Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains †
Abstract
:1. Introduction
- To propose a novel control strategy for UAVs, combining a Cascaded-PID with a fuzzy logic controller;
- To provide a method for fine tuning the fuzzy range of the PID gains values;
- To present a solution that can be embedded on UAV’s companion computers using ROS;
- To provide a testing solution using a state-of-the-art high-fidelity simulation engine such as Unreal Engine with AirSim.
2. Materials and Methods
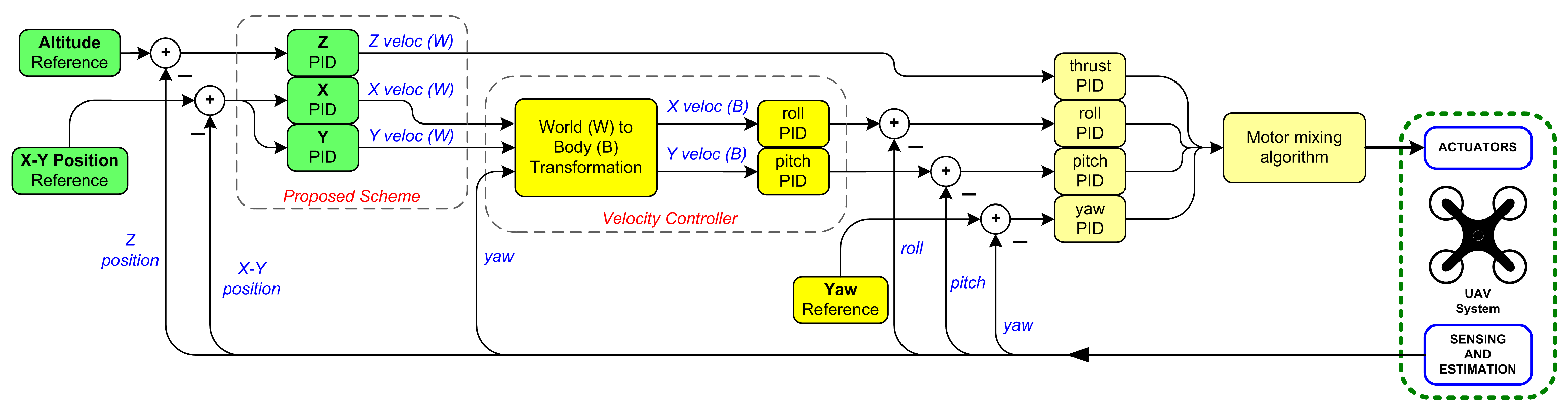
2.1. Cascaded-PID
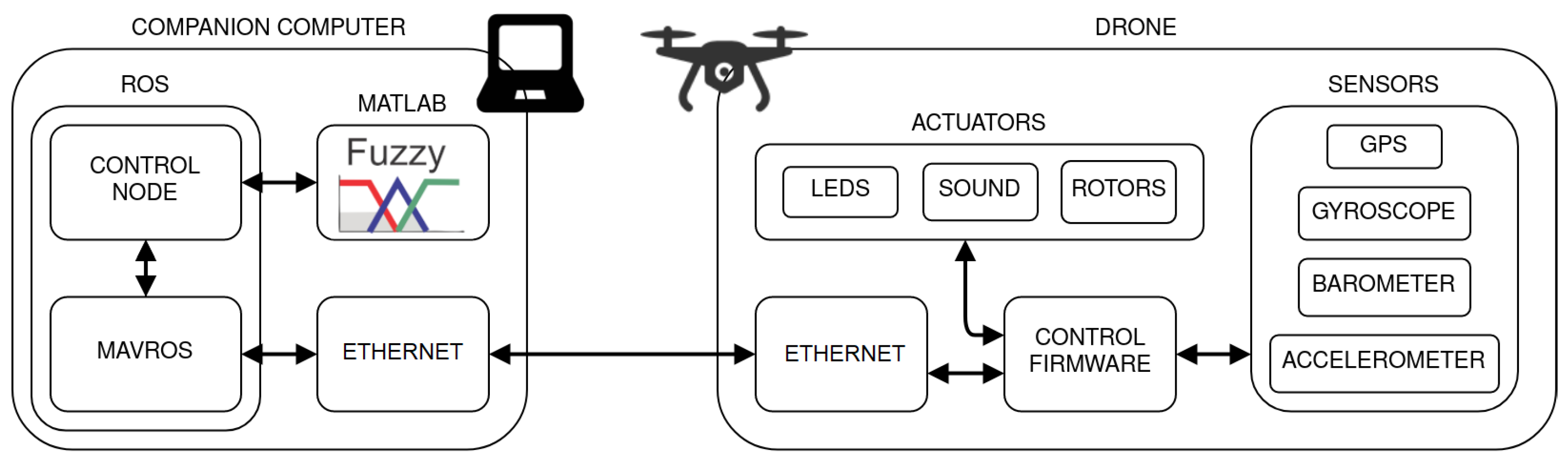
2.2. ROS Integration
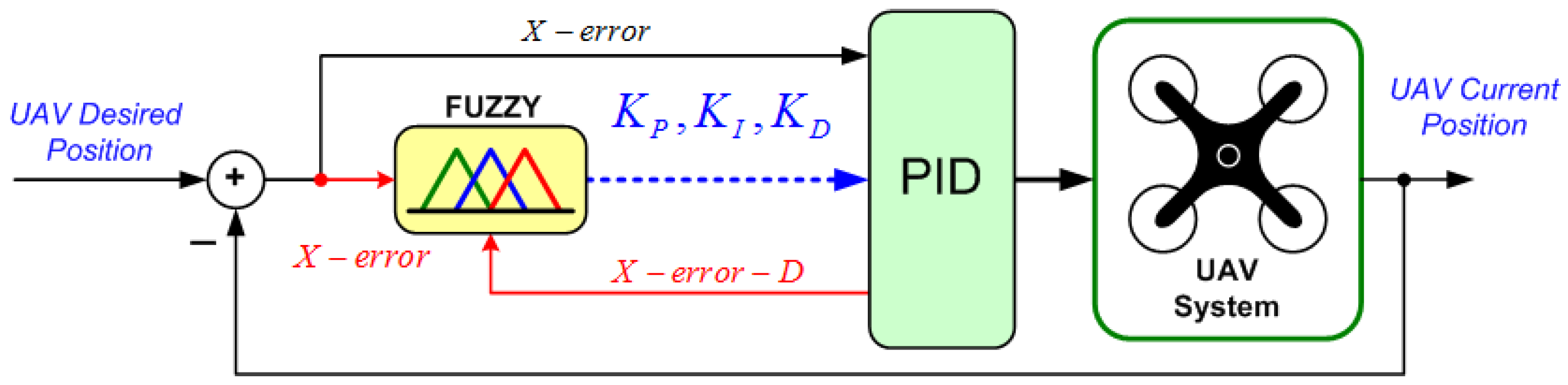
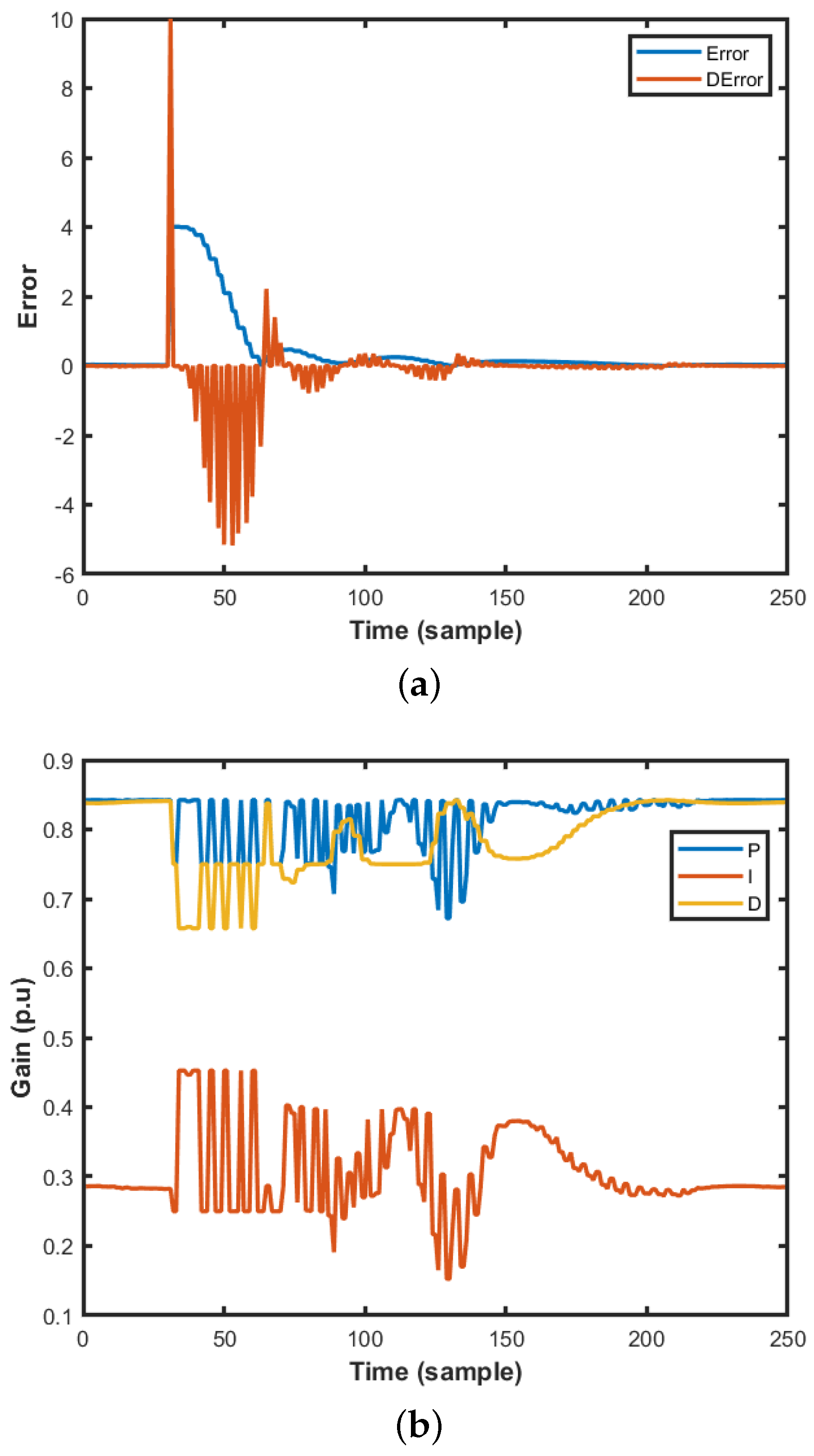
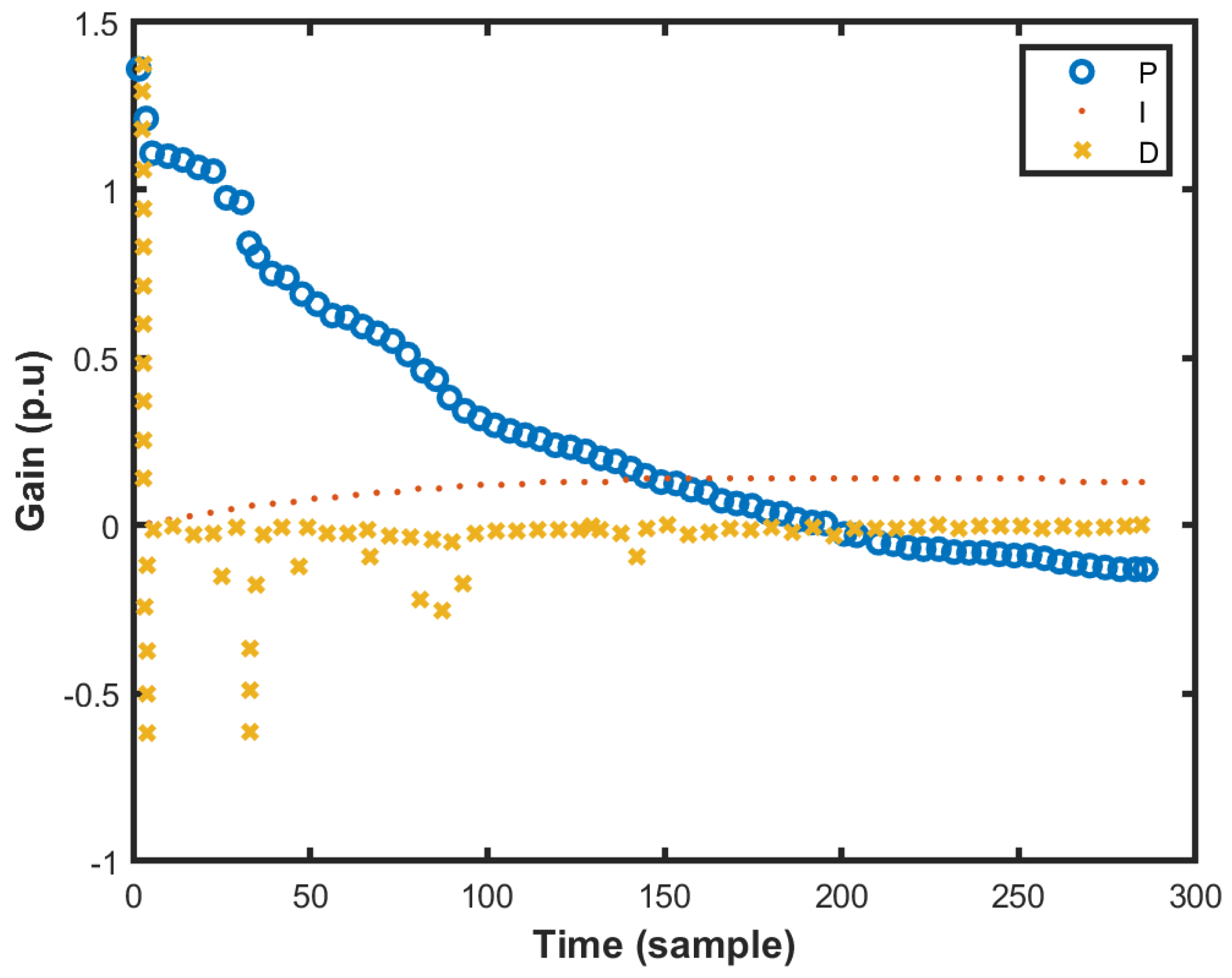
2.3. Fuzzy Logic PID Tuner
Selecting the Range of PID Gains for Horizontal Motion Control
3. Results
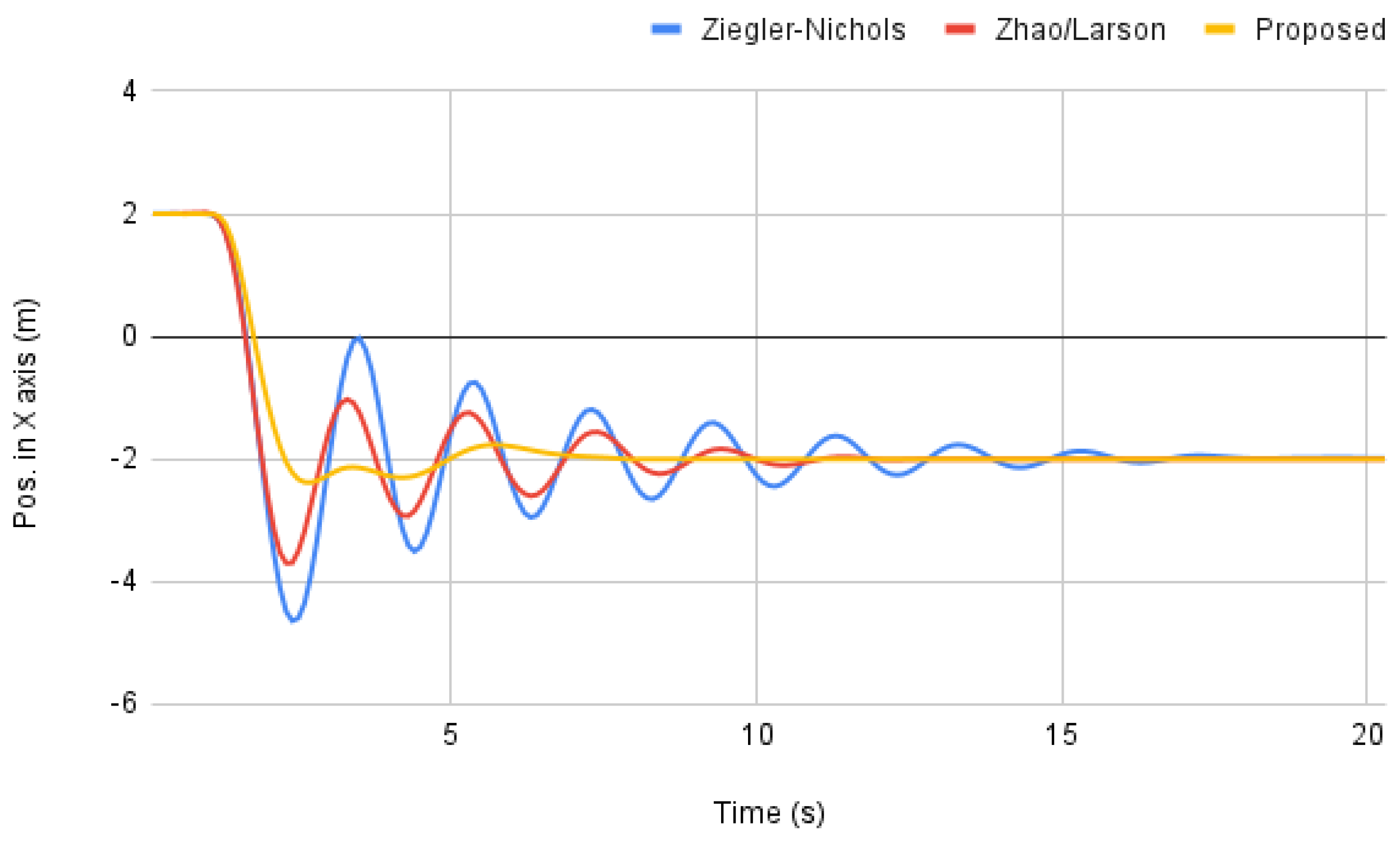
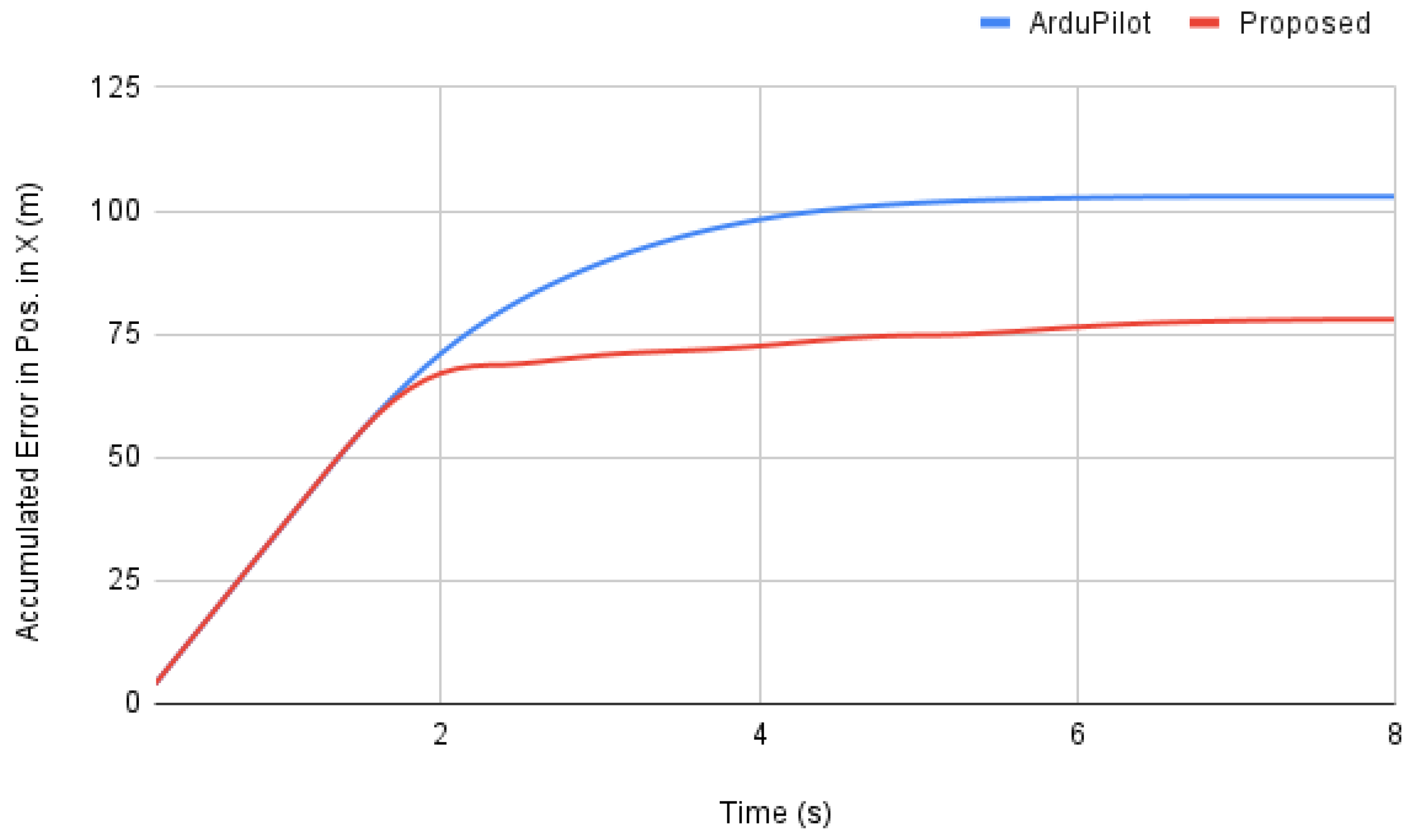
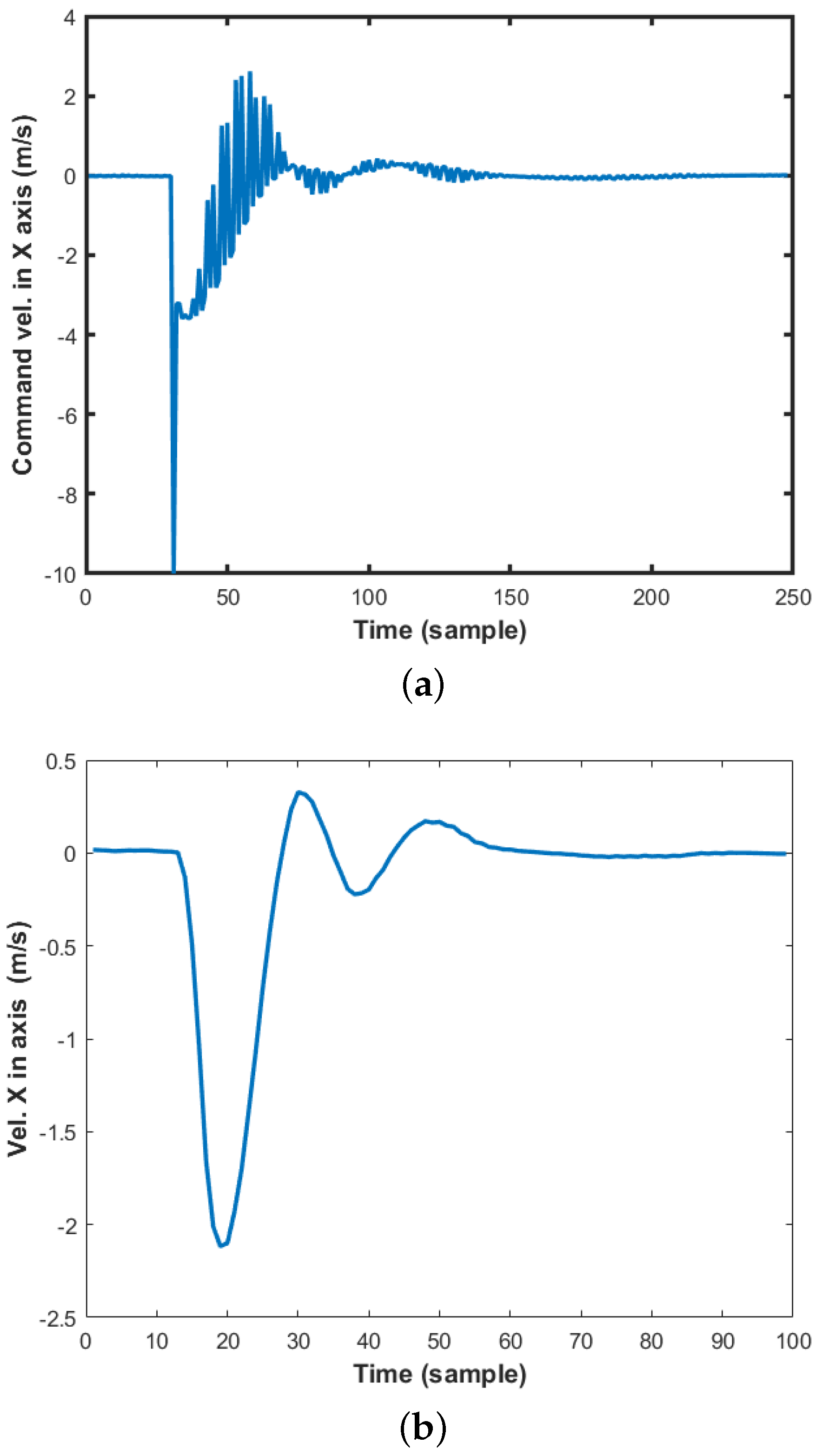
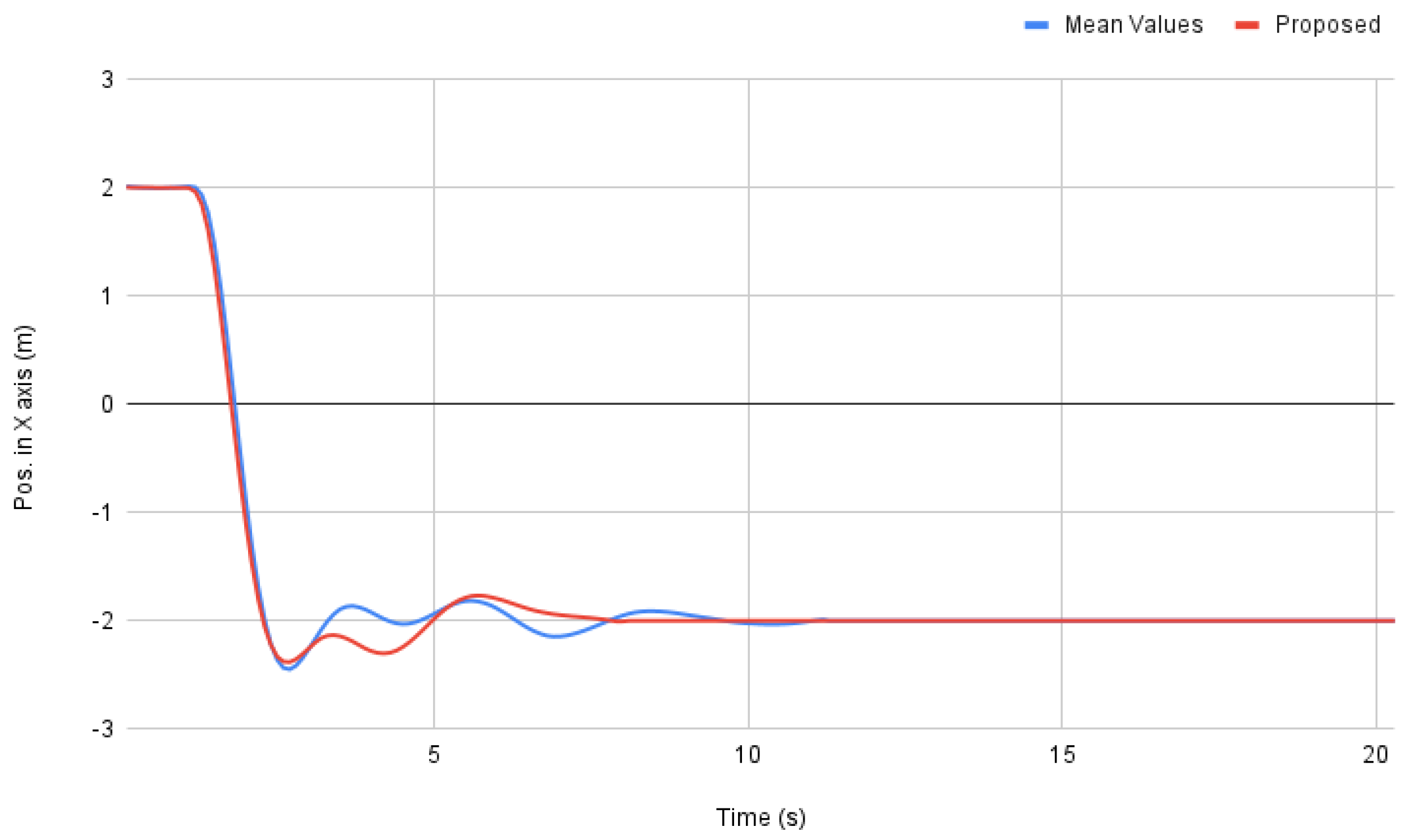
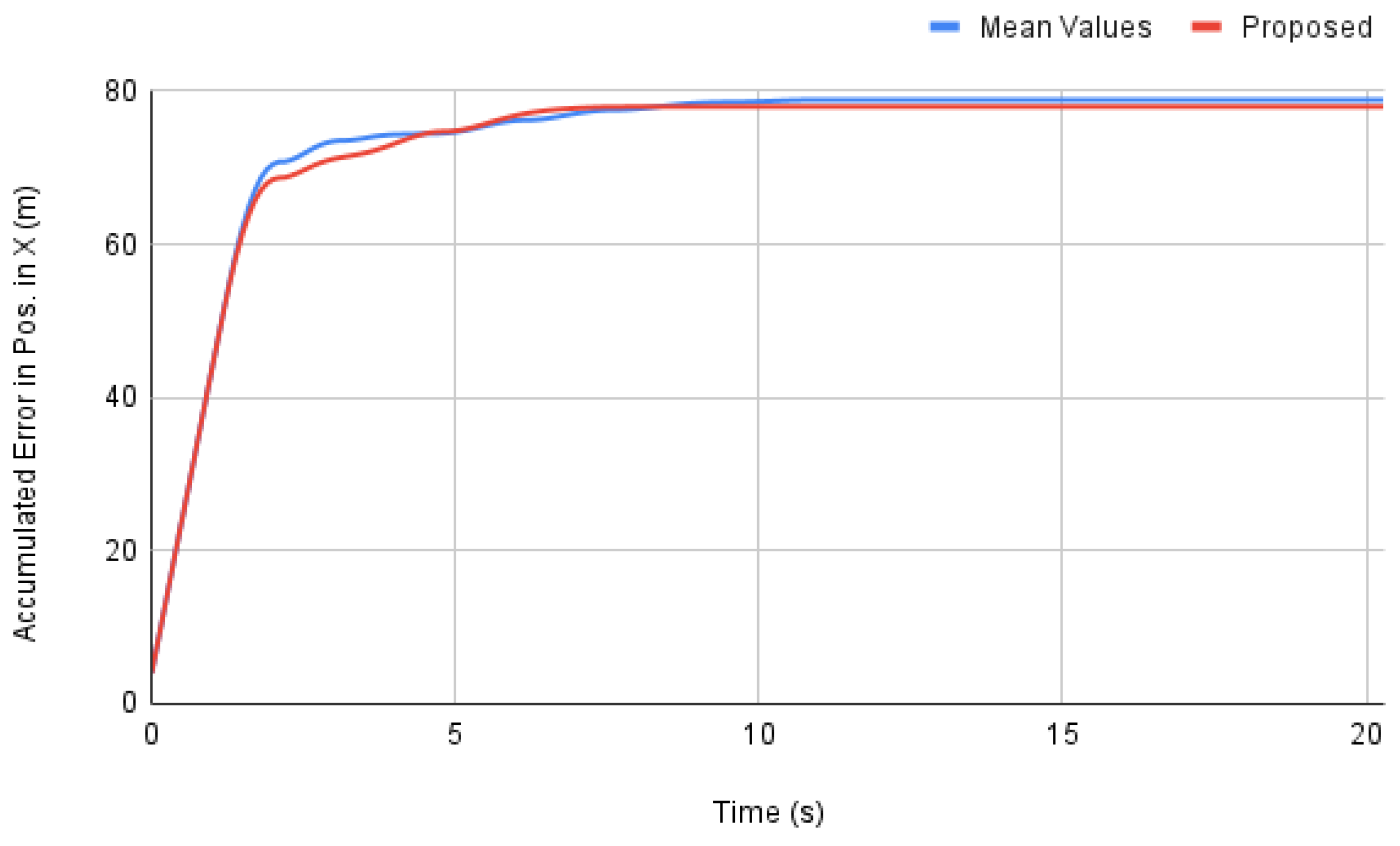
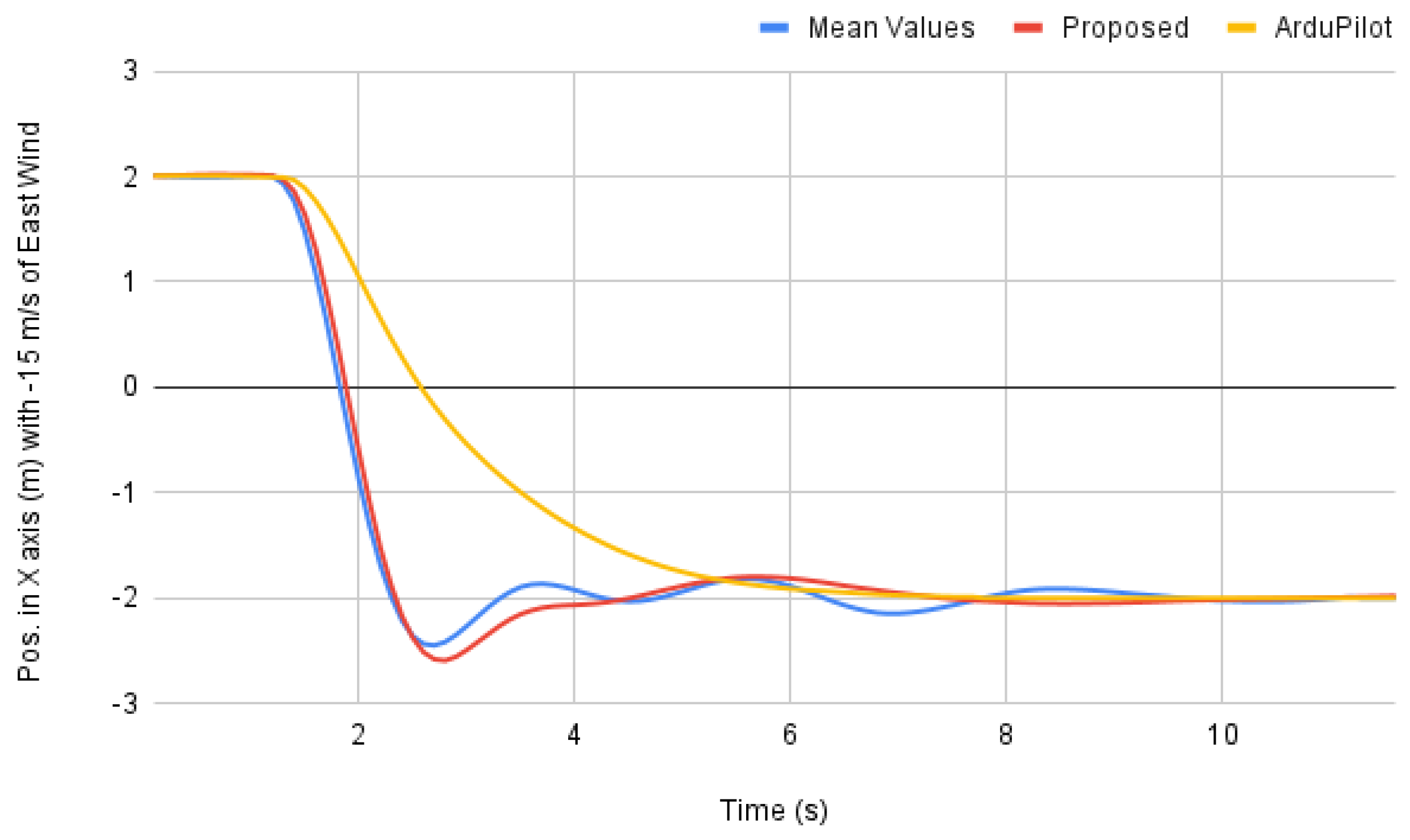
3.1. Horizontal Motion Control Tests in the Simulation Environment
- ArduPilot built-in GUIDED mode controller.
- Cascaded-PID solution tuned by the Ziegler-Nichols method.
Simulation Results
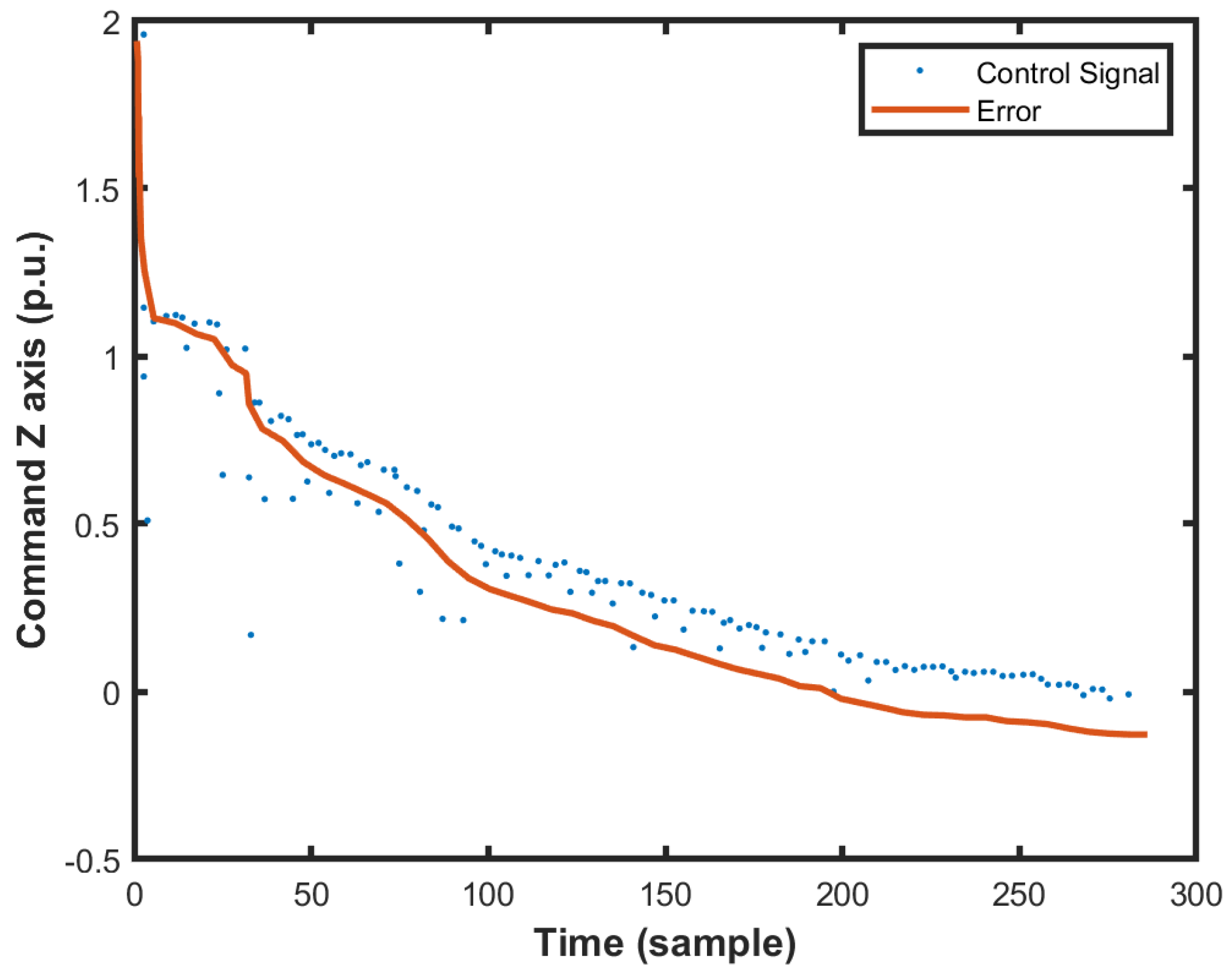
3.2. Altitude Control Tests in Real Flight
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| ROS | Robot Operating System |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| PID | Proportional-Integral-Derivative |
| FMU | Flight Management Unit |
References
- Biundini, I.Z.; Pinto, M.F.; Melo, A.G.; Marcato, A.L.; Honório, L.M.; Aguiar, M.J. A Framework for Coverage Path Planning Optimization Based on Point Cloud for Structural Inspection. Sensors 2021, 21, 570. [Google Scholar] [CrossRef]
- Pinto, M.F.; Honorio, L.M.; Melo, A.; Marcato, A.L. A Robotic Cognitive Architecture for Slope and Dam Inspections. Sensors 2020, 20, 4579. [Google Scholar] [CrossRef] [PubMed]
- Kong, W.; Zhou, D.; Yang, Z.; Zhao, Y.; Zhang, K. UAV Autonomous Aerial Combat Maneuver Strategy Generation with Observation Error Based on State-Adversarial Deep Deterministic Policy Gradient and Inverse Reinforcement Learning. Electronics 2020, 9, 1121. [Google Scholar] [CrossRef]
- Pinto, M.F.; Honório, L.M.; Marcato, A.L.; Dantas, M.A.; Melo, A.G.; Capretz, M.; Urdiales, C. ARCog: An Aerial Robotics Cognitive Architecture. Robotica 2021, 39, 483–502. [Google Scholar] [CrossRef]
- Cabral, K.M.; dos Santos, S.R.B.; Givigi, S.N.; Nascimento, C.L. Design of model predictive control via learning automata for a single UAV load transportation. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Melo, A.G.; Pinto, M.F.; Marcato, A.L.; Honório, L.M.; Coelho, F.O. Dynamic Optimization and Heuristics Based Online Coverage Path Planning in 3D Environment for UAVs. Sensors 2021, 21, 1108. [Google Scholar] [CrossRef]
- Fernández-Caramés, T.M.; Blanco-Novoa, O.; Froiz-Míguez, I.; Fraga-Lamas, P. Towards an autonomous industry 4.0 warehouse: A UAV and blockchain-based system for inventory and traceability applications in big data-driven supply chain management. Sensors 2019, 19, 2394. [Google Scholar] [CrossRef] [Green Version]
- Pinto, M.F.; Melo, A.G.; Marcato, A.L.; Urdiales, C. Case-based reasoning approach applied to surveillance system using an autonomous unmanned aerial vehicle. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1324–1329. [Google Scholar]
- Li, X.; Duan, H.; Li, J.; Deng, Y.; Wang, F.Y. Biological eagle eye-based method for change detection in water scenes. Pattern Recognit. 2022, 122, 108203. [Google Scholar] [CrossRef]
- Cabassi, J.; Lazzaroni, M.; Giannini, L.; Mariottini, D.; Nisi, B.; Rappuoli, D.; Vaselli, O. Continuous and near real-time measurements of gaseous elemental mercury (GEM) from an Unmanned Aerial Vehicle: A new approach to investigate the 3D distribution of GEM in the lower atmosphere. Chemosphere 2022, 288, 132547. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Zarzour, H.; Taberkit, A.M.; Kechida, A. A review on early wildfire detection from unmanned aerial vehicles using deep learning-based computer vision algorithms. Signal Process. 2022, 190, 108309. [Google Scholar] [CrossRef]
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transp. Res. Part C Emerg. Technol. 2020, 110, 368–398. [Google Scholar] [CrossRef]
- Madridano, Á.; Al-Kaff, A.; Martín, D. 3d trajectory planning method for UAVs swarm in building emergencies. Sensors 2020, 20, 642. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Liu, R.; Sun, L.; Nie, H.; Wang, X. UAV swarm based radar signal sorting via multi-source data fusion: A deep transfer learning framework. Inf. Fusion 2022, 78, 90–101. [Google Scholar] [CrossRef]
- Zapico, I.; Laronne, J.B.; Sánchez Castillo, L.; Martín Duque, J.F. Improvement of Workflow for Topographic Surveys in Long Highwalls of Open Pit Mines with an Unmanned Aerial Vehicle and Structure from Motion. Remote Sens. 2021, 13, 3353. [Google Scholar] [CrossRef]
- An Unmanned Aerial Vehicle for Greenhouse Navigation and Video-Based Tomato Phenotypic Data Collection. In Proceedings of the 2021 ASABE Annual International Virtual Meeting, Anaheim, CA, USA, 11–14 July 2021; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2021. [CrossRef]
- Smrcka, D.; Baca, T.; Nascimento, T.; Saska, M. Admittance Force-Based UAV-Wall Stabilization and Press Exertion for Documentation and Inspection of Historical Buildings. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 552–559. [Google Scholar] [CrossRef]
- Casella, E.; Rovere, A.; Pedroncini, A.; Stark, C.P.; Casella, M.; Ferrari, M.; Firpo, M. Drones as tools for monitoring beach topography changes in the Ligurian Sea (NW Mediterranean). Geo-Mar. Lett. 2016, 36, 151–163. [Google Scholar] [CrossRef]
- Pinto, M.F.; Marcato, A.L.; Melo, A.G.; Honório, L.M.; Urdiales, C. A framework for analyzing fog-cloud computing cooperation applied to information processing of UAVs. Wirel. Commun. Mob. Comput. 2019, 2019, 7497924. [Google Scholar] [CrossRef] [Green Version]
- Addabbo, P.; Angrisano, A.; Bernardi, M.L.; Gagliarde, G.; Mennella, A.; Nisi, M.; Ullo, S.L. UAV system for photovoltaic plant inspection. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 58–67. [Google Scholar] [CrossRef]
- Aghaei, M.; Bellezza Quater, P.; Grimaccia, F.; Leva, S.; Mussetta, M. Unmanned aerial vehicles in photovoltaic systems monitoring applications. In Proceedings of the European Photovoltaic Solar Energy 29th Conference and Exhibition, Amsterdam, The Netherlands, 22–26 September 2014; pp. 2734–2739. [Google Scholar]
- Joyo, M.K.; Hazry, D.; Ahmed, S.F.; Tanveer, M.H.; Warsi, F.A.; Hussain, A. Altitude and horizontal motion control of quadrotor UAV in the presence of air turbulence. In Proceedings of the 2013 IEEE Conference on Systems, Process & Control (ICSPC), Kuala Lumpur, Malaysia, 13–15 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 16–20. [Google Scholar]
- Tanveer, M.H.; Hazry, D.; Ahmed, S.F.; Joyo, M.K.; Warsi, F.A.; Kamaruddin, H.; Razlan, Z.M.; Wan, K.; Shahriman, A. NMPC-PID based control structure design for avoiding uncertainties in attitude and altitude tracking control of quad-rotor (UAV). In Proceedings of the 2014 IEEE 10th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 7–9 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 117–122. [Google Scholar]
- Wang, B.; Zhang, Y. Adaptive Sliding Mode Fault-Tolerant Control for an Unmanned Aerial Vehicle. Unmanned Syst. 2017, 5, 209–221. [Google Scholar] [CrossRef]
- Yuan, X.; Ren, X.; Zhu, B.; Zheng, Z.; Zuo, Z. Robust H Control for Hovering of a Quadrotor UAV with Slung Load. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 114–119. [Google Scholar]
- Liu, D.; Liu, H.; Lewis, F.L.; Wan, Y. Robust Fault-Tolerant Formation Control for Tail-Sitters in Aggressive Flight Mode Transitions. IEEE Trans. Ind. Inform. 2020, 16, 299–308. [Google Scholar] [CrossRef]
- Le Nhu Ngoc Thanh, H.; Hong, S.K. Quadcopter Robust Adaptive Second Order Sliding Mode Control Based on PID Sliding Surface. IEEE Access 2018, 6, 66850–66860. [Google Scholar] [CrossRef]
- Eltag, K.; Aslamx, M.S.; Ullah, R. Dynamic stability enhancement using fuzzy PID control technology for power system. Int. J. Control. Autom. Syst. 2019, 17, 234–242. [Google Scholar] [CrossRef]
- Hu, X.; Liu, J. Research on UAV Balance Control Based on Expert-fuzzy Adaptive PID. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 25–27 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 787–789. [Google Scholar]
- Ljubičić, R.; Strelnikova, D.; Perks, M.T.; Eltner, A.; Peña Haro, S.; Pizarro, A.; Dal Sasso, S.F.; Scherling, U.; Vuono, P.; Manfreda, S. A comparison of tools and techniques for stabilising unmanned aerial system (UAS) imagery for surface flow observations. Hydrol. Earth Syst. Sci. 2021, 25, 5105–5132. [Google Scholar] [CrossRef]
- Megyesi, D.; Bréda, R.; Schrötter, M. Adaptive Control and Estimation of the Condition of a Small Unmanned Aircraft Using a Kalman Filter. Energies 2021, 14, 2292. [Google Scholar] [CrossRef]
- Solihin, M.I.; Tack, L.F.; Kean, M.L. Tuning of PID controller using particle swarm optimization (PSO). In Proceeding of the International Conference on Advanced Science, Engineering and Information Technology, Bandar Baru Bangi, Malaysia, 14–15 January 2011; Volume 1, pp. 458–461. [Google Scholar]
- Aly, A.A. PID parameters optimization using genetic algorithm technique for electrohydraulic servo control system. Intell. Control Autom. 2011, 2, 69. [Google Scholar] [CrossRef] [Green Version]
- Doitsidis, L.; Valavanis, K.P.; Tsourveloudis, N.C.; Kontitsis, M. A framework for fuzzy logic based UAV navigation and control. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004 (Proceedings. ICRA’04), New Orleans, LA, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 4, pp. 4041–4046. [Google Scholar]
- Dong, J.; He, B. Novel fuzzy PID-type iterative learning control for quadrotor UAV. Sensors 2019, 19, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Shi, Y.; Cai, M.; Xu, W.; Yu, Q. Optimization of air–fuel ratio control of fuel-powered UAV engine using adaptive fuzzy-PID. J. Frankl. Inst. 2018, 355, 8554–8575. [Google Scholar] [CrossRef]
- Bucio-Gallardo, E.M.; Zavala-Yoé, R.; Ramírez-Mendoza, R.A. Mathematical Model and Intelligent Control of a Quadcopter, with Non-conventional Membership Functions. J. Energy Power Eng. 2016, 10, 634–642. [Google Scholar] [CrossRef]
- Demaya, B.; Palm, R.; Boverie, S.; Titli, A. Multilevel qualitative and numerical optimization of fuzzy controller. In Proceedings of the 1995 IEEE International Conference on Fuzzy Systems, Yokohama, Japan, 20–24 March 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 3, pp. 1149–1154. [Google Scholar]
- Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Peng-ya, X.; Yun-jie, W.; Jing-xing, Z.; Ling, C. Longitudinal attitude control of UAV based on fuzzy PID. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Carvalho, G.; Guedes, I.; Pinto, M.; Zachi, A.; Almeida, L.; Andrade, F.; Melo, A.G. Hybrid PID-Fuzzy controller for autonomous UAV stabilization. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1296–1302. [Google Scholar]
- Selvachandran, G.; Quek, S.G.; Lan, L.T.H.; Giang, N.L.; Ding, W.; Abdel-Basset, M.; Albuquerque, V.H.C. A new design of Mamdani complex fuzzy inference system for multi-attribute decision making problems. IEEE Trans. Fuzzy Syst. 2019, 29, 716–730. [Google Scholar] [CrossRef]
- Larson, K. Fuzzy Logic Tuning of a Proportional-Integral-Derivative Controller. Ph.D. Thesis, California State Polytechnic University, Pomona, CA, USA, 2016. [Google Scholar]
- Zhao, Z.Y.; Tomizuka, M.; Isaka, S. Fuzzy gain scheduling of PID controllers. IEEE Trans. Syst. Man Cybern. 1993, 23, 1392–1398. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. AirSim: High-Fidelity Visual and Physical Simulation for Autonomous Vehicles. In Field and Service Robotics; Springer: Cham, Swotzerland, 2017. [Google Scholar]

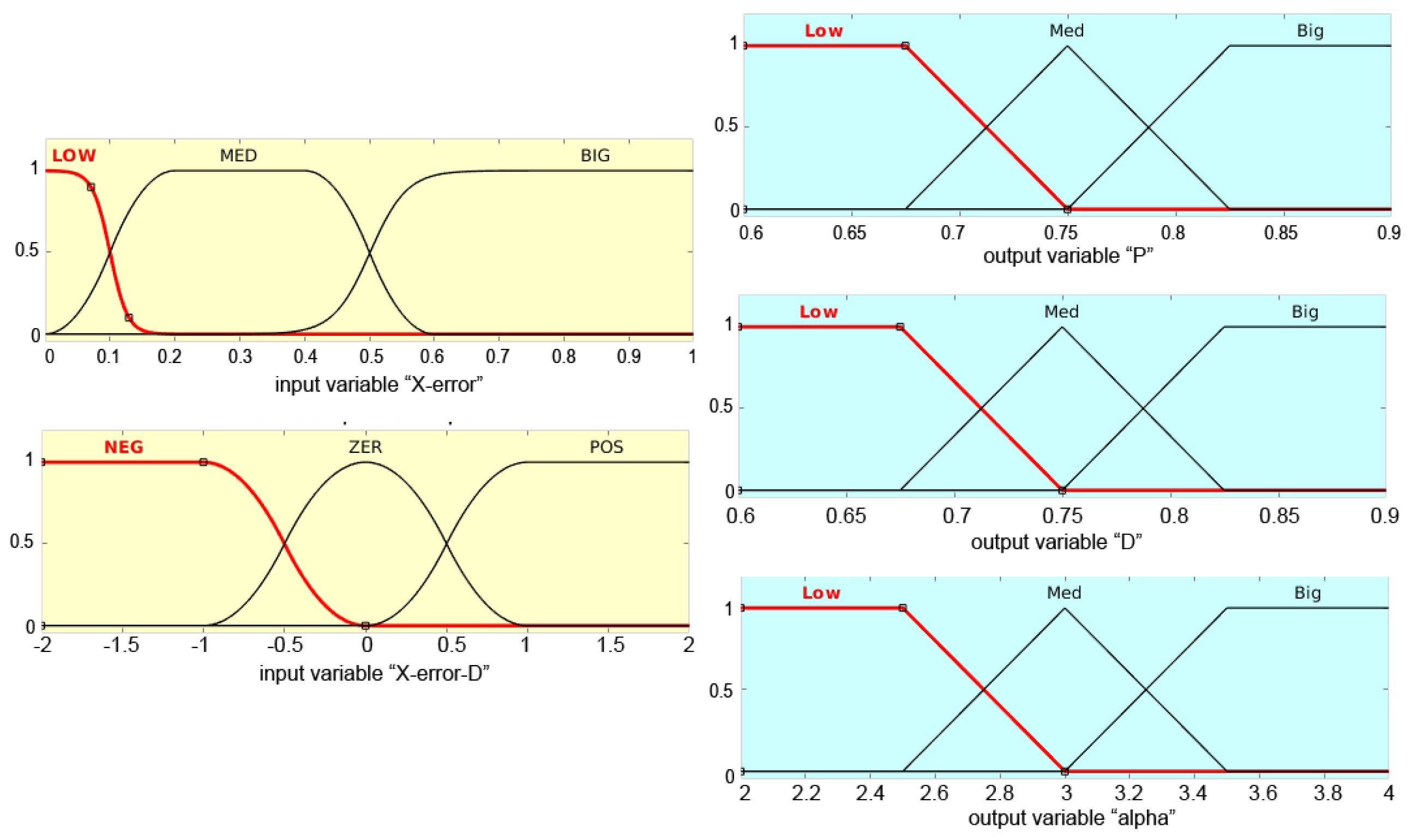





| Low | Medium | Big | |
| Negative | LBB | MMM | BLL |
| Zero | BBM | BML | BLL |
| Positive | LBB | MMM | BLL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade, F.A.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.L.; Haddad, D.B.; Almeida, L.F.; de Melo, A.G.; Pinto, M.F. Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains. Machines 2022, 10, 12. https://doi.org/10.3390/machines10010012
Andrade FAA, Guedes IP, Carvalho GF, Zachi ARL, Haddad DB, Almeida LF, de Melo AG, Pinto MF. Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains. Machines. 2022; 10(1):12. https://doi.org/10.3390/machines10010012
Chicago/Turabian StyleAndrade, Fabio A. A., Ihannah P. Guedes, Guilherme F. Carvalho, Alessandro R. L. Zachi, Diego B. Haddad, Luciana F. Almeida, Aurélio G. de Melo, and Milena F. Pinto. 2022. "Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains" Machines 10, no. 1: 12. https://doi.org/10.3390/machines10010012
APA StyleAndrade, F. A. A., Guedes, I. P., Carvalho, G. F., Zachi, A. R. L., Haddad, D. B., Almeida, L. F., de Melo, A. G., & Pinto, M. F. (2022). Unmanned Aerial Vehicles Motion Control with Fuzzy Tuning of Cascaded-PID Gains. Machines, 10(1), 12. https://doi.org/10.3390/machines10010012







