Heat Loss Analysis of a 2D Pump’s Transmission
Abstract
1. Introduction
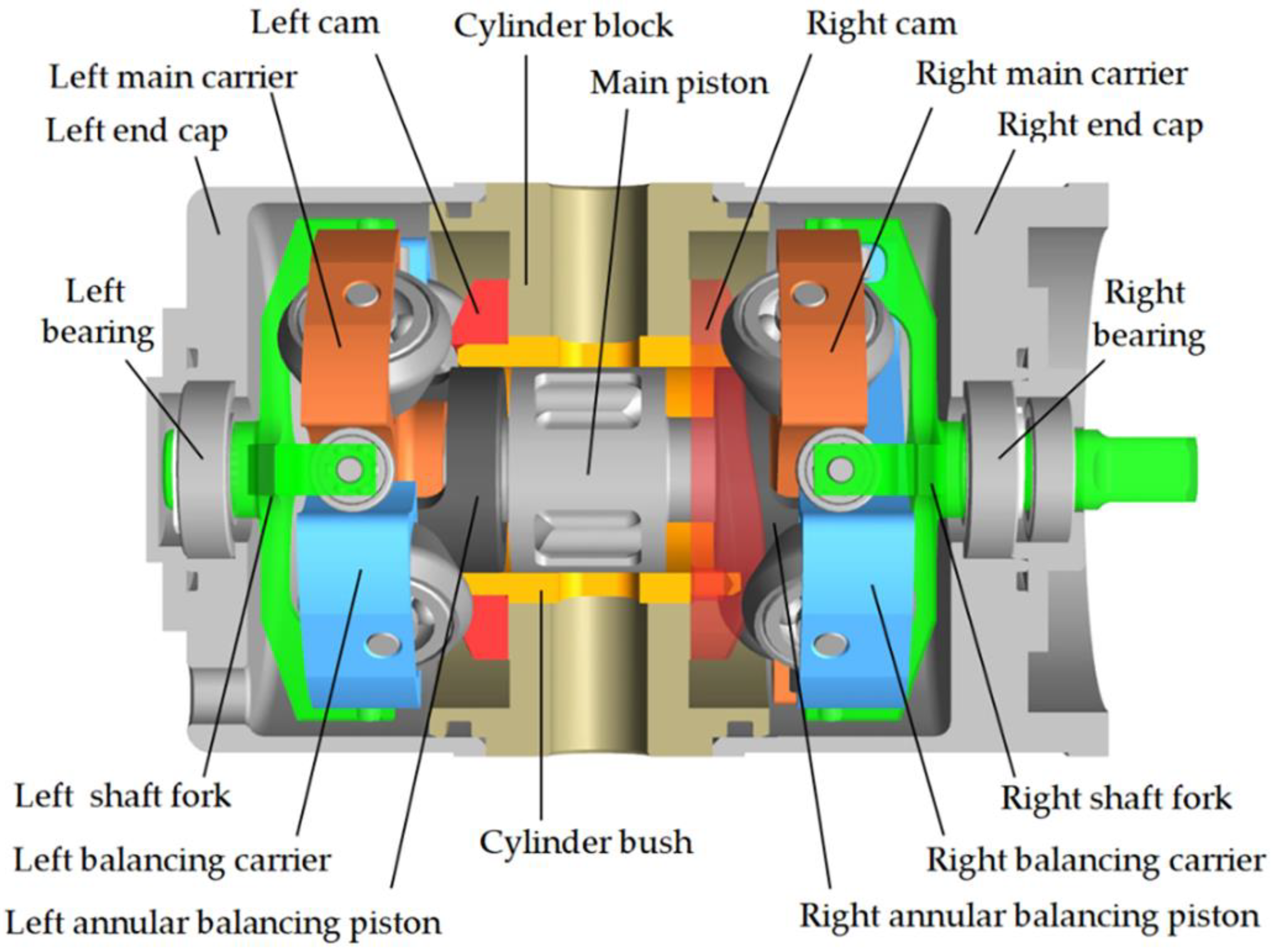
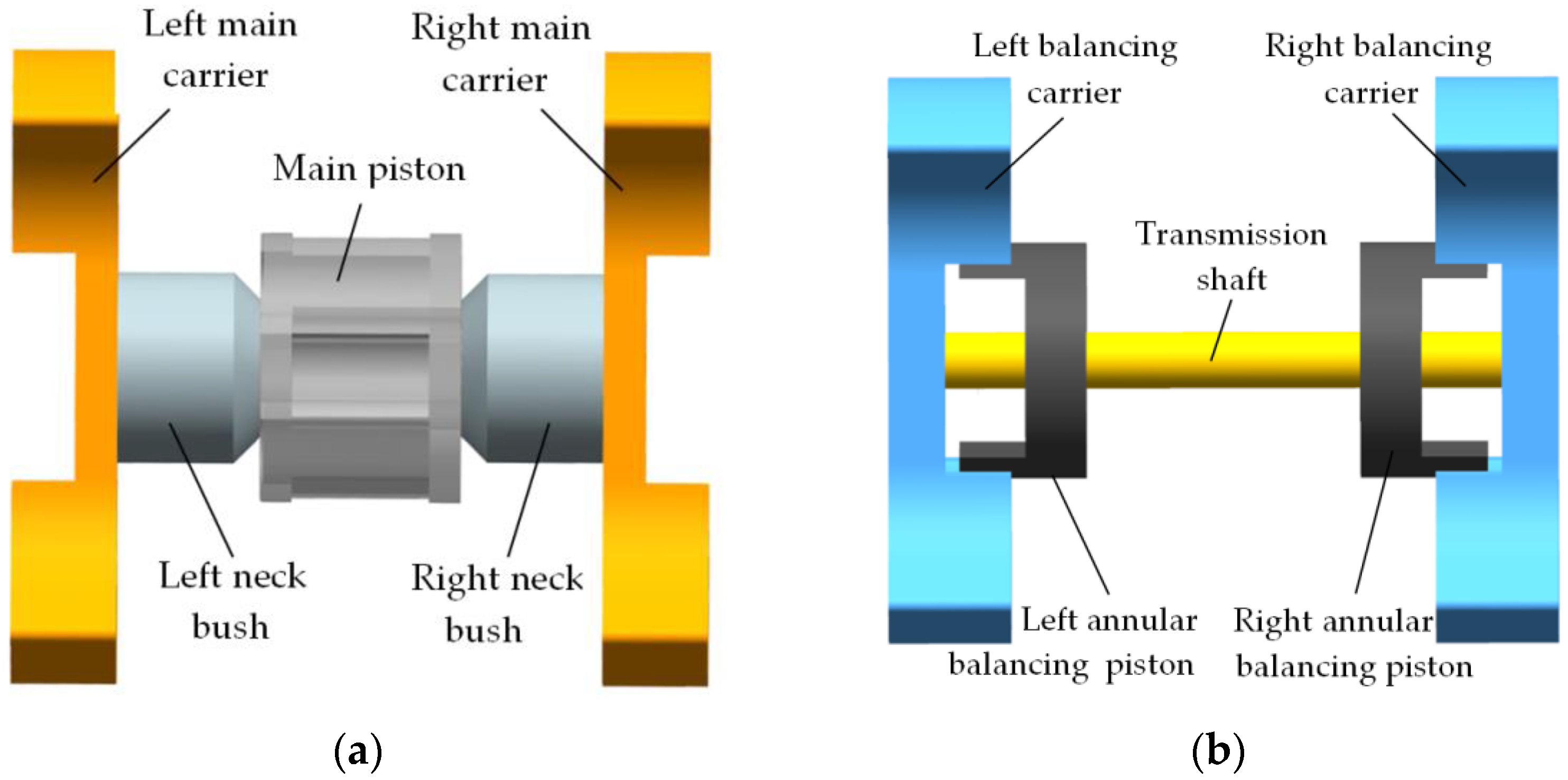
2. Structure and Working Principle
Mechanical Structure
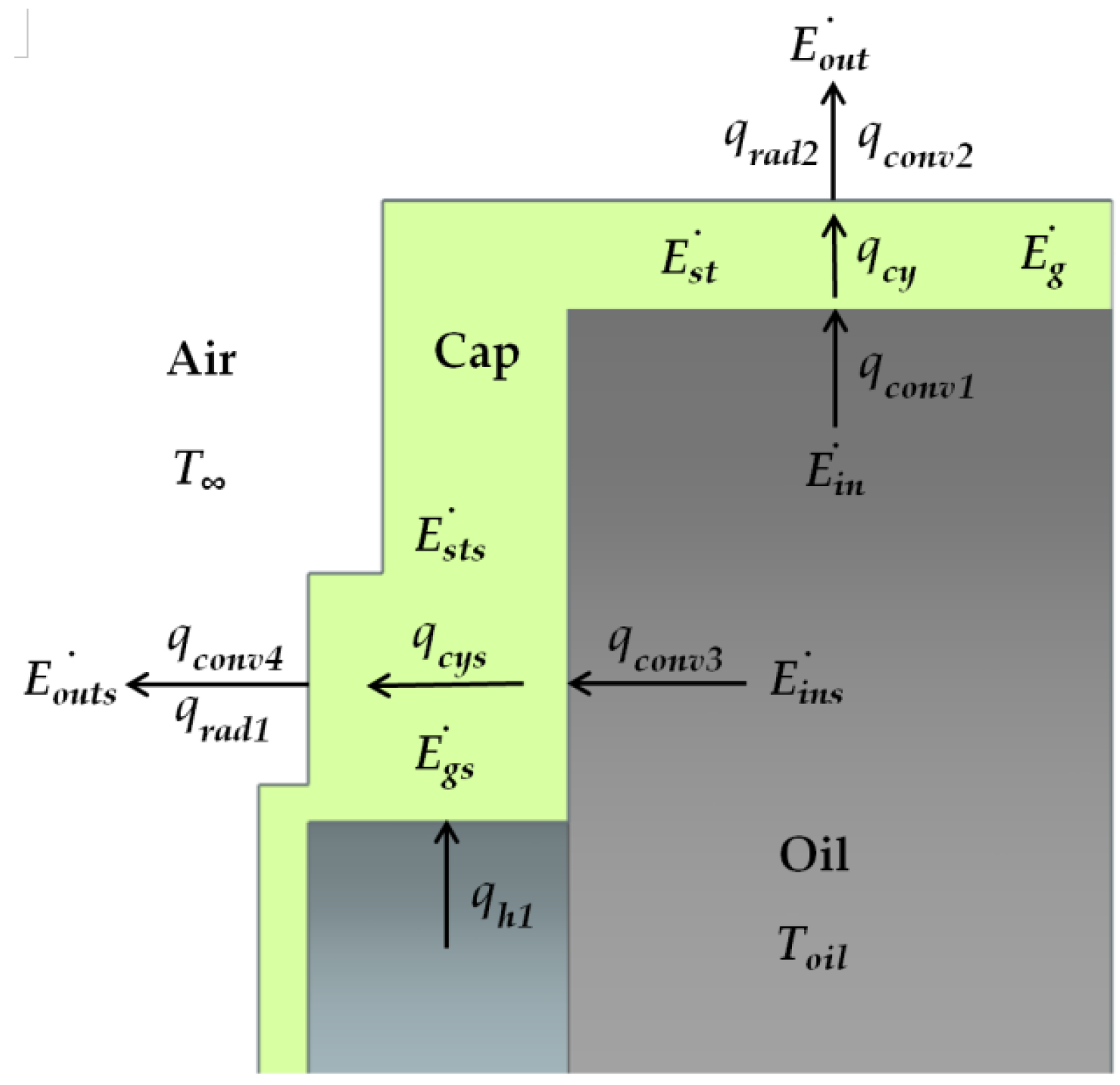
3. Heat Transfer Analysis
3.1. Heat Transfer Analysis of the 2D Pump Cap
3.1.1. Heat Transfer Analysis of Pump Cap’s Annulus
3.1.2. Heat Transfer Analysis of Pump Cap’s Head
3.2. Heat Transfer Analysis of Pump Cylinder’s Head
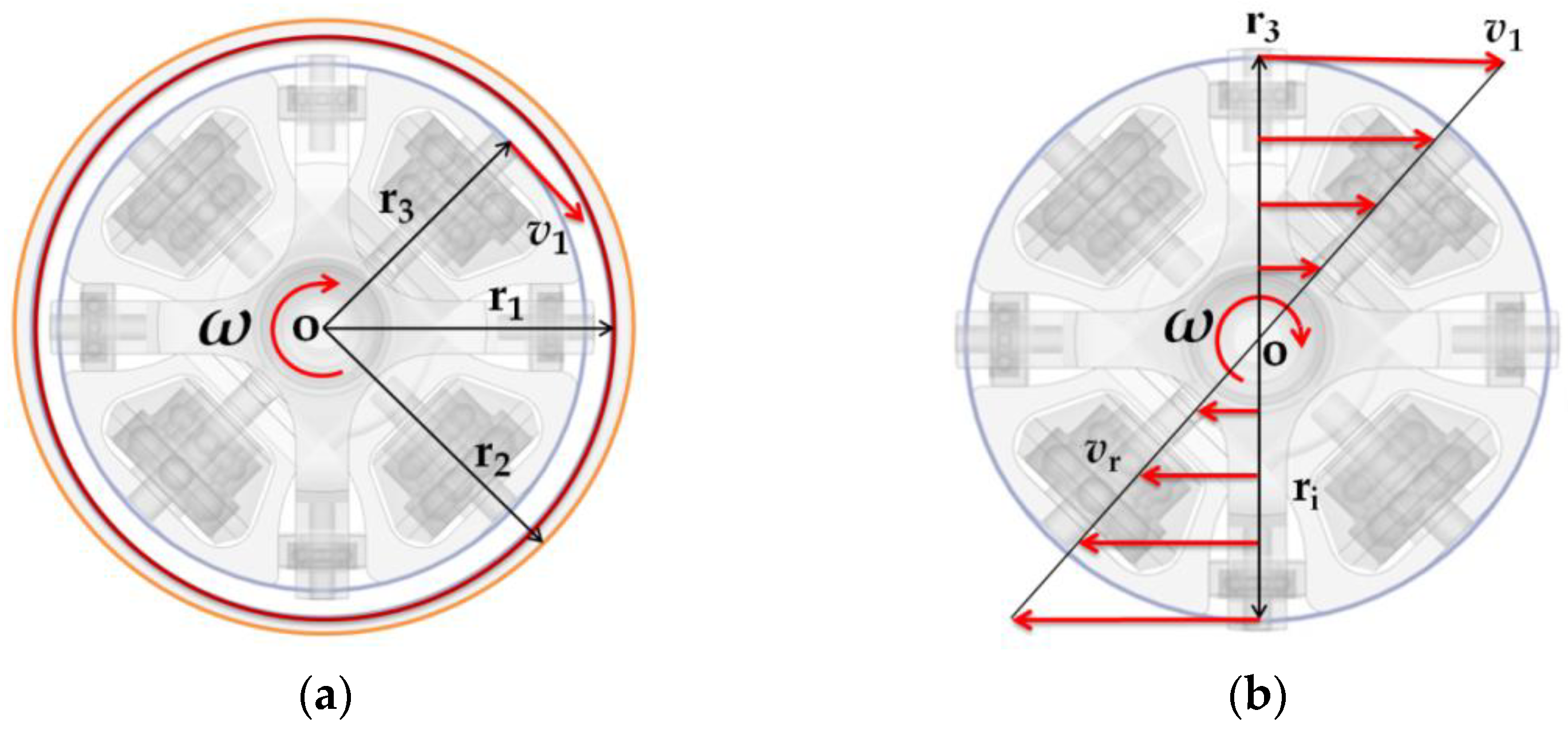
3.3. Heat Transfer Analysis of the Inner Cylinder
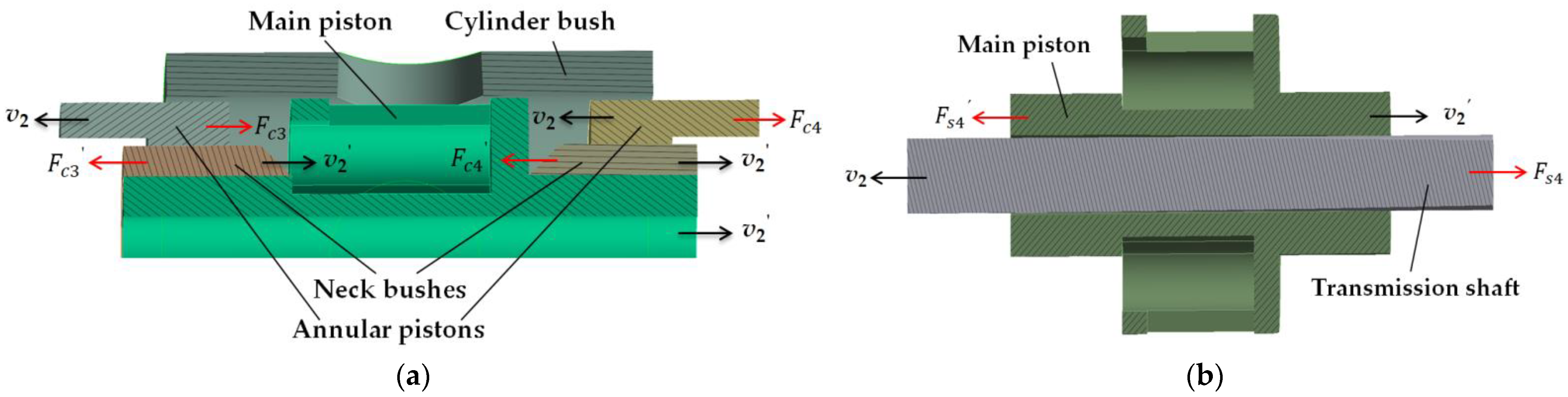
3.4. Heat Transfer between the 2D Pump’s Piston and Transmission Shaft
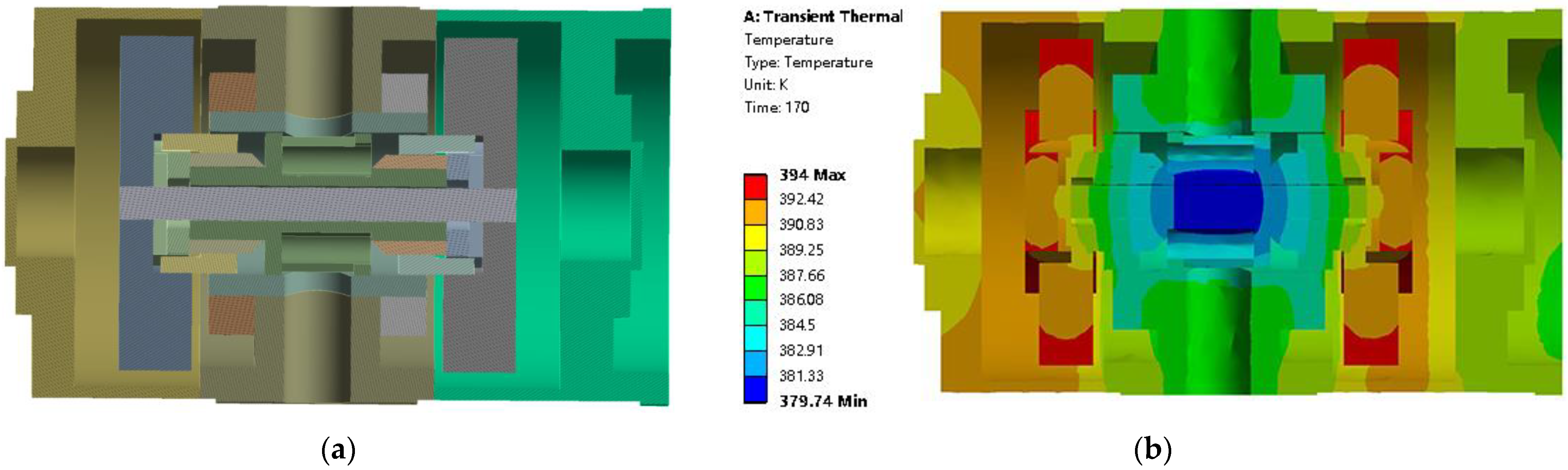
3.5. Heat Transfer Simulation Model
4. Experimental Study
5. Results and Discussion
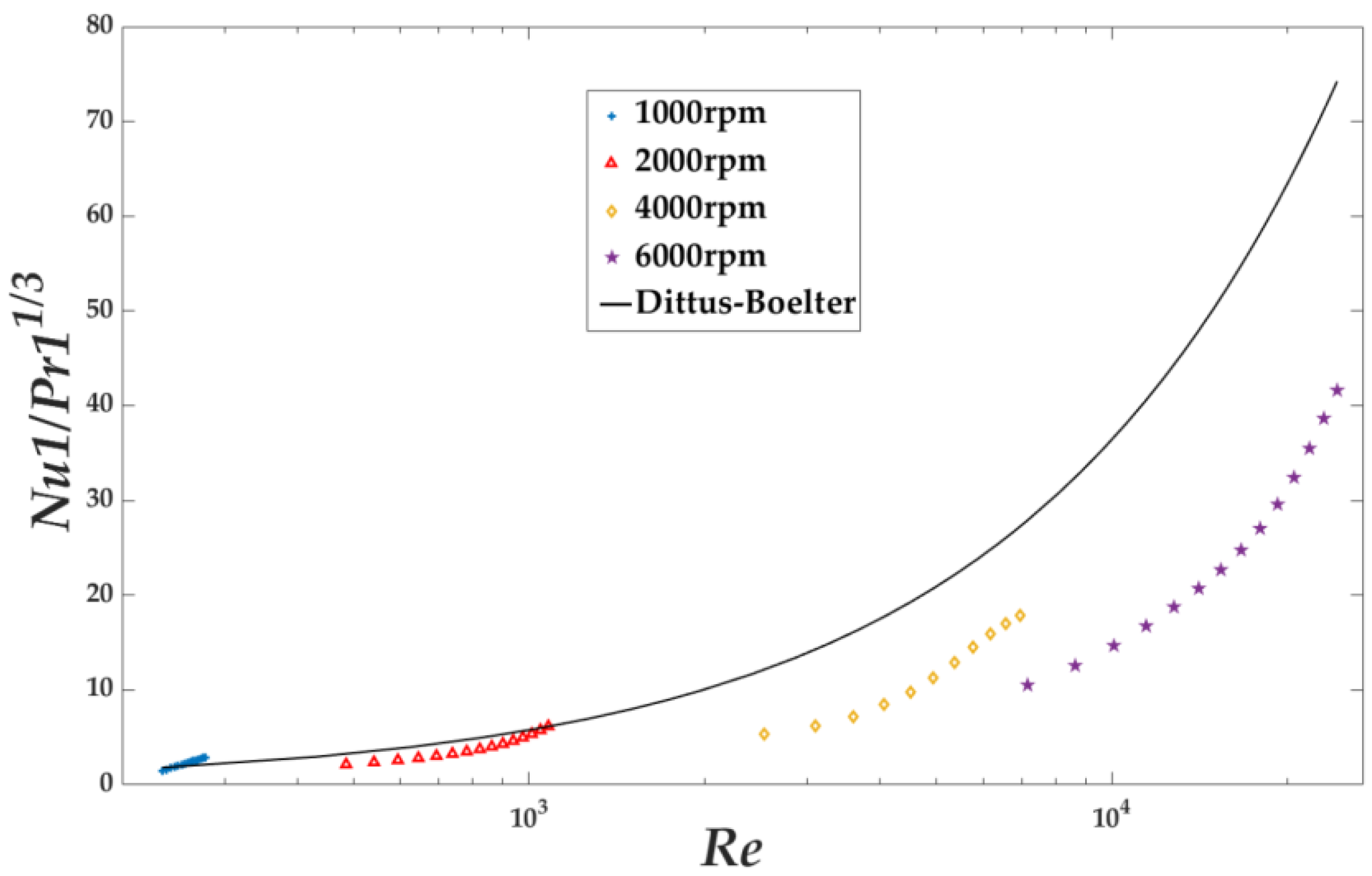
5.1. The Convective Heat Transfer Coefficients of the Pump Transmission
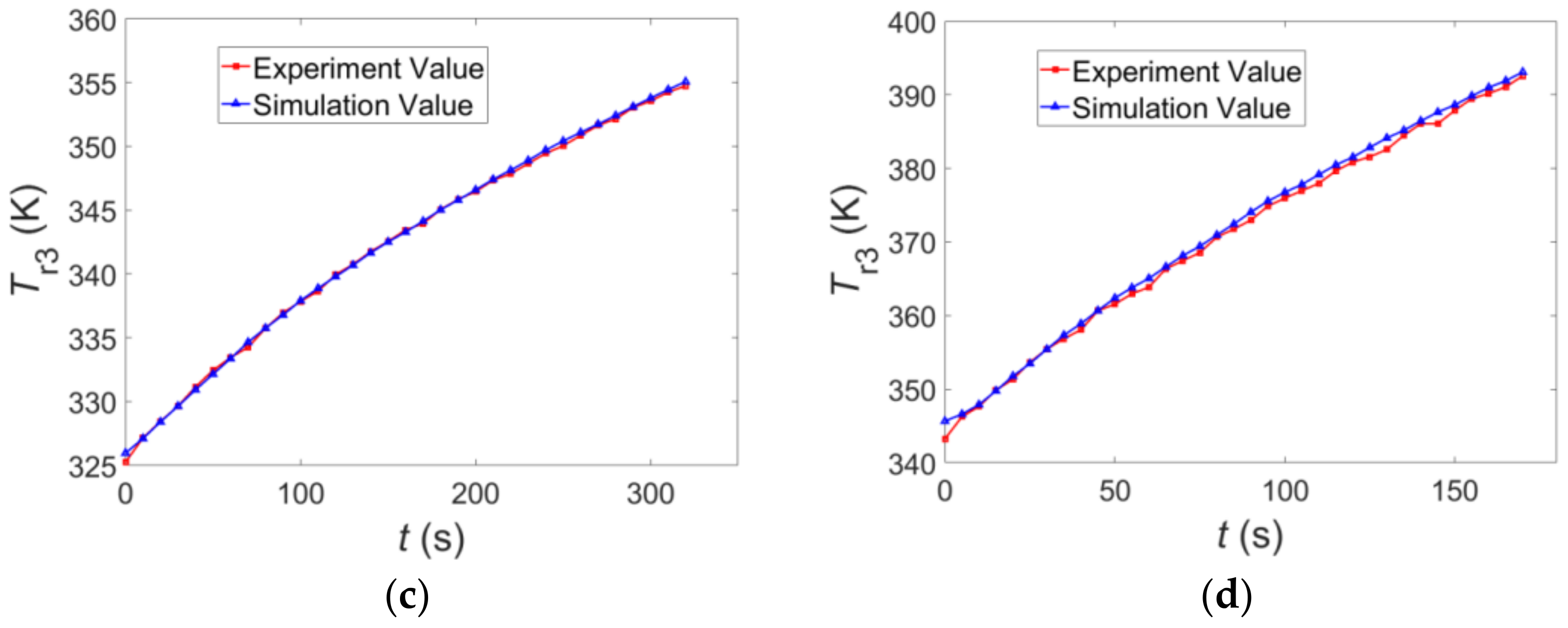
5.2. The Heat Loss Analysis of the Pump Transmission
6. Conclusions
- (1)
- The Dittus–Boelter relation cannot be applied directly to the pump transmission above 4000 rpm, so a corrected one was investigated to deal with the convective heat transfer of the vortex flows in it. The correction factor was determined through the Taylor flow heat transfer experiment. It is 1.155 at 1000 rpm, 0.789 at 2000 rpm, 0.546 at 4000 rpm, and 0.457 at 6000 rpm. In addition, the corrected relation was verified to be accurate.
- (2)
- With the rise of rotational speed, the transmission heat loss raises with the churning loss. At the same speed, as the oil temperature increases, the churning loss decreases gradually with the decrease of oil viscosity, and the heat loss is also reduced accordingly.
- (3)
- The heat loss simulation results are 6.27 W at 1000 rpm, 32.64 W at 2000 rpm, 93.06 W at 4000 rpm, and 312.87 W at 6000 rpm. They agree well with the reference churning loss experimental formula from 1000 rpm to 4000 rpm. At 6000 rpm, the heat loss is 44.35% higher than the reference value because of extra heat generated by the friction of the cam-roller set.
- (4)
- The distribution of the transient heat losses in the pump transmission are: 49.66% into the end cap, 27.74% into the cylinder head, 13.30% into the inner cylinder, and 9.30% into the oil. The pump cap carries away about 49.66% heat flow, which turns into its internal energy (12.85%) and transfers to the circumstances (36.81%). About 27.74% of the heat transfers into the cylinder head. In all, 77.40% of the heat transfers away from the transmission; 22.60% of the heat changes into its internal energy and makes its temperature rise.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Specific heat of the cylinder | kJ/kg·K | |
| Outer diameter of the annular piston | m | |
| Hydraulic diameter of the inner annulus | m | |
| Hydraulic diameter of the outer cylinder’s outer wall | m | |
| Hydraulic diameter of the cap head’s outer wall | m | |
| Hydraulic diameter of the cap head | m | |
| Hydraulic diameter of the cylinder head | m | |
| Inner diameter of the annular piston | m | |
| Diameter of the transmission shaft | m | |
| Diameter of the main piston | m | |
| Input energy rate of the annulus | kJ/s | |
| Annular input energy rate of the cap head | kJ/s | |
| Energy output rate of the oil | kJ/s | |
| Energy output rate of the annulus | kJ/s | |
| Energy output rate of the cap | kJ/s | |
| Energy output rate of the cap head | kJ/s | |
| Change rate of energy generation of the annulus | kJ/s | |
| Change rate of energy generation of the cap head | kJ/s | |
| Change rate of the cylinder’s internal energy of the annulus | kJ/s | |
| Change rate of the cylinder’s internal energy of the cap head | kJ/s | |
| Shearing force on the left annular piston | N | |
| Shearing force on the left neck bush | N | |
| Shearing force on the right annular piston | N | |
| Shearing force on the right neck bush | N | |
| Shearing force on the transmission shaft | N | |
| Shearing force on the main piston | N | |
| Maximum stroke of the piston | m | |
| Thickness between the annular piston and cylinder bush | m | |
| Thickness between the annular piston and neck bush | m | |
| Thickness between the main piston and transmission shaft | m | |
| Convective heat transfer coefficient between oil and inner wall | W/m2·K | |
| Convective heat transfer coefficient between oil and inner annulus wall | W/m2·K | |
| Convective heat transfer coefficient between surroundings and outer wall | W/m2·K | |
| Convective heat transfer coefficient between surroundings and cap head | W/m2·K | |
| Convective heat transfer coefficient between oil and cap head | W/m2·K | |
| Convective heat transfer coefficient between oil and left side of inner cylinder | W/m2·K | |
| Convective heat transfer coefficient between oil and cylinder head | W/m2·K | |
| Convective heat transfer coefficient between oil and right side of inner cylinder | W/m2·K | |
| Thermal conductivity of the oil | W/m·K | |
| Thermal conductivity of the air | W/m·K | |
| Fluid field length of the annular piston | m | |
| Fluid field length of the outer annulus | m | |
| Length of the annular piston | m | |
| Length of the main piston | m | |
| Bearing friction torque | N·m | |
| n | Rotational speed | rpm |
| Nusselt number of the inner wall | ||
| Nusselt number of the outer wall | ||
| Nusselt number of the cap head | ||
| Nusselt number of the cylinder head | ||
| Viscous resistance power on the cylinder bush | W | |
| Viscous resistance power on the annular piston | W | |
| Viscous resistance power on the left annular piston | W | |
| Viscous resistance power on the left neck bush | W | |
| Average viscous resistance power on the left annular piston | W | |
| Average viscous resistance power on the left neck bush | W | |
| Viscous resistance power on the right annular piston | W | |
| Viscous resistance power on the right neck bush | W | |
| Average viscous resistance power on the right annular piston | W | |
| Average viscous resistance power on the right neck bush | W | |
| Churning loss power | W | |
| Viscous resistance power on the transmission shaft | W | |
| Viscous resistance power on the main piston | W | |
| Average viscous resistance power on transmission shaft | W | |
| Average viscous resistance power on the main piston | W | |
| Prandtl number of the outer wall | ||
| Prandtl number of the cap head oil | ||
| Prandtl number of the cylinder head oil | ||
| Heat-transfer rate of the oil and cylinder bush | kJ/s | |
| Heat-transfer rate of the oil and annular piston | kJ/s | |
| Heat-transfer rate of the oil and inner wall | kJ/s | |
| Heat-transfer rate of the oil and inner annulus | kJ/s | |
| Heat-transfer rate of the air and outer wall | kJ/s | |
| Heat-transfer rate of the oil and cap head | kJ/s | |
| Heat-transfer rate of the oil and left side of the inner cylinder | kJ/s | |
| Heat-transfer rate of the air and cap head | kJ/s | |
| Heat-transfer rate of the air and cylinder head | kJ/s | |
| Heat-transfer rate of the air and right side of the inner cylinder | kJ/s | |
| Heat-transfer rate of the annulus | kJ/s | |
| Heat-transfer rate of the cap head | kJ/s | |
| Heat-transfer rate of the cap’s bearing housing | kJ/s | |
| Radiation heat transfer rate of the cap head and surroundings | kJ/s | |
| Radiation heat transfer rate of the outer wall and surroundings | kJ/s | |
| Radius of the inner wall | m | |
| Radius of the outer wall | m | |
| Radius of inner annulus | m | |
| Rayleigh number of the outer wall | ||
| Reynolds number of the cap head oil | ||
| Reynolds number of the cylinder head oil | ||
| Area of the cap head | m2 | |
| Area of the left side of the inner cylinder | m2 | |
| Area of the cylinder head | m2 | |
| Area of the right side of the inner cylinder | m2 | |
| Area of the inner annulus | m2 | |
| Time | s | |
| Time per round | s | |
| Shearing torque on the cylinder bush | N·m | |
| Shearing torque on the annular piston | N·m | |
| Churning loss torque | N·m | |
| Cylinder temperature | K | |
| Oil temperature | K | |
| Inner wall temperature | K | |
| Inner Wall temperature of annulus | K | |
| Outer wall temperature of outer cylinder | K | |
| Outer wall temperature of cap head | K | |
| Inner wall temperature of cap head | K | |
| Right side wall temperature of the inner cylinder | K | |
| Wall temperature of cylinder head | K | |
| Left side wall temperature of the inner cylinder | K | |
| Temperature of surroundings | K | |
| Environment temperature | K | |
| Inner annular tangential velocity | m/s | |
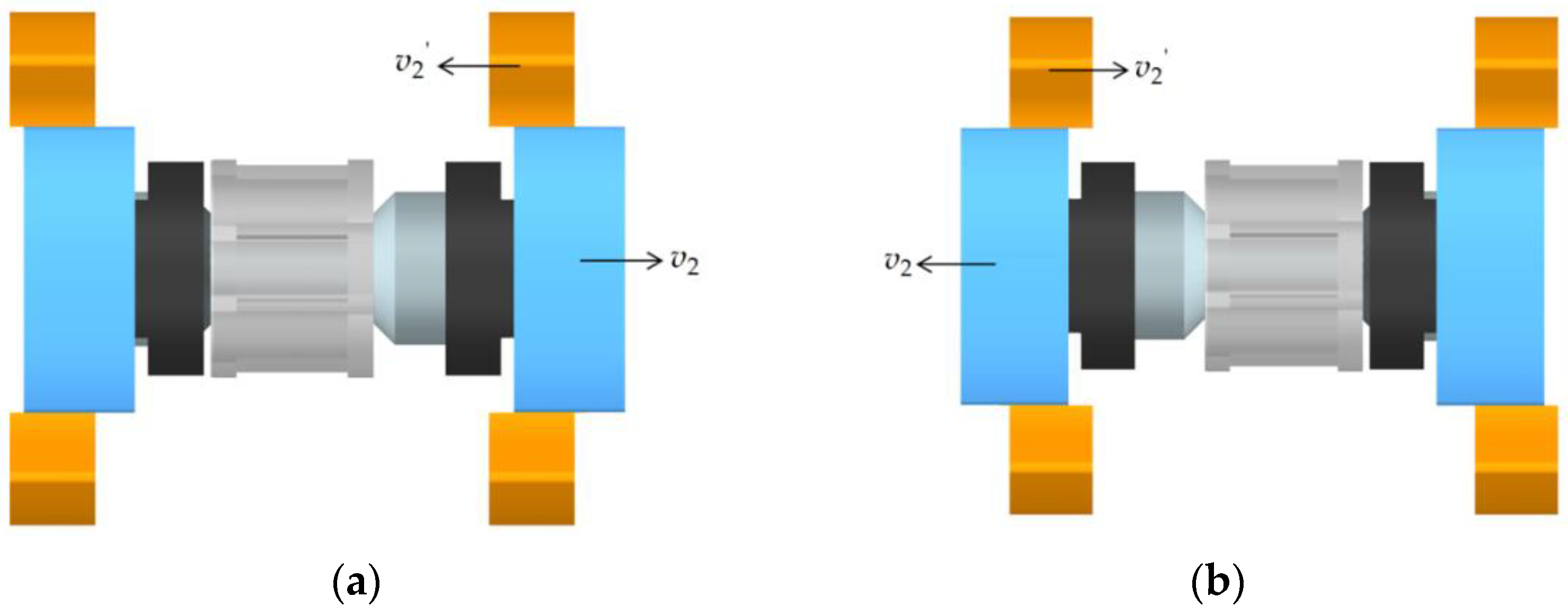
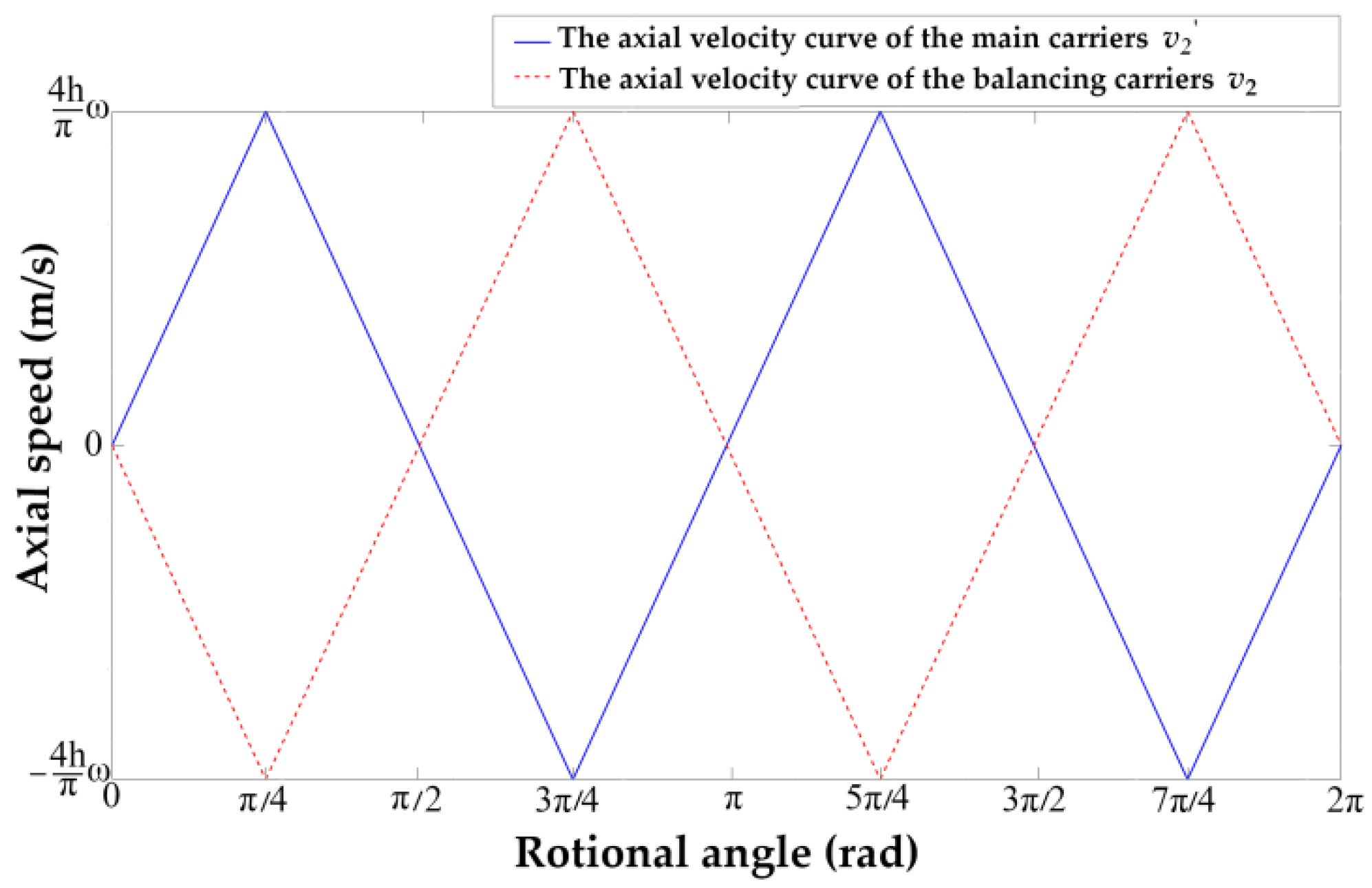
| Axial velocity of the main carrier | m/s | |
| Axial velocity of the balancing carrier | m/s | |
| Mean velocity of the cap head oil | m/s | |
| Mean velocity of the cylinder head oil | m/s | |
| Effective velocity of the carrier | m/s | |
| Volume of the cylinder | m3 | |
| Work performed by the shearing force on the left annular piston per revolution | J | |
| Work performed by the shearing force on the transmission shaft per revolution | J | |
| Work performed by the shearing force on the main piston per revolution | J |
Greek Symbols
| Kinematic viscosity of the oil | m2/s | |
| Dynamic viscosity of the oil between cylinder bush and annular piston | N·s/m2 | |
| Dynamic viscosity of the oil between neck bush and annular piston | N·s/m2 | |
| Dynamic viscosity of the oil between transmission shaft and main piston | N·s/m2 | |
| Density of the cylinder | kg/m3 | |
| Angular velocity | rad/s | |
| Correction factor | ||
| Stefan–Boltzmann constant | ||
| Emissivity |
References
- Yang, H.; Pan, M. Engineering research in fluid power: A review. J. Zhejiang Univ. A Sci. 2015, 16, 427–442. [Google Scholar] [CrossRef]
- Gracey, M.T. High Pressure Pumps, 1st ed.; Gulf Professional Publishing: Burlington, OH, USA, 2006; p. 197. [Google Scholar]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: Challenges and solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Li, C.; Jiao, Z. Thermal-hydraulic modeling and simulation of piston pump. Chin. J. Aeronaut. 2006, 19, 354–358. [Google Scholar] [CrossRef]
- Li, C.; Jiao, Z. Calculation method for thermal-hydraulic system simulation. J. Heat Transf. 2008, 130. [Google Scholar] [CrossRef]
- Banaszek, A.; Petrovi, R. Calculations of the unloading operation in liquid cargo service with high density on modern product and chemical tankers equipped with hydraulic submerged cargo pumps. Stroj. Vestn. J. Mech. Eng. 2010, 56, 186–194. [Google Scholar]
- Manring, N.D.; Mehta, V.S.; Nelson, B.E.; Graf, K.J.; Kuehn, J.L. Scaling the speed limitations for axial-piston swash-plate type hydrostatic machines. J. Dyn. Syst. Meas. Control 2014, 136, 031004. [Google Scholar] [CrossRef]
- Sidders, J.A.; Tilley, D.G.; Chapple, P.J. Thermal-hydraulic performance prediction in fluid power systems. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 1996, 210, 231–242. [Google Scholar] [CrossRef]
- Eduardo, D.L.; Victor Juliano, D.N. A new evaluation method for hydraulic gear pump efficiency through temperature measurements. SAE Tech. Pap. 2006, 1, 3503. [Google Scholar]
- Iben, U.; Wrona, F.; Munz, C.D. Cavitation in hydraulic tools based on thermodynamic properties of liquid and gas. J. Fluids Eng. 2002, 124, 1011–1017. [Google Scholar] [CrossRef]
- Green, T.E.; Snell, J.R. Thermographic inspection of hydraulic systems. In Proceedings of the Thermosense XVIII: An International Conference on Thermal Sensing and Imaging Diagnostic Applications, Orlando, FL, USA, 15 March 1996; pp. 25–30. [Google Scholar]
- Ivantysynova, M.; Lasaar, R. An investigation into micro and macrogeometric design of piston/cylinder assembly of swash plate machines. Int. J. Fluid Power 2004, 5, 23–36. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xu, B.; Chen, X.; Pan, M. Churning losses analysis on the thermal-hydraulic model of a high-speed electro-hydrostatic actuator pump. Int. J. Heat Mass Transf. 2018, 127, 1023–1030. [Google Scholar] [CrossRef]
- Xing, T.; Xu, Y.; Ruan, J. Two-dimensional piston pump: Principle, design, and testing for aviation fuel pumps. Chin. J. Aeronaut. 2020, 33, 1349–1360. [Google Scholar] [CrossRef]
- Dingcan, J.; Jian, R.; Sheng, L.; Bin, M.; Lingfeng, W. Modelling and validation of a roller-cam rail mechanism used in a 2D piston pump. J. Zhejiang Univ. A Sci. 2019, 20, 201–217. [Google Scholar] [CrossRef]
- Zhu, K.; Ruan, C.; Wang, H.; Li, S.; Ruan, J. Analysis of the torque loss of high-speed transmission mechanism with a stacked roller set. Machines 2021, 9, 140. [Google Scholar] [CrossRef]
- Wang, H.; Ding, C.; Huang, Y.; Li, S.; Jian, R. Design and research of 2D piston pumps with a stacked cone roller set. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 2128–2146. [Google Scholar] [CrossRef]
- Shentu, S.; Ruan, J.; Qian, J.; Meng, B.; Wang, L.; Guo, S. Study of flow ripple characteristics in an innovative two-dimensional fuel piston pump. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 464. [Google Scholar] [CrossRef]
- Huang, Y.; Ruan, J.; Zhang, C.; Ding, C.; Li, S. Research on the mechanical efficiency of high-speed 2D piston pumps. Processes 2020, 8, 853. [Google Scholar] [CrossRef]
- Wang, H.; Tong, C.; Ruan, C.; Ding, C.; Li, S.; Ruan, J. Optimization of mechanical efficiency models for 2D piston pumps with a stacked taper roller set. Machines 2022, 10, 180. [Google Scholar] [CrossRef]
- Zhang, C.; Jian, R.; Xing, T.; Li, S.; Ding, C. Research on the volumetric efficiency of a novel stacked roller 2D piston pump. Machines 2021, 9, 128. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, C.; Wang, H.; Ruan, J. Numerical and experimental study on the churning losses of 2D high-speed piston pumps. Eng. Appl. Comput. Fluid Mech. 2020, 14, 764–777. [Google Scholar] [CrossRef]
- Ding, C.; Zhu, Y.; Liu, L.; Tong, C.; Ruan, J. Research on a novel flowmeter with parallel two-dimensional pistons as its metering units. IEEE Access 2019, 7, 110912–110927. [Google Scholar] [CrossRef]
- Miller, R.; Miller, M.R.; Stewart, H. Pumps and Hydraulics, 6th ed.; Wiley Publishing: Indianapolis, IN, USA, 2004; p. 239. [Google Scholar]
- Childs, P.R.N.; Long, C.A. A review of forced convective heat transfer in stationary and rotating annuli. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1996, 210, 123–134. [Google Scholar] [CrossRef]
- Yong, N.L.; Minkowycz, W.J. Heat transfer characteristics of the annulus of twocoaxial cylinders with one cylinder rotating. Int. J. Heat Mass Transf. 1989, 32, 711–722. [Google Scholar] [CrossRef]
- Incroprera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavinne, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Churchill, S.W.; Chu, H.H.S. Correlating equations for laminar and turbulent free convection from a horizontal cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Hannon, W.M. Rolling-element bearing heat transfer—Part I: Analytic model. J. Tribol. 2015, 137, 031102. [Google Scholar] [CrossRef]
- Hamakawa, H.; Mori, H.; Iino, M.; Hori, M.; Yamasaki, M.; Setoguchi, T. Experimental study of heating fluid between two concentric cylinders with cavities. J. Therm. Sci. 2008, 17, 175–180. [Google Scholar] [CrossRef][Green Version]



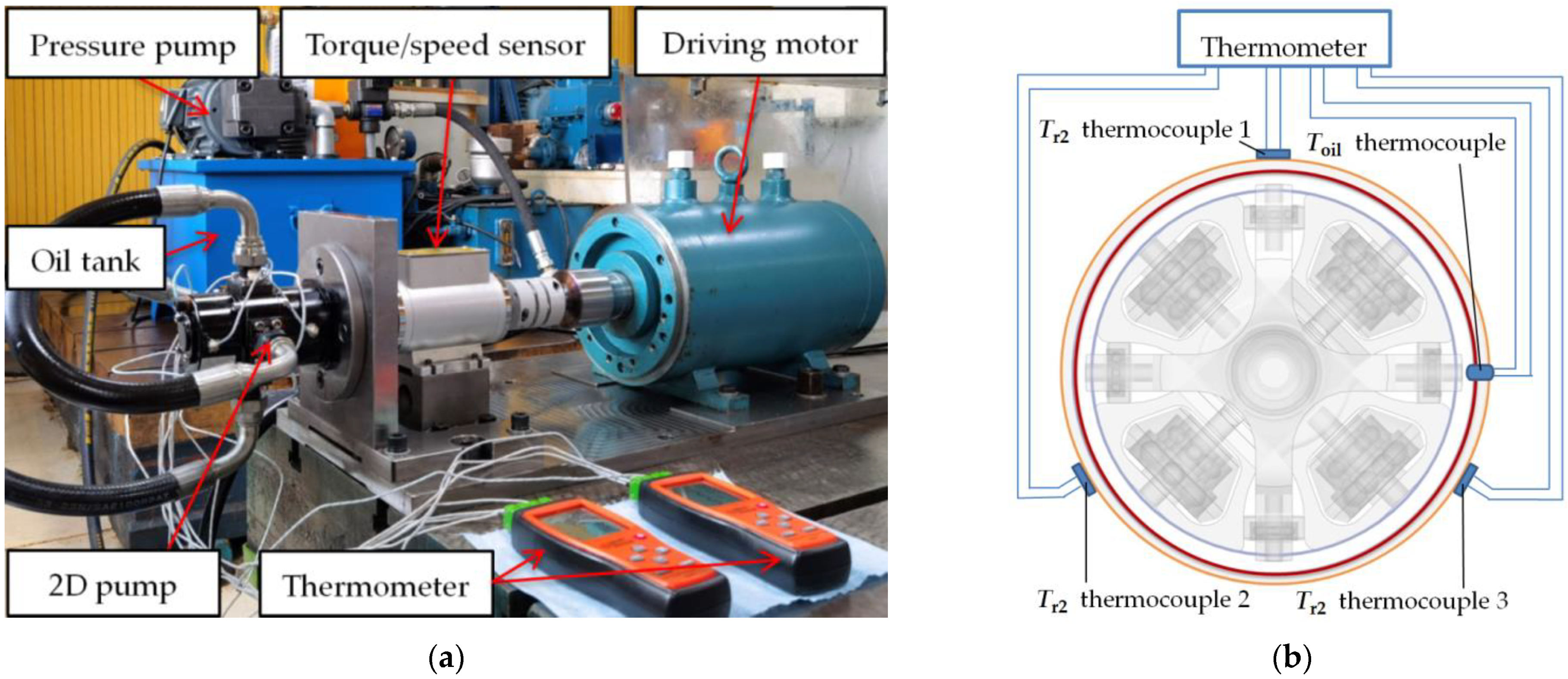


| Description | Value |
|---|---|
| Sanjing SL06 torque/speed sensor | Range 0~10 Nm, accuracy ± 0.1%; Rotational speed range 0~18,000 rpm |
| Smart Sensor AS887 thermometer | Range −200~1372 °C, accuracy ± 0.1% °C |
| K-type thermocouple | Range −50~300 °C, accuracy ±1.5% |
| Atmospheric pressure | 101.16 kPa |
| Rotational speed | 1000~6000 rpm |
| Initial surrounding temperature | 23.5 °C |
| Initial environment temperature | 23.5 °C |
| Speed (rpm) | Relative Deviation Range | Average Deviation | Correction Factor |
|---|---|---|---|
| 1000 | −19.78~38.87% | 15.49% | 1.155 |
| 2000 | −33.57~0.52% | −21.11% | 0.789 |
| 4000 | −56.21~−34.32% | −45.41% | 0.546 |
| 6000 | −62.34~−43.94% | −54.31% | 0.457 |
| Speed (rpm) | Relative Deviation Range | Mean Deviation |
|---|---|---|
| 1000 | 0.01~0.07% | 0.04% |
| 2000 | 0.02~0.24% | 0.08% |
| 4000 | −0.09~0.22% | 0.03% |
| 6000 | −0.05~0.70% | 0.19% |
| Speed (rpm) | Mean Heat Loss (W) | Churning Loss (W) | Relative Deviation Range | Mean Deviation |
|---|---|---|---|---|
| 1000 | 6.27 | 7.33 | −38.02~3.75% | −14.43% |
| 2000 | 32.64 | 28.27 | −15.68~53.90% | 15.45% |
| 4000 | 93.06 | 104.71 | −29.92~9.39% | −11.12% |
| 6000 | 312.87 | 216.75 | −6.13~67.33% | 44.35% |
| Speed (rpm) | ||||||
|---|---|---|---|---|---|---|
| 1000 | 9.58% | 14.18% | 32.89% | 14.14% | 29.21% | 36.04% |
| 2000 | 9.89% | 14.57% | 35.92% | 12.09% | 27.52% | 37.90% |
| 4000 | 9.07% | 12.71% | 37.54% | 12.46% | 28.22% | 35.38% |
| 6000 | 8.67% | 11.75% | 41.11% | 12.45% | 26.01% | 37.90% |
| Mean values | 9.30% | 13.30% | 36.87% | 12.79% | 27.74% | 36.81% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, L.; Li, Z.; Li, S.; Jia, W.; Ruan, J. Heat Loss Analysis of a 2D Pump’s Transmission. Machines 2022, 10, 860. https://doi.org/10.3390/machines10100860
Chang L, Li Z, Li S, Jia W, Ruan J. Heat Loss Analysis of a 2D Pump’s Transmission. Machines. 2022; 10(10):860. https://doi.org/10.3390/machines10100860
Chicago/Turabian StyleChang, Liang, Zhiwei Li, Sheng Li, Wenang Jia, and Jian Ruan. 2022. "Heat Loss Analysis of a 2D Pump’s Transmission" Machines 10, no. 10: 860. https://doi.org/10.3390/machines10100860
APA StyleChang, L., Li, Z., Li, S., Jia, W., & Ruan, J. (2022). Heat Loss Analysis of a 2D Pump’s Transmission. Machines, 10(10), 860. https://doi.org/10.3390/machines10100860






