Lightweight Design Optimization of Nonpneumatic Tires under Radial-Stiffness Constraints

Abstract

Nonpneumatic tires (NPTs) have good safety and a good load-carrying capacity, and they replace the function of air in pneumatic tires with a solid spoke component. The radial stiffness and weight are the important indexes for evaluating the performance of an NPT. In this research, we designed an NPT according to the requirements of vehicle Chery eQ1 based on weight minimization. Taking the radial stiffness related to the bearing-capacity performance as the constraint condition, a topology-optimization algorithm is proposed to find the best thickness distribution of the spokes with the objective of minimizing the mass. First, the mechanical properties of the material were obtained with the test. Then, the FE model of an NPT with a Fibonacci spoke structure was built and validated with a radial-stiffness test on a five rigid test machine. The optimization algorithm was carried out by searching for the best thickness distribution of the spoke after verifying the reliability of the FE model. Finally, the optimized tire was manufactured, and the stiffness test was carried out to verify the feasibility of the optimization results. The results show that the spoke mass can be reduced by 9% by using the proposed optimization algorithm while satisfying the radial-stiffness constraint.

1. Introduction

Nonpneumatic tires (NPTs) can completely achieve the functions of traditional pneumatic tires, such as supporting the vehicle, providing sufficient traction for driving and braking, cushioning the vehicle, and so on. More importantly, they can work without maintaining the air pressure, and with this characteristic, the serious traffic accidents caused by punctures, scratches, leaks, and even blowouts in tires can be overcome [1].

Figure 1 shows a variety of NPTs. A new concept NPT Tweel with the significant advantages of no bursting and no leakage was produced by Michelin [2]. Since then, more attention has been paid to NPTs. In 2008, Resilient Technology and the University of Wisconsin jointly developed a new honeycomb NPT made of polyurethane, which was designed with the tensile deformation of a honeycomb structure [3,4,5]. Bridgestone launched air-free concept NPTs in 2012 and 2014. In 2015, iFlex was launched by the Hantai Company [6,7]. In 2021, Jihua Lab developed an NPT with the structural characteristics of variable-thickness tires for vehicle Chery eQ1, and we present details on the lightweight design of this NPT in this paper.

The radial stiffness is used to evaluate the bearing capacity of an NPT. The radial stiffness also affects the rolling damping and buffering performance. Over the last decade, researchers have studied the load-bearing properties of NPTs. Jang designed the stiffness of an NPT with topology-optimization technology [8]. Zhao investigated the static stiffness of a new NPT with a hinge using numerical simulations and experiments [9]. In order to obtain NPTs with high load capacities, the bionic structure was introduced into the spoke design. Ganniari quantified the effect of a wide range of internal geometrical parameters on a honeycomb tire’s weight and mechanical behavior [10]. Zang proposed a design method for a honeycomb structure to direct the design of NPTs [11]. Zhang established an NPT with the characteristics of a kangaroo’s lower-limb structure and carried out a stiffness simulation for the NPT [12]. Chiral structures have been developed for NPTs due to their unique optical and mechanical properties. Wu developed a gradient anti-tetrarchical structure to replace the pneumatic parts of standard pneumatic tires, and the tires had a good load-carrying capacity [13].

Weight is also one of the important performance factors of NPTs. The reduction in the unsprung mass of a vehicle is conducive to fuel economy and smoothness [14]. The thickness of the spokes is also one of the main design variables of NPTs, and it has a great impact on not only their load-bearing capacity, but also their weight. However, variable-thickness structures have excellent performances and are widely used in automobiles, aviation, and other industrial fields [15,16,17]. The variable-thickness-structure design methods (e.g., the surrogate-model method [18,19,20] and intelligent-algorithm method [21,22,23]) have been widely used in the past few decades. In recent years, the topology-optimization method [24,25,26] has been applied to the design of variable-thickness structures because it is more efficient for optimization with a large number of variables. The abovementioned design method can make the components lightweight while satisfying the established requirements for the mechanical properties.

In this research, a lightweight NPT with radial-stiffness requirements was created. The improved topology-optimization algorithm was used for the NPT-spoke-thickness optimization, and it was proven to be effective with a radial-stiffness test. The continuously changing thickness of the spoke was taken as the design variable, while the radial stiffness was taken as the design constraint. The minimum mass was the optimization objective. In Section 2, we present the optimization-design-problem statement, the sensitivity analysis of the thickness-design variables, and the distribution constraints of the thickness. Section 3 describes how the mechanical properties of the polyurethane materials of the spoke were obtained with a test. The finite-element (FE) model of the NPT was built for lightweight design work, and the accuracy of the model was verified with a tire-radial-stiffness test. Section 4 describes how the optimized thickness distribution of the spokes was carried out with the proposed method, and how the lightweight tire was manufactured and verified again. The conclusions are given in Section 5.

2. Design Problem and Optimization Method

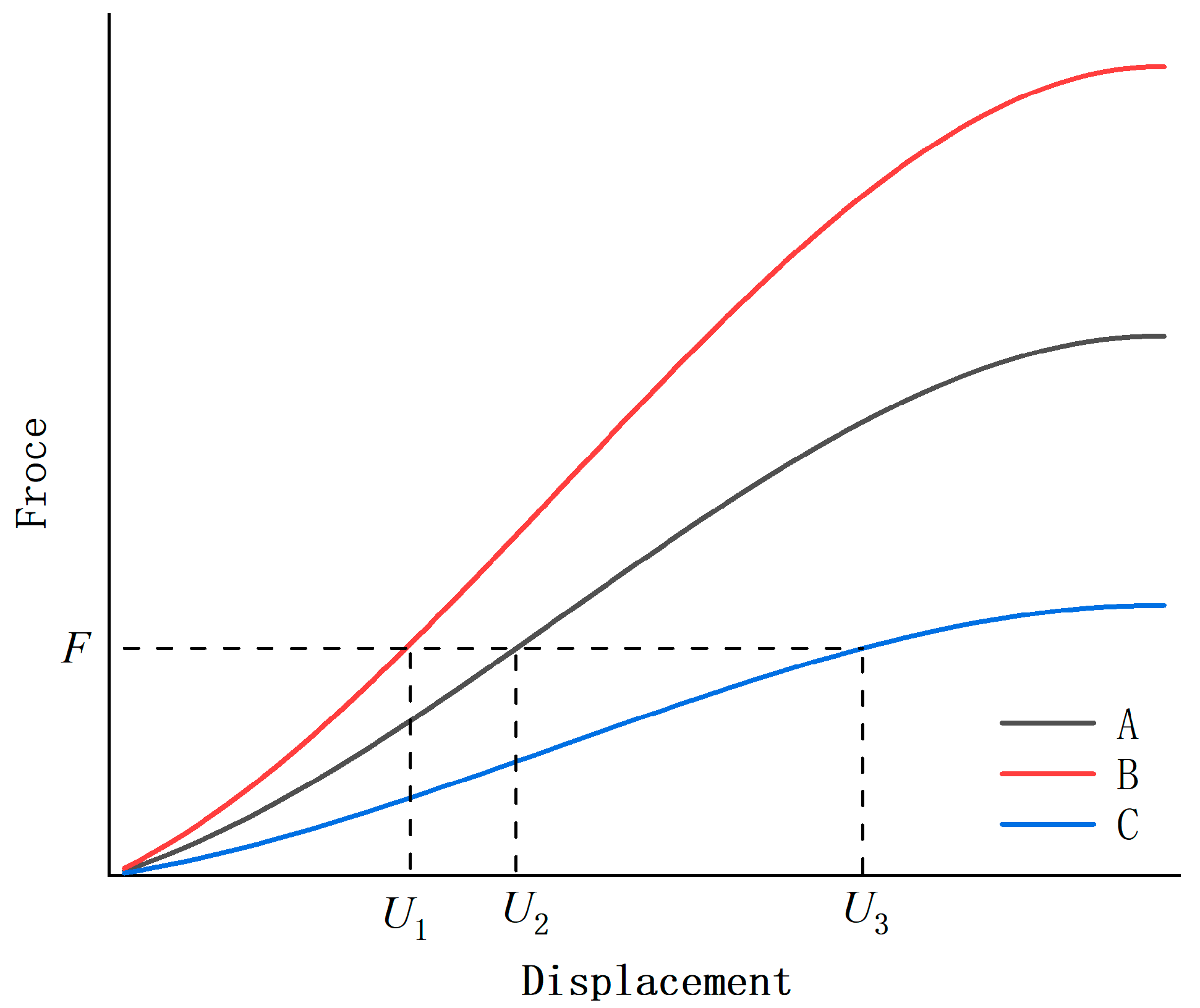
2.1. Design-Problem Statement

The appropriate radial stiffness of a tire can balance the performance requirements between the driving safety, handling stability, fuel economy, and vehicle ride comfort. Figure 2 shows the force-displacement curve of three different tire-radial-load tests. It can be seen from the figure that the radial stiffness of Tire B is the highest, and that of Tire C is the lowest. It is incorrect to think that the best curve is the one with the greatest stiffness. Actually, the best stiffness curve should be the best matching for the corresponding car. Therefore, it is reasonable to use stiffness as a constraint in tire optimization.

It is assumed that the radial-force-displacement curve of the tire in Figure 3 is tailored for an actual automobile. U* is the maximum radial-deformation displacement of the tire. F* is the radial reaction force with the maximum deformation displacement. The process of the loading tire displacement can be divided into many steps. Uⁱ and Fⁱ represent the radial force and radial deformation of the tire in the i-th step, respectively. These two physical quantities are applied to the derivation of the sensitivity, as described in the next section.

Due to the radial stiffness being tailored for an actual automobile, the mathematical model of the lightweight tire design can be described as shown in Equation (1). f(t_e) is the target, representing the mass of the tire; ${\rho }_e$ is the element density; $s_e$ is the area of the element of the number (e); t_e is the design variable for the spoke thickness; t_max and t_min are the maximum thickness and minimum thickness, respectively; U* and F* are described in the previous section; N is the total shell-element number.

$$\begin{array}{l}\mathrm{Minimize}\begin{array}{cc}& f(t_e)\end{array}={\displaystyle {\sum }_{e=1}^{e=N}{\rho }_e{t}_e{s}_e}\\ \mathrm{Subject}\begin{array}{cc}\begin{array}{c}\end{array}\mathrm{to}& U_{\max }\end{array}=U^{*}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{c}\begin{array}{cc}& \end{array}\end{array}\end{array}& F_{\max }\end{array}=F^{*}\\ \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{c}\begin{array}{cc}& \end{array}\end{array}\end{array}& t_e\end{array}\in [t_{\min },t_{\max }]\begin{array}{cc}& e=1,\dots \dots ,N\end{array}\end{array}$$

(1)

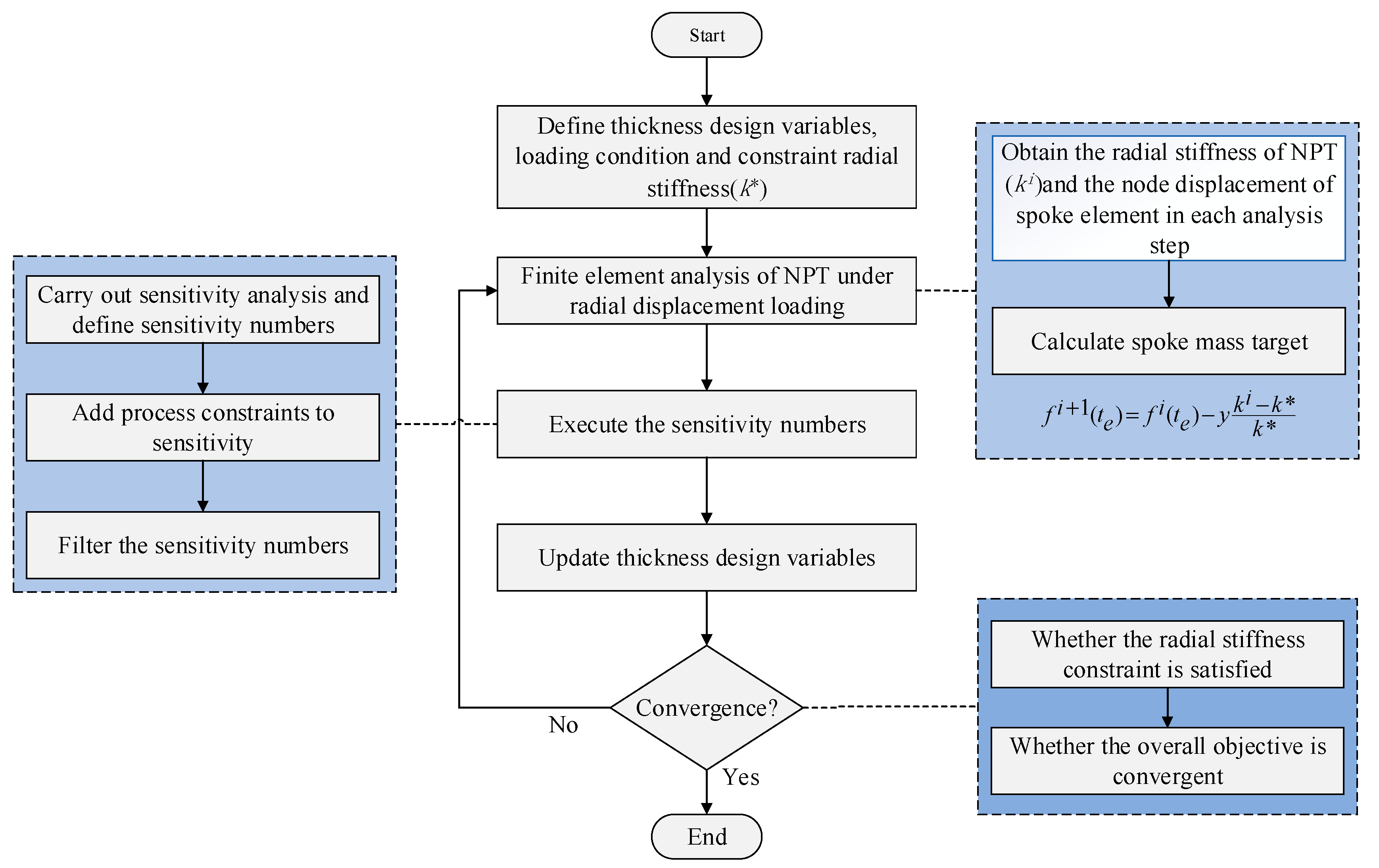
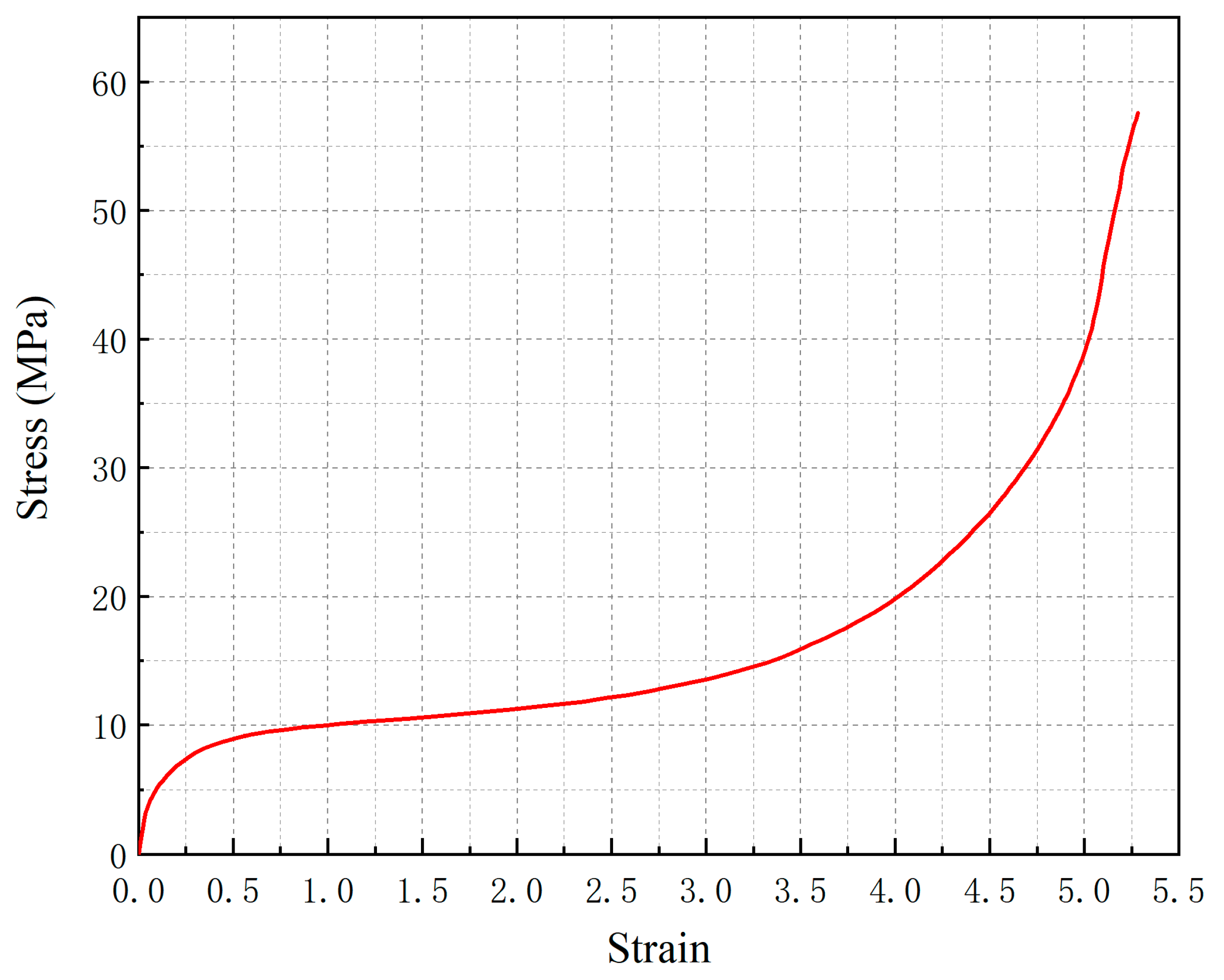
2.2. Sensitivity Analysis for Thickness

U* is the external displacement loading that can be loaded in the FE model. The force constraint can be added to the objective function by introducing a Lagrangian multiplier (λ):

$$f(t_e)={\displaystyle {\sum }_{t_e=1}^{t_e=N}{\rho }_e{t}_e{s}_e}+\lambda (F-F^{*})$$

(2)

The modified objective function is equivalent to the original objective function, and the Lagrangian multiplier (λ) can be any constant if the force constraint is satisfied. The derivative of the modified objective function (f(t_e)) is:

$$\frac{df(t_e)}{d{t}_e}={\displaystyle {\sum }_{t_e=1}^{t_e=N}{\rho }_e{s}_e}+\frac{\lambda dF}{d{t}_e}$$

(3)

To calculate the $\frac{\lambda dF}{d{t}_e}$, we introduce a virtual unit displacement (u^k), and the expression of F can be expressed as:

$$F=(u^k{)}^{\mathrm{T}}F$$

(4)

The radial loading of the tire is related to the geometric and material nonlinearity. The reaction force is calculated as follows in the FE analysis, where K¹ is the stiffness matrix of the unloaded spoke, and U⁰ = 0. The n is the total number of load increments.

$$\begin{array}{l}\Delta F^i=K^i(U^i-U^{i-1})\\ \Delta F^{i-1}=K^{i-1}(U^{i-1}-U^{i-2})\\ .\\ .\\ \Delta F^1=K^1(U^1-U^0)\\ F=\Delta F^1+\Delta F^2+\dots .\Delta F^i={\displaystyle {\sum }_{i=1}^{i=n}{K}^i(U^i-U^{i-1})}\end{array}$$

(5)

By simultaneously solving Equations (3)–(5), the derivative of the objective function (f(t_e)) can be rewritten as:

$$\frac{df(t_e)}{d{t}_e}={\displaystyle {\sum }_{t_e=1}^{t_e=N}{\rho }_e{s}_e}+\lambda \frac{{\displaystyle {\sum }_{i=1}^{i=n}{(u^k)}^T{K}^i(U^i-U^{i-1})}}{d{t}_e}$$

(6)

The spoke was modeled with the shell elements, and the stiffness matrix for the shell consists of the membrane, bending, and shear stiffness, which can be expressed by:

$$K(t_e)=K_m(t_e)+K_b(t_e)+K_s(t_e)$$

(7)

Furthermore, the shell-element-stiffness matrix can be expressed as:

$$\begin{array}{l}D=\frac{E}{(1-v^2)}\left[\begin{array}{ccc}1& v& 0\\ v& 1& 0\\ 0& 0& \frac{1-v}{2}\end{array}\right],D_b=\frac{E}{12(1-v^2)}\left[\begin{array}{ccc}1& v& 0\\ v& 1& 0\\ 0& 0& \frac{1-v}{2}\end{array}\right],D_s=\frac{G}{k}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\\ k=1.2\\ K_m(t_e)=t_e{\displaystyle \underset{A^e}{\int }{B}^{T}D}BdA,\hspace{1em}{K}_b(t_e)=t_e^3{\displaystyle \underset{A^e}{\int }{B}_{{}^b}^T{D}_b}{B}_{b}dA,\hspace{1em}{K}_s(t_e)=t_e{\displaystyle \underset{A^e}{\int }{B}_{{}^s}^T{D}_s}{B}_{s}dA\end{array}$$

(8)

where D, D_b, and D_s are the material matrixes, v is the Poisson’s ratio, E is the Young’s modulus, G is the shear modulus, and k is the shear-stress-distribution coefficient. By simultaneously solving Equations (6) and (8), the sensitivity of the element of the number (e) is finally obtained. When the area of each FE mesh approaches equality, λ can be taken from (0,1]:

$${\alpha }_e={\rho }_e{s}_e+\lambda {\displaystyle {\sum }_{i=1}^{i=n}(u^k}{)}^T({\displaystyle \underset{A^e}{\int }{B}_e^i{}^T{D}_e^i}{B}_e^{i}dA+3t_e^2{\displaystyle \underset{A^e}{\int }{B}_{b,e}^i{}^T{D}_{b,e}^i}{B}_{b,e}^{i}dA+{\displaystyle \underset{A^e}{\int }{B}_{s,e}^i{}^T{D}_{s,e}^i}{B}_{s,e}^{i}dA)(U_e^i-U_e^{i-1})$$

(9)

2.3. Sensitivity with Process Constraints

Although taking each shell element as an independent optimization design variable can obtain a structure with a better performance, it will increase the difficulty of the manufacturing. In Figure 4, it can be seen that the thickness of Plate A/B changes along the Y-axis direction/X-axis direction, which is more conducive to demolding from the X-axis direction/Y-axis direction.

In Figure 5, the variable-thickness plate is divided into M1 × M2 grids. Each grid has a thickness sensitivity, and the thickness sensitivity of the variable-thickness plate is in the form of a two-dimensional matrix. In order to make the thickness change only in one direction, we convert the thickness-sensitivity two-dimensional matrix into a one-dimensional matrix, and we constrain the sensitivity according to Formula (10). The x_j and y_k represent the thickness design variables of the i-th row and k-th column, respectively. m1 is the total number of thickness design variables in the X direction, and m2 is the total number of thickness design variables in the Y direction.

$${\alpha }_e(x_j)=\frac{{\displaystyle {\sum }_{j=1}^{j=m1}{\alpha }_e(x_j,y_k)}}{m1}\mathrm{or}{\alpha }_e(y_k)=\frac{{\displaystyle {\sum }_{k=1}^{k=m2}{\alpha }_e(x_j,y_k)}}{m2}$$

(10)

2.4. Sensitivity Filtering

There are areas with rapid thickness changes in the structure, which will increase the risk of failure in the manufacturing process. In order to mitigate the gradient of the thickness change, it is necessary to weight-average the thickness sensitivities of adjacent areas, as shown in Formula (11). L is the filtration range. When the L is increased, the thickness change is slower; otherwise, the thickness change is more intense:

$$\begin{array}{l}{\alpha }_e(y_k)=\frac{1}{{\displaystyle {\sum }_{f1=1}^{f1=m2}{H}_{f1}}}{\displaystyle {\sum }_{f1=1}^{f1=m2}{H}_{f1}{\alpha }_e(y_k)}\\ {\alpha }_e(x_j)=\frac{1}{{\displaystyle {\sum }_{f2=1}^{f2=m1}{H}_{f2}}}{\displaystyle {\sum }_{f2=1}^{f2=m1}{H}_{f2}{\alpha }_e(x_j)}\\ H_{f1}=\max (L-\mathrm{dist}(y_k-y_{f1}),0)\\ H_{f2}=\max (L-\mathrm{dist}(x_j-x_{f2}),0)\end{array}$$

(11)

2.5. Update Rule for Thickness

A lighter structure requires a higher load efficiency, for which the inefficient materials should be eliminated, while the efficient materials should be retained in the design domain. The idea of optimizing the thickness is also consistent with this. In order to estimate the contribution of the thickness of each element to the whole design field, we introduce the criterion ${\alpha }_{av}$:

$$\begin{array}{l}{t}_e^{i+1}=\\ \{\begin{array}{c}\mathrm{if}-b\le \frac{{\alpha }_e-{\alpha }_{av}}{{\alpha }_{av}}\le b\\ \min (t_{\max },\max (t_e^i+\frac{{\alpha }_e-{\alpha }_{av}}{{\alpha }_{av}},t_{\min })\\ \mathrm{if}b\le \frac{{\alpha }_e-{\alpha }_{av}}{{\alpha }_{av}}\\ \min (t_{\max },\max (t_e^i+b,t_{\min })\\ \mathrm{if}\frac{{\alpha }_e-{\alpha }_{av}}{{\alpha }_{av}}\le -b\\ \min (t_{\max },\max (t_e^i-b,t_{\min })\end{array}\end{array}$$

(12)

where b is the maximum step size of the thickness update, and $t_e^i,t_e^{i+1}$ are the thicknesses of Step i and Step i + 1, respectively. It is worth noting that, when the mass of the updated thickness is greater than the target value of the current iteration mass, let ${\alpha }_{\min }={\alpha }_{av}$; conversely, let ${\alpha }_{\max }={\alpha }_{av}$.

Figure 6 shows the whole process of thickness optimization. y can be determined according to the order of magnitude of the target. In this study, because the target is the mass fraction, y is taken as 1.

3. Automotive NPT

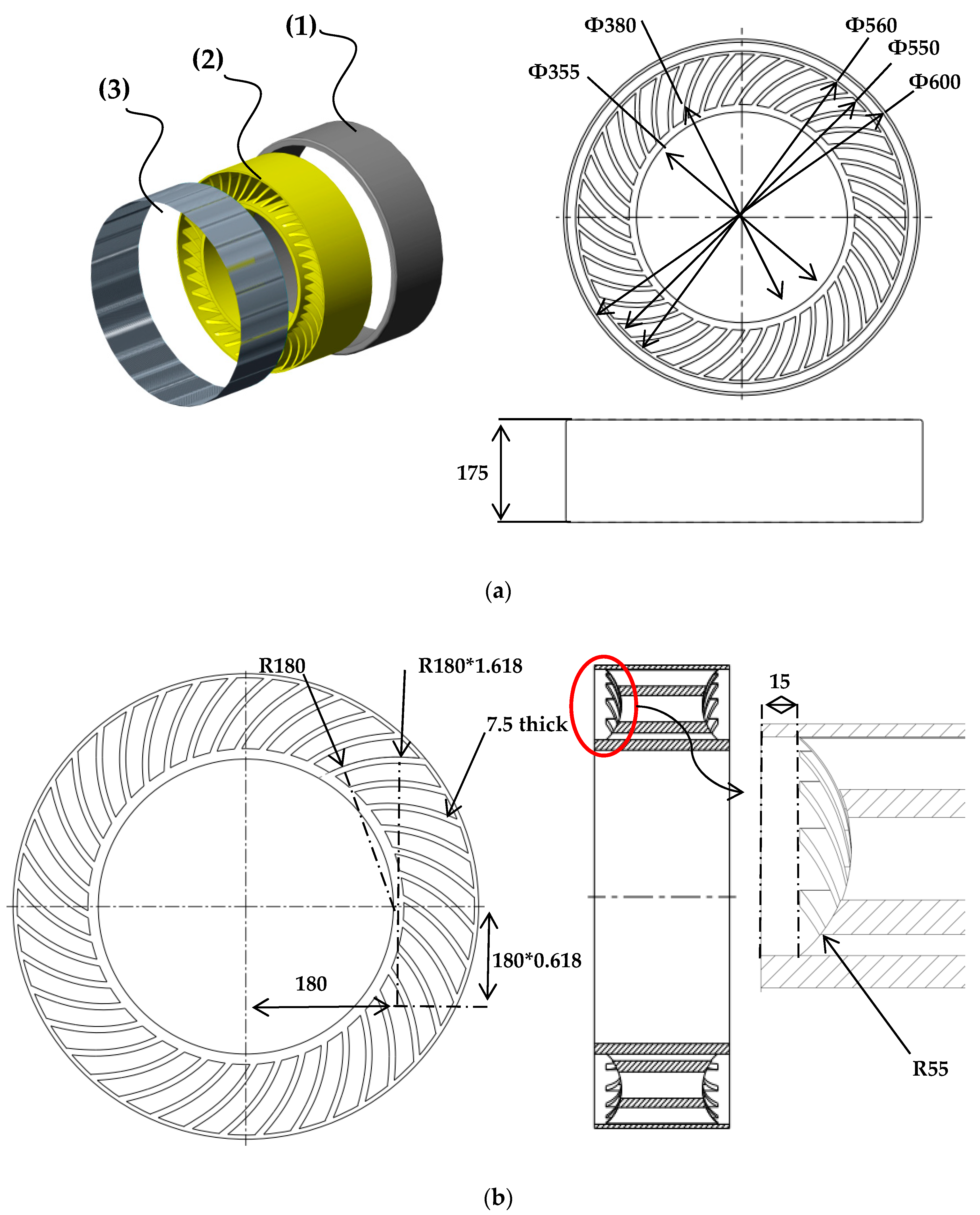
3.1. The Geometry of the Fibonacci-Spoke NPT

As shown in Figure 7a, the NPT is mainly composed of a tread (1), spoke (2), and ply layer (3). The diameter of the tire is 600 mm, and the width is 175 mm. The tread thickness is 20 mm. The wire-laying angle of the tire cord is 0, and the number of laying layers is 2. There are forty support bars on the spokes, and each of them is 7.5 mm thick. It can be seen from Figure 7b that the radius of the first circular arc of the Fibonacci spokes is 180 mm, and the radius of the second circular arc is 1.618 times that of the first circular arc. The spoke side dimensions and thickness dimensions can also be obtained from Figure 7b.

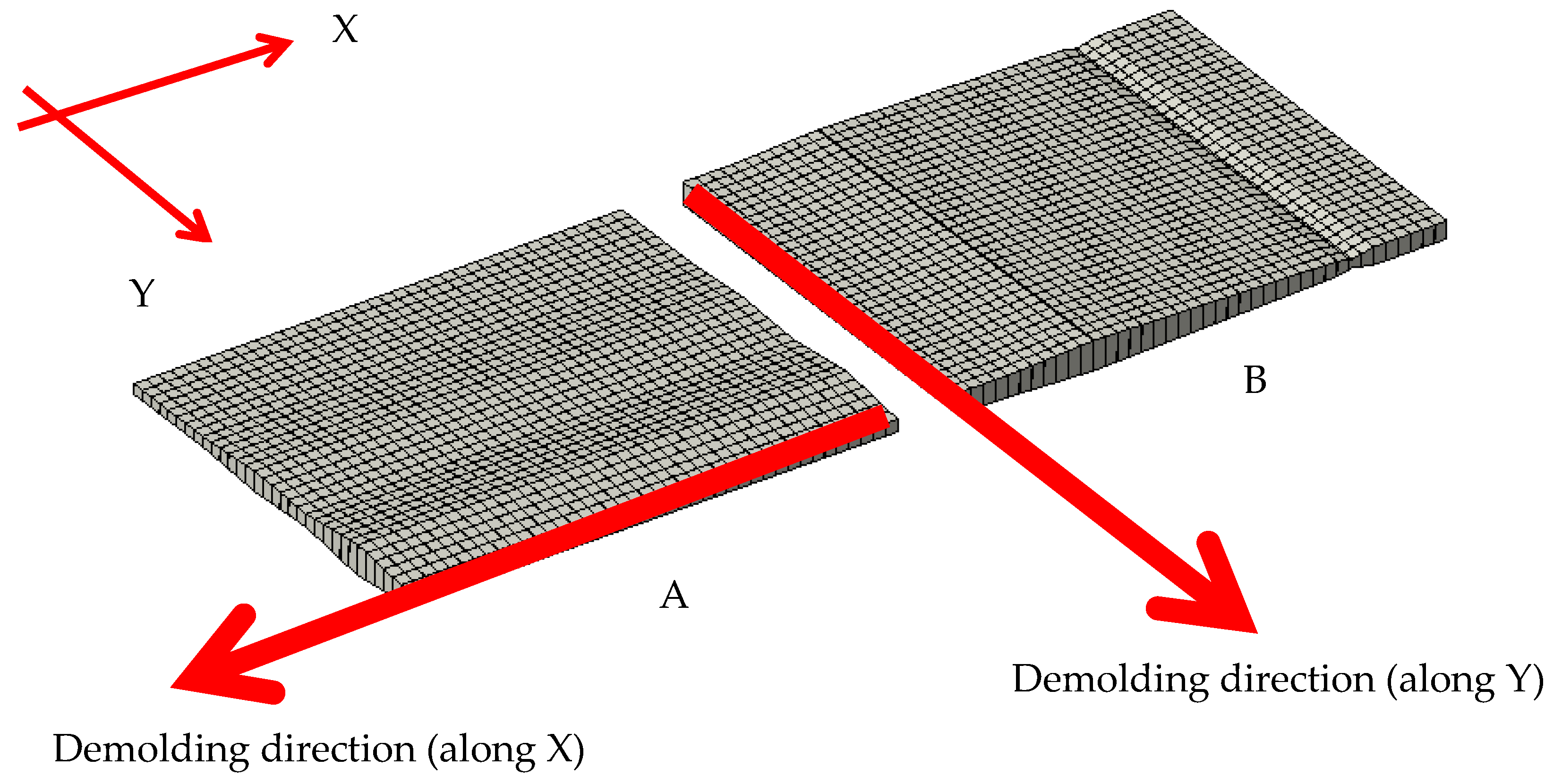
3.2. NPT Manufacturing

The spoke is formed by pouring. As shown in Figure 8, the spoke mold consists of an upper mold, lower mold, outer ring, and deflector. First, the mold is heated to between 120 °C and 140 °C. Molten material enters the mold cavity through the sprue and freezes within three minutes. After 24 h of vulcanization, the spoke can be demolded. It is notable that the thermal expansion of the material should be considered in the dimensional design of the mold. However, the thickness of the spoke was not 7.5 mm but 6.7 mm, which was caused by the wrong estimation of the thermal-expansion parameters of the material, and we modified the variable-thickness-spoke mold.

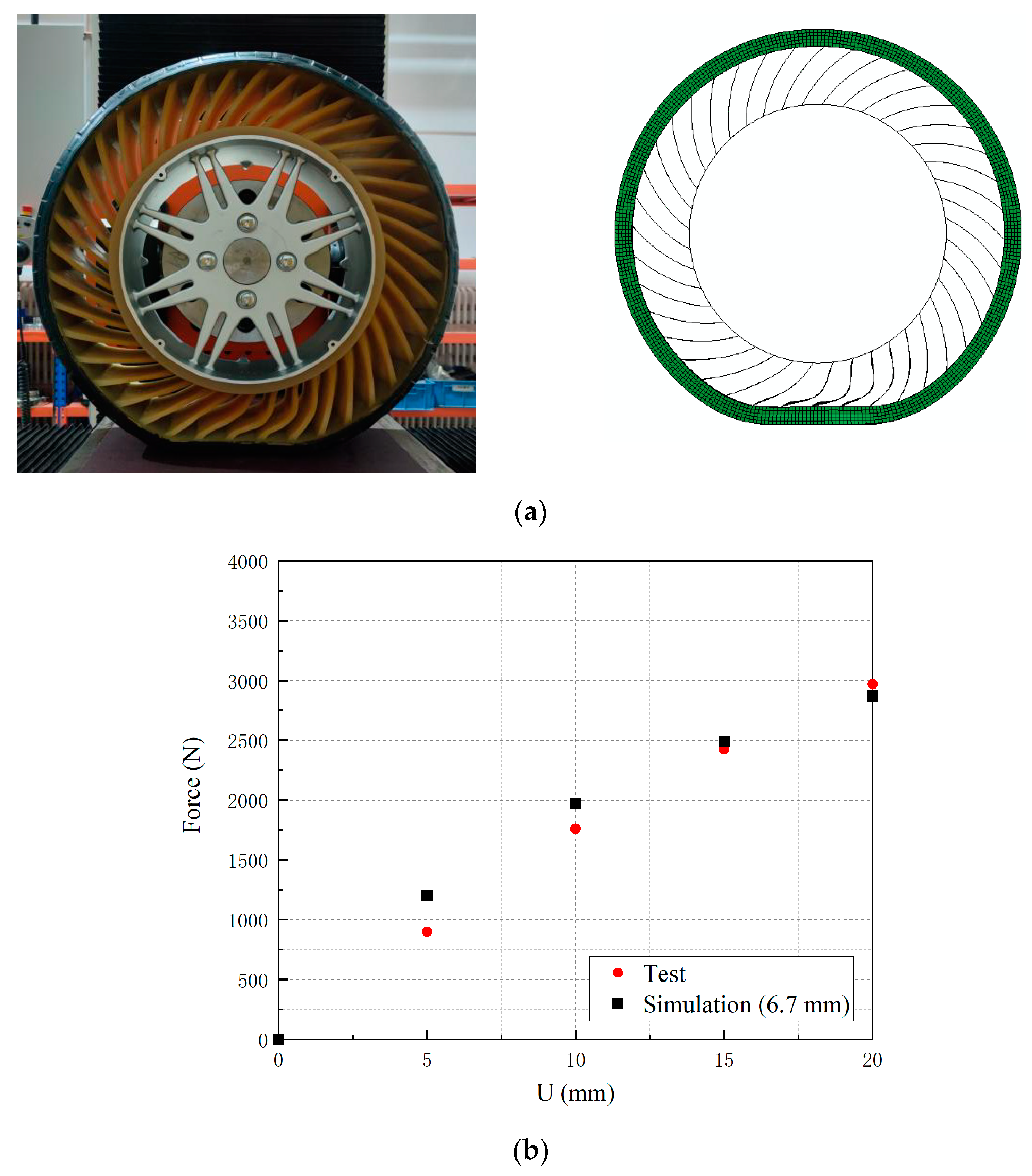
3.3. FE Model and Experimental Validation

The FE analysis was conducted with the implicit FE code ABAQUS. The spoke was modeled with S4R shell elements, and the other parts were modeled with C3D8RH hexahedron elements. The spoke is made of hyperelastic material, the mechanical properties of which are shown in Figure 9. The tread material is natural rubber, the mechanical performance of which can be defined by C10 and C01 in ABAQUS. In this tire model, C10 = 0.5 and C01 = 0.04. The material of the tire cord in the ply layer is steel, with the mechanical properties of the density ($\rho$ = 7.8 × 103 kg/m³), Young’s modulus (E = 210 GPa), and Poisson’s ratio ($\mu$ = 0.30).

In Figure 10, the NPT is fixed on the central axis on a five rigid test machine test bench, and it moves down with a velocity of 50 mm/min to press the test-bench ground until it reaches a 20 mm displacement. The FE model of the NPT was established according to the test conditions.

Figure 11a displays the experimental and simulation results of the NPT deformation, and Figure 11b displays the force-displacement curves for the test and simulation. The simulation curve is basically consistent with that of the test. The NPT FE model can be applied to the following optimization process.

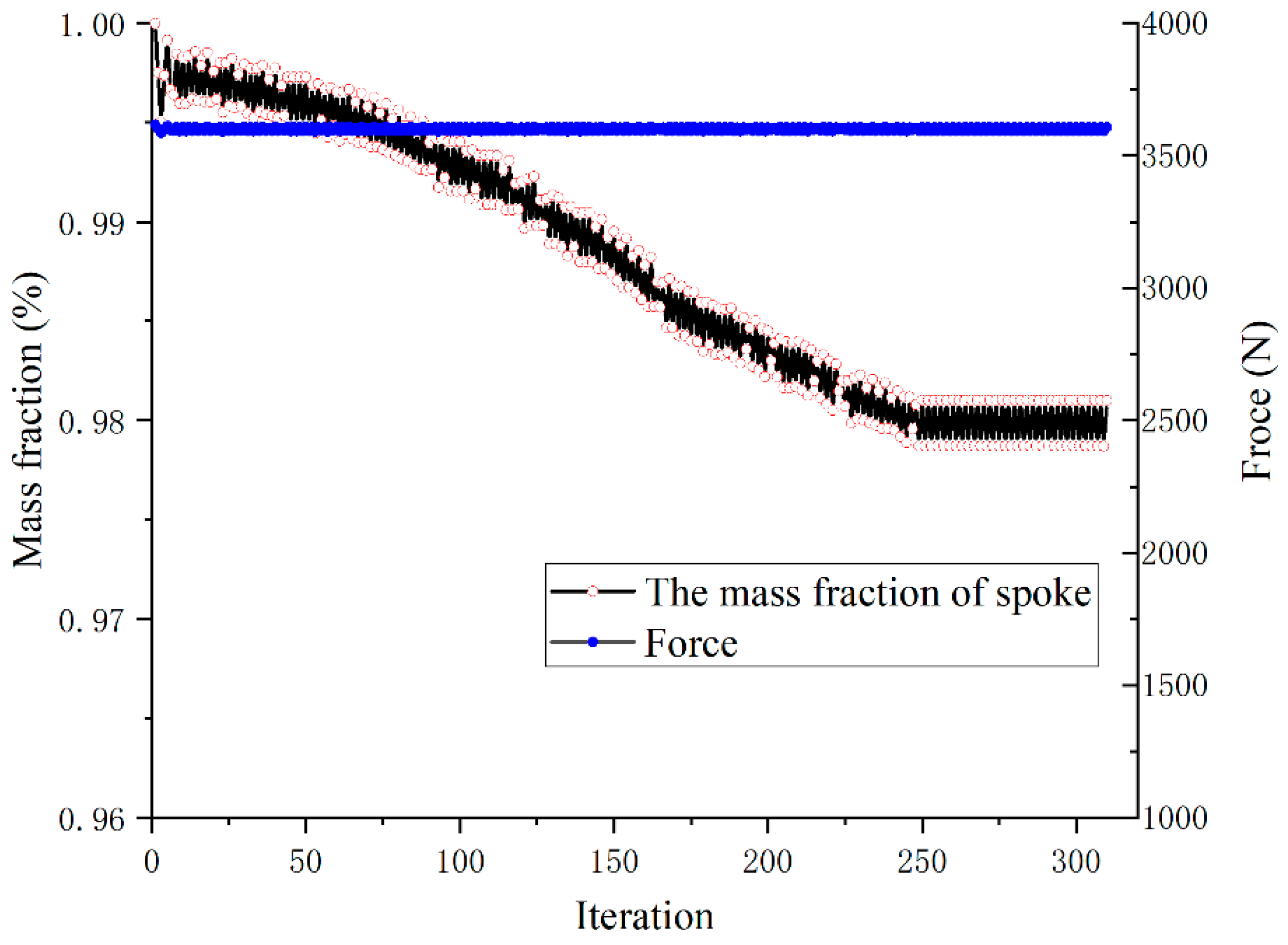
4. Thickness Optimization

The object was to minimize the spoke mass. When the deformation of the tire is close to 20 mm, the reaction force reaches 3600 N (the specification of a vehicle Chery eQ1 tire is 165/65 R15, its radial deformation is 20 mm, and the corresponding rated load is 360 kg).

Theoretically, the higher the thickness variable is set, the better the optimal solution obtained. We regarded the number of the radial and axial meshes of the spokes as the number of thickness variables. In order to balance the contradiction between the computational cost and optimization effect, we set the grid size to 1 mm. Thus, there were 26 and 30 design variables for the thickness in the radial and width directions of the tire, respectively. The spoke with 7.5 mm and a 3600 N reaction force was selected to be the initial model, and the total mass of all the spokes was 4.70 kg. The thickness was limited to a range from 4 mm to 10 mm.

4.1. Thickness Optimization in Tire Radial Direction

After 130 generations of iterations, it can in Figure 12 that the maximum thickness is 8.8 mm, and the minimum thickness is 4.0 mm. The thicker regions focus on the middle of the spoke in the tire radial direction. As shown in Figure 13, the reaction force converges to around 3600 N, and the mass of the spoke is reduced by 9%. The final total mass of all the spokes is 4.28 kg.

4.2. Thickness Optimization in Tire-Width Direction

As shown in Figure 14, the thicker regions are located in the middle and at both sides of the spoke in the direction of the tire width. It can be seen that the maximum thickness is 10 mm, and the minimum thickness is 4.0 mm.

Figure 15 shows that the optimized iterations for the spoke thickness are in the direction of the tire width. After 300 optimization calculations, the mass of the spoke was reduced by only 2% with the force = 3600 N constraint.

4.3. Experimental Validation for Optimized Spoke

The spoke with the variable thickness of the tire radial direction was selected and applied to the test. From Figure 16, it can be seen that the deformation of the spoke was consistent in both the test and simulation. For the same displacement constraint, the radial forces for the test and simulation had good consistency.

5. Conclusions

In this paper, we propose an optimization algorithm for the thickness distribution in the hyperelasticity problem with the force constraint. In Section 2, we establish the functional relationship between the thickness design variables and the target, and we present the thickness-sensitivity analysis. The thickness-sensitivity-constraint method and sensitivity-filtering method are proposed to ensure manufacturability. Section 3 describes how the FE model of the tire was built and validated with the radial-stiffness test. In Section 4, the proposed optimization method is adopted in the tire-mass-minimization problem. The optimized results show that the spoke with variable thicknesses in the tire radial direction can reduced the weight by 9% and met the radial-stiffness requirements. The spoke with variable thicknesses in the tire-width direction reduced the weight by 2% and met the radial-stiffness requirements. Then, the optimized tire was manufactured, and the stiffness test was carried out. The simulation results of the test and optimization are consistent. In summary, the thickness-optimization method that we propose can effectively realize lightweight NPTs.

Through the joint operation of MATLAB and ABAQUS, we realized the lightweight design of variable-thickness spokes of NPTs. At present, this method has certain limitations. It can only reduce the discontinuity of the thickness of the adjacent elements by increasing the number of thickness design variables and filtering. However, the discontinuity of the thickness of the adjacent elements has not been eliminated. In planned follow-up work, we intend to establish the relationship between the nodes of the shell element and thickness, and we will take the nodes of the shell element as the carrier of the thickness variable so as to eliminate the thickness discontinuity of the adjacent elements.