Response Surface Method for Optimization of Synchronous Reluctance Motor Rotor
Abstract
:1. Introduction
2. Design Optimization
- Mapping the response surface (display) in a specific interest area. This gives the designer understanding of what is expected as a result of changes in the parameters of the system or process. For this purpose, different graphical displays are applied: 3D surfaces and counter plots. The problem is that in the case of a larger number of input factors, it is only possible to create section graphics, i.e., record some factors with constant values, and view the other two factors graphically.
- Optimization of the response. Optimization using computer programs is usually not difficult for approximated models. If there is more than one optimization criterion, Pareto ideology or method weighted criteria can be applied. However, optimal result validation is always required. In addition, it may appear that the approximated model has a major error, and its optimum is not applicable to the physical model. Then the whole RSM process must be repeated, adding experimental tests and other regression functions.
- Change product or process parameters to adjust to standard specifications or customer requirements. The main problem of the response surface problem is the number of responses that should be analyzed simultaneously. If a client has determined a certain concentration in its project, the designer must reach this level at a minimum cost.
- Today, the Response Surface Methodology has evolved into a Metamodeling Methodology but is often also referred to as the Response Surface Method. The most significant development of RSM began with the onset of numerical experiments. There are mathematical models for numerical experiments often the Finite Elements (FE) model is applied. In this model, it is possible to calculate responses at the given input parameter values. However, the relationship between input factors and responses is not analytically describable. Numerical experiments and approximations are carried out to obtain an understandable mathematical model. These approximations are the exact approximation of the FE model, which is referred to as a metamodel or surrogate model [10].
- Aim and objective;
- Factors and range;
- Plan of numerical experiment;
- Modelling of experiment;
- Synthesis of metamodel;
- Verify prediction.
3. Design of the Experiment
4. Experimental Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A


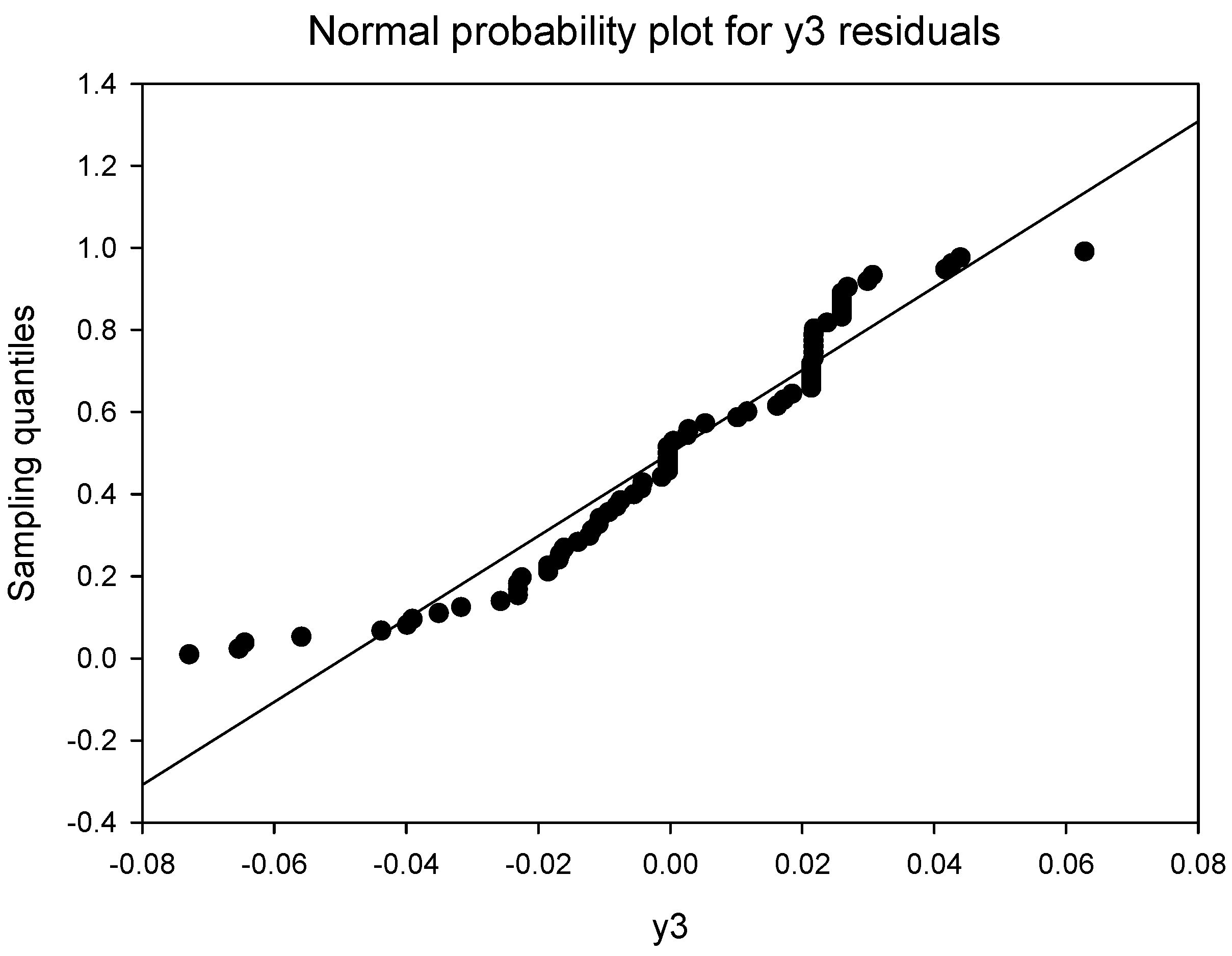
References
- Orlova, S.; Pugachov, V.; Auzins, J.; Rassolkin, A. Metamodel-based Optimization of Synchronous Reluctance Motor Rotor. In Proceedings of the 2021 28th International Workshop on Electric Drives: Improving Reliability of Electric Drives (IWED), Moscow, Russia, 27–29 January 2021. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2016. 2016. Available online: https://www.iea.org/newsroom/news/2016/november/world-energy-outlook-2016.html (accessed on 12 April 2022).
- Waide, P.; Brunner, C.U. Energy-Efficiency Policy Opportunities for Electric Motor Driven Systems; International Energy Agency: Paris, France, 2011; Available online: http://en.pgnig.pl/documents/18252/382674/EE_for_Electric_Systems.pdf (accessed on 12 April 2022).
- Dmitrievskii, V.; Prakht, V.; Kazakbaev, V.; Oshurbekov, S. Optimum Design of IE5 Energy-Efficiency Class Synchronous Reluctance Motor. In Proceedings of the 2019 20th International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 23–26 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- IEC 60034-30-1:2014; IEC 60034-30-1 Standard on Efficiency Classes for Low Voltage AC Motors. International Electrotechnical Commission: Geneva, Switzerland, 2014. Available online: https://library.e.abb.com/public/db64d153e3c346938e18916e66fb1d0d/9AKK107319%20EN%2005-2018_20848_ABB_Technical_note_IEC_60034_30_1.pdf (accessed on 7 August 2020).
- EU Ecodesign Regulation for Motors and Drives. Available online: https://library.e.abb.com/public/70f0664c6ece4f608bdb976019cf87c0/ABB_ecodesign_brochure_9AKK108373_EN052021_WEB.pdf?x-sign=kJQSFZnTJxSs3El6tbYqAklyX3cSMakevZOb8eawItxjk6yHRE5HHuiVFVaZx (accessed on 12 April 2022).
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Moghaddam, R.R. Synchronous Reluctance Machine (SynRM) Design. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2007; pp. 1–103. [Google Scholar]
- Orlova, S.; Pugachov, V.; Rassnlkin, A.; Kallaste, A.; Vaimann, T. Design of rotors for synchronous reluctance motor: Analytical treatment and optimization. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications, EPE 2019 ECCE Europe, Genova, Italy, 3–5 September 2019. [Google Scholar] [CrossRef]
- Auzins, J.; Janushevskis, A.; Janushevskis, J.; Skukis, E. Software EDAOpt for experimental design, analysis and multiobjective robust optimization. In Proceedings of the OPT-i 2014—1st International Conference on Engineering and Applied Sciences Optimization, Island, Greece, 4–6 June 2014; pp. 1055–1077, ISBN 978-960-99994-5-8. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments: Response Surface Method and Designs; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Khuri, A.I.; Cornell, J.A. Response Surfaces, 2nd ed.; Marcel Dekker: New York, NY, USA, 1996. [Google Scholar]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments, 2nd ed.; Springer: New York, NY, USA, 2018; Springer Series in Statistics. [Google Scholar]
- Bursztyn, D.; Steinberg, D.M. Comparison of Designs for Computer Experiments. J. Stat. Plan. Inference 2016, 136, 1103–1119. [Google Scholar] [CrossRef]
- Pánek, D.; Orosz, T.; Karban, P. Artap: Robust Design Optimization Framework for Motorering Applications. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakech, Morocco, 28–30 October 2019. [Google Scholar]
- Dirba, J.; Lavrinovicha, L.; Dobriyan, R. Prospects for use of synchronous reluctance motors in low-power electrical devices. Latv. J. Phys. Tech. Sci. 2015, 52, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Lavrinovicha, L.; Dirba, J.; Sejejs, K.; Kamolins, E. Synthesis of Electronically Commutated Synchronous Motors with Predefined Characteristics. Latv. J. Phys. Tech. Sci. 2019, 56, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Kamolins, E.; Gorobecs, M.; Burenin, V.; Zarembo, J.; Sejejs, K. 180 kW Synchronous Reluctance Motor for Mass Transit Electrical Traction Application. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications, EPE 2021 ECCE Europe, Ghent, Belgium, 6–10 September 2021; ISBN 978-907581537-5. [Google Scholar]
- Gulbis, K.; Brakanskis, U.; Kamolins, E.; Zarembo, J. Parameter Calculation Method of Synchronous Reluctance Motor including Cross Magnetic Saturation. In Proceedings of the 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 5–7 November 2020. [Google Scholar] [CrossRef]
- Berrar, D. Cross-validation. Encycl. Bioinform. Comput. Biol. 2019, 1, 542–545. [Google Scholar] [CrossRef]
- Allen, D.M. The Relationship between Variable Selection and Data Agumentation and a Method for Prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Stone, M. An Asymptotic Equivalence of Choice of Model by Cross-Validation and Akaike’s Criterion. J. R. Stat. Soc. Ser. B 1977, 39, 44–47. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Bradley, N. Response surface methodology. Nippon. Shokuhin Kagaku Kogaku Kaishi 2013, 60, 728–729. [Google Scholar] [CrossRef]
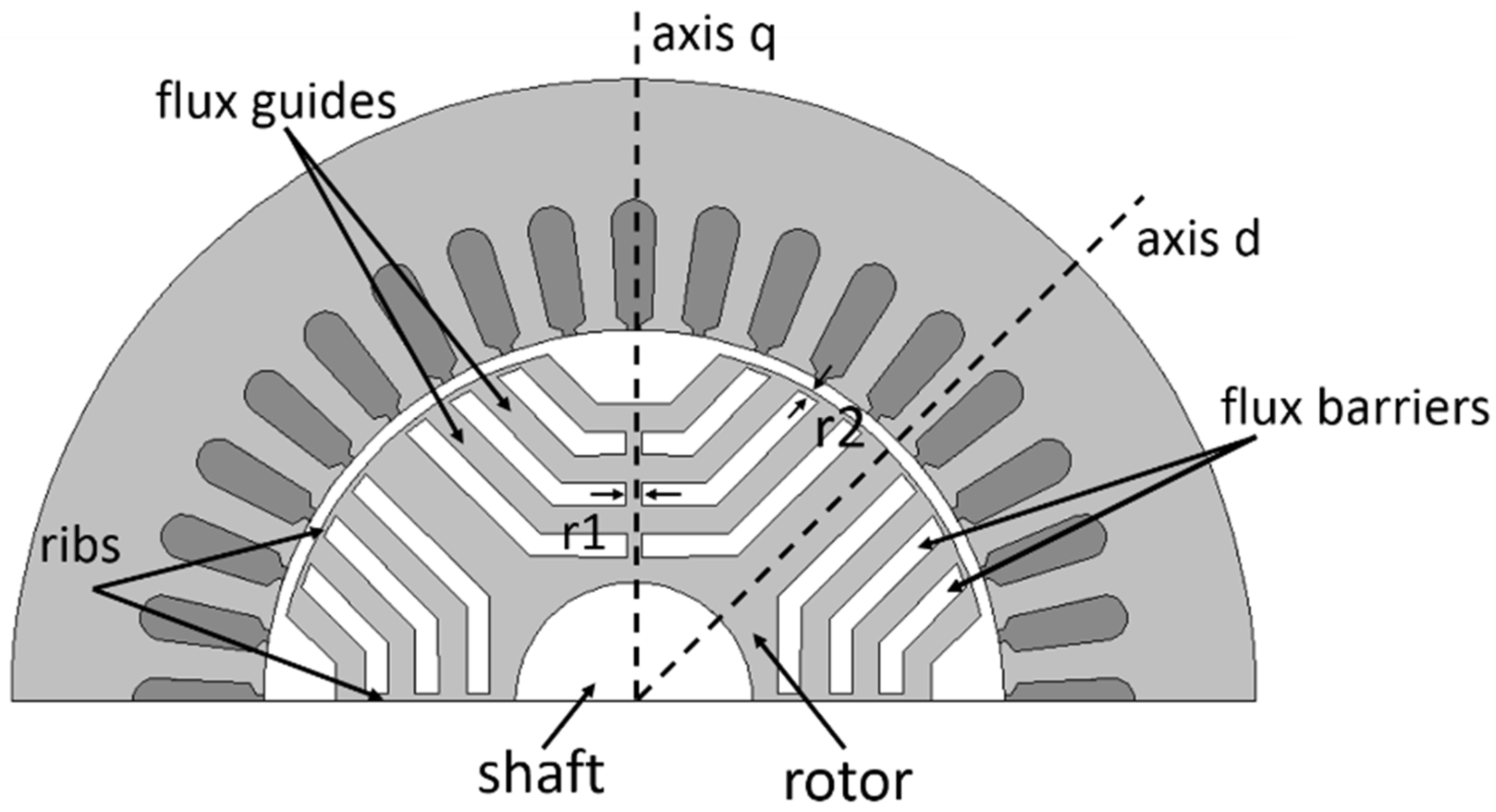
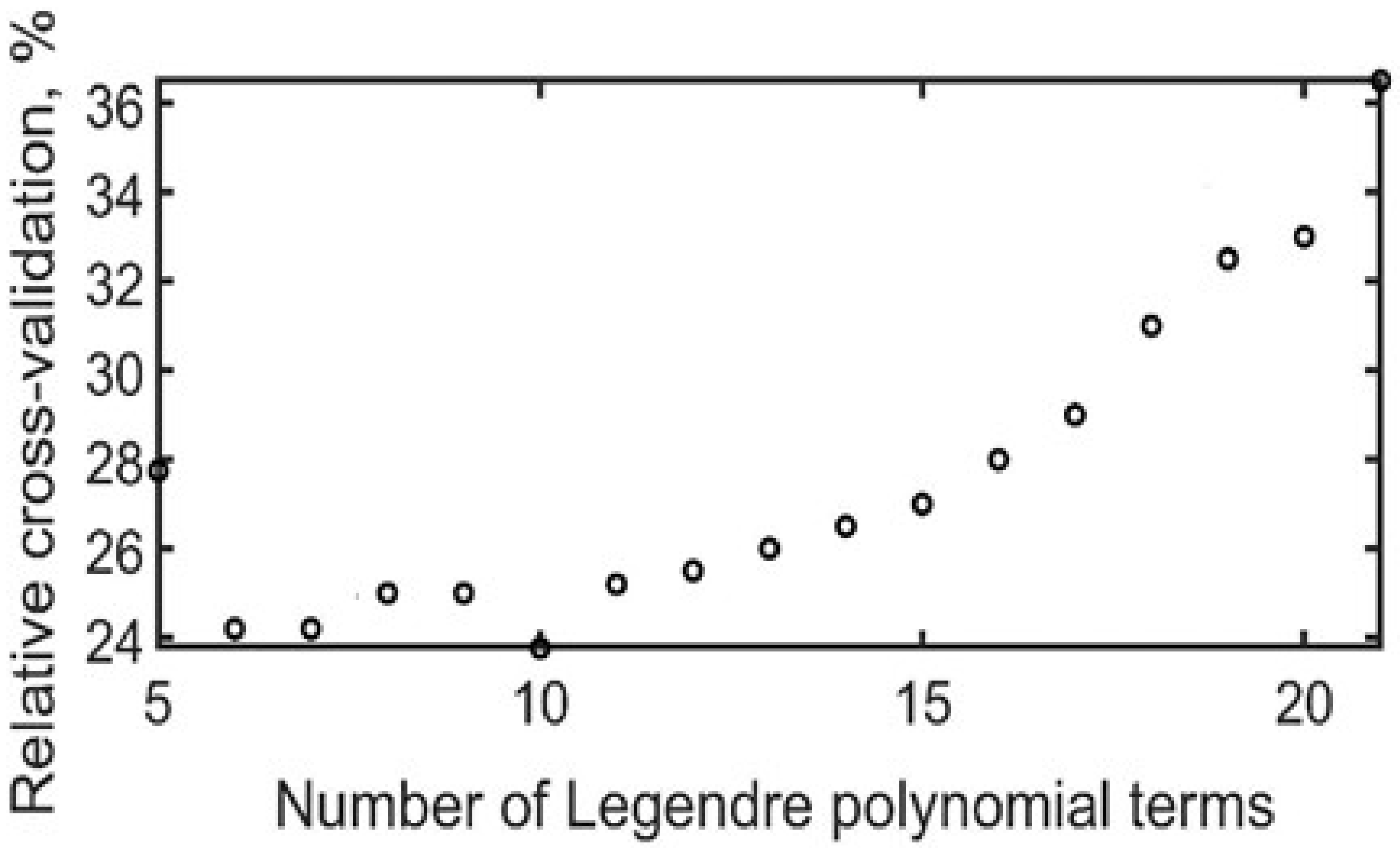


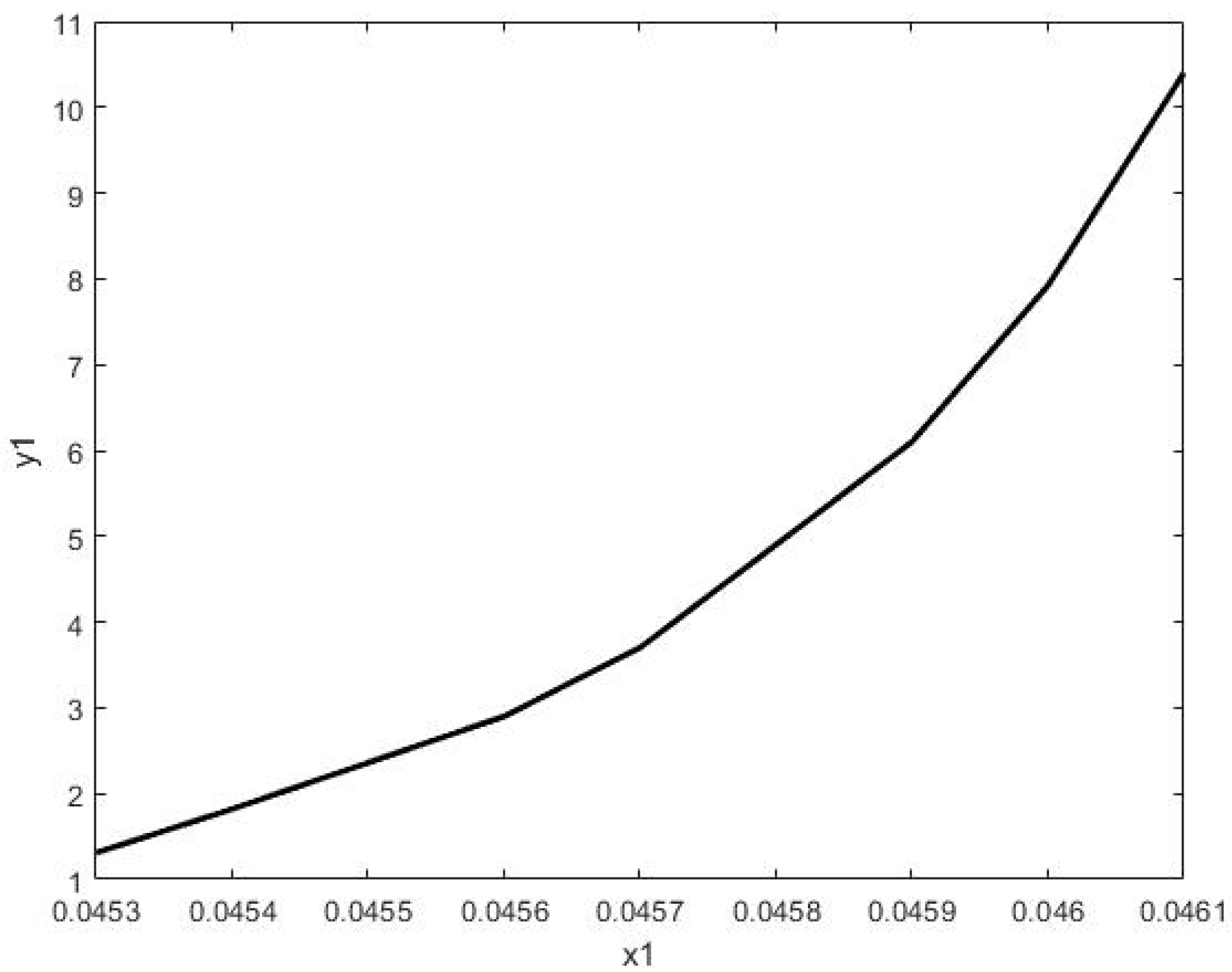




 | Parameters | Value |
| Number of slots | 36 | |
| Outer diameter | 139 mm | |
| Inner diameter | 92.7 mm | |
| Stack length | 110 mm | |
| Number of turns | 47 | |
| Number of parallel paths | 2 | |
| Coil pitch | 1–8 | |
| Filling factor | 69.48% | |
| Wire diameter | 0.56 mm |
| Variables | Unit | Limits | |
|---|---|---|---|
| Rotor outer radius | mm | 45.25 < < 46.05 | |
| Radial rib | mm | 1 < < 3 | |
| Tangential rib | mm | 1 < < 3 | |
| Insulation ratio | - | 0.2 < < 1.2 | |
| Number of barriers | - | 1 < < 5 |
| Variables | Unit | Aim | |
|---|---|---|---|
| Torque | Nm | Maximize | |
| Specific torque | Nm/kg | Maximize | |
| Efficiency | % | Maximize |
| Criterion | −10.443548 | −3.5202343 | −0.95434034 |
| 0.0461 | 0.0461 | 0.0461 | |
| 0.001 | 0.001 | 0.001 | |
| 0.001 | 0.001 | 0.001 | |
| 0.69776964 | 1.2 | 0.33468864 | |
| 1 | 1 | 5 | |
| 10.443548 | 9.7631095 | 9.4437398 | |
| 3.0903761 | 3.5202343 | 2.527117 | |
| 0.86956646 | 0.80096256 | 0.95687512 |
| Voltage (V) | 220 | 290 | 340 | 385 |
| Phase current (A) | 1.33 | 1.33 | 1.33 | 1.33 |
| Speed (rpm) | 750 | 1050 | 1347 | 1500 |
| Voltage (V) | 380 | 380 | 380 | 380 | 380 | 380 |
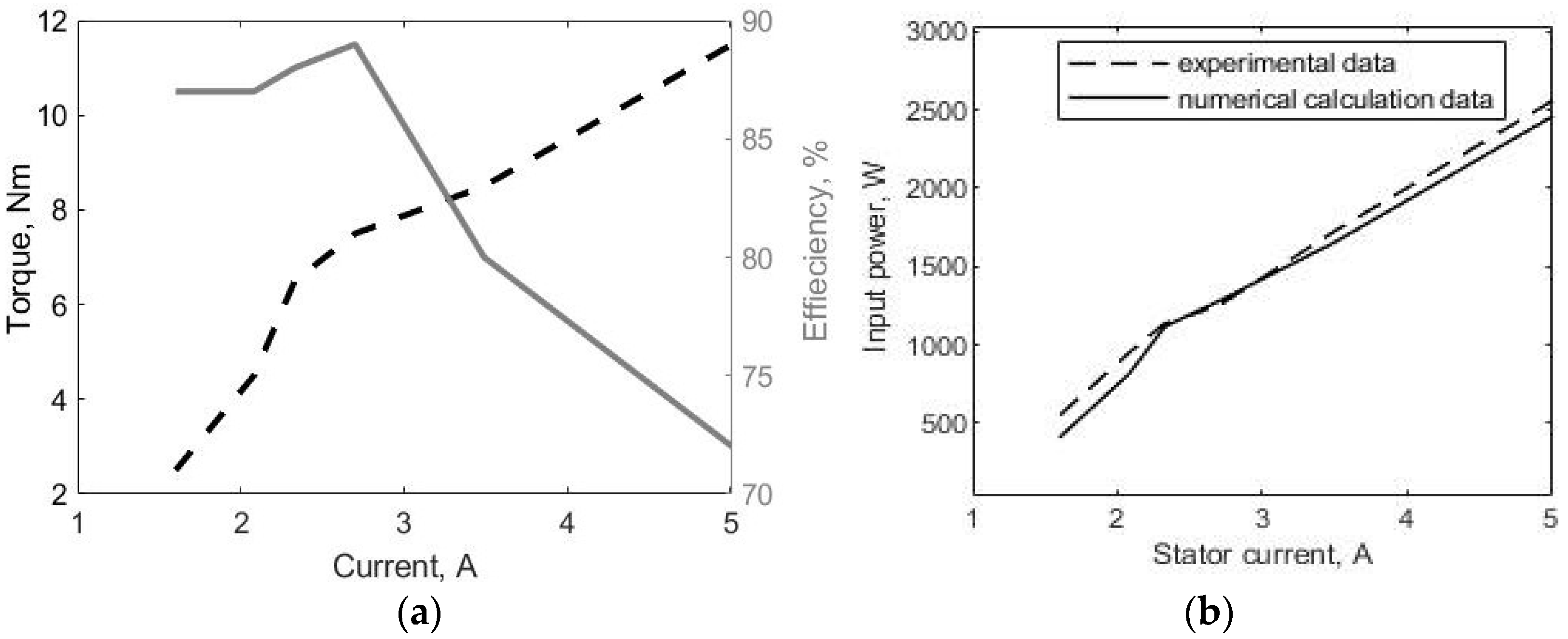
| Phase current (A) | 1.6 | 2.08 | 2.33 | 2.7 | 3.49 | 5.01 |
| Input power (W) | 410 | 814 | 1118 | 1280 | 1650 | 2460 |
| Torque (Nm) | 2.5 | 4.5 | 6.5 | 7.5 | 8.5 | 11.5 |
| Output power (W) | 368 | 670 | 988 | 1140 | 1319 | 1770 |
| Efficiency | 87 | 87 | 88 | 89 | 80 | 72 |
| Speed (rpm) | 1500 | 1500 | 1500 | 1500 | 1500 | 1500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orlova, S.; Auzins, J.; Pugachov, V.; Rassõlkin, A.; Vaimann, T. Response Surface Method for Optimization of Synchronous Reluctance Motor Rotor. Machines 2022, 10, 897. https://doi.org/10.3390/machines10100897
Orlova S, Auzins J, Pugachov V, Rassõlkin A, Vaimann T. Response Surface Method for Optimization of Synchronous Reluctance Motor Rotor. Machines. 2022; 10(10):897. https://doi.org/10.3390/machines10100897
Chicago/Turabian StyleOrlova, Svetlana, Janis Auzins, Vladislav Pugachov, Anton Rassõlkin, and Toomas Vaimann. 2022. "Response Surface Method for Optimization of Synchronous Reluctance Motor Rotor" Machines 10, no. 10: 897. https://doi.org/10.3390/machines10100897
APA StyleOrlova, S., Auzins, J., Pugachov, V., Rassõlkin, A., & Vaimann, T. (2022). Response Surface Method for Optimization of Synchronous Reluctance Motor Rotor. Machines, 10(10), 897. https://doi.org/10.3390/machines10100897









