Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results
Abstract
:1. Introduction
- A side branch stub introduced to correct the acoustic field within the looped-tube engine altered by the installation of a linear alternator [16].
- A side-branched Helmholtz resonator to control and tune the phase angle between the velocity and pressure amplitude in looped-tube traveling-wave thermoacoustic engine [17].
- A compliance and an inertance tube are proposed as the phase adjustor to control the acoustic field in a looped-type thermoacoustic engine [18].
- The introduction of a phase modulation object (ellipse) at the acoustic power output port to adjust the acoustic field distribution and improve impedance matching [19].
- An in-line piston located inside the main resonator introduced in order to optimise the acoustic field from any disturbances [20].
- A compliance serves as a tuner for the phase difference between the volume flow rate and the pressure oscillation in the core section of a closed-loop system [21].
2. Demonstrator Computational Model
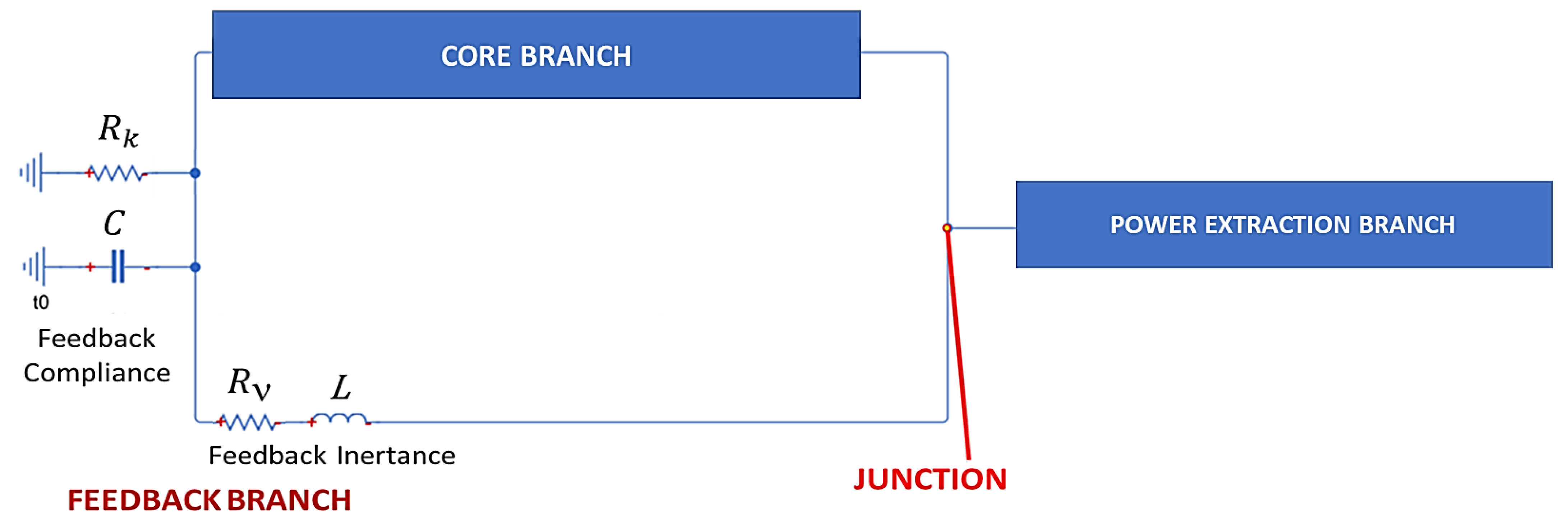
Energetic Analysis Based on the RAP Methodology
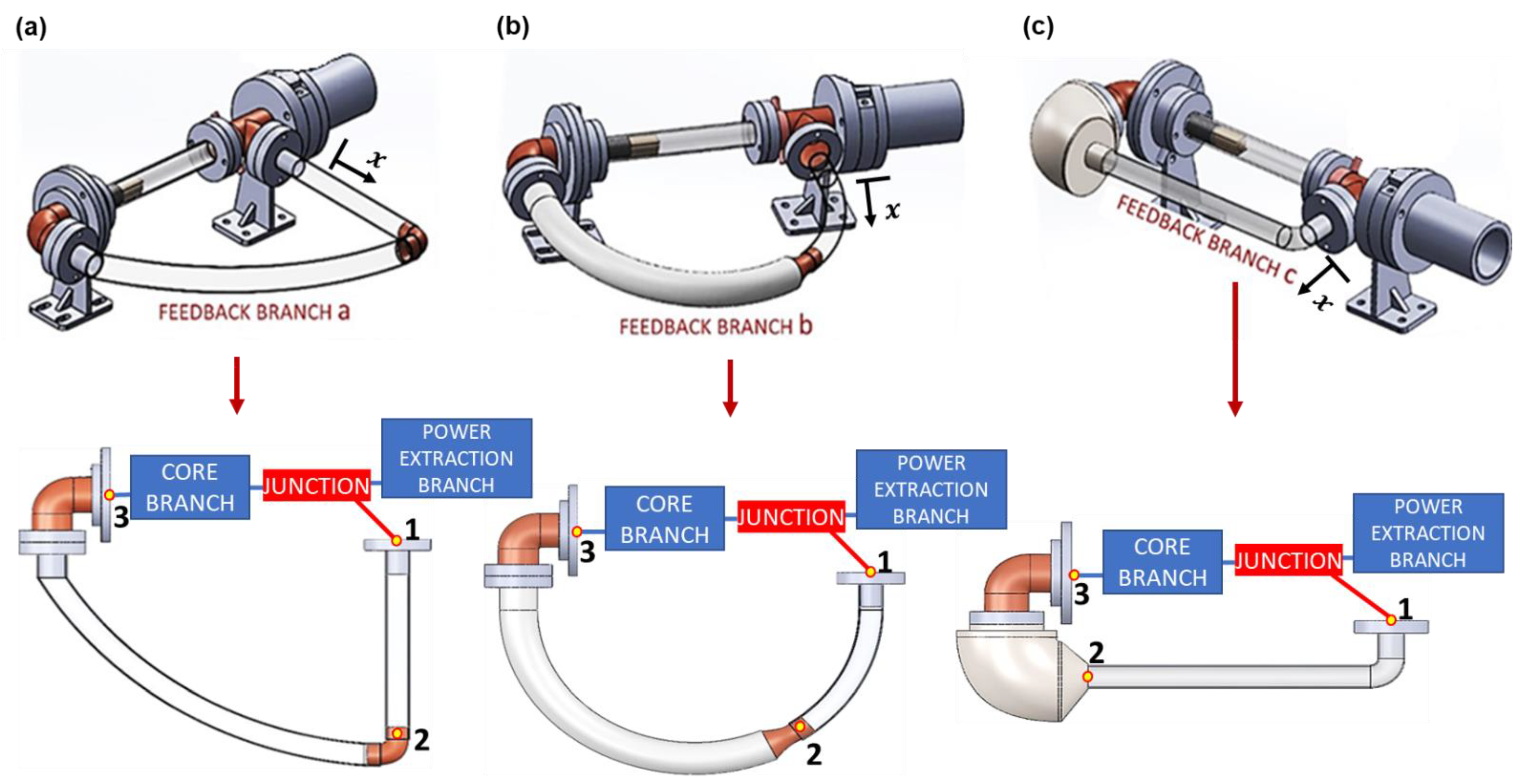
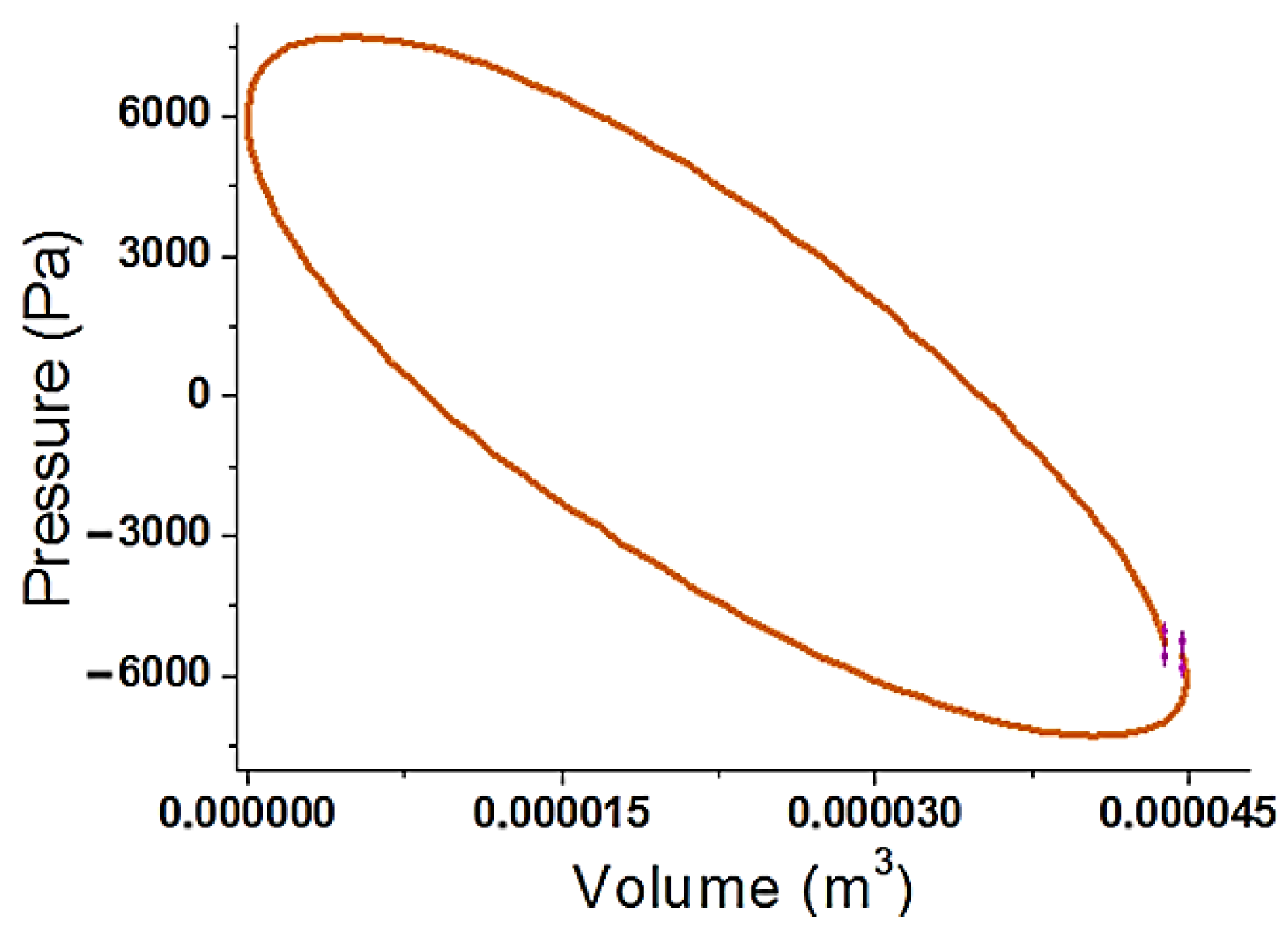
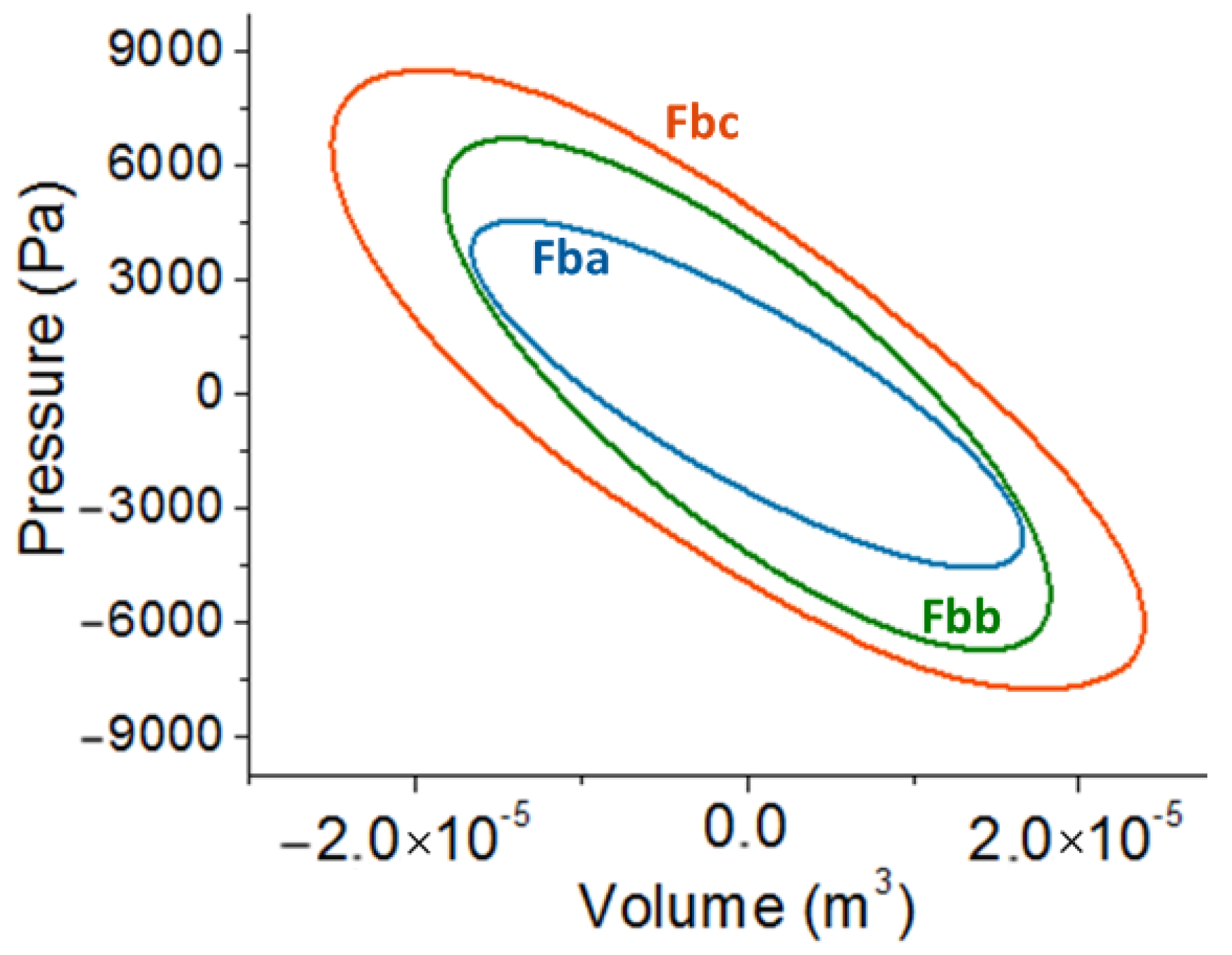
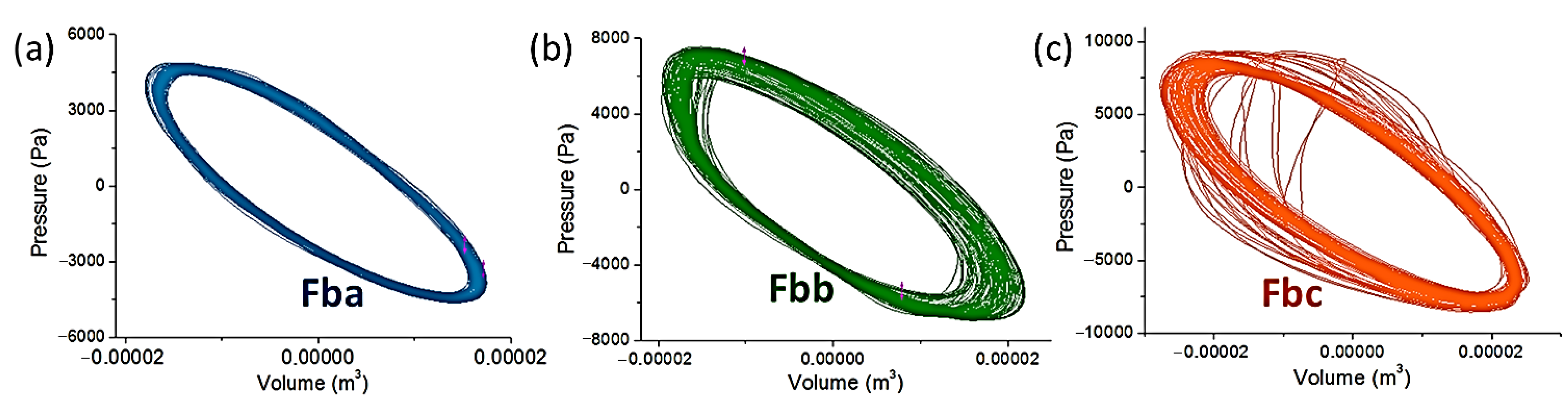
- Reference model “Fba” for the feedback design, shown in Figure 2a: DeltaEC multi-parametric fitting method satisfies a variety of mixed boundary conditions and allows the user choosing which variables are calculated as outputs. Therefore, active and reactive acoustic power are numerically calculated at any particular location of the engine.
- Modified model “Fbb”, shown in Figure 2b: by increasing the compliance inner diameter to 25 mm and shortening its length to 33 cm. The procedure is the same, and DeltaEC calculates the active and reactive acoustic power along with the rest of the parameters indicated for “Fba”.
- Modified model “Fbc”, shown in Figure 2c: by increasing again the compliance inner diameter to 63 mm and shortening its length to 12 cm; alike the previous two models, DeltaEC provides again the new active and reactive acoustic power, along with the rest of the parameters indicated above.
3. Laboratory Demonstrator
3.1. Apparatus Assembly
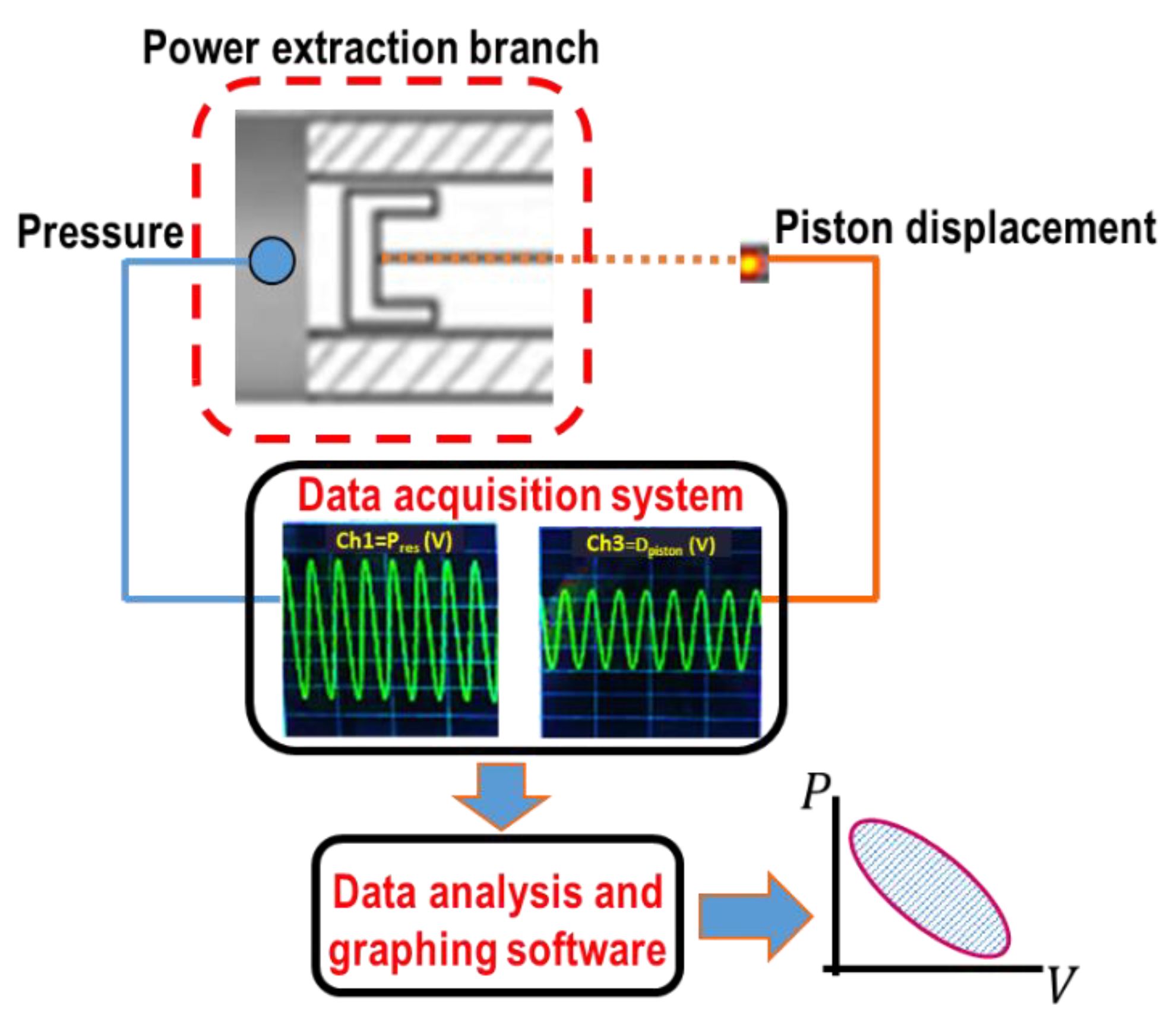
3.2. Power Extraction Branch Measurements
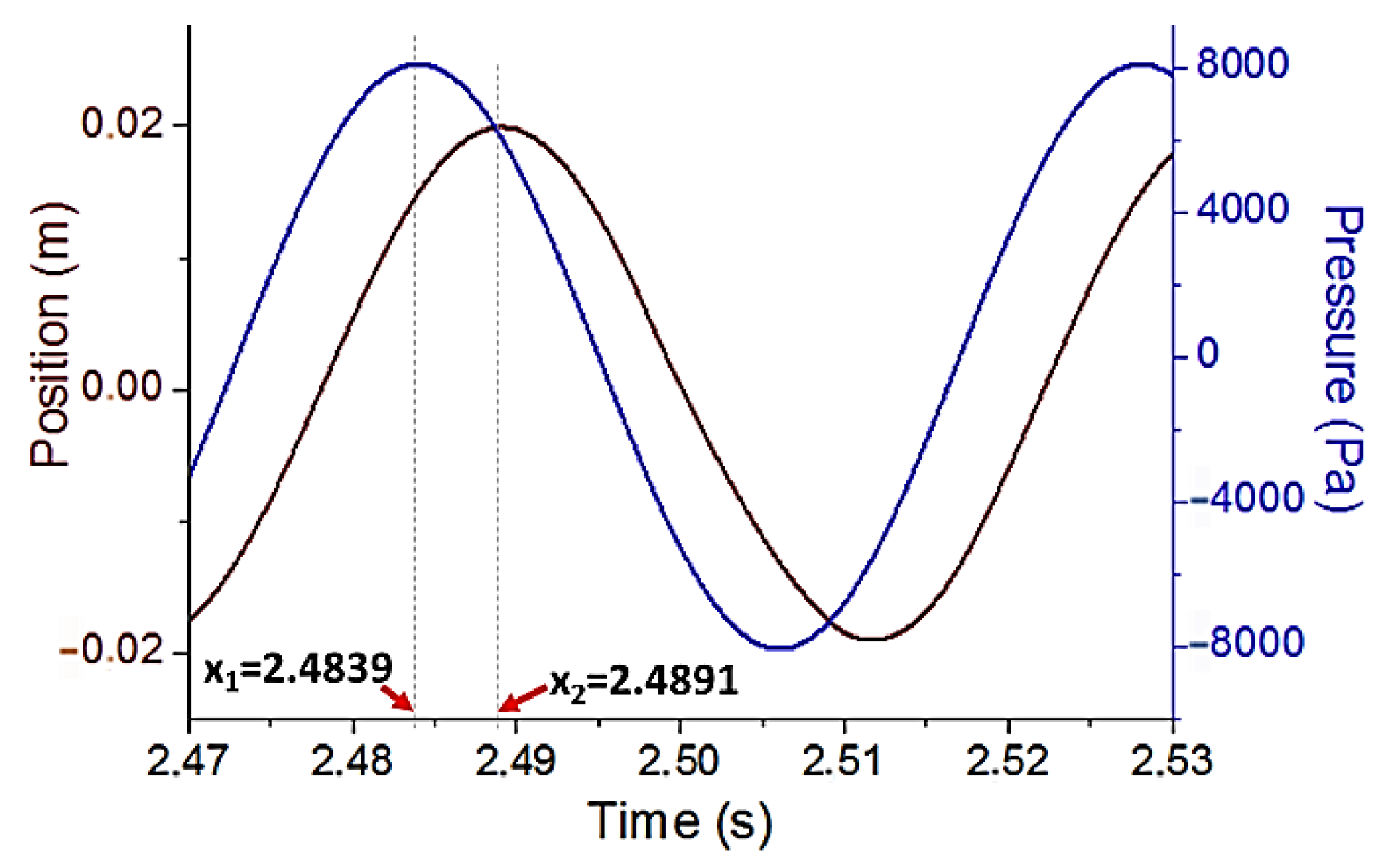
4. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernández-Yáñez, P.; Gómez, A.; García-Contreras, R.; Armas, O. Evaluating thermoelectric modules in diesel exhaust systems: Potential under urban and extra-urban driving conditions. J. Clean. Prod. 2018, 182, 1070–1079. [Google Scholar] [CrossRef]
- Ezzitouni, S.; Fernández-Yáñez, P.; Sánchez, L.; Armas, O. Global energy balance in a diesel engine with a thermoelectric generator. Appl. Energy 2020, 269, 115139. [Google Scholar] [CrossRef]
- Sharif, P.M.; Hairuddin, A.A.; As’arry, A.; Rezali, K.A.M.; Noor, M.M.; Norhafana, M.; Mossa, M.A.A.; Shareef, S.M. Shareef International Regulation of Vehicle Emissions Control Rules and Its Influence on Academic Engine Development Experimental Study and Vehicle Manufacturing. In Proceedings of the 1st International Postgraduate Conference on Mechanical Engineering, Pahang, Malaysia, 31 October 2018; pp. 1–15. [Google Scholar]
- Kölsch, B.; Radulovic, J. Utilisation of diesel engine waste heat by Organic Rankine Cycle. Appl. Therm. Eng. 2015, 78, 437–448. [Google Scholar] [CrossRef] [Green Version]
- Aghaali, H.; Angstrom, H.-E. Demonstration of Air-Fuel Ratio Role in One-Stage Turbocompound Diesel Engines. In Proceedings of the SAE/KSAE 2013 International Powertrains, Fuels & Lubricants Meeting, Seoul, Korea, 21–23 October 2013. Technical Paper 2013-01-2703. [Google Scholar]
- Liu, X.; Li, C.; Deng, Y.; Su, C. An energy-harvesting system using thermoelectric power generation for automotive application. Int. J. Electr. Power Energy Syst. 2015, 67, 510–516. [Google Scholar] [CrossRef]
- Zhou, J.; Karlsson, M.; Abom, M. Study of Thermoacoustic Engine for Automotive Exhaust Waste Heat Recovery. SAE Tech. Paper 2019, 2019-01-1257, 1–13. [Google Scholar] [CrossRef]
- Fernández-Yáñez, P.; Armas, O.; Kiwan, R.; Stefanopoulou, A.; Boehman, A. A thermoelectric generator in exhaust systems of spark-ignition and compression-ignition engines. A comparison with an electric turbo-generator. Appl. Energy 2018, 229, 80–87. [Google Scholar] [CrossRef]
- Nader, W.B.; Chamoun, J.; Dumand, C. Optimization of the thermodynamic configurations of a thermoacoustic engine auxiliary power unit for range extended hybrid electric vehicles. Energy 2020, 195, 116952. [Google Scholar] [CrossRef]
- Ceperley, P.H. A pistonless Stirling engine—The traveling wave heat engine. J. Acoust. Soc. Am. 1979, 66, 1508–1513. [Google Scholar] [CrossRef]
- Backhaus, S.; Swift, G.W. A thermoacoustic Stirling heat engine. Nature 1999, 399, 335–338. [Google Scholar] [CrossRef]
- Sugita, H.; Matsubara, Y.; Kushino, A.; Ohnishi, T.; Kobayashi, H.; Dai, W. Experimental study on thermally actuated pressure wave generator for space cryocooler. Cryogenics 2004, 44, 431–437. [Google Scholar] [CrossRef]
- Iniesta, C.; Olazagoitia, J.L.; Vinolas, J.; Aranceta, J. Review of travelling-wave thermoacoustic electric-generator technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 940–957. [Google Scholar] [CrossRef]
- Ward, B.; Clark, J.; Swift, G. Design Environment for Low-Amplitude Thermoacoustic Energy Conversion DeltaEC Version 6.4b2.7. Users Guide; Los Alamos National Laboratory: Los Alamos, NM, USA, 2017. [Google Scholar]
- Swift, G.W. Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, 2nd ed.; ASA Press/Springer: Cham, Switzerland, 2017; ISBN 978-3-319-66932-8. [Google Scholar]
- Jaworski, A.J.; Mao, X. Development of thermoacoustic devices for power generation and refrigeration. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Al-Kayiem, A.; Yu, Z. Using Side-Branched Helmholtz Resonator to Tuna Phase in Looped-Tube Travelling Wave Thermoacoustic Engine. In Proceedings of the Conference on Thermal Energy Systems: Production, Storage, Utilization and the Environment, Napoli, Italy, 17–20 May 2015; pp. 1–7. [Google Scholar]
- Jin, T.; Yang, R.; Wang, Y.; Liu, Y.; Feng, Y. Phase adjustment analysis and performance of a looped thermoacoustic prime mover with compliance/resistance tube. Appl. Energy 2016, 183, 290–298. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Li, Q. A novel method for improving the performance of thermoacoustic electric generator without resonator. Energy Convers. Manag. 2016, 110, 135–141. [Google Scholar] [CrossRef]
- Dhuchakallaya, I.; Saechan, P. The effect of phase-adjuster on the performance of a thermoacoustic Stirling heat engine. Therm. Sci. Eng. Prog. 2020, 20, 100665. [Google Scholar] [CrossRef]
- Tavakolpour-Saleh, A.; Zare, S. Justifying performance of thermo-acoustic Stirling engines based on a novel lumped mechanical model. Energy 2021, 227, 120466. [Google Scholar] [CrossRef]
- Iniesta, C.; Olazagoitia, J.L.; Vinolas, J.; Gros, J. New method to analyse and optimise thermoacoustic power generators for the recovery of residual energy. Alex. Eng. J. 2020, 59, 3907–3917. [Google Scholar] [CrossRef]
- Kruse, A.; Ruziewicz, A.; Nemś, A.; Tajmar, M. Numerical analysis of competing methods for acoustic field adjustment in a looped-tube thermoacoustic engine with a single stage. Energy Convers. Manag. 2019, 181, 26–35. [Google Scholar] [CrossRef]
- Hu, Z.J.; Li, Z.Y.; Li, Q. Evaluation of thermal efficiency and energy conversion of thermoacoustic Stirling engines. Energy Convers. Manag. 2010, 51, 802–812. [Google Scholar] [CrossRef]
- Wheatley, J.C.; Swift, G.W.; Migliori, A. Method of Measuring Reactive Acoustic Power Density in a Fluid. U.S. Patent 4538464, 3 September 1985. [Google Scholar]
- Jin, T.; Zhang, B.S.; Zhong, X.M.; Chen, G.B. Preliminary Study on Circuit Simulation of Thermo Acoustic Engines. In Proceedings of the AIP Conference Proceedings, AIP, Keystone, CO, USA, 29 August–2 September 2005; Volume 823, pp. 1103–1108. [Google Scholar]


| Parameter | Value |
|---|---|
| Operating frequency (f) | 22.7 Hz |
| Mean pressure (Pm) | Pa |
| Thermal input power () | 40 W |
| Hot air temperature ) | 429 °C |
| Cold air temperature ) | 30 °C |
| Calculated Parameters | “Fba” | “Fbb” | “Fbc” |
|---|---|---|---|
| Reactive acoustic power supplied to the core branch, (VAr) | 1.408 | 1.104 | 0.855 |
| Active acoustic power loss through the feedback branch, (W) | 0.185 | 0.157 | 0.255 |
| Amplification of the active acoustic power through the core branch, (W) | 1.672 | 1.721 | 2.482 |
| Acoustic power delivered to the power extraction branch, (W) | 1.487 | 1.564 | 2.227 |
| Parameters | Values |
|---|---|
| Feedback Branch “a” (“Fba”) | |
| Compliance: Internal diameter (𝐷𝐶𝑎) | 0.02 m |
| Length (𝐿𝐶𝑎) | 0.52 m |
| Volume (𝑉𝐶𝑎) | 163 × 10−5 m3 |
| Inertance: Internal diameter (𝐷𝐿𝑎) | 0.015 m |
| Length (𝐿𝐿𝑎) | 0.18 m |
| Feedback Branch “b” (“Fbb”) | |
| Compliance: Internal diameter (𝐷𝐶𝑏) | 0.025 m |
| Length (𝐿𝐶𝑏) | 0.33 m |
| Volume (𝑉𝐶𝑏) | 13.4 × 10−5 m3 |
| Inertance: Internal diameter (𝐷𝐿𝑏) | 0.015 m |
| Length (𝐿𝐿𝑏) | 0.15 m |
| Feedback Branch “c” (“Fbc”) | |
| Compliance: Internal diameter (𝐷𝐶𝑐) | 0.063 m |
| Length (𝐿𝐶𝑐) | 0.12 m |
| Volume (𝑉𝐶𝑐) | 37.4 × 10−5 m3 |
| Inertance: Internal diameter (𝐷𝐿𝑐) | 0.015 m |
| Length (𝐿𝐿𝑐) | 0.19 m |
| Parameters | Values | |
| Core branch | ||
| Main cooler: | ) | 0.013 m |
| ) | 98% | |
| Regenerator: | ) | 0.025 m |
| ) | 75% | |
| ) | 0.00033 m | |
| Heater: | ) | 0.026 m |
| ) | 91.6% | |
| ) | 40 W | |
| TBT: | ) | 0.085 m |
| ) | 0.00025 m2 | |
| Secondary cooler: | ) | 0.013 m |
| ) | 100% | |
| Parameters | Values |
|---|---|
| Power Extraction Branch | |
| Resonator Cylinder Internal Diameter (𝐷𝑅𝐸𝑆) | 0.04 m |
| Length of the resonator cylinder (𝐿𝑅𝐸𝑆) | 0.085 m |
| Length of the power extraction branch (𝐿𝑃𝐸𝐵) | 0.135 m |
| Piston mass (𝑀𝑝𝑖𝑠𝑡𝑜𝑛) | 0.023 kg |
| Piston length (𝐿𝑝𝑖𝑠𝑡𝑜𝑛) | 0.02 m |
| Acoustic Power Delivered towards the Power Extraction Branch | Simulation Result (W) | Experimental Result (W) | Error (%) |
|---|---|---|---|
| Feedback “Fba” 1.408 (VAr) | 1.49 | 1.37 | 8.8 |
| Feedback “Fbb” 1.104 (VAr) | 1.56 | 1.41 | 10.6 |
| Feedback “Fbc” 0.855 (VAr) | 2.23 | 2.03 | 9.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iniesta, C.; Olazagoitia, J.L.; Vinolas, J.; Gros, J. Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results. Machines 2022, 10, 958. https://doi.org/10.3390/machines10100958
Iniesta C, Olazagoitia JL, Vinolas J, Gros J. Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results. Machines. 2022; 10(10):958. https://doi.org/10.3390/machines10100958
Chicago/Turabian StyleIniesta, Carmen, José Luis Olazagoitia, Jordi Vinolas, and Jaime Gros. 2022. "Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results" Machines 10, no. 10: 958. https://doi.org/10.3390/machines10100958
APA StyleIniesta, C., Olazagoitia, J. L., Vinolas, J., & Gros, J. (2022). Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results. Machines, 10(10), 958. https://doi.org/10.3390/machines10100958









