Acoustic Feature Extraction Method of Rotating Machinery Based on the WPE-LCMV
Abstract
:1. Introduction
- (1)
- In order to more effectively extract fault features in a complex sound field, a multi-channel acoustic signal enhancement method is proposed for rotating machinery based on WPE-LCMV.
- (2)
- The composition and the transmission paths of the rotating machinery acoustic signal are analyzed in detail.
- (3)
- In order to obtain signals with a more obvious impact and a higher correlation with the original signal in different sound fields, the range of kurtosis is selected as the index of parameter selection of the WPE de-reverberation algorithm.
- (4)
- The problem of calculating the incident angle in the LCMV method is solved by using the sound field distribution.
2. Background and Theory
2.1. Acoustic Field Model
2.2. Reverberation Mechanism
2.3. De-Reverberation Principle of the WPE
2.4. Principle of the LCMV
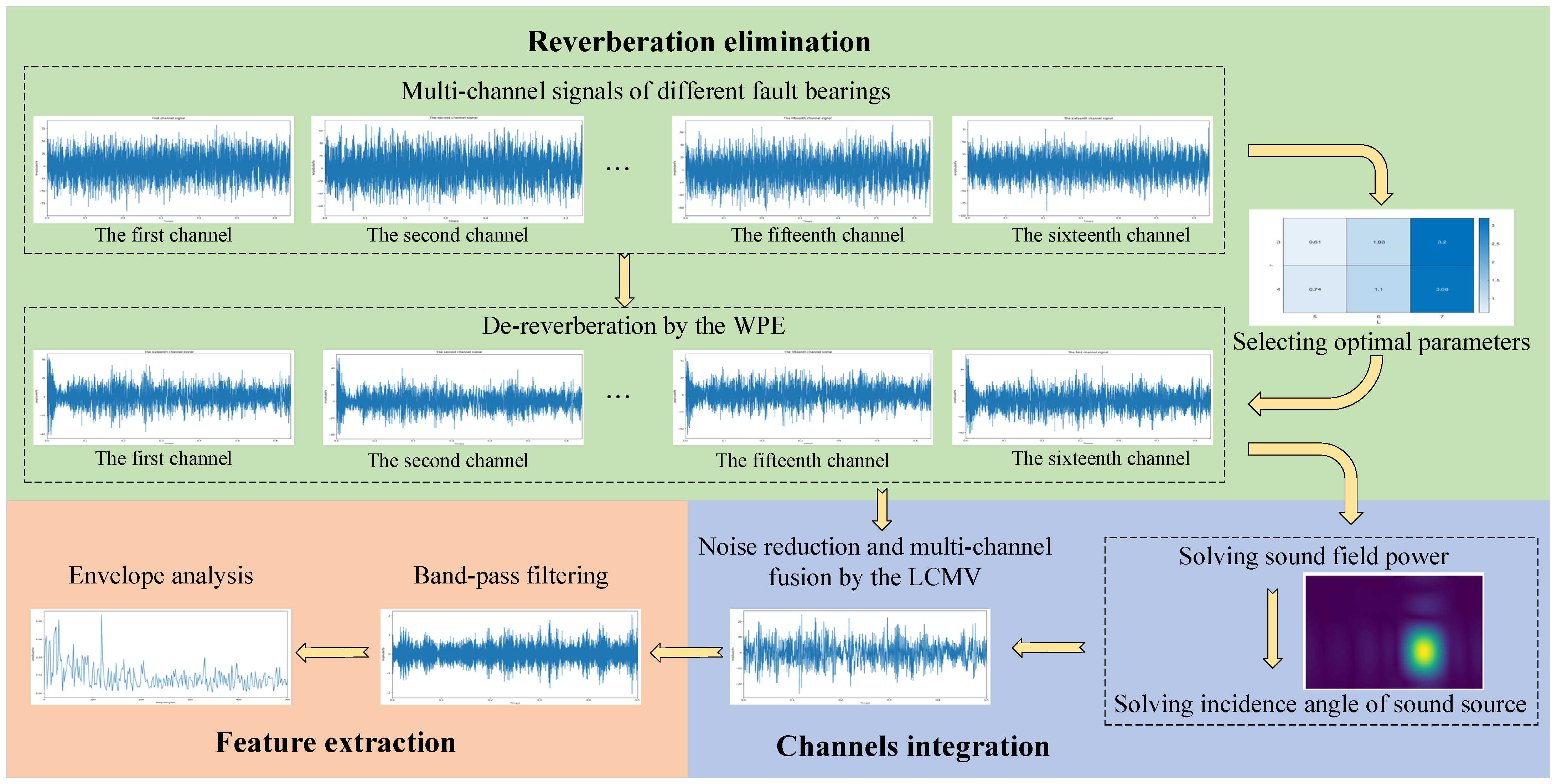
3. Acoustic Fault Feature Extraction Method Based on the WPE-LCMV
- (1)
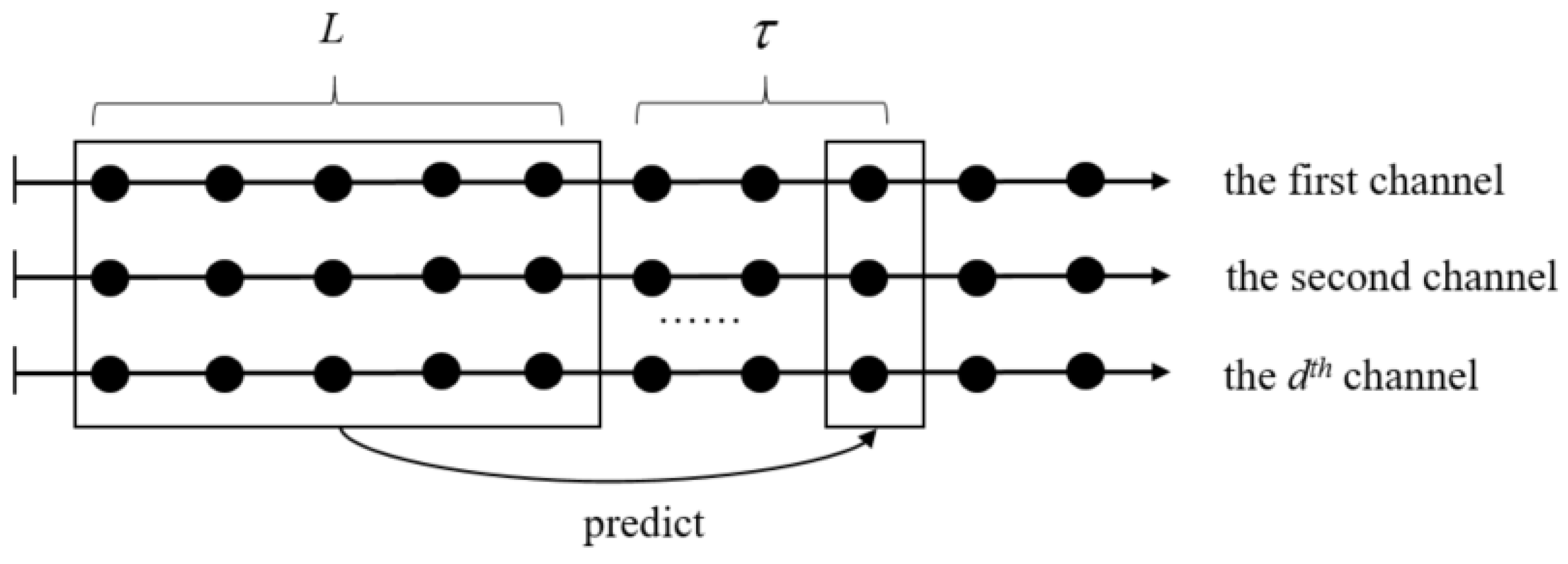
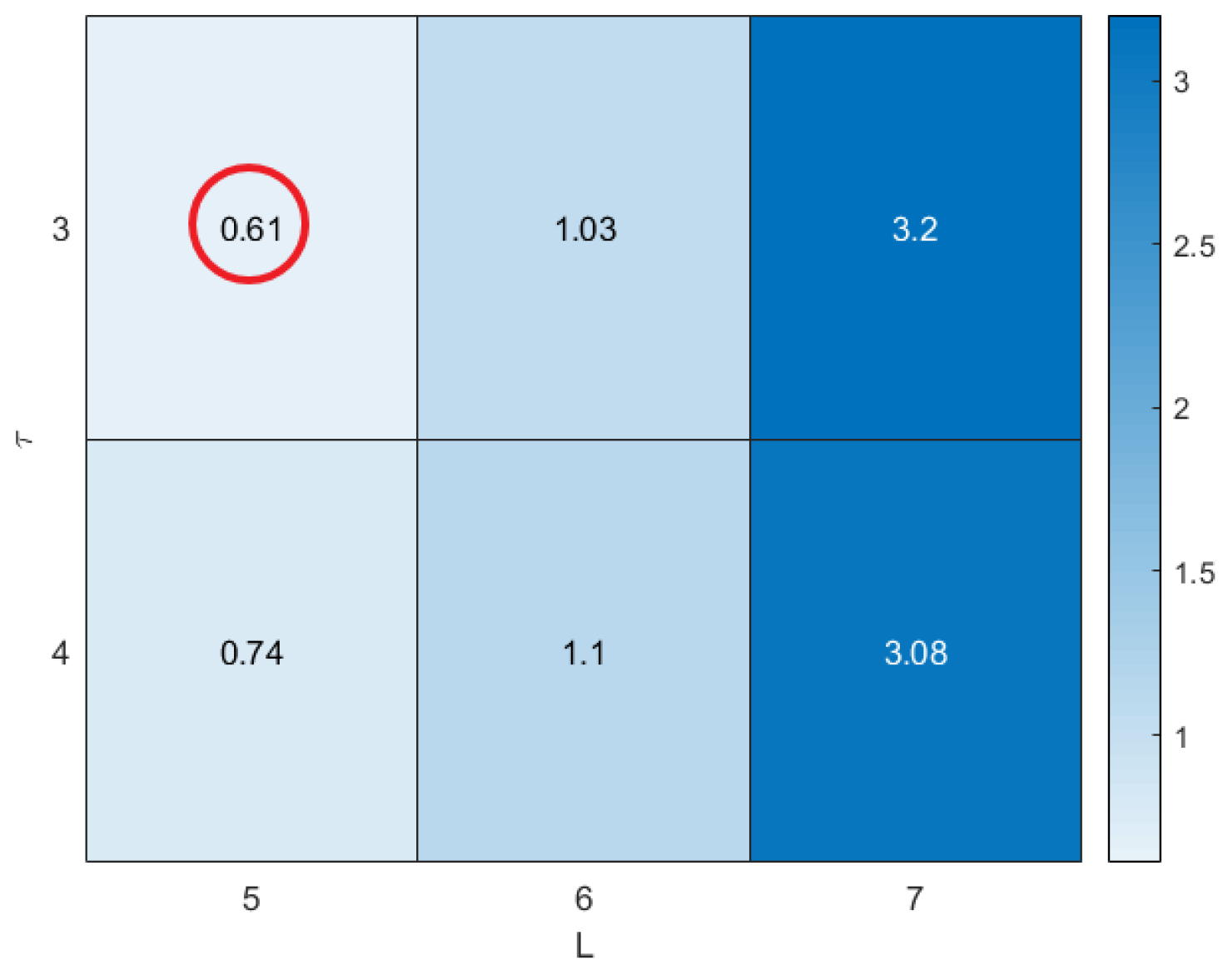
- Reverberation elimination: The delay coefficient and the number of prediction filter taps in the WPE method have a great influence on the de-reverberation effect and the signal correlation. From [31], it is clear that the delay coefficient is usually valued to be equal to 1, 2, 3 or 4 and the number of prediction filter taps is equal to 5, 6, 7, 8, 9 or 10. The delay coefficient is adjusted to separate the previous L frames signal from a frame signal that will forecast the late reverberation. This lowers the continuity between the two signals and prevents the signal from becoming too whitened. When the delay coefficient increases, the de-reverberation effect is enhanced, so it is initially selected as 3 or 4. In addition, more reference information can be obtained by increasing the taps of the prediction filter, so as to predict the late reverberation more effectively and improve the de-reverberation performance. However, beyond a certain range, excessive de-reverberation leads to signal distortion and reduces the signal correlation., where the prediction filter taps are initially selected as 5, 6 or 7. The specific methods for determining the delay coefficient and the prediction filter taps are as follows:
| Algorithm 1. Method: Optimal Selection Process of L and |
| Input: multichannel fault sound signals, multiple sets of L and Processing: repeating the following steps for each set of parameters:
else; abandoning; Return: selecting a set of parameters with the smallest kurtosis range. |
- (2)
- Channels integration: Due to the late reverberation of the delayed frames in prediction by the WPE based on the previous K frames of signals, the de-reverberation effect may be poor the signal of (L + − 1) frames at the beginning of each set of data, in order to reduce the interference with fault feature extraction, the signal of (L + − 1) frames at the beginning of each set of data is discarded when performing channels integration. The scanning range Scanxz is selected according to the size of the rotating equipment. To obtain a higher scanning accuracy, the scanning step is set to 0.01 m.where (x, z) is the coordinates in the scanning plane, (xmin, xmax) is the coordinate range in x direction and (zmin, zmax) is the coordinate range in z direction.
- (3)
- Feature extraction: The faulty features of the rolling bearing are extracted by filtering and envelope analysis of the fused signal to achieve the fault feature extraction of rotating machinery.
4. Experimental Validation
4.1. Experimental Platform and Experimental Design
4.2. Data Analysis
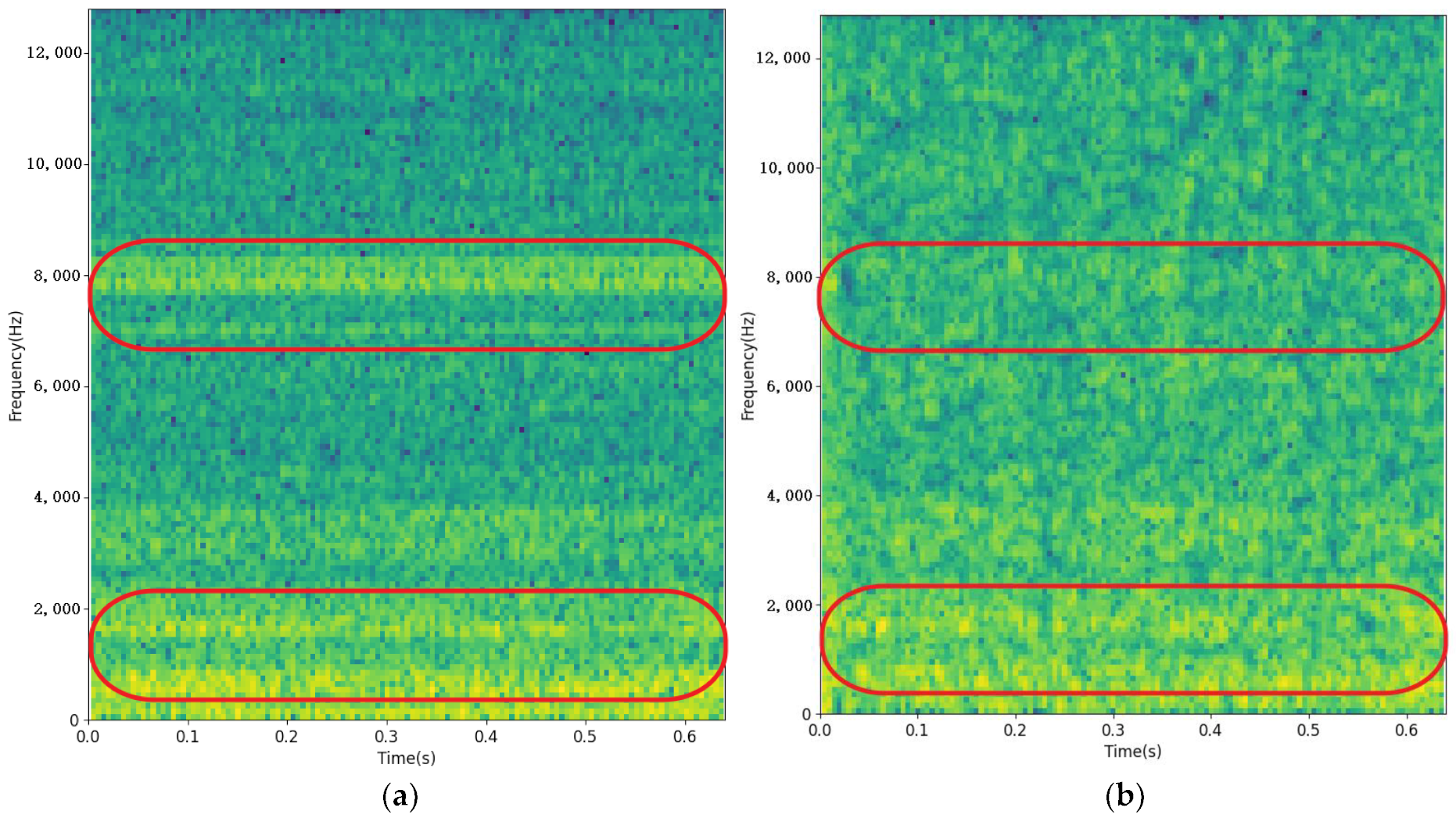
4.3. Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Liu, J.; Liu, F.; Geng, Z. An Intelligent Moving Window Sparse Principal Component Analysis-Based Case Based Reasoning for Fault Diagnosis: Case of the Drilling Process. ISA Trans. 2022, 128, 242–254. [Google Scholar] [CrossRef]
- Geng, Z.; Duan, X.; Han, Y.; Liu, F.; Xu, W. Novel Variation Mode Decomposition Integrated Adaptive Sparse Principal Component Analysis and It Application in Fault Diagnosis. ISA Trans. 2022, 128, 21–31. [Google Scholar] [CrossRef]
- Hou, J.; Ma, B.; Liang, L.; Zhang, M. An Early Warning Method for Mechanical Fault Detection Based on Adversarial Auto-Encoders. J. Adv. Manuf. Sci. Technol. 2022, 2, 2022006. [Google Scholar] [CrossRef]
- Yao, J.; Liu, C.; Song, K.; Feng, C.; Jiang, D. Fault Diagnosis of Planetary Gearbox Based on Acoustic Signals. Appl. Acoust. 2021, 181, 108151. [Google Scholar] [CrossRef]
- Qin, C.; Wang, D.; Xu, Z.; Tang, G. Improved Empirical Wavelet Transform for Compound Weak Bearing Fault Diagnosis with Acoustic Signals. Appl. Sci. 2020, 10, 682. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Hu, D.; Yu, G.; Liao, A.; Shi, W. Trackside Acoustic Detection of Axle Bearing Fault Using Wavelet Domain Moving Beamforming Method. Appl. Acoust. 2022, 195, 108851. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Lu, J.; Yang, F.; Dong, H.; Li, G. Feature Extraction Method of Pipeline Signal Based on Parameter Optimized Vocational Mode Decomposition and Exponential Entropy. Trans. Inst. Meas. Control 2022, 44, 216–231. [Google Scholar] [CrossRef]
- Wang, Y.; Chi, Y.; Wu, X.; Liu, C. Extracting Acoustical Impulse Signal of Faulty Bearing Using Blind Deconvolution Method. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; pp. 590–594. [Google Scholar]
- Yu, G.; Ma, B.; Yan, G. Acoustic Diagnosis of a Rolling Bearing Based on Resonance Sparse Decomposition and Sub-band Enhancement. J. Beijing Univ. Chem. Technol. (Nat. Sci.) 2021, 48, 49–57. [Google Scholar]
- Yu, G.; Yan, G.; Ma, B. Feature Enhancement Method of Rolling Bearing Acoustic Signal Based on RLS-RSSD. Measurement 2022, 192, 110883. [Google Scholar] [CrossRef]
- Marxim Rahula Bharathi, B.; Mohanty, A.R. Underwater Sound Source Localization by EMD-Based Maximum Likelihood Method. Acoust. Aust. 2018, 46, 193–203. [Google Scholar] [CrossRef]
- Huang, G.; Chen, J.; Benesty, J.; Cohen, I.; Zhao, X. Steerable Differential Beamformers with Planar Microphone Arrays. EURASIP J. Audio Speech Music Process. 2020, 2020, 15. [Google Scholar] [CrossRef]
- Ikeshita, R.; Kinoshita, K.; Kamo, N.; Nakatani, T. Online Speech Dereverberation Using Mixture of Multichannel Linear Prediction Models. IEEE Signal Process. Lett. 2021, 28, 1580–1584. [Google Scholar] [CrossRef]
- Ikeshita, R.; Kamo, N.; Nakatani, T. Blind Signal Dereverberation Based on Mixture of Weighted Prediction Error Models. IEEE Signal Process. Lett. 2021, 28, 399–403. [Google Scholar] [CrossRef]
- Nakatani, T.; Kinoshita, K. A Unified Convolutional Beamformer for Simultaneous Denoising and Dereverberation. IEEE Signal Process. Lett. 2019, 26, 903–907. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.Z.U.; Malik, A.N.; Zaman, F.; Qureshi, I.M. Robust LCMV Beamformer for Direction of Arrival Mismatch without Beam Broadening. Wirel. Pers. Commun. 2019, 104, 21–36. [Google Scholar] [CrossRef]
- Gosling, N.; Hadad, E.; Gannot, S.; Doclo, S. Binaural LCMV Beamforming with Partial Noise Estimation. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 2942–2955. [Google Scholar] [CrossRef]
- Pandey, O.J.; Gautam, V.; Nguyen, H.H.; Shukla, M.K.; Hegde, R.M. Fault-Resilient Distributed Detection and Estimation Over a SW-WSN Using LCMV Beamforming. IEEE Trans. Netw. Serv. Manag. 2020, 17, 1758–1773. [Google Scholar] [CrossRef]
- Hassani, A.; Plata-Chaves, J.; Bahari, M.H.; Moonen, M.; Bertrand, A. Multi-Task Wireless Sensor Network for Joint Distributed Node-Specific Signal Enhancement, LCMV Beamforming and DOA Estimation. IEEE J. Sel. Top. Signal Process. 2017, 11, 518–533. [Google Scholar] [CrossRef]
- Ribeiro, L.N.; de Almeida, A.L.; Mota, J.C. Separable Linearly Constrained Minimum Variance Beamformers. Signal Process. 2019, 158, 15–25. [Google Scholar] [CrossRef]
- Omologo, M.; Svaizer, P.; Matassoni, M. Environmental Conditions and Acoustic Transduction in Hands-Free Speech Recognition. Speech Commun. 1998, 25, 75–95. [Google Scholar] [CrossRef]
- Ma, B.; Yan, G.; Yu, G. Bogie Running-in Test of Fault Monitoring Experiment on Rolling Stock Based on Microphone Array. Electr. Drive Locomot. 2019, 6, 95–99. [Google Scholar]
- Zheng, K.; Zheng, C.; Sang, J.; Zhang, Y.; Li, X. Noise-Robust Blind Reverberation Time Estimation Using Noise-Aware Time–Frequency Masking. Measurement 2022, 192, 110901. [Google Scholar] [CrossRef]
- Purushothaman, A.; Sreeram, A.; Kumar, R.; Ganapathy, S. Dereverberation of Autoregressive Envelopes for Far-Field Speech Recognition. Comput. Speech Lang. 2022, 72, 101277. [Google Scholar] [CrossRef]
- Ullah, R.; Shohidul Islam, M.; Imran Hossain, M.; Wahab, F.E.; Ye, Z. Single Channel Speech Dereverberation and Separation Using RPCA and SNMF. Appl. Acoust. 2020, 167, 107406. [Google Scholar] [CrossRef]
- Yoshioka, T.; Sehr, A.; Delcroix, M.; Kinoshita, K.; Maas, R.; Nakatani, T.; Kellermann, W. Making Machines Understand Us in Reverberant Rooms: Robustness against Reverberation for Automatic Speech Recognition. IEEE Signal Process. Mag. 2012, 29, 114–126. [Google Scholar] [CrossRef]
- Scamoni, F.; Scrosati, C.; Depalma, M.; Barozzi, B. Experimental Evaluations of Acoustic Properties and Long-Term Analysis of a Novel Indoor Living Wall. J. Build. Eng. 2022, 47, 103890. [Google Scholar] [CrossRef]
- Yoshioka, T.; Nakatani, T. Generalization of Multi-Channel Linear Prediction Methods for Blind MIMO Impulse Response Shortening. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2707–2720. [Google Scholar] [CrossRef]
- Parchami, M.; Amindavar, H.; Zhu, W.-P. Speech Reverberation Suppression for Time-Varying Environments Using Weighted Prediction Error Method with Time-Varying Autoregressive Model. Speech Commun. 2019, 109, 1–14. [Google Scholar] [CrossRef]
- Frost, O.L. An Algorithm for Linearly Constrained Adaptive Array Processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Drude, L.; Heymann, J.; Boeddeker, C.; Haeb-Umbach, R. NARA-WPE: A Python Package for Weighted Prediction Error Dereverberation in Numpy and Tensorflow for Online and Offline Processing. In Proceedings of the Speech Communication, 13th ITG-Symposium, Oldenburg, Germany, 10–12 October 2018; pp. 1–5. [Google Scholar]
- Zhou, T.; Huang, J.; Du, W.; Shen, J.; Yuan, W. 2-D Deconvolved Conventional Beamforming for a Planar Array. Circuits Syst. Signal Process. 2021, 40, 5572–5593. [Google Scholar] [CrossRef]
- Gao, J.; Wu, H.; Jiang, W. Dipole-Based Beamforming Method for Locating Dipole Sources with Unknown Orientations in Three-Dimensional Domains. J. Acoust. Soc. Am. 2020, 147, 125–136. [Google Scholar] [CrossRef]
- Tan, Y.; Ma, B.; Zhang, Q. Rotating Machinery Fault Source Location Method Based on Sensitive Characteristic Frequency Band. J. Mech. Electr. Eng. 2022, 39, 1080–1087+1095. [Google Scholar]
- Xu, X.; Zhao, M.; Lin, J.; Lei, Y. Envelope Harmonic-to-Noise Ratio for Periodic Impulses Detection and Its Application to Bearing Diagnosis. Measurement 2016, 91, 385–397. [Google Scholar] [CrossRef]

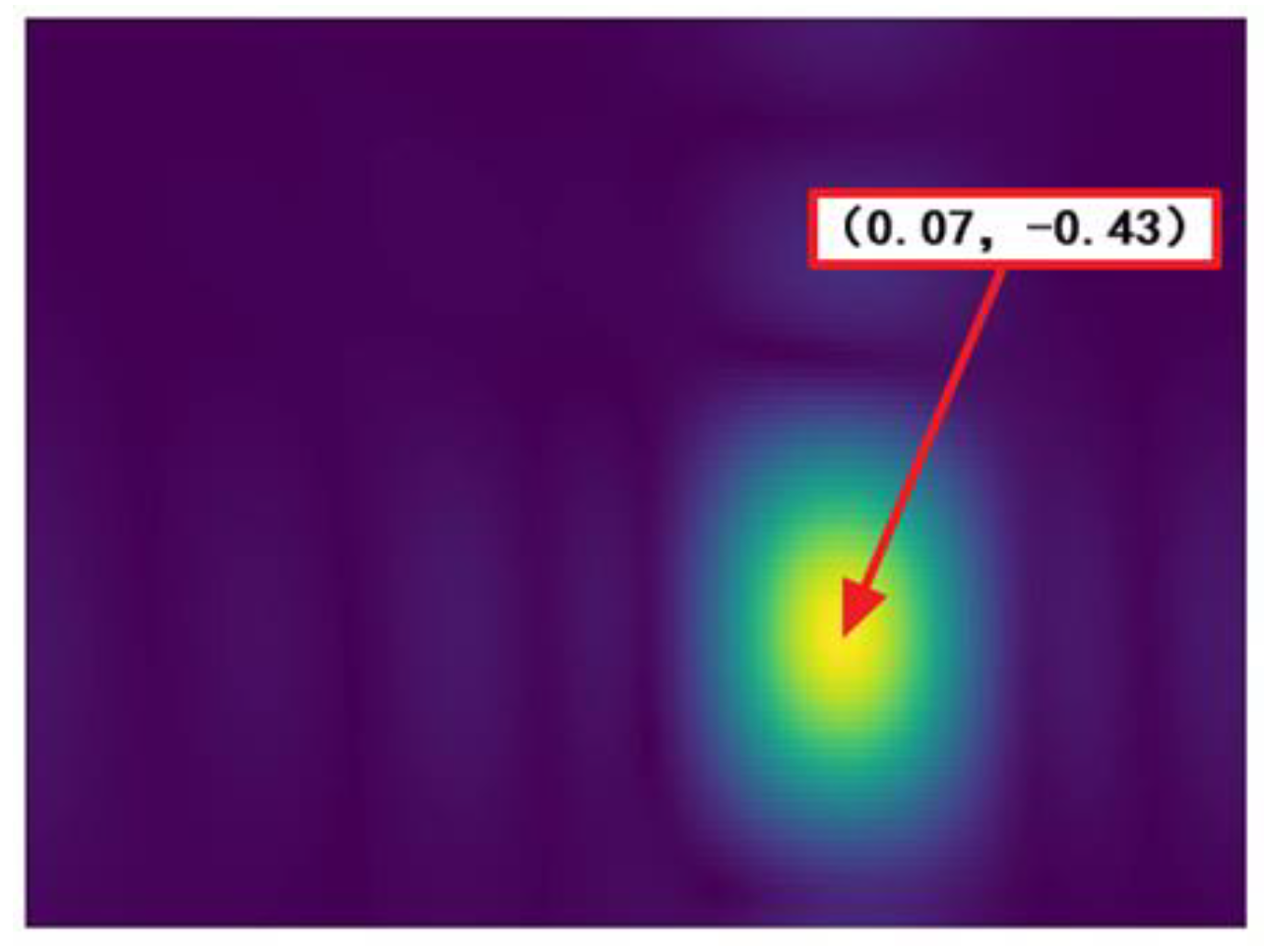
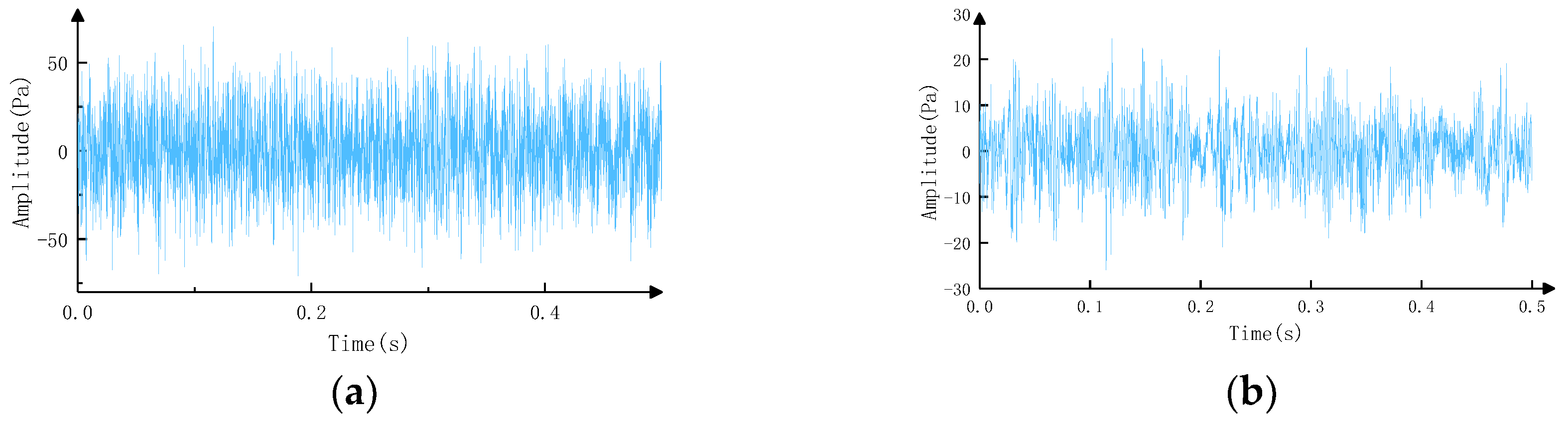


| Parameter | fs | P | c | λ | dm |
|---|---|---|---|---|---|
| Value | 25,600 Hz | 16,384 | 340 m/s | 0.17 m | 0.085 m |
| Groups | Fault Location | Defect Number | Defect Depth /mm | Defect Frequency /Hz | Rotation Speed/(r/min) |
|---|---|---|---|---|---|
| 1 | outer ring | 2 | 1 × 0.5 | 118.70 | 1800 |
| 2 | inner ring | 2 | 0.5 × 0.5 | 181.30 | |
| 3 | roller | 1 | 4 × 0.2 | 68.74 | |
| 4 | cage | 1 | 0.2 | 11.87 |
| Parameter | The Average Sound Absorption Coefficient | Temperature | The Relative Humidity | The Sound Energy Decay Constant |
|---|---|---|---|---|
| Value | 0.05 | 5 °C | 30% | 0.07 |
| Channel | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Weight | 0.067 | 0.077 | 0.078 | 0.040 | 0.050 | 0.10 | 0.088 | 0.061 |
| Channel | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Weight | 0.031 | 0.075 | 0.066 | 0.035 | 0.043 | 0.075 | 0.074 | 0.038 |
| Groups | Fault Location | WPE-LCMV | RLS-RSSD | The Parameter Optimized VMD | Original Signal |
|---|---|---|---|---|---|
| 1 | inner ring fault | 6.85 | 5.73 | 5.39 | 3.27 |
| 2 | roller fault | 8.13 | 4.71 | 3.78 | 2.61 |
| 3 | cage fault | 7.46 | 5.82 | 5.78 | 3.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Yu, G.; Dong, N.; Ma, B. Acoustic Feature Extraction Method of Rotating Machinery Based on the WPE-LCMV. Machines 2022, 10, 1170. https://doi.org/10.3390/machines10121170
Wu P, Yu G, Dong N, Ma B. Acoustic Feature Extraction Method of Rotating Machinery Based on the WPE-LCMV. Machines. 2022; 10(12):1170. https://doi.org/10.3390/machines10121170
Chicago/Turabian StyleWu, Peng, Gongye Yu, Naiji Dong, and Bo Ma. 2022. "Acoustic Feature Extraction Method of Rotating Machinery Based on the WPE-LCMV" Machines 10, no. 12: 1170. https://doi.org/10.3390/machines10121170





