Model-Based Control Design of an EHA Position Control Based on Multicriteria Optimization
Abstract
:1. Introduction
- Modeling of an EHA with a comprehensive grey-box model independent of data from bench tests, with the publication of all relevant parameters.
- Application of a method for multi-objective optimization of PID control for optimal control parameters of the EHA using a simulation model and two load cases.
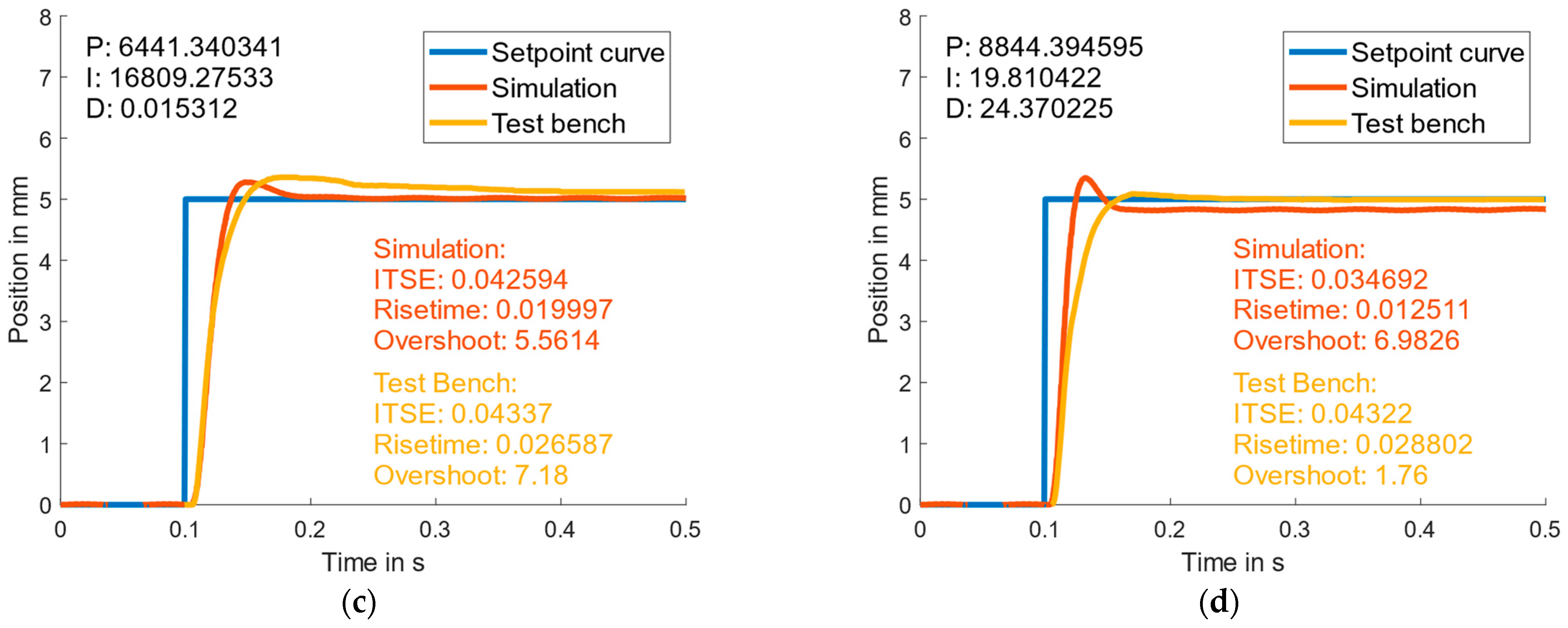
- Comparison of the system behavior between the simulation model and the test bench with the help of step responses using the optimized control parameters for both load cases.
2. Materials and Methods
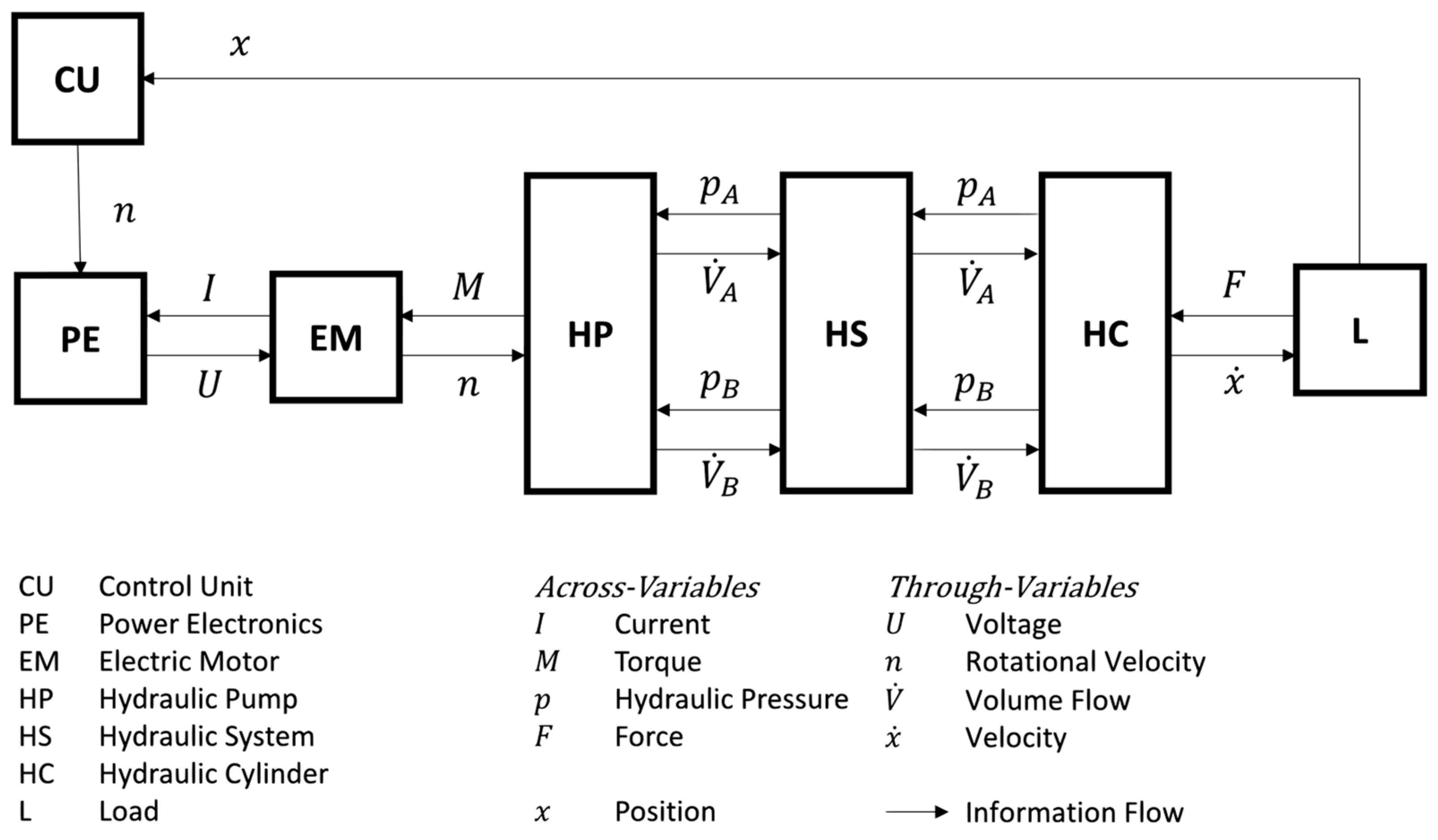
2.1. Electro-Hydraulic Actuator and Simulation Model
2.1.1. Control Unit (CU)
2.1.2. Power Electronics (PE)
2.1.3. Electric Motor (EM)
2.1.4. Hydraulic Pump (HP)
2.1.5. Hydraulic System (HS)
2.1.6. Hydraulic Cylinder (HC)
2.2. Method for Multi-Objective Optimization of PID Control
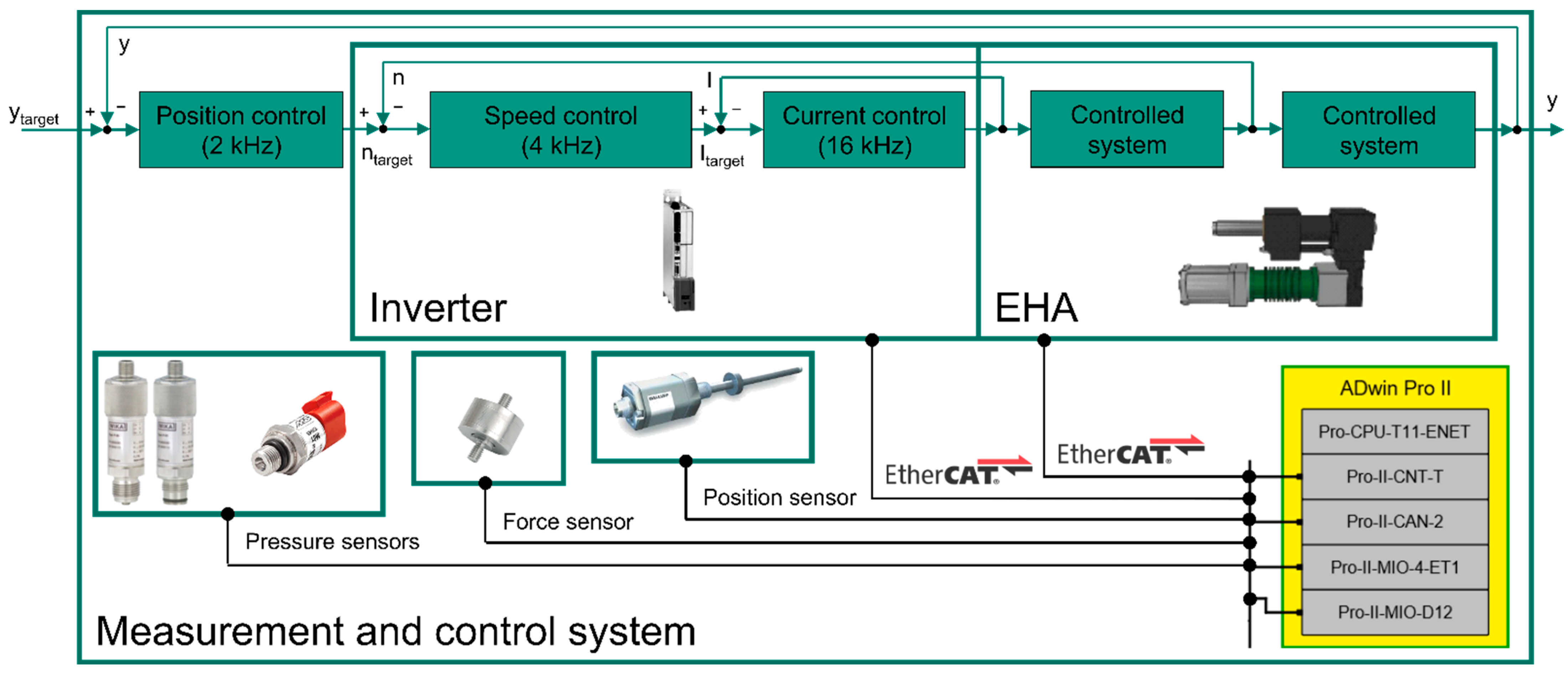
2.3. Test Bench for Validation of the Simulation Model
3. Results
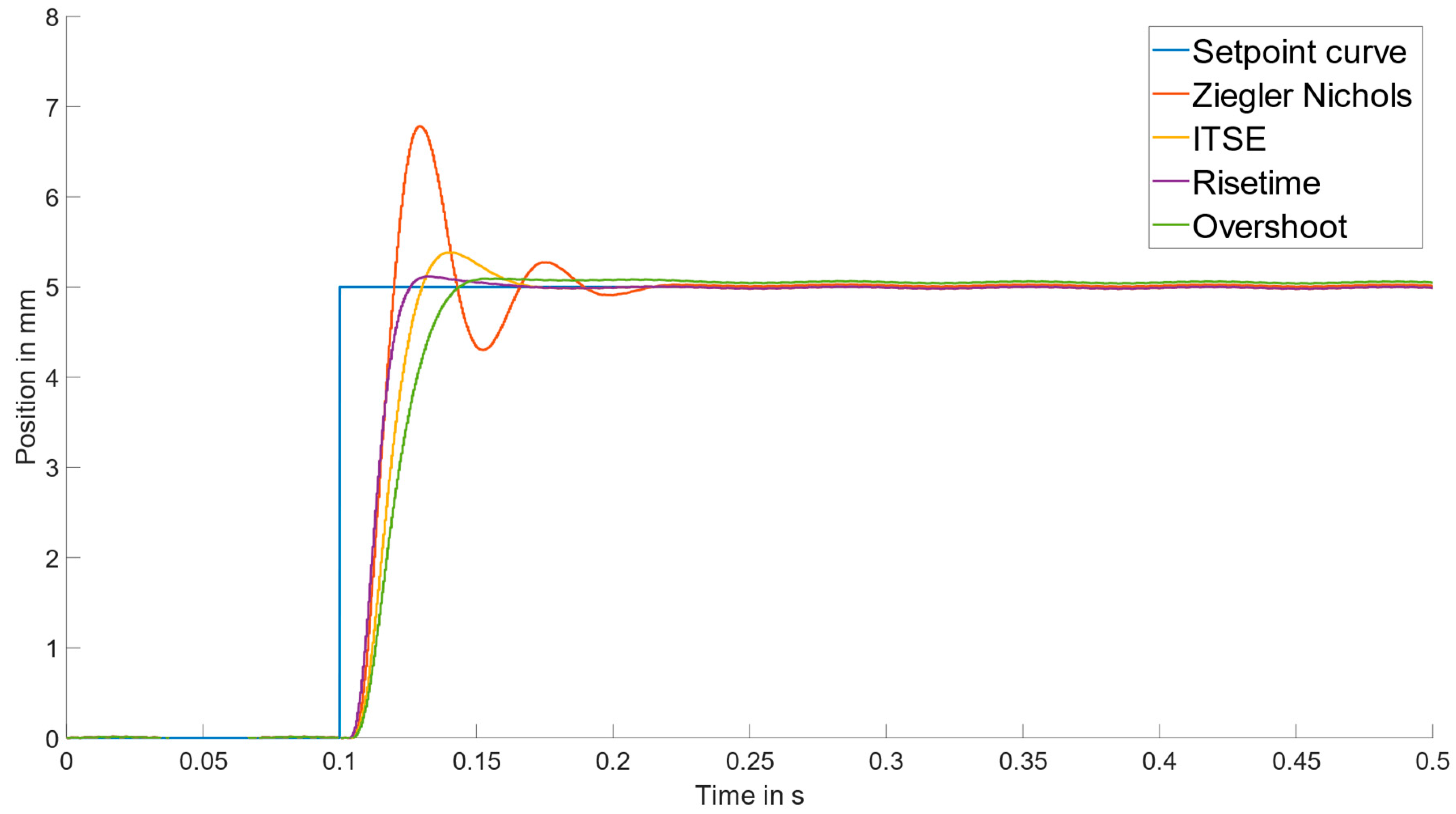
3.1. Results of the Method for Multi-Objective Optimization of PID Control for the Simulation Model
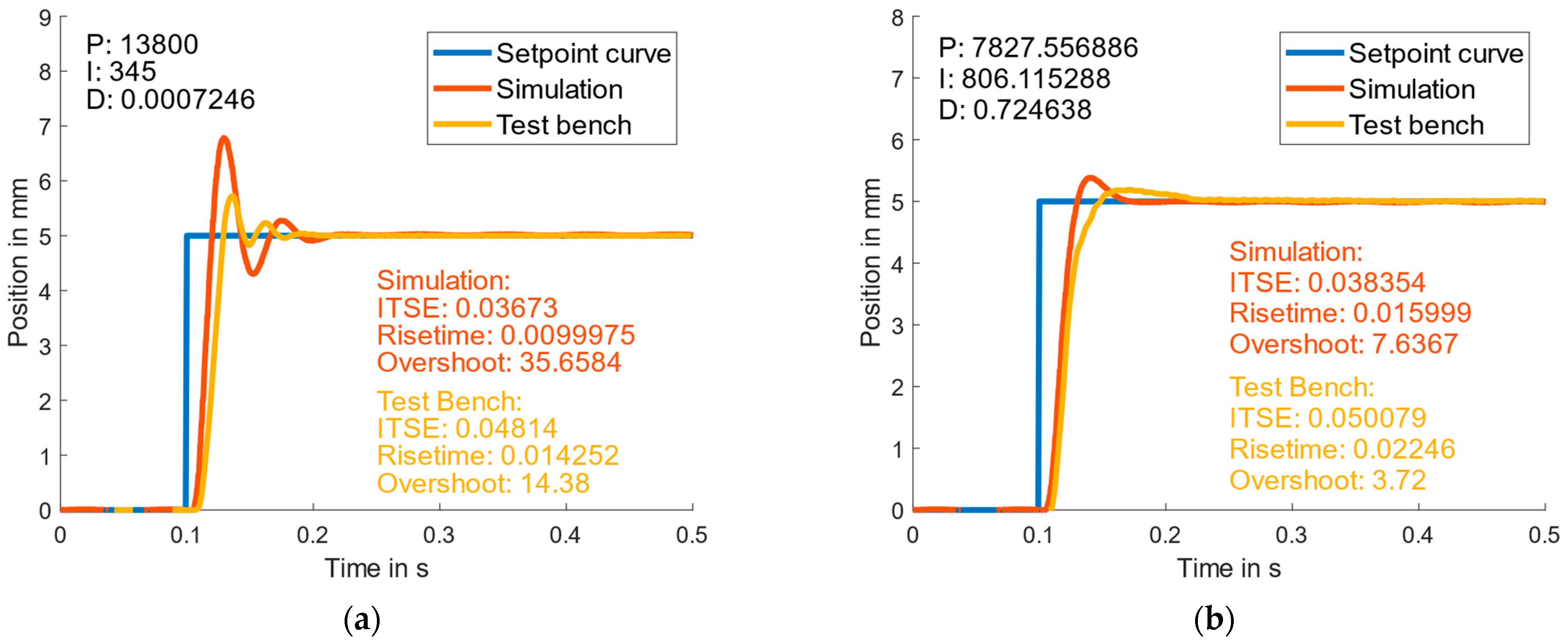
3.2. Validation of the Simulation Model for the Electro-Hydraulic Actuator
4. Discussion
4.1. Discussion of the Results of the Method for Multi-Objective Optimization of PID Control
4.2. Validation of the Simulation Model with the Test Bench
4.3. Limitations and Further Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EHA | Electro-Hydraulic Actuators |
| PID | Proportional–Integral–Derivative |
| ARX | Auto-Regressive Exogenous |
| PSO | Particle Swarm Optimization |
| CU | Control Unit |
| PE | Power Electronics |
| EM | Electric Motor |
| PMSM | Permanent Magnet Synchronous Motor |
| HC | Hydraulic Pump |
| HP | Hydraulic System |
| HC | Hydraulic Cylinder |
| ITSE | Integrated Time Weighted Square Error |
Appendix A
| Parameter | Value | |
|---|---|---|
| Power Electronics (PE) | ||
| Current controller proportional gain D-axis | 12.6 | V/A |
| Current controller proportional gain Q-axis | 20.1 | V/A |
| Current controller integral part | 2320 | V/A∗s |
| Current controller bandwidth | 200 | Hz |
| Speed controller frequency | 2000 | Hz |
| Speed controller proportional gain | 1000 | 1/s |
| Speed controller integral part | 100 | 1/s2 |
| Setpoint speed filter | 0.63 × 10−3 | 1/s |
| Actual speed filter | 1.23 × 10−3 | 1/s |
| Acceleration precontrol filter | 1.25 × 10−3 | s |
| Electric Motor (EM) | ||
| Nominal speed | 40 | 1/s |
| Nominal torque | 24.8 | Nm |
| Maximal torque | 90 | Nm |
| Nominal power motor | 6200 | W |
| Reduced rotational inertia | 1566 | kg/mm2 |
| Number of rotor polepairs | 5 | |
| DC link voltage | 560 | V |
| Nominal current | 13.8 | A |
| Current limit | 55.2 | A |
| D-inductance (field) | 10 | mH |
| Q-inductance (torque) | 16 | mH |
| Resistance (at 20°C) | 1.5 | Ω |
| Flux linkage established by magnets | 0.214 | Vs |
| Factor of induced voltage | 0.137 | V(RMS)/rpm |
| Limit speed for static friction | 0.001 | rad/s |
| Static friction torque | 0.5 | Nm |
| Viscous damping | 0.005 | Nm*s/rad |
| Hydraulic System (HS) | ||
| Hydraulic fluid density | 864 | kg/m3 |
| Hydraulic fluid bulk modulus | 1.448 × 109 | N/m2 |
| System pressure | 2 | bar |
| Tube A length | 160 | mm |
| Tube B length | 420 | mm |
| Tube A inner radius | 9.0 | mm |
| Tube B inner radius | 9.0 | mm |
| Elbow A quantity | 1 | |
| Elbow B quantity | 3 | |
| Elbow bending radius | 40 | mm |
| Hydraulic Cylinder (HC) | ||
| Piston radius | 25 | mm |
| Rod radius | 16 | mm |
| Dead volume A-Side | 2.90 × 10−5 | m3 |
| Dead volume B-Side | 2.90 × 10−5 | m3 |
| Moving mass of piston and rod | 4.19 | kg |
| Coulomb friction force | 150 | N |
| Viscous friction coefficient | 200 | Ns/m |
References
- Sohl, G.A.; Bobrow, J.E. Experiments and simulations on the nonlinear control of a hydraulic servosystem. IEEE Trans. Control Syst. Technol. 1999, 7, 238–247. [Google Scholar] [CrossRef] [PubMed]
- Doan, N.; Yoon, J.I.; Ahn, K.K. Position control of Electro hydrostatic actuator (EHA) using a modified back stepping controller. J. Korean Soc. Fluid Power Constr. Equip. 2012, 9, 16–22. [Google Scholar] [CrossRef] [Green Version]
- Kundu, S.; Bhattacharjee, R.; Chaudhuri, S. Evaluation of Fuzzy-Logic based Position Control Strategies for an Electrohydraulic Actuation System. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–7. [Google Scholar]
- Bessa, W.M.; Dutra, M.S.; Kreuzer, E. Sliding Mode Control with Adaptive Fuzzy Dead-Zone Compensation of an Electro-hydraulic Servo-System. J. Intell. Robot. Syst. 2010, 58, 3–16. [Google Scholar] [CrossRef]
- Guo, Q.; Shi, G.; Wang, D. Adaptive Composite Fuzzy Dynamic Surface Control for Electro-Hydraulic-System, with Variable-Supply-Pressure. Asian J. Control 2020, 22, 521–535. [Google Scholar] [CrossRef]
- Guo, K.; Wei, J.; Fang, J.; Feng, R.; Wang, X. Position tracking control of electro-hydraulic single-rod actuator based on an extended disturbance observer. Mechatronics 2015, 27, 47–56. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Dao, H.V.; Ahn, K.K. Active Disturbance Rejection Control for Position Tracking of Electro-Hydraulic Servo Systems under Modeling Uncertainty and External Load. Actuators 2021, 10, 20. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-Gain Disturbance Observer-Based Backstepping Control With Output Tracking Error Constraint for Electro-Hydraulic Systems. IEEE Trans. Control Syst. Technol. 2015, 23, 787–795. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A Review of High-Speed Electro-Hydrostatic Actuator Pumps in Aerospace Applications: Challenges and Solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Wang, P.; Dong, Z.; Jiang, D.; Sha, T. A novel architecture of electro-hydrostatic actuator with digital distribution. Chin. J. Aeronaut. 2021, 34, 224–238. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Deng, W.; Yao, J. Observer-based motion axis control for hydraulic actuation systems. Chin. J. Aeronaut. 2022, in press. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Doan, N.C.N.; Hyung, G.P.; Kyoung, K. Trajectory control of an electro hydraulic actuator using an iterative backstepping control scheme. Mechatronics 2015, 29, 96–102. [Google Scholar] [CrossRef]
- Yang, X.; Deng, W.; Yao, J. Neural Adaptive Dynamic Surface Asymptotic Tracking Control of Hydraulic Manipu-lators With Guaranteed Transient Performance. IEEE Trans. Neural Netw. Learn. Syst. 2022, 2022, 3141463. [Google Scholar] [CrossRef]
- Chen, G.; Liu, H.; Jia, P.; Qiu, G.; Yu, H.; Yan, G.; Ai, C.; Zhang, J. Position Output Adaptive Backstepping Control of Electro-Hydraulic Servo Closed-Pump Control System. Processes 2021, 9, 2209. [Google Scholar] [CrossRef]
- Cerman, O.; Hušek, P. Adaptive fuzzy sliding mode control for electro-hydraulic servo mechanism. Expert Syst. Appl. 2012, 39, 10269–10277. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, Y.; Burton, R. Modeling and Robust Discrete-Time Sliding-Mode Control Design for a Fluid Power Electrohydraulic Actuator (EHA) System. IEEE ASME Trans. Mechatron. 2013, 18, 1–10. [Google Scholar] [CrossRef]
- Feng, L.; Yan, H. Nonlinear Adaptive Robust Control of the Electro-Hydraulic Servo System. Appl. Sci. 2020, 10, 4494. [Google Scholar] [CrossRef]
- Izzuddin, N.H.; Faudzi, A.M.; Johari, M.R.; Osman, K. System identification and predictive functional control for electro-hydraulic actuator system. In Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Langkawi, Malaysia, 18–20 October 2015; pp. 138–143. [Google Scholar]
- Liang, X.W.; Mohd Faudzi, A.A.; Ismail, Z.H. System Identification and Model Predictive Control using CVXGEN for Electro-Hydraulic Actuator. Int. J. Integr. Eng. 2019, 11, 04018. [Google Scholar] [CrossRef]
- Ishak, N.; Yusof, N.M.; Azahar, W.N.A.W.; Adnan, R.; Tajudin, M. Model identifiction and controller design of a hydraulic cylinder based on pole placement. In Proceedings of the 2015 IEEE 11th International Colloquium on Signal Processing & Its Applications (CSPA), Kuala Lumpur, Malaysia, 6–8 March 2015; pp. 198–202, ISBN 978-1-4799-8249-3. [Google Scholar]
- Rahmat, M.F.; Rozali, S.M.; Wahab, N.A.; Jusoff, K. Modeling and Controller Design of an Electro-Hydraulic Actuator System. Am. J. Appl. Sci. 2010, 7, 1100–1108. [Google Scholar] [CrossRef] [Green Version]
- Wonohadidjojo, D.M.; Kothapalli, G.; Hassan, M.Y. Position Control of Electro-hydraulic Actuator System Using Fuzzy Logic Controller Optimized by Particle Swarm Optimization. Int. J. Autom. Comput. 2013, 10, 181–193. [Google Scholar] [CrossRef] [Green Version]
- Shern, C.M.; Ghazali, R.; Horng, C.; Jaafar, H.I.; Chong, C.S.; Md Sam, Y. Performance Analysis of Position Tracking Control with PID Controller using an Improved Optimization Technique. Int. J. Mech. Eng. Robot. Res. 2019, 8, 401–405. [Google Scholar] [CrossRef]
- Shern, C.M.; Ghazali, R.; Horng, C.S.; Soon, C.C.; Ghani, M.F.; Sam, Y.M.; Has, Z. The Effects of Weightage Values with Two Objective Functions in iPSO for Electro-Hydraulic Actuator System. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 81, 98–109. [Google Scholar] [CrossRef]
- Bellad, K.; Hiremath, S.S.; Singaperumal, M.; Karunanidhi, S. Optimization of PID Parameters in Electro-Hydraulic Actuator System Using Genetic Algorithm. Appl. Mech. Mater. 2014, 592–594, 2229–2233. [Google Scholar] [CrossRef]
- Elbayomy, K.M.; Zongxia, J.; Huaqing, Z. PID Controller Optimization by GA and Its Performances on the Electro-hydraulic Servo Control System. Chin. J. Aeronaut. 2008, 21, 378–384. [Google Scholar] [CrossRef] [Green Version]
- Zaki Fadel, M.; Rabie, M.; Youssef, A. Optimization of Control Parameters Based on Genetic Algorithm Technique for Integrated Electrohydraulic Servo Actuator System. Int. J. Mechatron. Autom. 2020, 6, 24–37. [Google Scholar]
- Tajjudin, M.; Ishak, N.; Ismail, H.; Rahiman, M.H.F.; Adnan, R. Optimized PID control using Nelder-Mead method for electro-hydraulic actuator systems. In Proceedings of the 2011 IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 27–28 June 2011; pp. 90–93. [Google Scholar] [CrossRef]
- Rahmat, M.F.; Marhainis Othman, S.; Rozali, S.M.; Has, Z. Optimization of Modified Sliding Mode Control for an Electro-Hydraulic Actuator System with Mismatched Disturbance. In Proceedings of the 2018 5th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Malang, Indonesia, 16–18 October 2018; pp. 1–6. [Google Scholar]
- Fan, Y.; Shao, J.; Sun, G. Optimized PID Controller Based on Beetle Antennae Search Algorithm for Electro-Hydraulic Position Servo Control System. Sensors 2019, 19, 2727. [Google Scholar] [CrossRef] [Green Version]
- Leitenberger, F.; Gwosch, T.; Matthiesen, S. Architecture of the Digital Twin in Product Validation for the Application in Virtual-Physical Testing to Investigate System Reliability. In Proceedings of the 32nd Symposium Design for X. Design for X Symposium, Online, 27–28 September 2021. [Google Scholar] [CrossRef]
- Torque-Based, Field-Oriented Controller for an Internal Permanent Magnet Synchronous Motor—Simulink. Available online: https://www.mathworks.com/help/releases/R2021a/autoblks/ref/interiorpmcontroller.html (accessed on 23 September 2022).
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Li, M.; He, J.; Demerdash, N.A.O. A flux-weakening control approach for interior permanent magnet synchronous motors based on Z-source inverters. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Briz, F.; Degner, M.W.; Lorenz, R.D. Analysis and design of current regulators using complex vectors. IEEE Trans. Ind. Appl. 2000, 36, 817–825. [Google Scholar] [CrossRef] [Green Version]
- Briz, F.; Diez, A.; Degner, M.W.; Lorenz, R.D. Current and flux regulation in field-weakening operation [of induction motors]. IEEE Trans. Ind. Appl. 2001, 37, 42–50. [Google Scholar] [CrossRef]
- SEW Eurodrive. System Manual—MOVIAXIS® Multi-Axis Servo Inverter. Available online: https://download.sew-eurodrive.com/download/pdf/20062532.pdf (accessed on 23 September 2022).
- Kundur, P.S. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 1993. [Google Scholar]
- Anderson, P.M. Analysis of Faulted Power Systems; IEEE Press: New York, NY, USA, 1995; ISBN 978-0-780-31145-9. [Google Scholar]
- Qu, S.; Fassbender, D.; Vacca, A.; Busquets, E. A Cost-Effective Electro-Hydraulic Actuator Solution with Open Circuit Architecture. TJFP 2021, 22, 2224. [Google Scholar] [CrossRef]
- Engineering Department. Flow of Fluids Through Valves, Fittings and Pipe: Crane Technical Paper No. 410; Crance Company: Stamford, CT, USA, 2009; ISBN 1-40052-712-0. [Google Scholar]
- Glöckler, M. Simulation Mechatronischer Systeme; Springer Fachmedien: Wiesbaden, Germany, 2018; ISBN 978-3-658-20702-1. [Google Scholar]
- Wolter, K. A Method for User-Friendly PID-Parameter Optimization for Highly Dynamic Component Test Benches. In Proceedings of the FISITA 2020 Web Congress, Online, 24 November 2020. [Google Scholar]
- Frischemeier, S. Electrohydrostatic actuators for aircraft primary flight control—Types, modelling and evaluation. In Proceedings of the 5th Scandinavian International Conference on Fluid Power, SICFP’97, Linköping, Sweden, 28–30 May 1997. [Google Scholar] [CrossRef]





| Frequency | Amplitude |
|---|---|
| 15 Hz | |
| 200 Hz | |
| 400 Hz |
| Population size of PSO in all loops | 125 |
| Generations of PSO in all loops | 10 |
| Objective in system characterization | ITSE ( |
| Objective in first optimization loop | Rise time ( |
| Objective in second optimization loop | Overshoot ( |
| Range of first system characterization loop | [ |
| Range of second optimization loop | [ |
| Range of third optimization loop | [ |
| Inertia Load of 11.8 kg | |||
|---|---|---|---|
| Ziegler and Nichols | 13,800 | 345 | 0.0007246 |
| System characterization (ITSE) | 7827.556886 | 806.115288 | 0.724638 |
| First optimization loop (Rise time) | 9441.263070 | 0.806115 | 25.386430 |
| Second optimization loop (Overshoot) | 6167.990306 | 495.702891 | 0.025386 |
| Spring Stiffness 241.381 N/mm | |||
|---|---|---|---|
| Ziegler and Nichols | 13,800 | 345 | 0.0007246 |
| System characterization (ITSE) | 7663.036665 | 19,810.42218 | 0.677059 |
| First optimization loop (Rise time) | 8844.394595 | 19.810422 | 24.370225 |
| Second optimization loop (Noise) | 6441.340341 | 16809.27533 | 0.015312 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dörr, M.; Leitenberger, F.; Wolter, K.; Matthiesen, S.; Gwosch, T. Model-Based Control Design of an EHA Position Control Based on Multicriteria Optimization. Machines 2022, 10, 1190. https://doi.org/10.3390/machines10121190
Dörr M, Leitenberger F, Wolter K, Matthiesen S, Gwosch T. Model-Based Control Design of an EHA Position Control Based on Multicriteria Optimization. Machines. 2022; 10(12):1190. https://doi.org/10.3390/machines10121190
Chicago/Turabian StyleDörr, Matthias, Felix Leitenberger, Kai Wolter, Sven Matthiesen, and Thomas Gwosch. 2022. "Model-Based Control Design of an EHA Position Control Based on Multicriteria Optimization" Machines 10, no. 12: 1190. https://doi.org/10.3390/machines10121190
APA StyleDörr, M., Leitenberger, F., Wolter, K., Matthiesen, S., & Gwosch, T. (2022). Model-Based Control Design of an EHA Position Control Based on Multicriteria Optimization. Machines, 10(12), 1190. https://doi.org/10.3390/machines10121190






