Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors
Abstract
:1. Introduction
- (1)
- Fault detection and isolation (FDI): its objective is to process input/output data, in order to detect the existence of a fault, to isolate it from other faults or alterations of the system [5];
- (2)
- Tolerant control algorithm: its objective is to adjust the controller to compensate for the effect of a fault, based on the information provided by the fault detector [3].
- Four online neural classifiers are proposed to deal with actuator and sensor faults;
- Classifiers are tested online with experimental data;
- A real-world problem for actuator and sensor fault classification is included;
- A detailed comparative analysis was performed for the four proposed classifiers to deal with actuator and sensor faults.
- Proposed methodology can be easily extended to different real-world fault diagnosis and classification problems.
2. Review of the Analyzed System
3. Deep Neural Networks
3.1. Multilayer Networks
3.2. Long Short-Term Memory Recurrent Neural Network
3.3. Bidirectional LSTM
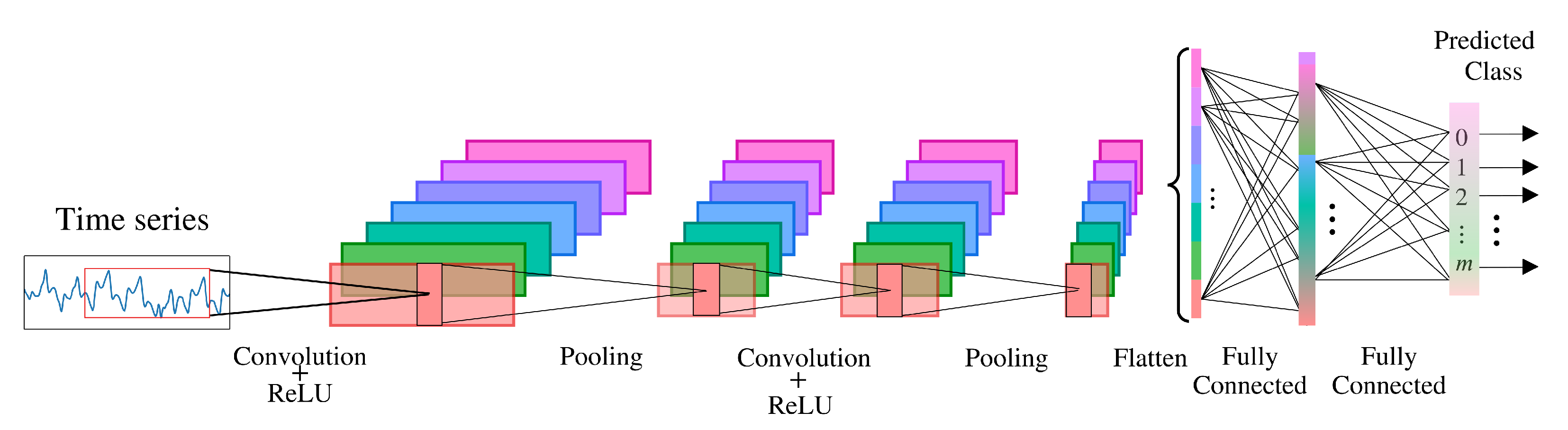
3.4. Convolutional Neural Network
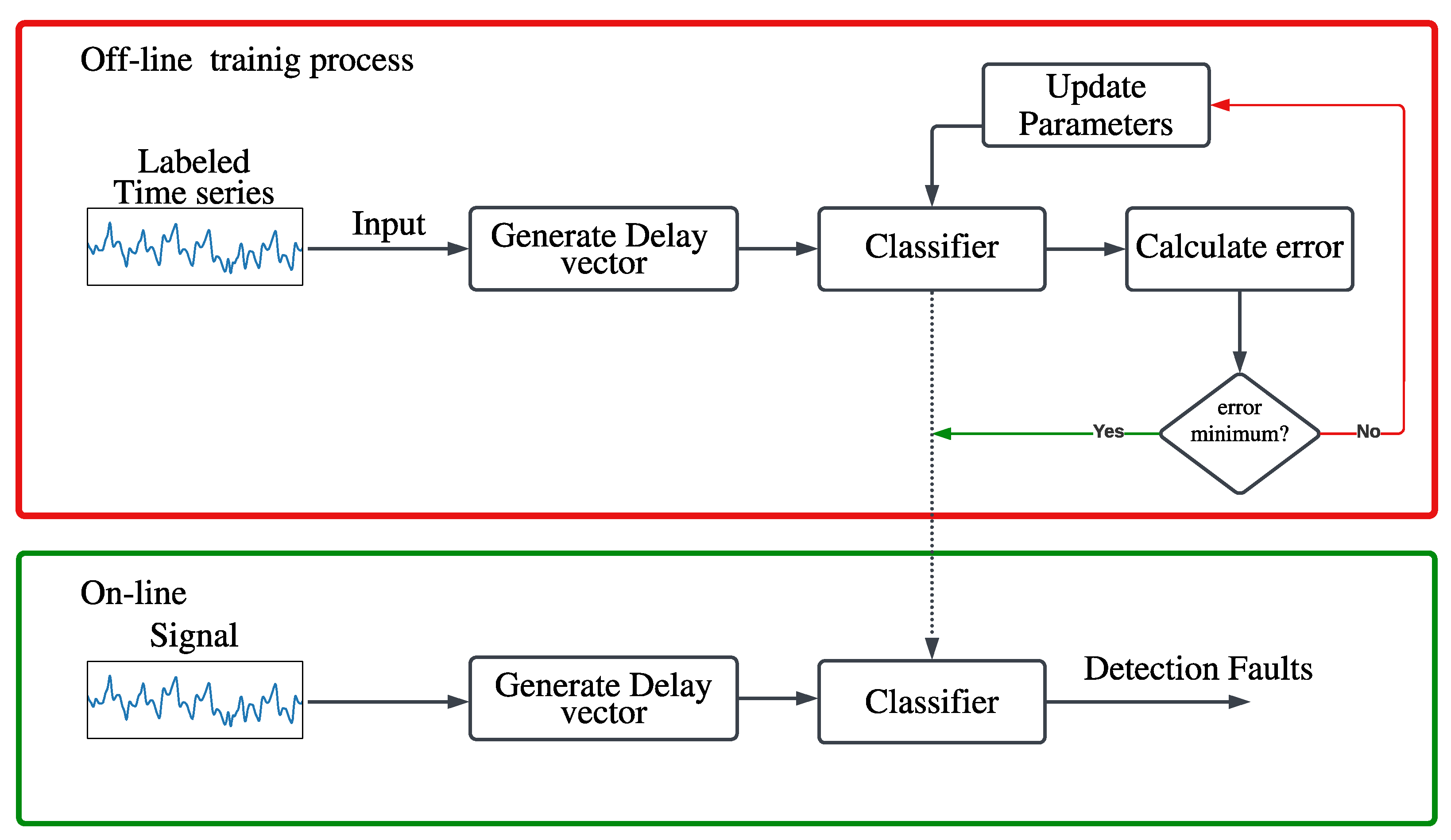
4. Proposed Method Based on Deep Neural Networks
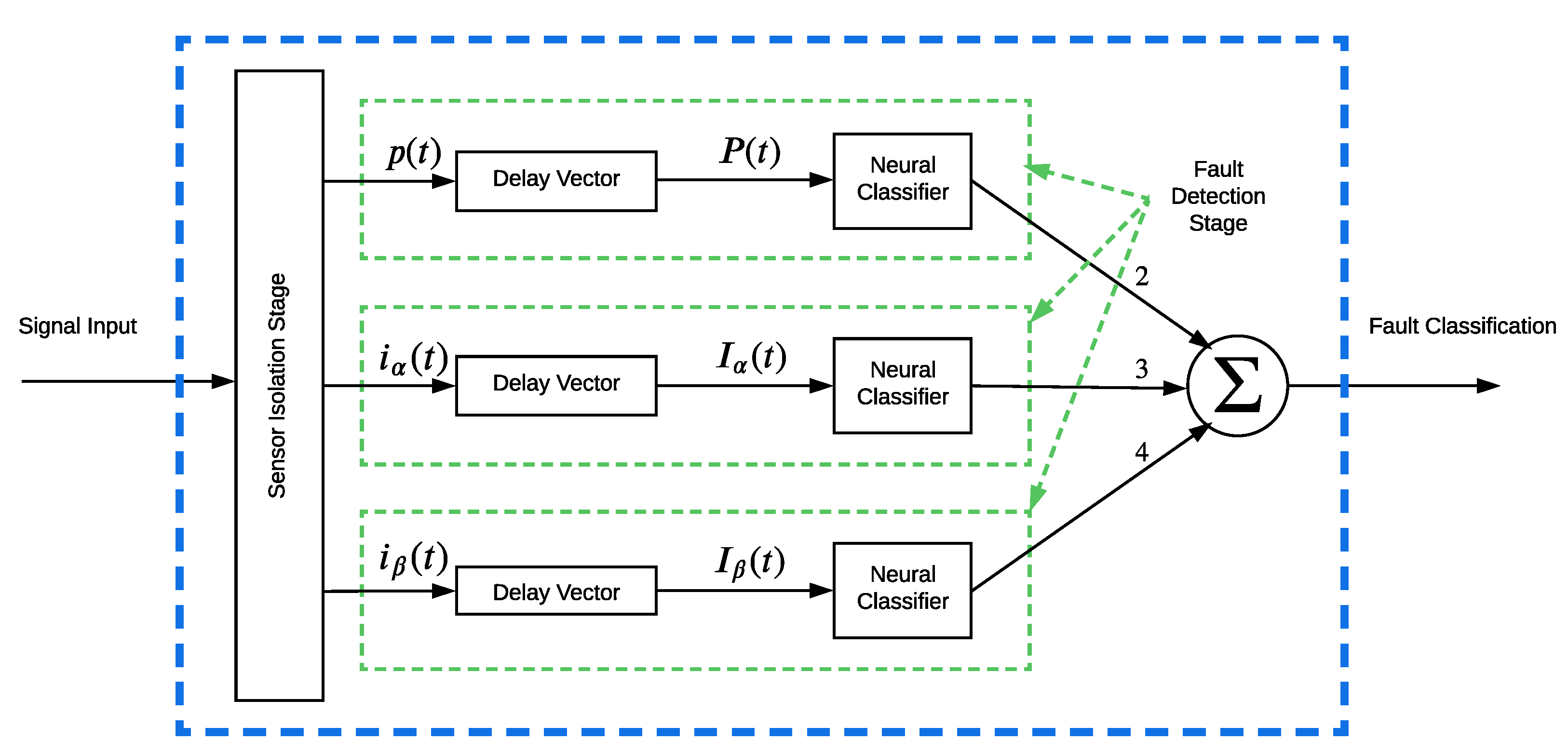
4.1. Fault-Isolation Logic
4.2. Fault-Detection Logic
4.3. Architecture of the Proposed NN Classifier
- Position channel neural classifier architecture: For the fault classification of the position sensor, the four proposed neural networks were tested. Each neural network has two inputs, corresponding to the delayed vector that is generated to add context to the classification. All neural networks have one output. The hidden layers and neurons for each neural network are as follows: MLP has 2 hidden layers with 20 neurons in each layer; LSTM contains 1 hidden layer with 15 LSTM cells; BiLSTM contains 1 layer with 15 LSTM cells for the forward state and 15 neurons for the hidden backward state layer; finally, the CNN contains 1 convolution + ReLu layer with 20 filters, followed by 1 pooling and 2 dense layers.
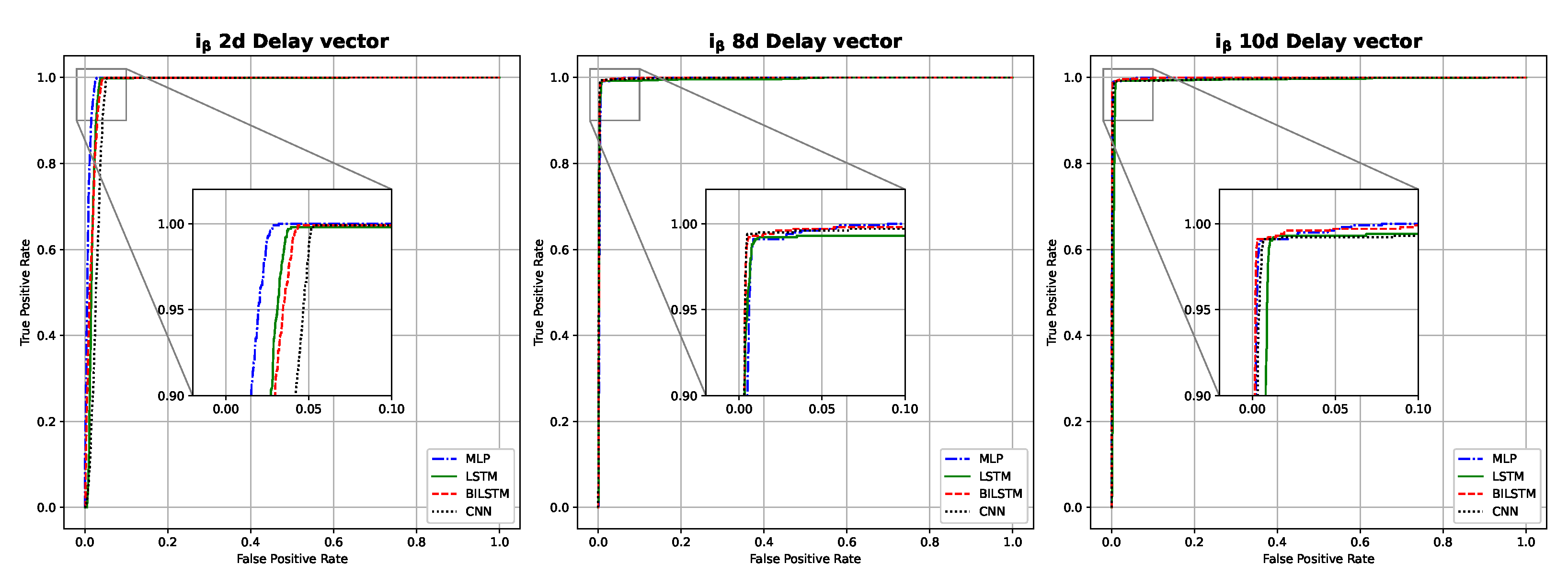
- Current channel neural classifier architecture: In the current sensors, different dimensions are explored for the delay vectors. These are dimension 8, the delay vector ; and dimension 10, , where t is the current sample. Therefore, the numbers of inputs of the neural networks are 8 and 10, and there is only 1 output. The numbers of hidden layers and neurons are the same as the aforementioned for all inputs for the MLP, LSTM and BiLSTM. The CNN has a convolution + ReLu layer, a pooling layer and two dense fully connected layers; the numbers of filters and neurons per layer are as shown in Table 3:
| Inputs | Convolution + ReLu | Dense | Dense | Outputs |
|---|---|---|---|---|
| + Pooling Layer | Layer 1 | Layer 2 | ||
| 8 | 20 | 140 | 100 | 1 |
| 10 | 20 | 180 | 100 | 1 |
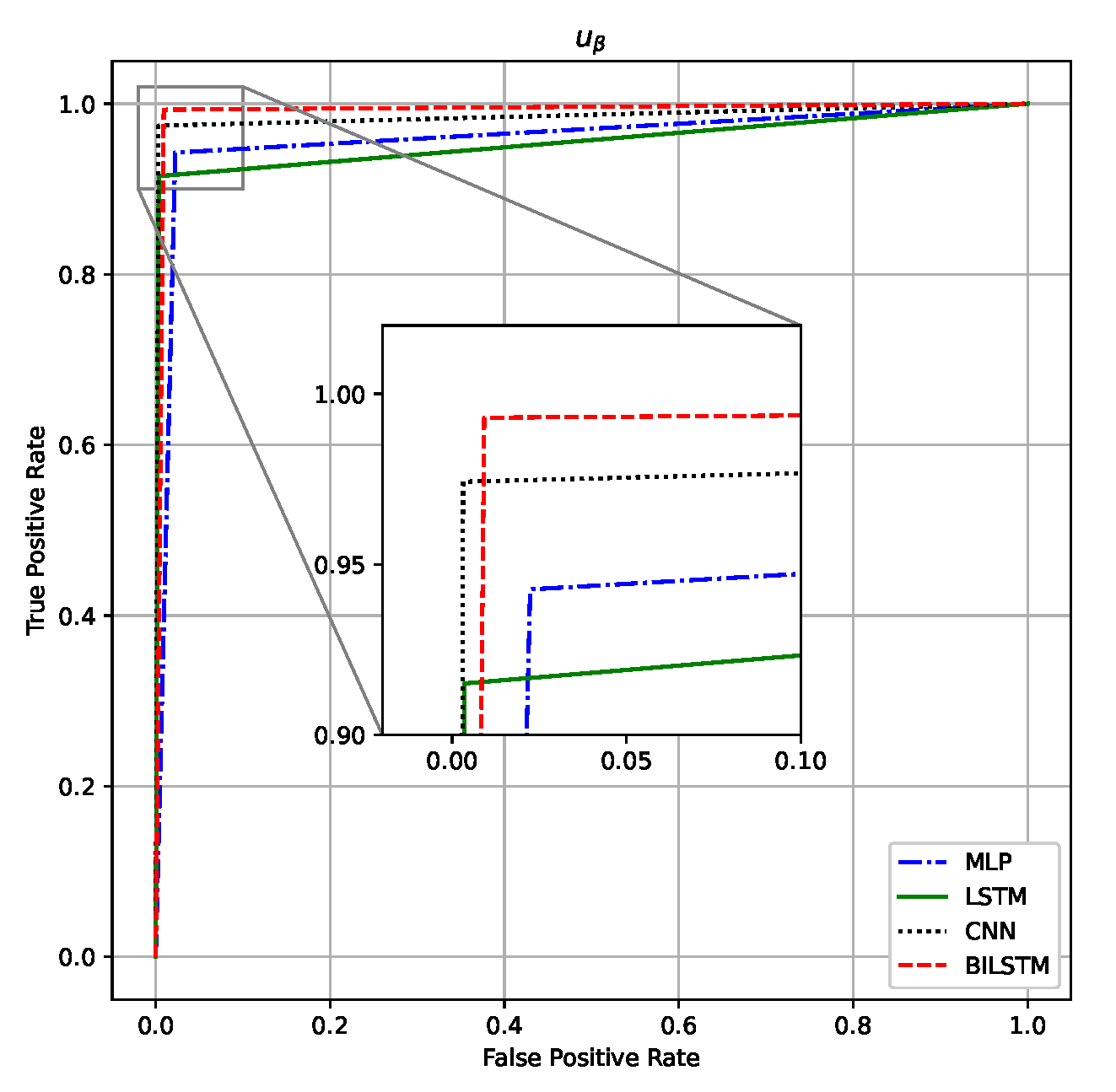
- Actuator voltage channel neural classifier architecture: Similarly, for the actuator voltages, the delay vector dimensions of 8 and 10 were used, so the vectors were and . Since the actuator voltage channel signals are similar to the current channel signals, the same architecture was used.
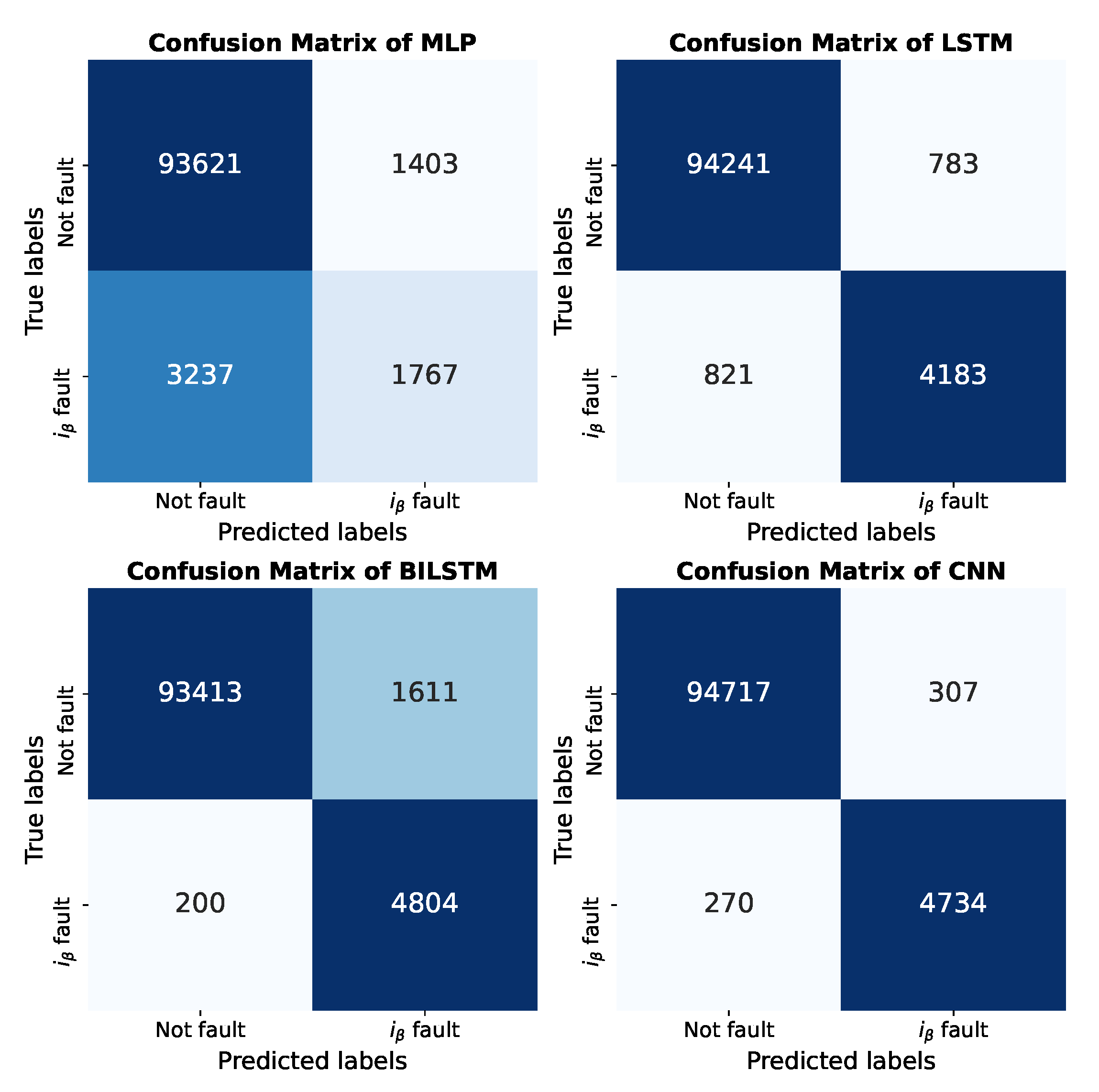
5. Results
Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alanis, A.Y.; Alvarez, J.G. Real-time model-free resilient control for discrete nonlinear systems. Asian J. Control 2021, 23, 2097–2111. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Zhang, H. Neural network-based model-free adaptive fault-tolerant control for discrete-time nonlinear systems with sensor fault. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2351–2362. [Google Scholar] [CrossRef]
- Bonivento, C.; Isidori, A.; Marconi, L.; Paoli, A. Implicit fault-tolerant control: Application to induction motors. Automatica 2004, 40, 355–371. [Google Scholar] [CrossRef]
- Abid, A.; Khan, M.T.; Lang, H.; de Silva, C.W. Adaptive system identification and severity index-based fault diagnosis in motors. IEEE/ASME Trans. Mechatron. 2019, 24, 1628–1639. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; De Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Trans. Mechatron. 2017, 23, 101–110. [Google Scholar] [CrossRef]
- Rodriguez-Guerra, J.; Calleja, C.; Pujana, A.; Elorza, I.; Macarulla, A.M. Fault-tolerant control study and classification: Case study of a hydraulic-press model simulated in real-time. Int. J. Electr. Inf. Eng. 2019, 13, 115–127. [Google Scholar]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1700–1716. [Google Scholar] [CrossRef]
- Gouichiche, A.; Safa, A.; Chibani, A.; Tadjine, M. Global fault-tolerant control approach for vector control of an induction motor. Int. Trans. Electr. Energy Syst. 2020, 30, e12440. [Google Scholar] [CrossRef]
- Raisemche, A.; Boukhnifer, M.; Larouci, C.; Diallo, D. Two active fault-tolerant control schemes of induction-motor drive in EV or HEV. IEEE Trans. Veh. Technol. 2013, 63, 19–29. [Google Scholar] [CrossRef]
- Raisemche, A.; Boukhnifer, M.; Diallo, D. New fault-tolerant control architectures based on voting algorithms for electric vehicle induction motor drive. Trans. Inst. Meas. Control 2016, 38, 1120–1135. [Google Scholar] [CrossRef]
- Salmasi, F.R.; Najafabadi, T.A. An adaptive observer with online rotor and stator resistance estimation for induction motors with one phase current sensor. IEEE Trans. Energy Convers. 2011, 26, 959–966. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Wang, B.; Huang, X.; Xu, D. Current sensor fault diagnosis and tolerant control for VSI-based induction motor drives. IEEE Trans. Power Electron. 2017, 33, 4238–4248. [Google Scholar] [CrossRef]
- Manohar, M.; Das, S. Current sensor fault-tolerant control for direct torque control of induction motor drive using flux-linkage observer. IEEE Trans. Ind. Inform. 2017, 13, 2824–2833. [Google Scholar] [CrossRef]
- Romero, M.; Seron, M.; De Dona, J. Sensor fault-tolerant vector control of induction motors. IET Control Theory Appl. 2010, 4, 1707–1724. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, S.; Liu, X. Neural network-based model-free adaptive near-optimal tracking control for a class of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6227–6241. [Google Scholar] [CrossRef]
- Yin, X.; Jiang, Z.; Pan, L. Recurrent neural network based adaptive integral sliding mode power maximization control for wind power systems. Renew. Energy 2020, 145, 1149–1157. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Challenges and opportunities of deep learning models for machinery fault detection and diagnosis: A review. IEEE Access 2019, 7, 122644–122662. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.D.; Koo, I.S. A distributed sensor-fault detection and diagnosis framework using machine learning. Inf. Sci. 2021, 547, 777–796. [Google Scholar] [CrossRef]
- Rkhissi-Kammoun, Y.; Ghommam, J.; Boukhnifer, M.; Mnif, F. Two current sensor fault detection and isolation schemes for induction motor drives using algebraic estimation approach. Math. Comput. Simul. 2019, 157, 39–62. [Google Scholar] [CrossRef]
- Junior, R.F.R.; dos Santos Areias, I.A.; Campos, M.M.; Teixeira, C.E.; da Silva, L.E.B.; Gomes, G.F. Fault detection and diagnosis in electric motors using 1d convolutional neural networks with multi-channel vibration signals. Measurement 2022, 190, 110759. [Google Scholar] [CrossRef]
- Leite, D.; Martins Jr, A.; Rativa, D.; De Oliveira, J.F.; Maciel, A.M. An Automated Machine Learning Approach for Real-Time Fault Detection and Diagnosis. Sensors 2022, 22, 6138. [Google Scholar] [CrossRef]
- Shahnazari, H. Fault diagnosis of nonlinear systems using recurrent neural networks. Chem. Eng. Res. Des. 2020, 153, 233–245. [Google Scholar] [CrossRef]
- Ghosh, A.; Wang, G.N.; Lee, J. A novel automata and neural network based fault diagnosis system for PLC controlled manufacturing systems. Comput. Ind. Eng. 2020, 139, 106188. [Google Scholar] [CrossRef]
- Taqvi, S.A.; Tufa, L.D.; Zabiri, H.; Maulud, A.S.; Uddin, F. Fault detection in distillation column using NARX neural network. Neural Comput. Appl. 2020, 32, 3503–3519. [Google Scholar] [CrossRef]
- Alrifaey, M.; Lim, W.H.; Ang, C.K.; Natarajan, E.; Solihin, M.I.; Juhari, M.R.M.; Tiang, S.S. Hybrid deep learning model for fault detection and classification of grid-connected photovoltaic system. IEEE Access 2022, 10, 13852–13869. [Google Scholar] [CrossRef]
- Parisi, L.; Zaernia, A.; Ma, R.; Youseffi, M. m-ark-Support Vector Machine for Early Detection of Parkinson’s Disease from Speech Signals. Int. J. Math. Comput. Simul. 2021, 15, 34. [Google Scholar] [CrossRef]
- Maragatham, G.; Devi, S. LSTM model for prediction of heart failure in big data. J. Med. Syst. 2019, 43, 111. [Google Scholar] [CrossRef]
- Verner, A.; Mukherjee, S. An LSTM-Based Method for Detection and Classification of Sensor Anomalies. In Proceedings of the 2020 5th International Conference on Machine Learning Technologies, Beijing, China, 19–21 June 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 39–45. [Google Scholar] [CrossRef]
- Chen, K.Y.; Chen, L.S.; Chen, M.C.; Lee, C.L. Using SVM based method for equipment fault detection in a thermal power plant. Comput. Ind. 2011, 62, 42–50. [Google Scholar] [CrossRef]
- Rodriguez, A.; Bourne, D.; Mason, M.; Rossano, G.F.; Wang, J. Failure detection in assembly: Force signature analysis. In Proceedings of the 2010 IEEE International Conference on Automation Science and Engineering, Mexico City, Mexico, 20–24 August 2010; pp. 210–215. [Google Scholar] [CrossRef]
- Abdul, Z.K.; Al-Talabani, A.K.; Ramadan, D.O. A Hybrid Temporal Feature for Gear Fault Diagnosis Using the Long Short Term Memory. IEEE Sens. J. 2020, 20, 14444–14452. [Google Scholar] [CrossRef]
- Chu, R.; Zhang, R.; Huang, Q.; Yang, K. TDV-LSTM: A New Methodology for Series Arc Fault Detection in Low Power AC Systems. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; pp. 2319–2324. [Google Scholar] [CrossRef]
- Sabir, R.; Rosato, D.; Hartmann, S.; Guehmann, C. LSTM Based Bearing Fault Diagnosis of Electrical Machines using Motor Current Signal. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning Additionally, Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 613–618. [Google Scholar] [CrossRef]
- Zhang, J.; Swain, A.K.; Nguang, S.K. Robust Observer-Based Fault Diagnosis for Nonlinear Systems Using MATLAB®; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Ogunmolu, O.; Gu, X.; Jiang, S.; Gans, N. Nonlinear systems identification using deep dynamic neural networks. arXiv 2016, arXiv:1610.01439. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- Sejnowski, T.J.; Rosenberg, C.R. Parallel networks that learn to pronounce English text. Complex Syst. 1987, 1, 145–168. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhai, X.; Ali, A.A.S.; Amira, A.; Bensaali, F. MLP neural network based gas classification system on Zynq SoC. IEEE Access 2016, 4, 8138–8146. [Google Scholar] [CrossRef]
- Lim, T.; Ratnam, M.; Khalid, M. Automatic classification of weld defects using simulated data and an MLP neural network. Insight-Non Test. Cond. Monit. 2007, 49, 154–159. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Qi, C.; Li, Y.; Wu, Z. Prediction and Compensation of Contour Error of CNC Systems Based on LSTM Neural-Network. IEEE/ASME Trans. Mechatron. 2021, 27, 572–581. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time series classification using multi-channels deep convolutional neural networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; pp. 298–310. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef] [Green Version]
- Pang, X.; Xue, X.; Jiang, W.; Lu, K. An Investigation into Fault Diagnosis of Planetary Gearboxes using a Bispectrum Convolutional Neural Network. IEEE/ASME Trans. Mechatron. 2020, 26, 2027–2037. [Google Scholar] [CrossRef]
- Chen, S.; Meng, Y.; Tang, H.; Tian, Y.; He, N.; Shao, C. Robust deep learning-based diagnosis of mixed faults in rotating machinery. IEEE/ASME Trans. Mechatron. 2020, 25, 2167–2176. [Google Scholar] [CrossRef]
- Xing, Z.; Pei, J.; Keogh, E. A brief survey on sequence classification. ACM SIGKDD Explor. Newsl. 2010, 12, 40–48. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S. Bayesian common spatial patterns for multi-subject EEG classification. Neural Netw. 2014, 57, 39–50. [Google Scholar] [CrossRef]
- Fu, Y. Human Activity Recognition and Prediction; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Geurts, P. Pattern extraction for time series classification. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery, Freiburg, Germany, 3–5 September 2001; pp. 115–127. [Google Scholar]
- Pavlovic, V.; Frey, B.J.; Huang, T.S. Time-series classification using mixed-state dynamic Bayesian networks. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), Fort Collins, CO, USA, 23–25 June 1999; Volume 2, pp. 609–615. [Google Scholar]
- Yu, Z.; Lee, M. Real-time human action classification using a dynamic neural model. Neural Netw. 2015, 69, 29–43. [Google Scholar] [CrossRef]
- Perea, J.A.; Harer, J. Sliding windows and persistence: An application of topological methods to signal analysis. Found. Comput. Math. 2015, 15, 799–838. [Google Scholar] [CrossRef] [Green Version]
- Cerda, J.; Cifuentes, L. Uso de curvas ROC en investigación clínica: Aspectos teórico-prácticos. Rev. Chil. Infectol. 2012, 29, 138–141. [Google Scholar] [CrossRef]
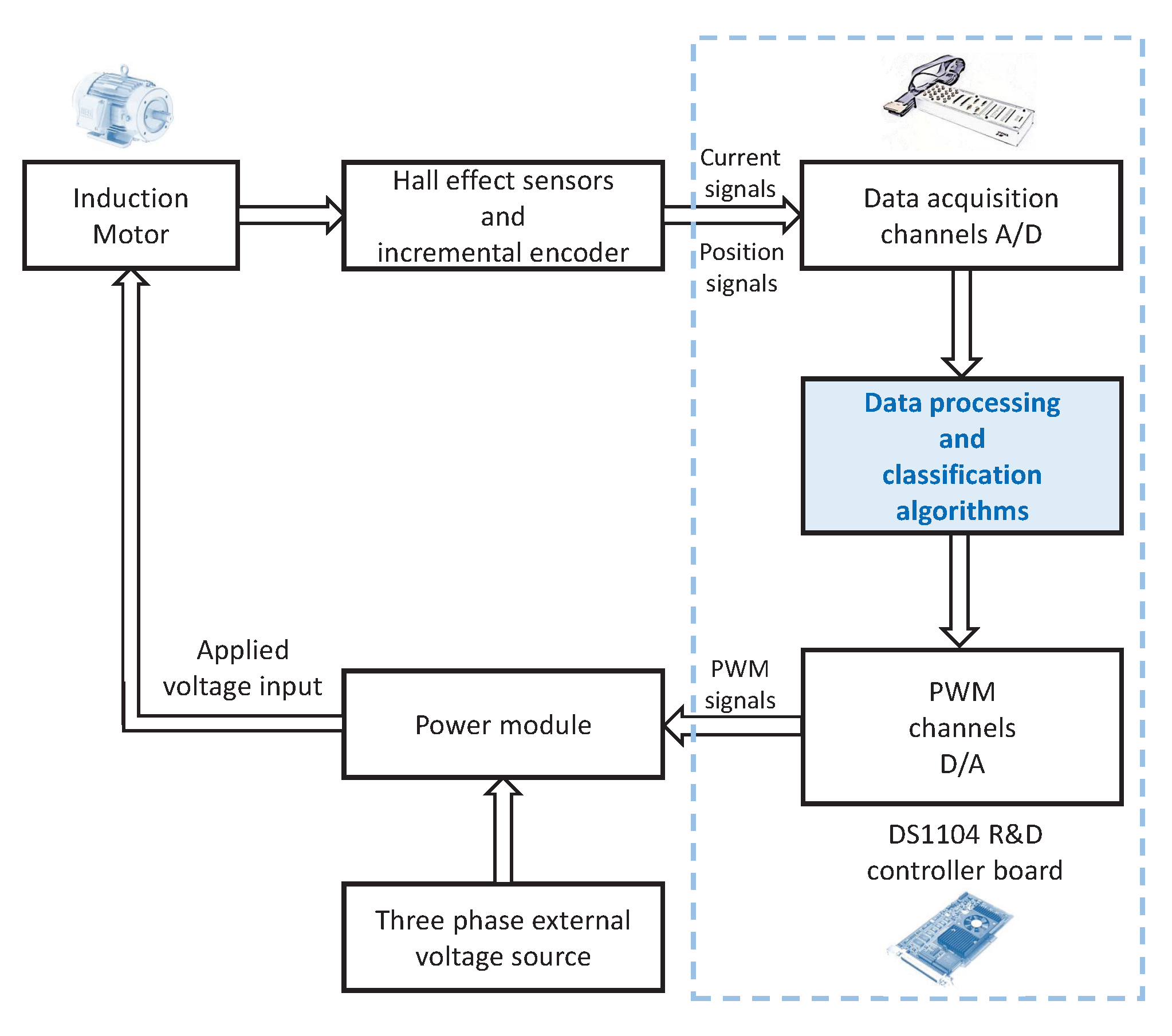
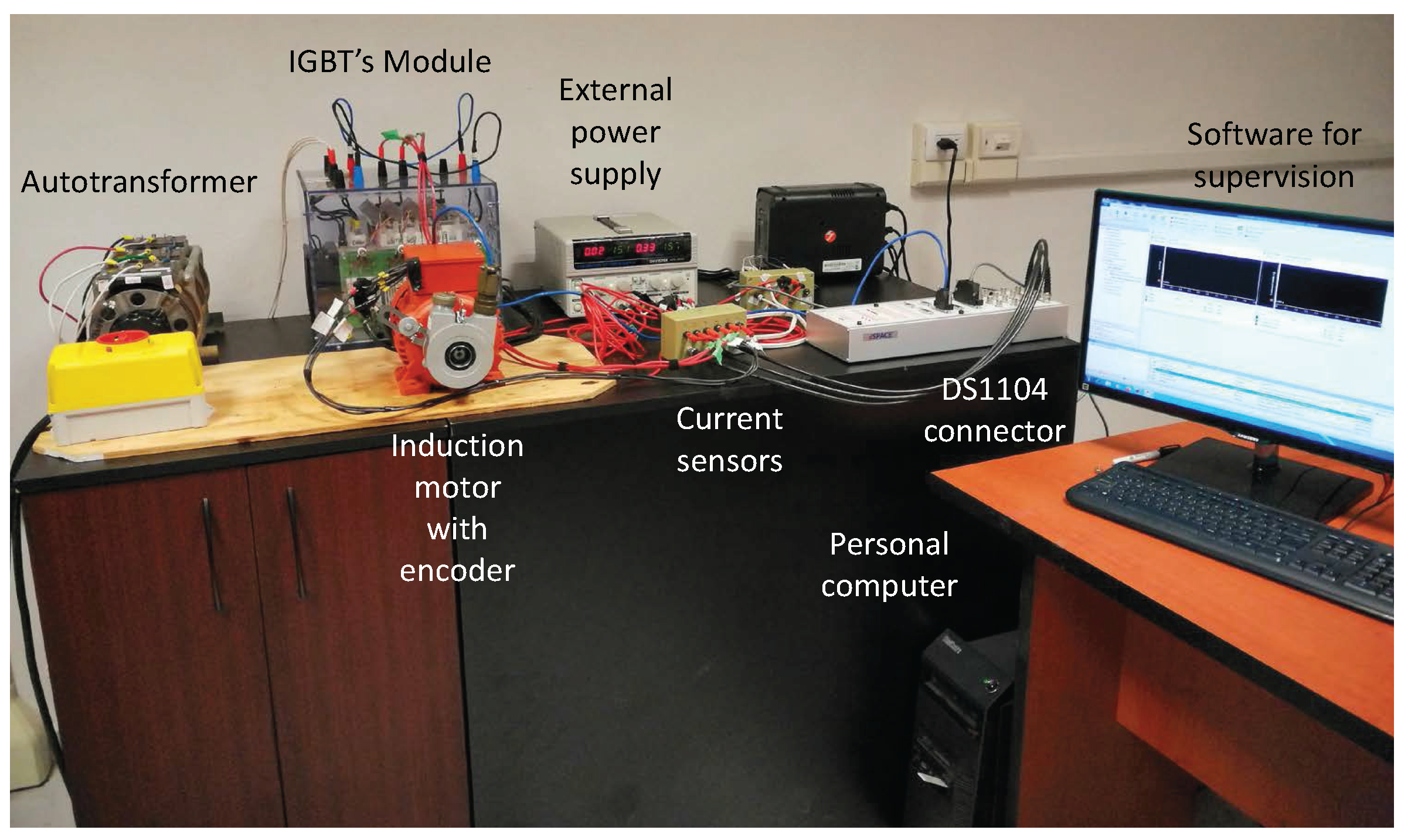










| Label | Fault |
|---|---|
| 0 | Healthy |
| 1 | None |
| 2 | Position |
| 3 | Current |
| 4 | Current |
| 5 | Position and current |
| 6 | Position and current |
| 7 | Current and current |
| 8 | None |
| 9 | Position, current and current |
| Label | Fault |
|---|---|
| 0 | Healthy |
| 1 | Voltage |
| 2 | Voltage |
| 3 | Voltage and voltage |
| Neural Network | MLP | LSTM | BiLSTM | CNN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Channel | Sensor | d | AUC | CA | AUC | CA | AUC | CA | AUC | CA |
| 1 | Position | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | Current | 8 | 0.9790 | 0.9665 | 0.9864 | 0.9778 | 0.9873 | 0.9381 | 0.9845 | 0.9665 |
| 10 | 0.9783 | 0.9666 | 0.9791 | 0.9675 | 0.9787 | 0.9318 | 0.9965 | 0.9909 | ||
| 3 | Current | 8 | 0.9867 | 0.9741 | 0.9954 | 0.9892 | 0.9914 | 0.9823 | 0.9878 | 0.9731 |
| 10 | 0.9862 | 0.9718 | 0.9961 | 0.9896 | 0.9902 | 0.9821 | 0.9983 | 0.9942 | ||
| 4 | Voltage | 8 | 0.9801 | 0.9678 | 0.9971 | 0.9905 | 0.9962 | 0.9887 | 0.9963 | 0.9807 |
| 10 | 0.9758 | 0.9759 | 0.9972 | 0.9907 | 0.9964 | 0.9890 | 0.9987 | 0.9957 | ||
| 5 | Voltage | 8 | 0.9883 | 0.8737 | 0.9973 | 0.9911 | 0.9971 | 0.9907 | 0.9920 | 0.9753 |
| 10 | 0.9846 | 0.8823 | 0.9972 | 0.9845 | 0.9965 | 0.9909 | 0.9985 | 0.9930 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez, O.D.; Martinez-Soltero, G.; Alvarez, J.G.; Alanis, A.Y. Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors. Machines 2022, 10, 1198. https://doi.org/10.3390/machines10121198
Sanchez OD, Martinez-Soltero G, Alvarez JG, Alanis AY. Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors. Machines. 2022; 10(12):1198. https://doi.org/10.3390/machines10121198
Chicago/Turabian StyleSanchez, Oscar D., Gabriel Martinez-Soltero, Jesus G. Alvarez, and Alma Y. Alanis. 2022. "Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors" Machines 10, no. 12: 1198. https://doi.org/10.3390/machines10121198
APA StyleSanchez, O. D., Martinez-Soltero, G., Alvarez, J. G., & Alanis, A. Y. (2022). Real-Time Neural Classifiers for Sensor and Actuator Faults in Three-Phase Induction Motors. Machines, 10(12), 1198. https://doi.org/10.3390/machines10121198







