Hybrid Feature Selection Framework for Bearing Fault Diagnosis Based on Wrapper-WPT
Abstract
1. Introduction
- (1)
- the proposed bearing feature-selection method based on Wrapper-WPT is constructed to avoid the common disadvantage of homogeneous energy feature extraction from the reconstructed signals by extracting a variety of heterogenous features with various sensitivities;
- (2)
- the proposed method allows the most discriminant information from the whole WPT decomposition level to be obtained, without any premature decisions on the usability of certain nodes for inter-class data separation based on various metrics at the signal processing stage.
2. Bearing Faults Theoretical Background
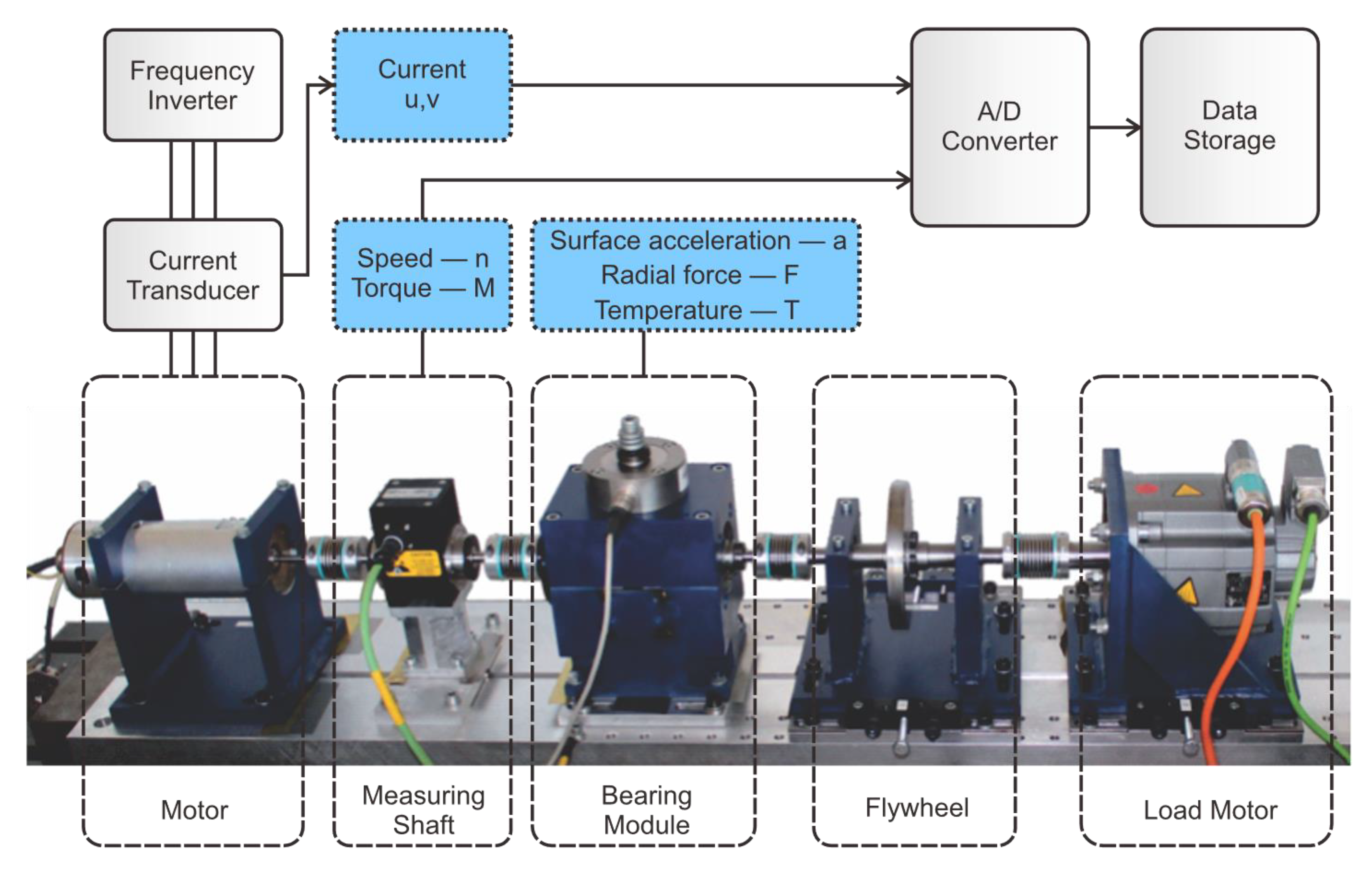
3. Experimental Setup and Data Collection
3.1. Paderborn University Bearing Dataset
3.2. Case Western Reserve University Bearing Dataset
4. Proposed Methodology
4.1. Bearing Vibration Signal Preprocessing
Hilbert Transform Envelope
4.2. Wrapper-WPT
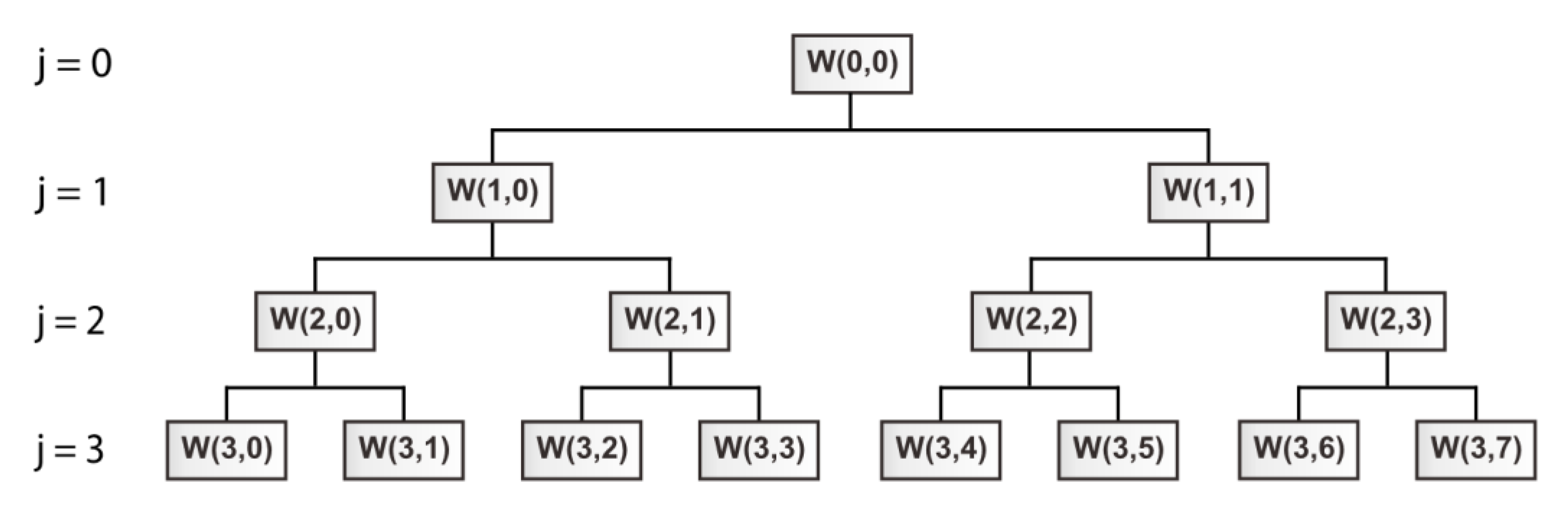
4.2.1. Wavelet Packet Transform Base Theory
4.2.2. Mother Wavelet Selection
4.3. Feature Extraction and Selection
4.3.1. Boruta Feature Selection
- The Boruta algorithm creates several copies of all original attributes—Shadow Attributes (SA);
- Then, the attributes are shuffled and permutated to remove their correlation with the response. The obtained randomized feature set is added to the original feature set to bring randomness to the feature attributes, constructing the Extended Information System (EIS);
- The Random Forest classifier is fitted to the EIS several times. The SA within the EIS is randomized for each run. Thus, every SA part of the EIS is unique for every iteration;
- The importance of every feature attribute, called the Z score, is computed for each run. In order to compute the Z scores, the EIS is divided into several bootstrapped sets of samples (BSSs) equal to the number of decision trees used for training the Random Forest algorithm. Accordingly, the same number of the out of the bag samples (OBSs) are used for testing the performance of each corresponding decision tree. The number of votes for the correct class is recorded for every attribute from the EIS. After that, the values of the OBSs are permutated and the class votes of the DTs are recorded once again. The importance value for the attribute for each DT—mean decrease in accuracy (MDA) is calculated as follows:The importance of the attribute values for the whole Random Forest are calculated as follows:The final importance score is calculated as:
- The maximum Z score among shadow attributes (MZSA) is found. A hit is assigned to every real attribute with a Z score higher than MZSA;
- The real attributes that scored significantly lower than MZSA are deemed as non-important and eliminated;
- The real attributes that scored significantly higher than MZSA are deemed as important;
- All Shadow Attributes are removed;
- The procedure is repeated until the importance is assigned to each attribute or the algorithm has reached the user-defined limit of Random Forest runs.
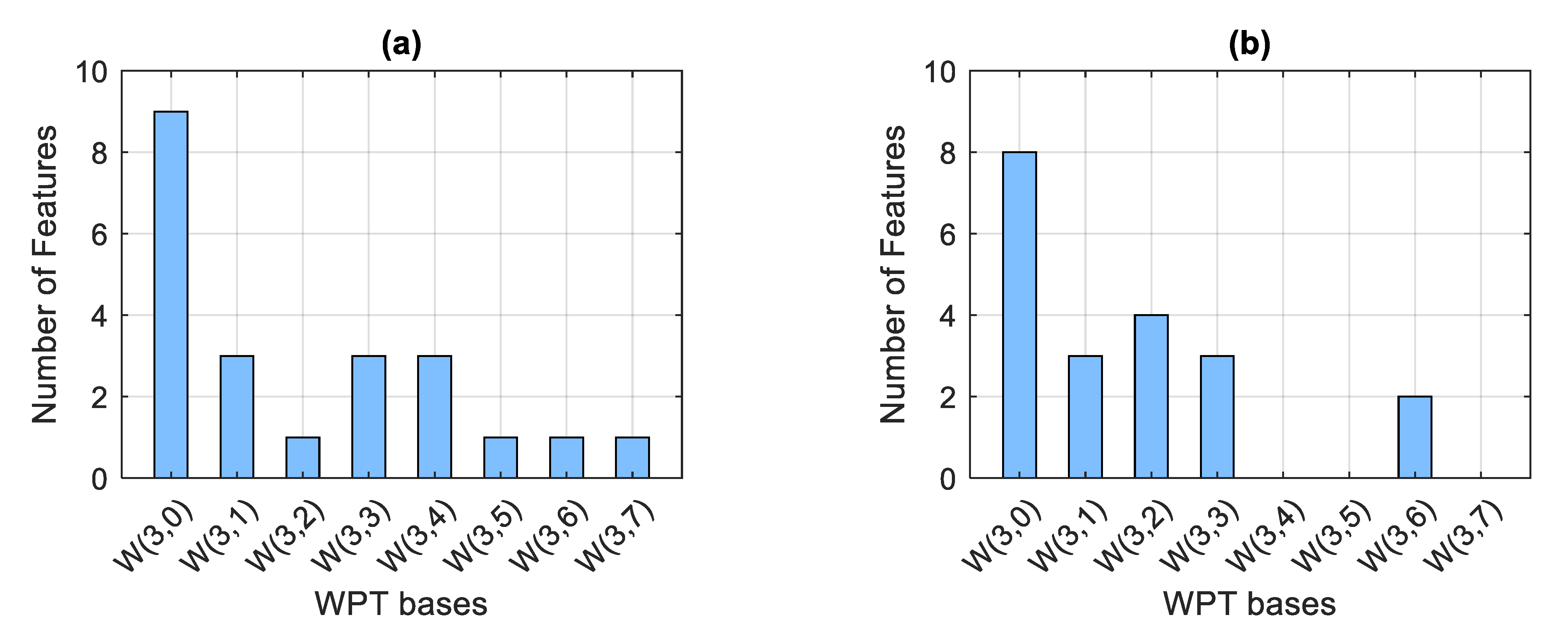
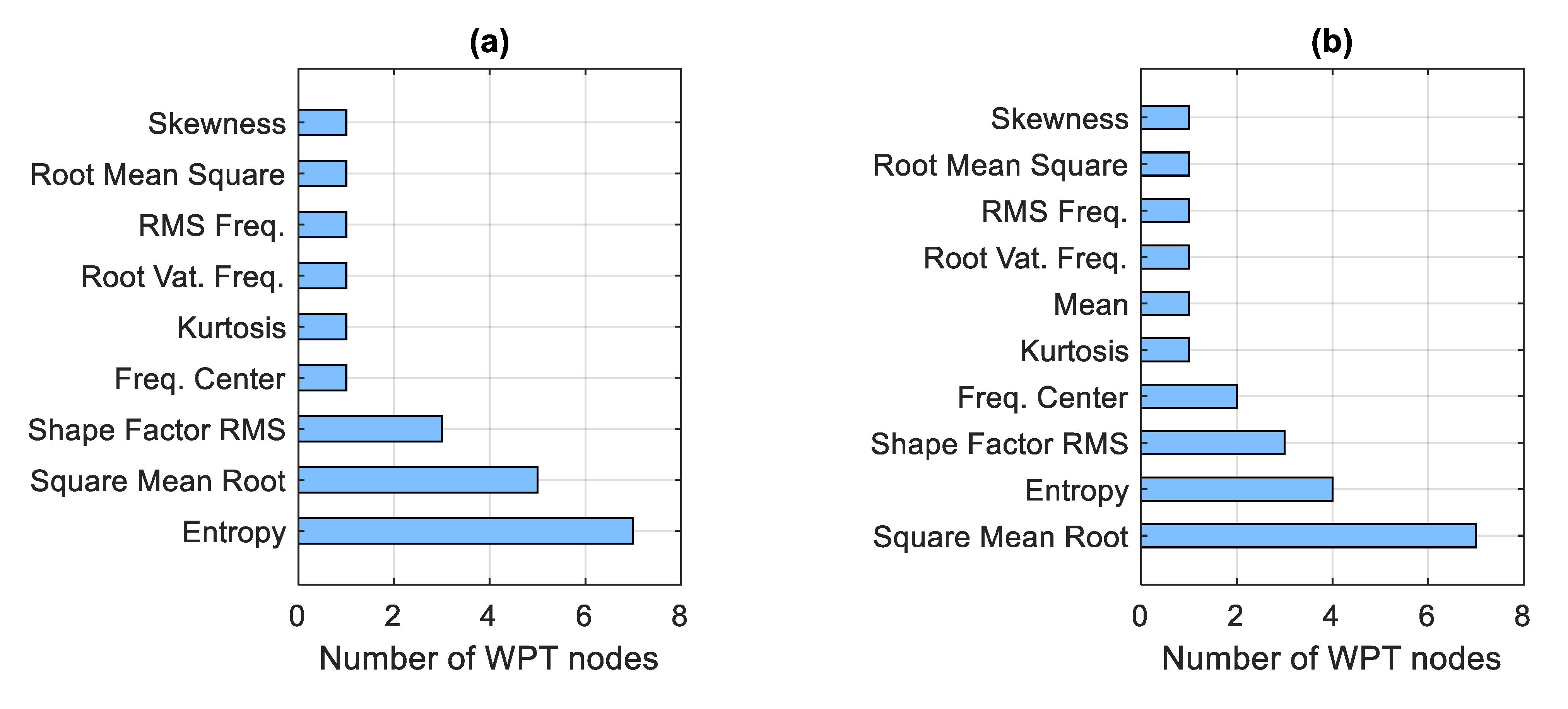
4.3.2. Selected Feature Set Analysis
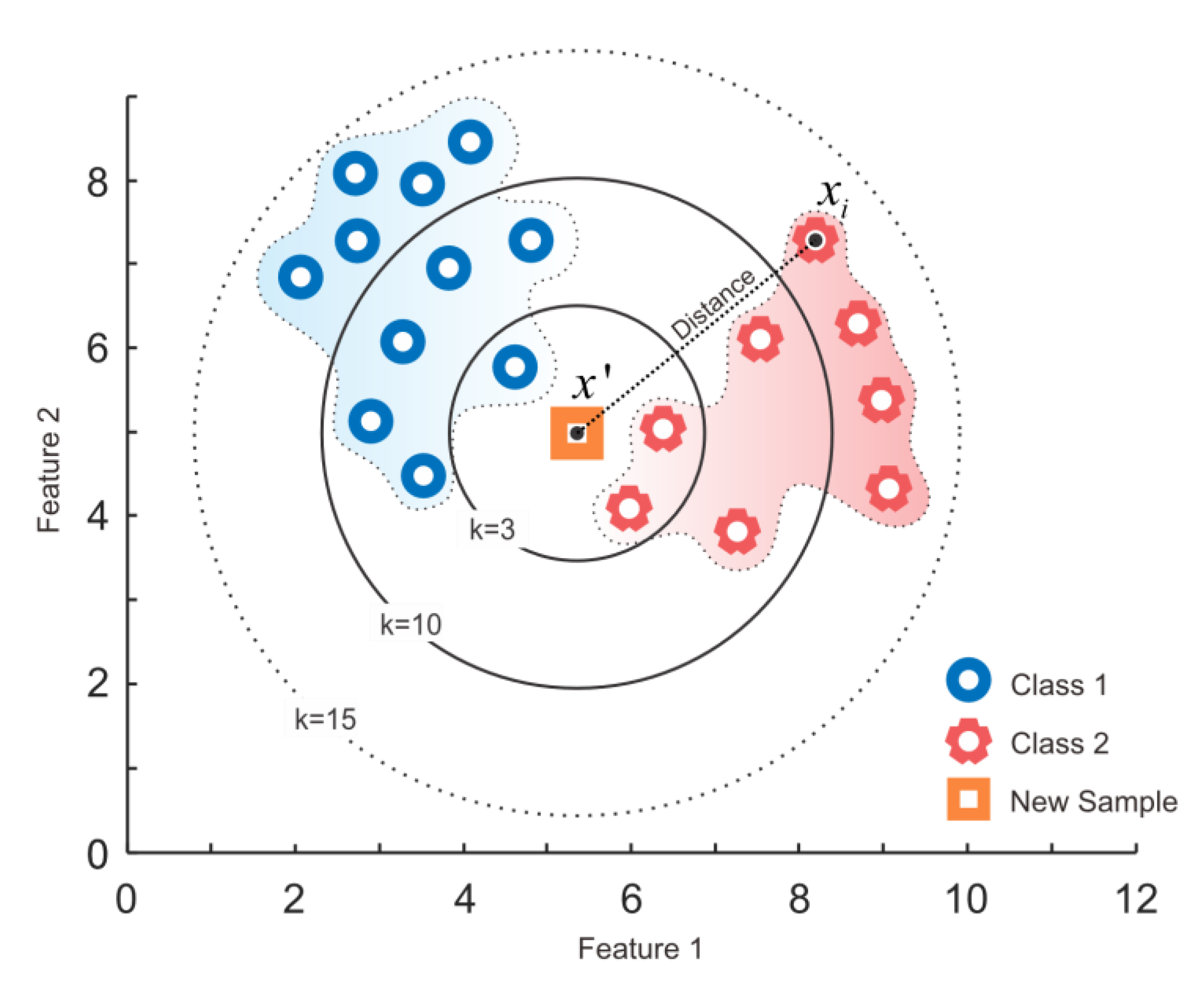
4.4. Subspace k-NN
5. Results and Performance Evaluation for Fault Identification
Performance Comparison
- (1)
- Yan et al. [18] extracted energy features from a WPT decomposed signal and used the Random Forest algorithm for classification. After extracting the same energy features from the decomposed signal using the PU experimental data and applying Random Forest, we obtained a 99.70% accuracy result for the real fault data and 94.10% for the artificial data, which is less than the proposed method, though this method has the closest performance levels among the comparison methods. This can be explained by the fact that both the proposed method and the method developed by Yan et al. utilized a powerful Random Forest algorithm, inside the Boruta feature selection for the first and as a classifier for the latter. However, the drawback of the comparison method is that there is no feature variability. The single energy feature compared to a set of different statistical features from time and frequency domain lacks sensitivity and thus yields less discriminant information;
- (2)
- For the second comparison, as demonstrated in the method developed by Surti et al. [58], the bearing vibration signal from the PU experiment data was decomposed using WPT and the statistical features from Table 5 were extracted. Classification was completed using k-NN with five nearest neighbors. The method yielded 92.12% accuracy for real fault data and 90.19% for artificial fault data. The underperformance of this method in comparison with the proposed method can be attributed to the absence of feature selection and thus presence of the less discriminant or possibly junk features detrimental for classification performance in the method’s feature vector. Additionally, the simple k-NN algorithm is known as a weaker classifier compared with Subspace k-NN;
- (3)
- The method developed by Yadavar Nikravesh [30] et al. decomposed the bearing vibration signal using WPT, extracted energy features and forwards the feature set to a Gaussian kernel SVM for classification. To make a correct comparison, the energy features were extracted from WPT decomposed experimental data bearing vibration signal and classification was executed by the Gaussian kernel SVM classifier. Accuracy yielded by the comparison method with real fault data is 89.96% and accuracy with the artificial fault data is 90.76%, which is lower than the proposed method for the reason of low feature variability similarly to the method developed by Yan et al, meaning that this comparison method is likely to show a better performance on the feature vector that would contain features of different domains;
- (4)
- For the fourth comparison method, the best energy node out of the third decomposition level was selected, then statistical features from Table 5 were extracted and the resulting feature set was forwarded to the Subspace k-NN for classification. The accuracy result for the real fault data is 93.07% and 91.58% for the artificial fault data. The lower accuracy in comparison with the proposed method can be explained by not utilizing the whole WPT decomposition level, which means leaving a significant amount of fault-related information untouched. Then, for the same reason, utilization of the whole WPT decomposition level by the proposed method becomes an advantage and is considered as a part of the proposed method contribution;
- (5)
- The proposed method together with Chi-Squared test for feature selection instead of Boruta algorithm showed slightly lower accuracies for two PU datasets; however, it performed better on the CWRU dataset. This close performance can be explained by the fact that this comparison method shares most of the structure with the proposed method and only differs in the feature selection step; however, we observed that the feature pools created by this algorithm for all datasets contain energy of signal feature as a predominant one which strongly resembles the feature pools of comparison method one and three, which utilized only energy of signal features;
- (6)
- The last comparison method is the Deep Learning Attention Stream Network. This method showed very high classification performance without any signal preprocessing. However, the authors believe that if WPT signal processing had been considered, the accuracy of this method on given data would have reached 100%.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bazurto, A.J.; Quispe, E.C.; Mendoza, R.C. Causes and failures classification of industrial electric motor. In Proceedings of the 2016 IEEE ANDESCON, Arequipa, Peru, 19–21 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Shen, W.; Huang, C. Online Fault Diagnosis Method Based on Transfer Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2020, 69, 509–520. [Google Scholar] [CrossRef]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace, and Automotive Applications; Wiley: Chichester, UK; Hoboken, NJ, USA, 2011. [Google Scholar]
- Maliuk, A.S.; Prosvirin, A.E.; Ahmad, Z.; Kim, C.H.; Kim, J.-M. Novel Bearing Fault Diagnosis Using Gaussian Mixture Model-Based Fault Band Selection. Sensors 2021, 21, 6579. [Google Scholar] [CrossRef] [PubMed]
- Tandon, N. A comparison of some vibration parameters for the condition monitoring of rolling element bearings. Measurement 1994, 12, 285–289. [Google Scholar] [CrossRef]
- Sun, J.; Yan, C.; Wen, J. Intelligent Bearing Fault Diagnosis Method Combining Compressed Data Acquisition and Deep Learning. IEEE Trans. Instrum. Meas. 2018, 67, 185–195. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Gong, H.; Deng, X. Multimodal loosening detection for threaded fasteners based on multiscale cross fuzzy entropy. Mech. Syst. Signal Process. 2023, 186, 109834. [Google Scholar] [CrossRef]
- Honarvar, F.; Martin, H.R. New Statistical Moments for Diagnostics of Rolling Element Bearings. J. Manuf. Sci. Eng. 1997, 119, 425–432. [Google Scholar] [CrossRef]
- Martin, H.R.; Honarvar, F. Application of statistical moments to bearing failure detection. Appl. Acoust. 1995, 44, 67–77. [Google Scholar] [CrossRef]
- Skora, M.; Ewert, P.; Kowalski, C.T. Selected Rolling Bearing Fault Diagnostic Methods in Wheel Embedded Permanent Magnet Brushless Direct Current Motors. Energies 2019, 12, 4212. [Google Scholar] [CrossRef]
- Chen, L.; Xu, G.; Tao, T.; Wu, Q. Deep Residual Network for Identifying Bearing Fault Location and Fault Severity Concurrently. IEEE Access 2020, 8, 168026–168035. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A Motor Current Signal-Based Bearing Fault Diagnosis Using Deep Learning and Information Fusion. IEEE Trans. Instrum. Meas. 2020, 69, 3325–3333. [Google Scholar] [CrossRef]
- Long, J.; Qin, Y.; Yang, Z.; Huang, Y.; Li, C. Discriminative feature learning using a multiscale convolutional capsule network from attitude data for fault diagnosis of industrial robots. Mech. Syst. Signal Process. 2023, 182, 109569. [Google Scholar] [CrossRef]
- Pang, S.; Yang, X. A Cross-Domain Stacked Denoising Autoencoders for Rotating Machinery Fault Diagnosis Under Different Working Conditions. IEEE Access 2019, 7, 77277–77292. [Google Scholar] [CrossRef]
- Cui, M.; Wang, Y.; Lin, X.; Zhong, M. Fault Diagnosis of Rolling Bearings Based on an Improved Stack Autoencoder and Support Vector Machine. IEEE Sens. J. 2021, 21, 4927–4937. [Google Scholar] [CrossRef]
- Toma, R.N.; Piltan, F.; Kim, J.-M. A Deep Autoencoder-Based Convolution Neural Network Framework for Bearing Fault Classification in Induction Motors. Sensors 2021, 21, 8453. [Google Scholar] [CrossRef] [PubMed]
- Saucedo-Dorantes, J.J.; Arellano-Espitia, F.; Delgado-Prieto, M.; Osornio-Rios, R.A. Diagnosis Methodology Based on Deep Feature Learning for Fault Identification in Metallic, Hybrid and Ceramic Bearings. Sensors 2021, 21, 5832. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Mu, H.; Yi, X.; Yang, Y.; Chen, G. Fault Diagnosis of Rolling Bearing with Small Samples Based on Wavelet Packet Theory and Random Forest. In Proceedings of the 2019 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 15–17 August 2019; pp. 305–310. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, T.; Luo, Z.; Sun, K. A Novel Rolling Bearing Fault Diagnosis and Severity Analysis Method. Appl. Sci. 2019, 9, 2356. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Chen, Z.; Xu, X. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Transform and Convolutional Neural Network. Appl. Sci. 2020, 10, 770. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Wang, F.; Sun, S. A Fault Diagnosis Method of Rolling Bearing Based on Wavelet Packet Analysis and Deep Forest. Symmetry 2022, 14, 267. [Google Scholar] [CrossRef]
- Zhu, H.; He, Z.; Wei, J.; Wang, J.; Zhou, H. Bearing Fault Feature Extraction and Fault Diagnosis Method Based on Feature Fusion. Sensors 2021, 21, 2524. [Google Scholar] [CrossRef]
- Bastami, A.R.; Aasi, A.; Arghand, H.A. Estimation of Remaining Useful Life of Rolling Element Bearings Using Wavelet Packet Decomposition and Artificial Neural Network. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 233–245. [Google Scholar] [CrossRef]
- Guo, W.; Wu, C.; Ding, Z.; Zhou, Q. Prediction of surface roughness based on a hybrid feature selection method and long short-term memory network in grinding. Int. J. Adv. Manuf. Technol. 2021, 112, 2853–2871. [Google Scholar] [CrossRef]
- Lu, P.; Sorathiya, V.; Lavadiya, S.; Luo, Y.; Nguyen, T.K.; Dhasarathan, V. A hybrid feature selection combining wavelet transform for quantitative analysis of heat value of coal using laser-induced breakdown spectroscopy. Appl. Phys. B 2021, 127, 19. [Google Scholar] [CrossRef]
- Hussein, A.M.; Obed, A.A.; Zubo, R.H.; Al-Yasir, Y.I.; Saleh, A.L.; Fadhel, H.; Sheikh-Akbari, A.; Mokryani, G.; Abd-Alhameed, R.A. Detection and Diagnosis of Stator and Rotor Electrical Faults for Three-Phase Induction Motor via Wavelet Energy Approach. Electronics 2022, 11, 1253. [Google Scholar] [CrossRef]
- Rapur, J.S.; Tiwari, R. Experimental fault diagnosis for known and unseen operating conditions of centrifugal pumps using MSVM and WPT based analyses. Measurement 2019, 147, 106809. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy 2019, 21, 865. [Google Scholar] [CrossRef]
- Feng, H.; Chen, R.; Wang, Y. Feature extraction for fault diagnosis based on wavelet packet decomposition: An application on linear rolling guide. Adv. Mech. Eng. 2018, 10, 168781401879636. [Google Scholar] [CrossRef]
- Nikravesh, S.Y.; Rezaie, H.; Kilpatrik, M.; Taheri, H. Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM). J. Manuf. Mater. Process. 2019, 3, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Feng, T.; Sun, Y.; Zhang, X. Research on Rotating Machinery Fault Diagnosis Method Based on Energy Spectrum Matrix and Adaptive Convolutional Neural Network. Processes 2020, 9, 69. [Google Scholar] [CrossRef]
- Wu, C.-S.; Peng, Y.-X.; Zhuo, D.-B.; Zhang, J.-Q.; Ren, W.; Feng, Z.-Y. Energy Ratio Variation-Based Structural Damage Detection Using Convolutional Neural Network. Appl. Sci. 2022, 12, 10220. [Google Scholar] [CrossRef]
- Qian, H.; Zhang, Y.; Li, Y.; Gao, J.; Song, J. Damage Monitoring of Engineered Cementitious Composite Beams Reinforced with Hybrid Bars Using Piezoceramic-Based Smart Aggregates. Sensors 2022, 22, 7184. [Google Scholar] [CrossRef]
- Yuan, X.; Fan, Y.; Zhou, C.; Wang, X.; Zhang, G. Fault Diagnosis of Check Valve Based on KPLS Optimal Feature Selection and Kernel Extreme Learning Machine. Coatings 2022, 12, 1320. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z.; Wang, Z.; Wang, X. Fault Detection and Identification Method for Quadcopter Based on Airframe Vibration Signals. Sensors 2021, 21, 581. [Google Scholar] [CrossRef] [PubMed]
- Al Tobi, M.; Bevan, G.; Wallace, P.; Harrison, D.; Okedu, K.E. Using MLP-GABP and SVM with wavelet packet transform-based feature extraction for fault diagnosis of a centrifugal pump. Energy Sci. Eng. 2022, 10, 1826–1839. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, J.; Wu, Y.; Zhen, D.; Zhang, M. Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis. Appl. Sci. 2020, 10, 7715. [Google Scholar] [CrossRef]
- Gao, L.; Yang, Z.; Cai, L.; Wang, H.; Chen, P. Roller Bearing Fault Diagnosis Based on Nonlinear Redundant Lifting Wavelet Packet Analysis. Sensors 2010, 11, 260–277. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Cai, W.; Liu, W.; Shang, Z.; Liu, G. A Lighted Deep Convolutional Neural Network Based Fault Diagnosis of Rotating Machinery. Sensors 2019, 19, 2381. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Zhang, W.-A.; Guo, F.; Liu, W.; Shi, X. Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Cybern. 2021, 1–11. [Google Scholar] [CrossRef]
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Deep Residual Networks With Dynamically Weighted Wavelet Coefficients for Fault Diagnosis of Planetary Gearboxes. IEEE Trans. Ind. Electron. 2018, 65, 4290–4300. [Google Scholar] [CrossRef]
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Multiple Wavelet Coefficients Fusion in Deep Residual Networks for Fault Diagnosis. IEEE Trans. Ind. Electron. 2019, 66, 4696–4706. [Google Scholar] [CrossRef]
- Xiong, S.; Zhou, H.; He, S.; Zhang, L.; Xia, Q.; Xuan, J.; Shi, T. A Novel End-To-End Fault Diagnosis Approach for Rolling Bearings by Integrating Wavelet Packet Transform into Convolutional Neural Network Structures. Sensors 2020, 20, 4965. [Google Scholar] [CrossRef]
- Huang, H.; Tang, B.; Luo, J.; Pu, H.; Zhang, K. Residual Gated Dynamic Sparse Network for Gearbox Fault Diagnosis Using Multisensor Data. IEEE Trans. Ind. Inform. 2022, 18, 2264–2273. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. In Proceedings of the PHM Society European Conference, Bilbao, Spain, 5–8 July 2016; p. 17. [Google Scholar]
- Welcome to the Case Western Reserve University Bearing Data Center Website|Case School of Engineering|Case Western Reserve University. Case School of Engineering. 10 August 2021. Available online: https://engineering.case.edu/bearingdatacenter/welcome (accessed on 20 October 2022).
- Yang, J.; Zhou, C. A Fault Feature Extraction Method Based on LMD and Wavelet Packet Denoising. Coatings 2022, 12, 156. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R. Wavelets; Springer: Boston, MA, USA, 2011. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R. Selection of Base Wavelet. In Wavelets; Springer: Boston, MA, USA, 2011; pp. 165–187. [Google Scholar] [CrossRef]
- Agrawal, P.; Jayaswal, P. Diagnosis and Classifications of Bearing Faults Using Artificial Neural Network and Support Vector Machine. J. Inst. Eng. India Ser. C 2020, 101, 61–72. [Google Scholar] [CrossRef]
- Strömbergsson, D.; Marklund, P.; Berglund, K.; Saari, J.; Thomson, A. Mother wavelet selection in the discrete wavelet transform for condition monitoring of wind turbine drivetrain bearings. Wind Energy 2019, 22, 1581–1592. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Hasan, M.J.; Sohaib, M.; Kim, J.-M. An Explainable AI-Based Fault Diagnosis Model for Bearings. Sensors 2021, 21, 4070. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Grus, J. Data Science from Scratch: First Principles with Python, 1st ed.; O’Reilly: Sebastopol, CA, USA, 2015. [Google Scholar]
- Nearest Ho, T.K. Nearest neighbours in random subspaces. In Advances in Pattern Recognition. SSPR/SPR 1998; Amin, A., Dori, D., Pudi, P., Freeman, H., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 1998. [Google Scholar] [CrossRef]
- Surti, K.V.; Naik, C.A. Bearing Condition Monitoring of Induction Motor Based on Discrete Wavelet Transform & K-nearest Neighbor. In Proceedings of the 2018 3rd International Conference for Convergence in Technology (I2CT), Pune, India, 6 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Plakias, S.; Chasiotis, I.D. Extracting spatially global and local attentive features for rolling bearing fault diagnosis in electrical machines using attention stream networks. IET Electr. Power Appl. 2021, 15, 903–915. [Google Scholar] [CrossRef]






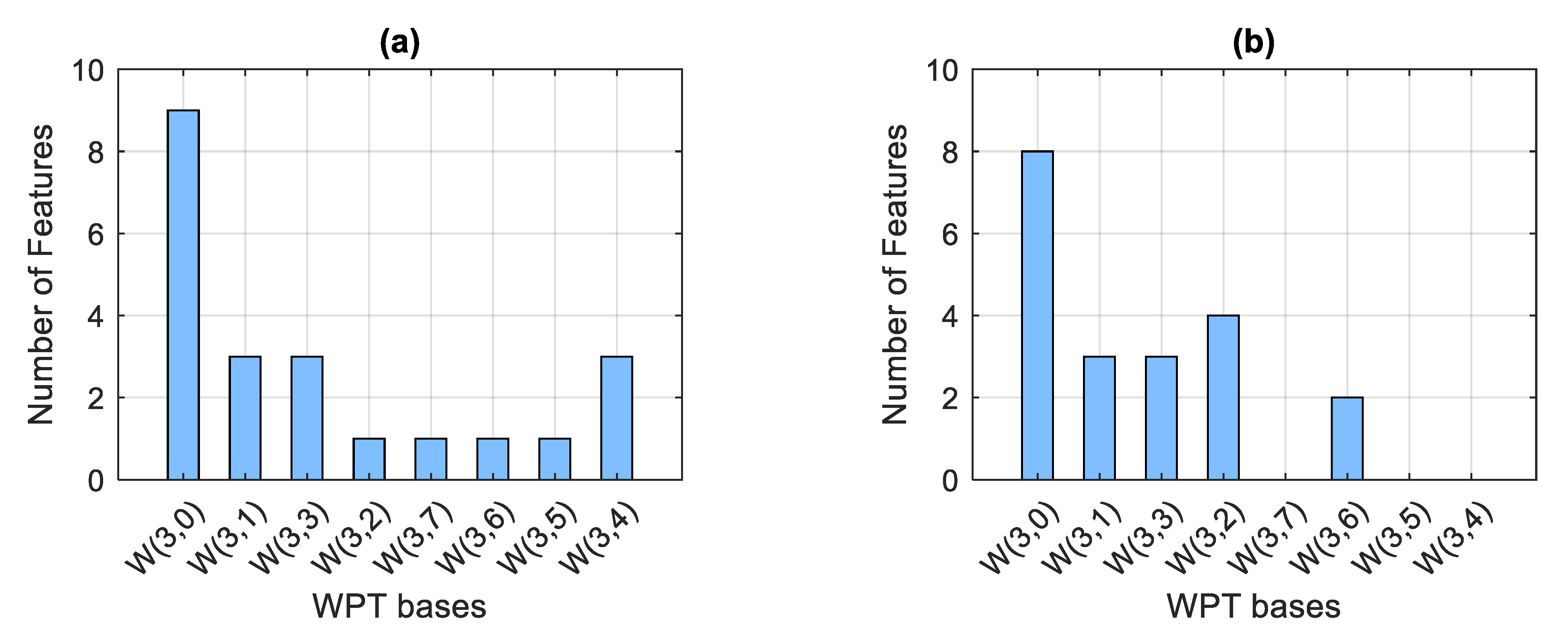

| No. | Rotational Speed (rpm) | Load Torque (Nm) | Radial Force (N) |
|---|---|---|---|
| 0 | 1500 | 0.7 | 1000 |
| 1 | 900 | 0.7 | 1000 |
| 2 | 1500 | 0.1 | 1000 |
| 3 | 1500 | 0.7 | 400 |
| Bearing Type | Bearing Code | Class Label |
|---|---|---|
| Healthy | K001 | H |
| K002 | ||
| K003 | ||
| K004 | ||
| K005 | ||
| K006 | ||
| Outer Ring Damage | KA01 | OR |
| KA03 | ||
| KA05 | ||
| KA06 | ||
| KA07 | ||
| KA08 | ||
| KA09 | ||
| Inner Ring Damage | KI01 | IR |
| KI03 | ||
| KI05 | ||
| KI07 | ||
| KI08 |
| Bearing Type | Bearing Code | Class Label |
|---|---|---|
| Healthy | K001 | H |
| K002 | ||
| K003 | ||
| K004 | ||
| K005 | ||
| K006 | ||
| Outer Ring Damage | KA04 | OR |
| KA15 | ||
| KA16 | ||
| KA22 | ||
| KA30 | ||
| Inner Ring Damage | KI04 | IR |
| KI14 | ||
| KI16 | ||
| KI17 | ||
| KI18 | ||
| KI21 | ||
| Outer + Inner Ring Damage | KB23 | |
| KB24 | OR + IR | |
| KB27 |
| Bearing Type | Bearing Code | Class Label |
|---|---|---|
| Healthy | 97–100 | H |
| Outer Ring Damage | 130–133 | OR |
| 144–147 | ||
| 156–160 | ||
| 197–200 | ||
| 234–237 | ||
| 246–249 | ||
| 258–261 | ||
| Inner Ring Damage | 056–059 | IR |
| 105–108 | ||
| 169–172 | ||
| 209–212 | ||
| Ball Damage | 048–051 | B |
| 118–121 | ||
| 185–188 | ||
| 222–225 |
| Statistical Feature | Formula | Statistical Feature | Formula |
|---|---|---|---|
| Peak value | Fifth normalized moment | ||
| Root-mean square | Sixth normalized moment | ||
| Kurtosis | Skewness | ||
| Crest factor | Shape factor RMS | ||
| Clearance factor | Peak-to-peak value | ||
| Impulse factor | Energy of signal | ||
| Shape factor SMR | Frequency center | ||
| Entropy | RMS frequency | ||
| Mean | Root variance frequency | ||
| Square mean root |
| Dataset | Precision | Recall | F1-Score | FIA |
|---|---|---|---|---|
| PU Artificial faults | 99.39% | 99.39% | 99.39% | 99.39% |
| PU Real faults | 99.92% | 99.92% | 99.92% | 99.92% |
| CWRU | 98.77% | 98.77% | 98.77% | 98.77% |
| Number | Method | Accuracy (PU Real Fault Data) | Accuracy (PU Artificial Fault Data) | Accuracy (CWRU Data) |
|---|---|---|---|---|
| Proposed | 99.92% | 99.39% | 98.77% | |
| 1 | WPT Energy Feature + Random Forest [18] | 98.70% | 94.10% | 98.62% |
| 2 | WPT + k-NN [58] | 92.12% | 90.19% | 91.51% |
| 3 | WPT Energy Feature + Gaussian kernel SVM [30] | 89.96% | 90.76% | 88.87% |
| 4 | Best Energy WPT Node + Subspace k-NN | 93.07% | 91.58% | 94.71% |
| 5 | Proposed + Chi-Squared test | 99.35% | 98.35% | 99.02% |
| 6 | Attention Stream Network [59] | 99.37% | 99.28% | 99.60% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maliuk, A.S.; Ahmad, Z.; Kim, J.-M. Hybrid Feature Selection Framework for Bearing Fault Diagnosis Based on Wrapper-WPT. Machines 2022, 10, 1204. https://doi.org/10.3390/machines10121204
Maliuk AS, Ahmad Z, Kim J-M. Hybrid Feature Selection Framework for Bearing Fault Diagnosis Based on Wrapper-WPT. Machines. 2022; 10(12):1204. https://doi.org/10.3390/machines10121204
Chicago/Turabian StyleMaliuk, Andrei S., Zahoor Ahmad, and Jong-Myon Kim. 2022. "Hybrid Feature Selection Framework for Bearing Fault Diagnosis Based on Wrapper-WPT" Machines 10, no. 12: 1204. https://doi.org/10.3390/machines10121204
APA StyleMaliuk, A. S., Ahmad, Z., & Kim, J.-M. (2022). Hybrid Feature Selection Framework for Bearing Fault Diagnosis Based on Wrapper-WPT. Machines, 10(12), 1204. https://doi.org/10.3390/machines10121204








