Flow Loss Analysis and Optimal Design of a Diving Tubular Pump
Abstract
:1. Introduction
2. Numerical Method
2.1. Flow Control Equations
2.2. Theory of Entropy Generation
3. Numerical Simulation and Optimization Potential Analysis of Internal Flow
3.1. Computational Domain Model
3.2. Grid Division of a Computational Domain
3.3. Boundary Condition Setting
3.4. Performance Analysis of the Initial Model
3.5. Analysis of Entropy Generation
4. Optimal Design
4.1. Optimal Design Based on the Empirical Method
4.1.1. Hydraulic Design of the Impeller and Guide Vanes
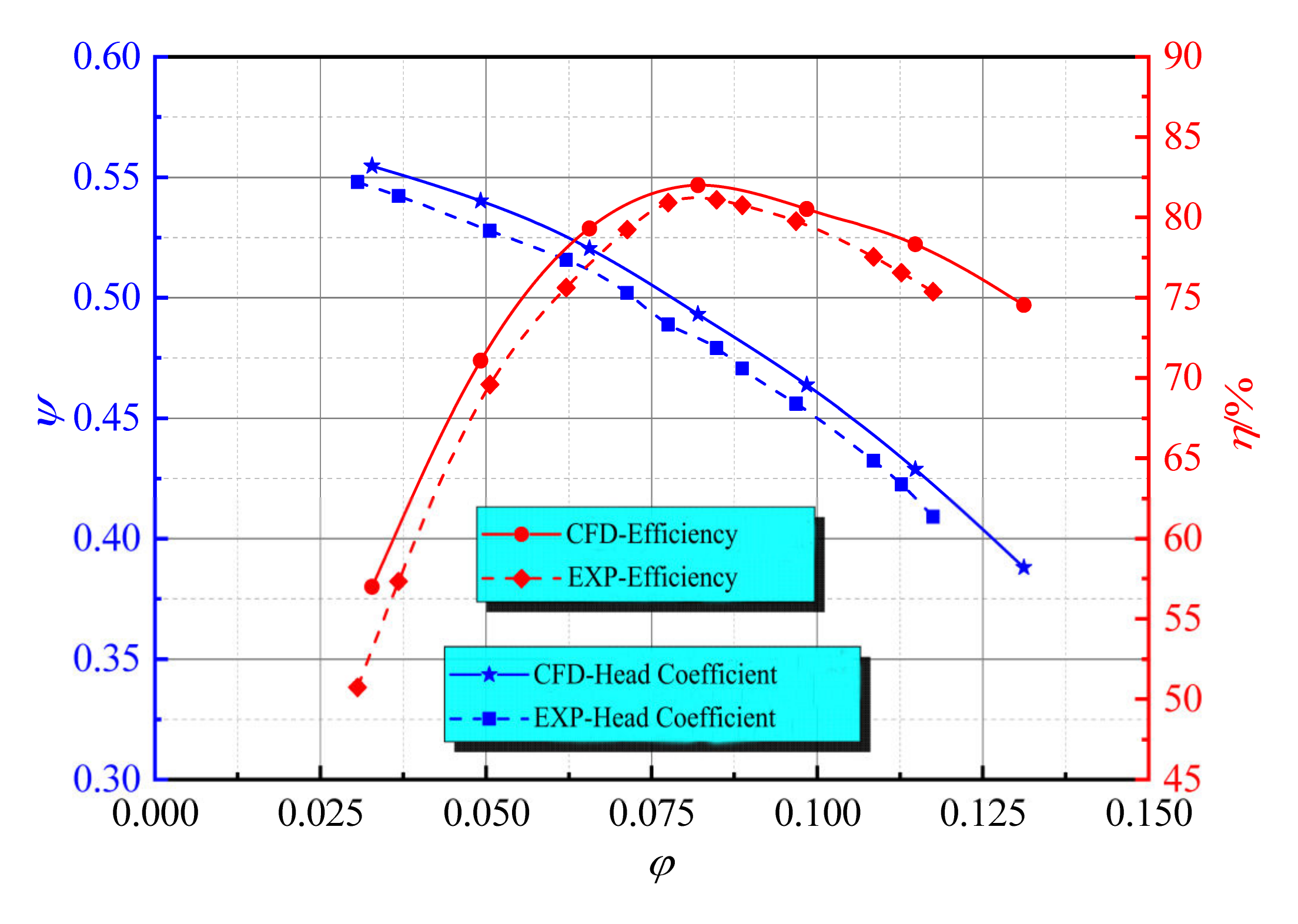
4.1.2. The Results of Numerical Calculation
4.2. Optimal Design Based on the Full-Factorial Experiment
4.2.1. Optimization Object
4.2.2. Full-Factor Design of the Experiment
4.3. Optimal Design Based on Surface Response Experimental Method
4.4. Optimization Results
4.4.1. Comparison of Optimization Effects on Pump Performance
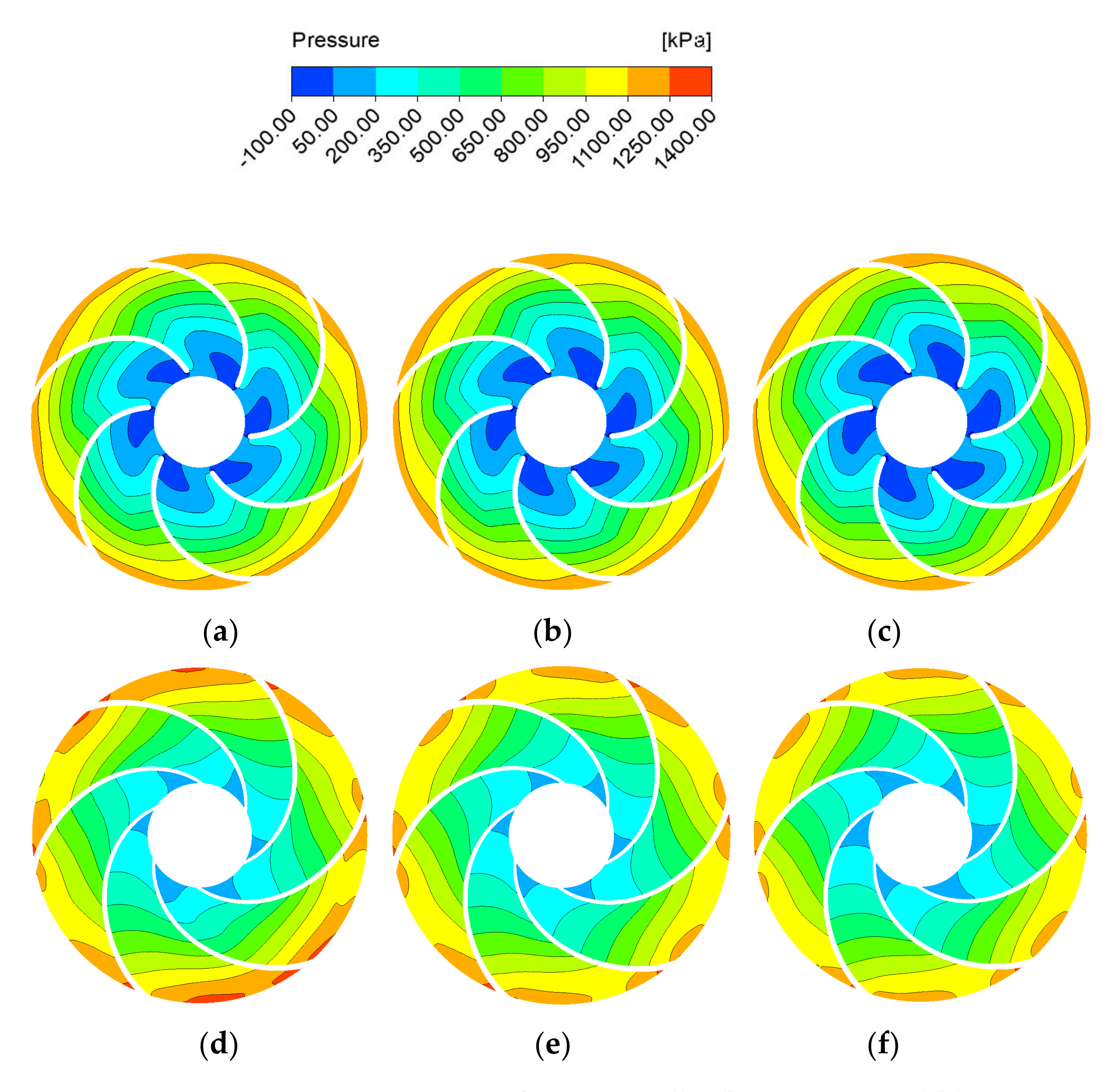
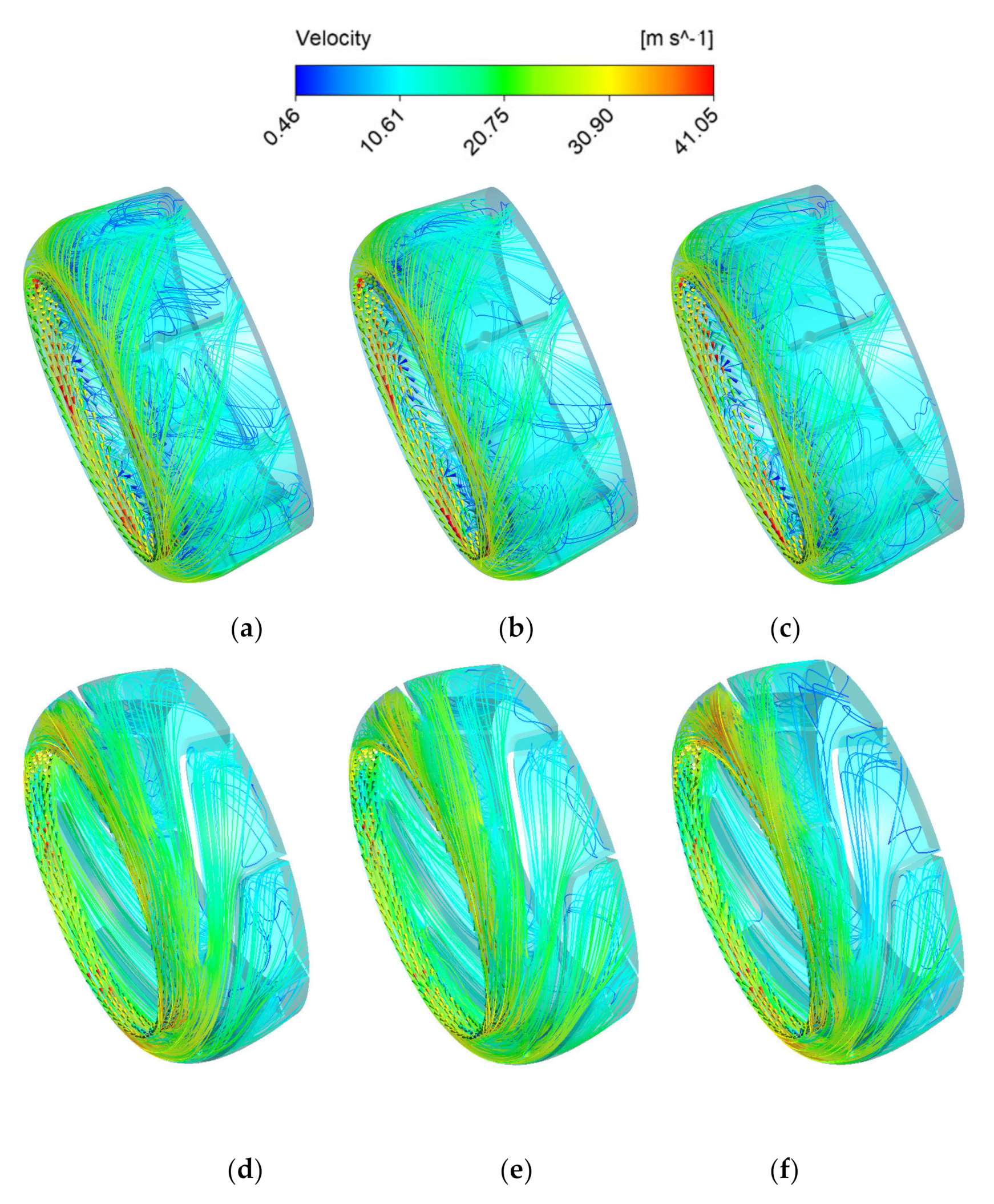
4.4.2. Analysis of Internal Flow Characteristics
5. Conclusions
- (1)
- Entropy generation can effectively visualize the flow loss distribution caused by turbulent dissipation and flow separation. The internal flow loss of the diving tubular pump is mainly concentrated in the inlet and outlet area of the impeller and the inlet area of the guide vane. The main cause of flow loss is that the angle of attack between the relative liquid flow angle and the blade placement angle at the inlet of the impeller blade is too large; the matching between the guide vane and the impeller is poor, and the guide vane design is unreasonable.
- (2)
- The streamline placement angle (A) of the front cover of the impeller blade, the placement angle (B) of the middle streamline inlet, and the placement angle (C) of the streamline inlet of the rear cover are all significant factors that affect the efficiency. The order of the influencing factors from strong to weak is as follows: A2 (p = 0.000) > C (p = 0.007) = A * B (p = 0.007) > B (p = 0.023) > B2 (p = 0.066) > A * C (p = 0.094) > A (p = 0.162) > C2 (p = 0.386) > A * B (p = 0.421). The best combination of response variables after surface response test design is A = 9°, B = 31°, and C = 36°.
- (3)
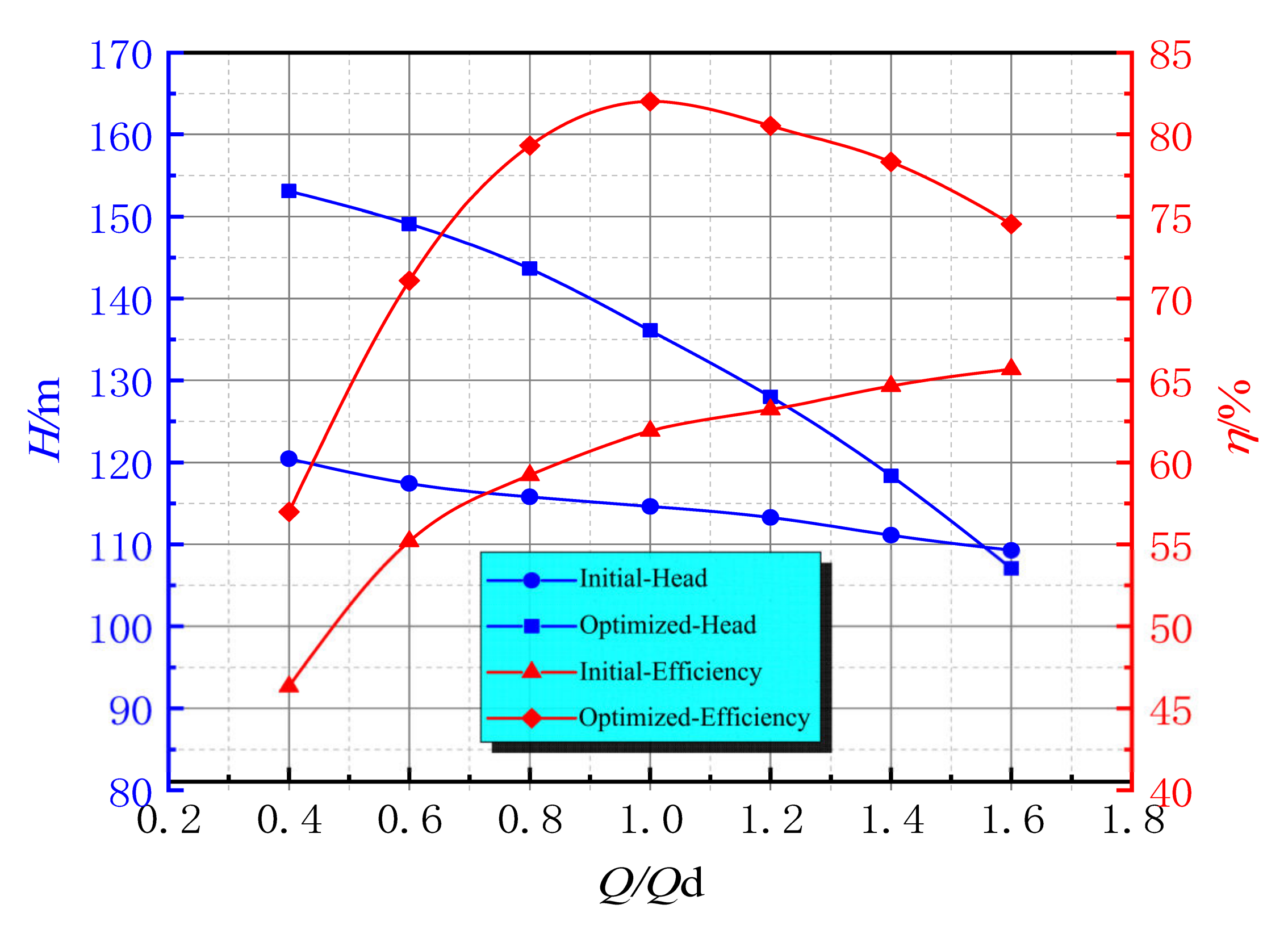
- The optimization process successfully improves the head and efficiency by 32.99% and 18.71%, respectively, compared to those of the initial pump. The optimized simulation data of the diving tubular pump are in good agreement with the test data. After optimization, the large-scale separation vortex inside the impeller is significantly reduced and no backflow occurs. The internal outflow area of the guide vane is significantly reduced after optimization, and the internal flow is greatly improved because the flow is more uniform and smoother.
- (4)
- The optimization method in this study is universal and can be applied to conduct optimization of other fluid machinery. This study focuses on only some parameters of the impeller, and more parameters can be studied as variables in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| u v w | Cartesian velocity components |
| x y z | Coordinate components |
| t | Time |
| p | Pressure |
| μ | Dynamic viscosity |
| ν | Kinematic viscosity |
| ε | Turbulent eddy dissipation |
| T | Temperature |
| s | Entropy |
| p1 | Pressure of the pump inlet |
| p2 | Pressure of the pump outlet |
| v1 | Velocity of the pump inlet |
| v2 | Velocity of the pump outlet |
| z1 | Installation height of the pump inlet |
| z2 | Installation height of the pump outlet |
| P | Shaft power |
| The viscous dissipation term of mechanical energy | |
| The dissipation term generated by heat transfer due to temperature difference | |
| Viscous entropy generation | |
| Turbulent kinetic energy entropy generation | |
| Wall entropy generation | |
| Wall shear stress | |
| The average velocity | |
| Q | Rate flow |
| H | Head |
| n | Rotational speed |
| η | Efficiency |
| Dh | Hub diameter |
| Dj | Impeller inlet diameter |
| D2 | Impeller outlet diameter |
| b2 | Impeller outlet width |
| Blade wrap angle | |
| φ2 | Blade outlet angle |
| Z | Blade number |
| b3 | Guide vane inlet width |
| D3 | Maximum diameter of an inner streamline of the guide vane |
| D4 | Maximum diameter of an outer streamline of the guide vane |
| D5 | Inside diameter of the guide vane outlet |
| D6 | Outside diameter of the guide vane outlet |
| L | Axial length of the guide vane |
| Z | Number of guide vanes |
| α3 | Guide vane inlet angle |
| α4 | Guide vane outlet angle |
| Guide vane wrap angle | |
| Flow coefficient | |
| Head coefficient | |
| A | The streamline placement angle of the front cover of the impeller blade |
| B | The placement angle of the middle streamline inlet |
| C | The placement angle of the rear cover flowline inlet |
| Superscripts | |
| - | Time-averaged value |
| ‘ | Fluctuating component |
References
- Shi, L.J.; Zhang, W.P.; Jiao, H.F.; Tang, F.P.; Wang, L.; Sun, D.D.; Shi, W. Numerical simulation and experimental study on the comparison of the hydraulic characteristics of an axial-flow pump and a full tubular pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Abdelaziz, E.A.; Saidur, R.; Mekhilef, S. A review on energy saving strategies in industrial sector. Renew. Sustain. Energy Rev. 2011, 15, 150–168. [Google Scholar] [CrossRef]
- Edwards, G.; Spence, D. The European Commission. Dev. Eur. 1997, 8, 14–26. [Google Scholar]
- Shankar, A.; Kalaiselvan, V.; Subramaniam, U.; Shanmugam, P.; Hanigovszki, N. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system. Appl. Energy 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Denton, J.D. Loss Mechanisms in Turbomachines. Trans ASME J. Turbomach. 1993, 115, 10–23. [Google Scholar] [CrossRef]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Gu, Y.; Pei, J.; Yuan, S.; Wang, W.; Zhang, F.; Wang, P. Clocking Effect of Vaned Diffuser on Hydraulic Performance of High-Power Pump by Using the Numerical Flow Loss Visualization Method. Energy 2019, 170, 986–997. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.C.; Wu, D.H.; Li, X.J. Influence of guide ring on energy loss in a multistage centrifugal pump. J. Fluids Eng. 2019, 141, 0613021–06130213. [Google Scholar]
- Zhang, F.; Appiah, D.; Hong, F.; Zhang, J.; Wei, X. Energy loss evaluation in a side channel pump under different wrapping angles using entropy production method. Int. Commun. Heat Mass Transf. 2020, 113, 104526. [Google Scholar] [CrossRef]
- Hao, C.; Shi, W.D.; Li, W.; Liu, J.R. Energy loss analysis of novel self-priming pump based on the entropy production theory. J. Therm. Sci. 2019, 28, 150–162. [Google Scholar]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Hou, H.; Zhang, J.; Xu, C. Entropy production diagnostic analysis of energy consumption for cavitation flow in a two-stage lng cryogenic submerged pump. Int. J. Heat Mass Transf. 2019, 129, 342–356. [Google Scholar] [CrossRef]
- Si, Q.; Lu, R.; Shen, C.; Xia, S.; Sheng, G.; Yuan, J. An intelligent cfd-based optimization system for fluid machinery: Automotive electronic pump case application. Appl. Sci. 2020, 10, 366. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.Y.; Cai, S.J.; Li, Y.J.; Zhou, X.; Zhang, Y.X. Optimization design of multiphase pump impeller based on combined genetic algorithm and boundary vortex flux diagnosis. J. Hydrodyn. 2017, 29, 1023–1034. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.H.; Husain, A.; Kim, K.Y. Multi-objective optimization of a centrifugal compressor impeller through evolutionary algorithms. Proc. Inst. Mech. Eng. J. Power Energy 2010, 224, 711–721. [Google Scholar] [CrossRef]
- Kang, H.S.; Song, Y.J.; Kim, Y.J. Optimal Design of Impeller for Centrifugal Compressor Under the Influence of Fluid-Structure Interaction. J. Mech. Sci. Technol. 2016, 30, 3953–3959. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-Disciplinary optimization design of axial-flow pump impellers based on the approximation model. Energies 2020, 13, 779. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Tan, L.; Cao, S. Design method of controllable blade angle and orthogonal optimization of pressure rise for a multiphase pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Bonaiuti, D.; Arnone, A.; Ermini, M.; Baldassarre, L. Analysis and optimization of transonic centrifugal compressor impellers using the design of experiments technique. J. Turbomach. 2006, 128, 647–652. [Google Scholar] [CrossRef]
- Lee, K.Y.; Choi, Y.S.; Kim, Y.L.; Yun, J.H. Design of axial fan using inverse design method. J. Mech. Sci. Technol. 2008, 22, 1883–1888. [Google Scholar] [CrossRef]
- Thakkar, S.; Vala, H.; Patel, V.K.; Patel, R. Performance improvement of the sanitary centrifugal pump through an integrated approach based on response surface methodology, multi-objective optimization and cfd. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–15. [Google Scholar] [CrossRef]
- Nataraj, M.; Ragoth, S.R. Analyzing pump impeller for performance evaluation using RSM and CFD. Desalination Water Treat. 2014, 52, 6822–6831. [Google Scholar] [CrossRef]
- Wang, W.; Pei, J.; Yuan, S.; Zhang, J.; Yuan, J.; Xu, C. Application of different surrogate models on the optimization of centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 567–574. [Google Scholar] [CrossRef]
- Yang, F.; Jin, Y.; Liu, C.; Tang, F.; Cheng, L.; Yang, H. Numerical analysis and performance test on diving tubular pumping system with symmetric aerofoil blade. Trans. Chin. Soc. Agric. Eng. 2012, 28, 60–67. [Google Scholar]
- Lu, R.; Yuan, J.; Wei, G.; Zhang, Y.; Lei, X.; Si, Q. Optimization Design of Energy-Saving Mixed Flow Pump Based on MIGA-RBF Algorithm. Machines 2021, 9, 365. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, H.; Zhang, J.; Zhang, J.; Zhao, J. Experiment and numerical study of a new generation three-stage multiphase pump. J. Pet. Sci. Eng. 2018, 169, 471–484. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Li, W.; Shi, W.; Wang, C. PIV validation of different turbulence models used for numerical simulation of a centrifugal pump diffuser. Eng. Computations 2018, 35, 2–17. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Effects of different turbulence models on three-dimensional unsteady cavitating flows in the centrifugal pump and performance prediction. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 487–509. [Google Scholar] [CrossRef]
- Lu, R.; Yuan, J.P.; Wang, L.Y.; Fu, Y.X.; Hong, F.; Wang, W.J. Effect of volute tongue angle on the performance and flow unsteadiness of an automotive electronic cooling pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 235, 227–241. [Google Scholar] [CrossRef]
- Herwig, H.; Gloss, D.; Wenterodt, T. A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 2008, 613, 35–53. [Google Scholar] [CrossRef]
- Xiang, Z. Energy conversion characteristic within impeller of low specific speed centrifugal pump. Trans. Chin. Soc. Agric. Mach. 2011, 42, 75–81. [Google Scholar]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the impeller blade with a slot structure on the centrifugal pump performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, X.; Wang, Z. Evaluating the transient energy dissipation in a centrifugal impeller under rotorstator interaction. Entropy 2019, 21, 271. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Tan, L. Spatial-temporal evolution of tip leakage vortex in a mixed flow pump with tip clearance. J. Fluids Eng. 2019, 141, 081302. [Google Scholar] [CrossRef]
- Ran, H.; Luo, X.; Zhu, L.; Zhang, Y.; Wang, X.; Xu, H. Experimental study of the pressure fluctuations in a pump turbine at large partial flow conditions. Chin. J. Mech. Eng. 2012, 25, 1205–1209. [Google Scholar] [CrossRef]
- Lu, L.G.; Chen, J.; Liang, J.D.; Leng, Y. Optimal hydraulic design of bulb tubular pump system. J. Hydraul. Eng. 2008, 39, 355–360. [Google Scholar]
- Zhou, L.; Yang, Y.; Shi, W.; Lu, W.; Ye, D. Influence of outlet edge position of diffuser vane on performance of deep-well centrifugal pump. J. Drain. Irrig. Mach. Eng. 2016, 34, 1028–1034. [Google Scholar]
- Cheng, X.; Zhang, X.; Wei, Y.; Zhang, S.; Wang, P. Influence of outlet edge position of guide vane on performance of well submersible pump. Trans. Chin. Soc. Agric. Eng. 2018, 34, 68–75. [Google Scholar]
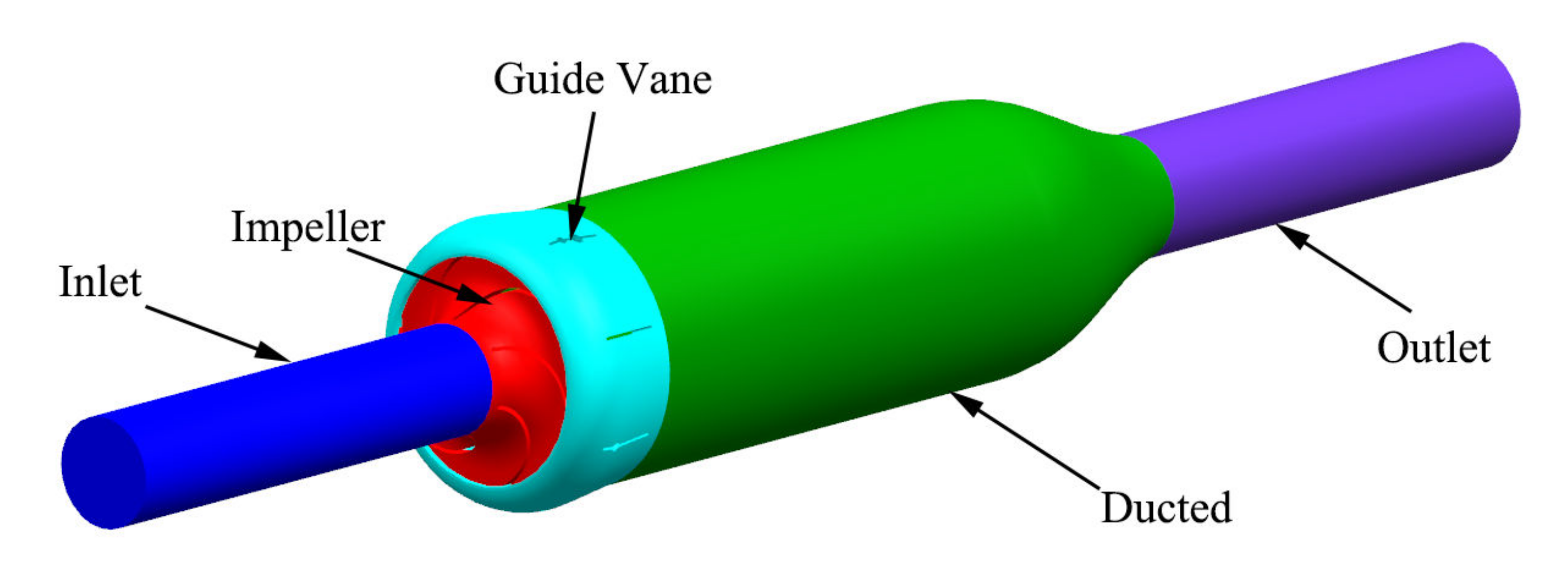
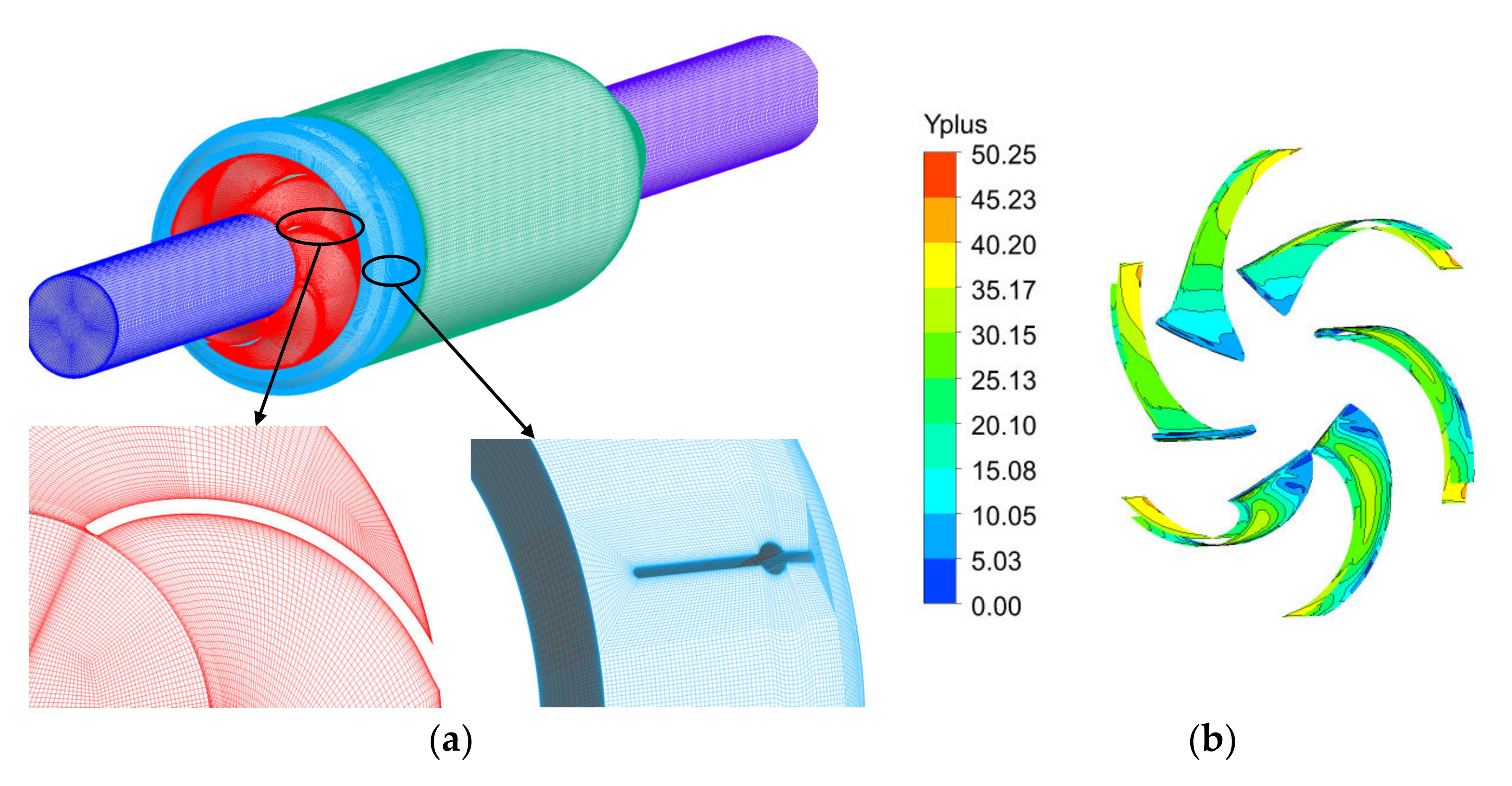

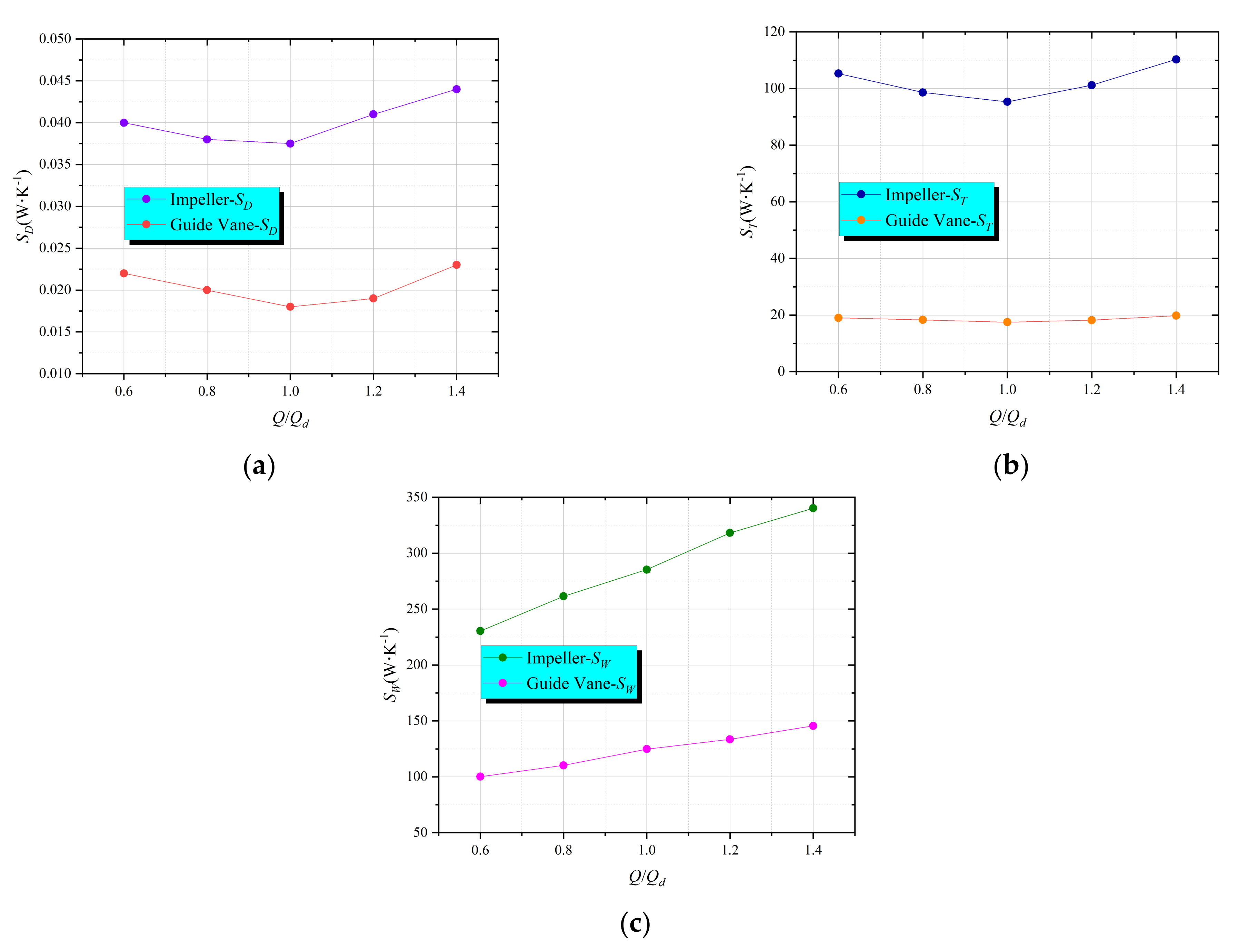


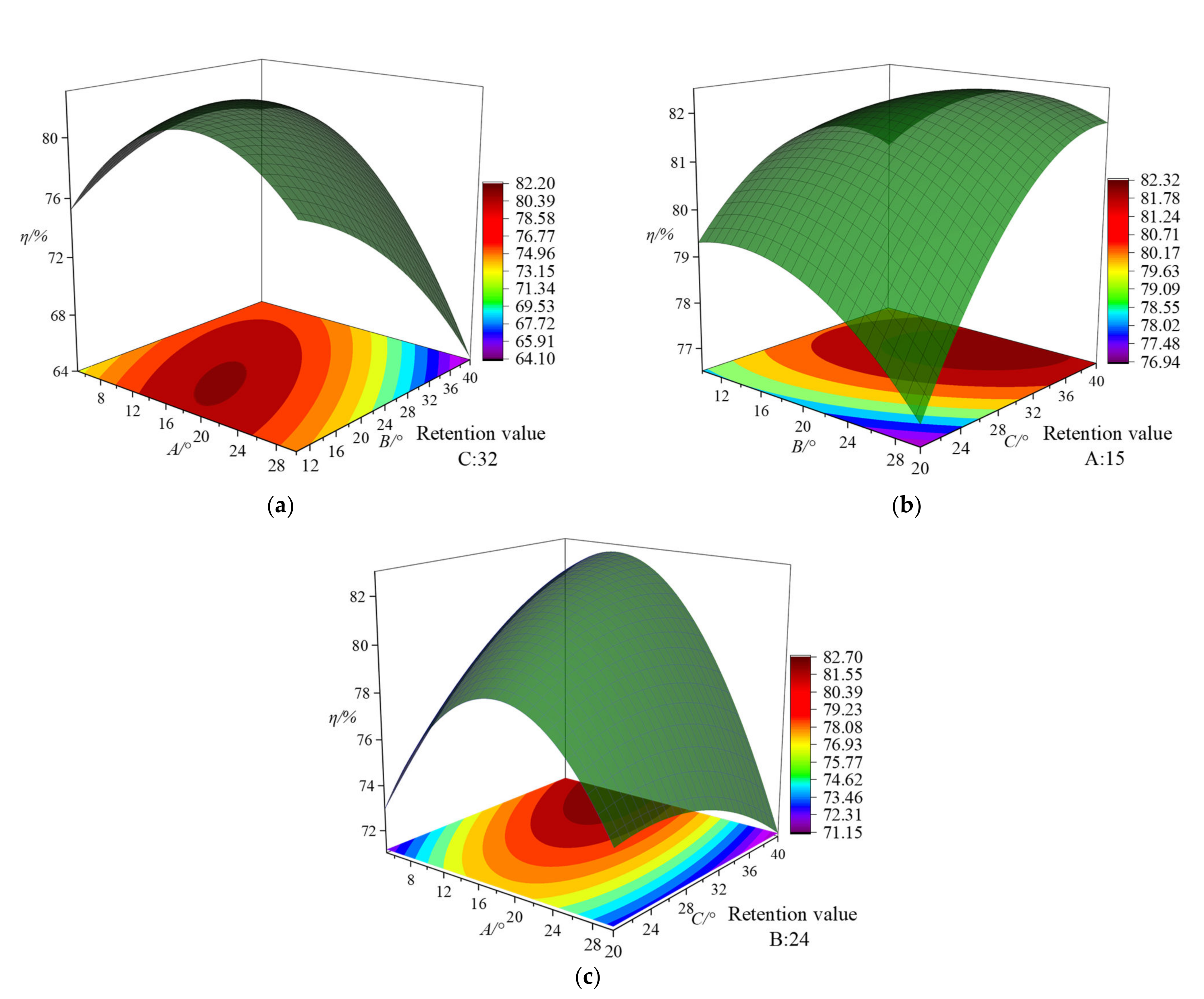
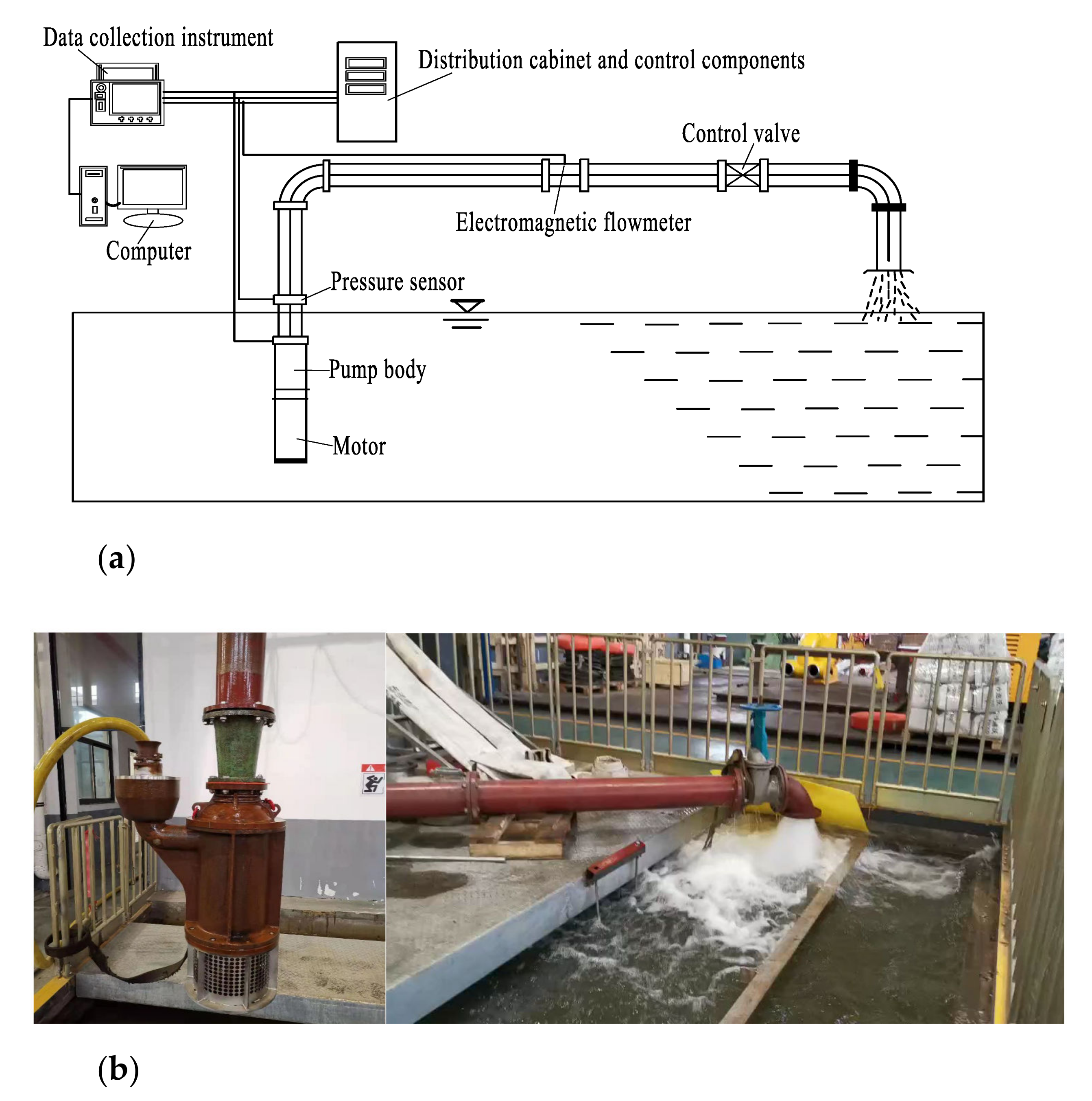
| Parameters | Symbols | Value |
|---|---|---|
| Rate flow | Qd | 240 m3/h |
| Head | Hd | 120 m |
| Rotational speed | n | 3600 r/min |
| Impeller suction diameter | Dj | 276 mm |
| Impeller outlet diameter | D2 | 110 mm |
| Impeller outlet width | b2 | 18 mm |
| Blade number | z | 6 |
| Element Count (Million) | H (m) | Relative Error (%) | Efficiency (%) | Relative Error (%) |
|---|---|---|---|---|
| 5.79 | 113.97 | - | 61.35 | - |
| 6.36 | 114.64 | 0.58% | 61.04 | 0.51% |
| 7.68 | 115.52 | 0.76% | 61.91 | 1.42% |
| 8.56 | 115.57 | 0.04% | 62.01 | 0.16% |
| 9.72 | 115.56 | 0.01% | 61.98 | 0.04% |
| Parameters | Symbols | Value |
|---|---|---|
| Hub diameter | dh | 0 mm |
| Impeller inlet diameter | Dj | 110 mm |
| Impeller outlet diameter | D2 | 276 mm |
| Impeller outlet width Blade wrap angle Blade outlet angle Number of blades | b2 Φ φ2 Z | 18 mm 140° 29° 6 |
| Guide vane inlet width | b3 | 38 mm |
| Maximum diameter of an inner streamline of the guide vane | D3 | 144 mm |
| Maximum diameter of an outer streamline of the guide vane | D4 | 176 mm |
| Inside diameter of the guide vane outlet | D5 | 132.9 mm |
| Outside diameter of the guide vane outlet Axial length of the guide vane Number of guide vanes Guide vane inlet angle Guide vane outlet angle Guide vane wrap angle | D6 L z α3 α4 φ0 | 167 mm 147 mm 8 12° 89.71° 65.2° |
| Q/Qd | Head (m) | Efficiency (%) |
|---|---|---|
| 0.75 | 140.80 | 71.09 |
| 1 | 134.95 | 75.38 |
| 1.2 | 130.81 | 73.59 |
| Factors | A | B | C | |
|---|---|---|---|---|
| Levels | ||||
| −1 | 9 | 17 | 28 | |
| 0 | 15 | 24 | 32 | |
| 1 | 21 | 31 | 36 | |
| Standard Order | Operation Order | Center Point | Zone | A | B | C | Efficiency (%) | Head (m) |
|---|---|---|---|---|---|---|---|---|
| 9 | 1 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 10 | 2 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 7 | 3 | 1 | 1 | 9 | 31 | 36 | 82.38 | 136.81 |
| 6 | 4 | 1 | 1 | 21 | 17 | 36 | 81.65 | 133.50 |
| 2 | 5 | 1 | 1 | 21 | 17 | 28 | 81.32 | 134.04 |
| 1 | 6 | 1 | 1 | 9 | 17 | 28 | 79.88 | 130.93 |
| 5 | 7 | 1 | 1 | 9 | 17 | 36 | 81.66 | 137.19 |
| 3 | 8 | 1 | 1 | 9 | 31 | 28 | 78.86 | 129.05 |
| 11 | 9 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 8 | 10 | 1 | 1 | 21 | 31 | 36 | 77.65 | 126.66 |
| 4 | 11 | 1 | 1 | 21 | 31 | 28 | 77.06 | 126.71 |
| Source | Degree of Freedom | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 6 | 35.066 | 5.84437 | 30.14 | 0.003 |
| Linearity | 3 | 17.2534 | 75.75113 | 29.93 | 0.003 |
| A | 1 | 3.2704 | 3.27040 | 17.02 | 0.015 |
| B | 1 | 9.1485 | 9.14850 | 47.61 | 0.002 |
| C | 1 | 4.8345 | 4.83450 | 25.16 | 0.007 |
| Two-factor interaction | 2 | 10.3243 | 5.16217 | 26.86 | 0.005 |
| A × B | 1 | 7.9142 | 7.91423 | 41.18 | 0.003 |
| A × C | 1 | 2.4101 | 2.41011 | 12.54 | 0.024 |
| Bending | 1 | 7.4885 | 7.48848 | 38.97 | 0.003 |
| Error | 4 | 0.7687 | 0.19217 | ||
| Lack of fit | 2 | 0.7687 | 0.38434 | ||
| Pure error | 2 | 0.0000 | 0.00000 | ||
| Total | 10 | 35.8349 |
| Standard Order | Operation Order | Center Point | Zone | A | B | C | Efficiency (%) | Head (m) |
|---|---|---|---|---|---|---|---|---|
| 18 | 1 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 19 | 2 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 8 | 3 | 1 | 1 | 21 | 31 | 36 | 77.64 | 126.66 |
| 12 | 4 | −1 | 1 | 15 | 35.8 | 32 | 80.70 | 131.09 |
| 9 | 5 | −1 | 1 | 4.9 | 24 | 32 | 78.41 | 127.51 |
| 14 | 6 | −1 | 1 | 15 | 24 | 38.7 | 81.76 | 135.13 |
| 1 | 7 | 1 | 1 | 9 | 17 | 28 | 79.88 | 130.93 |
| 3 | 8 | 1 | 1 | 9 | 31 | 28 | 78.86 | 129.05 |
| 7 | 9 | 1 | 1 | 9 | 31 | 36 | 82.38 | 136.81 |
| 6 | 10 | 1 | 1 | 21 | 17 | 36 | 81.65 | 133.50 |
| 11 | 11 | −1 | 1 | 15 | 12.2 | 32 | 80.55 | 131.55 |
| 15 | 12 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 10 | 13 | −1 | 1 | 25 | 24 | 32 | 78.67 | 127.96 |
| 13 | 14 | −1 | 1 | 15 | 24 | 25.2 | 80.94 | 133.47 |
| 2 | 15 | 1 | 1 | 21 | 17 | 28 | 81.32 | 134.04 |
| 16 | 16 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 17 | 17 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 5 | 18 | 1 | 1 | 9 | 17 | 36 | 81.66 | 137.19 |
| 20 | 19 | 0 | 1 | 15 | 24 | 32 | 81.91 | 136.92 |
| 4 | 20 | 1 | 1 | 21 | 31 | 28 | 77.06 | 126.71 |
| Source | Degree of Freedom | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 9 | 43.9376 | 4.8820 | 6.94 | 0.003 |
| Linearity | 3 | 10.8785 | 3.6262 | 5.16 | 0.021 |
| A | 1 | 1.6022 | 1.6022 | 2.28 | 0.162 |
| B | 1 | 5.0415 | 5.0415 | 7.17 | 0.023 |
| C | 1 | 4.8345 | 4.83450 | 25.16 | 0.007 |
| Square | 3 | 22.2402 | 7.4134 | 10.54 | 0.002 |
| A2 | 1 | 20.5424 | 20.5424 | 29.2 | 0.000 |
| B2 | 1 | 2.9996 | 2.9996 | 4.26 | 0.066 |
| C2 | 1 | 0.5769 | 0.5769 | 0.82 | 0.386 |
| Two-factor interaction | 3 | 10.8189 | 3.6063 | 5.13 | 0.021 |
| A × B | 1 | 7.9142 | 7.9142 | 11.25 | 0.007 |
| A × C | 1 | 2.4101 | 2.4101 | 3.43 | 0.094 |
| B × C | 1 | 0.4945 | 0.4945 | 0.70 | 0.421 |
| Error | 10 | 7.0342 | 0.7034 | ||
| Lack of fit | 5 | 7.0342 | 1.4068 | ||
| Pure error | 5 | 0.0000 | 0.0000 | ||
| Total | 19 | 50.9718 |
| Initial | Optimized | |||
|---|---|---|---|---|
| Q/Qd | Head (m) | Efficiency (%) | Head (m) | Efficiency (%) |
| 0.4 | 120.46 | 46.34 | 153.09 | 56.99 |
| 0.6 | 117.43 | 55.19 | 149.09 | 71.08 |
| 0.8 | 115.80 | 59.23 | 143.63 | 79.31 |
| 1.0 | 114.64 | 61.91 | 136.09 | 82.34 |
| 1.2 | 113.28 | 63.22 | 127.99 | 80.52 |
| 1.4 | 111.12 | 64.66 | 118.36 | 78.32 |
| 1.6 | 109.27 | 65.69 | 107.08 | 74.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Tian, D.; Si, Q.; Liao, M.; He, J.; He, X.; Liu, Z. Flow Loss Analysis and Optimal Design of a Diving Tubular Pump. Machines 2022, 10, 175. https://doi.org/10.3390/machines10030175
Yang X, Tian D, Si Q, Liao M, He J, He X, Liu Z. Flow Loss Analysis and Optimal Design of a Diving Tubular Pump. Machines. 2022; 10(3):175. https://doi.org/10.3390/machines10030175
Chicago/Turabian StyleYang, Xiao, Ding Tian, Qiaorui Si, Minquan Liao, Jiawei He, Xiaoke He, and Zhonghai Liu. 2022. "Flow Loss Analysis and Optimal Design of a Diving Tubular Pump" Machines 10, no. 3: 175. https://doi.org/10.3390/machines10030175
APA StyleYang, X., Tian, D., Si, Q., Liao, M., He, J., He, X., & Liu, Z. (2022). Flow Loss Analysis and Optimal Design of a Diving Tubular Pump. Machines, 10(3), 175. https://doi.org/10.3390/machines10030175







