Synchronization of Four Axisymmetrically Distributed Eccentric Rotors in a Vibration System
Abstract
:1. Introduction
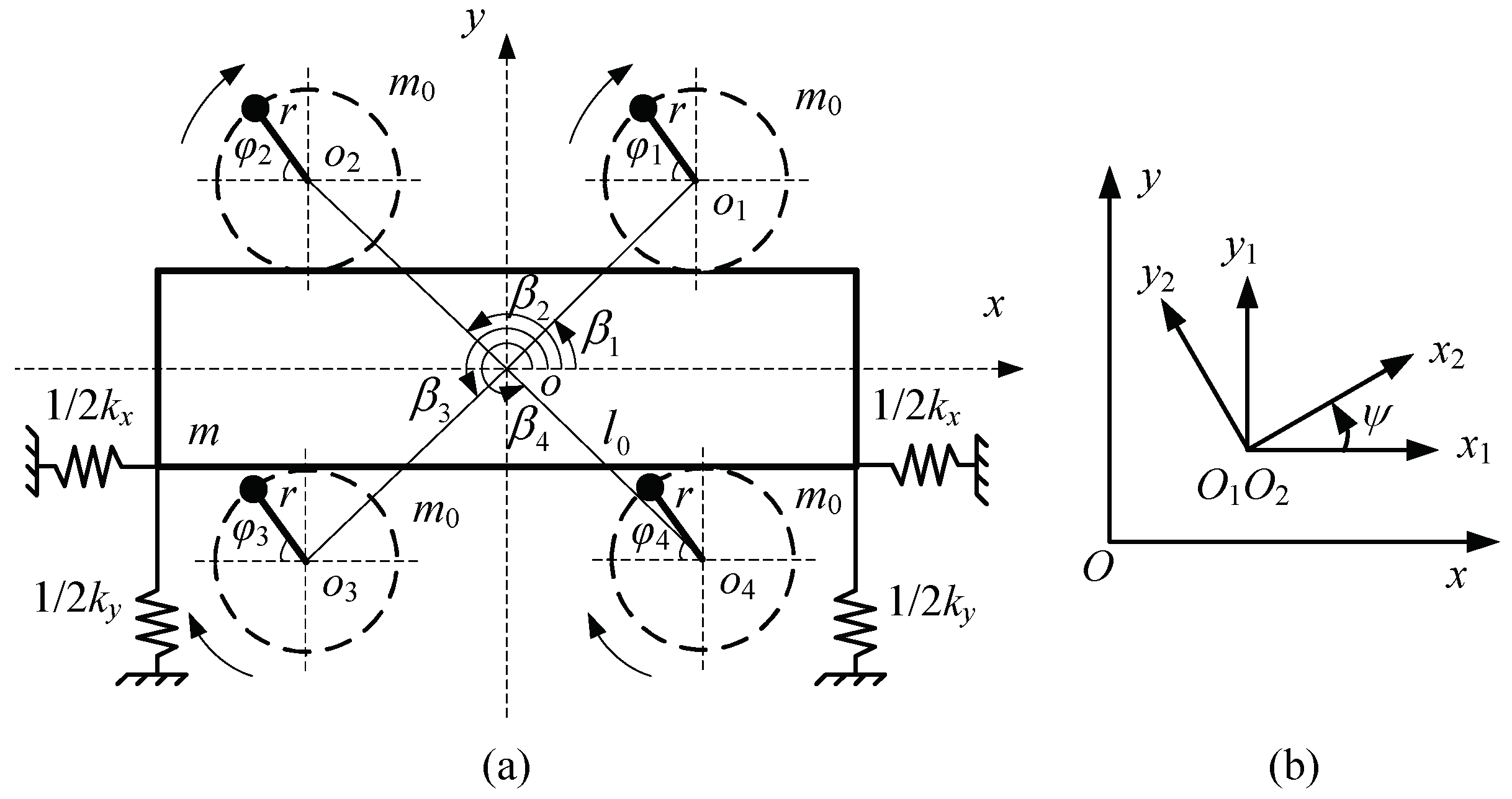
2. Dynamic Model and Motion Differential Equations
3. Theoretical Derivation
3.1. Synchronization of Vibration System
3.2. Stability Condition of Synchronous State
4. Numerical Analysis
5. Experiment
5.1. Experimental Machine
5.2. The System Is in the Sub-Reasonant State
5.3. The System Is in the Super-Resonant State
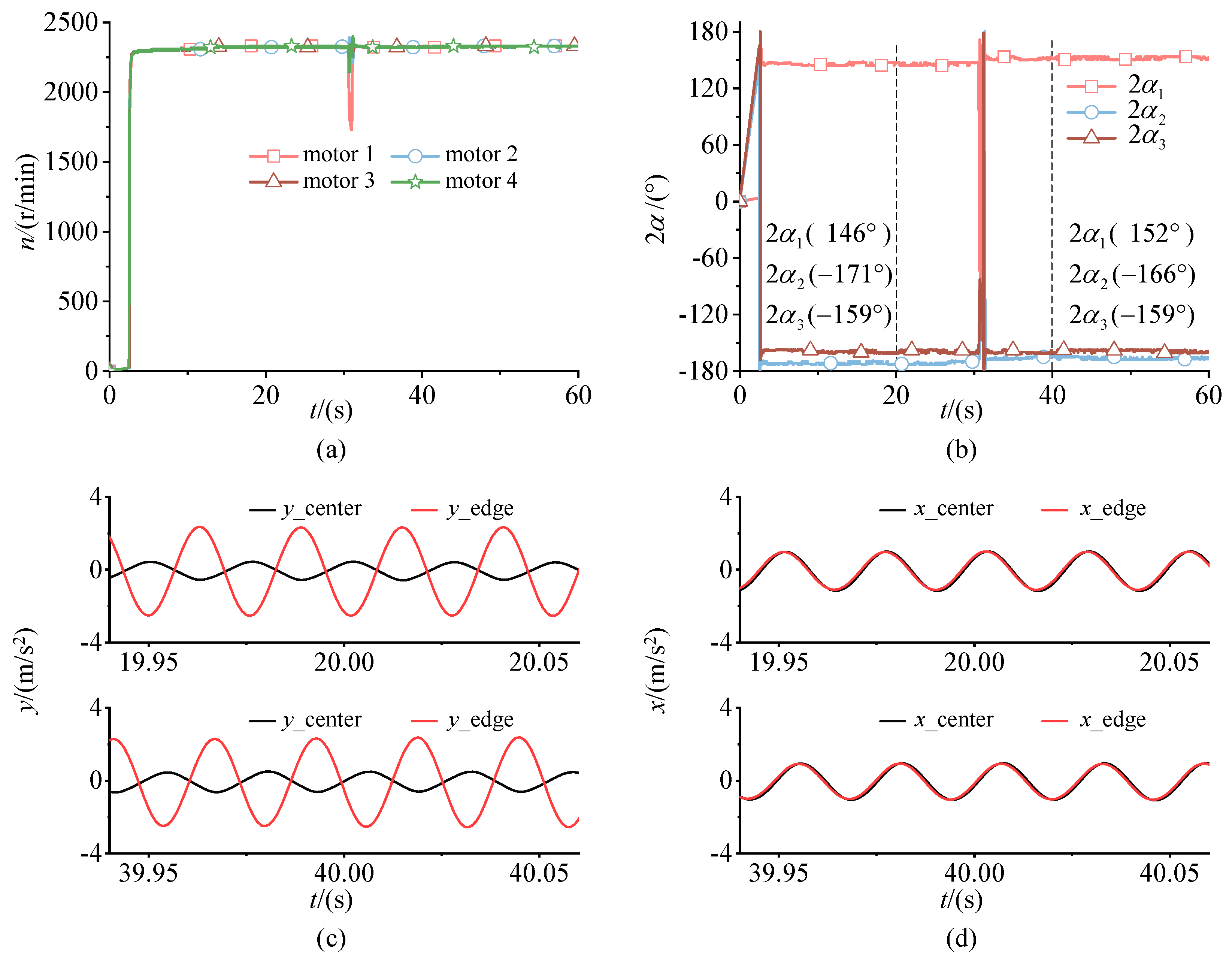
5.3.1. Steady State One
5.3.2. Steady State Two
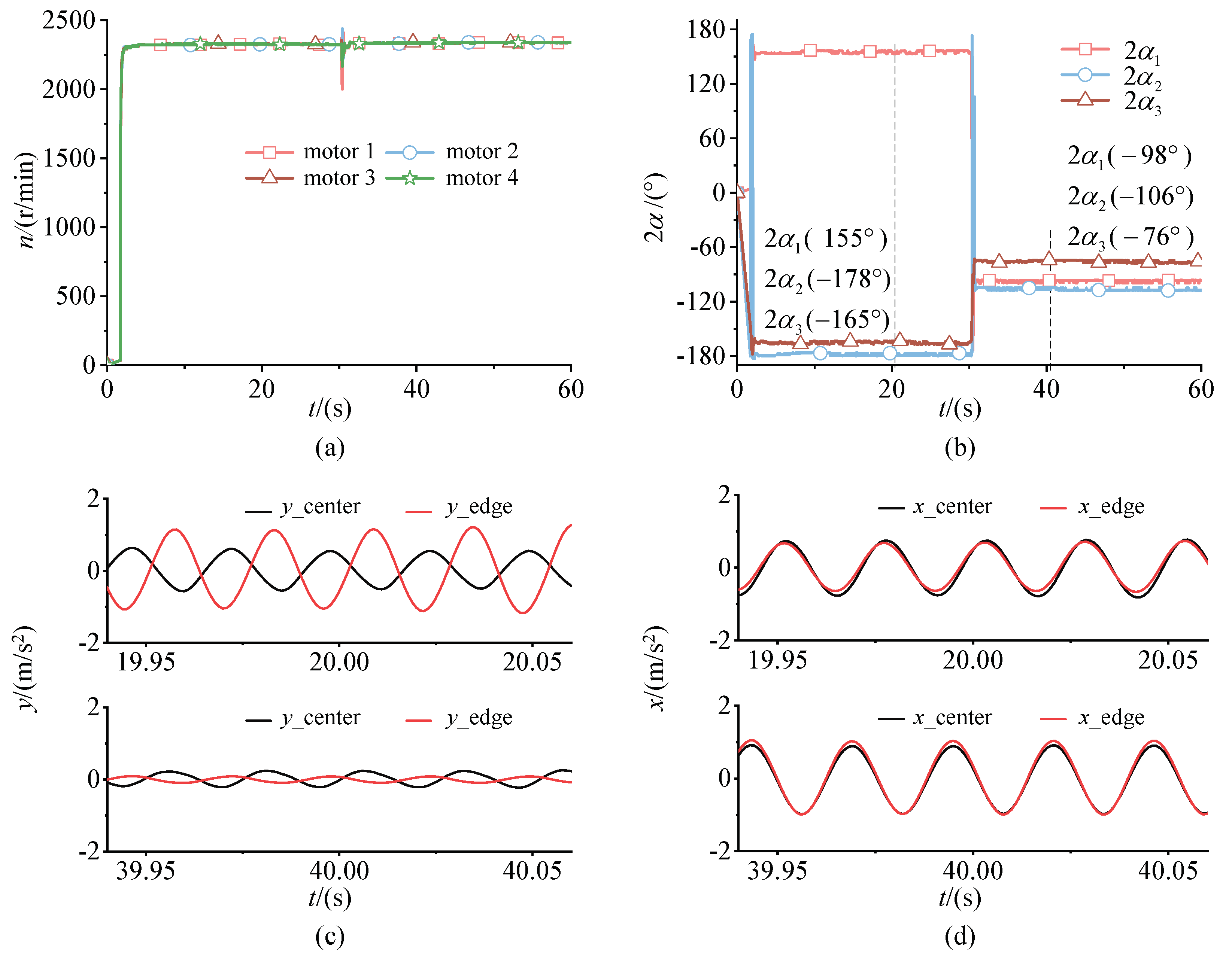
5.3.3. Steady State Three
5.3.4. Steady State Four
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Blekhman, I.I.; Fradkov, A.L.; Tomchina, O.P.; Bogdanov, D.E. Self-synchronization and controlled synchronization: General definition and example design. Math. Comput. Simul. 2002, 58, 367–384. [Google Scholar] [CrossRef]
- Blekhman, I.I.; Sorokin, V.S. On the separation of fast and slow motions in mechanical systems with high-frequency modulation of the dissipation coefficient. J. Sound Vib. 2010, 329, 4936–4949. [Google Scholar] [CrossRef]
- Czolczynski, K.; Okolewski, A.; Blazejczyk-Okolewska, B. Lyapunov exponents in discrete modelling of a cantilever beam impacting on a moving base. Int. J. Non-Linear Mech. 2017, 88, 74–84. [Google Scholar] [CrossRef]
- Dudkowski, D.; Czolczynski, K.; Kapitaniak, T. Multistability and synchronization: The co-existence of synchronous patterns in coupled pendula. Mech. Syst. Signal Process. 2022, 166, 108446. [Google Scholar] [CrossRef]
- Kibirktis, E.; Pauliukaitis, D.; Miliunas, V.; Ragulskis, K. Synchronization of pneumatic vibroexciters operating on air cushion with feeding pulsatile pressure under autovibration regime. J. Mech. Sci. Technol. 2018, 32, 81–89. [Google Scholar] [CrossRef]
- Miklos, A.; Szabo, Z. Simulation and experimental validation of the dynamical model of a dual-rotor vibrotactor. J. Sound Vib. 2015, 334, 98–107. [Google Scholar] [CrossRef] [Green Version]
- Gu, D.; Zhang, X.; Zhang, J.; Liu, Y.; Wen, B. Synchronization and coupling dynamic characteristics of an exciter and two cylindrical rollers in a vibrating system. J. Sound Vib. 2019, 456, 353–373. [Google Scholar] [CrossRef]
- Chen, X.; Kong, X.; Dou, J.; Liu, Y.; Wen, B. Numerical and experimental investigation on self-synchronization of two eccentric rotors in the vibration system. J. Vibroeng. 2016, 18, 744–758. [Google Scholar]
- Chen, X.; Kong, X.; Zhang, X.; Li, L.; Wen, B. On the Synchronization of Two Eccentric Rotors with Common Rotational Axis: Theory and Experiment. Shock Vib. 2016, 2016, 6973597. [Google Scholar] [CrossRef] [Green Version]
- Zou, M.; Fang, P.; Hou, Y.; Peng, H. Investigation on multiple-frequency synchronization experiment of vibration system with dual-rotor actuation. Mech. Syst. Signal Process. 2022, 164, 108261. [Google Scholar] [CrossRef]
- Li, L.; Chen, X. Times-frequency synchronization of two exciters with the opposite rotating directions in a vibration system. J. Sound Vib. 2019, 443, 591–604. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, H.; Zhang, Y.; Wen, B. Synchronization of two coupled exciters in a vibrating system of spatial motion. Acta Mech. Sin. 2010, 26, 477–493. [Google Scholar] [CrossRef]
- Fang, P.; Zou, M.; Peng, H.; Du, M.; Hu, G.; Hou, Y. Spatial synhronization of unbalanced rotors excited with paralleled and counterrotating motors in s far resonance system. J. Theor. Appl. Mech. 2019, 57, 723–738. [Google Scholar] [CrossRef]
- Chen, B.; Xia, X.O.; Wang, X. Synchronization and vibratory synchronization transmission of a weakly damped far-resonance vibrating system. PLoS ONE 2019, 14, e0209703. [Google Scholar] [CrossRef] [PubMed]
- Shishkin, E.V.; Kazakov, S.V. Application of vibratory-percussion crusher for disintegration of supertough materials. IOP Conf. Ser.-Earth Environ. Sci. 2017, 87, 022018. [Google Scholar] [CrossRef] [Green Version]
- Djanan, A.A.N.; Nbendjo, B.R.N.; Woafo, P. Self-synchronization of two motors on a rectangular plate and reduction of vibration. J. Vib. Control 2015, 21, 2114–2123. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Wei, X.; Wen, B. Self-synchronization theory of a nonlinear vibration system driven by two exciters. Part 1: Theoretical analysis. J. Vibroeng. 2014, 16, 725–734. [Google Scholar]
- Zhang, X.; Wen, B.; Zhao, C. Theoretical, numerical and experimental study on synchronization of three identical exciters in a vibrating system. Chin. J. Mech. Eng. 2013, 26, 746–757. [Google Scholar] [CrossRef]
- Chen, X.; Li, L. Phase Synchronization Control of Two Eccentric Rotors in the Vibration System with Asymmetric Structure Using Discrete-Time Sliding Mode Control. Shock Vib. 2019, 2019. [Google Scholar] [CrossRef]
- Chen, X.; Li, L. Selected synchronous state of the vibration system driven by three homodromy eccentric rotors. J. Low Freq. Noise Vib. Act. Control 2020, 39, 352–367. [Google Scholar] [CrossRef] [Green Version]
- Fang, P.; Wang, Y.; Hou, Y.; Wu, Y. Synchronous Control of Multi-Motor Coupled with Pendulum in a Vibration System. IEEE Access 2020, 8, 51964–51975. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Li, L. Dynamics of the Vibration System Driven by Three Homodromy Eccentric Rotors Using Control Synchronization. Appl. Sci. 2021, 11, 7691. [Google Scholar] [CrossRef]
- Jia, L.; Zhang, J.; Zhou, L.; Wen, B. Multifrequency-controlled synchronization of three eccentric rotors driven by induction motors in the same direction. J. Low Freq. Noise Vib. Act. Control 2019, 38, 615–632. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Liu, T.; Yue, H.; Zhang, X. Coupling synchronization principle of two pairs counter-rotating unbalanced rotors in the different resonant conditions. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1149–1165. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Wang, Z.; Cui, S. Synchronous Stability of Four Homodromy Vibrators in a Vibrating System with Double Resonant Types. Shock Vib. 2018, 2018, 9641231. [Google Scholar] [CrossRef]
- Kong, X.; Wen, B. Composite synchronization of a four eccentric rotors driven vibration system with a mass-spring rigid base. J. Sound Vib. 2018, 427, 63–81. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, H.; Wang, R.; Wen, B. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion. Part I: Theoretical analysis. Shock Vib. 2009, 16, 505–515. [Google Scholar] [CrossRef]
- Blekhman, I.I. Selected Topics in Vibrational Mechanics; World Scientific: Singapore, 2004; pp. 179–251. [Google Scholar]
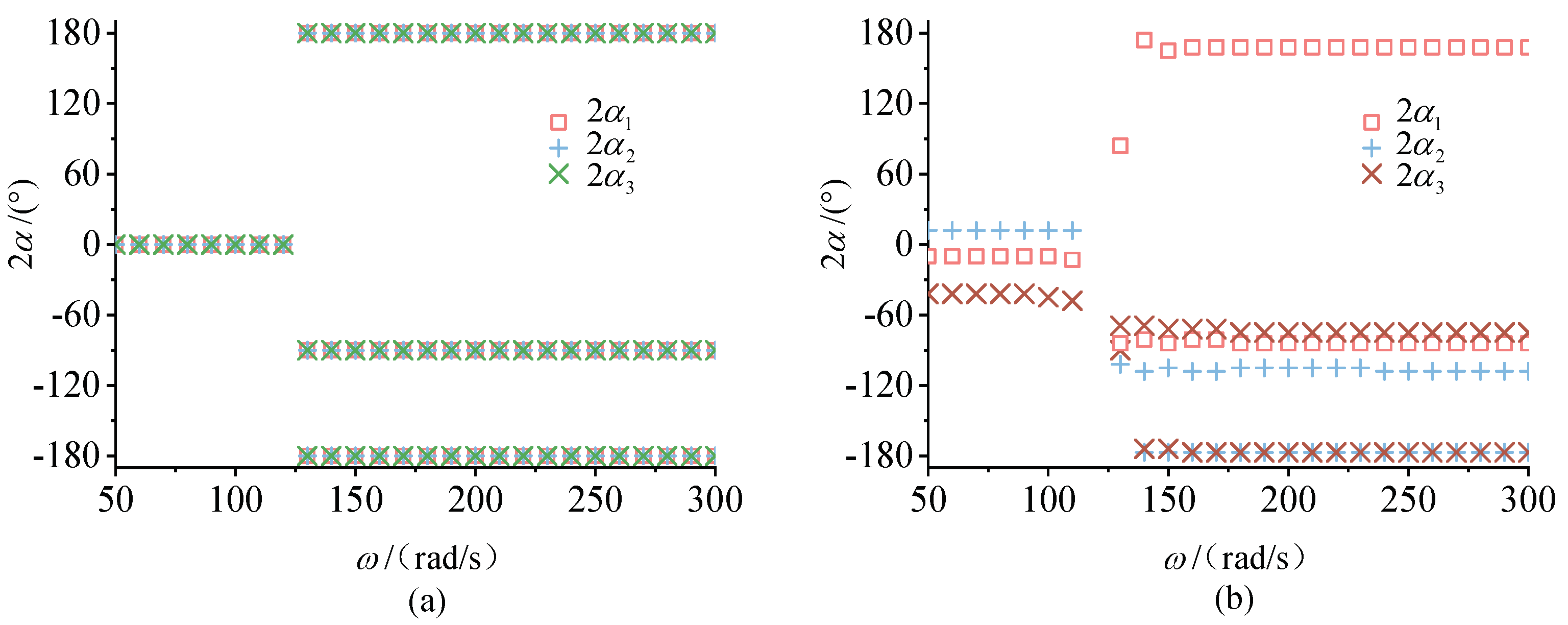








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, J.; Zhang, J.; Li, L. Synchronization of Four Axisymmetrically Distributed Eccentric Rotors in a Vibration System. Machines 2022, 10, 457. https://doi.org/10.3390/machines10060457
Chen X, Liu J, Zhang J, Li L. Synchronization of Four Axisymmetrically Distributed Eccentric Rotors in a Vibration System. Machines. 2022; 10(6):457. https://doi.org/10.3390/machines10060457
Chicago/Turabian StyleChen, Xiaozhe, Junqi Liu, Jiaqi Zhang, and Lingxuan Li. 2022. "Synchronization of Four Axisymmetrically Distributed Eccentric Rotors in a Vibration System" Machines 10, no. 6: 457. https://doi.org/10.3390/machines10060457
APA StyleChen, X., Liu, J., Zhang, J., & Li, L. (2022). Synchronization of Four Axisymmetrically Distributed Eccentric Rotors in a Vibration System. Machines, 10(6), 457. https://doi.org/10.3390/machines10060457




