Proximate Model of Gear Drive Units Based on Dimensional Analysis for Wear Process Evaluation
Abstract
:1. Introduction
2. Selection of Similar Parameters
2.1. Similarity Criterion for Gears
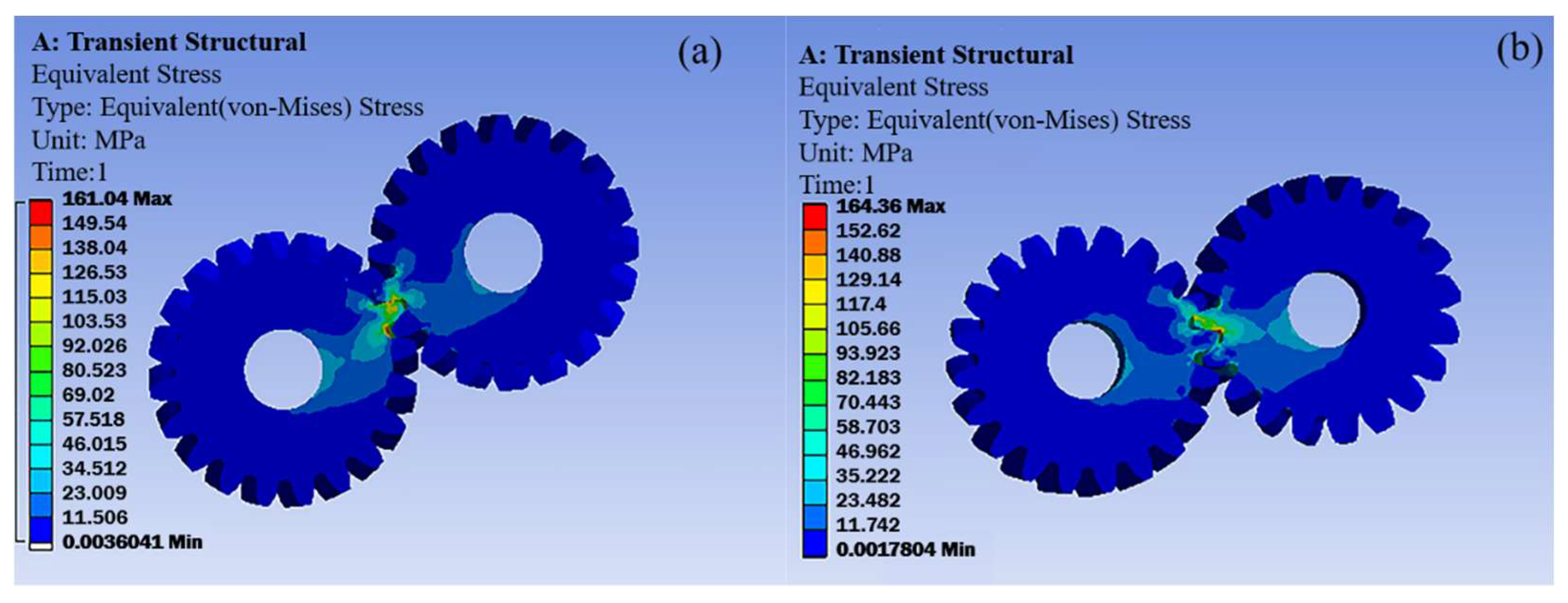
2.2. Finite Element Analysis to Verify
3. Experiment and Methods
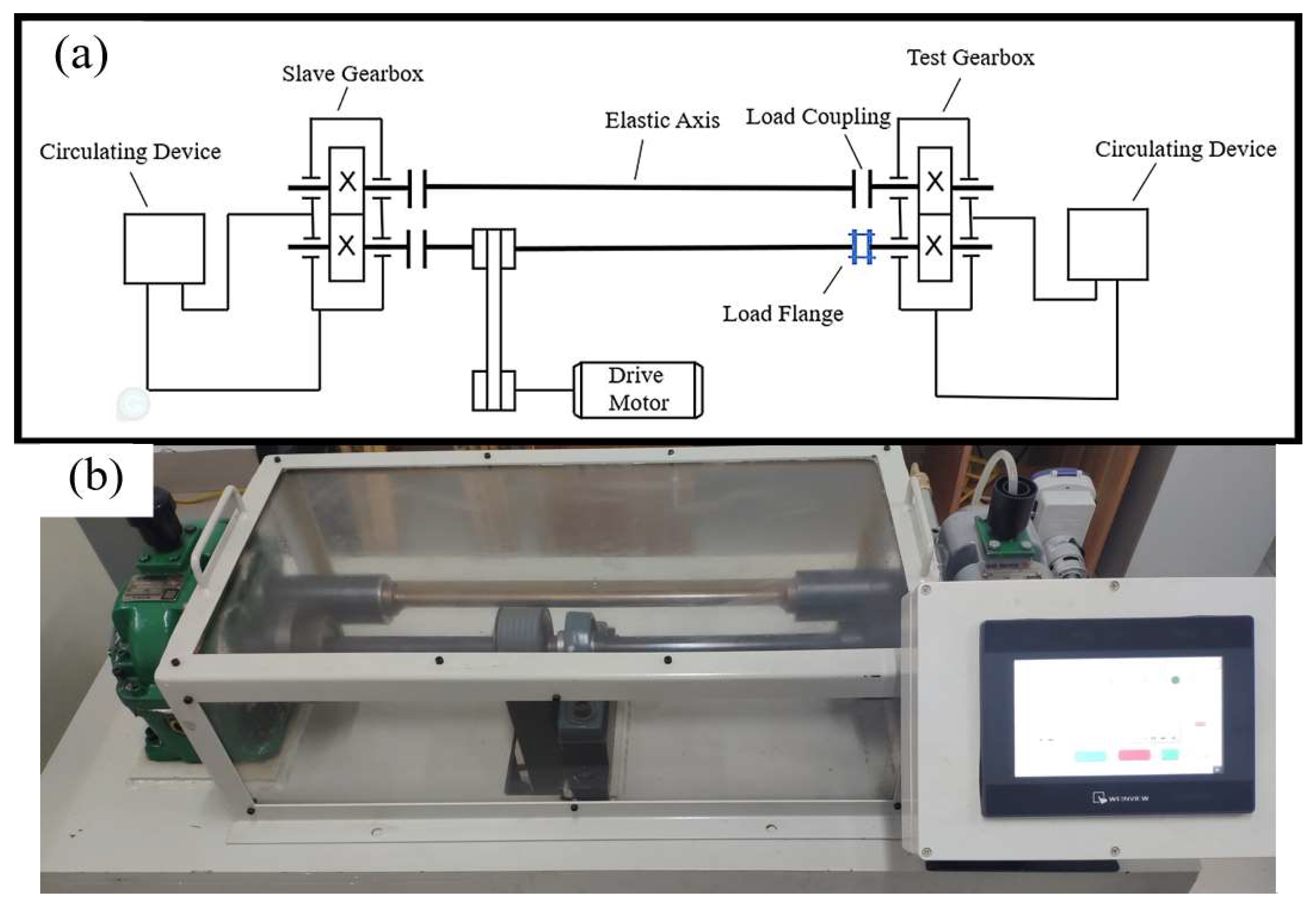
3.1. Gear Test Platform
3.2. Test Condition Set
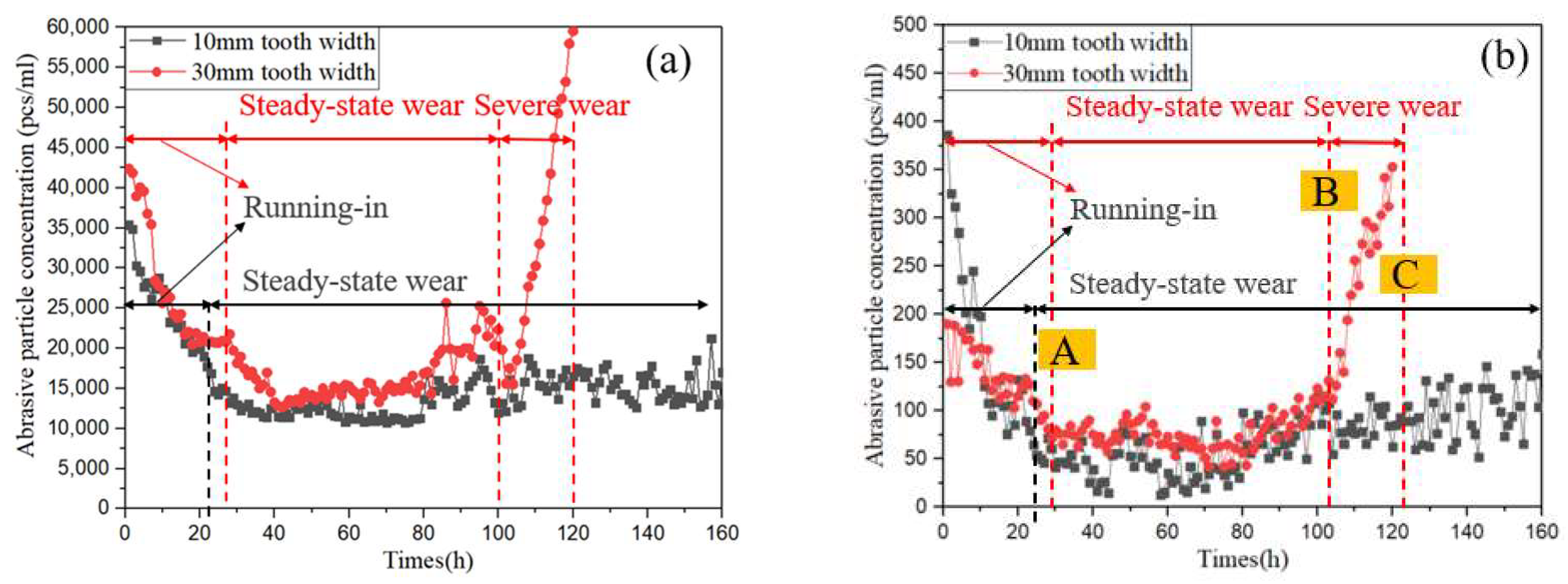
4. Results and Discussion
5. Conclusions
- Two pairs of gears with similar parameters are established, and the finite element analysis results showed that the maximum equivalent stress ratio was 0.98, which was about 1, which showed that the similarity relationship derived from the Buckingham pi-theorem based on dimensional analysis was feasible for predicting the friction and wear process of gears in simulation.
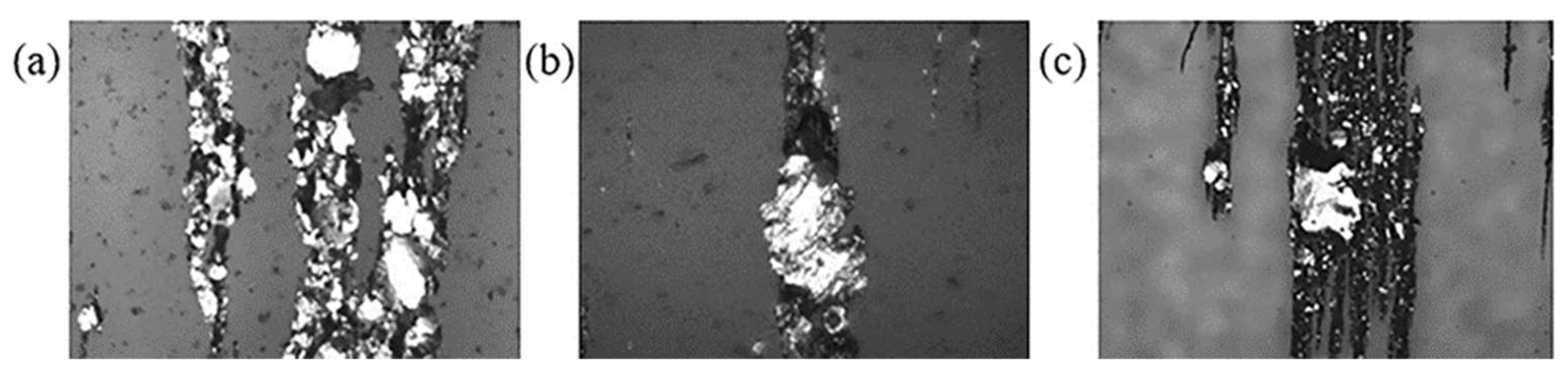
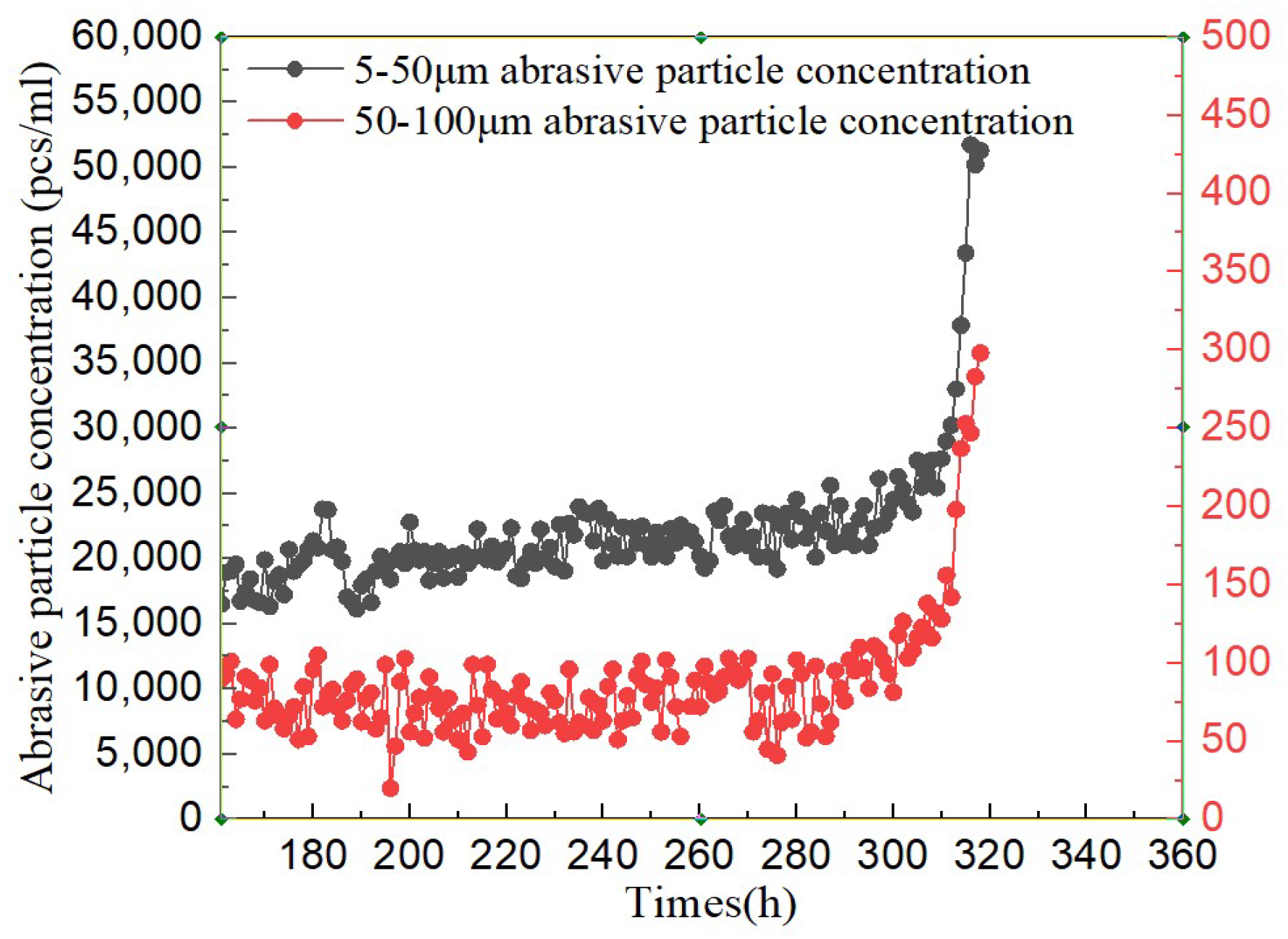
- A gear wear test platform was established. By analyzing the change of the abrasive particle concentration in the test gear, three wear stages during the gear operation were obtained. The friction and wear process of the 30 mm tooth width gear set was shortened. Compared with the 10 mm tooth width gear and the similar ratio tend to be consistent. The wear situation reflected by the ferrogram was consistent with the three stages of abrasive particle concentration change. The increase in abrasive particle concentration during abnormal wear was related to the generation of large-sized abrasive particles.
- By building a similar test model platform, the design and fault monitoring of similar ratio gears can be realized.
Author Contributions
Funding
Conflicts of Interest
References
- Yan, Y. Load characteristic analysis and fatigue reliability prediction of wind turbine gear transmission system. Int. J. Fatigue 2019, 130, 105259. [Google Scholar] [CrossRef]
- Nutakor, C.; Kłodowski, A.; Sopanen, J.; Mikkola, A.; Pedrero, J.I. Planetary gear sets power loss modeling: Application to wind turbines. Tribol. Int. 2017, 105, 42–54. [Google Scholar] [CrossRef]
- Fotso, H.R.F.; Kazé, C.V.A.; Kenmoé, G.D. Real-time rolling bearing power loss in wind turbine gearbox modeling and prediction based on calculations and artificial neural network. Tribol. Int. 2021, 163, 107171. [Google Scholar] [CrossRef]
- Kandukuri, S.T.; Klausen, A.; Karimi, H.R.; Robbersmyr, K.G. A review of diagnostics and prognostics of low-speed machinery towards wind turbine farm-level health management. Renew. Sustain. Energy Rev. 2016, 53, 697–708. [Google Scholar] [CrossRef]
- Wehrle, E.; Gufler, V.; Vidoni, R. Optimal In-Operation Redesign of Mechanical Systems Considering Vibrations—A New Methodology Based on Frequency-Band Constraint Formulation and Efficient Sensitivity Analysis. Machines 2020, 8, 11. [Google Scholar] [CrossRef]
- Dong, W.B.; Nejad, A.R.; Moan, T.; Gao, Z. Structural reliability analysis of contact fatigue design of gears in wind turbine drivetrains. J. Loss Prev. Process Ind. 2020, 65, 104115. [Google Scholar] [CrossRef]
- Hemalatha, S.; Selwyn, T.S. Computation of mechanical reliability for Sub- assemblies of 250 kW wind turbine through sensitivity analysis. Mater. Today Proc. 2020, 46, 3180–3186. [Google Scholar] [CrossRef]
- Ma, Y.; Cheng, J.; Wang, P.; Wang, J.; Yang, Y. A novel Lanczos quaternion singular spectrum analysis method and its application to bevel gear fault diagnosis with multi-channel signals. Mech. Syst. Signal. Process. 2021, 168, 108679. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Xu, Y.; Jia, M. Multichannel fault diagnosis of wind turbine driving system using multivariate singular spectrum decomposition and improved Kolmogorov complexity. Renew. Energy 2021, 178, 724–748. [Google Scholar] [CrossRef]
- Liu, Z.; Ding, K.; Lin, H.; He, G.; Du, C.; Chen, Z. A Novel Impact Feature Extraction Method Based on EMD and Sparse Decomposition for Gear Local Fault Diagnosis. Machines 2022, 10, 242. [Google Scholar] [CrossRef]
- Shboul, B.; AL-Arfi, I.; Michailos, S.; Ingham, D.; AL-Zoubi, O.H.; Ma, L.; Hughes, K. Mohamed Pourkashanian Design and Techno-economic assessment of a new hybrid system of a solar dish Stirling engine instegrated with a horizontal axis wind turbine for microgrid power generation. Energy Convers. Manag. 2021, 245, 114587. [Google Scholar] [CrossRef]
- Shivsharan, B.A.; Magade, P.B.; Chavan, S.; Magade, S. Experimental design, development and testing of novel aluminum mini wind turbine. Mater. Today Proc. 2020, 43, 1304–1312. [Google Scholar] [CrossRef]
- Ajirlo, K.S.; Tari, P.H.; Gharali, K.; Zandi, M. Development of a wind turbine simulator to design and test micro HAWTs—ScienceDirect. Sustain. Energy Technol. Assess. 2021, 43, 100900. [Google Scholar]
- Rohrmoser, A.; Kraus, M.; Merklein, M. Forming of Components with Microgearings from Coil Material—Numerical Modeling of the Process Chain and Experimental V alidatio. Micromachines 2021, 12, 1456. [Google Scholar] [CrossRef] [PubMed]
- Giraud, M.; Gatumel, C.; Vaudez, S.; Nos, J.; Gervais, T.; Bernard-Granger, G.; Berthiaux, H. Investigating grinding mechanisms and scaling criteria in a ball mill by dimensional analysis. Adv. Powder Technol. 2021, 32, 2988–3001. [Google Scholar] [CrossRef]
- Jadhav, P.M.; Kumbhar, S.G.; Desavale, R.G.; Patil, S.B. Distributed Fault Diagnosis of Rotor-Bearing System using Dimensional Analysis and Experimental Methods. Measurement 2020, 166, 108239. [Google Scholar] [CrossRef]
- Patil, M.S.; Mathew, J.; Rajendrakumar, P.K.; Desai, S. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing. Int. J. Mech. Sci. 2010, 52, 1193–1201. [Google Scholar] [CrossRef]
- Roylance, B.J. Ferrography—Then and now. Tribol. Int. 2005, 38, 857–862. [Google Scholar] [CrossRef]
- Khan, M.A.; Starr, A.G. Wear debris: Basic features and machine health diagnostics. OR Insight 2006, 48, 470–476. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, D.; Mishra, A.K. Analysis of ISO VG 68 bearing oil for condition monitoring collected from an externally pressurized ball bearing system. Mater. Today Proc. 2021, 44, 4602–4606. [Google Scholar] [CrossRef]
- Li, S. Experimental investigation and FEM analysis of resonance frequency behavior of three-dimensional, thin-walled spur gears with a power-circulating test rig. Mech. Mach. Theory 2008, 43, 934–963. [Google Scholar] [CrossRef]
- Feng, S.; Fan, B.; Mao, J.; Xie, Y. Prediction on wear of a spur gearbox by on-line wear debris concentration monitoring. Wear 2015, 336–337, 1–8. [Google Scholar] [CrossRef]
- Singh, D.K.; Kurien, J.; Villayamore, A. Study and analysis of wind turbine gearbox lubrication failure and its mitigation process. Mater. Today: Proc. 2020, 44, 3976–3983. [Google Scholar] [CrossRef]
- Marafona, J.D.; Marques, P.M.; Martins, R.C.; Seabra, J.H. Mesh stiffness models for cylindrical gears: A detailed review. Mech. Mach. Theory 2021, 166, 104472. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A scuffing model for spur gear contacts. Mech. Mach. Theory 2021, 156, 104161. [Google Scholar] [CrossRef]









| Type | Physical Quantity | Symbol | Dimension |
|---|---|---|---|
| Pitch circle diameter | d | L | |
| Modulus | m | L | |
| Geometric feature | Tooth width | b | L |
| Number of teeth | z | -- | |
| Helix angle | β | -- | |
| Stress | σ | ML−1T−2 | |
| Material feature | Density | ρ | ML−3 |
| Elastic modulus | E | ML−1T−2 | |
| Poisson’s ratio | ν | -- | |
| Load | F | MLT−2 | |
| Kinetic feature | Rotating speed | n | T−1 |
| Time | t | T |
| d | m | b | z | β | σ | ρ | E | υ | F | n | t | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| L | 1 | 1 | 1 | 0 | 0 | −1 | −3 | −1 | 0 | 1 | 0 | 0 |
| T | 0 | 0 | 0 | 0 | 0 | −2 | 0 | −2 | 0 | −2 | −1 | 1 |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | |
|---|---|---|---|---|---|---|---|---|---|
| M | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| L | 1 | 1 | 1 | −1 | −3 | −1 | 1 | 0 | 0 |
| T | 0 | 0 | 0 | −2 | 0 | −2 | −2 | −1 | 1 |
| d | m | b | σ | ρ | E | F | n | t | |
|---|---|---|---|---|---|---|---|---|---|
| π1 | −1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| π2 | −1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| π3 | 0 | 0 | 0 | 1 | 0 | −1 | 0 | 0 | 0 |
| π4 | −2 | 0 | 0 | 0 | 0 | −1 | 1 | 0 | 0 |
| π5 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| π6 | −1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Parameter | m | b | z | β | σ | υ | F | n | t |
|---|---|---|---|---|---|---|---|---|---|
| Similarity | |||||||||
| Contact | 1 | 1 | 1 |
| Coordinate System Type | Contact | Constrain | Solver Type | ||
|---|---|---|---|---|---|
| Type | Location | Type | Location | ||
| Cylindrical Coordinate System | Frictional:0.2 | Contact: big gear | Joint- moment | Axial surface of small gear | Equivalent stress |
| Interface treatment: adjust to touch | Target: small gear | Axial surface of small gear | |||
| Parameter | Symbol | Prototype Gear | Model Gear |
|---|---|---|---|
| Pitch circle diameter (mm) | d | 60 | 30 |
| Number of teeth | z | 20 | 20 |
| Tooth width (mm) | b | 8 | 4 |
| Modulus (mm) | m | 3 | 1.5 |
| Pressure angle (°) | α | 20 | 20 |
| Helix angle (°) | β | 15 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yuan, W.; Zhu, Y.; Guo, Q.; Chi, B.; Wang, H.; Yang, X. Proximate Model of Gear Drive Units Based on Dimensional Analysis for Wear Process Evaluation. Machines 2022, 10, 474. https://doi.org/10.3390/machines10060474
Wang W, Yuan W, Zhu Y, Guo Q, Chi B, Wang H, Yang X. Proximate Model of Gear Drive Units Based on Dimensional Analysis for Wear Process Evaluation. Machines. 2022; 10(6):474. https://doi.org/10.3390/machines10060474
Chicago/Turabian StyleWang, Wenhua, Wei Yuan, Yuqi Zhu, Qianjian Guo, Baotao Chi, Haixiao Wang, and Xianhai Yang. 2022. "Proximate Model of Gear Drive Units Based on Dimensional Analysis for Wear Process Evaluation" Machines 10, no. 6: 474. https://doi.org/10.3390/machines10060474
APA StyleWang, W., Yuan, W., Zhu, Y., Guo, Q., Chi, B., Wang, H., & Yang, X. (2022). Proximate Model of Gear Drive Units Based on Dimensional Analysis for Wear Process Evaluation. Machines, 10(6), 474. https://doi.org/10.3390/machines10060474






