1. Introduction
Continuing development of technology has shown its impact in different areas of production. The fashion industry has adapted these technologies to revolutionize it brands. However, one of the main requests is fulfilling or meeting consumers’ preferences, especially the preferences regarding product personalization. Digitalization in the fashion industry speeds up product customization through different technologies, as part of the fourth industrial revolution. Industry 4.0, even known as smart manufacturing because of its main pillars such as 3D modeling, simulation, additive manufacturing, and digital data processing, has optimized the development of a wide range of products. Moreover, I4.0 is a synonym for sustainable production. As a sensitive topic, it has gained the attention of various researchers who highlight that there is a link between Industry 4.0 and sustainability, where I4.0 is a key factor in speeding up sustainable development [
1].
The fashion industry is more exposed to the issue of sustainability due to its negative contribution through fast fashion, overconsumption, technological process, etc. Due to this fact, there are initiatives from companies that try to make an impact or give their contribution to sustainable ways of production. Improvements are seen in developed countries which are more likely to adopt Industry 4.0, but its implementation is still in its infancy [
2]. In addition, researchers have found that retail companies are the first to use pillars of Industry 4.0 compared to textile companies. However, findings reveal a wide spread in fashion management [
3]. Among the pillars of I4.0, 3D printing is a well-known technology for various applications in developing fashion products. Having a wide range of applications is driven by improvements in technology and a wide range of materials available. Of increasing interest are the applications for fashion products in order to improve or add functionalities. Objects are created by laying down on the printing support successive layers of materials extruded from the heated nozzle. Combinations of printing materials with textile fabric can be a great solution to add functionalities to garments or technical textiles. The composite structure created by these combinations may present adhesion problems that are linked with textile properties and 3D printing parameters. Various researchers have studied the influence of these parameters in order to find the optimum value or parameters that result in good adhesion [
4,
5].
According to Denker et al. [
6], 3D printers are widely used devices because they make prototyping easy, but they come with limitations such as the type of material used and the relatively long printing time. The authors point out that the use of fabric as the main material on which to print overcomes some of the limitations of 3D printers. This expands the application of 3D printers in general.
The technology for 3D printing on fabrics was developed by Peng et al. [
7]. The authors propose a technology in which the textile fabric is cut with a laser and applied layer by layer until a three-dimensional object is obtained. The method is suitable for the development of touch-sensitive sensing devices applied directly to the textile fabric. The disadvantage of this technology is that it requires complex equipment and long preparation of the 3D CAD model before its physical production.
Effective results with 3D printing on fabrics were reported by Pei et al. [
8]. The authors managed to combine polymer with textile fabrics. According to the authors, the advantage of combining the two materials is that the textile fabric is a breathable and deformable material, and the polymer can strengthen its structure. As a result of this study, PLA exhibited the best properties compared to other polymer threads. Tested on eight types of fabrics, the material has good adhesion, low distortion, satisfactory bending strength, and high print quality. Grimmelsmann et al. [
4] explored the possibilities of the presented 3D printing technologies as a tool for adding sensors and actuators to textile fabrics and creating smart products. The authors point out that it is necessary for the electronic devices attached by 3D printing to retain the characteristics for the entire planned service life of the textile fabrics. In addition, more research is needed on the combination of textile fabrics and polymeric materials that will ensure the efficient use of electronic devices for smart textiles.
Another interesting application is embroideries created by 3D printing on textile fabric. Three-dimensional printing in the form of embroidery on textile fabrics is proposed by Goudswaard et al. [
5]. The authors apply their development as non-retaining buttons for smart textiles. The authors point out that more research is needed to find methods for maintaining flexibility and a design approach to making smart textiles using 3D printing techniques.
One of the important characteristics of fabrics is their drape. A number of methods have been developed to determine it. Methods for obtaining, processing, and analyzing images are suitable for such purposes as obtaining fabric drapes. They are affordable, and they do not require complex equipment and complex computational procedures. They are suitable for application directly on the production line when assessing the condition and quality of textile fabrics with 3D prints on them.
Modifications of the existing method for automated evaluation of drapery characteristics are proposed by Sanad et al. [
9]. The authors found that image processing techniques were more effective for weaving drapes in nonwovens than in woolen fabrics.
Capdevila et al. [
10], determine the drape characteristics of woolen fabrics with an accuracy of 76%. Using classifiers, the authors reported errors of up to 4% when using data from color digital images to determine the drape of woolen textile fabrics.
A modified method for determining the drape characteristics of digital images is proposed by Ragab et al. [
11] by achieving a maximum accuracy of 90% compared with the standard method for determining the drape characteristics.
It has been found that the direct use of data on textile fibers embedded in textile fabrics is not a sufficient source of informative data when predicting the characteristics of draperies. In another work proposed by Pan et al. [
12], the accuracy achieved is only 55–84% when using data on the characteristics of textile fibers to predict the drape of textile fabrics on their color digital images.
The characteristics of textile fabrics were used as input data to predict the drape characteristics. Using digital image data, Hussain et al. [
13] achieved an accuracy of 76–82% through a modified draping coefficient and degree of bending of the textile fabric.
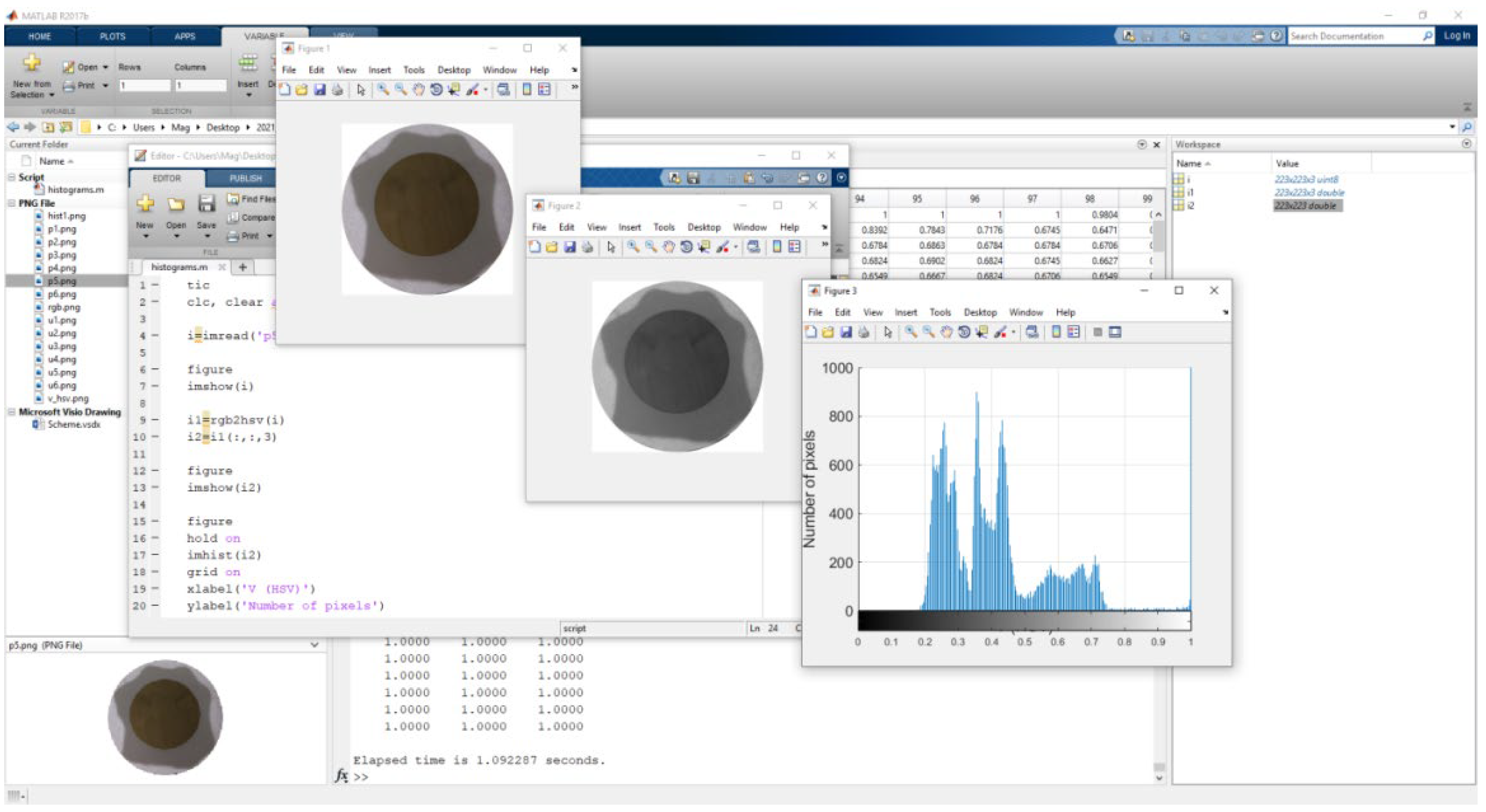
From the review of the available literature sources, it can be summarized that it is necessary to look for more effective methods for the analysis of images of draperies. The aim is to make them suitable for use in practice. One such method is image histogram analysis [
14]. The advantage of histogram analysis is that it is an affordable image analysis method that does not require complex computational procedures and does not require a long time to process the data obtained. In this method, a digital image is divided into multiple segments, sets of pixels, also known as regions of interest in the image. This type of analysis is not sufficiently applied in the analysis of fabric drapes, on their color digital images.
An important practical application of the drape images, which has become necessary in recent years, is their use for three-dimensional visualization and simulation in the analysis of textile fabrics. According to Petrak et al. [
15], an important parameter for adjustment in the 3D simulation of garments is the density of the used grid of the polygonal model. By optimally choosing this density, the resulting three-dimensional model will be simple enough and will carry enough information about the condition of the drapery.
Comparative analysis of actually measured drape characteristics and results of three-dimensional simulation was performed by Rudolf et al. [
16]. The authors point out that there is no complete correspondence between the obtained 3D model and the real drape. According to them, it is necessary to look for more methods that will lead to sufficient accuracy in the three-dimensional drape simulation. One such solution is the precise determination and importation of characteristics of the fabrics in the simulation software, as indicated by Han et al. [
17].
Suitable for determining the fabric drape are methods developed using 3D scanning and stereo video cameras. The disadvantage of these methods is that they are time-consuming and require the use of complex equipment for operation and maintenance, at high cost.
Methods for a more accurate 3D drape suitable for use with CAD systems have been proposed. Efendioglu et al. [
18] indicate that 3D scanning, laser scanning, and stereo video cameras are applicable for this purpose. Common disadvantages of these methods are that they require the use of complex technical equipment, require a long time to obtain the three-dimensional shape of the scanned fabric drape, and involve a high cost of technical means used for this purpose.
Ju et al. [
19] offer options, using different methods of draping the fabric and three-dimensional scanning. Such draping methods are hanging drape, Cusick’s drapemeter, and modified Cusick’s drapemeter.
Improving the 3D simulations of drapery requires prior knowledge of the composition and properties of the fabric, as well as accurate determination of the drape characteristics of their digital images. When looking for a connection between the type of fibers used in the textile fabric and the drape characteristics, it is necessary to look for appropriate calculation procedures because the direct use of data on the types of fibers in the fabric does not provide sufficient accuracy.
From the review of the available literature sources related to obtaining a three-dimensional shape of the fabric drape, it can be concluded that the existing approaches cannot provide sufficient accuracy of the obtained results. There are also insufficiently defined criteria for an objective assessment of the resulting drape from different types of fabrics.
The Cusick’s drape method is suitable for creating three-dimensional shapes of fabric drapes on their two-dimensional visual images. Creating an algorithm through which it is possible to reproduce 3D drapery is suitable. The main research on the automation of this method aims to determine the drape parameters on 2D images. Insufficient research has been found in the available literature related to the reproduction of a three-dimensional shape from two-dimensional images obtained by this method. Reproduction of 3D shapes of fabric drapes obtained from 2D images is possible because the conditions under which the images were obtained, the location of the object in space, and the physical dimensions of the object are known in advance.
The aim of the present work is to review the possibilities, limitations, and evaluation of fabric drape with 3D printed geometries through comparative analyses and application of methods for image processing and analysis.
The main contributions that can be defined are as follows:
A comparative analysis was performed on the use of histograms of images as a criterion for assessing changes in textile fabrics with and without printed 3D elements on them.
An algorithm is proposed that realizes the basic principles for obtaining a 3D shape of fabric drape based on its 2D images. The algorithm is supplemented with basic functions to estimate the changes in the fabric drape after 3D printing geometries.
A comparative analysis is performed between the results obtained with the proposed algorithm and a standard drape tester. It was found that the proposed algorithm can be used to determine the characteristics of a fabric drape with printed 3D geometries with sufficient accuracy.
The article is organized in the following order: After the literature review and definition of the main problems and limitations related to the analysis of fabric drapes with 3D printed geometries, color digital images describe the materials and methods used to solve some of these problems. Textile fabrics, 3D printing materials, and methodology for image analysis of histograms are described. The main criteria for evaluating the changes on fabric drapes after printing 3D geometries are presented. The results of comparative analyses related to the determination of the drape coefficient by a standard method and by image analysis of histograms are reported. Finally, a discussion is presented in which the results obtained are compared with those of the available literature, and the content of the present work is summarized as conclusions.
4. Discussion
In the present work, the results indicated in the available literature are supplemented, updated, and partially improved. Three-dimensional printing technologies have been proven to be an effective method for improving the appearance and properties of textile fabrics. This complements the summaries of Denker et al. [
6], according to which the use of fabric as the main material on which to print overcomes some of the limitations of 3D printers.
In this paper, a clear and objective assessment of the properties of the obtained textile fabrics with 3D printing is proposed. The results of Capdevila et al. [
10] depict that an accuracy of 76% was achieved in the analysis of draperies of woolen fabrics. In the present work, a close accuracy of 70% has been achieved in the analysis of textile linen fabrics. Compared to the standard method, the errors are of the order of 4%. In addition, in the present work, the data for fabrics are enriched with 3D elements printed on them.
The results obtained here complement those of Hussain et al. [
13]. By using histograms of images, an accuracy of over 80% was achieved compared to the standard method for determining drape characteristics, close to that of the presented authors. An accuracy higher than this was achieved by Ragab et al. [
11], who reported a maximum accuracy of 90%.
Sanad et al. [
9] found that image processing techniques are more effective for weaving draperies in nonwovens than in woolen fabrics. This is complemented in the present work by methods for analyzing histograms of images, as well as an algorithm for obtaining three-dimensional shapes from two-dimensional images, with added features to assess the basic drape characteristics.
The methods proposed here for obtaining the 3D shape of drapes from their 2D images are suitable for use with 3D CAD systems. This complements the findings of Efendioglu et al. [
18], who showed that 3D scanning, laser scanning, and stereo video cameras are applicable for this purpose. The use of color digital images removes the limitations of these methods, which require the use of complex technical equipment and a long time to obtain the three-dimensional shape of the scanned fabric drape. The use of digital images does not require complex and expensive equipment or complex computational procedures for processing the data obtained.
The results of the present work fulfill one of the recommendations of Rudolf et al. [
16], which indicates that it is necessary to look for more methods that will lead to sufficient accuracy in the three-dimensional simulation of fabric drape. The algorithm proposed in this paper for obtaining a 3D shape of the fabric drape implements the recommendation.
The following research will be related to removing the limitations of the algorithm proposed here. More research is needed to assess the impact of factors influencing textile drape. This will improve the accuracy of the laziness obtained by removing the limitations of the algorithm proposed here.
5. Conclusions
The drape is an important property for garment appearance and is considered by pattern makers for garment design and production. Effects of design or seams are studied by different authors to modify garment drapes. With the application of innovative technologies such as 3D printing, we have tested the effect of 3D printing various geometries according to number, shape, and positioning or arrangement on linen fabric. Drape coefficients measured on pure fabric and fabric with 3D printed patterns depict another way to modify fabric drape and create complex shapes by using less material compared to the traditional manufacturing methods, which is seen as an advantage in the fashion industry.
A comparative analysis of the use of image histograms as a criterion for assessing changes in textile fabrics with and without printed 3D elements on them was conducted. It was found that in the textile fabrics without printed 3D elements, the region of interest in the histogram has a smaller range and more pixels compared to the textile fabrics on which 3D elements are printed. The results were confirmed by the measurement with a standard drape tester. In this analysis, higher values of the draping coefficient were obtained for fabrics without 3D elements than for those without such elements. The difference in the drape coefficient is up to 4% for both types of fabrics.
An algorithm is proposed that implements the basic principles for obtaining a 3D shape of a drape based on its 2D images. The algorithm is supplemented with basic functions for estimating the changes in fabric drape after printing 3D elements on it. Compared to the standard drape tester, the proposed algorithm offers 70% accuracy in determining the drape characteristics of fabrics with 3D printed shapes on them.
From the comparative analysis of the results obtained in the present work with those indicated in the available literature, it was found that the data from the available literature have been updated, improved, and supplemented. Software and hardware are offered, through which the characteristics of fabric drape with and without 3D printed elements can be determined in an accessible and objective way. These instruments can be used for these purposes, ensuring sufficient accuracy of measurements.
The achieved accuracy is sufficient for the application of the algorithm for practical purposes, in determining the drape characteristics and their 3D reproduction from their two-dimensional color digital images.
The methods and technical means proposed in the present work can be used in the analysis of fabrics from which to produce garments, curtains, upholstery, etc.