A Novel Hybrid Whale Optimization Algorithm for Flexible Job-Shop Scheduling Problem
Abstract
:1. Introduction
2. Problem Description
- (1)
- In the Total Flexible Job Shop Scheduling Problem (T-FJSP), any operation in any job can choose any machine from all machines for operations, as shown in Table 2;
- (2)
- Partial Flexible Job Shop Scheduling Problem (P-FJSP), where each operation of each job can be operated by some of all the machines shown in Table 3.
3. Whale Optimization Algorithm
3.1. Encircling the Prey
3.2. Search for The Prey (Exploration Phase)
3.3. Bubble-Net Attacking (Exploitation Phase)
4. Proposed HWOA
4.1. Encoding and Decoding
4.2. Population Initialization
| Algorithm 1. The population is initialized by the good point set. |
| 1.Let the population size be G. |
| 2. for n = 1:G do |
| 3. for k = 1:m do |
| 4. P takes the smallest prime number that satisfies p ≥ 2m + 3 |
| 5. A matrix with n as rows, m as columns, and all elements in the columns as n |
| 6. Calculate the value by Equation (22) |
| 7. The initial population location is calculated by Equation (20) |
| 8. end for |
| 9. end for |
4.3. Nonlinear Convergence Factor
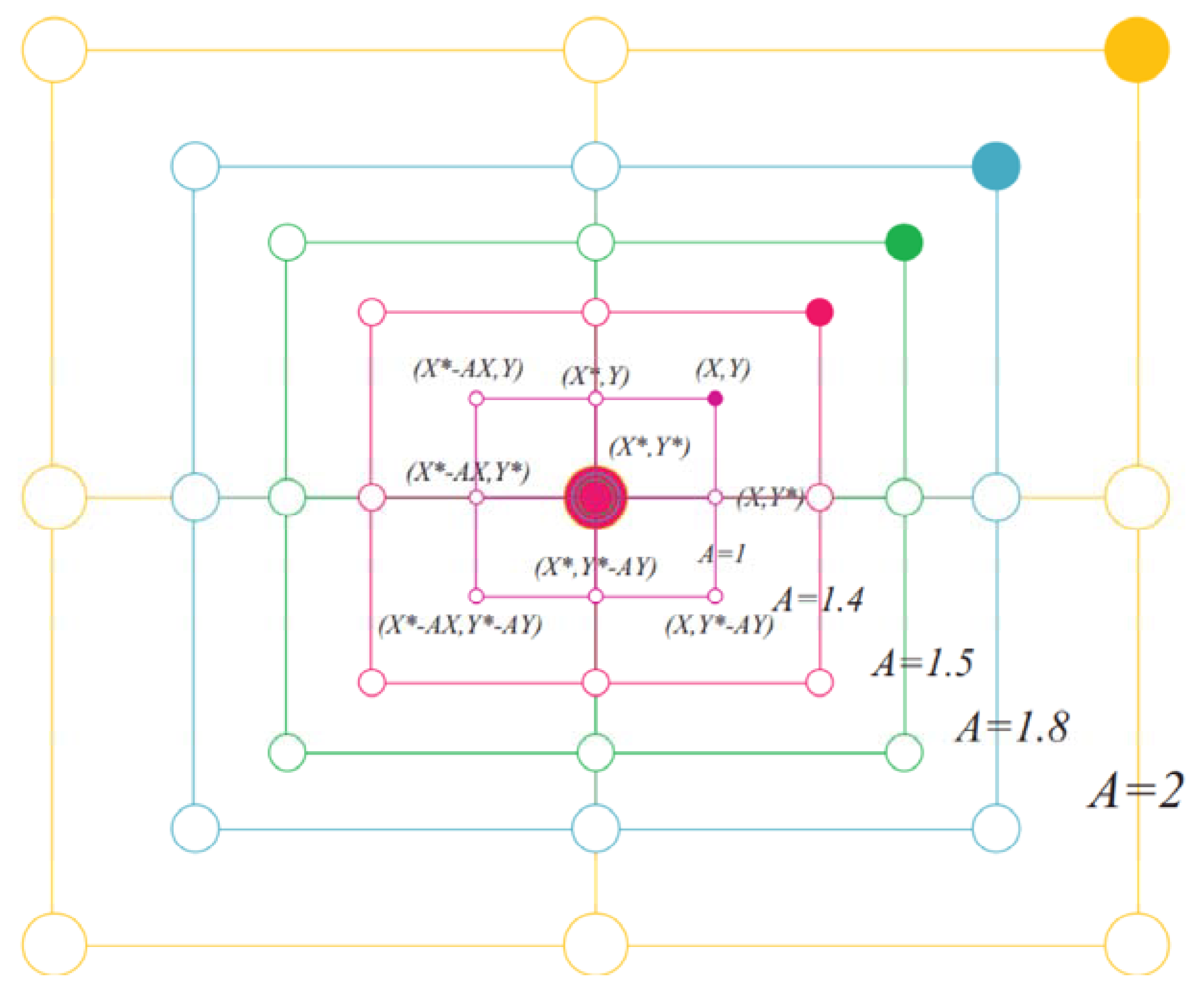
4.4. Multi-Neighborhood Structure
4.4.1. Neighborhood Structure N1
4.4.2. Neighborhood Structure N2
4.4.3. Neighborhood Structure N3
| Algorithm 2. Core operation across-machine gene reinforcement mechanism. |
| 1. Let the current core operation arrangement code be , the machine arrangement code be , the length of the core path set composed of core operations be , and the fitness function be F |
| 2. for 3. Select the operation on the core path, and the set composed of its operation set and machine set is denoted as . |
| 4. The across-machine gene reinforcement operation is performed on , and the newly generated machine set is noted as , and the set of newly generated machine set and operation set is noted as 5. if F() < F() 6. |
| 7. end if |
| 8. end for |
4.5. Diversity Reception Mechanism
| Algorithm 3. HWOA. |
| 1. Initialize the parameters and population 2. Calculate the fitness value and save the optimal individual position 3. while do 4. for do 5. Calculate the value of according to Equation (10), the value of according to Equation (11) and the value of the nonlinear convergence factor according to Equation (23) 6. Generate a random number within 7. if do 8. if do 9. Update individual whale positions according to Equation (8) 10. else if 11. Update individual whale positions according to Equation (13) 12. end if 13. else if 14. Update individual whale positions according to Equation (17) 15. end if 16. end for 17. Perform multi-neighborhood structure updates and retain the resulting improved solutions 18. Carry out the diversity reception mechanism 19. Update the optimal individual position 20. t = t + 1 21. end while |
| 22. end |
5. Experimental Analysis
5.1. Benchmark Functions Test
5.2. Performance Evaluation Compared with Other Algorithms
5.3. Application to Flexible Job Shop Scheduling
5.3.1. Experimental Settings
5.3.2. Strategy Validity Verification
5.3.3. Performance Verification
Comparison Experiment 1
Comparison Experiment 2
Comparison Experiment 3
Comparison Experiment 4
Comparison Experiment 5
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Ihlow, J.; Lehmann, C. A genetic algorithm for flexible job-shop scheduling. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; pp. 1120–1125. [Google Scholar]
- Du, X.; Li, Z.; Xiong, W. Flexible Job Shop scheduling problem solving based on genetic algorithm with model constraints. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008; pp. 1239–1243. [Google Scholar]
- Bowman, E.H. The schedule-sequencing problem. Oper. Res. 1959, 7, 621–624. [Google Scholar] [CrossRef]
- Wu, X.; Wu, S. An elitist quantum-inspired evolutionary algorithm for the flexible job-shop scheduling problem. J. Intell. Manuf. 2017, 28, 1441–1457. [Google Scholar] [CrossRef] [Green Version]
- Brucker, P.; Schlie, R. Job-shop scheduling with multi-purpose machines. Computing 1990, 45, 369–375. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Niar, S.; Ammari, A.C. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem. J. Intell. Manuf. 2015, 29, 603–615. [Google Scholar] [CrossRef]
- Huang, X.; Chen, S.; Zhou, T.; Sun, Y. A new neighborhood structure for solving the flexible job-shop scheduling problem. Syst. Eng.-Theory Pract. 2021, 41, 2367–2378. [Google Scholar]
- Xue, L. Block structure neighborhood search genetic algorithm for job-shop scheduling. Comput. Integr. Manuf. Syst. 2021, 27, 2848–2857. [Google Scholar]
- Driss, I.; Mouss, K.N.; Laggoun, A. A new genetic algorithm for flexible job-shop scheduling problems. J. Mech. Sci. Technol. 2015, 29, 1273–1281. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C. Application of Grey Wolf Optimization for Solving Combinatorial Problems: Job Shop and Flexible Job Shop Scheduling Cases. IEEE Access 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Liang, X.; Huang, M.; Ning, T. Flexible job shop scheduling based on improved hybrid immune algorithm. J. Ambient Intell. Humaniz. Comput. 2016, 9, 165–171. [Google Scholar] [CrossRef]
- Caldeira, R.H.; Gnanavelbabu, A. Solving the flexible job shop scheduling problem using an improved Jaya algorithm. Comput. Ind. Eng. 2019, 137, 106064. [Google Scholar] [CrossRef]
- Wu, M.; Yang, D.; Zhou, B.; Yang, Z.; Liu, T.; Li, L.; Wang, Z.; Hu, K. Adaptive population nsga-iii with dual control strategy for flexible job shop scheduling problem with the consideration of energy consumption and weight. Machines 2021, 9, 344. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, L.; Shi, Y. An effective genetic algorithm for the flexible job-shop scheduling problem. Expert Syst. Appl. 2011, 38, 3563–3573. [Google Scholar] [CrossRef]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Zhang, S.; Du, H.; Borucki, S.; Jin, S.; Hou, T.; Li, Z. Dual resource constrained flexible job shop scheduling based on improved quantum genetic algorithm. Machines 2021, 9, 108. [Google Scholar] [CrossRef]
- Singh, M.R.; Mahapatra, S.S. A quantum behaved particle swarm optimization for flexible job shop scheduling. Comput. Ind. Eng. 2016, 93, 36–44. [Google Scholar] [CrossRef]
- Wang, L.; Cai, J.; Li, M.; Liu, Z. Flexible Job Shop Scheduling Problem Using an Improved Ant Colony Optimization. Sci. Program. 2017, 2017, 9016303. [Google Scholar] [CrossRef]
- Cruz-Chávez, M.A.; Martínez-Rangel, M.G.; Cruz-Rosales, M.H. Accelerated simulated annealing algorithm applied to the flexible job shop scheduling problem. Int. Trans. Oper. Res. 2017, 24, 1119–1137. [Google Scholar] [CrossRef]
- Chenyang, G.; Yuelin, G.; Shanshan, L. Improved simulated annealing algorithm for flexible job shop scheduling problems. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 2191–2196. [Google Scholar]
- Vijaya Lakshmi, A.; Mohanaiah, P. WOA-TLBO: Whale optimization algorithm with Teaching-learning-based optimization for global optimization and facial emotion recognition. Appl. Soft Comput. 2021, 110, 107623. [Google Scholar] [CrossRef]
- Medani, K.b.O.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Huang, X.; Wang, R.; Zhao, X.; Hu, K. Aero-engine performance optimization based on whale optimization algorithm. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 11437–11441. [Google Scholar]
- Yan, Q.; Wu, W.; Wang, H. Deep Reinforcement Learning for Distributed Flow Shop Scheduling with Flexible Maintenance. Machines 2022, 10, 210. [Google Scholar] [CrossRef]
- Dao, T.-K.; Pan, T.-S.; Pan, J.-S. A multi-objective optimal mobile robot path planning based on whale optimization algorithm. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 337–342. [Google Scholar]
- Oliva, D.; Abd El Aziz, M.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Liang, R.; Chen, Y.; Zhu, R. A novel fault diagnosis method based on the KELM optimized by whale optimization algorithm. Machines 2022, 10, 93. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; El-Shahat, D.; Mirjalili, S. A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem. Future Gener. Comput. Syst. 2018, 85, 129–145. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Yao, X.; Li, Y. Hybrid whale optimization algorithm enhanced with Lévy flight and differential evolution for job shop scheduling problems. Appl. Soft Comput. 2020, 87, 105954. [Google Scholar]
- Luan, F.; Cai, Z.; Wu, S.; Liu, S.Q.; He, Y. Optimizing the Low-Carbon Flexible Job Shop Scheduling Problem with Discrete Whale Optimization Algorithm. Mathematics 2019, 7, 688. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, M.; Amiri, M.; Zandieh, M. Flexible job-shop scheduling with parallel variable neighborhood search algorithm. Expert Syst. Appl. 2010, 37, 678–687. [Google Scholar] [CrossRef]
- Hua, L.; Wang, Y. Application of Number Theory in Approximate Analysis; Science Press: Bejing, China, 1978; p. 248. [Google Scholar]
- Lv, H.; Feng, Z.; Wang, X.; Zhou, W.; Chen, B. Structural damage identification based on hybrid whale annealing algorithm and sparse regularization. J. Vib. Shock. 2021, 40, 85–91. [Google Scholar]
- Yang, W.; Yang, Z.; Chen, Y.; Peng, Z. Modified Whale Optimization Algorithm for Multi-Type Combine Harvesters Scheduling. Machines 2022, 10, 64. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar]
- Ding, H.; Gu, X. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Comput. Oper. Res. 2020, 121, 104951. [Google Scholar] [CrossRef]
- Xing, L.-N.; Chen, Y.-W.; Wang, P.; Zhao, Q.-S.; Xiong, J. A Knowledge-Based Ant Colony Optimization for Flexible Job Shop Scheduling Problems. Appl. Soft Comput. 2010, 10, 888–896. [Google Scholar] [CrossRef]
- Ziaee, M. A heuristic algorithm for solving flexible job shop scheduling problem. Int. J. Adv. Manuf. Technol. 2013, 71, 519–528. [Google Scholar] [CrossRef]
- Luan, F.; Cai, Z.; Wu, S.; Jiang, T.; Li, F.; Yang, J. Improved Whale Algorithm for Solving the Flexible Job Shop Scheduling Problem. Mathematics 2019, 7, 384. [Google Scholar] [CrossRef] [Green Version]
- Xiong, W.; Fu, D. A new immune multi-agent system for the flexible job shop scheduling problem. J. Intell. Manuf. 2015, 29, 857–873. [Google Scholar] [CrossRef]
- Jiang, T. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm. Control Decis. 2018, 33, 503–508. [Google Scholar]
- Phuang, A. The flower pollination algorithm with disparity count process for scheduling problem. In Proceedings of the 2017 9th International Conference on Information Technology and Electrical Engineering (ICITEE), Phuket, Thailand, 12–13 October 2017; pp. 1–5. [Google Scholar]
- Demir, Y.; İşleyen, S.K. Evaluation of mathematical models for flexible job-shop scheduling problems. Appl. Math. Model. 2013, 37, 977–988. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, M.; Yang, Z.; Feng, W.; Yang, D. A Grasshopper Optimization Algorithm for the Flexible Job Shop Scheduling Problem. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; pp. 873–877. [Google Scholar]
- Bagheri, A.; Zandieh, M.; Mahdavi, I.; Yazdani, M. An artificial immune algorithm for the flexible job-shop scheduling problem. Future Gener. Comput. Syst. 2010, 26, 533–541. [Google Scholar] [CrossRef]
- Teekeng, W.; Thammano, A.; Unkaw, P.; Kiatwuthiamorn, J. A new algorithm for flexible job-shop scheduling problem based on particle swarm optimization. Artif. Life Robot. 2016, 21, 18–23. [Google Scholar] [CrossRef]
- Hurink, J.; Jurisch, B.; Thole, M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper.-Res.-Spektrum 1994, 15, 205–215. [Google Scholar] [CrossRef] [Green Version]
- Wei, F.; Cao, C.; Zhang, H. An Improved Genetic Algorithm for Resource-Constrained Flexible Job-Shop Scheduling. Int. J. Simul. Model. 2021, 20, 201–211. [Google Scholar] [CrossRef]
























| Symbols | Description |
|---|---|
| Total number of jobs | |
| Total number of machines | |
| Total number of operations | |
| Number of operations for each job | |
| Number of operations assigned to machine | |
| operation of job | |
| operation of job on machine | |
| operation of job | |
| operation of job | |
| Makespan | |
| operation of job . | |
| Operation sequence | |
| Machine sequence | |
| The length of the core path set composed of core operations | |
| Good point set initialization | |
| Nonlinear convergence factor | |
| Multiple neighborhood structure | |
| Diversity receiving mechanism | |
| Self-deviation percentage | |
| Relative lift percentage | |
| Lower bound of test instances | |
| Upper bound for test instances | |
| Deviation percentage |
| Job | Operation | Machine | |||
|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | ||
| 6 | 3 | 7 | 3 | ||
| 3 | 2 | 6 | 1 | ||
| 5 | 1 | 6 | 4 | ||
| 3 | 6 | 3 | 7 | ||
| 2 | 7 | 1 | 2 | ||
| 7 | 3 | 4 | 4 | ||
| Job | Operation | Machine | |||
|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | ||
| - | 3 | - | 3 | ||
| 3 | 2 | - | 1 | ||
| - | 1 | - | 4 | ||
| 3 | - | 3 | - | ||
| 2 | 5 | 1 | - | ||
| - | 3 | 4 | - | ||
| Job | Operation | Machine | ||
|---|---|---|---|---|
| M1 | M2 | M3 | ||
| - | 3 | 3 | ||
| 3 | 2 | 1 | ||
| 1 | 4 | |||
| 3 | - | 3 | ||
| 2 | 5 | 1 | ||
| - | 3 | 4 | ||
| Name | Function | C | Search Range | Min |
|---|---|---|---|---|
| Sphere | US | [−100, 100] | 0 | |
| Sumsquare | US | [−10, 10] | 0 | |
| Schwefel2.22 | UN | [−10, 10] | 0 | |
| Rosenbrock | UN | [−5, 10] | 0 | |
| Rastrigin | MS | [−5.12, 5.12] | 0 | |
| Ackley | MN | [−32, 32] | 0 | |
| Levy | MN | [−10, 10] | 0 |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| HWOA | Min | 3.42 × 10−132 | 6.04 × 10−132 | 2.61 × 10−78 | 2.62 × 101 | 0 | 8.88 × 10−16 | 2.68 × 10−2 |
| Mean | 2.22 × 10−120 | 4.45 × 10−120 | 2.29 × 10−71 | 2.68 × 101 | 0 | 3.14 × 10−15 | 1.40 × 10−1 | |
| Std | 1.13 × 10−119 | 2.41 × 10−119 | 7.84 × 10−71 | 2.36 × 10−1 | 0 | 1.98 × 10−15 | 1.08 × 10−1 | |
| WOA | Mean | 1.44 × 10−72 | 4.41 × 10−78 | 1.17 × 10−50 | 2.79 × 101 | 1.89 × 10−15 | 3.85 × 10−15 | 5.19 × 10−1 |
| Std | 7.22 × 10−72 | 1.58 × 10−77 | 2.77 × 10−50 | 4.79 × 10−1 | 1.04 × 10−14 | 2.48 × 10−15 | 2.08 × 10−1 | |
| sig | + | + | + | + | + | = | + | |
| MFO | Mean | 2.34 × 103 | 6.04 × 102 | 3.64 × 101 | 5.35 × 106 | 1.59 × 102 | 1.46 × 101 | 2.24 × 102 |
| Std | 5.04 × 103 | 8.47 × 102 | 1.99 × 101 | 2.03 × 107 | 4.07 × 101 | 7.66 | 1.09 × 103 | |
| sig | + | + | + | + | + | + | + | |
| GWO | Mean | 1.65 × 10−27 | 2.44 × 10−28 | 1.08 × 10−16 | 2.70 × 101 | 2.88 | 1.05 × 10−13 | 6.53 × 10−1 |
| Std | 3.22 × 10−27 | 3.80 × 10−28 | 6.52 × 10−17 | 7.85 × 10−1 | 4.25 | 1.97 × 10−14 | 1.98 × 10−1 | |
| sig | + | + | + | + | + | + | + | |
| SCA | Mean | 1.11 × 101 | 2.12 | 2.23 × 10−2 | 6.33 × 104 | 2.64 × 101 | 1.45 × 101 | 1.13 × 105 |
| Std | 3.32 × 101 | 4.69 | 3.06 × 10−2 | 1.34 × 105 | 3.38 × 101 | 8.95 | 2.79 × 105 | |
| sig | + | + | + | + | + | + | + | |
| MVO | Mean | 1.31 × 10 | 1.40 | 1.25 × 101 | 4.76 × 102 | 1.27 × 102 | 1.54 | 2.19 × 10−1 |
| Std | 3.71 × 10−1 | 1.55 | 3.48 × 101 | 7.71 × 102 | 3.37 × 101 | 4.48 × 10−1 | 1.57 × 10−1 | |
| sig | + | + | + | + | + | + | + | |
| DA | Mean | 1.69 × 103 | 2.39 × 102 | 1.60 × 101 | 3.10 × 105 | 1.67 × 102 | 1.09 × 101 | 3.23 × 105 |
| Std | 6.59 × 102 | 1.95 × 102 | 5.52 | 3.06 × 105 | 3.77 × 101 | 1.90 | 3.98 × 105 | |
| sig | + | + | + | + | + | + | + | |
| SSA | Mean | 4.79 × 10−7 | 1.83 | 1.46 | 1.69 × 102 | 5.04 × 101 | 2.75 | 1.37 × 101 |
| Std | 1.14 × 10−6 | 1.54 | 1.02 | 2.63 × 102 | 1.38 × 101 | 6.48 × 10−1 | 1.54 × 101 | |
| sig | + | + | + | + | + | + | + |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| HWOA | Min | 0 | 0 | 2.17 × 10−310 | 2.34 × 10−2 | 0 | 8.88 × 10−16 | 9.69 × 10−4 |
| Mean | 0 | 0 | 4.92 × 10−295 | 4.76 × 10−1 | 0 | 3.02 × 10−15 | 7.16 × 10−2 | |
| Std | 0 | 0 | 0 | 4.90 × 10−1 | 0 | 2.57 × 10−15 | 1.01 × 10−1 | |
| WOA | Mean | 9.86 × 10−305 | 2.47 × 10−300 | 2.26 × 10−209 | 4.67 × 101 | 1.89 × 10−15 | 4.32 × 10−15 | 2.00 × 10−1 |
| Std | 0 | 0 | 0 | 6.10 × 10−1 | 1.04 × 10−14 | 2.72 × 10−15 | 1.33 × 10−1 | |
| sig | + | + | + | + | + | = | + | |
| MFO | Mean | 8.00 × 103 | 2.19 × 103 | 6.97 × 101 | 1.07 × 107 | 2.96 × 102 | 1.89 × 101 | 2.73 × 107 |
| Std | 8.47 × 103 | 1.93 × 103 | 3.59 × 101 | 2.77 × 107 | 4.65 × 101 | 2.85 × 100 | 1.04 × 108 | |
| sig | + | + | + | + | + | + | + | |
| GWO | Mean | 1.70 × 10−91 | 7.22 × 10−92 | 1.28 × 10−53 | 4.68 × 101 | 1.89 × 10−15 | 1.58 × 10−14 | 1.69 × 10 |
| Std | 4.06 × 10−91 | 2.82 × 10−91 | 1.73 × 10−53 | 7.93 × 10−1 | 1.04 × 10−14 | 2.54 × 10−15 | 2.88 × 10−1 | |
| sig | + | + | + | + | + | + | + | |
| SCA | Mean | 1.58 × 10−1 | 9.18 × 10−2 | 1.45 × 10−5 | 2.81 × 105 | 4.58 × 101 | 1.73 × 101 | 3.67 × 105 |
| Std | 3.33 × 10−1 | 2.64 × 10−1 | 4.26 × 10−5 | 1.19 × 106 | 3.91 × 101 | 7.02 × 10 | 1.29 × 106 | |
| sig | + | + | + | + | + | + | + | |
| MVO | Mean | 6.06 × 10−1 | 3.00 × 10 | 1.47 × 101 | 4.51 × 102 | 2.25 × 102 | 1.61 × 10 | 1.98 × 10−1 |
| Std | 1.54 × 10−1 | 2.44 × 10 | 4.47 × 101 | 6.51 × 102 | 4.70 × 101 | 5.53 × 10−1 | 1.38 × 10−1 | |
| sig | + | + | + | + | + | + | + | |
| DA | Mean | 2.78 × 103 | 5.71 × 102 | 2.64 × 101 | 4.02 × 105 | 2.98 × 102 | 9.83 × 10 | 1.61 × 105 |
| Std | 1.17 × 103 | 2.44 × 102 | 8.71 × 10 | 2.53 × 105 | 5.00 × 101 | 1.16 × 10 | 1.65 × 105 | |
| sig | + | + | + | + | + | + | + | |
| SSA | Mean | 3.08 × 10−8 | 7.72 × 10−1 | 2.34 × 10 | 1.04 × 102 | 1.01 × 102 | 2.75 × 10 | 3.99 × 101 |
| Std | 5.12 × 10−9 | 1.01 × 10 | 1.40 × 10 | 7.38 × 101 | 2.44 × 101 | 6.67 × 10−1 | 2.93 × 101 | |
| sig | + | + | + | + | + | + | + |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| HWOA | Min | 0 | 0 | 0 | 2.22 × 10−2 | 0 | 8.88 × 10−16 | 4.47 × 10−4 |
| Mean | 0 | 0 | 0 | 3.10 × 10−1 | 0 | 2.31 × 10−15 | 1.96 × 10−2 | |
| Std | 0 | 0 | 0 | 2.40 × 10−1 | 0 | 2.40 × 10−15 | 3.48 × 10−2 | |
| WOA | Mean | 0 | 0 | 0 | 9.50 × 101 | 0 | 3.73 × 10−15 | 2.76 × 10−2 |
| Std | 0 | 0 | 0 | 3.54 × 10−1 | 0 | 2.54 × 10−15 | 3.94 × 10−2 | |
| sig | = | = | = | + | = | + | + | |
| MFO | Mean | 1.95 × 104 | 1.47 × 104 | 1.25 × 102 | 4.58 × 107 | 6.40 × 102 | 1.99 × 101 | 1.39 × 108 |
| Std | 1.61 × 104 | 7.70 × 103 | 5.56 × 101 | 6.95 × 107 | 7.41 × 101 | 1.39 × 10−1 | 2.45 × 108 | |
| sig | + | + | + | + | + | + | + | |
| GWO | Mean | 1.98 × 10−265 | 8.93 × 10−266 | 3.26 × 10−156 | 9.72 × 101 | 0 | 1.51 × 10−14 | 5.71 |
| Std | 0 | 0 | 0 | 7.60 × 10−1 | 0 | 1.87 × 10−15 | 3.36 × 10−1 | |
| sig | + | + | + | + | = | + | + | |
| SCA | Mean | 1.84 × 102 | 5.11 × 101 | 4.13 × 10−7 | 4.21 × 106 | 1.03 × 102 | 1.94 × 101 | 2.10 × 107 |
| Std | 2.70 × 102 | 1.19 × 102 | 1.82 × 10−6 | 5.18 × 106 | 6.26 × 101 | 4.38 | 2.58 × 107 | |
| sig | + | + | + | + | + | + | + | |
| MVO | Mean | 6.05 × 10−1 | 1.04 × 101 | 7.14 × 104 | 4.12 × 102 | 5.81 × 102 | 4.07 | 1.13 |
| Std | 1.10 × 10−1 | 5.81 | 3.90 × 105 | 6.34 × 102 | 8.02 × 101 | 6.19 | 2.73 | |
| sig | + | + | + | + | + | + | + | |
| DA | Mean | 3.08 × 103 | 1.68 × 103 | 4.46 × 101 | 4.45 × 105 | 6.17 × 102 | 8.11 | 1.17 × 105 |
| Std | 1.36 × 103 | 7.42 × 102 | 1.66 × 101 | 3.44 × 105 | 1.49 × 102 | 1.93 | 2.29 × 105 | |
| sig | + | + | + | + | + | + | + | |
| SSA | Mean | 8.03 × 10−8 | 1.49 | 6.24 | 1.81 × 102 | 2.06 × 102 | 3.78 | 1.27 × 102 |
| Std | 8.91 × 10−9 | 1.79 | 3.27 | 1.61 × 102 | 4.48 × 101 | 7.02 × 10−1 | 2.63 × 101 | |
| sig | + | + | + | + | + | + | + |
| BRdata | n × m | LB | UB | WOA | HWOA-1 | HWOA-2 | HWOA | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MK01 | 10 × 6 | 36 | 42 | 42 | 45.7 | 42 | 44.3 | 40 | 41.8 | 40 | 41.3 |
| MK02 | 10 × 6 | 24 | 32 | 33 | 39.9 | 33 | 36.5 | 27 | 28.4 | 26 | 27.5 |
| MK03 | 15 × 8 | 204 | 211 | 231 | 235.1 | 223 | 228.3 | 204 | 213.1 | 204 | 207.4 |
| MK04 | 15 × 8 | 48 | 81 | 73 | 76.3 | 73 | 74.7 | 64 | 67.3 | 62 | 63.8 |
| MK05 | 15 × 4 | 168 | 186 | 175 | 181.5 | 175 | 181.9 | 173 | 177.3 | 173 | 174.5 |
| MK06 | 10 × 15 | 33 | 86 | 98 | 101.7 | 98 | 100.7 | 65 | 69.5 | 62 | 65.4 |
| MK07 | 20 × 5 | 133 | 157 | 154 | 158.7 | 155 | 160.7 | 145 | 147.6 | 143 | 145.2 |
| MK08 | 20 × 10 | 523 | 523 | 531 | 541.8 | 531 | 539.3 | 523 | 526.1 | 523 | 523 |
| MK09 | 20 × 10 | 299 | 369 | 379 | 392.5 | 383 | 391.5 | 312 | 327.9 | 310 | 319.9 |
| MK10 | 20 × 15 | 165 | 296 | 271 | 302.4 | 265 | 296.5 | 224 | 233.3 | 216 | 220.3 |
| Kacem, BRdata | n × m | LB | WOA | HWOA-1 | HWOA-2 | HWOA | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kac01 | 4 × 5 | 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Kac02 | 8 × 8 | 14 | 57.14 | 0.00 | 14.28 | 27.27 | 0.00 | 36.36 | 0.00 | 36.36 |
| Kac03 | 10 × 7 | 11 | 27.27 | 0.00 | 27.27 | 0.00 | 0.00 | 21.42 | 0.00 | 21.42 |
| Kac04 | 10 × 10 | 7 | 14.28 | 0.00 | 0.00 | 12.50 | 0.00 | 12.50 | 0.00 | 12.50 |
| Kac05 | 15 × 10 | 11 | 27.27 | 0.00 | 27.27 | 0.00 | 9.09 | 14.28 | 0.00 | 21.42 |
| MK01 | 10 × 6 | 36 | 5.00 | 0.00 | 5.00 | 0.00 | 0.00 | 4.76 | 0.00 | 4.76 |
| MK02 | 10 × 6 | 24 | 26.92 | 0.00 | 26.92 | 0.00 | 3.84 | 18.18 | 0.00 | 21.21 |
| MK03 | 15 × 8 | 204 | 13.23 | 0.00 | 9.31 | 3.46 | 0.00 | 11.68 | 0.00 | 11.68 |
| MK04 | 15 × 8 | 48 | 17.74 | 0.00 | 17.74 | 0.00 | 3.22 | 12.32 | 0.00 | 15.06 |
| MK05 | 15 × 4 | 168 | 1.15 | 0.00 | 1.15 | 0.00 | 0.00 | 1.14 | 0.00 | 1.14 |
| MK06 | 10 × 15 | 33 | 58.06 | 0.00 | 58.06 | 0.00 | 4.83 | 33.67 | 0.00 | 36.73 |
| MK07 | 20 × 5 | 133 | 7.69 | 0.00 | 8.39 | −0.64 | 1.39 | 5.84 | 0.00 | 7.14 |
| MK08 | 20 × 10 | 523 | 1.53 | 0.00 | 1.53 | 0.00 | 0.00 | 15.06 | 0.00 | 15.06 |
| MK09 | 20 × 10 | 299 | 22.25 | 0.00 | 19.06 | −1.05 | 0.64 | 17.67 | 0.00 | 18.20 |
| MK10 | 20 × 15 | 165 | 25.46 | 0.00 | 22.68 | 2.21 | 3.70 | 17.34 | 0.00 | 20.29 |
| Mean | - | - | 20.33 | 0.00 | 15.91 | 2.95 | 1.78 | 14.81 | 0.00 | 16.19 |
| BRdata | n × m | OPSO | PPSO | KBACO | Heuristic | IWOA | NIMASS | HWOA |
|---|---|---|---|---|---|---|---|---|
| MK01 | 10 × 6 | 41 | 40 | 39 | 42 | 40 | 40 | 40 |
| MK02 | 10 × 6 | 26 | 29 | 29 | 28 | 26 | 28 | 26 |
| MK03 | 15 × 8 | 207 | 204 | 204 | 204 | 204 | 204 | 204 |
| MK04 | 15 × 8 | 65 | 66 | 65 | 75 | 60 | 65 | 62 |
| MK05 | 15 × 4 | 171 | 175 | 173 | 179 | 175 | 177 | 173 |
| MK06 | 10 × 15 | 61 | 77 | 67 | 69 | 63 | 67 | 62 |
| MK07 | 20 × 5 | 173 | 145 | 144 | 149 | 144 | 144 | 143 |
| MK08 | 20 × 10 | 523 | 523 | 523 | 555 | 523 | 523 | 523 |
| MK09 | 20 × 10 | 307 | 320 | 311 | 342 | 339 | 312 | 310 |
| MK10 | 20 × 15 | 312 | 239 | 229 | 242 | 242 | 229 | 216 |
| BRdata | n × m | OPSO | PPSO | KBACO | Heuristic | IWOA | NIMASS | HWOA |
|---|---|---|---|---|---|---|---|---|
| MK01 | 10 × 6 | 11.11 | 11.11 | 8.33 | 16.67 | 11.11 | 11.11 | 11.11 |
| MK02 | 10 × 6 | 12.5 | 20.83 | 20.86 | 16.67 | 8.33 | 20.86 | 8.33 |
| MK03 | 15 × 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| MK04 | 15 × 8 | 29.16 | 37.50 | 35.41 | 56.25 | 25.00 | 35.41 | 29.16 |
| MK05 | 15 × 4 | 5.95 | 4.16 | 2.97 | 6.54 | 4.16 | 5.35 | 2.97 |
| MK06 | 10 × 15 | 136.36 | 133.33 | 103.03 | 109.09 | 90.90 | 103.03 | 87.87 |
| MK07 | 20 × 5 | 10.52 | 9.02 | 8.27 | 12.03 | 8.27 | 8.27 | 7.51 |
| MK08 | 20 × 10 | 0.00 | 0.00 | 0.00 | 6.12 | 0.00 | 0.00 | 0.00 |
| MK09 | 20 × 10 | 14.04 | 7.02 | 4.01 | 14.38 | 13.37 | 4.34 | 3.67 |
| MK10 | 20 × 15 | 50.91 | 44.84 | 38.78 | 46.66 | 46.66 | 38.78 | 30.90 |
| Mean | - | 27.05 | 26.78 | 22.16 | 28.44 | 20.78 | 22.71 | 18.15 |
| Kacem | n × m | KBACO | HGWO | IWOA | EQEA | HWOA |
|---|---|---|---|---|---|---|
| Kac01 | 4 × 5 | 11 | 11 | 11 | 11 | 11 |
| Kac02 | 8 × 8 | 14 | 14 | 14 | 14 | 14 |
| Kac03 | 10 × 7 | 11 | 11 | 13 | 11 | 11 |
| Kac04 | 10 × 10 | 7 | 7 | 7 | 7 | 7 |
| Kac05 | 15 × 10 | 11 | 13 | 14 | 11 | 11 |
| Kacem | n × m | KBACO | HGWO | IWOA | EQEA | HWOA |
|---|---|---|---|---|---|---|
| Kac01 | 4 × 5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Kac02 | 8 × 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Kac03 | 10 × 7 | 0.00 | 0.00 | 18.18 | 0.00 | 0.00 |
| Kac04 | 10 × 10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Kac05 | 15 × 10 | 0.00 | 18.18 | 27.27 | 0.00 | 0.00 |
| Fattahin | n × m | LB | FPA | M2 | HA | GOA | AIA | EPSO | HWOA |
|---|---|---|---|---|---|---|---|---|---|
| SFJS01 | 2 × 2 | 66 | 66 | 66 | 66 | 66 | 66 | 66 | 66 |
| SFJS02 | 2 × 2 | 107 | 107 | 107 | 107 | 107 | 107 | 107 | 107 |
| SFJS03 | 3 × 2 | 221 | 221 | 221 | 221 | 221 | 221 | 221 | 221 |
| SFJS04 | 3 × 2 | 355 | 355 | 355 | 355 | 355 | 355 | 355 | 355 |
| SFJS05 | 3 × 2 | 119 | 119 | 119 | 119 | 119 | 119 | 119 | 119 |
| SFJS06 | 3 × 3 | 320 | 320 | 320 | 320 | 320 | 320 | 320 | 320 |
| SFJS07 | 3 × 5 | 397 | 397 | 397 | 397 | 397 | 397 | 397 | 397 |
| SFJS08 | 3 × 4 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 |
| SFJS09 | 3 × 3 | 210 | 210 | 210 | 210 | 210 | 210 | 210 | 210 |
| SFJS10 | 4 × 5 | 516 | 516 | 516 | 516 | 533 | 516 | 516 | 516 |
| MFJS01 | 5 × 6 | 396 | 469 | 468 | 468 | 469 | 468 | 468 | 468 |
| MFJS02 | 5 × 7 | 396 | 446 | 446 | 446 | 457 | 448 | 446 | 446 |
| MFJS03 | 6 × 7 | 396 | 470 | 466 | 466 | 538 | 468 | 466 | 466 |
| MFJS04 | 7 × 7 | 496 | 554 | 564 | 554 | 610 | 554 | 554 | 554 |
| MFJS05 | 7 × 7 | 414 | 516 | 514 | 514 | 613 | 527 | 514 | 514 |
| MFJS06 | 8 × 7 | 469 | 636 | 634 | 634 | 721 | 635 | 634 | 634 |
| MFJS07 | 8 × 7 | 619 | 879 | 928 | 879 | 1092 | 879 | 879 | 879 |
| MFJS08 | 9 × 8 | 619 | 884 | - | 884 | 1095 | 884 | 884 | 884 |
| Fattahin | n × m | LB | FPA | M2 | HA | GOA | AIA | EPSO | HWOA |
|---|---|---|---|---|---|---|---|---|---|
| SFJS01 | 2 × 2 | 66 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS02 | 2 × 2 | 107 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS03 | 3 × 2 | 221 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS04 | 3 × 2 | 355 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS05 | 3 × 2 | 119 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS06 | 3 × 3 | 320 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS07 | 3 × 5 | 397 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS08 | 3 × 4 | 253 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS09 | 3 × 3 | 210 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SFJS10 | 4 × 5 | 516 | 0.00 | 0.00 | 0.00 | 3.29 | 0.00 | 0.00 | 0.00 |
| MFJS01 | 5 × 6 | 396 | 18.43 | 18.18 | 18.18 | 18.43 | 18.18 | 18.18 | 18.18 |
| MFJS02 | 5 × 7 | 396 | 12.62 | 12.62 | 12.62 | 15.40 | 13.13 | 12.62 | 12.62 |
| MFJS03 | 6 × 7 | 396 | 18.68 | 17.67 | 17.67 | 35.85 | 18.18 | 17.67 | 17.67 |
| MFJS04 | 7 × 7 | 496 | 11.69 | 13.71 | 11.69 | 22.98 | 11.69 | 11.69 | 11.69 |
| MFJS05 | 7 × 7 | 414 | 24.63 | 24.15 | 24.15 | 48.06 | 27.29 | 24.15 | 24.15 |
| MFJS06 | 8 × 7 | 469 | 35..60 | 35.18 | 35.18 | 53.73 | 35.39 | 35.18 | 35.18 |
| MFJS07 | 8 × 7 | 619 | 42.00 | 49.92 | 42.00 | 76.41 | 42.00 | 42.00 | 42.00 |
| MFJS08 | 9 × 8 | 619 | 42.81 | - | 42.81 | 76.89 | 42.81 | 42.81 | 42.81 |
| Vdata | N1-1000 | N2-1000 | IJA | HWOA |
|---|---|---|---|---|
| La01–La05 | 0.78 | 0.59 | 0.00 | 0.00 |
| La06–La10 | 0.20 | 0.15 | 0.00 | 0.00 |
| La11–La15 | 0.20 | 0.40 | 0.00 | 0.00 |
| La16–La20 | 0.00 | 0.00 | 0.00 | 0.00 |
| La21–La25 | 6.90 | 1.97 | 0.77 | 0.64 |
| La26–La30 | 0.26 | 0.25 | 0.13 | 0.09 |
| La31–La35 | 0.06 | 0.01 | 0.01 | 0.01 |
| La36–La40 | 0.00 | 0.00 | 0.00 | 0.00 |
| Mean | 1.050 | 0.421 | 0.114 | 0.093 |
| Ra | n × m | WOA | MWOA | IWOA | HWOA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ra01 | 30 × 15 | 2524 | 2664.6 | 152.77 | 2344 | 2419.2 | 106.13 | 2273 | 2397.2 | 169.36 | 1751 | 1857.7 | 96.81 |
| Ra02 | 45 × 15 | 3522 | 3691.2 | 203.04 | 3336 | 3417.5 | 114.91 | 3190 | 3354.1 | 223.03 | 2715 | 3939.2 | 116.45 |
| Ra03 | 50 × 10 | 3269 | 3382.4 | 152.77 | 3090 | 3168.2 | 95.82 | 3007 | 3193.4 | 169.36 | 2734 | 2878.4 | 98.84 |
| Ra04 | 60 × 15 | 4454 | 4660.6 | 283.36 | 4261 | 4318.2 | 153.72 | 3947 | 4231.9 | 310.01 | 3669 | 3836.3 | 137.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Su, J.; Yao, Y.; Yang, Z.; Yuan, Y. A Novel Hybrid Whale Optimization Algorithm for Flexible Job-Shop Scheduling Problem. Machines 2022, 10, 618. https://doi.org/10.3390/machines10080618
Yang W, Su J, Yao Y, Yang Z, Yuan Y. A Novel Hybrid Whale Optimization Algorithm for Flexible Job-Shop Scheduling Problem. Machines. 2022; 10(8):618. https://doi.org/10.3390/machines10080618
Chicago/Turabian StyleYang, Wenqiang, Jinzhe Su, Yunhang Yao, Zhile Yang, and Ying Yuan. 2022. "A Novel Hybrid Whale Optimization Algorithm for Flexible Job-Shop Scheduling Problem" Machines 10, no. 8: 618. https://doi.org/10.3390/machines10080618






