Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition and Genetic Algorithm-Optimized Wavelet Threshold Denoising
Abstract
:1. Introduction
2. Methodologies
2.1. VMD
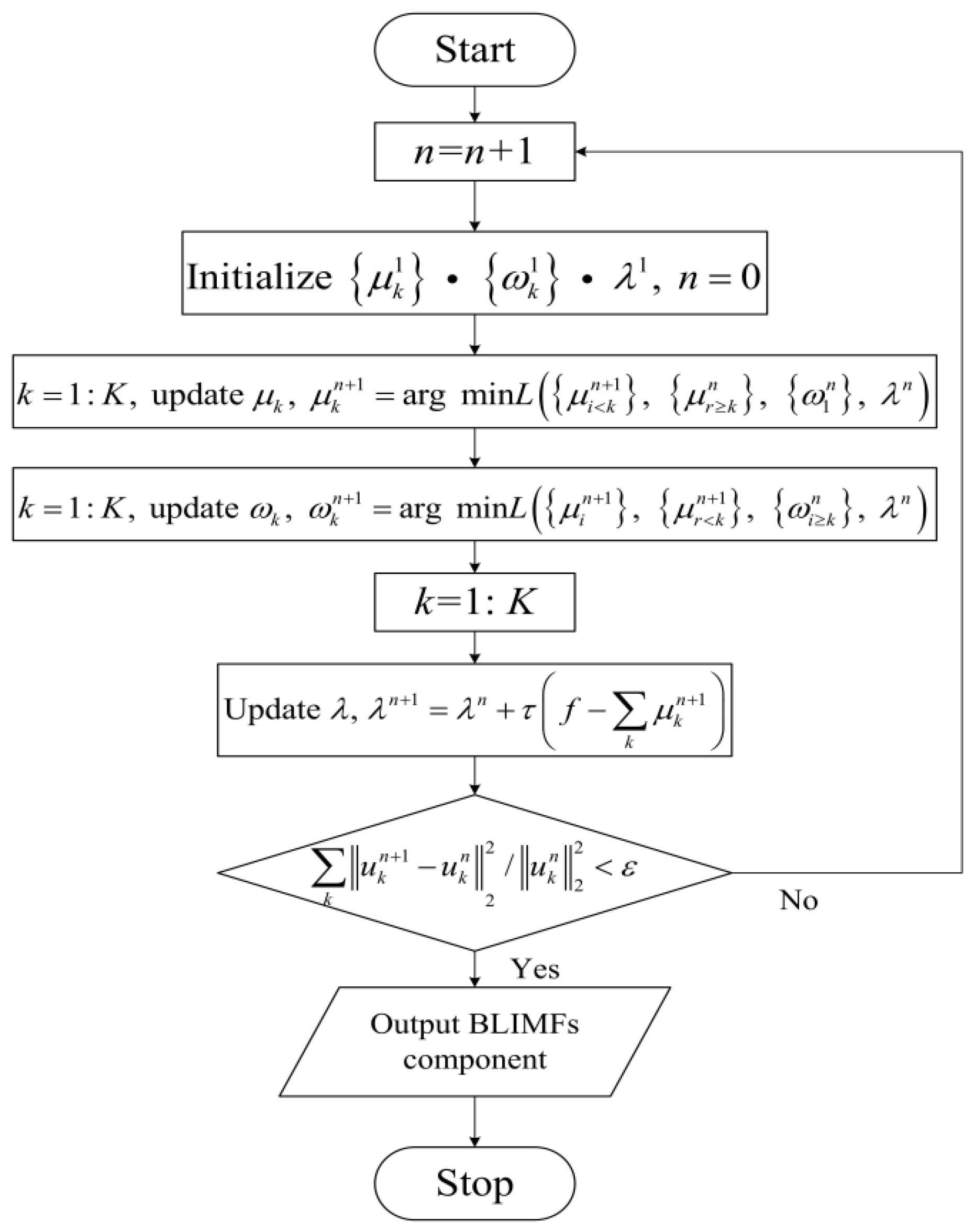
2.2. Optimized WT Denoising
2.3. Genetic Algorithm
- (1)
- The size of the initial population M specifies the number of individuals contained in the population and generally ranges from 20 to 100. Inbreeding occurs if the group size is too small, resulting in diseased genes; conversely, if the group size is too large, the convergence of the problem is difficult to achieve, leading to wasted resources and reduced robustness.
- (2)
- Crossover operation is the main method for generating new individuals in a genetic algorithm, so the crossover probability Pr should generally take a larger value. However, if Pr is too large, the good patterns in the group will be destroyed, which adversely affects the evolutionary operation. If Pr is too small, the speed at which new individuals are generated is slower. The recommended value of Pr is 0.4 to 0.99.
- (3)
- The mutation probability Pm controls how often the mutation operation is used. If Pm is too small, the population diversity declines too quickly, leading to the rapid loss of effective genes which is not easy to repair. If Pm is too large, although the population diversity is guaranteed, the probability of high-order patterns destroyed also increases. Therefore, the range of Pm is generally 0.0001–0.1.
- (4)
- The maximum evolutionary algebra T represents the termination condition of the genetic algorithm. If the T is too small, the algorithm cannot easily converge, and the population is not mature; if T is too large, the algorithm is already proficient or the population is too precocious, in which case it is impossible to obtain a converged solution. Generally, the value of T is set to be 100–500.
3. The Proposed VMD and Genetic Algorithm-Optimized Wavelet Threshold Denoising Approach
- (1)
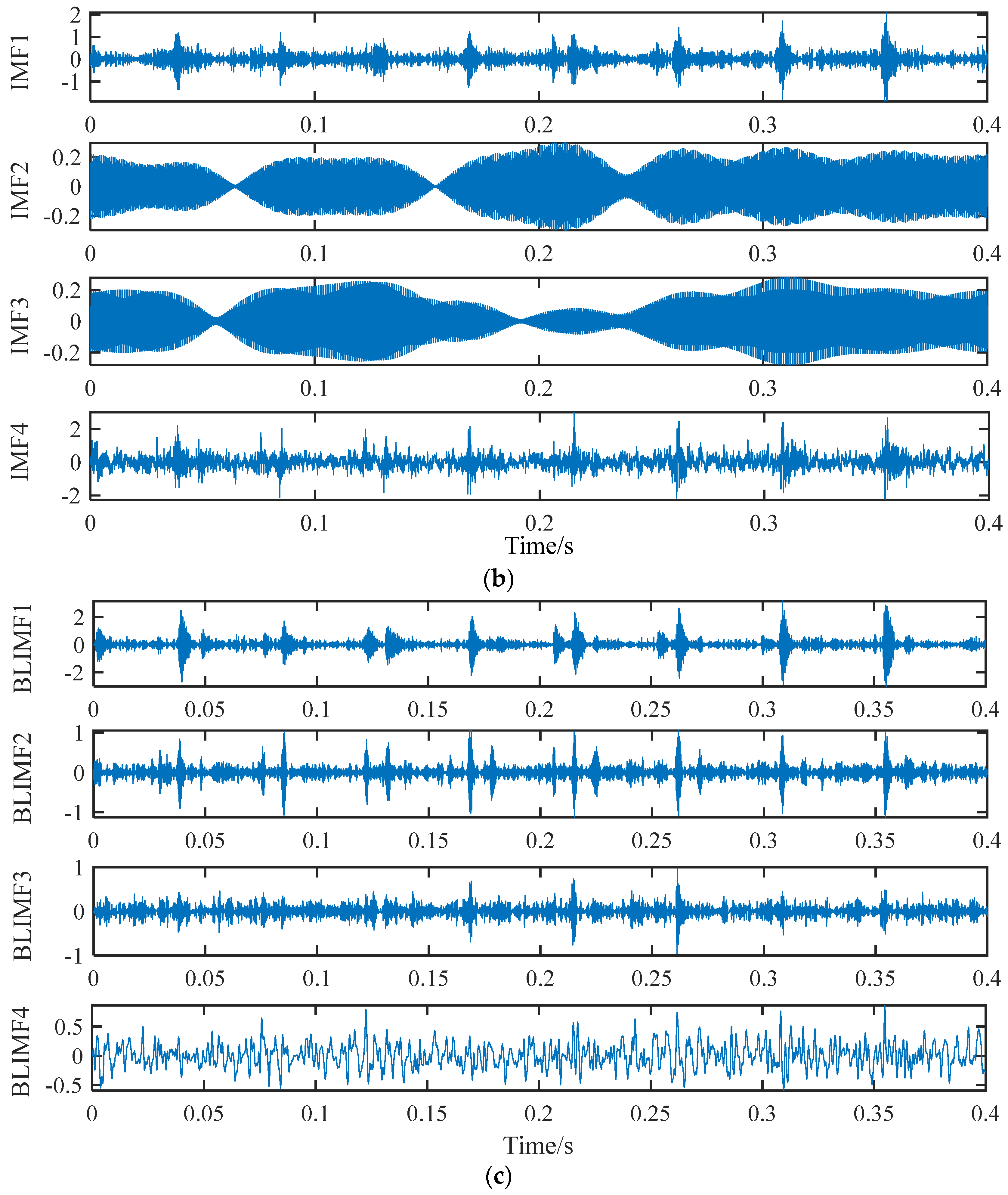
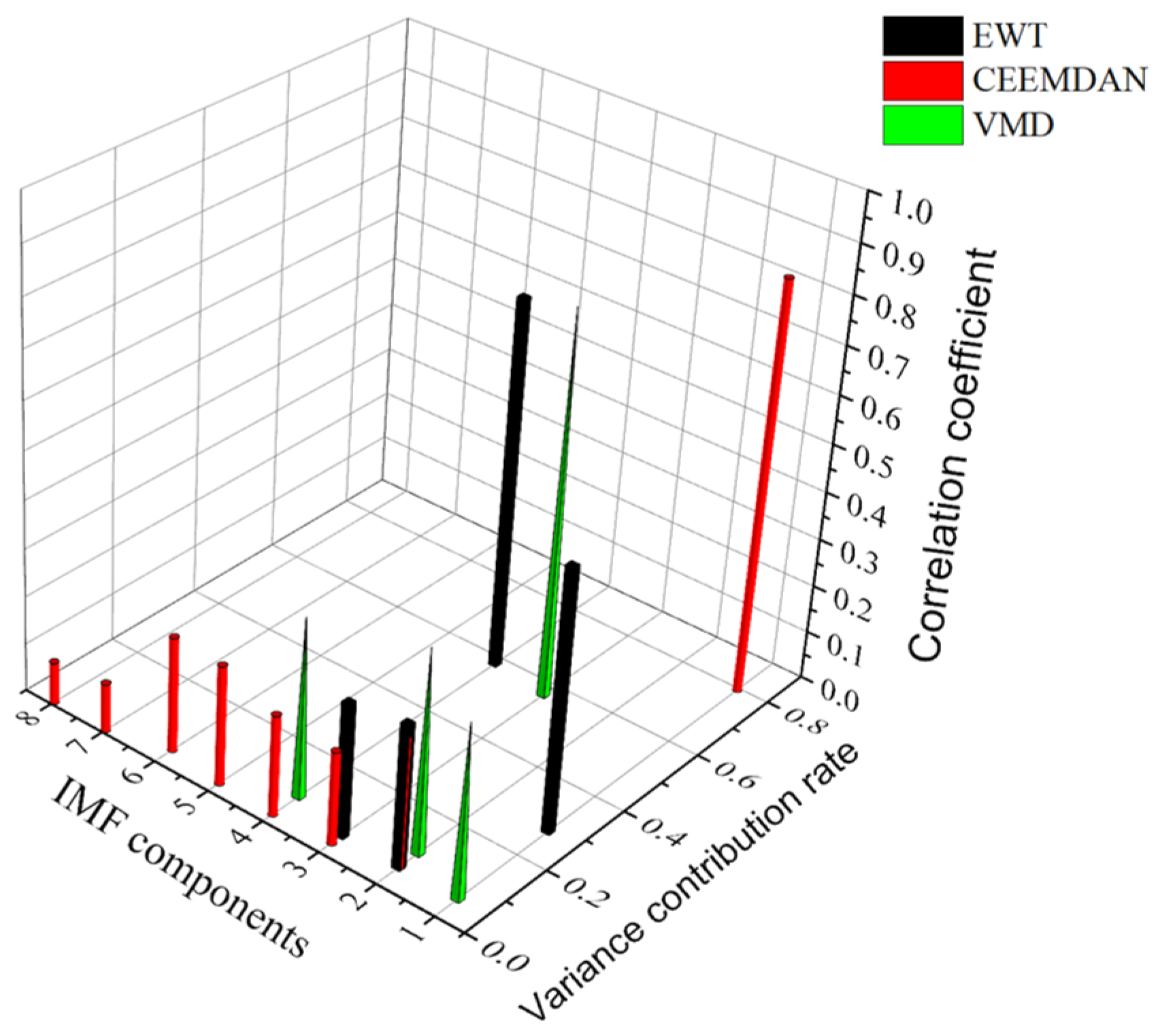
- VMD of faulty rolling bearing signals: K–L divergence is used to obtain the optimal penalty factor and mode number. After the determination of important parameters, the signals are decomposed into multiple BLIMFs by VMD. Then, the correlation coefficient and variance contribution rate of each component are analyzed, the effective components are screened out and the signals are reconstructed.
- (2)
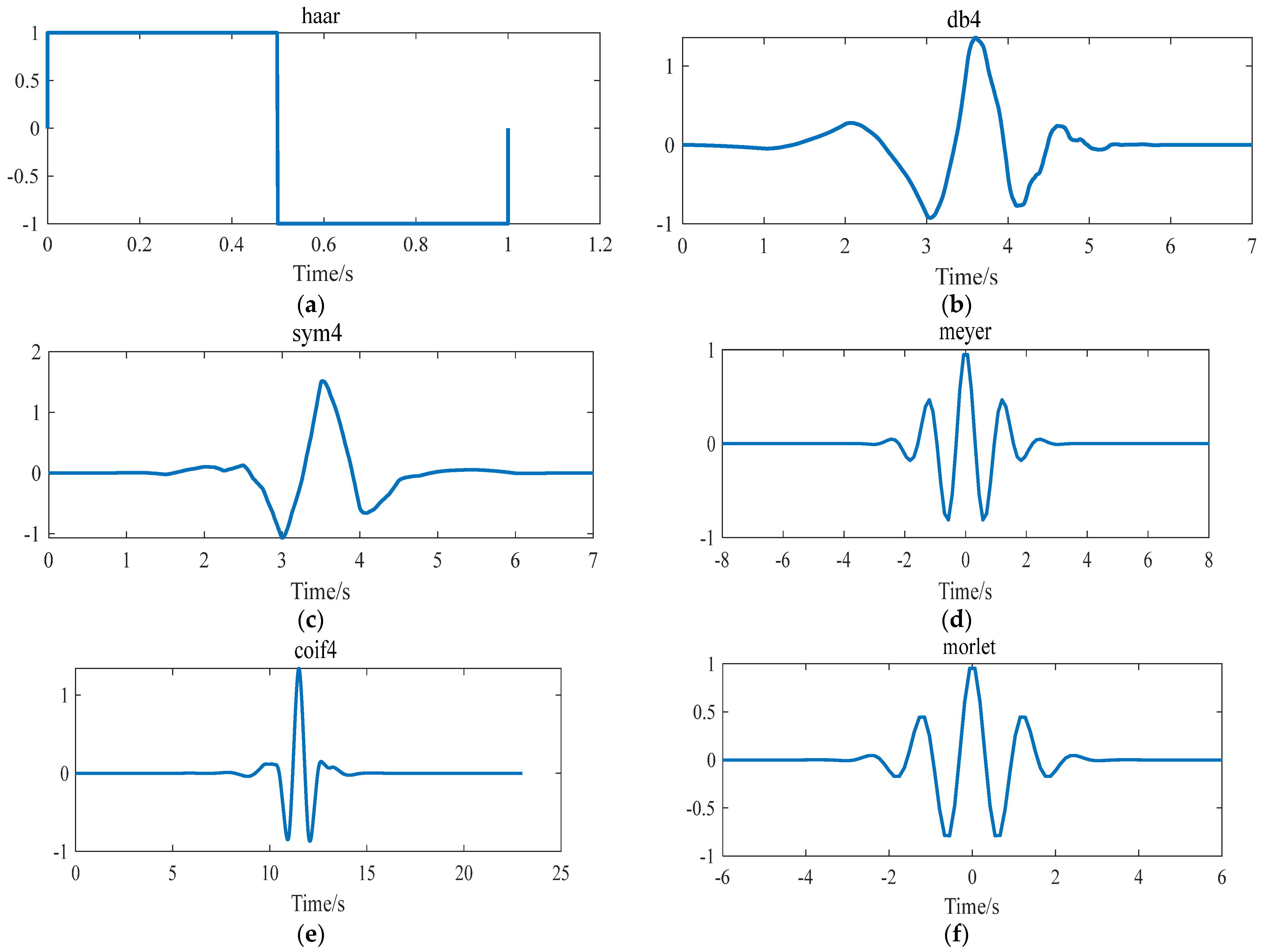
- Wavelet decomposition of the reconstructed signals: The db4 wavelet base is selected, the decomposition level j is determined to be 3 [28] (see Appendix A for parameter selection), and then 3-level decomposition of the reconstructed signals is carried out.
- (3)
- Threshold compression of wavelet decomposition coefficients: The optimal parameters are selected by using the genetic algorithm, and then the optimized wavelet threshold denoising is used to perform threshold compression on the low-frequency coefficients from the first to the third layers to remove the noise components.
- (4)
- Signal reconstruction: Signals are reconstructed on the processed low-frequency coefficients from the first to the third layers and the high-frequency coefficients in the third layer.
4. Numerical Simulation
4.1. Establishment of Simulation Signals
4.2. Simulation Signal Denoising
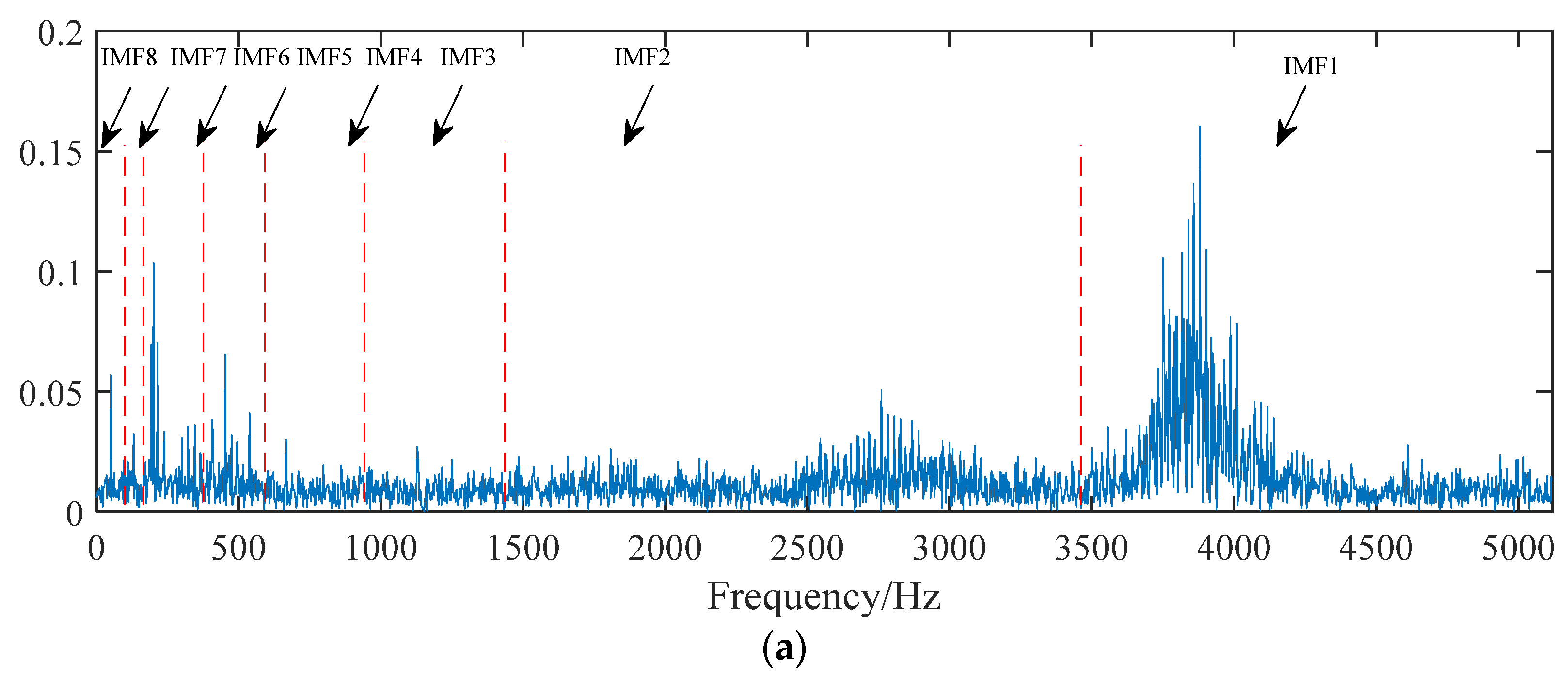
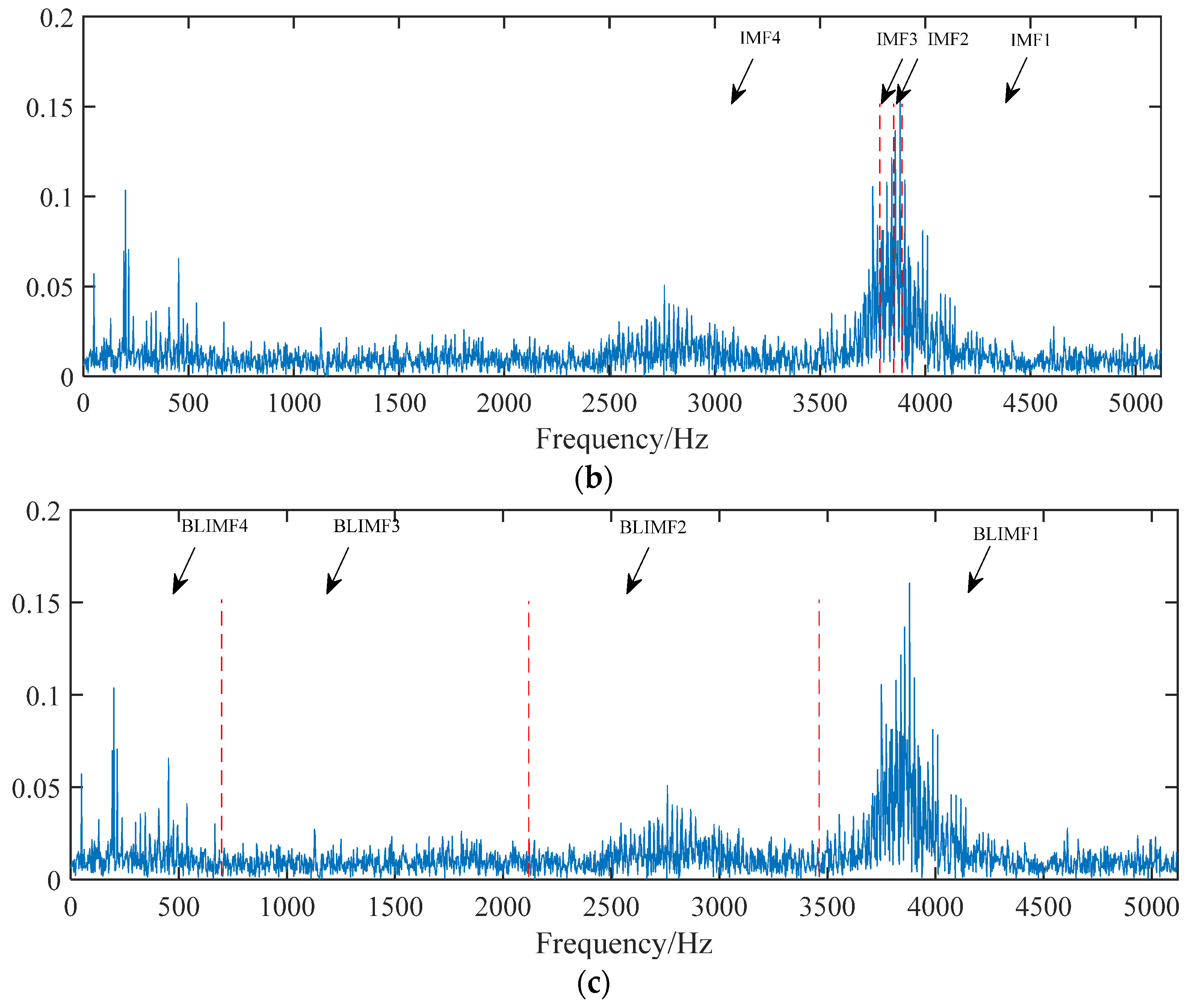
4.2.1. IMF and BLIMF Selection
4.2.2. Comparative Analysis
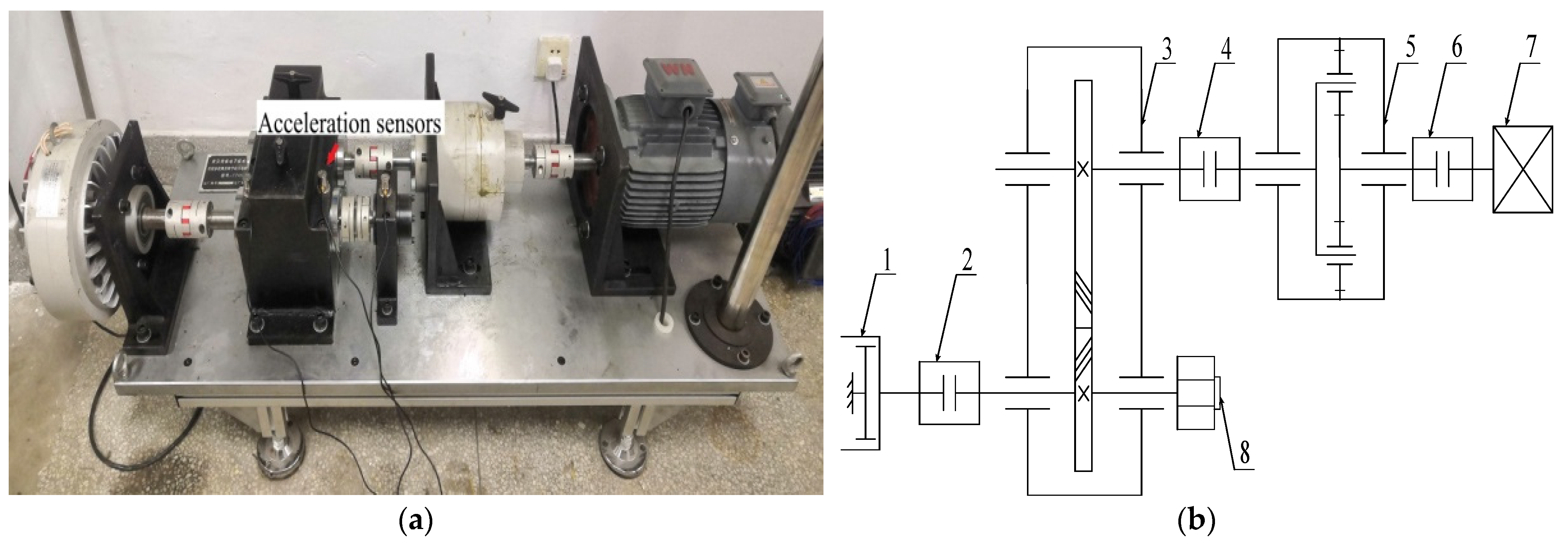
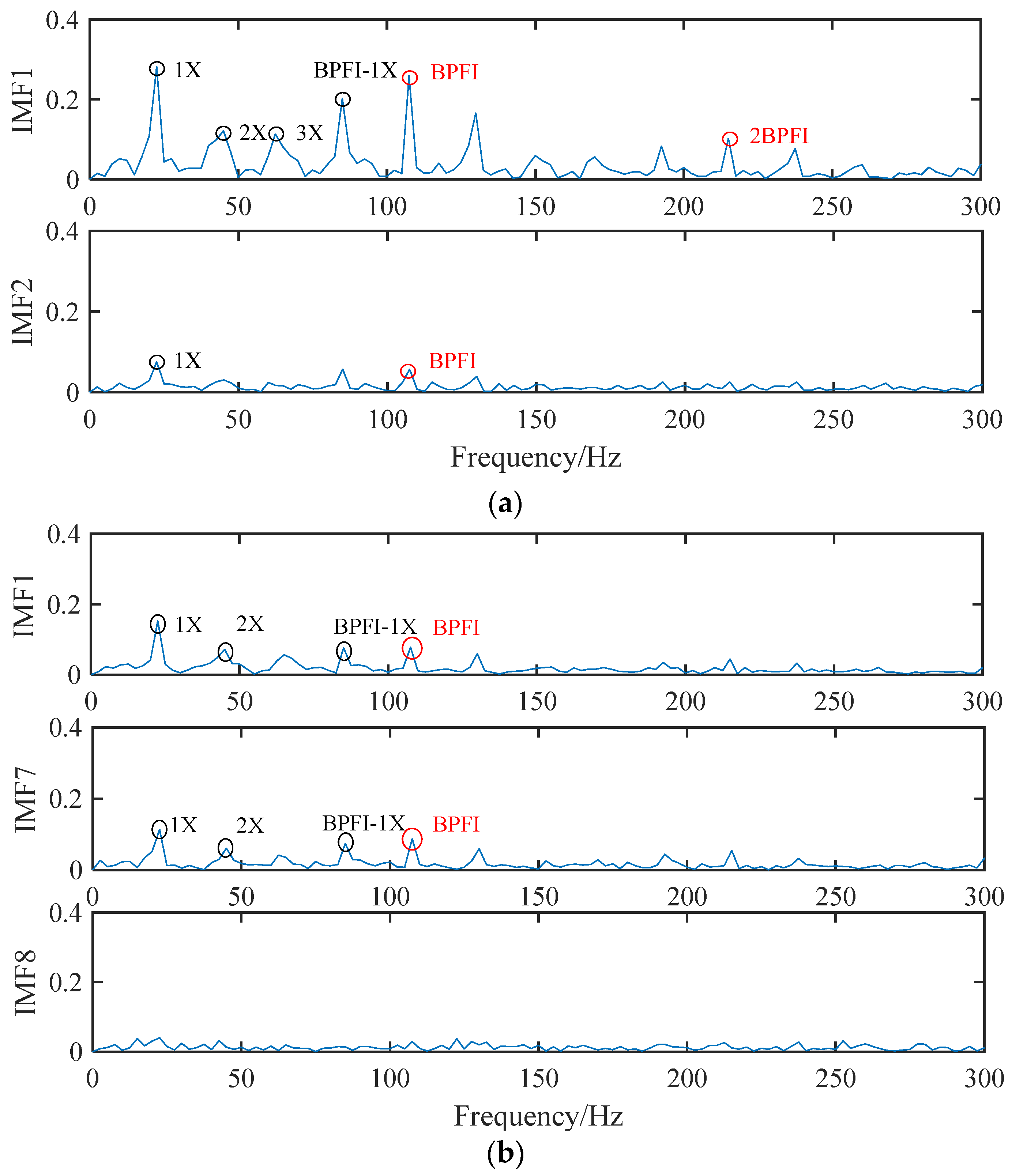
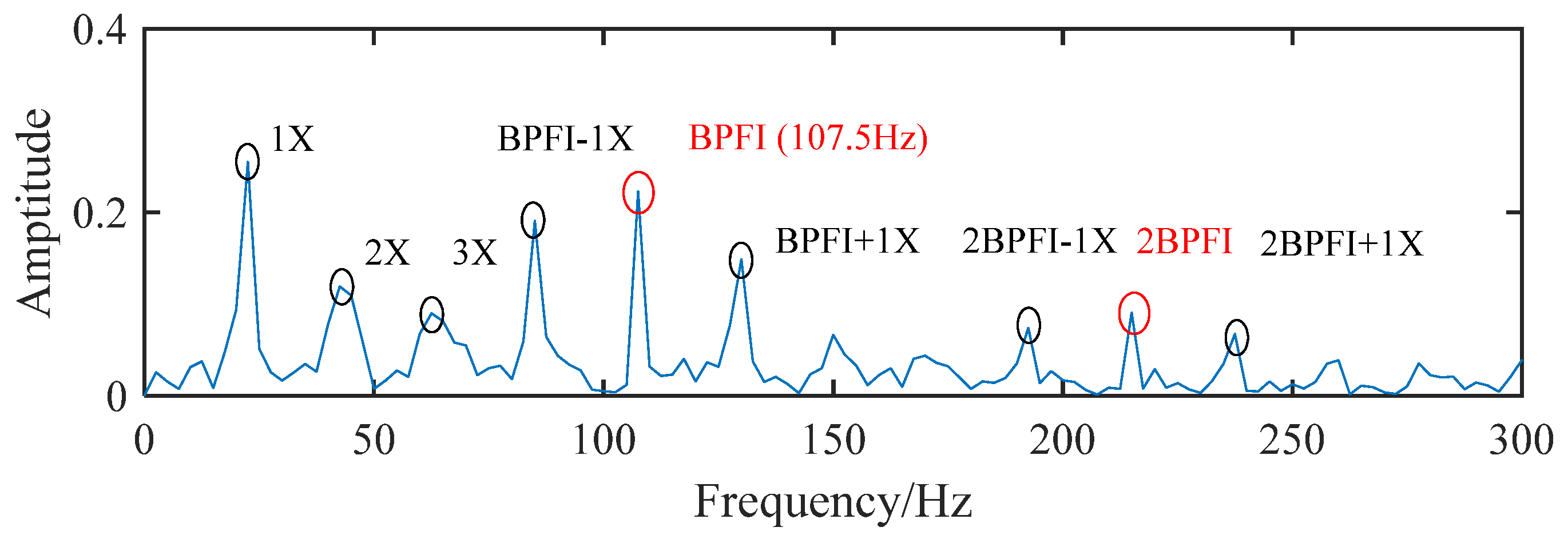
5. Actual Bearing Signal Noise Reduction
6. Conclusions
- (1)
- Artificial selection of parameters cannot yield the best results for VMD, so K–L divergence can be used to optimize the selection of parameters K and in VMD to reduce decomposition uncertainty.
- (2)
- The optimized wavelet threshold denoising approach proposed not only ensures the continuity of the threshold function but also avoids the fixed deviation of the soft threshold.
- (3)
- The verification results of simulation and measured signals show that the proposed approach can reduce noise interference and accurately extract fault features. Compared with the EMD, CEEMD, CEEMDAN–WPT, and EWT algorithms, the proposed approach boasts better noise reduction capability and hence higher application value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Selection of Decomposition Parameters
| Wavelet Function | Harr | Daubechies | Symlets | Meyer | Morlet | Coiflet |
|---|---|---|---|---|---|---|
| Symmetry | Yes | Far from | Near from | Yes | Yes | Near from |
| Orthogonal | Yes | Yes | Yes | Yes | No | Yes |
| Biorthogonal | Yes | Yes | Yes | Yes | No | Yes |
| Compact support | Yes | Yes | Yes | No | No | Yes |
| CWT | Possible | Possible | Possible | Possible | Possible | Possible |
| 6.5632 | 7.4970 | 6.3626 | 6.6082 | 7.2148 | 6.3298 |
Appendix B. Code for Optimized Wavelet Threshold Denoising

References
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Lu, Z.; Li, S.; Li, H. Robust fault diagnosis of rolling bearing via phase space reconstruction of intrinsic mode functions and neural network under various operating conditions. Struct. Health Monit. 2022, 14759217221091131. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J.; Bao, J.; Liu, Q.; Ding, K. Adaptive empirical fourier decomposition based mechanical fault diagnosis method. J. Mech. Eng. 2020, 56, 125–136. [Google Scholar]
- Sun, W.; An Yang, G.; Chen, Q.; Palazoglu, A.; Feng, K. Fault diagnosis of rolling bearing based on wavelet transform and envelope spectrum correlation. J. Vib. Control. 2013, 19, 924–941. [Google Scholar] [CrossRef]
- Chen, H.; Zheng, B. Signal noise reduction method of automata based on wavelet modulus maxima. Mech. Eng. Autom. 2010, 40, 36–37. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Xie, P.; Leng, A.; Peng, Y. Wavelet infrared image denoising with improved correlation between threshold and scale. Chin. J. Autom. 2011, 37, 1167–1174. [Google Scholar]
- Liu, X.; Hu, J.; Gao, L.; Li, T.; Bai, X. Micromachined gyroscope denoising method based on improved wavelet threshold. Chin. J. Inert. Technol. 2014, 22, 233–236. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Alam, S.M.S.; Bhuiyan, M.I.H. Detection of seizure and epilepsy using higher order statistics in the EMD domain. IEEE J. Biomed. Health Inform. 2013, 17, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Q.; Xu, Y.; Peng, Y.; Zhang, W.; Li, Y.; Tang, L. Low-speed rolling bearing fault diagnosis based on EMD denoising and parameter estimate with alpha stable distribution. J. Mech. Sci. Technol. 2017, 31, 1587–1601. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 207152935. [Google Scholar] [CrossRef]
- Gaci, S. A new ensemble empirical mode decomposition (EEMD) denoising method for seismic signals. Energy Procedia 2016, 97, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Lei, Y.; Liu, Z.; Ouazri, J.; Lin, J. A fault diagnosis method of rolling element bearings based on CEEMDAN. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1804–1815. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Jia, R.; Lu, X. Two-dimensional variational mode decomposition for seismic record denoising. J. Geophys. Eng. 2022, 19, 433–444. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, L. Application of variational mode decomposition in fault diagnosis of rotors. J. Vib. Test. Diagn. 2017, 37, 793–799. [Google Scholar]
- Zhao, H.; Guo, S.; Gao, D. Fault feature extraction of bearing faults based on singular value decomposition and variational modal decomposition. J. Vib. Shock. 2016, 35, 183–188. [Google Scholar]
- He, Y.; Wang, H.; Gu, S. A new method for bearing fault diagnosis based on VMD parameter optimization based on genetic algorithm. J. Vib. Shock. 2021, 40, 184–189. [Google Scholar]
- Xu, T.; Wang, H.; Song, Z.; Li, Y. Fault diagnosis of VMD instantaneous energy and PNN based on K-L dispersion. J. Electron. Meas. Instrum. 2019, 33, 117–123. [Google Scholar]
- Deng, P.; Zhang, L.; Liu, R.; Wang, B. Denoising of microgrid detection signal based on improved threshold function wavelets. Electr. Meas. Instrum. 2021, 58, 180–185. [Google Scholar]
- Dai, C.; Zhu, Y.; Chen, W. A New Wavelet Noise Cancellation Threshold Selection Method. Comb. Mach. Tool Autom. Mach. Technol. 2005, 6, 33–35. [Google Scholar]
- Wang, X.P.; Cao, L.M. Genetic Algorithm: Theory, Application and Software Implementation; Xi’an Jiaotong University Press: Xi’an, China, 2002; pp. 68–69. [Google Scholar]
- Jia, T. Research on the Fault Diagnosis of Rolling Bearings in the Running Section of Rail Trains; Beijing Jiaotong University: Beijing, China, 2011. [Google Scholar] [CrossRef]
- Tang, G.; Wang, X. Early fault diagnosis of rolling bearings fused with singular value differential spectra of IVMD. Vib. Test Diagn. 2016, 36, 700–707. [Google Scholar]
- Zheng, J.; Cao, S.; Pan, H.; Ni, Q. Spectral envelope-based adaptive empirical Fourier decomposition method and its application to rolling bearing fault diagnosis. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Wang, H.; Bai, H.; Zhao, Y.; Wang, B.; Wang, H. Denoising Method of Blasting Signal Based on Fourier Decomposition-Wavelet Packet Analysis. Blasting 2021, 38, 37–44. [Google Scholar]







| Genetic Algorithm Parameters | Values |
|---|---|
| M | 50 |
| Pr | 0.8 |
| Pm | 0.01 |
| T | 300 |
| Noise Reduction Method | RMSE | SNR | GSNR |
|---|---|---|---|
| EMD | 0.1740 | 3.4234 | 1.0583 |
| CEEMD | 0.1797 | 3.4797 | 1.0814 |
| EWT | 0.1687 | 3.9485 | 1.2271 |
| CEEMDAN + WPT | 0.1697 | 3.6651 | 1.1499 |
| The proposed approach | 0.0990 | 6.7350 | 2.1397 |
| Bearing Type | Sampling Frequency (Hz) | Rotating Speed (r/min) | Fault Characteristic Frequency (Hz) |
|---|---|---|---|
| SKF6308 | 10,204 | 1309 | 107.25 |
| Noise Reduction Method | RMSE | SNR |
|---|---|---|
| EMD | 0.3567 | 4.5971 |
| CEEMD | 0.3465 | 4.6352 |
| CEEMDAN-WPT | 0.3290 | 4.7264 |
| EWT | 0.2995 | 5.5910 |
| The proposed approach | 0.1981 | 7.1065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Xing, F.; Pan, S.; Yuan, R.; Lv, Y. Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition and Genetic Algorithm-Optimized Wavelet Threshold Denoising. Machines 2022, 10, 649. https://doi.org/10.3390/machines10080649
Hu C, Xing F, Pan S, Yuan R, Lv Y. Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition and Genetic Algorithm-Optimized Wavelet Threshold Denoising. Machines. 2022; 10(8):649. https://doi.org/10.3390/machines10080649
Chicago/Turabian StyleHu, Can, Futang Xing, Shuhan Pan, Rui Yuan, and Yong Lv. 2022. "Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition and Genetic Algorithm-Optimized Wavelet Threshold Denoising" Machines 10, no. 8: 649. https://doi.org/10.3390/machines10080649
APA StyleHu, C., Xing, F., Pan, S., Yuan, R., & Lv, Y. (2022). Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition and Genetic Algorithm-Optimized Wavelet Threshold Denoising. Machines, 10(8), 649. https://doi.org/10.3390/machines10080649








