Mathematical Modeling and Machining of the Internal Double-Arc Spiral Bevel Gear by Finger Milling Cutters for the Nutation Drive Mechanism †
Abstract
:1. Introduction
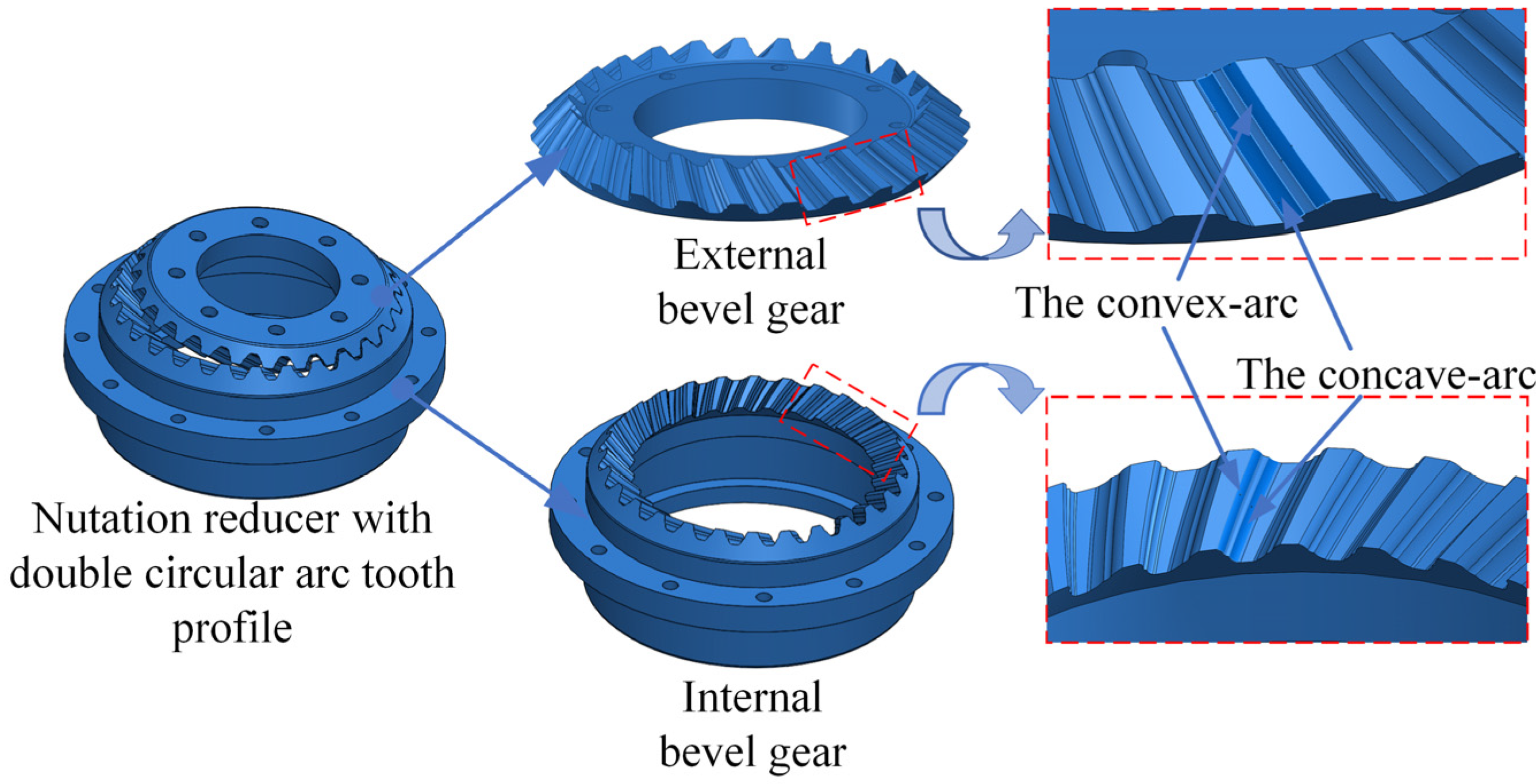
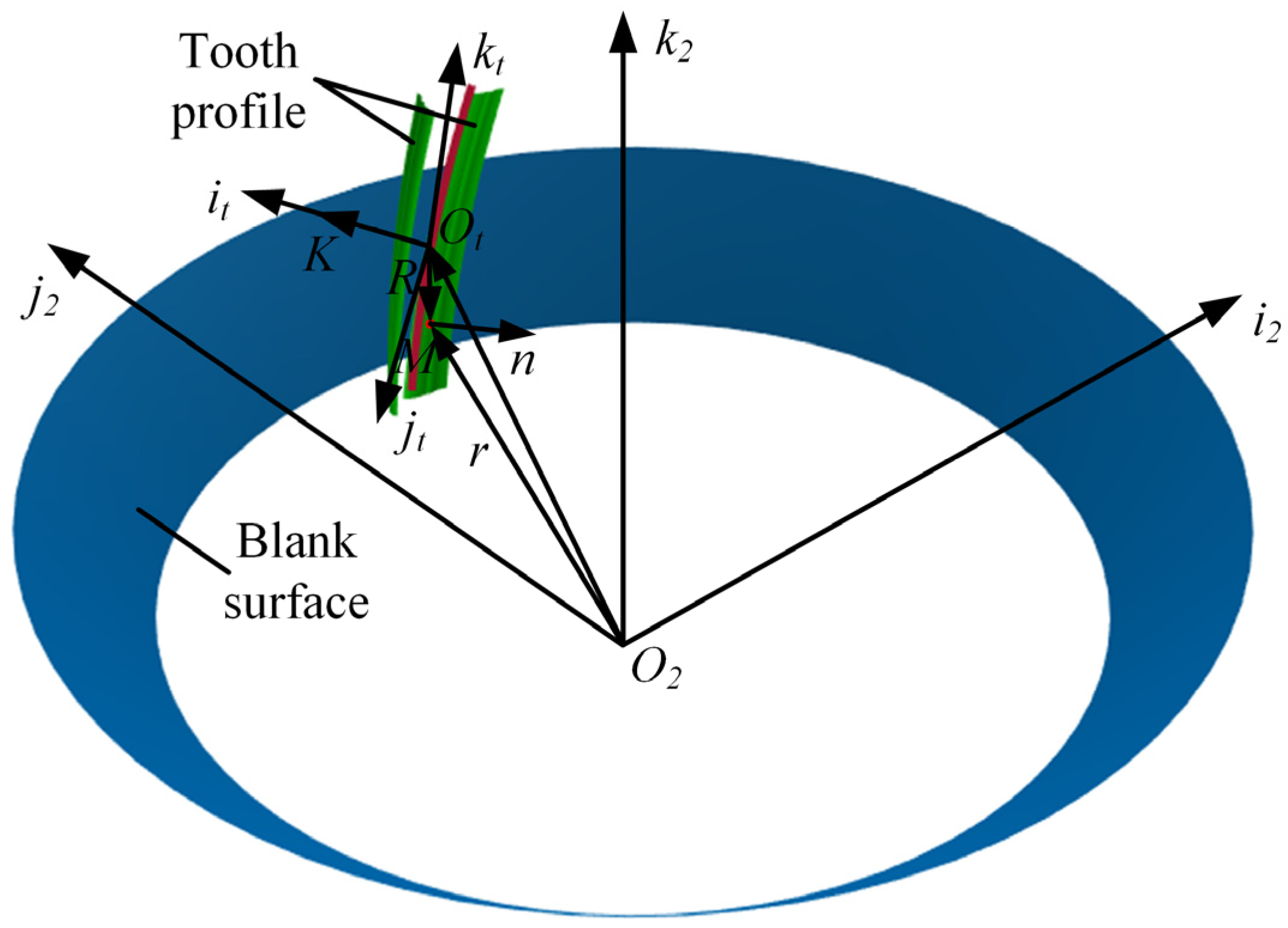
2. Mathematical Modeling of the Tooth Profile with a Double-Arc Internal Spiral Bevel Gear
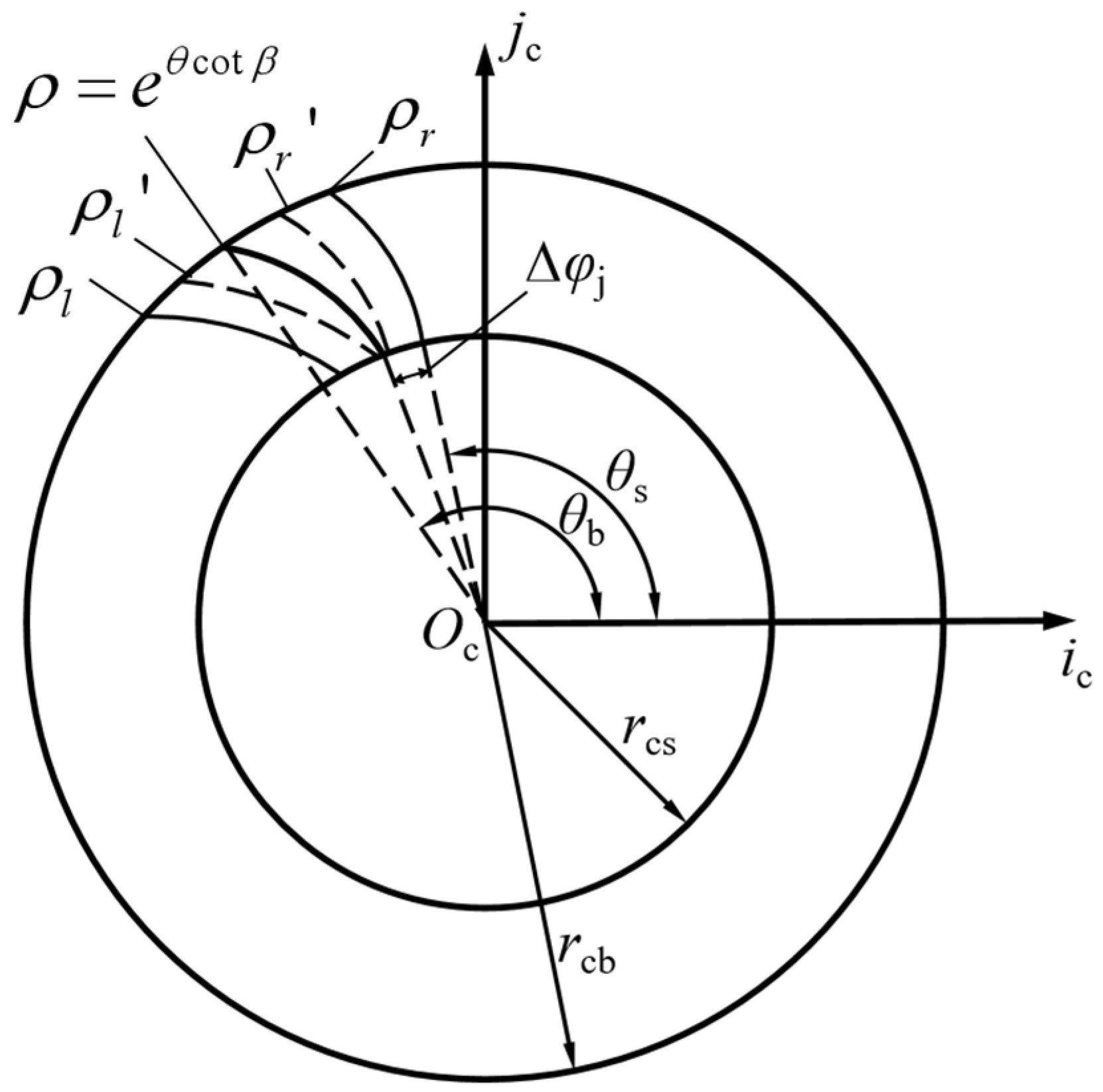
2.1. Tooth Profile Design
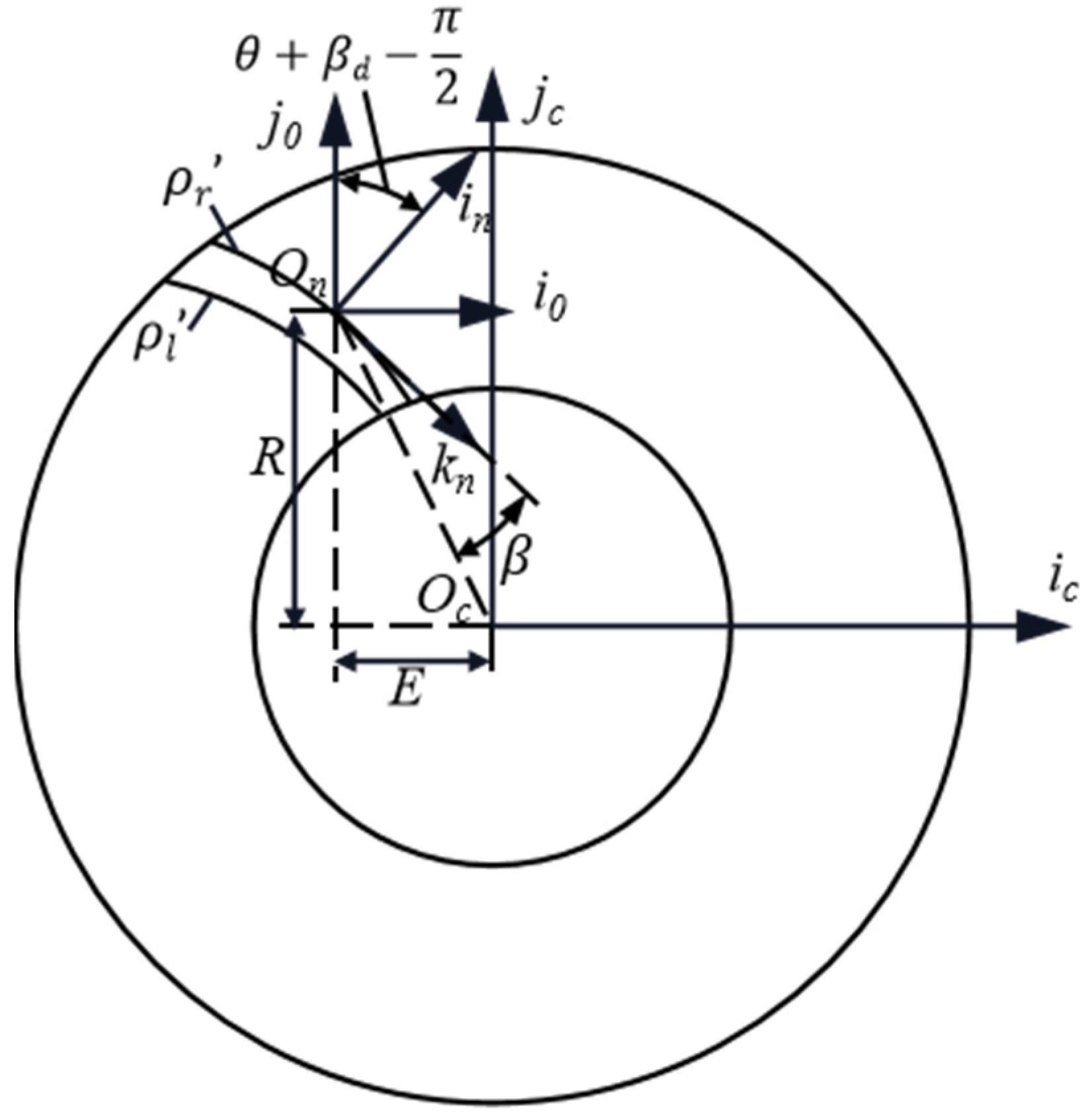
2.2. Tooth Alignment Curve Design
2.3. Tooth Alignment Curve Equation of the Internal Spiral Bevel Gear
2.4. Mathematical Modeling Method
3. The Design of the Finger Milling Cutter
3.1. Solving the Tool Rotation Surface with the Known Tooth Profile Equation
3.2. The Designing of Finger Milling Cutter
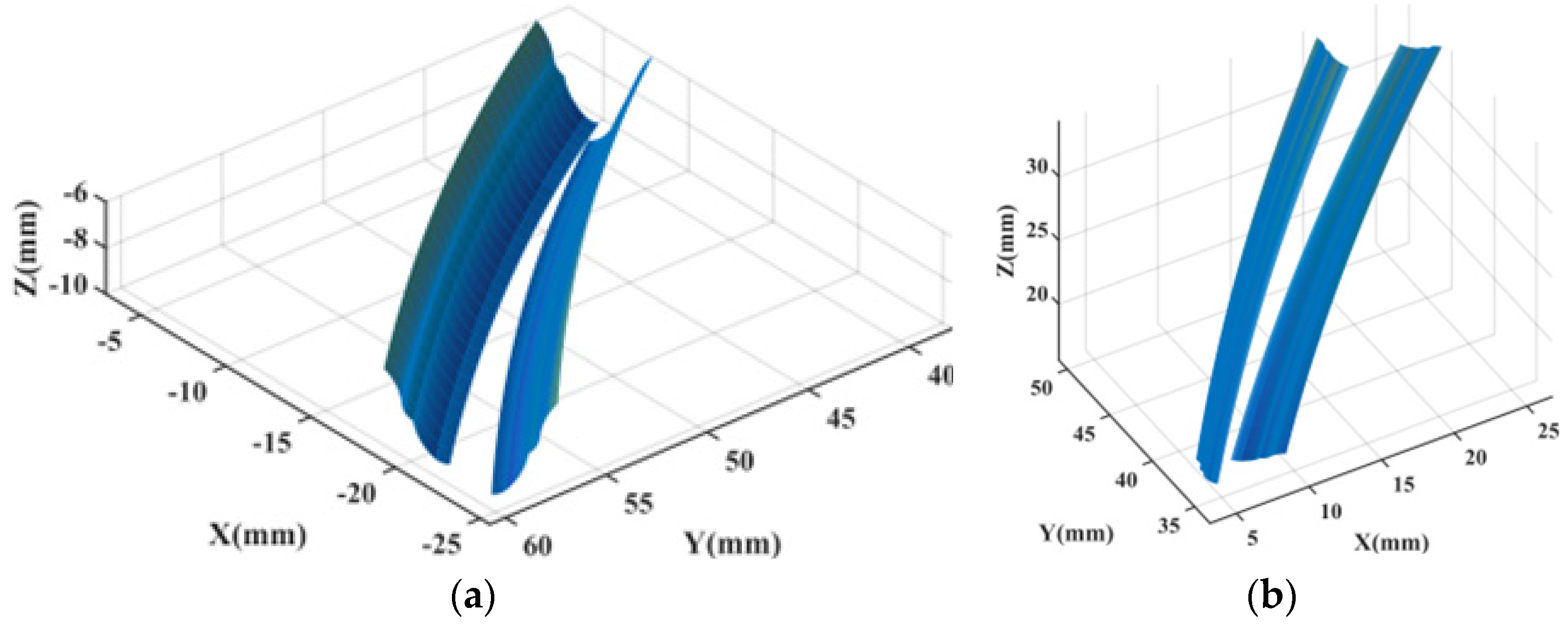
4. Simulation and Verification of the Tooth Surface of the Internal Spiral Bevel Gear
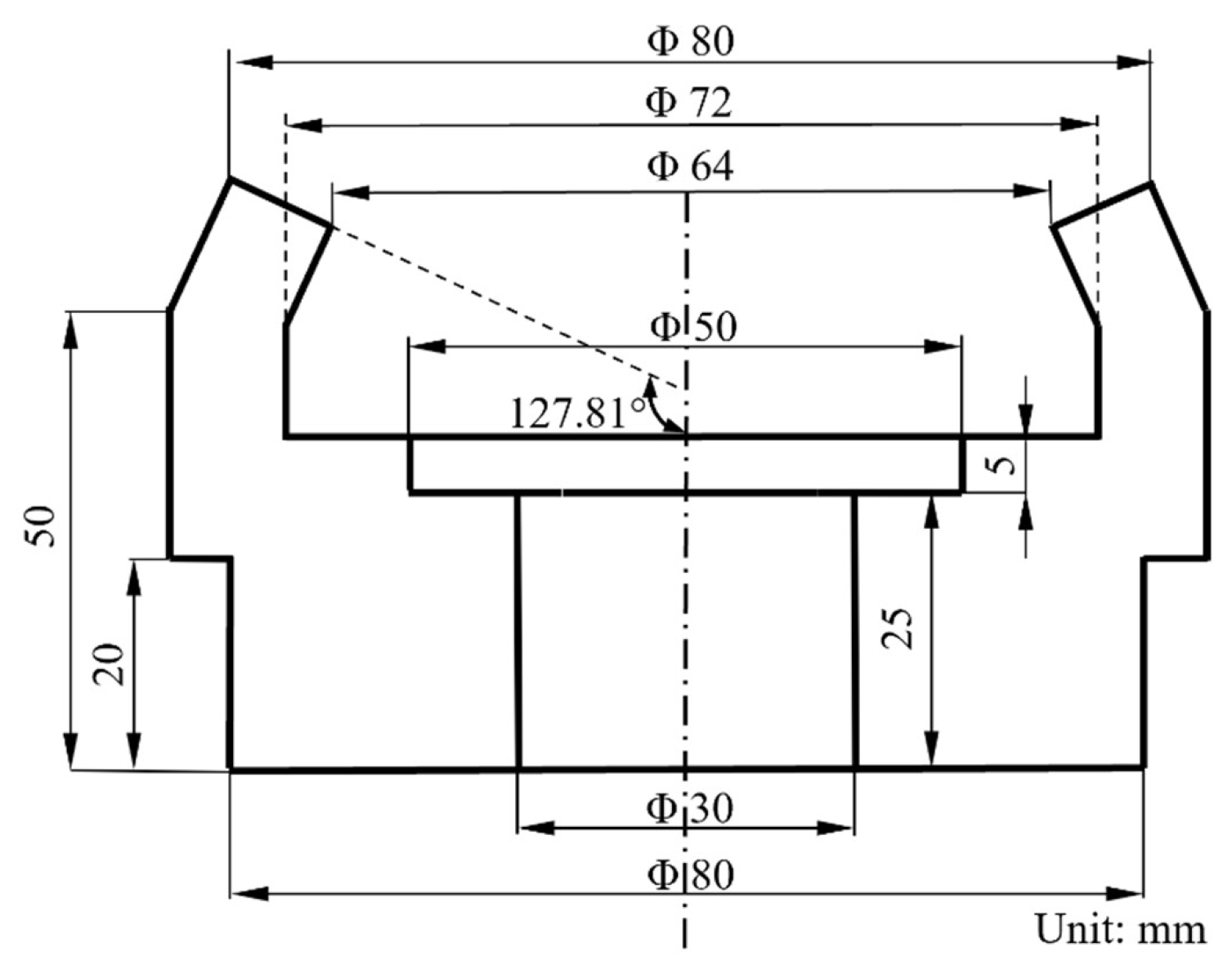
4.1. Determination of Machining Parameters
4.2. Simulation Machining Process of the Internal Spiral Bevel Gear
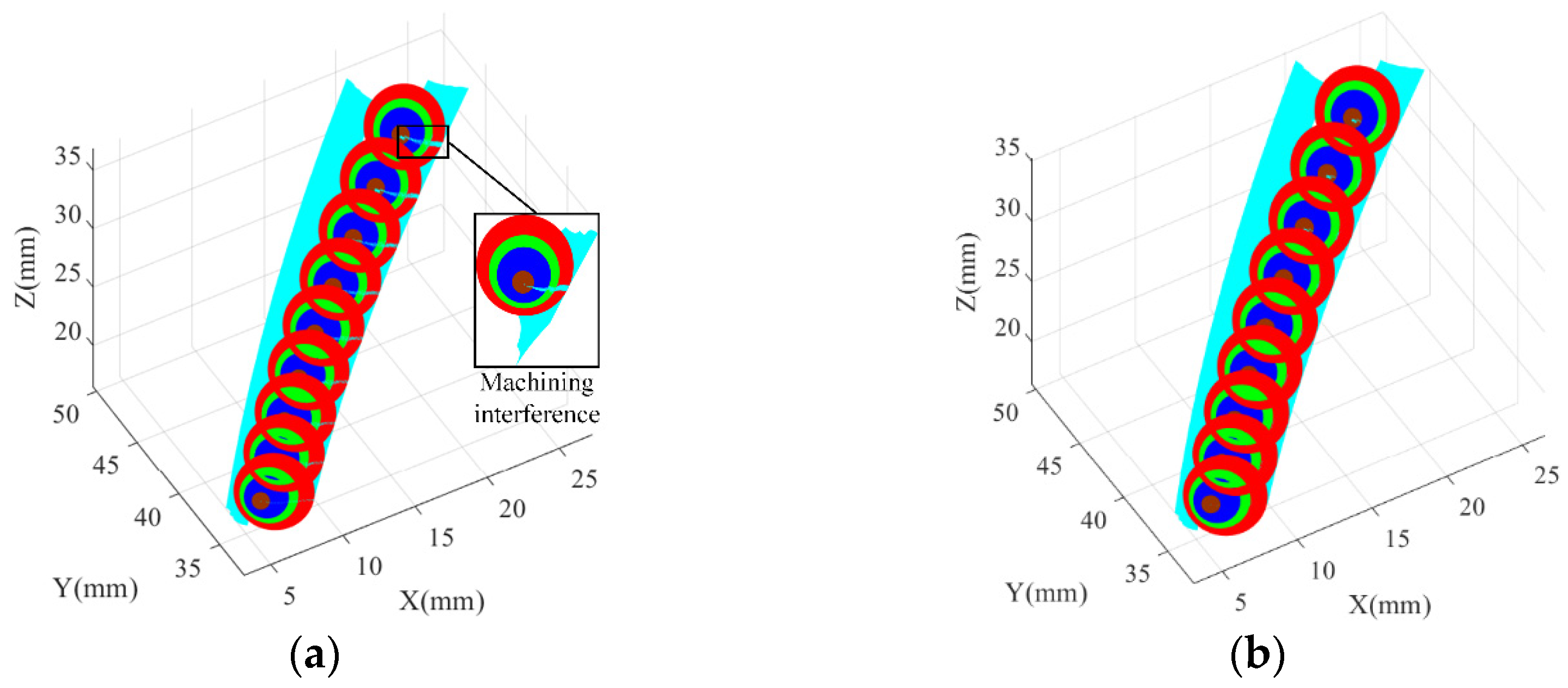
4.3. Machining Interference Inspection
4.4. Real Machining Process of the Internal Spiral Bevel Gear
5. Conclusions
- (1)
- Aiming at the proposed method of machining the internal double-arc spiral bevel gear with a finger milling cutter, the intercept equation of the finger milling cutter is solved. Considering the processing difficulty, it is divided into four finger milling cutters, which are used to process the convex tooth surface, transitional tooth surface, concave tooth surface and tooth root surface, respectively.
- (2)
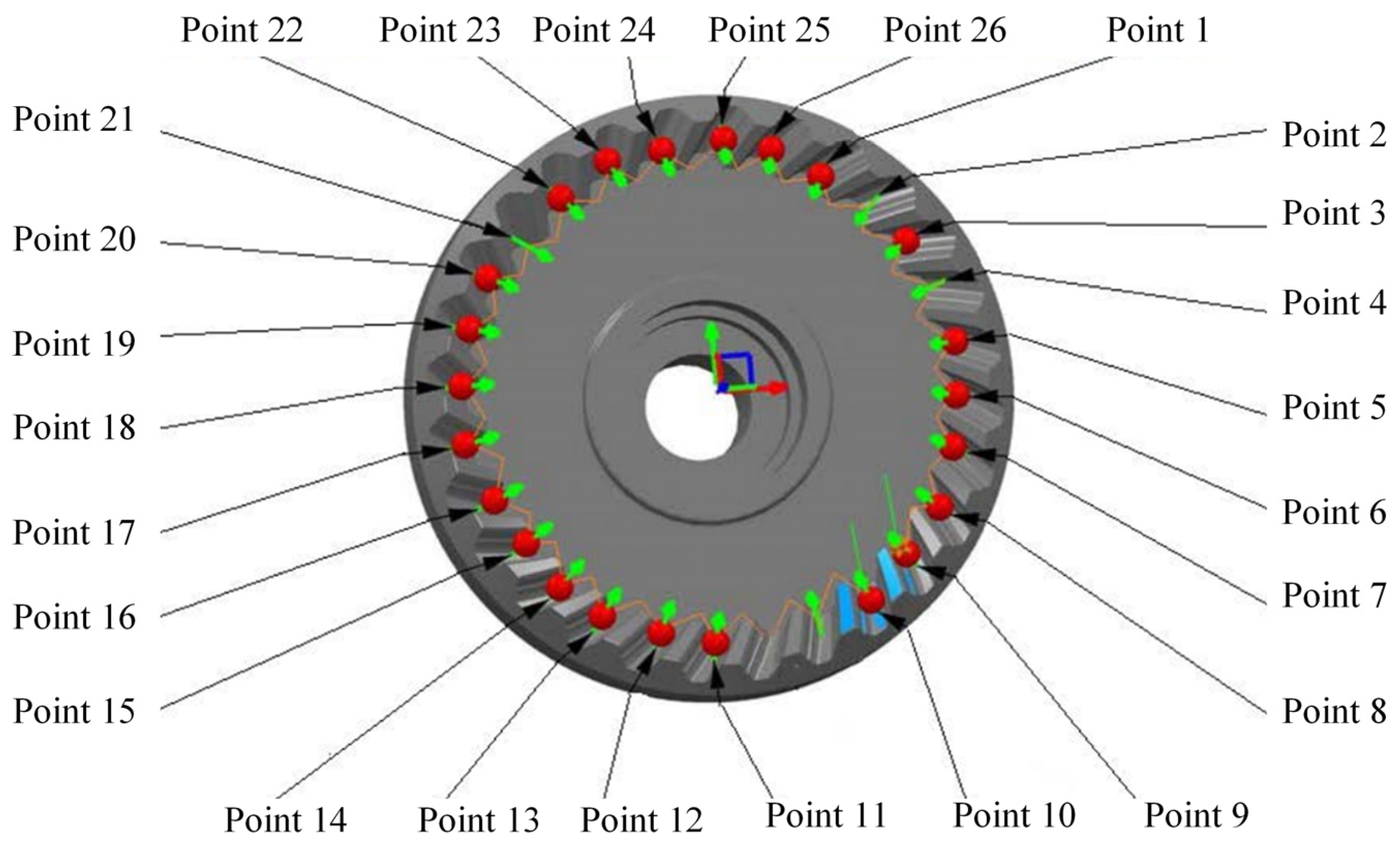
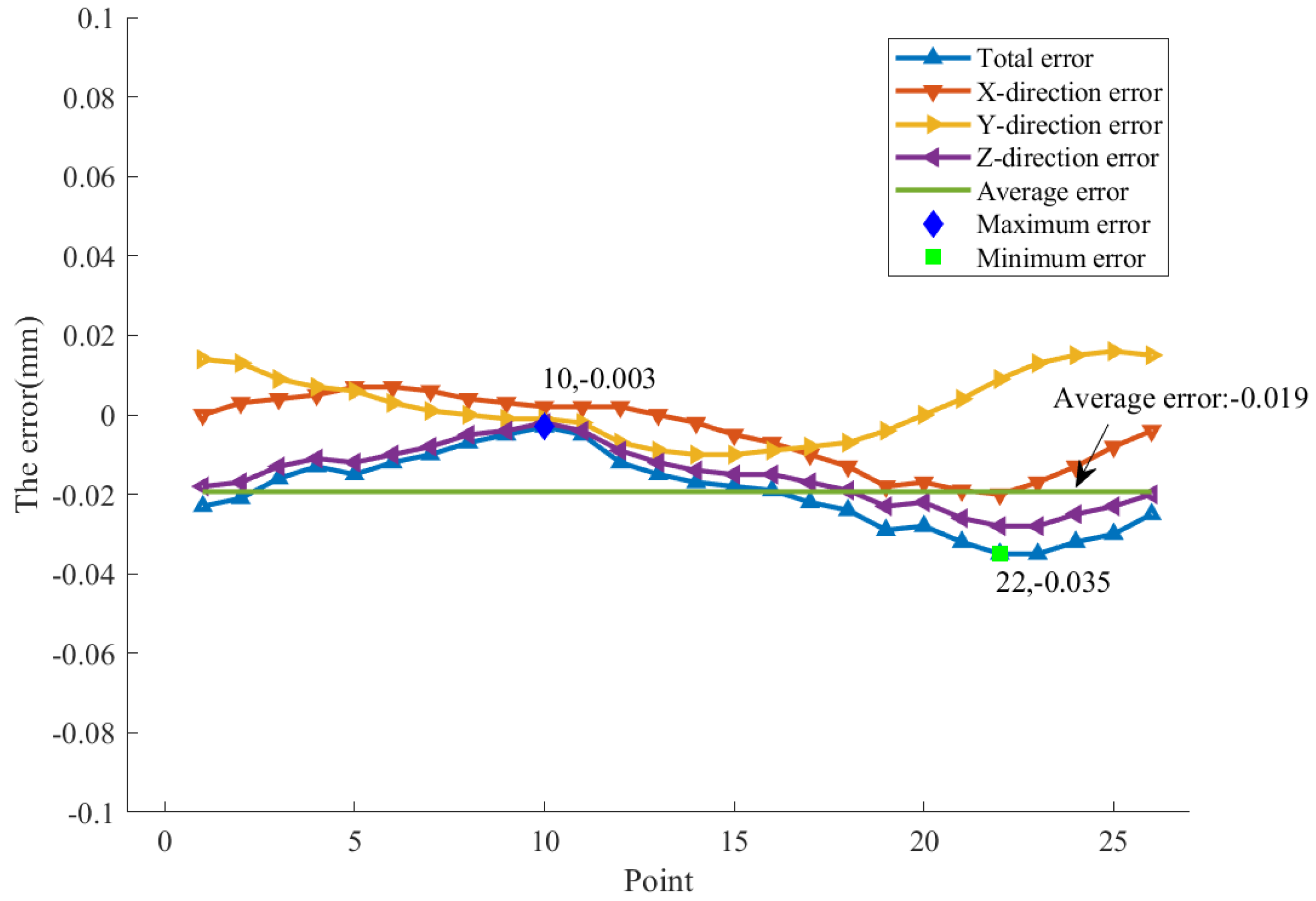
- A simulation machining experiment with the designed finger milling cutter was carried out. Compared with the ideal tooth surface, the error of the convex tooth surface is the smallest, which is 0.005 mm. The error of the concave tooth surface and transitional tooth surface is 0.030 mm, and the error of the tooth root surface is 0.032 mm. The 26 sample points on the machined gear were measured. The maximum error was 0.035 mm, the minimum error was 0.003 mm, and the average error was 0.019 mm, meeting the machining requirements. The Z-direction error has the greatest influence on the overall error.
- (3)
- This method requires the design and manufacture of special milling cutters, which increases the machining cost. The size of the tool is small, and it is easily deformed under stress and heat during machining. At the same time, many tool changes are required in the machining process, which result in the low efficiency of small batch production.
- (4)
- This method does not consider the heat and force generated in the processing process. Subsequent research can reduce the machining error and improve the machining accuracy by analyzing the coupling of the stress field and temperature field. Meanwhile, the tool structure can be optimized to improve the tool life and machining accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, Y.W.; Yao, L.G.; Zhang, J.; Xie, Z.Y.; Hong, J.L. Feasibility analysis of using a two-stage nutation drive as joint reducer for industrial robots. J. Mech. Sci. Technol. 2019, 33, 1799–1807. [Google Scholar] [CrossRef]
- Saribay, Z.B.; Bill, R.C. Design analysis of pericyclic mechanical transmission system. Mech. Mach. Theory 2013, 61, 102–122. [Google Scholar] [CrossRef]
- Uzuka, K.; Enomoto, I.; Suzumori, K. Comparative assessment of several nutation motor types. IEEE ASME Trans. Mechatron. 2009, 14, 82–92. [Google Scholar] [CrossRef]
- Mlendini, P.; Perrone, M.; Stam, S.; Barbagelate, A.; Primavori, M.; Appolonia, S.D. Wobbling gears achieve high ratios. ESA J. 2010, 10, 34–37. [Google Scholar]
- Yao, L.G.; Gu, B.; Huang, S.J.; Wu, W.G.; Dai, J.S. Mathematical modeling and simulation of the external and internal double circular-arc spiral bevel gears for the nutation drive. ASME J. Mech. Des. 2010, 132, 8–13. [Google Scholar] [CrossRef]
- Lin, Z.; Yao, L.G.; Zhang, J.; Su, T.K.; Chen, K.J. Tooth contact analysis with latent error of double circular-arc spiral bevel gears for industrial robot joint nutation drive. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 10. [Google Scholar] [CrossRef]
- Su, Y.J.; Yao, L.G.; Zhang, J. Contact dynamics analysis of nutation drive with double circular-arc spiral bevel gear based on mathematical modeling and numerical simulation. Mech. Sci. 2021, 12, 185–192. [Google Scholar] [CrossRef]
- Lou, M.Y.; Yao, L.G.; Zheng, Y.S. Numerical analysis on magnetic field and torque of a disk-type nutation magnetic drive. IEEE Trans. Magn. 2020, 56, 4900106. [Google Scholar] [CrossRef]
- Habibi, M.; Chen, Z.C. A semi-analytical approach to un-deformed chip boundary theory and cutting force prediction in face-hobbing of bevel gears. Comput. Aided Des. 2016, 73, 63–65. [Google Scholar] [CrossRef]
- Efstathiou, C.; Tapoglou, N. A novel CAD-based simulation model for manufacturing of spiral bevel gears by face milling. CIRP J. Manuf. Sci. Technol. 2021, 33, 277–292. [Google Scholar] [CrossRef]
- Wang, S.H.; Zhou, Y.S.; Liu, X.R.; Liu, S.J.; Tang, J.Y. An advanced comprehensive approach to accurately modeling the face-milled generated spiral bevel gears. J. Comput. Inf. Sci. Eng. 2021, 21, 041008. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Chen, Z.Z.C.; Tang, J.Y. A new method of designing the tooth surfaces of spiral bevel gears with ruled surface for their accurate five-axis flank milling. ASME J. Manuf. Sci. Eng. 2017, 139, 061004. [Google Scholar] [CrossRef]
- Zheng, F.; Hua, L.; Chen, D.; Han, X. Generation of noncircular spiral bevel gears by face-milling method. ASME J. Manuf. Sci. Eng. 2016, 138, 081013. [Google Scholar] [CrossRef]
- Zheng, F.; Hua, L.; Han, X.; Chen, D.F. Generation of non-circular bevel gears with free-form tooth profile and tooth lengthwise based on screw theory. ASME J. Mech. Des. 2016, 138, 064501. [Google Scholar] [CrossRef]
- Li, G.L.; Du, S.C.; Wang, B.; Lv, J.; Deng, Y.F. High definition metrology-based quality improvement of surface texture in face milling of workpieces with discontinuous surfaces. ASME J. Manuf. Sci. Eng. 2022, 144, 031001. [Google Scholar] [CrossRef]
- Li, G.L.; Du, S.C.; Huang, D.L.; Zhao, C.; Deng, Y.F. Dynamics modeling-based optimization of process parameters in face milling of workpieces with discontinuous surfaces. ASME J. Manuf. Sci. Eng. 2019, 141, 101009. [Google Scholar] [CrossRef]
- Shih, Y.; Zhang, C. Manufacture of spiral bevel gears using standard profile angle blade cutters on a five-axis computer numerical control machine. ASME J. Mech. Des. 2017, 139, 061017. [Google Scholar] [CrossRef]
- Bo, P.; González, H.; Calleja, A.; Lacalle, L.; Bartoň, M. 5-axis double-flank CNC machining of spiral bevel gears via custom-shaped milling tools—Part I: Modeling and simulation. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2020, 62, 204–212. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.F.; Luo, Q.S.; Wang, L.T.; Qiao, L.J.; Li, M.H. Review on logarithmic spiral bevel gear. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 400. [Google Scholar] [CrossRef]
- Hoai, N.H.; Yusuf, A. Modeling the dynamics of five-axis machine tool using the multibody approach. ASME J. Manuf. Sci. Eng. 2021, 143, 021012. [Google Scholar]
- Sun, H.; Zou, B.; Chen, W. Cutting performance of silicon-based ceramic end milling tools in high-efficiency machining of GH4099 under dry condition. Int. J. Adv. Manuf. Technol. 2021, 118, 1719–1732. [Google Scholar] [CrossRef]
- Perez, I.G.; Aznar, A.F. Reverse engineering of spiral bevel gear drives reconstructed from point clouds. Mech. Mach. Theory 2022, 170, 104694. [Google Scholar] [CrossRef]
- Perez, I.G.; Saura, P.L.; Aznar, A.F. Application of the bilateral filter for the reconstruction of spiral bevel gear tooth surfaces from point clouds. ASME J. Mech. Des. 2021, 143, 053401. [Google Scholar] [CrossRef]
- Álvarez, A.; Lacalle, L.; Olaiz, A. Large spiral bevel gears on universal 5-axis milling machines: A complete process. Manuf. Eng. Soc. Int. Conf. 2015, 132, 397–404. [Google Scholar] [CrossRef] [Green Version]
- Rong, K.; Ding, H.; Tang, J. Adaptive data-driven modular control approach to computer aided process planning for manufacturing spiral bevel and hypoid gears. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 514–532. [Google Scholar] [CrossRef]
- Gonzalez, I.; Fuentes, A. Conjugated action and methods for crowning in face-hobbed spiral bevel and hypoid gear drives through the spiral system. Mech. Mach. Theory 2019, 139, 109–130. [Google Scholar] [CrossRef]
- Celikag, H.; Ozturk, E.; Sims, N. Can mode coupling chatter happen in milling? Int. J. Mach. Tools Manuf. 2021, 165, 103738. [Google Scholar] [CrossRef]
- Tajima, S.; Sencer, B. Online interpolation of 5-axis machining toolpaths with global blending. Int. J. Mach. Tools Manuf. 2022, 175, 103862. [Google Scholar] [CrossRef]
- Franco, O.; Beudaert, X.; Iglesias, A.; Dombovari, Z.; Erkorkmaz, K.; Munoa, J. Optimal cutting condition selection for high quality receptance measurements by sweep milling force excitation. Int. J. Mach. Tools Manuf. 2022, 176, 103873. [Google Scholar] [CrossRef]
- Tehranizadeh, F.; Berenji, K.R.; Budak, E. Dynamics and chatter stability of crest-cut end mills. Int. J. Mach. Tools Manuf. 2021, 171, 103813. [Google Scholar] [CrossRef]



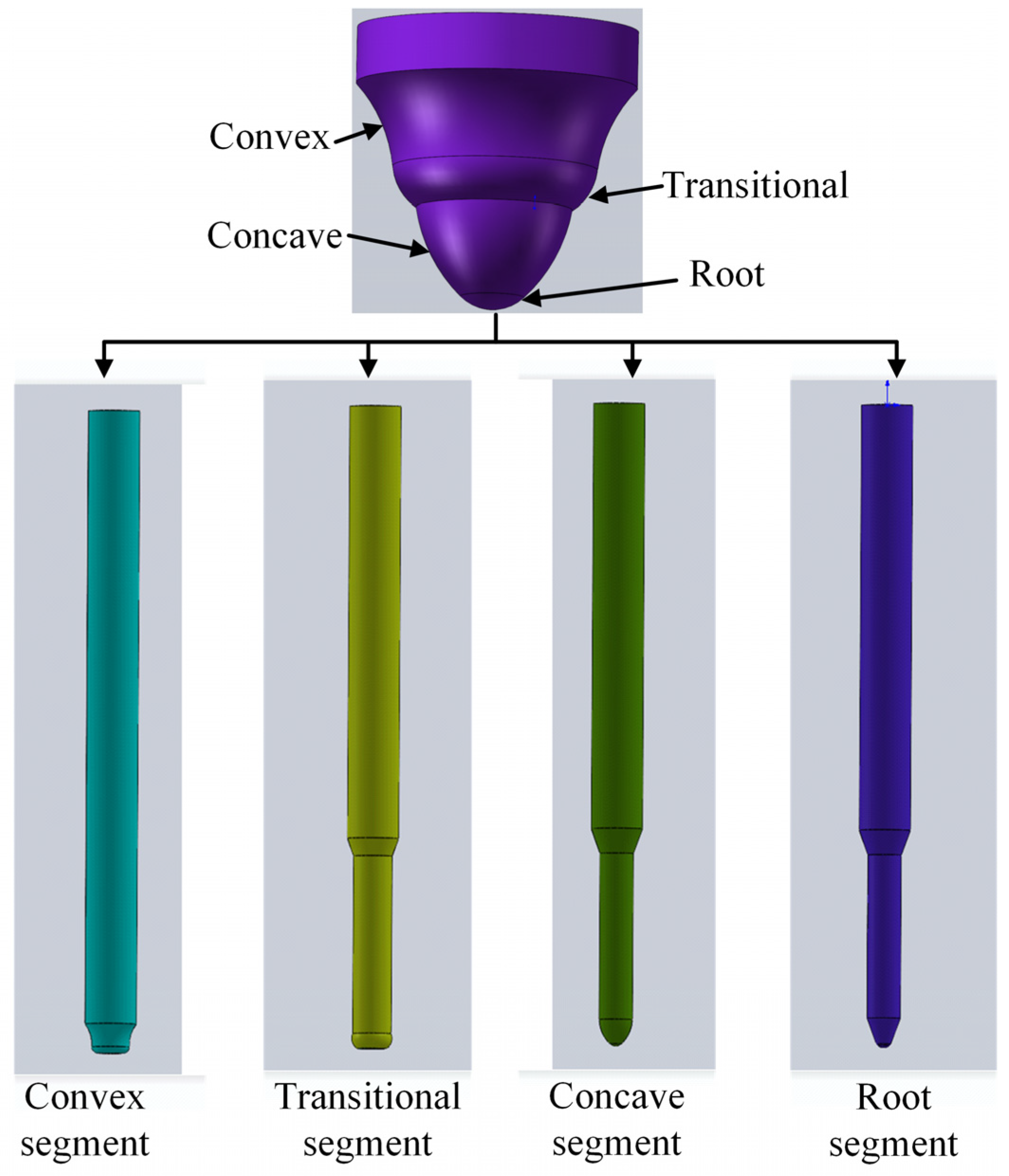





| Convex Arc | Transition Arc | Concave Arc | Root Arc |
|---|---|---|---|
| Gear Parameters | Numerical Value |
|---|---|
| Nutation dynamic angle | 5° |
| Spiral angle | 25° |
| Internal bevel gear knuckle taper angle | 127.81° |
| Spiral cone tooth taper | 50 mm |
| Number of internal bevel gear teeth | 28 |
| Normal face modulus | 2 mm |
| Point | X-Direction Error (mm) | Y-Direction Error (mm) | Z-Direction Error (mm) | Total error (mm) |
|---|---|---|---|---|
| 1 | 0.000 | 0.014 | −0.018 | −0.023 |
| 2 | 0.003 | 0.013 | −0.017 | −0.021 |
| 3 | 0.004 | 0.009 | −0.013 | −0.016 |
| 4 | 0.005 | 0.007 | −0.011 | −0.013 |
| 5 | 0.007 | 0.006 | −0.012 | −0.015 |
| 6 | 0.007 | 0.003 | −0.010 | −0.012 |
| 7 | 0.006 | 0.001 | −0.008 | −0.010 |
| 8 | 0.004 | 0.000 | −0.005 | −0.007 |
| 9 | 0.003 | −0.001 | −0.004 | −0.005 |
| 10 | 0.002 | −0.001 | −0.002 | −0.003 |
| 11 | 0.002 | −0.002 | −0.004 | −0.005 |
| 12 | 0.002 | −0.007 | −0.009 | −0.012 |
| 13 | 0.000 | −0.009 | −0.012 | −0.015 |
| 14 | −0.002 | −0.010 | −0.014 | −0.017 |
| 15 | −0.005 | −0.010 | −0.015 | −0.018 |
| 16 | −0.007 | −0.009 | −0.015 | −0.019 |
| 17 | −0.010 | −0.008 | −0.017 | −0.022 |
| 18 | −0.013 | −0.007 | −0.019 | −0.024 |
| 19 | −0.018 | −0.004 | −0.023 | −0.029 |
| 20 | −0.017 | 0.000 | −0.022 | −0.028 |
| 21 | −0.019 | 0.004 | −0.026 | −0.032 |
| 22 | −0.020 | 0.009 | −0.028 | −0.035 |
| 23 | −0.017 | 0.013 | −0.028 | −0.035 |
| 24 | −0.013 | 0.015 | −0.025 | −0.032 |
| 25 | −0.008 | 0.016 | −0.023 | −0.030 |
| 26 | −0.004 | 0.015 | −0.020 | −0.025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, Z.; Yao, L.; Xie, D. Mathematical Modeling and Machining of the Internal Double-Arc Spiral Bevel Gear by Finger Milling Cutters for the Nutation Drive Mechanism. Machines 2022, 10, 663. https://doi.org/10.3390/machines10080663
Zhang D, Wang Z, Yao L, Xie D. Mathematical Modeling and Machining of the Internal Double-Arc Spiral Bevel Gear by Finger Milling Cutters for the Nutation Drive Mechanism. Machines. 2022; 10(8):663. https://doi.org/10.3390/machines10080663
Chicago/Turabian StyleZhang, Dawei, Zhenya Wang, Ligang Yao, and Daizhi Xie. 2022. "Mathematical Modeling and Machining of the Internal Double-Arc Spiral Bevel Gear by Finger Milling Cutters for the Nutation Drive Mechanism" Machines 10, no. 8: 663. https://doi.org/10.3390/machines10080663
APA StyleZhang, D., Wang, Z., Yao, L., & Xie, D. (2022). Mathematical Modeling and Machining of the Internal Double-Arc Spiral Bevel Gear by Finger Milling Cutters for the Nutation Drive Mechanism. Machines, 10(8), 663. https://doi.org/10.3390/machines10080663






