Lateral Stability Control of a Tractor-Semitrailer at High Speed
Abstract
:1. Introduction
2. Dynamic Modelling
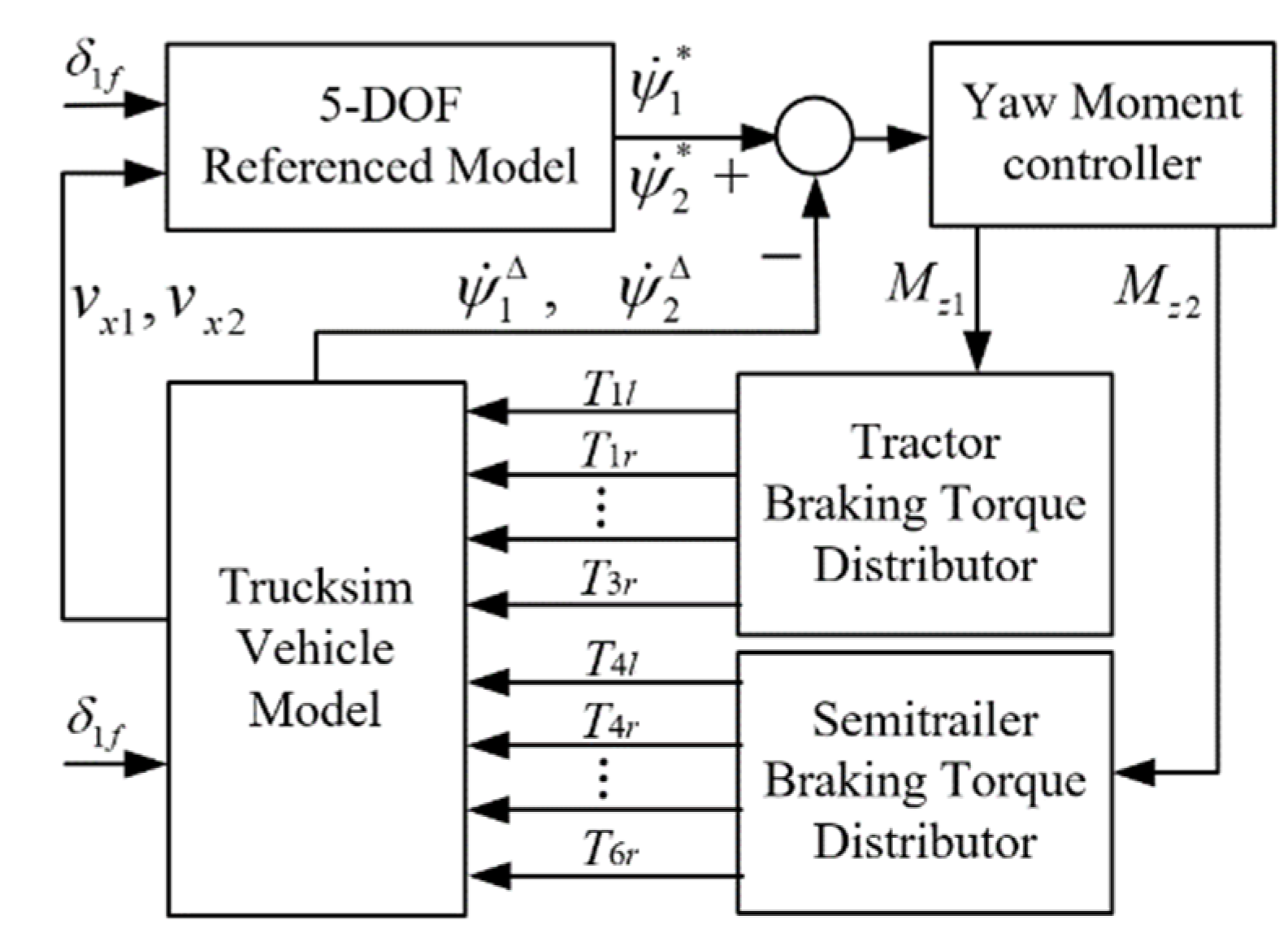
3. Stability Control System Design
3.1. Referenced Responses
3.2. Proportional-Derivative Control
3.3. Model Predictive Control
3.4. Braking Torque Distributor
4. Simulation Results
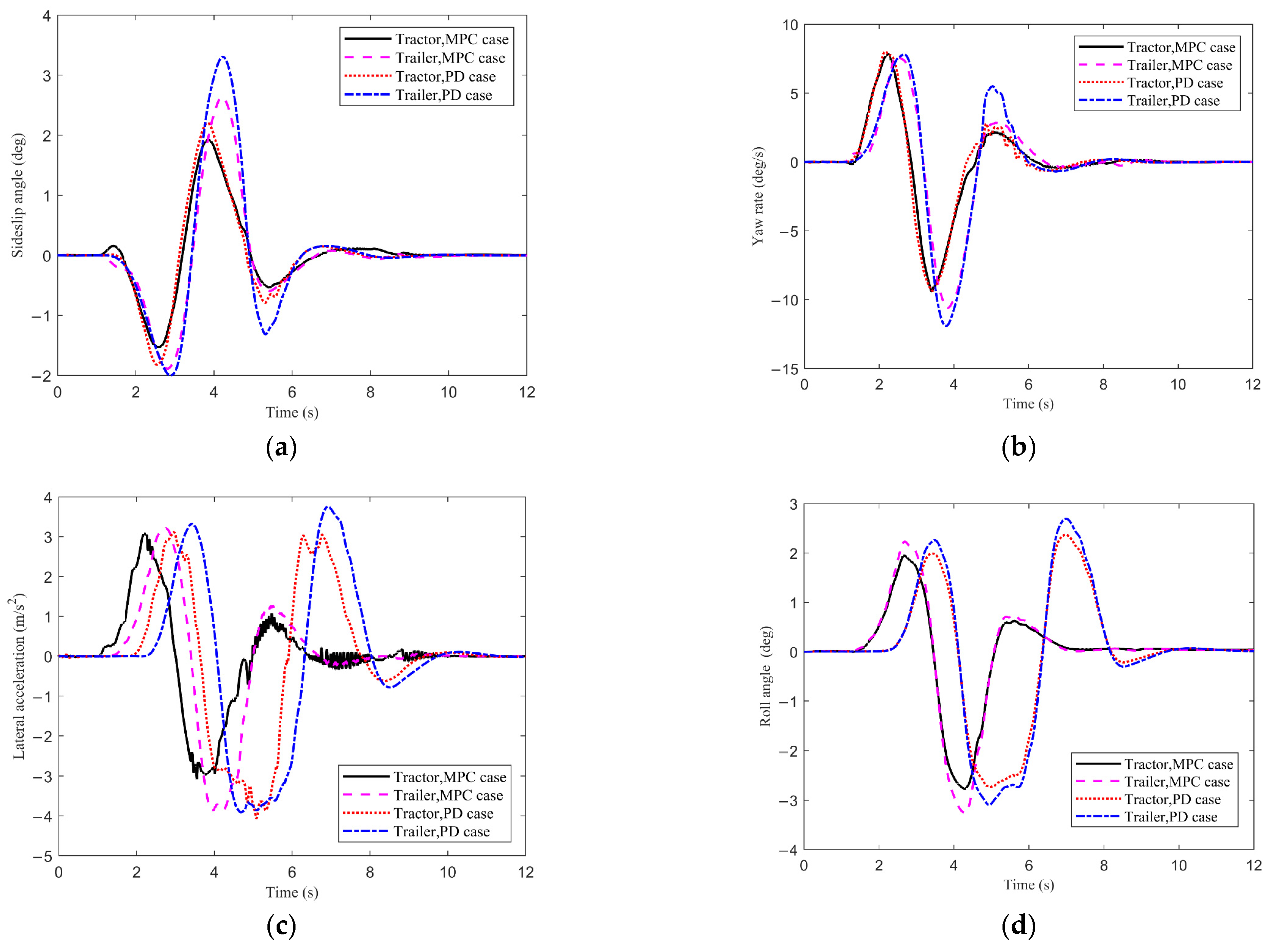
4.1. Single Lane-Change (SLC) Maneuver
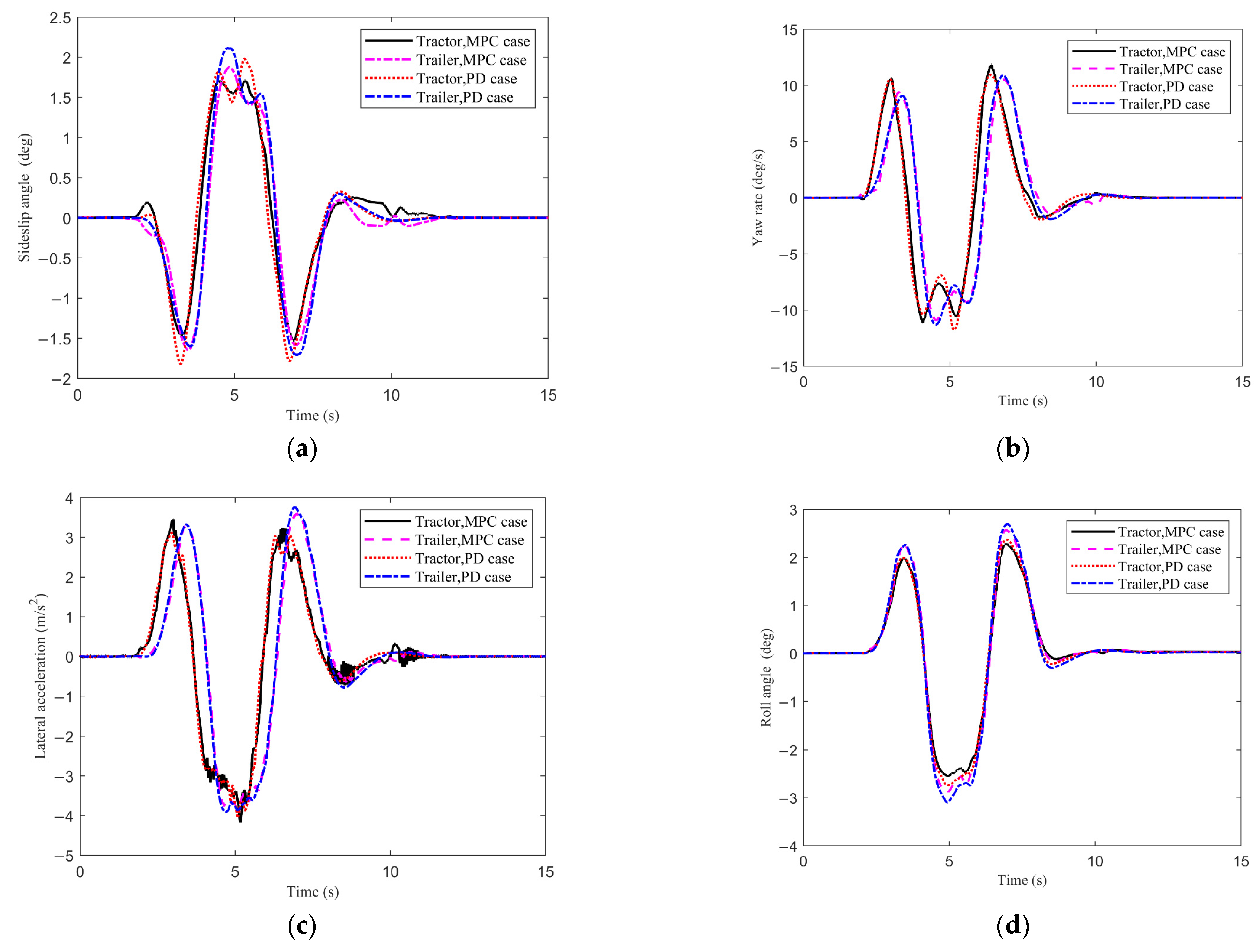
4.2. Double Lane-Change (DLC) Maneuver
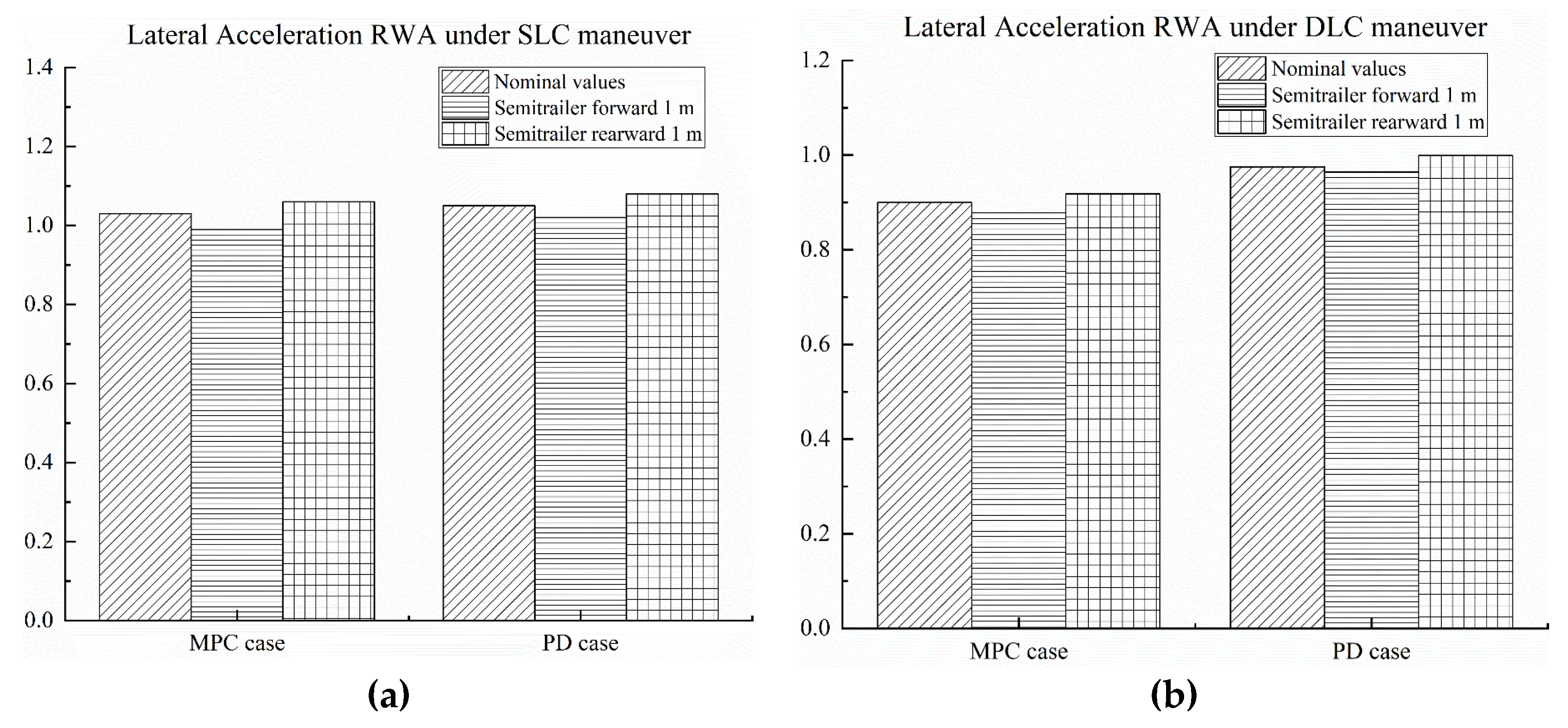
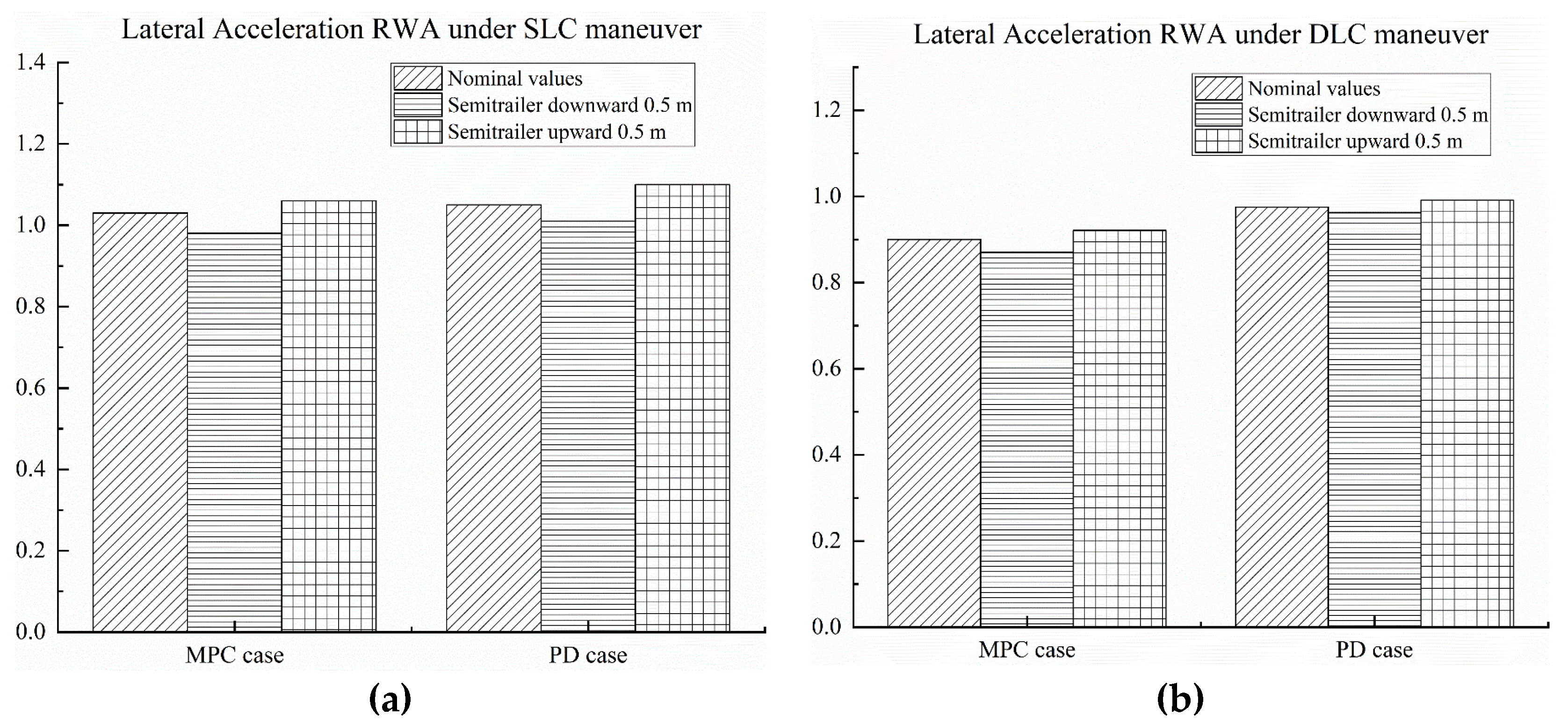
5. Controller Sensitivity to Parameter Uncertainties
6. Conclusions
- (1)
- The proposed high-speed lateral stability control strategy is feasible, which is based on the additional yaw moment caused by differential braking and can ensure the tractor-semitrailer to safely perform the SLC maneuver at 110 km/h and DLC maneuver at 88 km/h.
- (2)
- The yaw moment controller has significant influence on the lateral dynamic performance of the tractor-semitrailer, and the influence under the SLC maneuver is more notable than that under the DLC maneuver. Compared with the PD case, under the SLC maneuver the tractor-semitrailer with MPC has lower peak values of dynamic responses, shorter dynamic responding time, and can reach a new steady state after a shorter time. Under the DLC maneuver, the MPC yaw moment controller can reduce the peak values of the dynamic responses to a certain extent, but it has no obvious advantage over the PD controller in terms of the responding time.
- (3)
- The MPC and PD controllers exhibit good robustness to the considered vehicle parameter uncertainties. The robustness of the two controllers under the DLC maneuver is better than that under the SLC maneuver. Compared with the PD controller, the MPC can make the tractor-semitrailer obtain lower lateral acceleration RWA and better stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Description | Nominal Value |
|---|---|---|
| m1 | Total mass of the tractor | 6360 kg |
| m1s | Sprung mass of the tractor | 4455 kg |
| m2 | Total mass of the semitrailer | 25,910 kg |
| m2s | Sprung mass of the semitrailer | 23,840 kg |
| a1 | Distance between the center of gravity (CG) of the tractor and its front axle | 2.35 m |
| b1 | Distance between the CG of the tractor and its intermediate axle | 1.15 m |
| c1 | Distance between the hitch point and the intermediate axle of the tractor | 0.64 m |
| d1 | Distance between the hitch point and the rear axle of the tractor | 0.64 m |
| a2 | Distance between the hitch point and the CG of the semitrailer | 5.61 m |
| b2 | Distance between the CG of the semitrailer and its front axle | 1.11 m |
| c2 | Distance between the front axle and the intermediate axle of the semitrailer | 1.20 m |
| d2 | Distance between the rear axle and the intermediate axle of the semitrailer | 1.20 m |
| r1 | Rolling radius of the wheels on the front axle of the tractor | 0.52 m |
| r2 | Rolling radius of the wheels on the intermediate and rear axles of the tractor | 0.52 m |
| r3 | Rolling radius of the wheels of the semitrailer | 0.52 m |
| B1 | Track width between the front left and right wheels of the tractor | 2.03 m |
| B2 | Track width between the left and right wheels of the tractor intermediate and rear axles | 1.86 m |
| B3 | Track width between the left and right wheels of the semitrailer | 1.86 m |
| h1s | Height of the CG of the sprung mass for the tractor | 1.18 m |
| h2s | Height of the CG of the sprung mass for the semitrailer | 2.19 m |
| h1r | Height of the roll center of the sprung mass for the tractor | 0.61 m |
| h2r | Height of the roll center of the sprung mass for the semitrailer | 1.02 m |
| hp | Height of the hitch point | 1.10 m |
| I1zz | Yaw moment of inertia of the whole mass of the tractor | 45,075.9 kg m2 |
| I1sxx | Roll moment of inertia of the sprung mass of the tractor | 2283.9 kg m2 |
| I1sxz | Roll–yaw product of inertia of the sprung mass of the tractor | 1626 kg m2 |
| I2zz | Yaw moment of inertia of the whole mass of the semitrailer | 285,516 kg m2 |
| I2sxx | Roll moment of inertia of the sprung mass of the semitrailer | 21,802.3 kg m2 |
| I2sxz | Roll-yaw product of inertia of the sprung mass of the semitrailer | 0 kg m2 |
| K1* | Roll stiffness of the tractor | 1,631,140 N m/rad |
| K2* | Roll stiffness of the semitrailer | 4,265,880 N m/rad |
| K12 | Roll stiffness of the articulation joint between the tractor and semitrailer | 5,729,578 N m/rad |
| C1* | Roll damping of the tractor’s suspension | 48,150 N m s/rad |
| C2* | Roll damping of the semitrailer’s suspension | 45,000 N m s/rad |
| k1f | Tire cornering stiffness of the front axle of the tractor | −231,430 N/rad |
| k1m | Tire cornering stiffness of the intermediate axle of the tractor | −520,000 N/rad |
| k1r | Tire cornering stiffness of the rear axle of the tractor | −520,000 N/rad |
| k2f | Tire cornering stiffness of the front axle of the semitrailer | −553,000 N/rad |
| k2m | Tire cornering stiffness of the intermediate axle of the semitrailer | −553,000 N/rad |
| k2r | Tire cornering stiffness of the rear axle of the semitrailer | −553,000 N/rad |
| F1f/F1m/F1r | Lateral forces subjected by the front, intermediate and rear axles of the tractor | |
| F2f/F2m/F2r | Lateral forces subjected by the front, intermediate and rear axles of the semitrailer | |
| α1f/α1m/α1r | Tire slip angles for the front, intermediate and rear axles of the tractor | |
| α2f/α2m/α2r | Tire slip angles for the front, intermediate and rear axles of the semitrailer | |
| β1/β2 | Sideslip angles at CG of the tractor and semitrailer | |
| Yaw rates of the tractor and semitrailer | ||
| ϕ1/ϕ2 | Roll angles of the sprung mass of the tractor and semitrailer | |
| δ1f | Front wheel steering angle of the tractor | |
| h1cr/h2cr | Distances between the hitch point and roll center of the sprung mass for the tractor and semitrailer | |
| h1sr/h2sr | Distances between the CG and roll center of the sprung mass for the tractor and semitrailer | |
| F1oy/F2oy | Lateral reaction forces at the hitch point for the tractor and semitrailer | |
| vx1/vx2 | Longitudinal velocities of the tractor and semitrailer | |
| v1/v2 | Forward velocities of the tractor and semitrailer |
Appendix B. Relevant Matrices Definition
| , | |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | . |
| , | , |
| , | |
| , | |
| , | , |
| , | |
| , | |
| , | , |
| , | |
| , | , |
| , | , |
| . | |
References
- Xu, X.; Zhang, L.; Jiang, Y.; Chen, N. Active control on path following and lateral stability for truck-trailer combinations. Arab. J. Sci. Eng. 2019, 44, 1365–1377. [Google Scholar] [CrossRef]
- Li, Z.; Yao, J.; Xu, Y. Controlling the vertical shift of an isolated body based on the vibration of nonlinear systems with asymmetric damping forces. Meccanica 2022, 57, 1173–1191. [Google Scholar] [CrossRef]
- Li, Z.; Yao, J.; Xu, Y.; Jia, Y. Analysis of a novel methodology for shifting an isolated body based on nonlinear system vibration. J. Vib. Control 2022. [Google Scholar] [CrossRef]
- Li, B.; Zeng, L. Fractional calculus control of road vehicle lateral stability after a tire blowout. Mechanika 2021, 27, 475–482. [Google Scholar] [CrossRef]
- Zhang, R.; Peng, T.; Lv, Z.; Qiu, Z. Bifurcation and robust control analysis to tractor-semitrailer with interference on rainy slippery road. Future Gener. Comput. Syst. 2020, 107, 126–143. [Google Scholar] [CrossRef]
- Sun, H.; Yang, L.; Chen, Y.; Zhang, X. Controlling tractor-semitrailer vehicles in automated highway systems: Adaptive robust and Lyapunov minimax approach. Asian J. Control 2021, 23, 2642–2656. [Google Scholar] [CrossRef]
- Harun, M.H.; Hudha, K.; Samin, P.M.; Abu Bakar, S.A.; Amer, N.H.; Abd Kadir, Z. A modified odenthal rollover index algorithm for tractor-semitrailer using steering and vehicle speed inputs. Int. J. Heavy Veh. Syst. 2021, 28, 563–584. [Google Scholar] [CrossRef]
- Tian, J.; Ding, J.; Tai, Y.; Chen, N. Hierarchical control of nonlinear active four-wheel-steering vehicles. Energies 2018, 11, 2930. [Google Scholar] [CrossRef] [Green Version]
- Ni, Z.; He, Y. Design and validation of a robust active trailer steering system for multi-trailer articulated heavy vehicles. Veh. Syst. Dyn. 2019, 57, 1545–1571. [Google Scholar] [CrossRef]
- Tian, J.; Zeng, Q.K.; Wang, P.; Wang, X.Q. Active steering control based on preview theory for articulated heavy vehicles. PLoS ONE 2021, 16, e0252098. [Google Scholar] [CrossRef]
- Zong, C.; Zhu, T.; Wang, C.; Liu, H. Multi-objective stability control algorithm of heavy tractor semi-trailer based on differential braking. Chin. J. Mech. Eng. 2012, 25, 88–97. [Google Scholar] [CrossRef]
- Termous, H.; Shraim, H.; Talj, R.; Francis, C.; Charara, A. Coordinated control strategies for active steering, differential braking and active suspension for vehicle stability, handling and safety improvement. Veh. Syst. Dyn. 2018, 57, 1494–1529. [Google Scholar] [CrossRef]
- Tian, J.; Tong, J.; Luo, S. Differential Steering Control of Four-Wheel Independent-Drive Electric Vehicles. Energies 2018, 11, 2892. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Rakheja, S.; Feng, Y. Enhancement of vehicle stability through integration of direct yaw moment and active rear steering. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 830–840. [Google Scholar] [CrossRef]
- Elhemly, M.A.; Fayed, M.A.; Elmaihy, A.A. Tractor-semitrailer jackknifing elimination using semitrailer differential braking technique. Int. J. Heavy Veh. Syst. 2013, 20, 19–34. [Google Scholar] [CrossRef]
- Lee, E. Design Optimization of Active Trailer Differential Braking Systems for Car-Trailer Combinations; University of Ontario Institute of Technology: Oshawa, ON, Canda, 2017. [Google Scholar]
- Cui, Q.; Ding, R.; Wu, X.; Zhou, B. A new strategy for rear-end collision avoidance via autonomous steering and differential braking in highway driving. Veh. Syst. Dyn. 2020, 58, 955–986. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Lin, F.; Xiao, Z. Integrated yaw and rollover control based on differential braking for off-road vehicles with mechanical elastic wheel. J. Cent. South Univ. 2019, 26, 2354–2367. [Google Scholar] [CrossRef]
- Zhang, B.; Zong, C.; Chen, G.; Huang, Y.; Xu, T. A novel integrated stability control based on differential braking and active steering for four-axle trucks. Chin. J. Mech. Eng. 2019, 32, 1–21. [Google Scholar] [CrossRef]
- Bai, Z.; Lu, Y.; Li, Y. Method of improving lateral stability by using additional yaw moment of semi-Trailer. Energies 2020, 13, 6317. [Google Scholar] [CrossRef]
- Li, L.; Lu, Y.; Wang, R.; Chen, J. A three-dimensional dynamics control framework of vehicle lateral stability and rollover prevention via active braking with MPC. IEEE Trans. Ind. Electron. 2017, 64, 3389–3401. [Google Scholar] [CrossRef]
- Ataei, M.; Khajepour, A.; Jeon, S. Model predictive control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. Veh. Syst. Dyn. 2020, 58, 49–73. [Google Scholar] [CrossRef]
- Choi, M.; Choi, S.B. MPC for vehicle lateral stability via differential braking and active front steering considering practical aspects. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 459–469. [Google Scholar] [CrossRef]
- Jalali, M.; Khosravani, S.; Khajepour, A.; Chen, S.K. Model predictive control of vehicle stability using coordinated active steering and differential brakes. Mechatronics 2017, 48, 30–41. [Google Scholar] [CrossRef]
- Abroshan, M.; Hajiloo, R.; Hashemi, E.; Khajepour, A. Model predictive-based tractor-trailer stabilization using differential braking with experimental verification. Veh. Syst. Dyn. 2021, 59, 1190–1213. [Google Scholar] [CrossRef]
- Haung, H.H.; Yedavalli, R.K.; Guenther, D.A. Active roll control for rollover prevention of heavy articulated vehicles with multipe-rollover-index minimization. Veh. Syst. Dyn. 2012, 50, 471–493. [Google Scholar] [CrossRef]
- Jeong, D.; Ko, G.; Choi, S.B. Estimation of sideslip angle and cornering stiffness of an articulated vehicle using a constrained lateral dynamics model. Mechatronics 2022, 85, 102810. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, K.; Chung, K.W. Nonlinear analysis of a closed-loop tractor-semitrailer vehicle system with time delay. Mech. Syst. Signal Pr. 2016, 76–77, 696–711. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Ren, J.; Sun, T. A comparative study of control algorithms for active trailer steering systems of articulated heavy vehicles. In Proceedings of the American Control Conference Fairmont Queen Elizabeth, Montreal, QU, Canada, 27–29 June 2012. [Google Scholar]
- Cheng, Z.; Lu, Z. Research on load disturbance based variable speed PID control and a novel denoising method based effect evaluation of HST for agricultural machinery. Agriculture 2021, 11, 960. [Google Scholar] [CrossRef]
- Tai, Y.; Li, P.; Zheng, Y.; Tian, J. Entropy generation and thermoelastic damping in the in-plane vibration of microring resonators. Entropy 2019, 21, 631. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Huang, S.; Wu, S.; Fu, X. Direct yaw-moment control of electric vehicle with in-wheel motor drive system. Int. J. Auto. Technol. 2020, 21, 1013–1028. [Google Scholar] [CrossRef]
- Yang, X. Optimal reconfiguration control of the yaw stability of the tractor-semitrailer vehicle. Math. Probl. Eng. 2012, 2012, 602502. [Google Scholar] [CrossRef]


| Referenced Yaw Rate | Actual Yaw Rate | Yaw Rate Deviation | Direction of Mz1 | Target Braking Wheel |
|---|---|---|---|---|
| − | − | >0 | + | R1 |
| − | − | <0 | − | L2, L3 |
| + | + | >0 | − | L1 |
| + | + | <0 | + | R2, R3 |
| − | + | \ | − | L1 |
| − | − | \ | + | R1 |
| 0 | + | \ | − | L1 |
| 0 | − | \ | + | R1 |
| − | 0 | \ | − | L2, L3 |
| + | 0 | \ | + | R2, R3 |
| Referenced Yaw Rate | Actual Yaw Rate | Yaw Rate Deviation | Direction of Mz2 | Target Braking Wheel |
|---|---|---|---|---|
| − | − | + | + | R4, R5, R6 |
| − | − | − | − | L4, L5, L6 |
| + | + | + | − | L4, L5, L6 |
| + | + | − | + | R4, R5, R6 |
| − | + | \ | − | L4, L5, L6 |
| − | − | \ | + | R4, R5, R6 |
| 0 | + | \ | − | L4, L5, L6 |
| 0 | − | \ | + | R4, R5, R6 |
| − | 0 | \ | − | L4, L5, L6 |
| + | 0 | \ | + | R4, R5, R6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Xu, X. Lateral Stability Control of a Tractor-Semitrailer at High Speed. Machines 2022, 10, 716. https://doi.org/10.3390/machines10080716
Cai H, Xu X. Lateral Stability Control of a Tractor-Semitrailer at High Speed. Machines. 2022; 10(8):716. https://doi.org/10.3390/machines10080716
Chicago/Turabian StyleCai, Haohao, and Xiaomei Xu. 2022. "Lateral Stability Control of a Tractor-Semitrailer at High Speed" Machines 10, no. 8: 716. https://doi.org/10.3390/machines10080716
APA StyleCai, H., & Xu, X. (2022). Lateral Stability Control of a Tractor-Semitrailer at High Speed. Machines, 10(8), 716. https://doi.org/10.3390/machines10080716






