Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power
Abstract
:1. Introduction
2. Adaptive Control Principle Based on Process–Machine Interaction
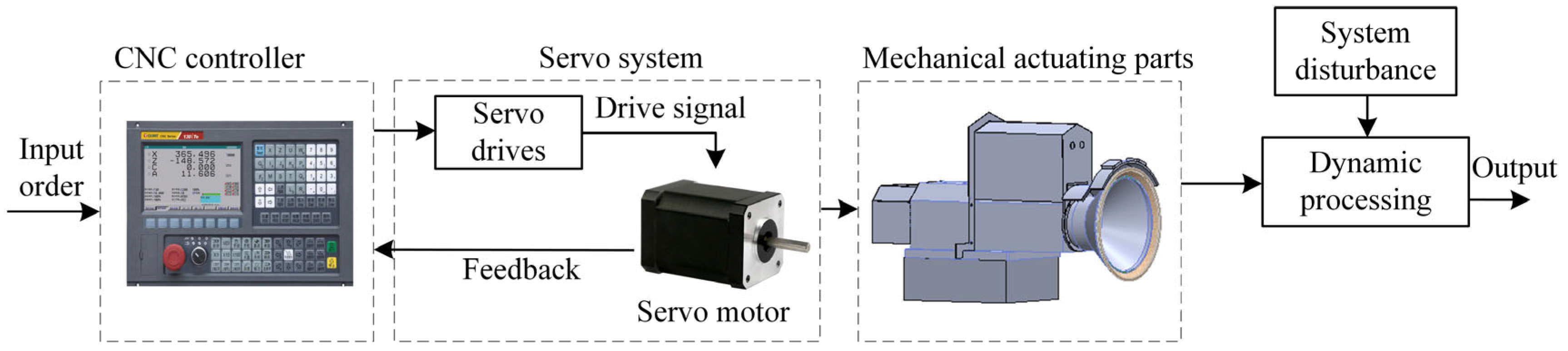
2.1. Adaptive Control Principle
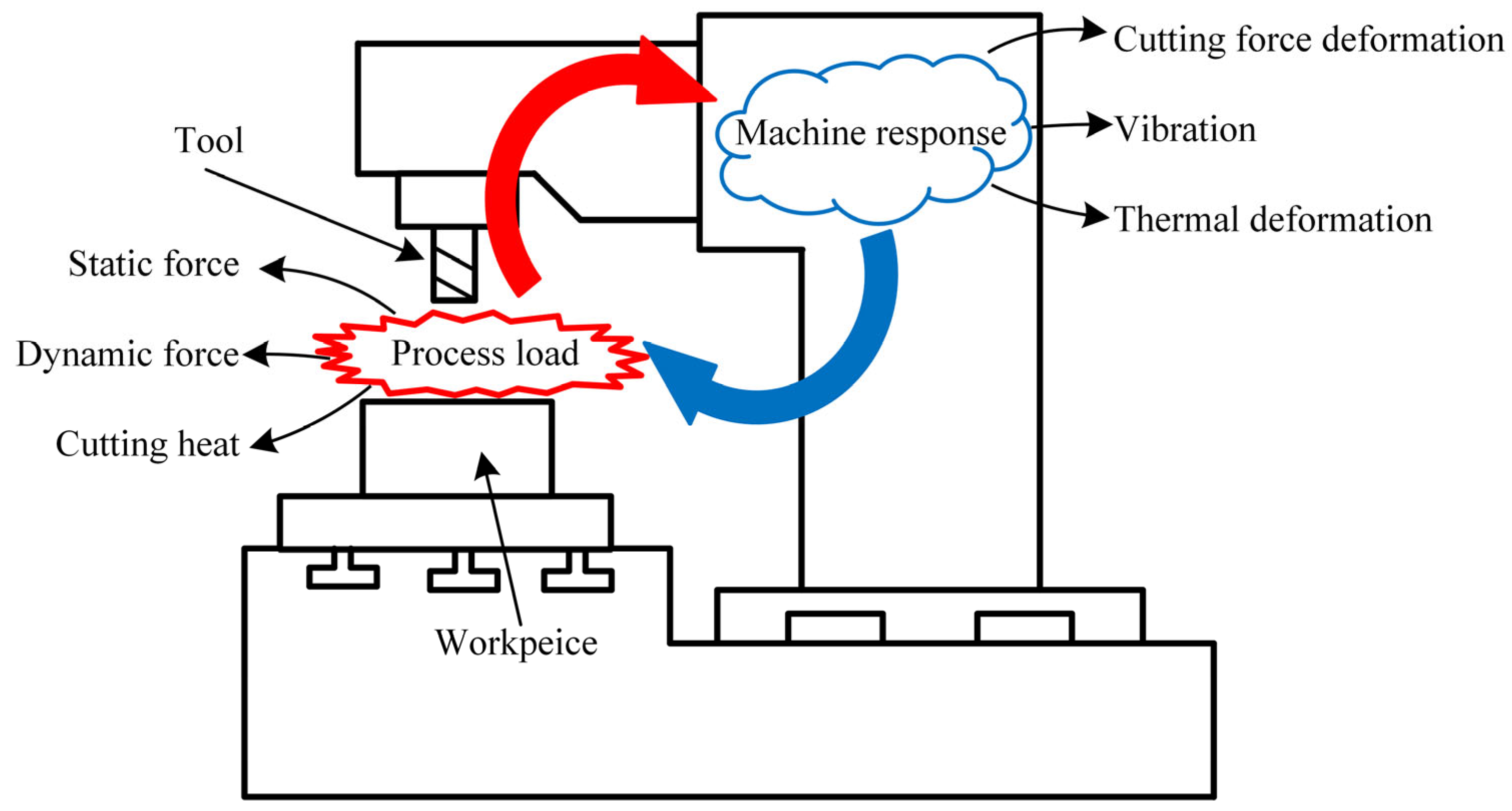
2.2. Principle of Process–Machine Interaction
3. Grinding Force Monitoring Method and Experimental Verification
3.1. Grinding Force Monitoring Method
3.2. Experimental Verification
4. Grinding Force Control Method and Experimental Verification
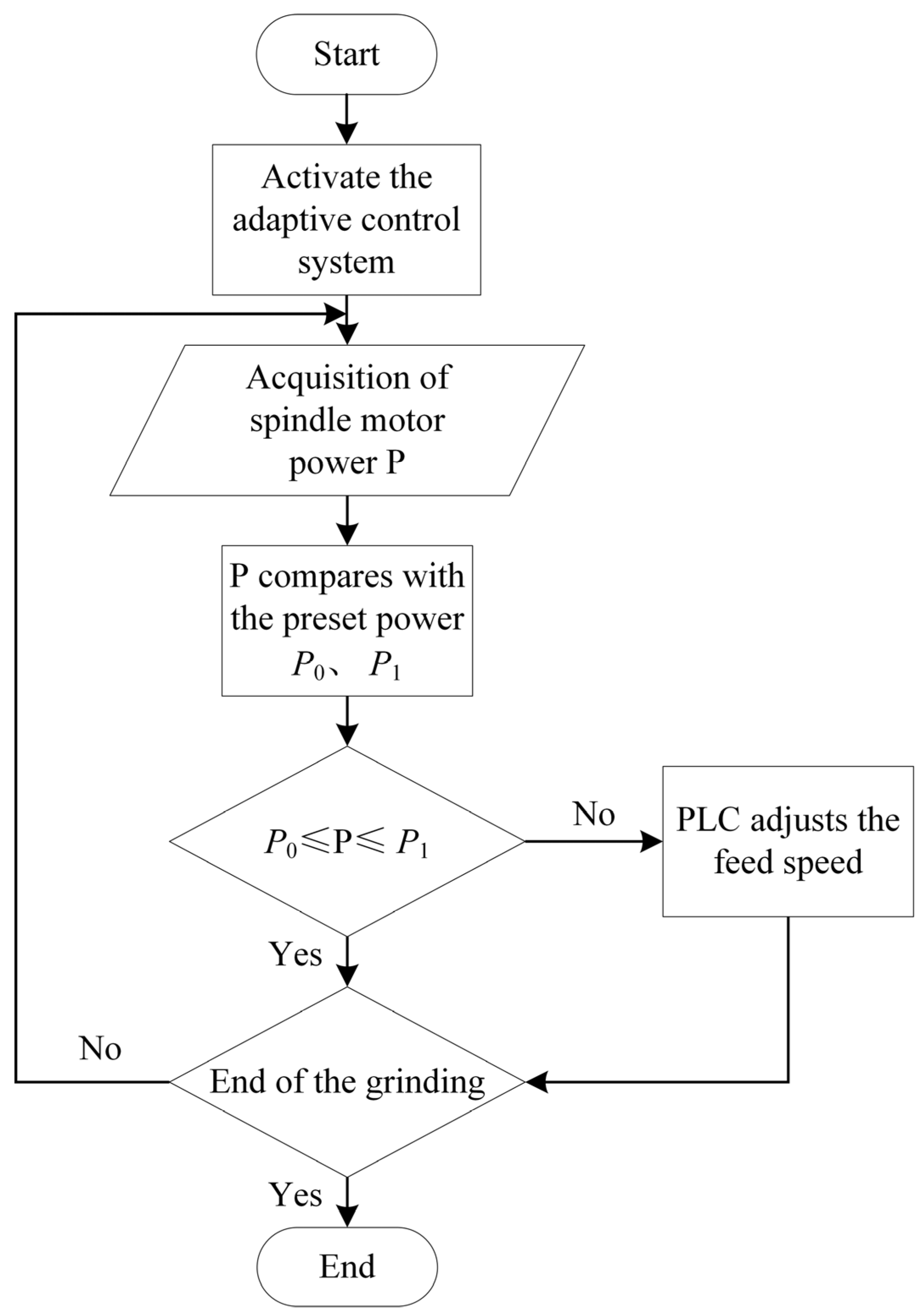
4.1. Feed Rate Compensation
4.2. Experimental Conditions
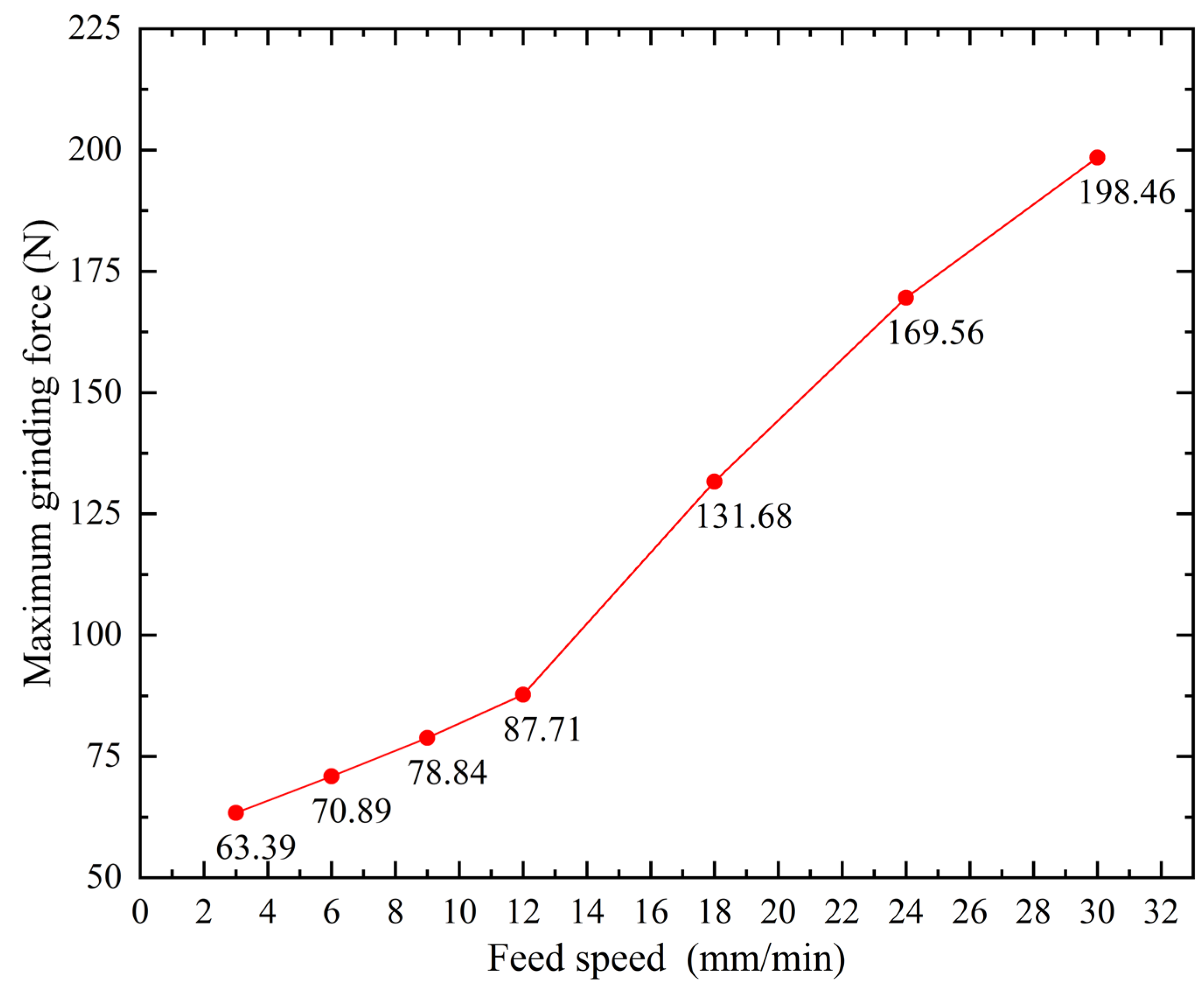
4.3. Experimental Results
5. Conclusions
- (1)
- The indirect monitoring method of grinding force based on spindle motor power is proposed, and the monitoring effect is good, with a maximum error of 9.85% and a minimum error of 0.96%;
- (2)
- Considering the process–machine interaction, an adaptive control approach for the grinding force is proposed, along with the controller’s compensating rules. The adaptive control system of grinding force substantially improves the grinding process’s efficiency;
- (3)
- Only a general explanation of the machine tool process interaction is provided in this work. Further research is required to completely comprehend the impact of the machine tool process interaction on the control effect;
- (4)
- A disadvantage of this work is that the adaptive control experiment is only conducted at 2000 r/min and 0.5mm grinding depth. Due to the fact that the effects of the machine tool process interaction on the control effect may vary under different processing conditions, it will be necessary to conduct more research that takes these variables into account.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, V.H.; Shin, S.G.; Ko, S.L. Development of CAM software to design and grind indexable inserts. Int. J. Precis. Eng. Manuf. 2015, 16, 869–876. [Google Scholar] [CrossRef]
- Zhan, Y.; Tian, X.; Xu, Y.; Jia, M. Study on the specific grinding energy of cemented carbide (YG8) grinding with a vitrified diamond wheel in high speed regime. Int. J. Abrasive Technol. 2019, 9, 286. [Google Scholar] [CrossRef]
- Cai, S.; Yao, B.; Zheng, Q.; Cai, Z.; He, Z. Dynamic grinding force model for carbide insert peripheral grinding based on grain element method. J. Manuf. Process. 2020, 58, 1200–1210. [Google Scholar] [CrossRef]
- Dai, S.; Zhao, Y.; Ji, W.; Mu, J.; Hu, F. Constant force control for aluminum wheel hub grinding based on ESO + backstepping. Ind. Robot 2022, 49, 824–834. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, T.; Tan, Y.; Lu, J. An adaptive grinding method for precision-cast blades with geometric deviation. Int. J. Adv. Des. Manuf. Technol. 2020, 108, 7–8. [Google Scholar] [CrossRef]
- Feng, G.; Wang, T.; Huang, Q.; Guo, W.; Liu, R. Experimental study on ultra-precision grinding characteristics of WC-Ni hard metals. Proc. Inst. Mech. Eng. Part B 2019, 234, 600–609. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Z.; Yu, Y.; Xu, X. Evaluation of Double-Sided Planetary Grinding Using Diamond Wheels for Sapphire Substrates. Crystals 2018, 8, 262. [Google Scholar] [CrossRef]
- Yang, F.; Sun, Y.; Wang, Y.; Mo, H.; Zhu, L.; Yuan, H.; Lu, B.; Zhang, G.; Zuo, D. Modeling and Experimental Verification of Surface Roughness for Grinding Monocrystalline Silicon Lens. Adv. Theory Simul. 2022, 5, 2100422. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.; Lv, L.; She, S.; Liu, W.; Luo, C. Experimental Analysis of Process Parameter Effects on Vibrations in the High-Speed Grinding of a Camshaft. Stroj. Vestn.—J. Mech. Eng. 2020, 66, 175–183. [Google Scholar] [CrossRef]
- Wu, C.; Guo, W.; Wu, Z.; Wang, Q.; Li, B. Ductility-oriented high-speed grinding of silicon carbide and process design for quality and damage control with higher efficiency. Int. J. Adv. Manuf. Technol. 2019, 105, 2771–2784. [Google Scholar] [CrossRef]
- Maeng, S.; Lee, P.A.; Bo, H.K.; Min, S. An analytical model for grinding force prediction in ultra-precision machining of WC with PCD micro grinding tool. Int. J. Precis. Eng. Manuf.-Green Technol. 2020, 7, 1031–1045. [Google Scholar] [CrossRef]
- Junejo, F. The application of artificial intelligence in grinding operation using sensor fusion. Int. J. Geomate 2017, 12, 11–18. [Google Scholar] [CrossRef]
- Jiang, C.; Li, H.; Mai, Y.; Guo, D. Material removal monitoring in precision cylindrical plunge grinding using acoustic emission signal. Proc. Inst. Mech. Eng. Part C 2014, 228, 715–722. [Google Scholar] [CrossRef]
- Teti, R.; Jemielniak, K.; O’Donnell, G.; Dornfeld, D. Advanced monitoring of machining operations. CIRP Ann. 2010, 59, 717–739. [Google Scholar] [CrossRef]
- Liu, C.S.; Li, Y.A. Evaluation of grinding wheel loading phenomena by using acoustic emission signals. Int. J. Adv. Manuf. Technol. 2018, 99, 1109–1117. [Google Scholar] [CrossRef]
- Chi, Y.; Li, H.; Chen, X. In-process monitoring and analysis of bearing outer race way grinding based on the power signal. Proc. Inst. Mech. Eng. Part B 2016, 231, 2622–2635. [Google Scholar] [CrossRef]
- Ma, Y.C.; Yang, J.G. Multi-Sensor Intelligent Monitoring of High-Speed Grinding for Brittle and Hard Materials. Appl. Mech. Mater. 2015, 741, 309–314. [Google Scholar] [CrossRef]
- Lee, C.H.; Jwo, J.S.; Hsieh, H.Y.; Lin, C.S. An intelligent system for grinding wheel condition monitoring based on machining sound and deep learning. IEEE Access 2020, 8, 58279–58289. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, M.; Li, J.; Ming, W.Y.; Shao, X.Y.; Huang, Y. Multi-objective optimization for surface grinding process using a hybrid particle swarm optimization algorithm. Int. J. Adv. Des. Manuf. Technol. 2014, 71, 1861–1872. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Yao, B.; Zhang, X.L.; Yao, B.S. Accuracy analysis of grinding indexable inserts related to the centrifugal force of high speed abrasive wheel. Adv. Mater. Res. 2012, 422, 606–609. [Google Scholar] [CrossRef]
- Zhang, X.-L.; Yao, B.; Chen, B.-Q.; Sun, W.-F.; Wang, M.-M.; Luo, Q. Thermo-mechanical properties of bowl-shaped grinding wheel and machining error compensation for grinding indexable inserts. J. Cent. South Univ. 2015, 22, 3830–3836. [Google Scholar] [CrossRef]
- Fountas, N.A.; Vaxevanidis, N.M. Optimization of Abrasive Flow Nano-Finishing Processes by Adopting Artificial Viral Intelligence. J. Manuf. Mater. Process. 2021, 5, 22. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Wang, H.; Feng, W.; Wang, Y.; Liu, S. Five-axis flank milling stability prediction by considering the tool-workpiece interactions and speed effect. Int. J. Adv. Des. Manuf. Technol. 2020, 108, 2037–2060. [Google Scholar] [CrossRef]
- Aurich, J.C.; Biermann, D.; Blum, H.; Brecher, C.; Carstensen, C.; Denkena, B.; Klocke, F.; Kröger, M.; Steinmann, P.; Weinert, K. Modelling and simulation of process: Machine interaction in grinding. Prod. Eng. 2009, 3, 111–120. [Google Scholar] [CrossRef]
- Brecher, C.; Esser, M.; Witt, S. Interaction of manufacturing process and machine tool. CIRP Ann. 2009, 58, 588–607. [Google Scholar] [CrossRef]
- Aurich, J.C.; Kirsch, B. Kinematic simulation of high-performance grinding for analysis of chip parameters of single grains. CIRP J. Maunf. Sci. Technol. 2012, 5, 164–174. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.; Zhang, J.; Li, S.; Zhou, H. Study on grinding force of Si3N4 ceramics in random rotation grinding with truncated polyhedral grains. Int. J. Adv. Manuf. Technol. 2021, 115, 3139–3148. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, F.; Luo, X.; Guo, X.; Cai, Y.; Chang, W.; Sun, J. A new grinding force model for micro grinding RB-SiC ceramic with grinding wheel topography as an input. Micromachines 2018, 9, 368. [Google Scholar] [CrossRef]
- Manea, H.; Cheng, X.; Ling, S.; Zheng, G.; Gao, X. Model for predicting the micro-grinding force of k9 glass based on material removal mechanisms. Micromachines 2020, 11, 969. [Google Scholar] [CrossRef]
- Li, D.; Xu, M.; Wei, C.; Hu, D.; Xu, L. A dynamic threshold-based fuzzy adaptive control algorithm for hard sphere grinding. Int. J. Adv. Manuf. Technol. 2012, 60, 923–932. [Google Scholar] [CrossRef]
- Hecker, R.L.; Liang, S.Y.; Wu, X.J.; Xia, P.; Jin, D.G.W. Grinding force and power modeling based on chip thickness analysis. Int. J. Adv. Manuf. Technol. 2007, 33, 449–459. [Google Scholar] [CrossRef]
- Mao, X.Y.; Liu, H.Q.; Bin, L.I. Time-frequency analysis and detecting method research on milling force token signal in spindle current signal. Sci. China 2009, 52, 2810–2813. [Google Scholar] [CrossRef]
- Chen, T.; Tian, X. Dimensional error prediction and its intelligent soft pre-compensation in batch manufacture. Int. J. Adv. Manuf. Technol. 2015, 77, 281–288. [Google Scholar] [CrossRef]







| Serial Number | Feed Speed (mm/min) | Grinding Depth (mm) |
|---|---|---|
| 1 | 2.4 | 0.08 |
| 2 | 12 | 0.05 |
| 3 | 2.4 | 0.4 |
| 4 | 6.0 | 0.2 |
| 5 | 2.4 | 0.2 |
| 6 | 12.0 | 0.4 |
| 7 | 18.0 | 0.4 |
| 8 | 24.0 | 0.4 |
| 9 | 30.0 | 0.4 |
| Linear Speed of Grinding Wheel (m/s) | Grinding Depth (mm) | Feed Speed (mm/min) |
|---|---|---|
| 50 | 0.4 | 3, 6, 9, 12, 18, 24, 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Zhang, X.; Feng, M.; Li, S.; Pan, X.; Feng, W. Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power. Machines 2022, 10, 802. https://doi.org/10.3390/machines10090802
Chen P, Zhang X, Feng M, Li S, Pan X, Feng W. Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power. Machines. 2022; 10(9):802. https://doi.org/10.3390/machines10090802
Chicago/Turabian StyleChen, Peng, Xianglei Zhang, Ming Feng, Sisi Li, Xiaoming Pan, and Wei Feng. 2022. "Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power" Machines 10, no. 9: 802. https://doi.org/10.3390/machines10090802
APA StyleChen, P., Zhang, X., Feng, M., Li, S., Pan, X., & Feng, W. (2022). Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power. Machines, 10(9), 802. https://doi.org/10.3390/machines10090802








