Modification and Validation of 1D Loss Models for the Off-Design Performance Prediction of Centrifugal Compressors with Splitter Blades
Abstract
:1. Introduction
2. Methodologies
2.1. Aerodynamic Calculation Method Using the 1D Single-Zone Model
2.2. Loss Models Used in the Single-Zone Model
2.2.1. Loss Models for Impellers
- Incidence loss model
- 2.
- Skin friction loss model
- 3.
- Blade-loading loss model
- 4.
- Tip clearance loss model
- 5.
- Mixing loss model
- 6.
- Viscosity loss
- 7.
- Shock loss
- 8.
- Disk friction loss
- 9.
- Recirculation loss model
- 10.
- Leakage loss model
2.2.2. Loss Models for Stationary Components
2.3. Multi-Objective Optimization Methodology
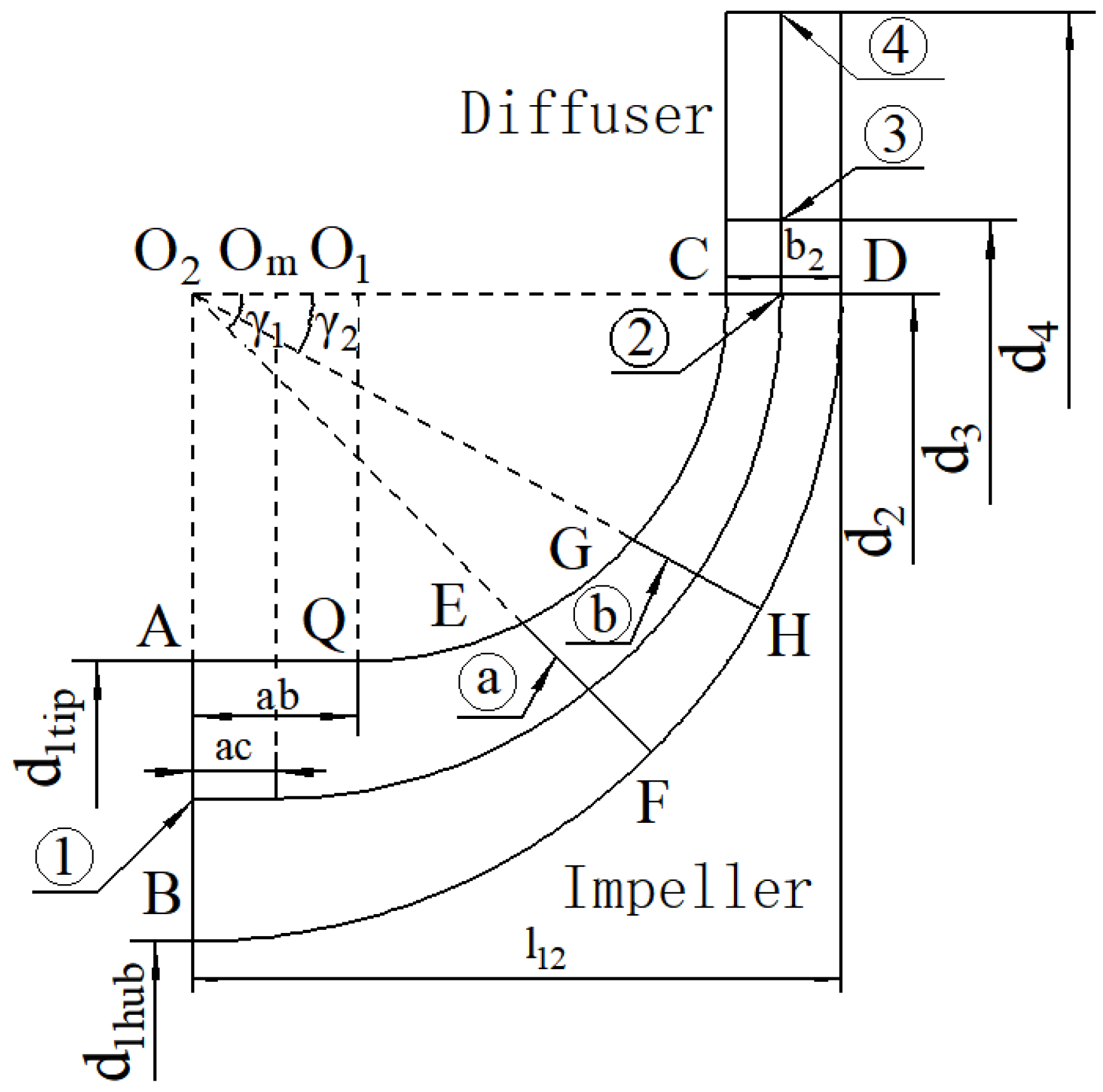
3. Description of Geometric Parameters and 1D Aerodynamic Calculation Procedure for Centrifugal Compressors with Splitter Blades
3.1. Calculation of Geometric Parameters
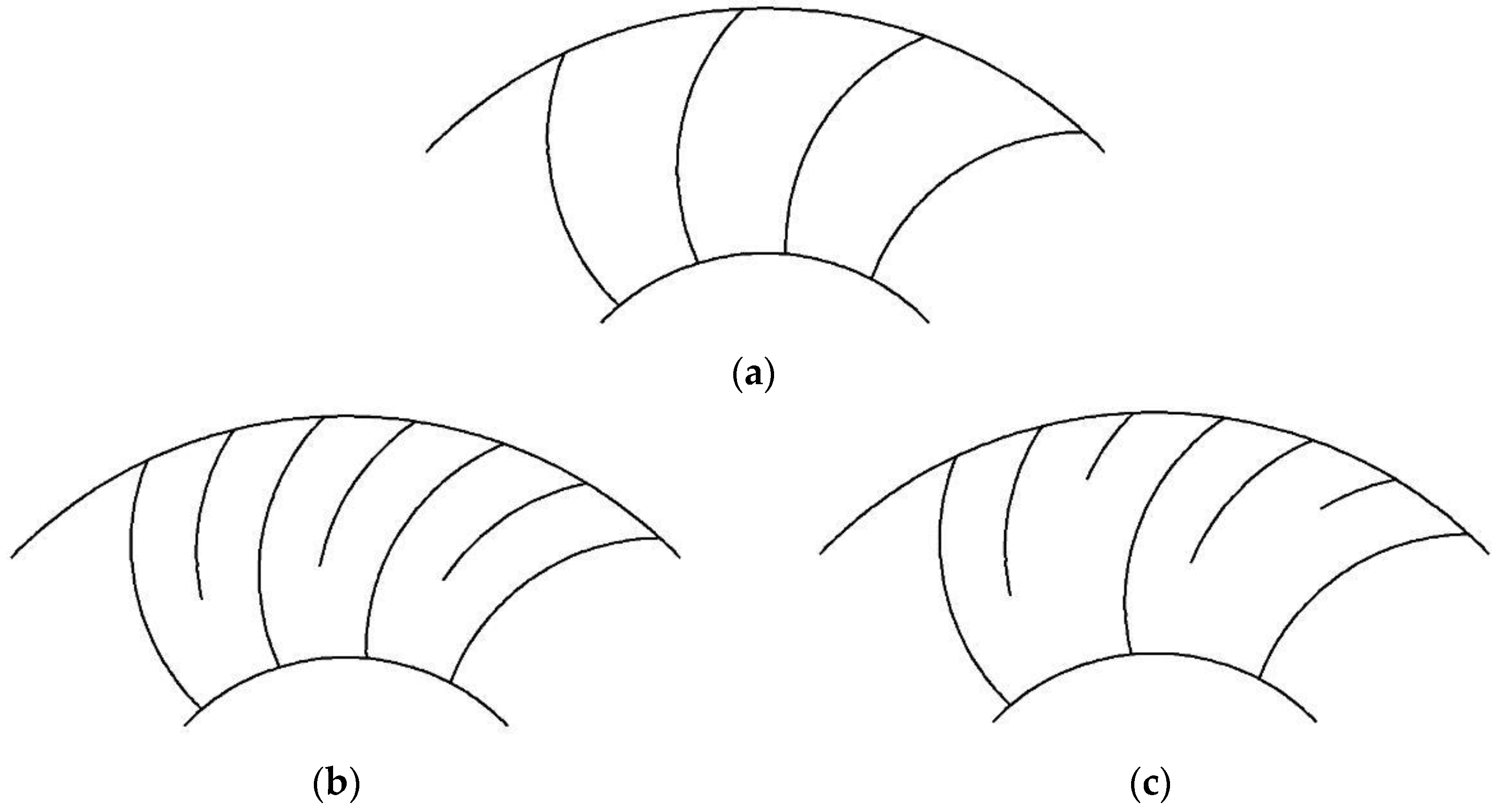
- (a)
- Impeller without splitter blades, Zi2 = Zi1;
- (b)
- Impeller with one row of splitter blades, Zi2 = 2 Zi1;
- (c)
- Impeller with two rows of splitter blades, Zi2 = 3 Zi1.
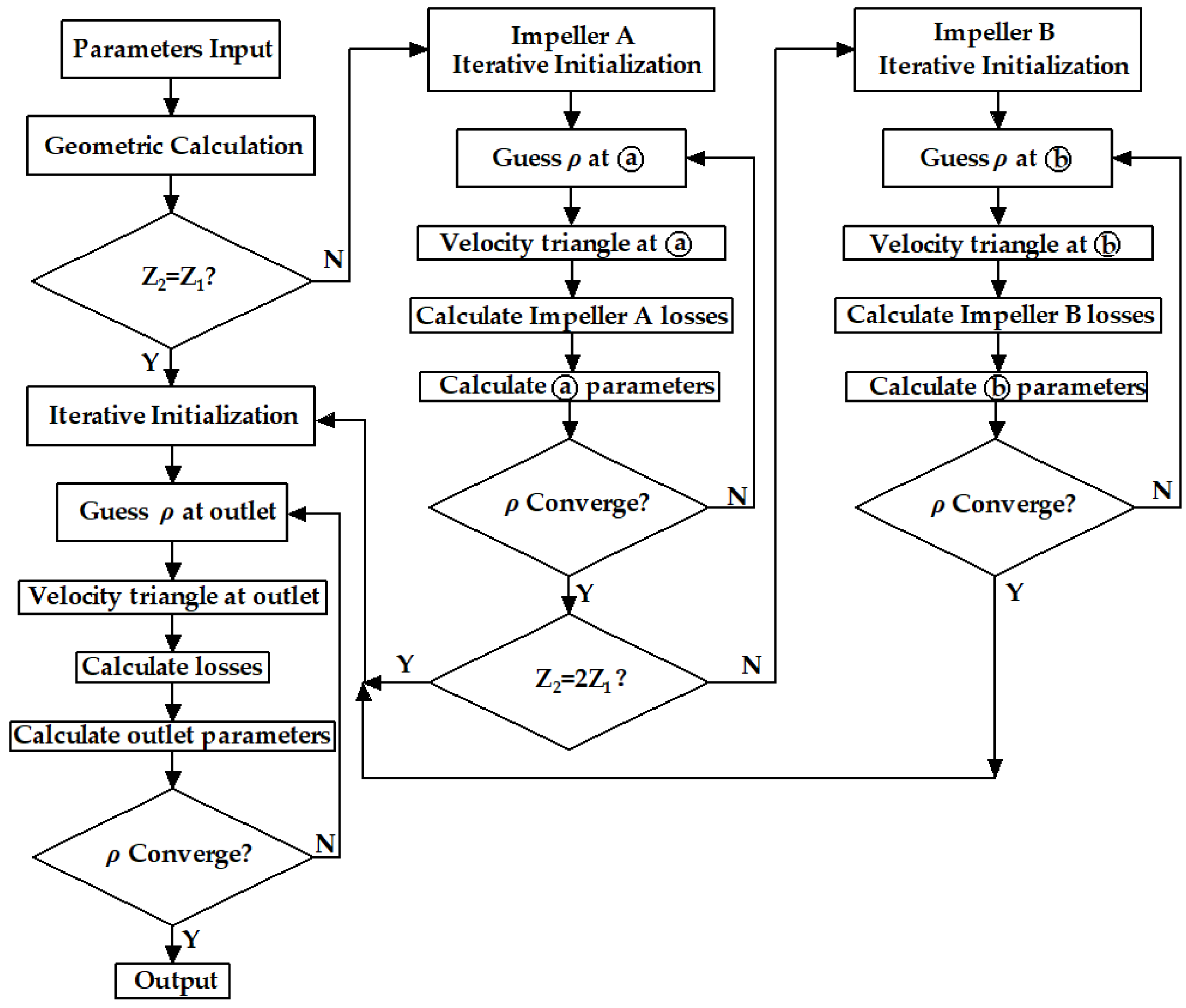
3.2. One-Dimensional Aerodynamic Calculation Procedure for Impellers with Splitter Blades
4. The Impellers Investigated
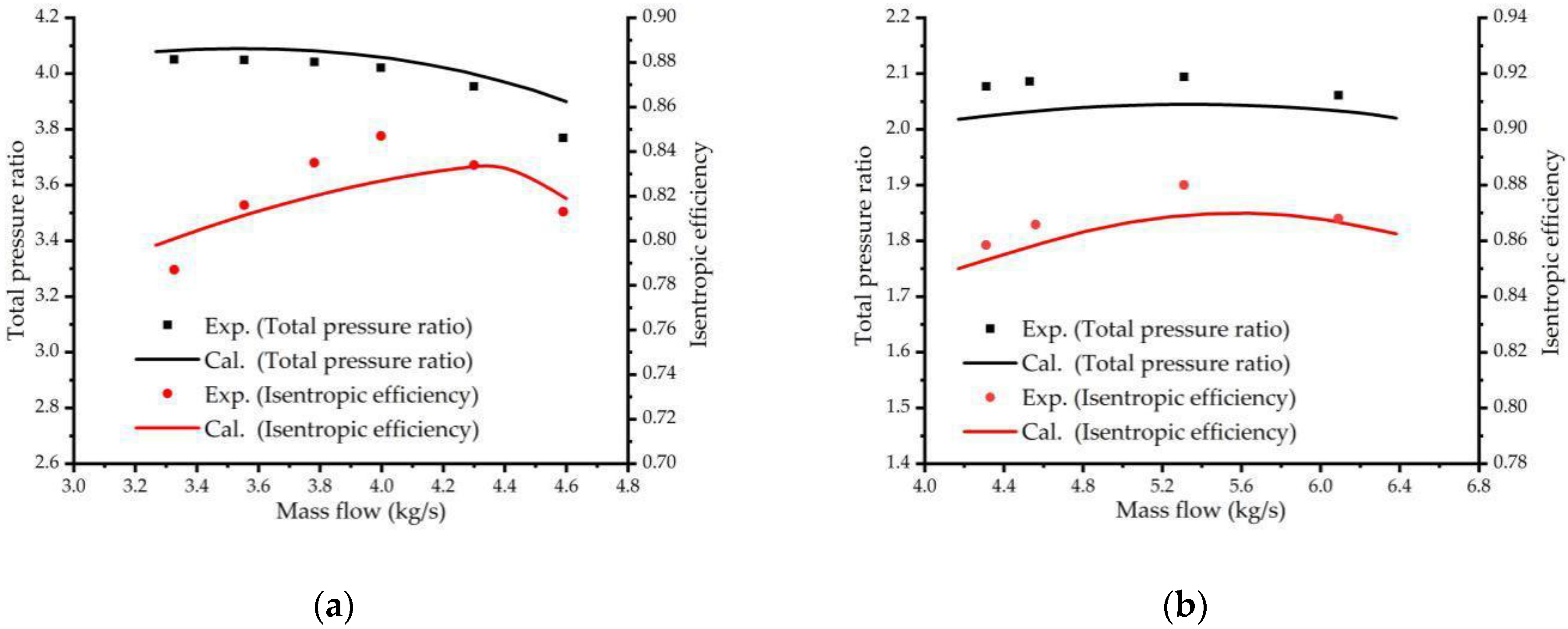
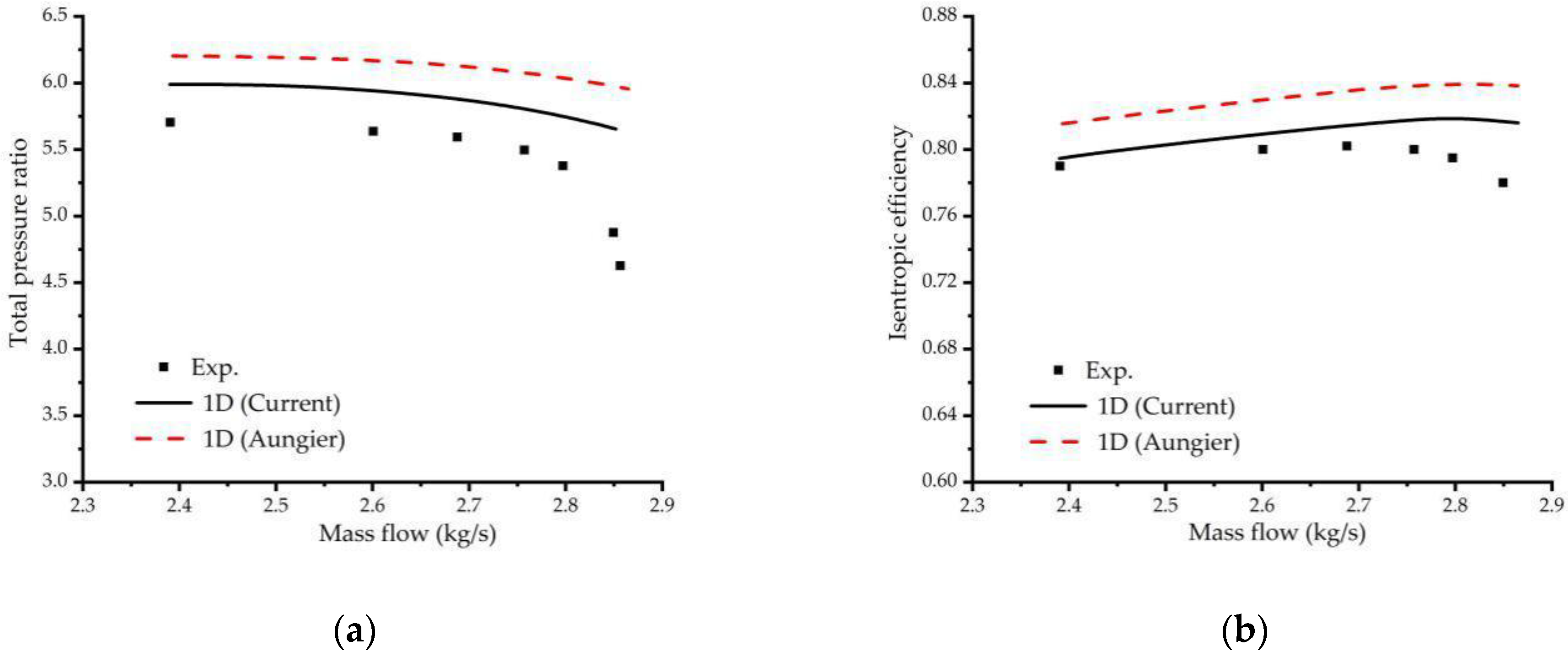
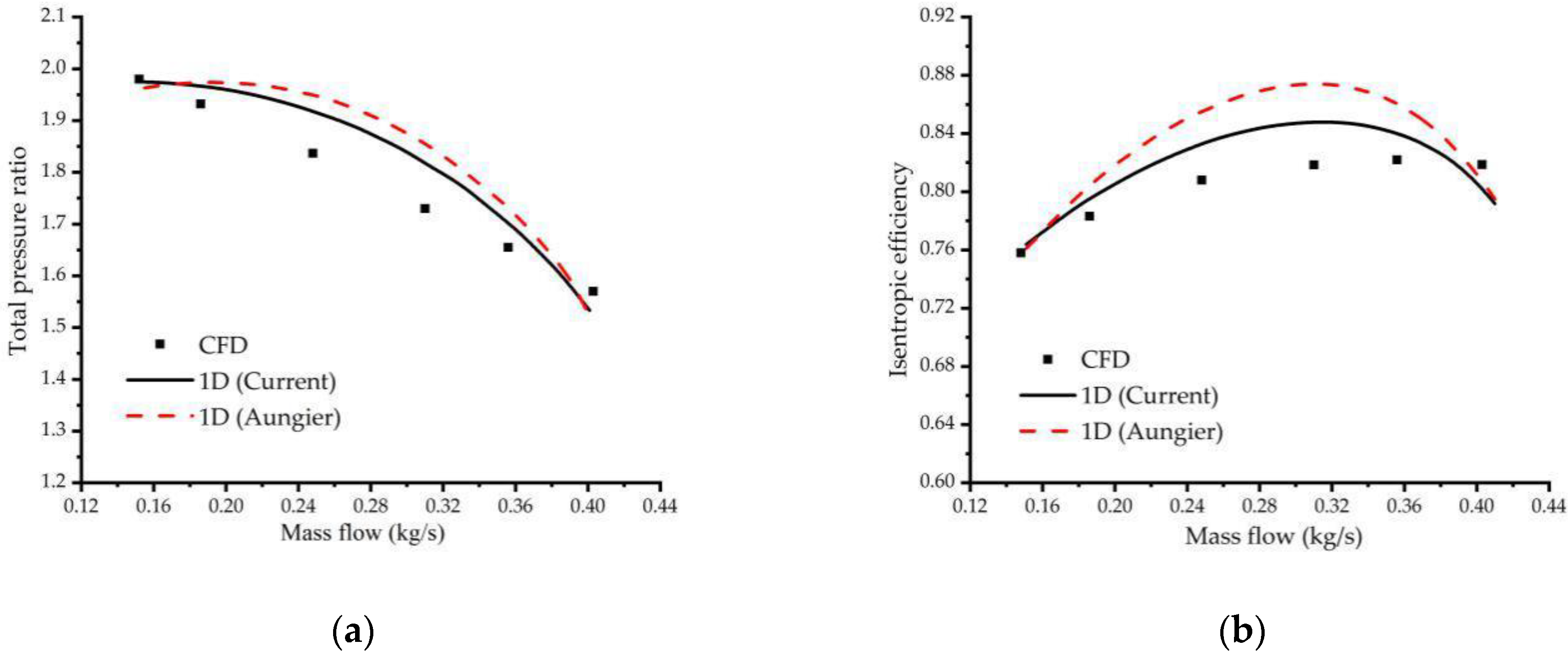
5. Validation of 1D Calculation Method
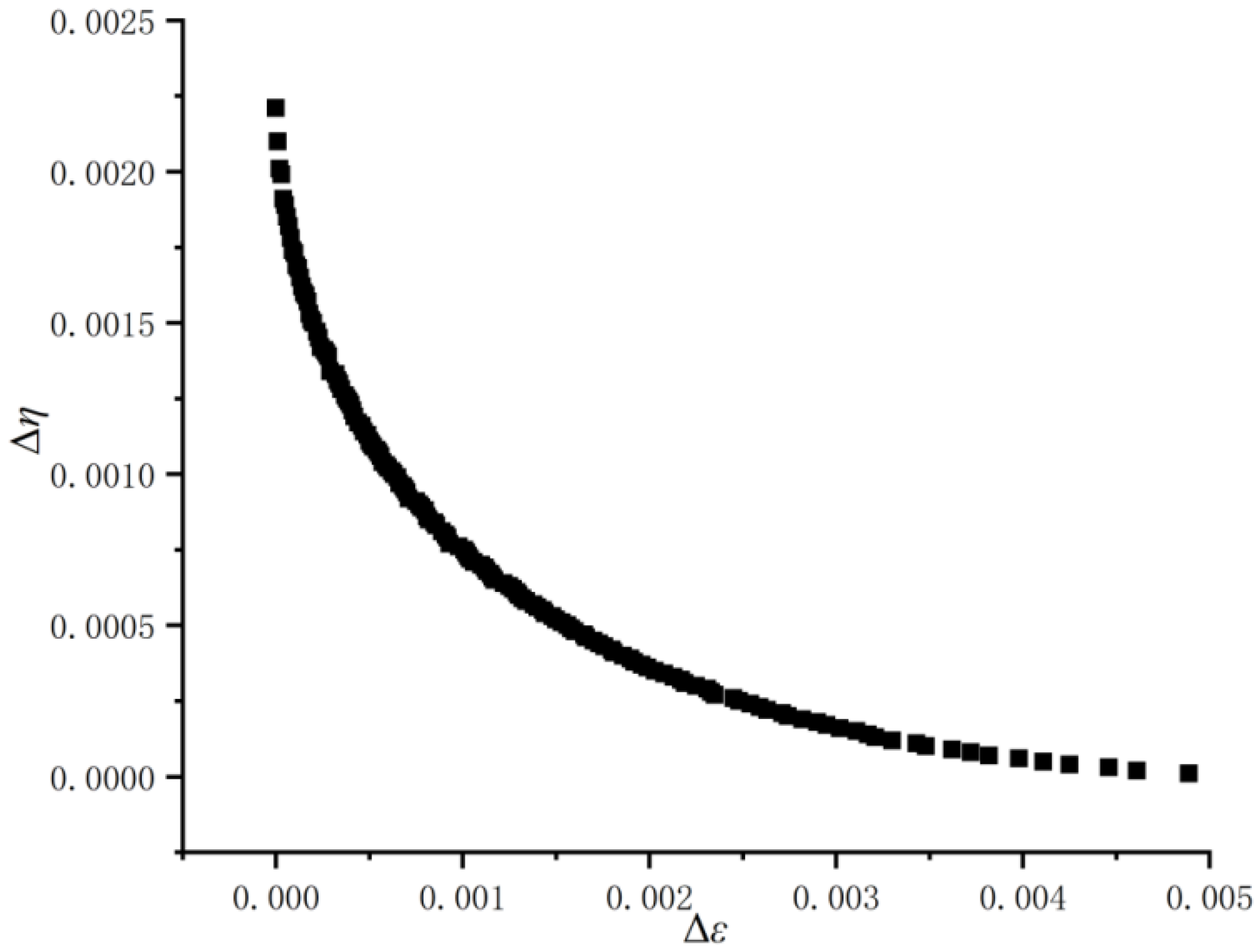
6. Modifications of Coefficients in Loss Models
7. Optimization Results
7.1. Results for the First Group of Impellers
7.2. Comparisons with Other Calculation Methods
7.3. Results for the Second Group of Impellers
7.4. Results for the Third Group of Impellers
7.5. Value Changes for the Coefficients Involved in the Loss Models
8. Conclusions
- (1)
- To reduce the geometric parameters required for calculation, a general meridional channel of the computational domain is established and the calculation method of the leading edge position of the splitter blade is offered. Based on the simplified computational domain, all the geometric parameters required for 1D performance calculations can be obtained.
- (2)
- Based on the geometric characteristics of impeller with splitter blades, a stepping calculation method is proposed for the impellers with different rows of splitter blades. Along the meridional channel, each section with the same number of blades is treated as an independent impeller. Each sub-impeller can be calculated in turn. Comparisons between predicted aerodynamic performances with experimental data or CFD results for different impellers have demonstrated that the current 1D calculation method is superior to the existing simplified calculation methods.
- (3)
- The most optimal loss model set, which is applicable to different types of impellers with different rows, is gained. Coefficients involved in loss models are optimized by using the multi-objective genetic algorithm (NSGA-II). The modified loss models greatly improve the prediction accuracy of the single-zone model. The coefficient optimization method provides a useful tool for improvement in accuracy of loss models.
- (4)
- In order to further improve the generality of the single-zone model, more impellers with splitter blades will be used for verification in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | impeller blade width at outlet |
| d | impeller outlet diameter |
| l | axial distance |
| sp | relative distance of the splitter blade |
| γ | angle of the splitter blade leading edge |
| T | Temperature |
| u | circumferential velocity |
| Cp | specific heat |
| ρ | Density |
| C | absolute velocity |
| Cr | radial component of the absolute velocity |
| β | blade angle |
| W | power/relative velocity |
| Cf | skin friction coefficient |
| dg | average hydraulic diameter |
| Df | diffusion factor |
| τ | tip clearance size |
| k | adiabatic index |
| kg | blockage ratio |
| kd | blade thickness coefficient |
| Re | Reynolds number |
| P | pressure |
| M | Mach number |
| mass flow rate | |
| ns | specific speed |
| V | volume |
| Z | number of blades |
| ε | total pressure ratio |
| η | isentropic efficiency |
| n | rotational speed |
| Subscripts | |
| FB | full blades |
| SB | splitter blades |
| i | impeller |
| 1 | inlet of impeller |
| 2 | outlet of impeller |
| cr | critical |
| r | radial direction |
| u | tangential direction |
| m | meridional direction |
| opt | optimal |
References
- Japikse, D. Assessment of Single-and Two-Zone Modeling of Centrifugal Compressors, Studies in Component Performance: Part 3; American Society of Mechanical Engineers: New York, NY, USA, 1985; Volume 79382, p. V001T003A023. [Google Scholar]
- Aungier, R.H.X. Mean streamline aerodynamic performance analysis of centrifugal compressors. J. Turbomach. 1995, 117, 360–366. [Google Scholar] [CrossRef]
- Cicciotti, M.; Martinez-Botas, R.; Gozalbo, R.; Geist, S.; Schild, A.; Thornhill, N.F.; Khars, O.; Reiser, W. Assessment of meanline models for centrifugal compressors in the process plant industry. In Proceedings of the 5th International Symposium on Fluid Machinery and Fluids Engineering (ISFMFE), Jeju, Republic of Korea, 24–27 October 2012. [Google Scholar]
- Cicciotti, M.; Martinez-Botas, R.F.; Romagnoli, A.; Thornhill, N.F.; Geist, S.; Schild, A. Systematic One Zone Meanline Modelling of Centrifugal Compressors for Industrial Online Applications; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55249, p. V06CT40A025. [Google Scholar]
- VeláSquez, E.I.G. Determination of a suitable set of loss models for centrifugal compressor performance prediction. Chin. J. Aeronaut. 2017, 30, 1644–1650. [Google Scholar] [CrossRef]
- Galvas, M.R. Fortran Program for Predicting Off-Design Performance of Centrifugal Compressors; National Aeronautics and Space Administration: Washington, DC, USA, 1973.
- Aungier, R.H.X. Centrifugal Compressors: A Strategy for Aerodynamic Design and Analysis; American Society of Mechanical Engineers Press: New York, NY, USA, 2000. [Google Scholar]
- Whitfield, A.; Baines, N.C. Design of Radial Turbomachines; Longman: London, UK, 1990. [Google Scholar]
- Li, P.-Y.; Gu, C.-W.; Song, Y. A new optimization method for centrifugal compressors based on 1D calculations and analyses. Energies 2015, 8, 4317–4334. [Google Scholar] [CrossRef]
- Sundström, E.; Kerres, B.; Sanz, S.; Mihăescu, M. On the Assessment of Centrifugal Compressor Performance Parameters by Theoretical and Computational Models; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 50800, p. V02CT44A029. [Google Scholar]
- Oh, H.W.; Yoon, E.S.; Chung, M.K. An optimum set of loss models for performance prediction of centrifugal compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 1997, 211, 331–338. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, X.; Liu, X.; Sun, Z.; Wu, S.; Gao, Q.; Tan, C. A method to select loss correlations for centrifugal compressor performance prediction. Aerosp. Sci. Technol. 2019, 93, 105335. [Google Scholar] [CrossRef]
- Harley, P.; Spence, S.; Filsinger, D.; Dietrich, M.; Early, J. Assessing 1D Loss Models for the Off-Design Performance Prediction of Automotive Turbocharger Compressors; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55249, p. V06CT40A005. [Google Scholar]
- Du, W.; Li, Y.; Li, L.; Lorenzini, G. A quasi-one-dimensional model for the centrifugal compressors performance simulations. Int. J. Heat Technol. 2018, 36, 391–396. [Google Scholar] [CrossRef]
- Abd El-Maksoud, R.M.; Bayomi, N.N.; Rezk, M.I.F. Prediction and Modification of Centrifugal Compressor Performance Maps. In Proceedings of the Al-Azhar Engineering Twelfth International Conference, Cairo, Egypt, 25–27 December 2012. [Google Scholar]
- Jiang, H.; Dong, S.; Liu, Z.; He, Y.; Ai, F. Performance prediction of the centrifugal compressor based on a limited number of sample data. Math. Probl. Eng. 2019, 2019, 5954128. [Google Scholar] [CrossRef] [Green Version]
- Bourabia, L.; Abed, C.B.; Cerdoun, M.; Khalfallah, S.; Deligant, M.; Khelladi, S.; Chettibi, T. Aerodynamic preliminary design optimization of a centrifugal compressor turbocharger based on one-dimensional mean-line model. Eng. Comput. 2021, 38, 3438–3469. [Google Scholar] [CrossRef]
- Massoudi, S.; Picard, C.; Schiffmann, J. Robust design using multiobjective optimisation and artificial neural networks with application to a heat pump radial compressor. Des. Sci. 2022, 8, e1. [Google Scholar] [CrossRef]
- Bicchi, M.; Biliotti, D.; Marconcini, M.; Toni, L.; Cangioli, F.; Arnone, A. An AI-Based Fast Design Method for New Centrifugal Compressor Families. Machines 2022, 10, 458. [Google Scholar] [CrossRef]
- Du, Y.; Yang, C.; Wang, H.; Hu, C. One-dimensional optimisation design and off-design operation strategy of centrifugal compressor for supercritical carbon dioxide Brayton cycle. Appl. Therm. Eng. 2021, 196, 117318. [Google Scholar] [CrossRef]
- Romei, A.; Gaetani, P.; Giostri, A.; Persico, G. The role of turbomachinery performance in the optimization of supercritical carbon dioxide power systems. J. Turbomach. 2020, 142, 071001. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Zhou, K.; Xia, J.; Li, Y.; Zhao, P.; Dai, Y. Design and performance analysis of compressor and turbine in supercritical CO2 power cycle based on system-component coupled optimization. Energy Convers. Manag. 2020, 221, 113179. [Google Scholar] [CrossRef]
- Conrad, O.; Raif, K.; Wessels, M. The calculation of performance maps for centrifugal compressors with vane-island diffusers. In Performance Prediction of Centrifugal Pumps and Compressors; American Society of Mechanical Engineers: New York, NY, USA, 1979; pp. 135–147. [Google Scholar]
- Jansen, W. A method for calculating the flow in a centrifugal impeller when entropy gradient are present. Inst. Mech. Eng. Intern. Aerodyn. 1970, 133–146. Available online: https://cir.nii.ac.jp/crid/1571135650145571968 (accessed on 10 October 2022).
- Coppage, J.E.; Dallenbach, F. Study of Supersonic Radial Compressors for Refrigeration and Pressurization Systems; Garrett Corp Los Angeles Ca AiResearch MFG DIV: Los Angeles, CA, USA, 1956. [Google Scholar]
- Rodgers, C. Paper 5: A Cycle Analysis Technique for Small Gas Turbines; SAGE Publications Sage UK: London, UK, 1968; Volume 183, pp. 37–49. [Google Scholar]
- Krylov, E.P.; Spunde, Y.A. About the Influence of the Clearance between the Working Blades and Housing of a Radial Turbine on Its Exponent; Air Force Systems Command Wright-Patterson AFB Oh Wright-Patterson AFB: Dayton, OH, USA, 1967. [Google Scholar]
- Алексеев. Принцип авиациoнных двигателей; Издательствo науки и правды: Volgogrd, Soviet Union, 1982. [Google Scholar]
- Johnston, J.P.; Dean, R.C., Jr. Losses in vaneless diffusers of centrifugal compressors and pumps: Analysis, experiment, and design. J. Eng. Power. 1966, 88, 49–60. [Google Scholar] [CrossRef]
- Daily, J.W.; Nece, R.E. Chamber dimension effects on induced flow and frictional resistance of enclosed rotating disks. J. Basic Eng. 1960, 82, 217–230. [Google Scholar] [CrossRef]
- Boyce, M.P. Centrifugal Compressors: A Basic Guide; PennWell Corporation: Tulsa, OK, USA, 2003. [Google Scholar]
- Stanitz, J.D. One-Dimensional Compressible Flow in Vaneless Diffusers of Radial-and Mixed-Flow Centrifugal Compressors, Including Effects of Friction, Heat Transfer and Area Change; National Advisory Committee for Aeronautics: Washington, DC, USA, 1952.
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Krain, H.; Hoffmann, B.; Pak, H. Aerodynamics of a Centrifugal Compressor Impeller with Transonic Inlet Conditions; American Society of Mechanical Engineers: New York, NY, USA, 1995; Volume 78781, p. V001T001A011. [Google Scholar]
- Eckardt, D. Instantaneous measurements in the jet-wake discharge flow of a centrifugal compressor impeller. J. Eng. Gas Turbines Power 1975, 97, 337–345. [Google Scholar] [CrossRef]
- Moore, J. Eckardt’s impeller: A ghost from ages past. NASA STI/Recon Tech. Rep. N 1976, 77, 28442. [Google Scholar]
- Eisenlohr, G.; Krain, H.; Richter, F.-A.; Tiede, V. Investigations of the flow through a high pressure ratio centrifugal impeller. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; Volume 3610, pp. 649–657. [Google Scholar]
- Britton, I.; Gauthier, J.E.D. Performance prediction of centrifugal impellers using a two-zone model. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 43161, pp. 1695–1704. [Google Scholar]



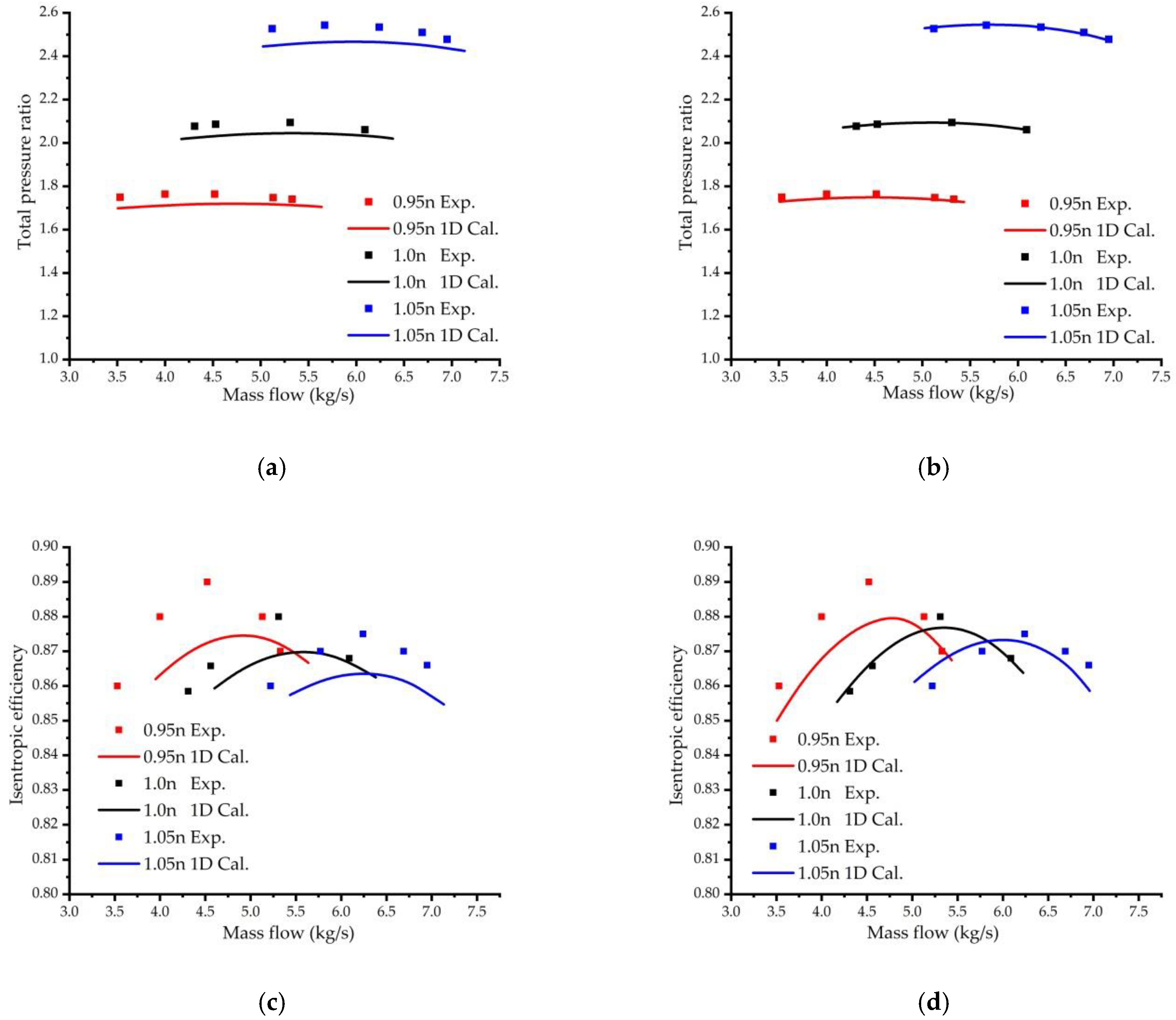
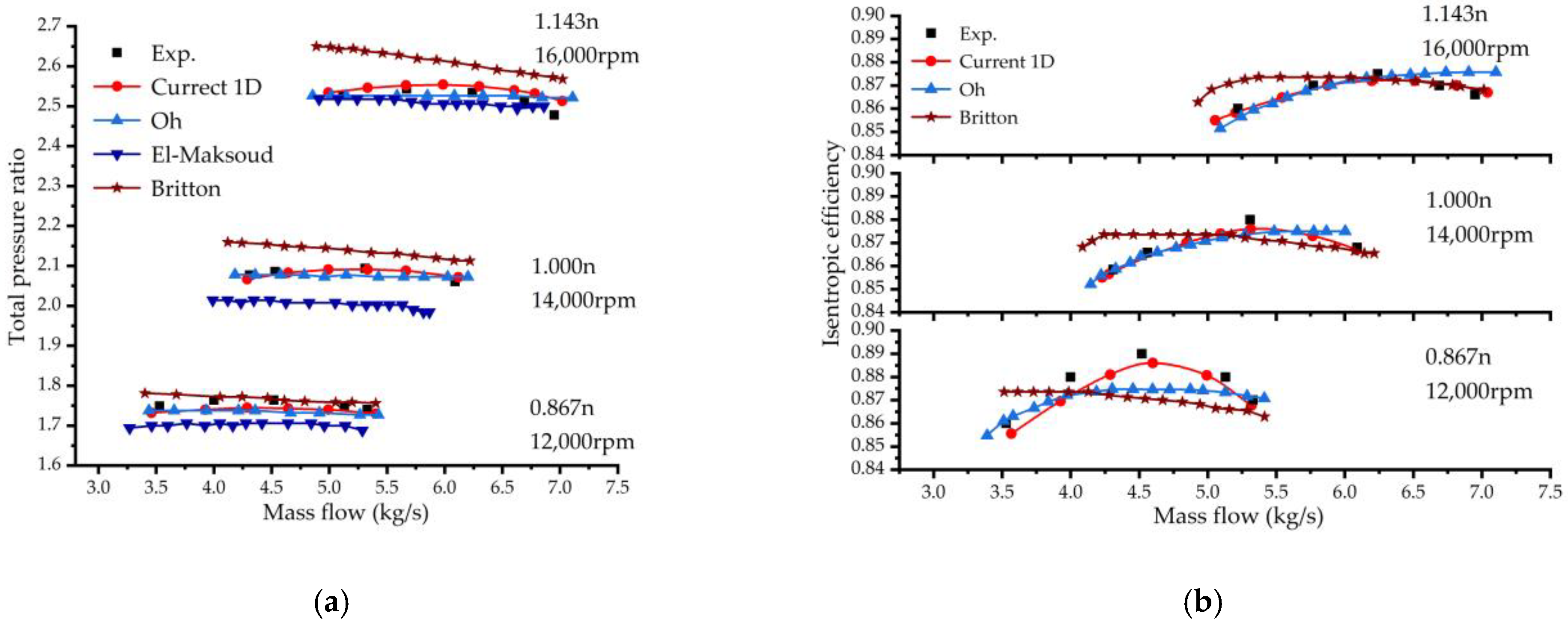
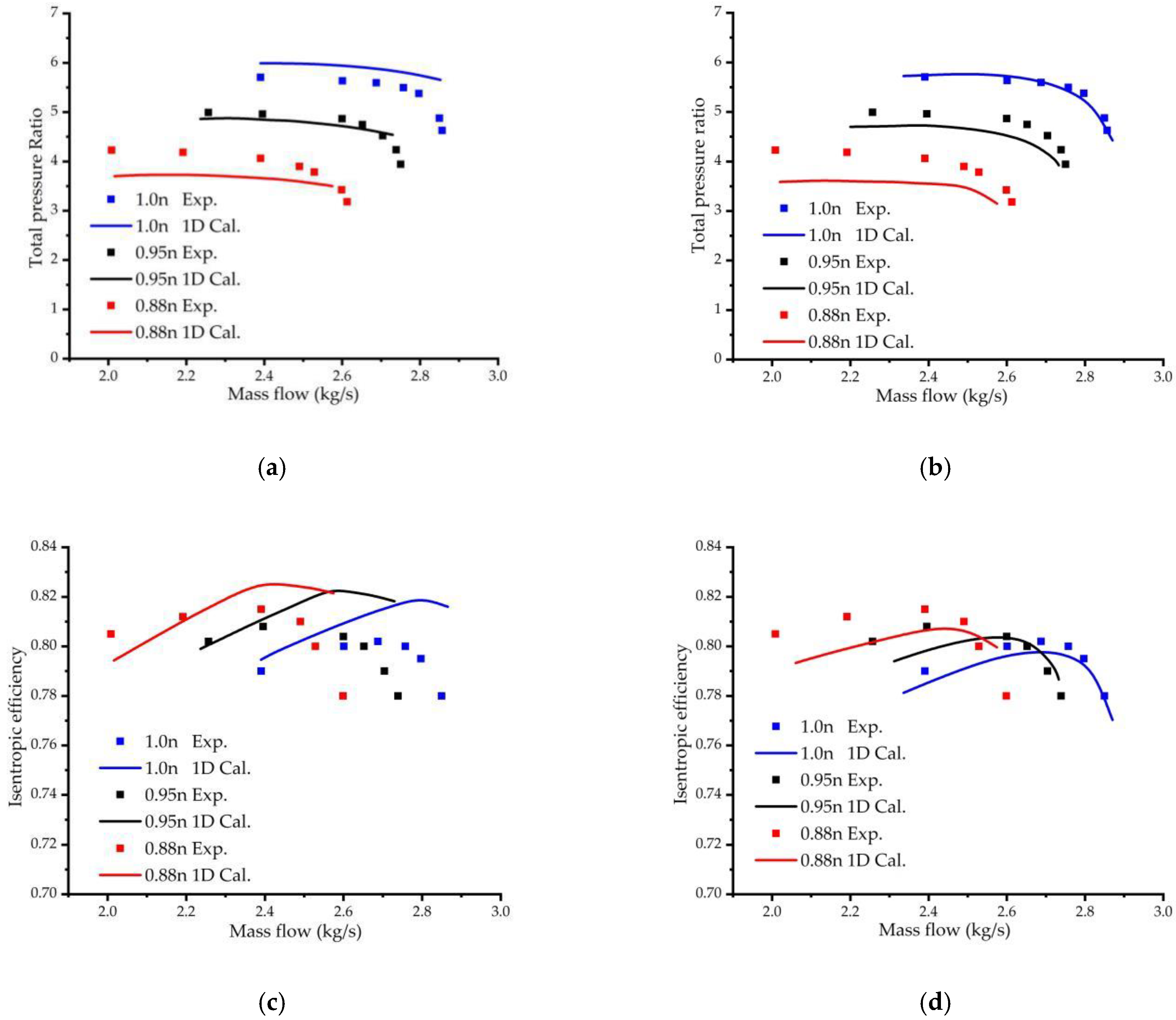
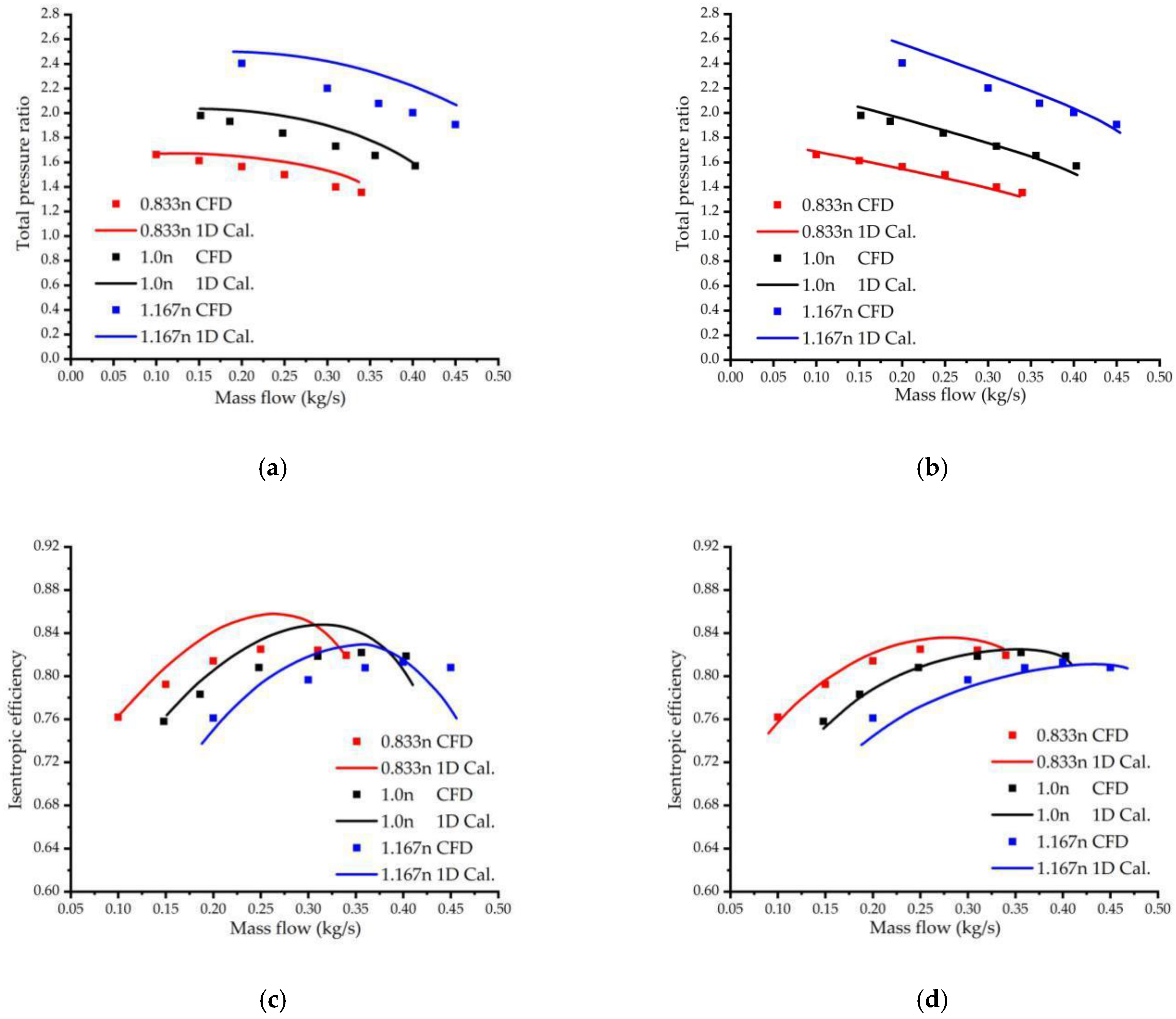

| Order | Categories | No Splitter Blade | One Row | Two Rows | ||
|---|---|---|---|---|---|---|
| 1 | Names of impeller | Krain | Ekcardt-O | SRV2-O | R | J |
| 2 | Axial length l12 (mm) | 120 | 130 | 75 | 30 | 68 |
| 3 | Inlet tip diameter d1tip (mm) | 226 | 280 | 156 | 68 | 117 |
| 4 | Inlet hub diameter d1hub (mm) | 90 | 90 | 60 | 20 | 44 |
| 5 | Impeller exit diameter d2 (mm) | 400 | 400 | 224 | 101 | 170 |
| 6 | Impeller exit width b2 (mm) | 14.7 | 26 | 10.2 | 5.1 | 10 |
| 7 | Tip clearance size τ (mm) | 0.4 | 0.6 | 0.5 | 0.2 | 0.2 |
| 8 | Number of inlet blades Z1 | 24 | 20 | 13 | 7 | 8 |
| 9 | Number of outlet blades Z2 | 24 | 20 | 26 | 14 | 24 |
| 10 | Inlet mean blade angle β1 (º) | 45 | 40 | 40 | 40 | 36 |
| 11 | The relative position of section ⓐ sp1 | - | - | 0.215 | 0.227 | 0.236 |
| 12 | Section ⓐ mean blade angle β12 (º) | - | - | 44 | 52 | 51 |
| 13 | The relative position of section ⓑ sp2 | - | - | - | - | 0.407 |
| 14 | Section ⓑ mean blade angle β13 (º) | - | - | - | - | 66 |
| 15 | Exit blade angle β2 (º) | 60 | 90 | 52 | 45 | 70 |
| 16 | Design rotational speed n (rpm) | 22,363 | 14,000 | 50,000 | 60,000 | 61,000 |
| 17 | Mass flow rate (kg/s) at design point | 4 | 5.31 | 2.55 | 0.31 | 1.55 |
| 19 | Total pressure ratio ε at design point | 4.1 | 2.09 | 5.7 | 1.62 | 7.18 |
| 18 | Specific speed ns | 0.239 | 0.355 | 0.324 | 0.403 | 0.316 |
| Component | Loss Models | Proposers | Models Used in This Study |
|---|---|---|---|
| Internal losses | Incidence loss | Galvas, Conrad, Aungier | Galvas |
| Skin friction loss | Jansen, Aungier | Jansen | |
| Blade loading loss | Coppage, Aungier | Coppage | |
| Tip clearance loss | Jansen, Roders, Krylov and Spunde | Jansen | |
| Mixing loss | Aлeкceeв, Aungier, Johnston and Dean | Aлeкceeв | |
| Viscosity loss | Aлeкceeв | Aлeкceeв | |
| Shock loss | Aungier, Whitfield and Baines, Aлeкceeв | Aлeкceeв | |
| External losses | Disk friction loss | Galvas, Aungier, Daily and Nece, Boyce | Galvas |
| Recirculation loss | Aлeкceeв, Roders, Coppage, Oh | Aлeкceeв | |
| Leakage loss | Aungier, Jansen | Aungier |
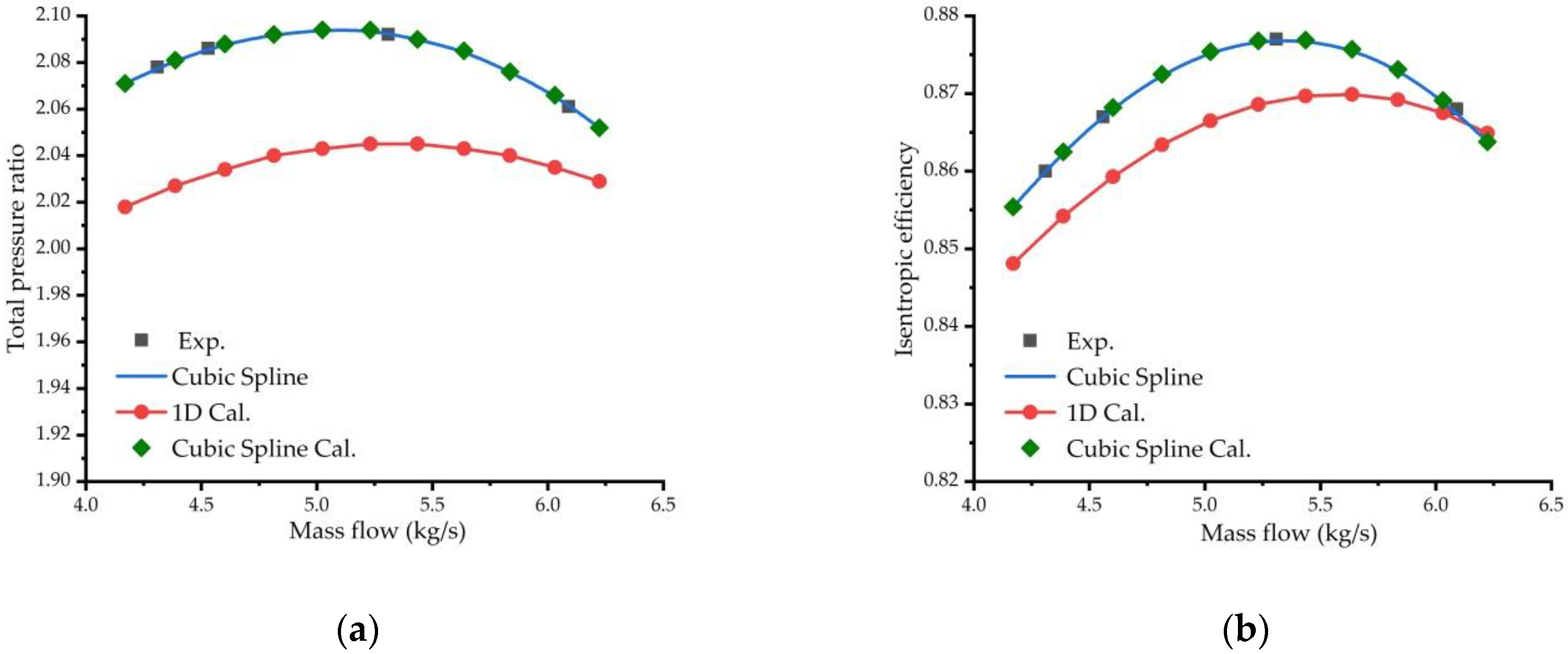
| Mass Flow | Total Pressure Ratio | Isentropic Efficiency | ||
|---|---|---|---|---|
| kg/s | 1D Cal. | Cubic spline | 1D Cal. | Cubic spline |
| 4.17 | 2.018 | 2.071 | 0.8481 | 0.8554 |
| 4.387 | 2.027 | 2.081 | 0.8542 | 0.8625 |
| 4.814 | 2.04 | 2.092 | 0.8634 | 0.8725 |
| 5.231 | 2.045 | 2.094 | 0.8686 | 0.8768 |
| 5.637 | 2.043 | 2.085 | 0.8699 | 0.8757 |
| 5.836 | 2.04 | 2.076 | 0.8692 | 0.8731 |
| 6.223 | 2.029 | 2.052 | 0.8649 | 0.8638 |
| Name | finc | fcl | fgpr | fbl | fdf | frc | fsf | foz |
|---|---|---|---|---|---|---|---|---|
| Eckardt-O | 1.58801 | 0.4796 | 4.7907 | 0.13334 | 2.93157 | 2.96052 | 0.96139 | |
| Krain | 2.78663 | 0.5242 | 2.08658 | 0.85853 | 0.14468 | 0.72164 | 1.58243 | |
| R | 1.0772 | 6.3912 | 5.2102 | 4.913 | 1.6832 | 0.1231 | 0.6838 | |
| SRV2-O | 3.74546 | 2.07457 | 3.12488 | 0.1213 | 1.32559 | 0.07233 | 1.32559 | 2.63154 |
| J | 6.03554 | 0.81823 | 3.33042 | 1.54833 | 2.84399 | 0.05061 | 1.77527 | 4.84246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Liu, Y.; Zhao, G. Modification and Validation of 1D Loss Models for the Off-Design Performance Prediction of Centrifugal Compressors with Splitter Blades. Machines 2023, 11, 118. https://doi.org/10.3390/machines11010118
Yang X, Liu Y, Zhao G. Modification and Validation of 1D Loss Models for the Off-Design Performance Prediction of Centrifugal Compressors with Splitter Blades. Machines. 2023; 11(1):118. https://doi.org/10.3390/machines11010118
Chicago/Turabian StyleYang, Xiuxin, Yan Liu, and Guang Zhao. 2023. "Modification and Validation of 1D Loss Models for the Off-Design Performance Prediction of Centrifugal Compressors with Splitter Blades" Machines 11, no. 1: 118. https://doi.org/10.3390/machines11010118
APA StyleYang, X., Liu, Y., & Zhao, G. (2023). Modification and Validation of 1D Loss Models for the Off-Design Performance Prediction of Centrifugal Compressors with Splitter Blades. Machines, 11(1), 118. https://doi.org/10.3390/machines11010118






