Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway
Abstract
:1. Introduction
2. Measurement Setup
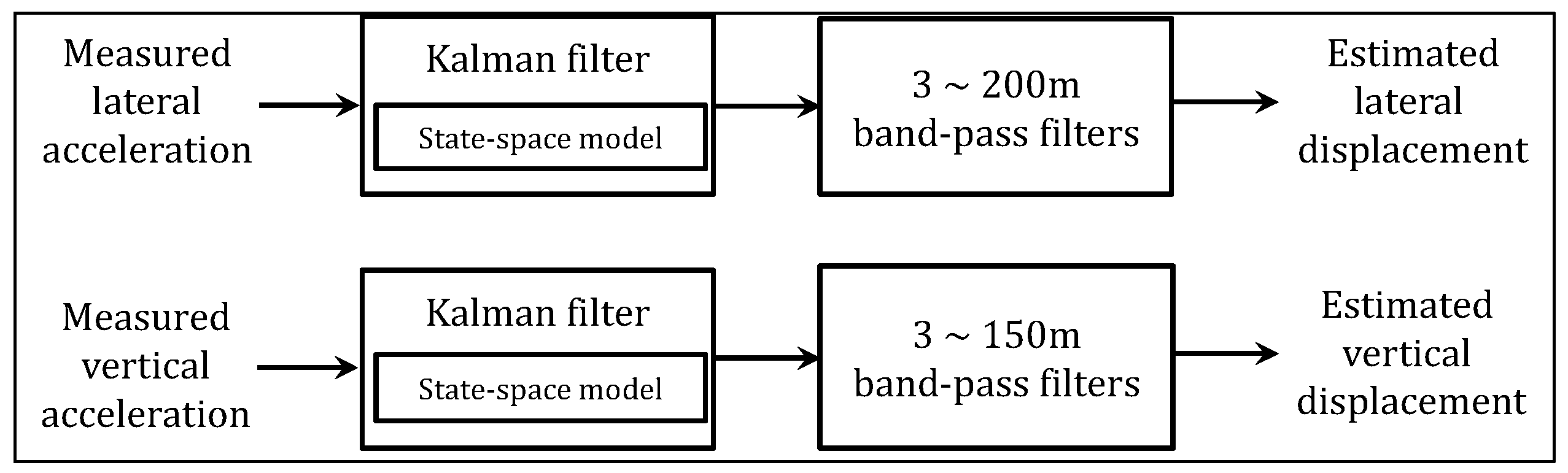
3. Displacement Estimation from Acceleration
- State model
- Space model
- Initial condition
- Recursion relations
- -
- Innovations:
- -
- Innovation covariance:
- -
- Kalman prediction gain:
- -
- State estimation:
- -
- State error covariance:
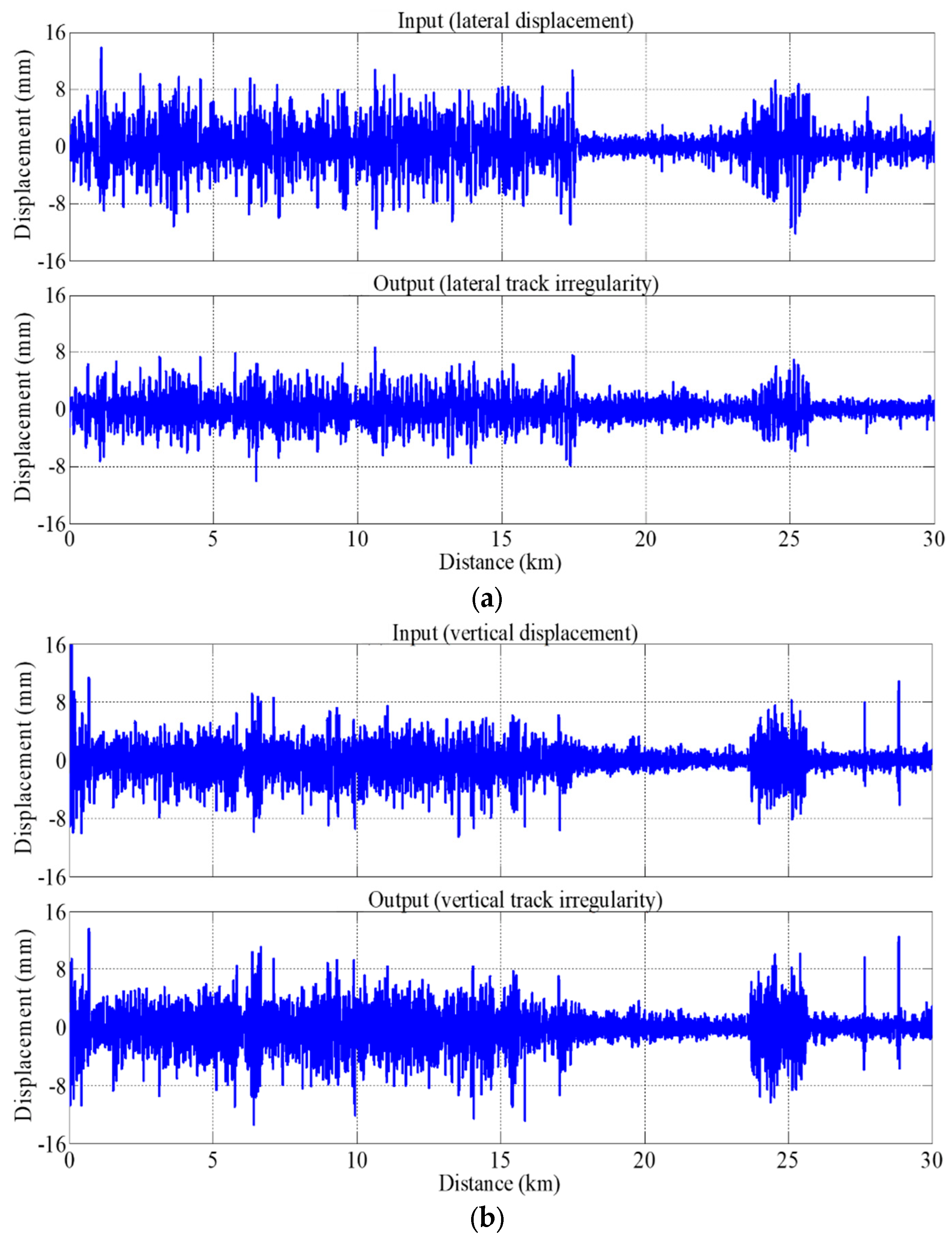
4. Model Setup and Identification
4.1. Concept
4.2. Model Setup
- -
- IIR model:
- -
- FIR model:
4.3. Adaptive Kalman Filter
- -
- State model
- -
- Space model:
- Initialization
- Recursions
- -
- Innovations:
- -
- Innovation covariance:
- -
- Kalman prediction gain:
- -
- State estimation:
- -
- State error covariance:
5. Identification of the Models
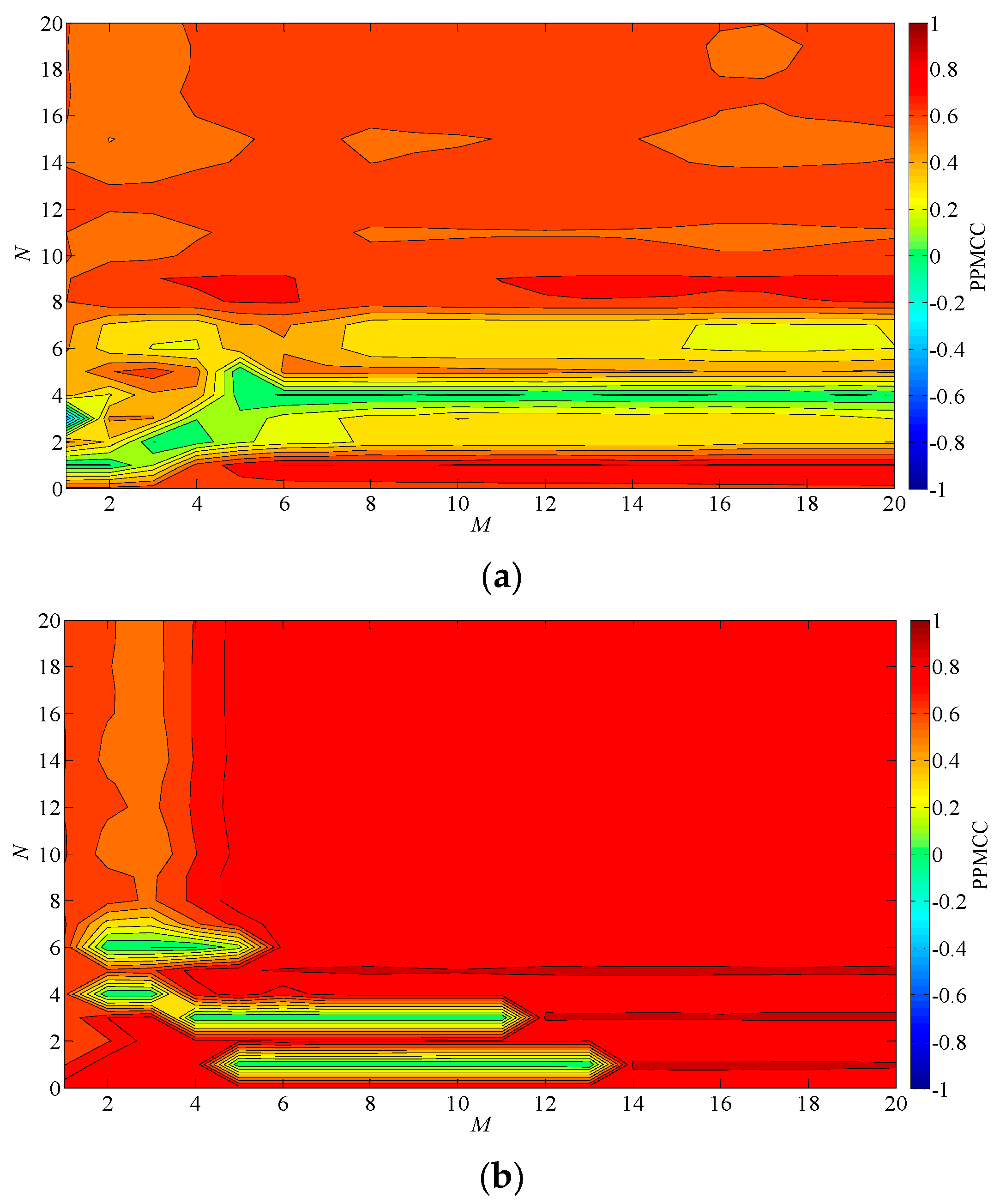
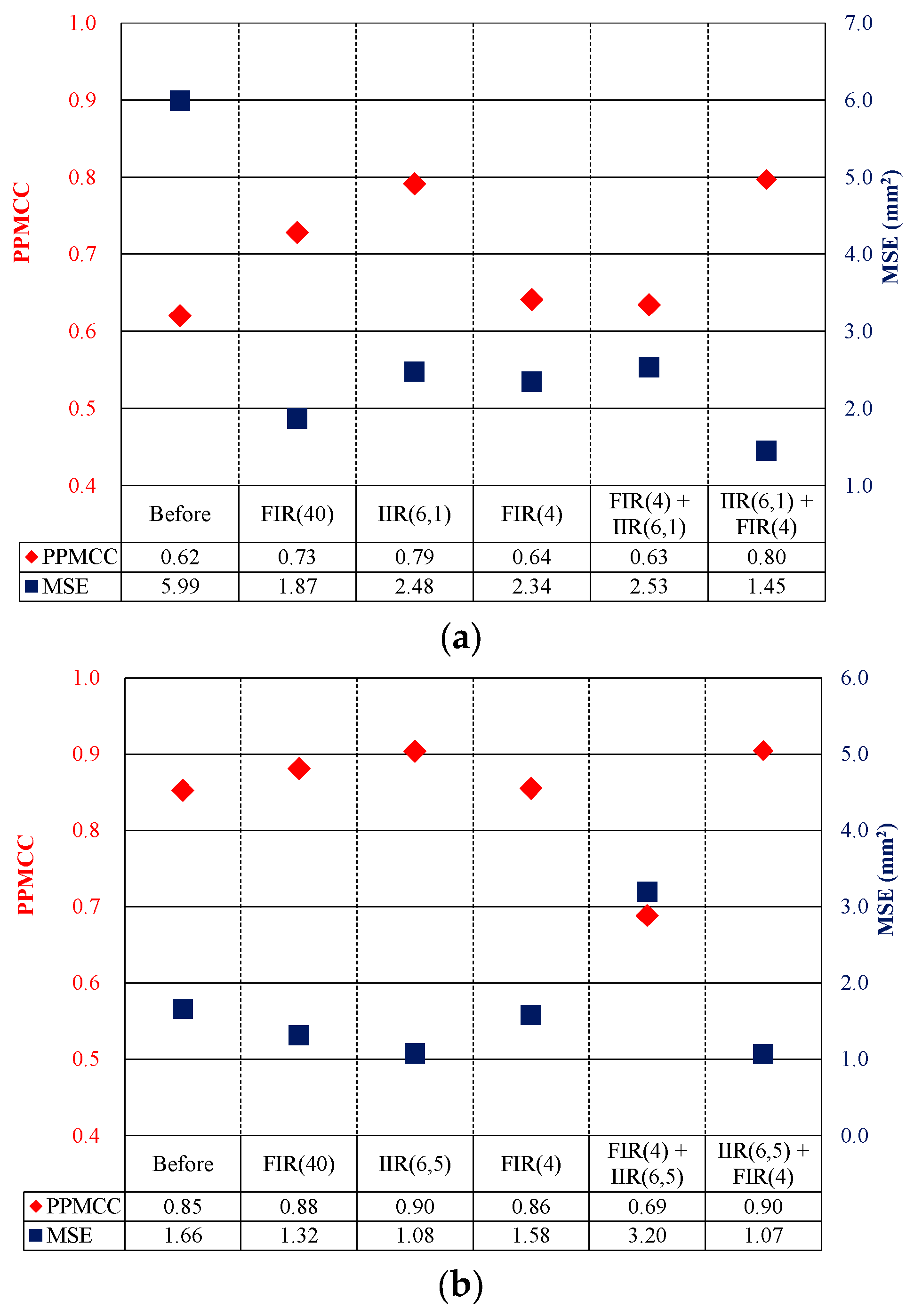
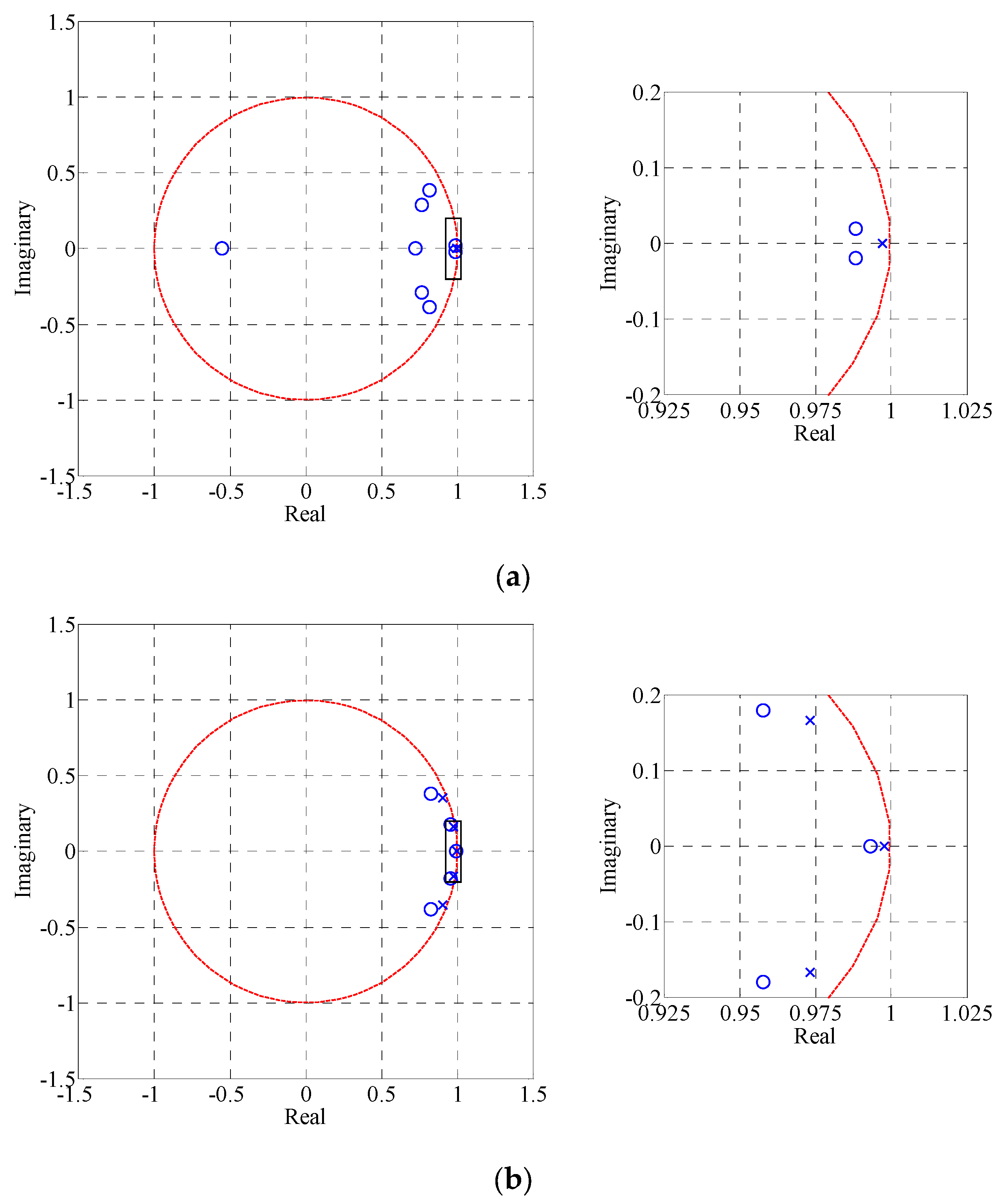
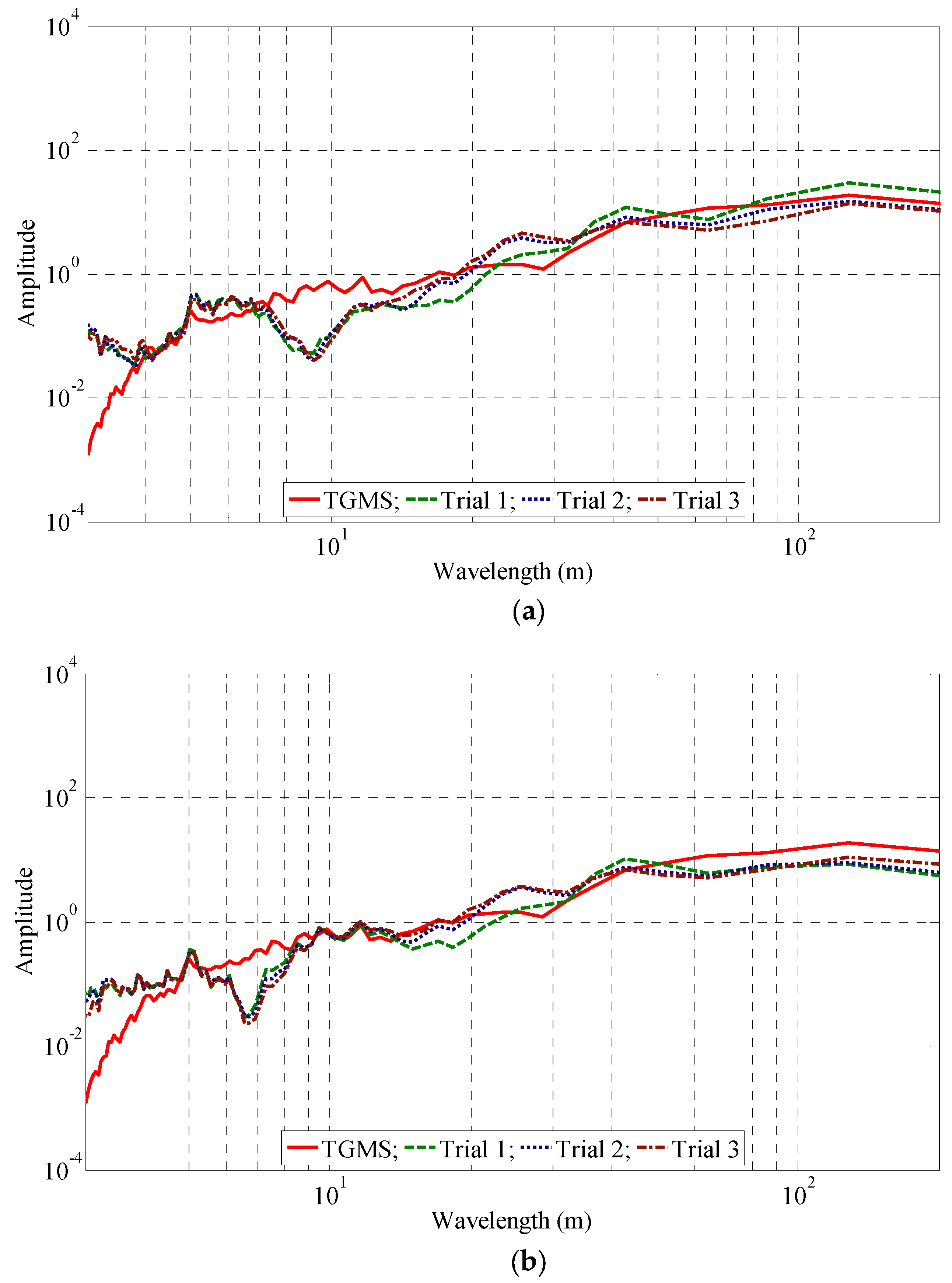
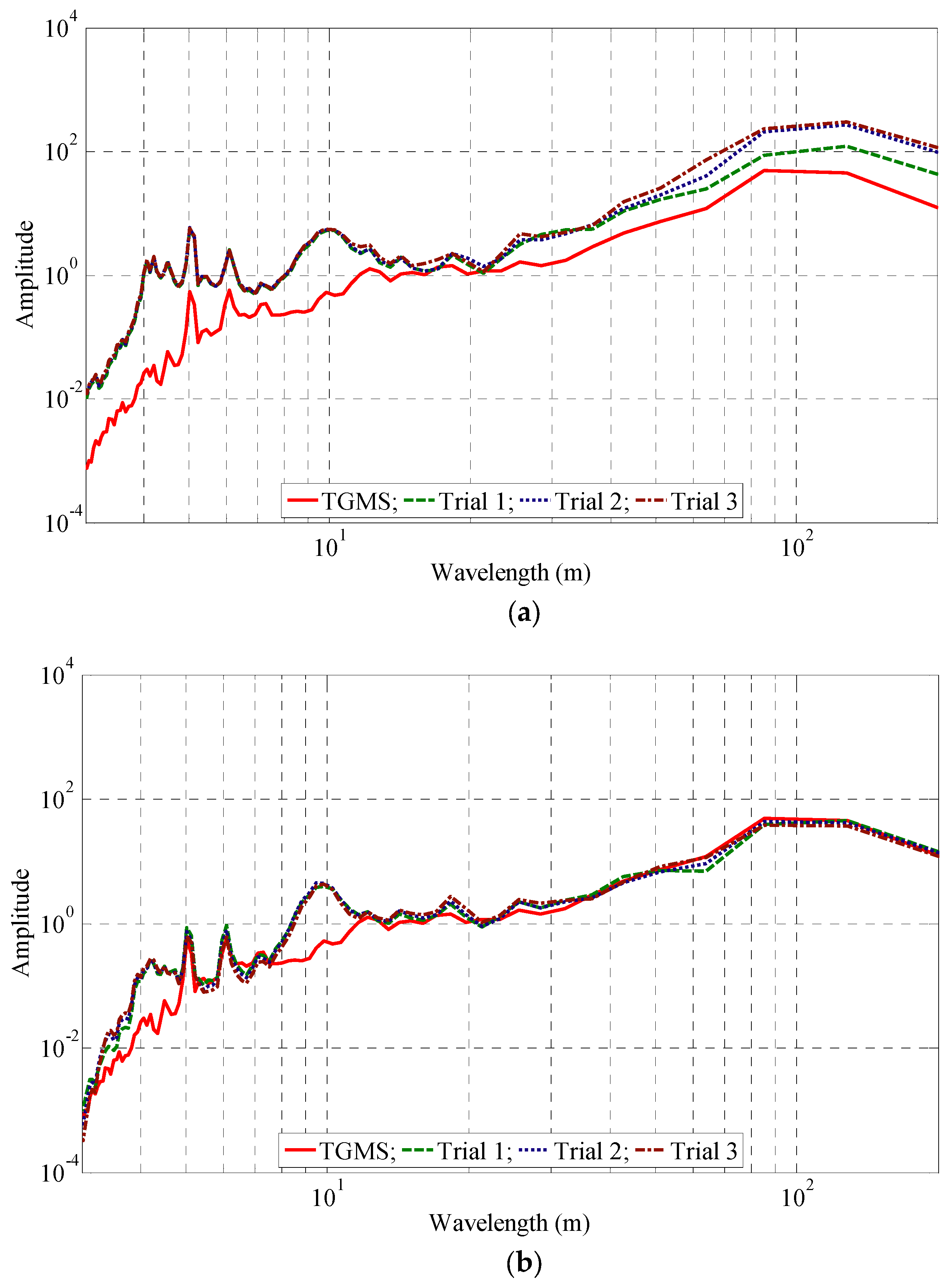
5.1. Model Selection
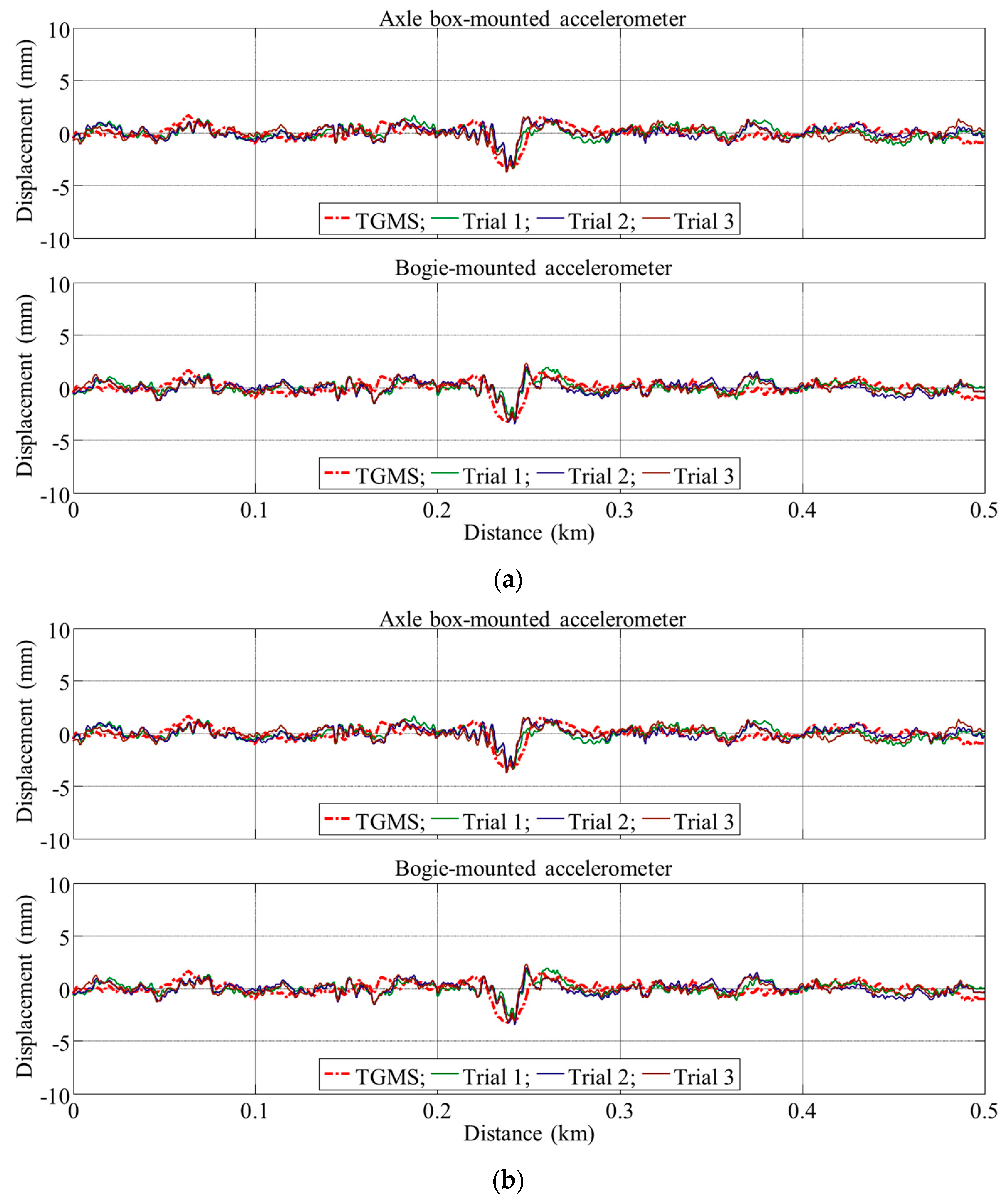
5.2. Model Validation
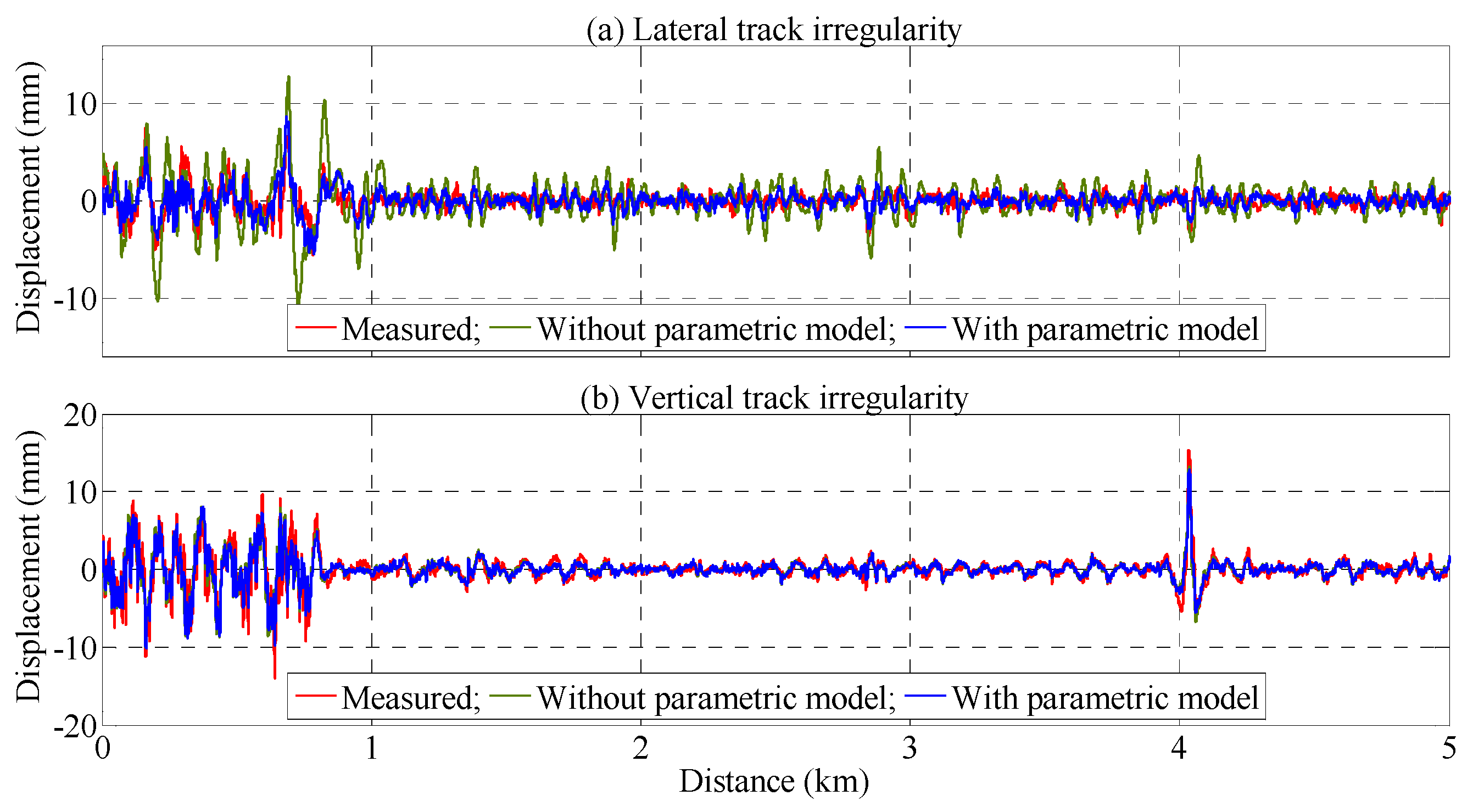
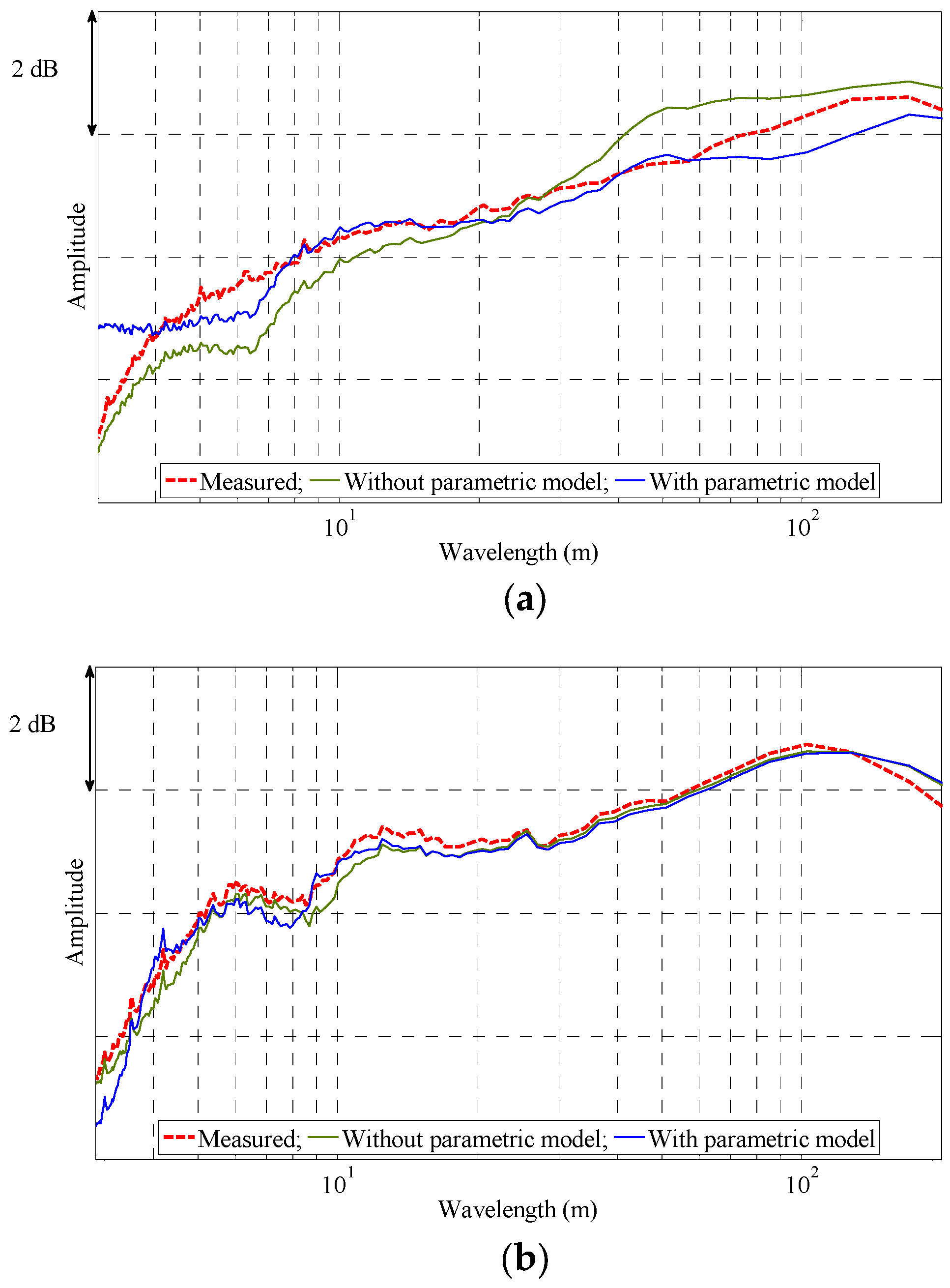
6. Track Irregularity Estimation Using Derived Models
7. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Track Recording Cars. Available online: https://www.plassertheurer.com/en/machine/measuring-work/overview (accessed on 10 November 2022).
- Track Geometry System. Available online: https://www.mermecgroup.com/measuring-trains-br-and-systems/track-measurement/185/track-geometry.php (accessed on 10 November 2022).
- Yang, J.; Li, J.B.; Lin, G. A simple approach to integration of acceleration data for dynamic soil-structure interaction analysis. Soil Dyn. Earthq. Eng. 2006, 26, 725–734. [Google Scholar] [CrossRef]
- Kawasaki, J.; Youcef-Toumi, K. Estimation of rail irregularities. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 3650–3660. [Google Scholar]
- Westeon, P.F.; Ling, C.S.; Roberts, C.; Goodman, C.J.; Li, P.; Goodall, R.M. Monitoring vertical track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2007, 221, 75–88. [Google Scholar] [CrossRef]
- Westeon, P.F.; Ling, C.S.; Goodman, C.J.; Roberts, C.; Li, P.; Goodall, R.M. Monitoring lateral track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2007, 221, 89–100. [Google Scholar] [CrossRef]
- Alfi, S.; Bruni, S. Estimation of long wavelength track irregularities from on board measurement. In Proceedings of the 4th IET International Conference on Railway Condition Monitoring, Derby, UK, 18–20 June 2008; pp. 1–6. [Google Scholar]
- Czop, P.; Mendrok, K.; Uhl, T. Application of inverse linear parametric models in the identification of rail track irregularities. Arch. Appl. Mech. 2011, 81, 1541–1554. [Google Scholar] [CrossRef]
- Hidalgo, A.; Ros, J.; Escalona, J. A Kalman filter-based algorithm for imu signals fusion applied to track geometry estimation. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Barcelona, Spain, 29 June–2 July 2015; pp. 1–13. [Google Scholar]
- Tsunashima, H.; Naganuma, Y.; Kobayashi, T. Track geometry estimation from car-body vibration. Veh. Syst. Dyn. 2014, 52, 207–219. [Google Scholar] [CrossRef]
- Muñoz, S.; Ros, J.; Urda, P.; Escalona, J.L. Estimation of lateral track irregularity through Kalman filtering techniques. IEEE Access 2021, 9, 60010–60025. [Google Scholar] [CrossRef]
- Lee, J.S.; Choi, S.; Kim, S.S.; Park, C.; Kim, Y.G. A mixed filtering approach for track condition monitoring using accelerometers on the axle-box and bogie. IEEE Trans. Instrum. Meas. 2012, 61, 749–758. [Google Scholar] [CrossRef]
- Kim, S.S.; Park, C.; Kim, Y.G.; Park, C. Parameter characteristics of rail inspection measurement system of HSR-350x. J. Mech. Sci. Technol. 2009, 23, 1019–1022. [Google Scholar] [CrossRef]
- Ogata, K. Discrete-Time Control Systems, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Sayed, A.H. Adaptive Filters, 1st ed.; Wisley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ljung, L.; Glad, T. Modeling of Dynamic Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Wickens, A.H. Fundamentals of Rail Vehicle Dynamics: Guidance and Stability; Swets & Zeitlinger, Lisse: Leiden, The Netherlands, 2003. [Google Scholar]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing, 4th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Pasquato, L.; Kale, I. System identification via hybrid FIR-IIR adaptive filtering. In Proceedings of the 16th IEEE Instrumentation and Measurement Technology Conference, Venice, Italy, 24–26 May 1999; pp. 1064–1069. [Google Scholar]
- Ljung, L. System Identification: Theory for User; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Hayter, A.J. Probability and Statistics for Engineers and Scientists, 4th ed.; Brooks/Cole: Boston, MA, USA, 2012. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S. Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway. Machines 2023, 11, 6. https://doi.org/10.3390/machines11010006
Choi S. Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway. Machines. 2023; 11(1):6. https://doi.org/10.3390/machines11010006
Chicago/Turabian StyleChoi, Sunghoon. 2023. "Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway" Machines 11, no. 1: 6. https://doi.org/10.3390/machines11010006
APA StyleChoi, S. (2023). Identifying Parametric Models Used to Estimate Track Irregularities of a High-Speed Railway. Machines, 11(1), 6. https://doi.org/10.3390/machines11010006




