Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body
Abstract
:1. Introduction
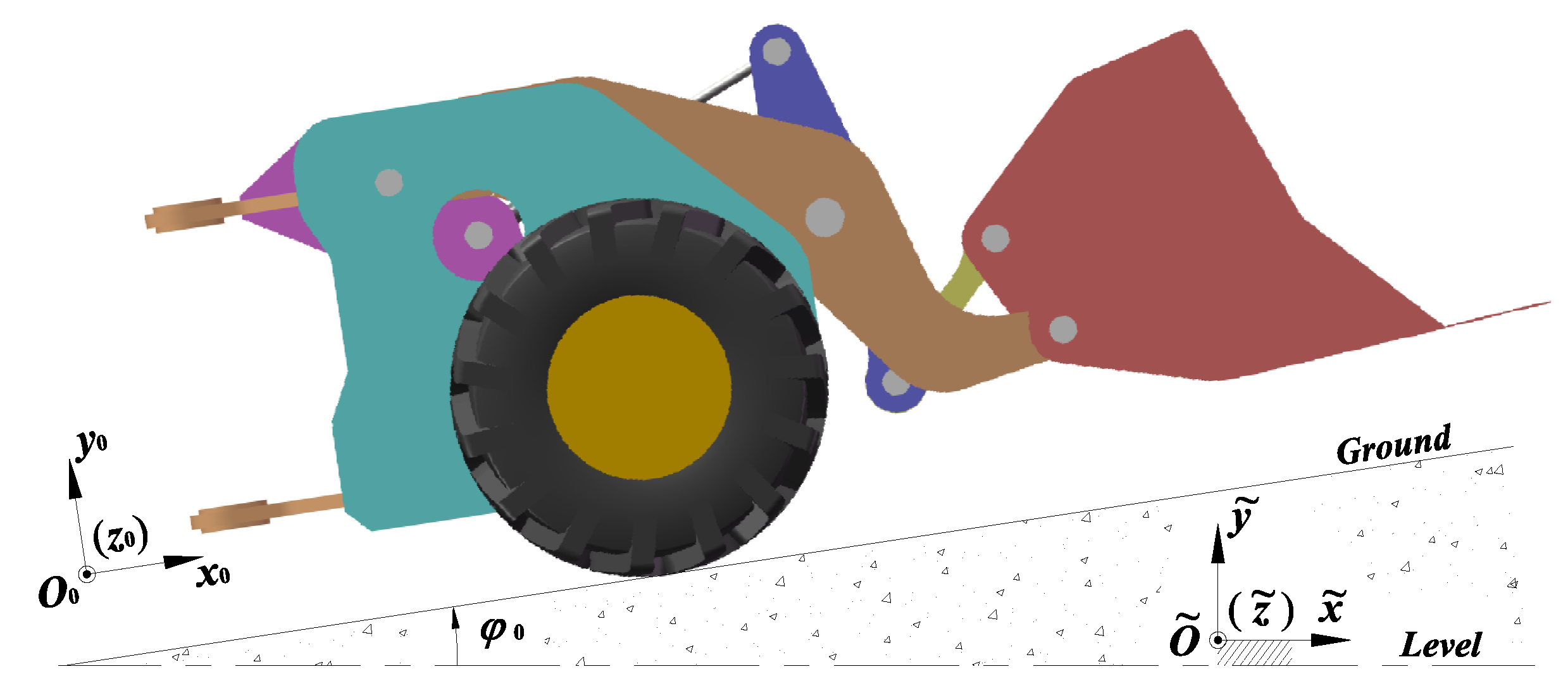
2. Drive Space and Parameters
3. Kinematic Description of Working Mechanism System
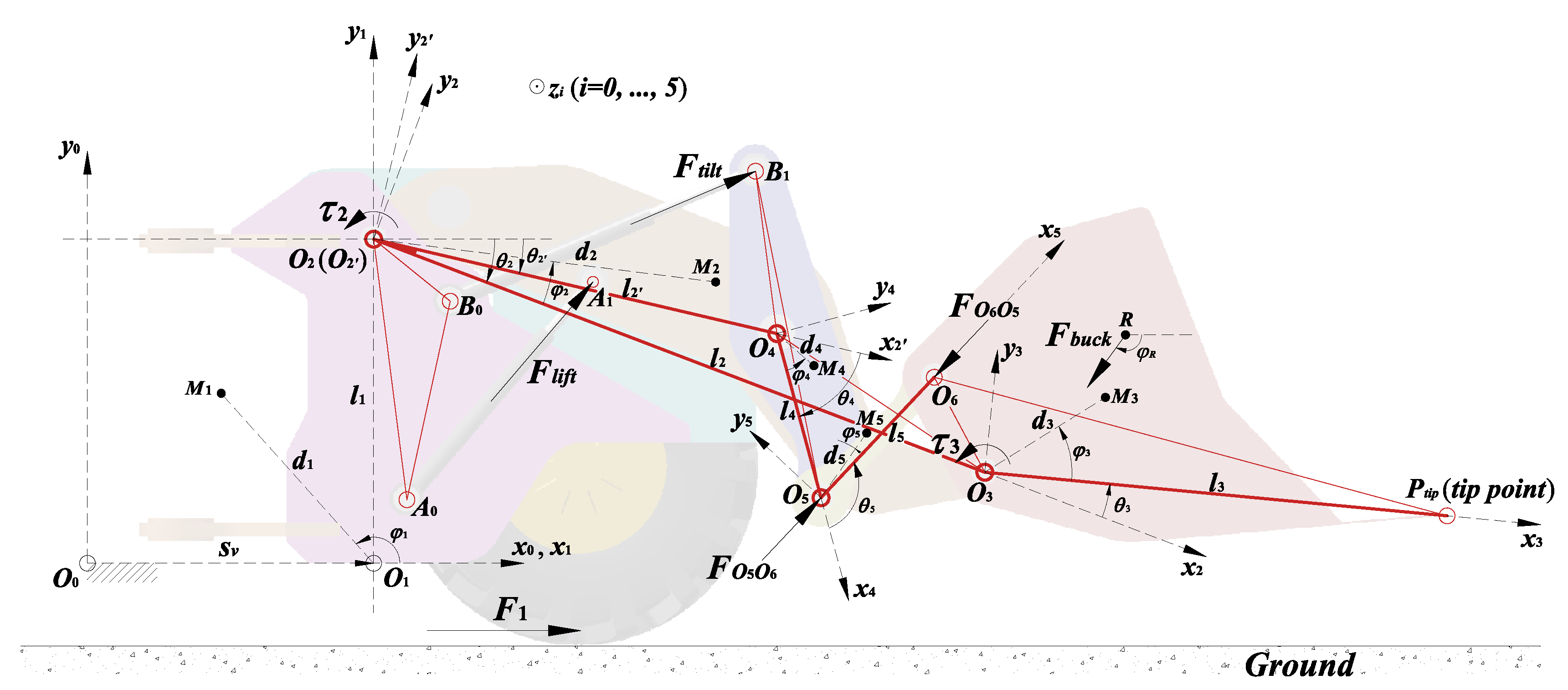
3.1. Kinematic Description in Joint Space
3.2. Kinematic Description in Drive Space
4. Dynamic Modeling of Working Mechanism System
4.1. Dynamic Model Based on Lagrange Method
4.2. Dynamic Model Derivation Based on Newton–Euler Method
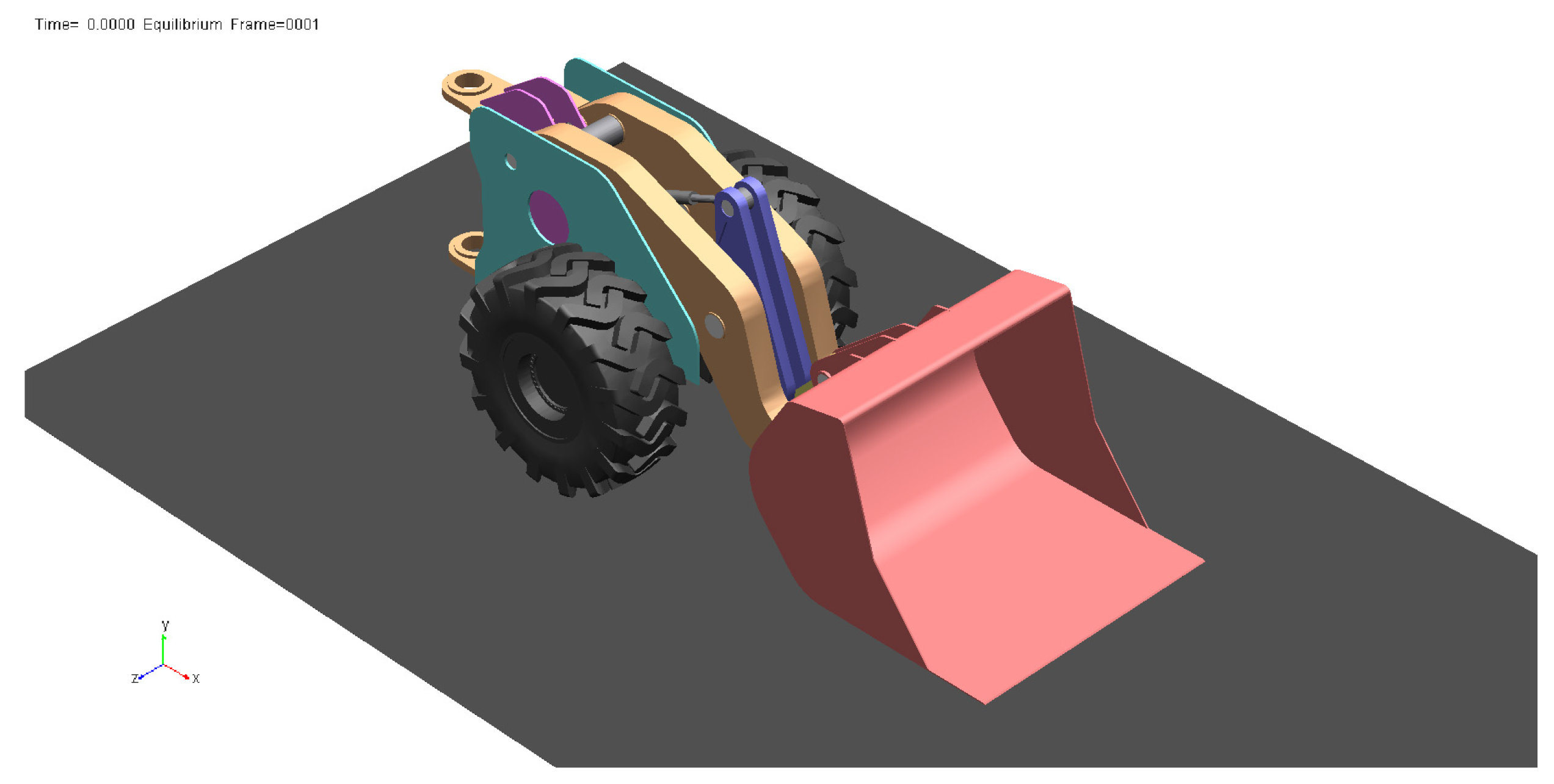
5. Validation and Analysis
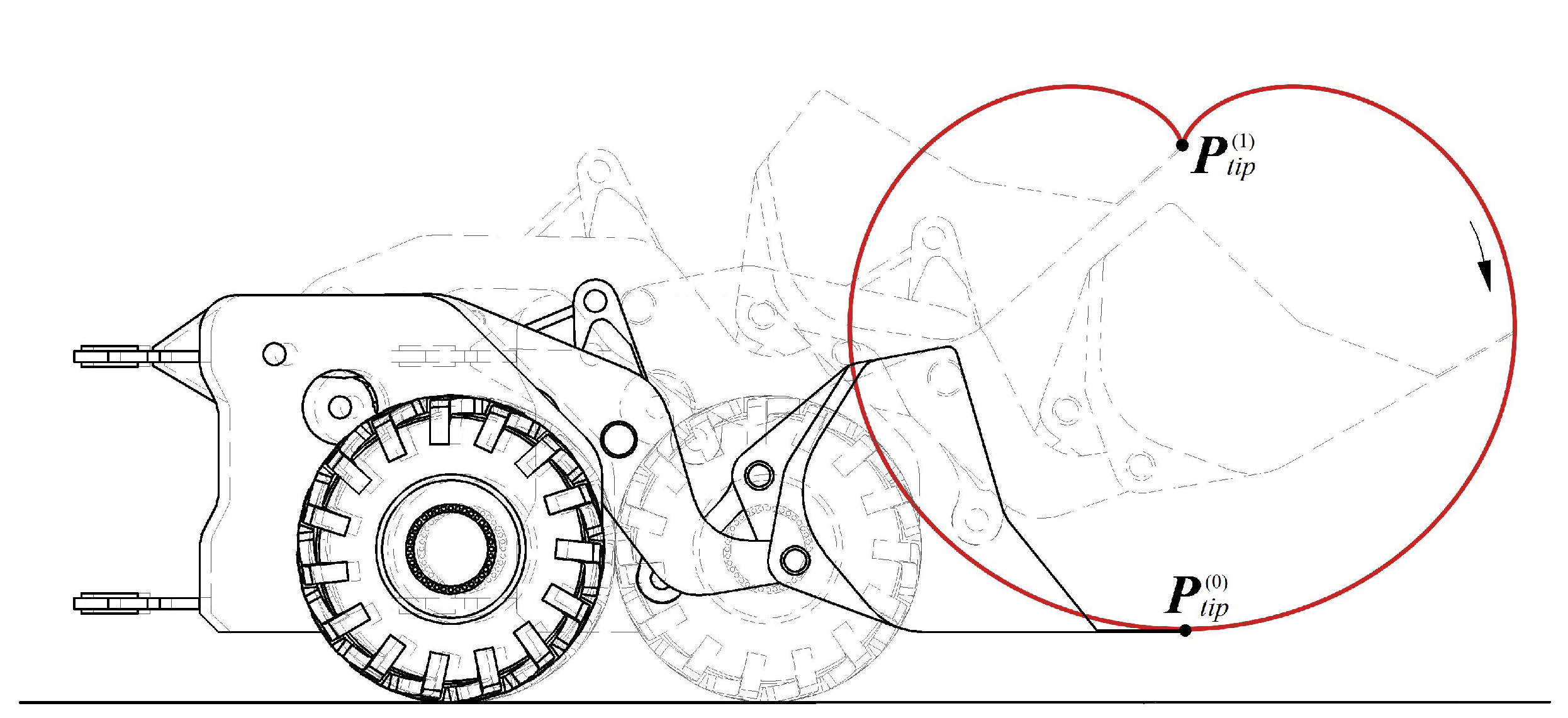
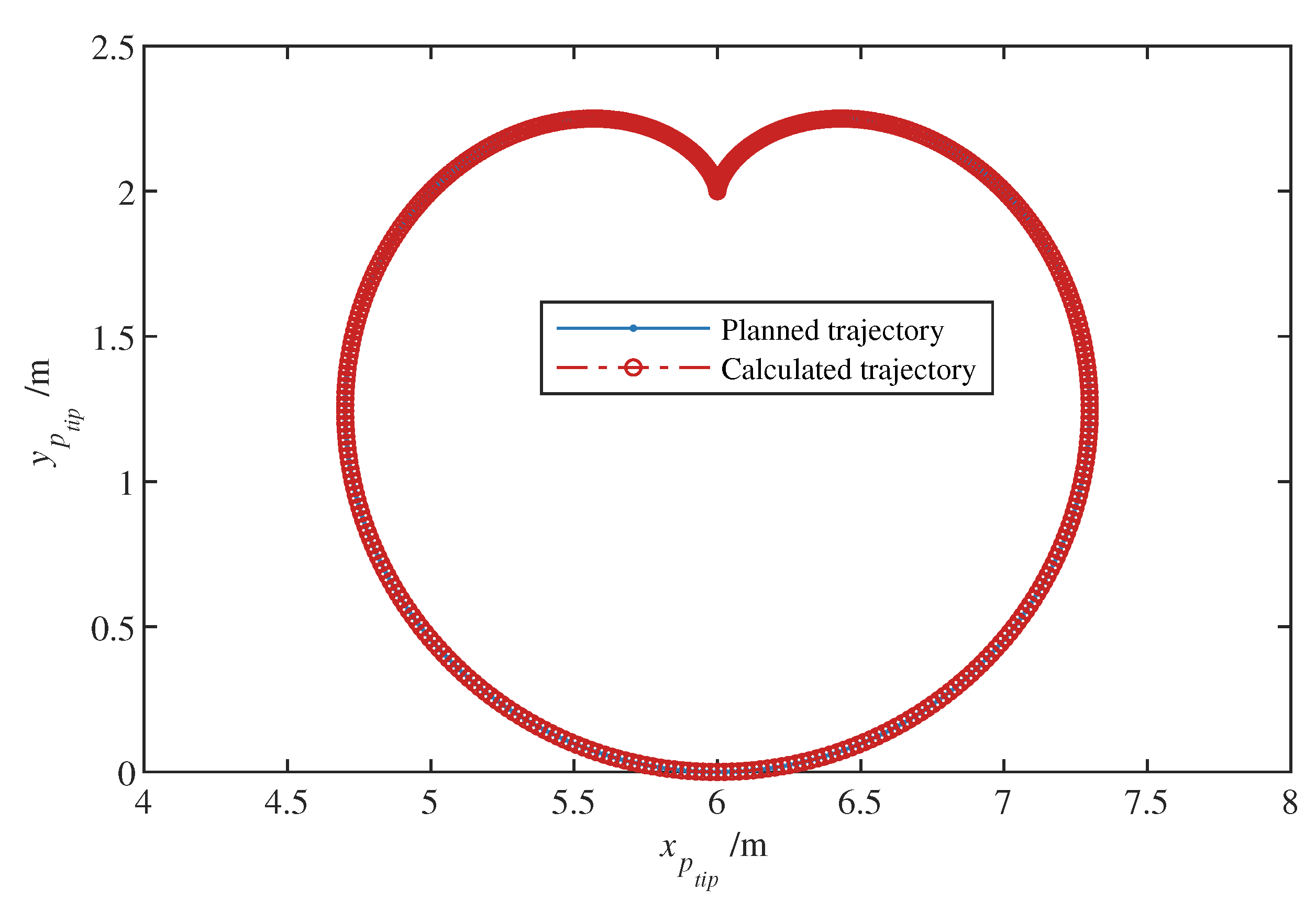
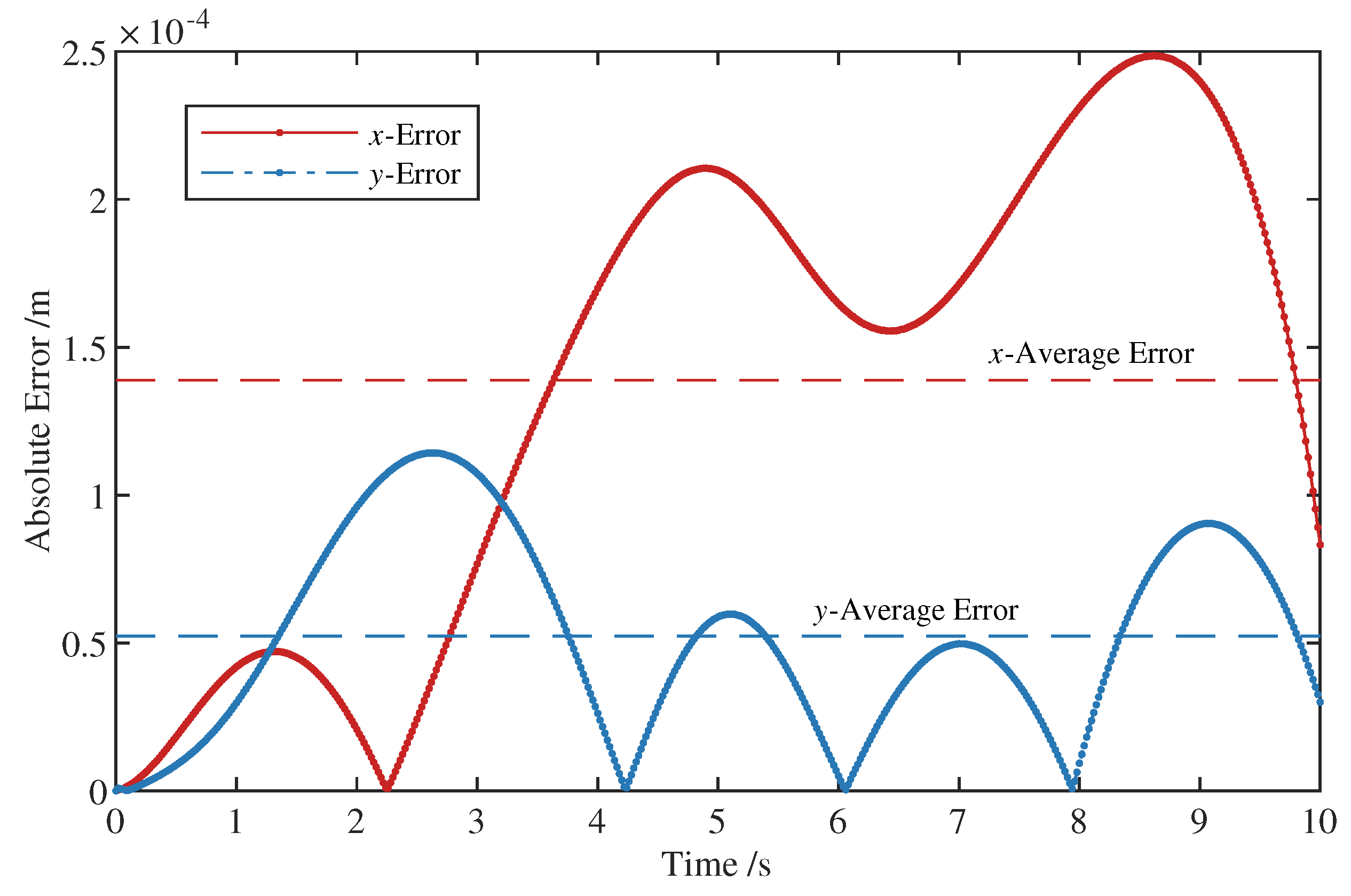
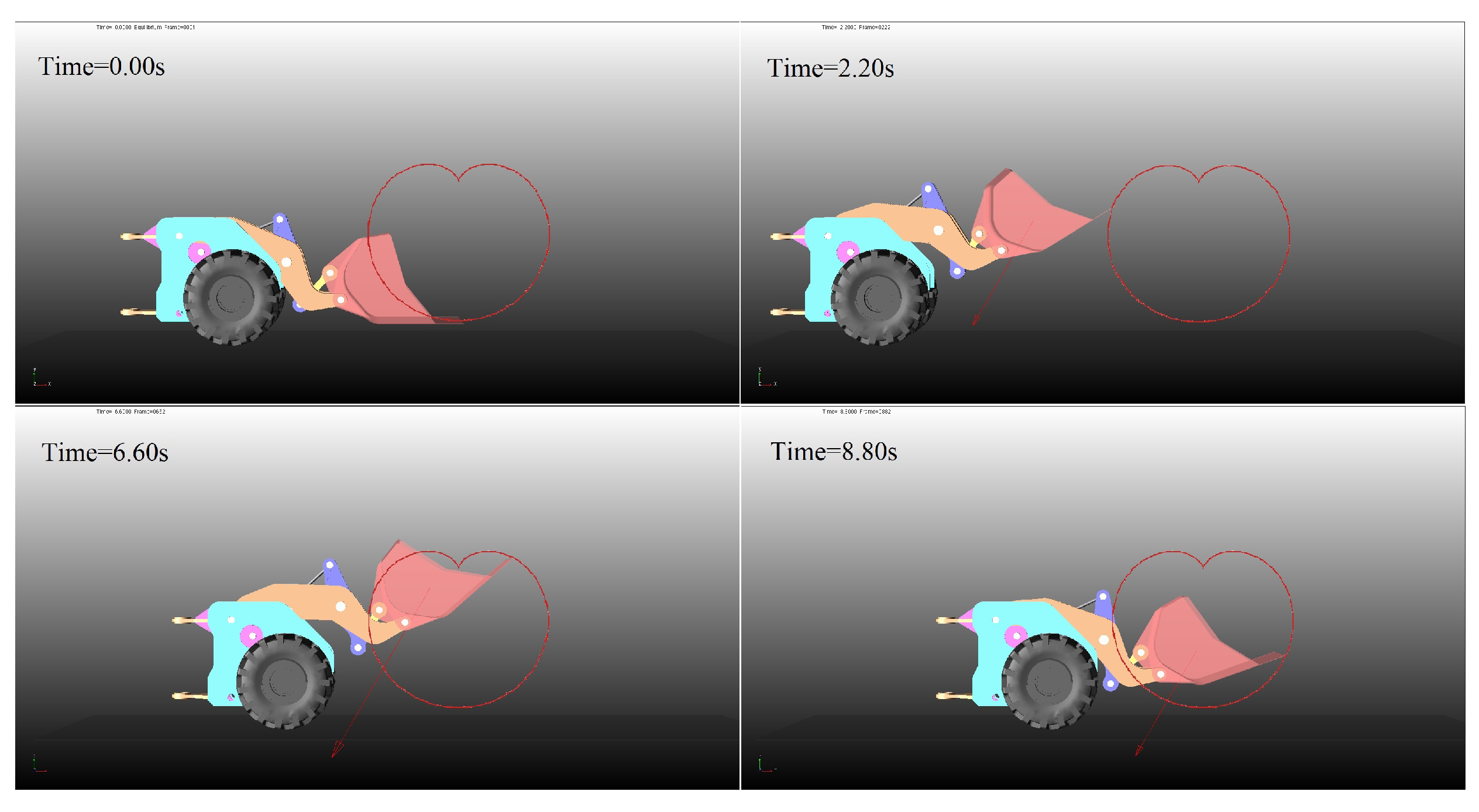
5.1. Validation of the Kinematic Model
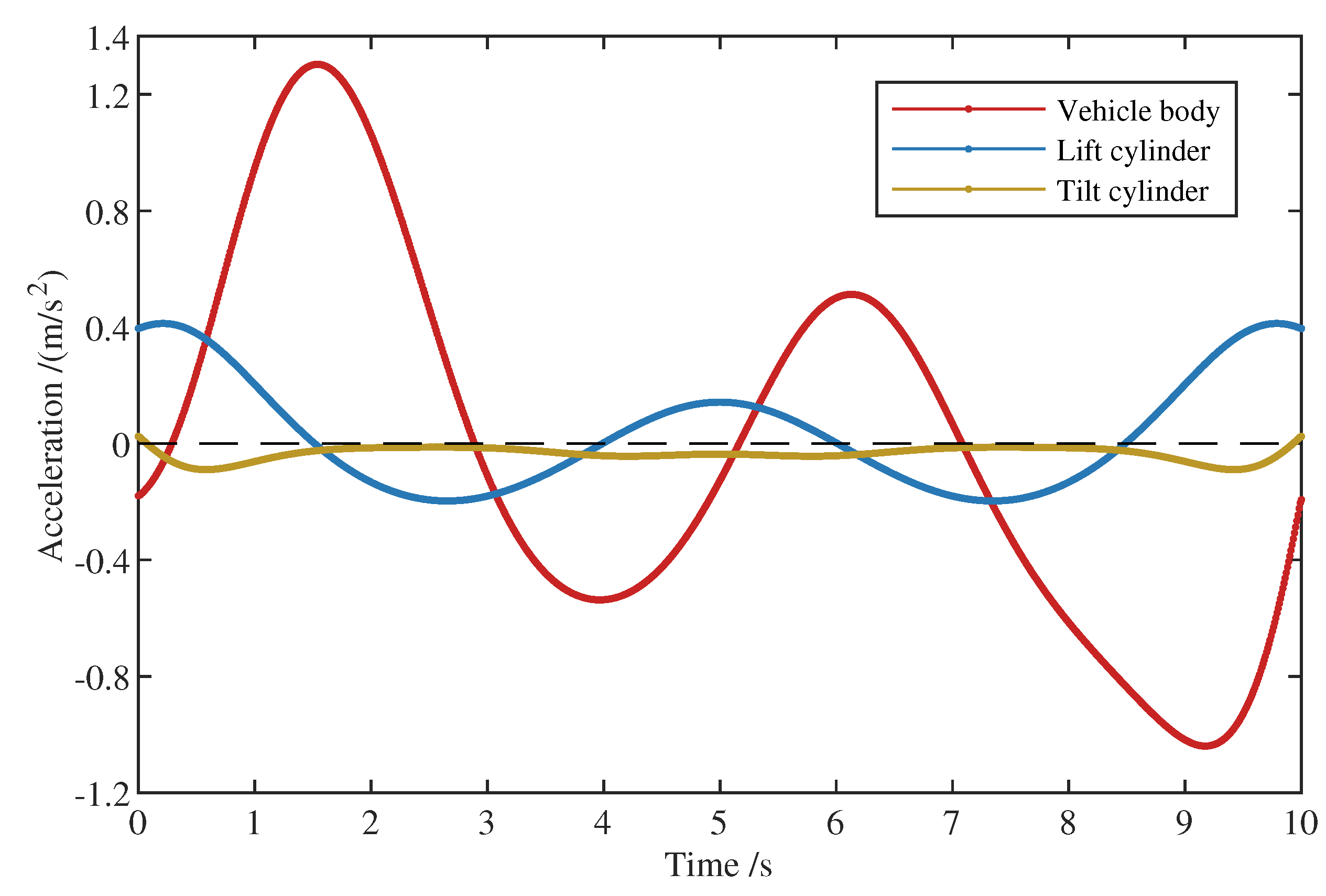
5.2. Validation and Analysis of the Dynamic Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| acceleration vector of any point of body i ; | |
| components of acceleration vector given in coordinate frame ; | |
| , | length vector from point to point () and its magnitude (), respectively; |
| ,, , | matrices of , , and dimensions for generalized force , respectively; |
| ,, , | items of matrices , , and , respectively; |
| , | matrices of and dimensions for kinetic energy , respectively; |
| , | items of matrices and , respectively; |
| matrix of dimensions for potential energy ; | |
| items of matrix ; | |
| unit vector of dimensions on i-th joint axis; | |
| components of unit vector given in coordinate frame ; | |
| skew-symmetric matrix associated with vector ; | |
| , | total kinetic energy and total potential energy of system, respectively; |
| , | kinetic energy and potential energy of body i, respectively; |
| , | matrices of kinetic energy and potential energy , respectively; |
| force matrix of , , ; | |
| , | total force vector of all non-conservative forces driving the vehicle’s motion and its magnitude, respectively; |
| piston force of lift hydraulic cylinder; | |
| piston force of tilt hydraulic cylinder; | |
| , | equivalent force vector exerted by the working load on the bucket and its magnitude, respectively; |
| , | component forces of on -axis and -axis in coordinate frame , respectively; |
| , | driving force vector for vehicle’s motion and its magnitude, respectively; |
| , | generalized force vector exerted by body 5 on body 4 and its magnitude, respectively; |
| , | generalized force vector exerted by body 5 on body 3 and its magnitude, respectively; |
| g | magnitude of gravity acceleration vector; |
| acceleration vector of gravity given in Earth’s inertial frame ; | |
| identity matrix of dimensions; | |
| inertia tensor of body j in local coordinate frame ; | |
| ,, | moments of inertia of body j relative to -axis, -axis and -axis, respectively; |
| , , | products of inertia of body j relative to -axis, -axis and -axis, respectively; |
| total length of lift hydraulic cylinder; | |
| , | First and second derivatives of , respectively; |
| total length of tilt hydraulic cylinder; | |
| , | First and second derivatives of , respectively; |
| , | length vector from point i to point j and its magnitude, respectively; |
| , | First and second derivatives of , respectively; |
| , | length vector from point to point () and its magnitude (), respectively; |
| components of length vector given in coordinate frame ; | |
| length vector from point to point (); | |
| components of length vector given in coordinate frame ; | |
| components of length vector from point to point () given in Earth’s inertial frame ; | |
| L | Lagrange function; |
| mass of body i; | |
| diagonal matrix of dimensions associated with mass ; | |
| mass center point of body i; | |
| ,, , | torques of forces , , , and to -axis in coordinate frame , respectively; |
| coordinate frame on i-th joint fixed to body i; | |
| coordinate frame fixed to Earth’s inertial system; | |
| coordinate frame on mass center fixed to body j; | |
| any point of body i; | |
| point of bucket tip; | |
| non-conservative generalized force on i-th generalized coordinate; | |
| force matrix of ; | |
| R | equivalent action point of on bucket; |
| transformation matrix from ground coordinate frame to Earth’s inertial reference frame ; | |
| , , | transformation matrix from to reference frame and its inverse matrix and transposition matrix, respectively; |
| Rodriguez matrix of dimensions; | |
| ; | |
| ; | |
| ; | |
| ; | |
| ; | |
| ; | |
| driving displacement of vehicle body; | |
| , | First and second derivatives of respectively; |
| components of driving displacement vector of vehicle body given in coordinate frame ; | |
| , | First and second derivatives of respectively; |
| t | time variable; |
| total time of a cycle for prototype simulation; | |
| velocity vector of any point of body i ; | |
| components of velocity vector given in coordinate frame ; | |
| velocity vector of mass center of body i given in coordinate frame ; | |
| , , | -axis, -axis, -axis of coordinate frame , respectively; |
| ,, | -axis, -axis, -axis of coordinate frame , respectively; |
| , | position coordinates of bucket tip in coordinate frame ; |
| angular acceleration of body i ; | |
| components of angular acceleration given in coordinate frame ; | |
| skew-symmetric matrix associated with vector ; | |
| angle ; | |
| , | First and second derivatives of respectively; |
| characteristic coefficient of Cartesian curve function; | |
| polar angle of Cartesian curve in polar coordinate frame; | |
| relative rotation angle of body i with respect to body i-1 carried out about the joint axis; | |
| , | First and second derivatives of , respectively; |
| attitude angle of bucket tip in coordinate frame ; | |
| generalized coordinate matrix of ; | |
| , | generalized coordinate and generalized velocity in system, respectively; |
| characteristic coefficient of expression about ; | |
| polar radius of Cartesian curve in polar coordinate frame; | |
| total torque of all non-conservative forces driving i-th joint rotating; | |
| inclination angle of working surface to level surface (regarded as pitch angle of vehicle body); | |
| rotation angle of relative to -axis; | |
| direction angle of in coordinate frame ; | |
| , | kinematic mapping functions; |
| , | dynamic mapping functions; |
| angular velocity of body i ; | |
| components of angular velocity given in coordinate frame ; | |
| skew-symmetric matrix associated with vector . |
References
- Dadhich, S.; Bodin, U.; Andersson, U. Key challenges in automation of earth-moving machines. Autom. Constr. 2016, 68, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Gao, G.; Wang, J.; Ma, T.; Han, Y.; Yang, X.; Li, X. Optimisation strategy of torque distribution for the distributed drive electric wheel loader based on the estimated shovelling load. Veh. Syst. Dyn. 2022, 60, 2036–2054. [Google Scholar] [CrossRef]
- Backman, S.; Lindmark, D.; Bodin, K.; Servin, M.; Mörk, J.; Löfgren, H. Continuous Control of an Underground Loader Using Deep Reinforcement Learning. Machines 2021, 9, 216. [Google Scholar] [CrossRef]
- Dadhich, S. Automation of Wheel-Loaders. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2018. [Google Scholar]
- Gong, J.; Cui, Y. Track planning for a wheel loader in a digging. J. Mech. Eng. 2009, 45, 29–34. [Google Scholar] [CrossRef]
- Liang, G.; Liu, L.; Meng, Y.; Gu, Q.; Fang, H. Dynamic modelling and accuracy analysis for front-end weighing system of LHD vehicles. Proc. Inst. Mech. Eng. Part K J. -Multi-Body Dyn. 2021, 235, 514–535. [Google Scholar] [CrossRef]
- Gong, J.; Bao, J.; Yi, G.; Cui, Y. Trajectory-following control for manipulator of wheel loaders based on computed torque. J. Mech. Eng. 2010, 46, 141–146. [Google Scholar] [CrossRef]
- Kang, H.; Jung, W.; Lee, C. Modeling and Measurement of Payload Mass of the Wheel Loader in the Dynamic State Based on Experimental Parameter Identification; Technical Report, SAE Technical Paper: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Kudryavcev, E. Modeling of Efforts on Cylinder of Boom Lift of Small Loader. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1079, p. 052045. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Yang, J.; Ge, L.; Hao, Y.; Quan, L. Research on the Characteristics of Wheel Loader Boom Driven by the Asymmetric Pump Controlled System. J. Mech. Eng. 2021, 57, 258–266, 284. [Google Scholar] [CrossRef]
- Fales, R.; Spencer, E.; Chipperfield, K.; Wagner, F.; Kelkar, A. Modeling and Control of a Wheel Loader With a Human-in-the-Loop Assessment Using Virtual Reality. J. Dyn. Syst. Meas. Control 2005, 127, 415–423. [Google Scholar] [CrossRef]
- Sarata, S.; Osumi, H.; Kawai, Y.; Tomita, F. Trajectory arrangement based on resistance force and shape of pile at scooping motion. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3488–3493. [Google Scholar] [CrossRef]
- Takahashi, Y.; Yasuhara, R.; Kanai, O.; Osumi, H.; Sarata, S. Development of bucket scooping mechanism for analysis of reaction force against rock piles. In Proceedings of the 23rd International Symposium on Automation and Robotics in Construction, Zadar, Croatia, 24–27 October 2006; pp. 476–481. [Google Scholar]
- Wang, W.; Wang, T.; Zhao, H.; Wei, H. Lean weight about dynamic weighing of loaders. J. Mech. Eng. 2007, 43, 106–110. [Google Scholar] [CrossRef]
- Worley, M.; La Saponara, V. A simplified dynamic model for front-end loader design. Proc. Inst. Mech. Eng. Part C Journal Mech. Eng. Sci. 2008, 222, 2231–2249. [Google Scholar] [CrossRef]
- Roskam, R.; Dobkowitz, D. Modeling of a front end loader for control design. In Proceedings of the 2015 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; pp. 442–447. [Google Scholar] [CrossRef]
- Yung, I.; Freidovich, L.; Vázquez, C. Payload estimation in front-end loaders. In Proceedings of the MCG 2016—5th International Conference on Machine Control & Guidance, Vichy, France, 5–6 October 2016. [Google Scholar]
- Lindmark, D.M.; Servin, M. Computational exploration of robotic rock loading. Robot. Auton. Syst. 2018, 106, 117–129. [Google Scholar] [CrossRef] [Green Version]
- Wan, Y.; Song, X.; Yu, L.; Yuan, Z. Load Identification Model and Measurement Method of Loader Working Device. J. Vib. Meas. Diagn. 2019, 39, 582–589. [Google Scholar] [CrossRef]
- Brinkschulte, L.; Hafner, J.; Geimer, M. Real-time load determination of wheel loader components. Atzheavy Duty Worldw. 2019, 12, 62–68. [Google Scholar] [CrossRef]
- Fernando, H.; Marshall, J.A.; Larsson, J. Iterative learning-based admittance control for autonomous excavation. J. Intell. Robot. Syst. 2019, 96, 493–500. [Google Scholar] [CrossRef] [Green Version]
- Madau, R.; Colombara, D.; Alexander, A.; Vacca, A.; Mazza, L. An online estimation algorithm to predict external forces acting on a front-end loader. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2021, 235, 1678–1697. [Google Scholar] [CrossRef]
- Yuan, Z.; Lu, Y.; Hong, T.; Ma, H. Research on the load equivalent model of wheel loader based on pseudo-damage theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1036–1048. [Google Scholar] [CrossRef]
- Frank, B.; Kleinert, J.; Filla, R. Optimal control of wheel loader actuators in gravel applications. Autom. Constr. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Sánchez, M.C.; Torres-Torriti, M.; Cheein, F.A. Online Inertial Parameter Estimation for Robotic Loaders. IFAC-PapersOnLine 2020, 53, 8763–8770. [Google Scholar] [CrossRef]
- Yuan, Z.; Ma, H.; Lu, Y.; Zhu, S.; Hong, T. The application of load identification model on the weld line fatigue life assessment for a wheel loader boom. Eng. Fail. Anal. 2019, 104, 898–910. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Šalinić, S.; Bošković, G.; Nikolić, M. Dynamic modelling of hydraulic excavator motion using Kane’s equations. Autom. Constr. 2014, 44, 56–62. [Google Scholar] [CrossRef]
- Angeles, J.; Ma, O.; Rojas, A. An algorithm for the inverse dynamics of n-axis general manipulators using Kane’s equations. Comput. Math. Appl. 1989, 17, 1545–1561. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, W.; Frimpong, S. Compound mechanism modeling of wheel loader front-end kinematics for advance engineering simulation. Int. J. Adv. Manuf. Technol. 2015, 78, 341–349. [Google Scholar] [CrossRef]
- Lurie, A.I. Analytical Mechanics; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Yin, J.; Shen, D.; Du, X.; Li, L. Distributed Stochastic Model Predictive Control With Taguchi’s Robustness for Vehicle Platooning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15967–15979. [Google Scholar] [CrossRef]
- Shen, D.; Chen, Y.; Li, L. State-feedback Switching Linear Parameter Varying Control for Vehicle Path Following Under Uncertainty and External Disturbances. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 3125–3132. [Google Scholar] [CrossRef]




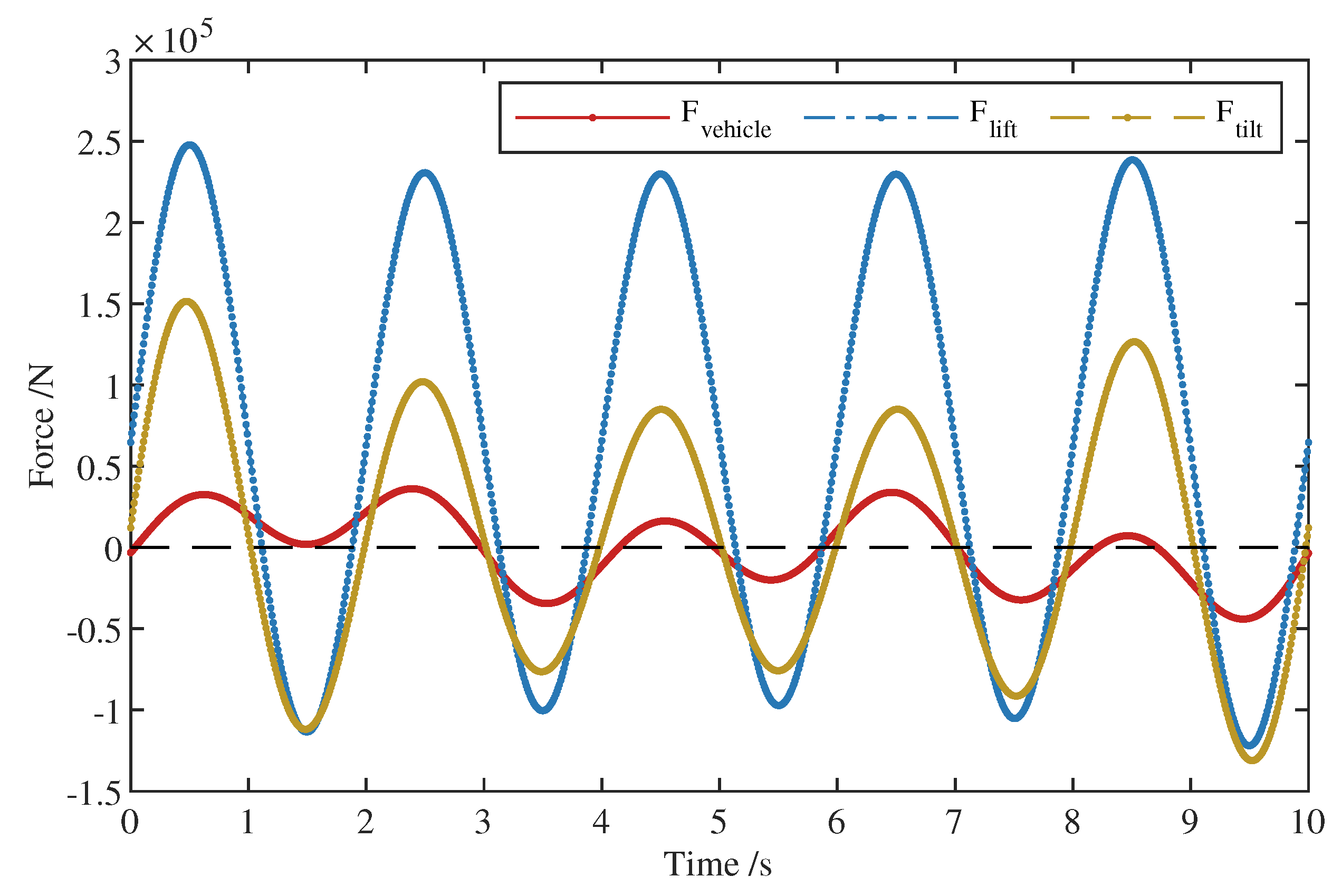

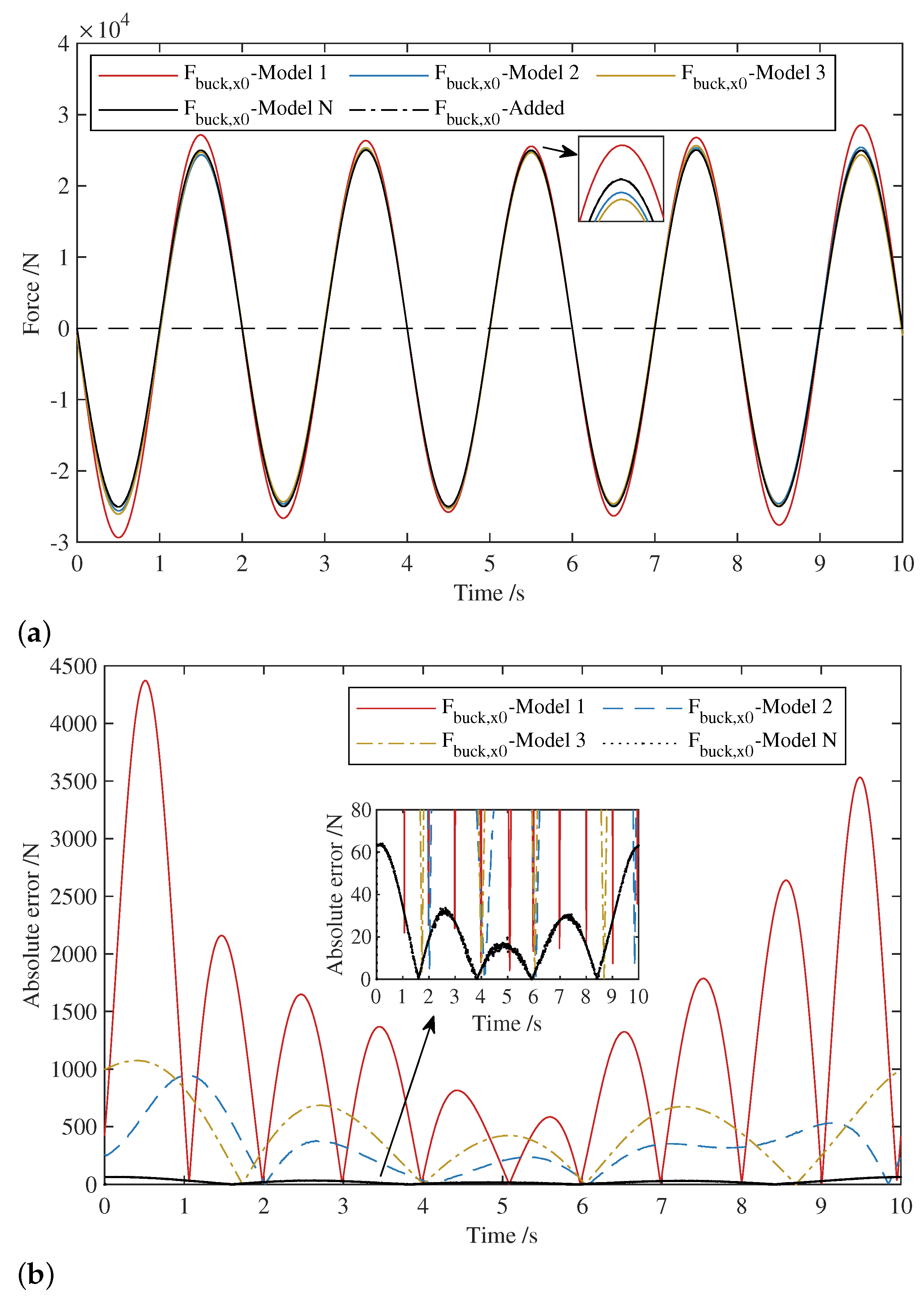
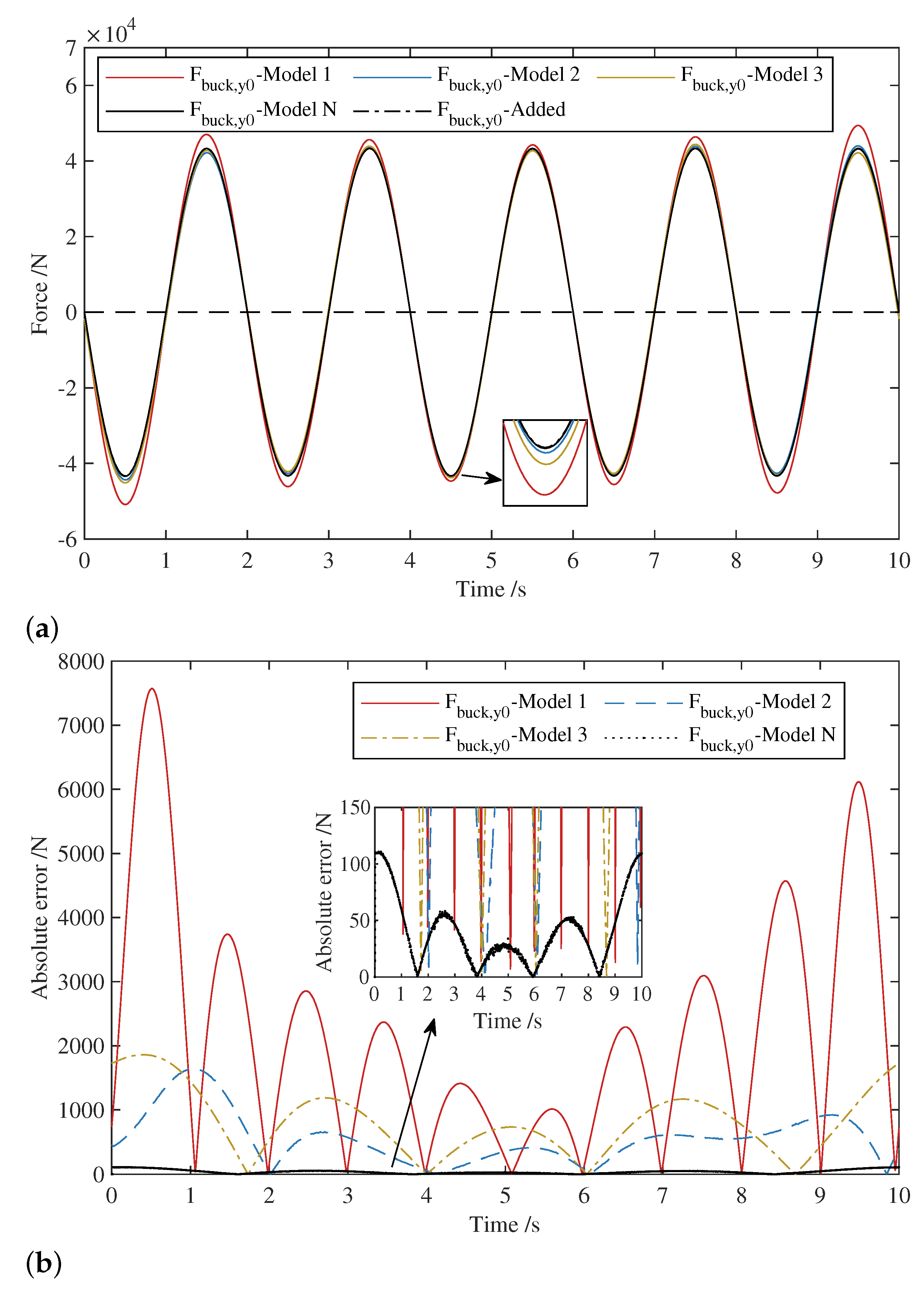
| Model 1 | Model 2 | Model 3 | Model N | ||
|---|---|---|---|---|---|
| 11,018.17 | 11,314.74 | 328.40 | 55.72 | ||
| /N | 1271.63 | 322.52 | 467.70 | 23.26 | |
| 2202.52 | 558.62 | 810.08 | 40.30 | ||
| 29,347.76 | 27,032.53 | 748.03 | 117.95 | ||
| /N | 4372.93 | 946.42 | 1074.77 | 63.96 | |
| 7574.14 | 1639.25 | 1861.56 | 110.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, G.; Liu, L.; Meng, Y.; Chen, Y.; Bai, G.; Fang, H. Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body. Machines 2023, 11, 9. https://doi.org/10.3390/machines11010009
Liang G, Liu L, Meng Y, Chen Y, Bai G, Fang H. Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body. Machines. 2023; 11(1):9. https://doi.org/10.3390/machines11010009
Chicago/Turabian StyleLiang, Guodong, Li Liu, Yu Meng, Yanhui Chen, Guoxing Bai, and Huazhen Fang. 2023. "Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body" Machines 11, no. 1: 9. https://doi.org/10.3390/machines11010009
APA StyleLiang, G., Liu, L., Meng, Y., Chen, Y., Bai, G., & Fang, H. (2023). Dynamic Modeling and Analysis of Loader Working Mechanism Considering Cooperative Motion with the Vehicle Body. Machines, 11(1), 9. https://doi.org/10.3390/machines11010009





