Influence of Rotation Speed and Gas Content on the Transient Gas–Liquid Two-Phase Flow of an Electric Submersible Pump

Abstract

In order to study the internal flow characteristics of the electric submersible pump (ESP) when the gas–liquid two-phase flow is conveyed by the variable frequency variable speed operation and the change of the imported gas content, the impeller of the Q10# ESP is taken as the research object, based on the Eulerian-Eulerian non-homogeneous phase. The flow model, the unsteady Reynolds time-averaged N-S equation, and the standard k-ε turbulence model are used for transient simulation calculations of the gas–liquid two-phase flow in the impeller of the ESP. Calculations show that with the rotation of the impeller, the gas phase is unevenly distributed in the flow channel. The gas phase is mainly concentrated on the inlet side of the flow channel near the front cover, and the gas phase exhibits periodic aggregation and diffusion in the flow channel. When the impeller speed increases, the period of periodic accumulation and diffusion of gas in the flow channel is shortened and the gas concentration in the impeller decreases, the overall flow velocity in the flow channel increases, and the pressure difference between the inlet and outlet increases. The pressure difference between the two sides of the blade is proportional to the speed of the impeller, and the fluctuation frequency of the blade surface also increases. As the gas content increases, the maximum concentration of gas phase in the flow channel increases. The area occupied by the high concentration of gas phase in the flow channel expands toward the blade’s working surface, and periodically accumulates, diffuses, and grows. The gas-liquid splitting area shrinks toward the front cover side and the pump. The internal pressure increases slightly, the main flow velocity increases, and the vortex action range increases.

1. Introduction

ESPs, due to their large displacement range, simple operation, convenient management, insensitivity to well deviation, and other advantages, have become the second-most used oil production equipment in the world of oil fields [1].

In recent years, the two-phase flow problem in ESPs has mainly been based on experimental methods. Pan Binghui et al. discussed the influence of gas concentration and gas phase particle diameter on the external characteristics of the pump when the ESP transports gas and liquid phases. Li Guidong [2] carried out a numerical simulation study on the internal flow pattern and force state of a certain model of ESP under gas–liquid two-phase flow, and studied the gas volume fraction and pressure pulsation in the pump. The results show that the main frequency of pressure pulsation at different monitoring points under different air content is equal to the passing frequency of the blade. With the increase in the gas volume fraction, the periodic change in the pressure amplitude of the monitoring point with time is destroyed, and the unevenness of the gas–liquid two-phase flow in the impeller channel is aggravated. Treviso of the University of Tulsa applied a high-speed camera to a research experiment of the two-phase flow of the ESP affected by the viscosity and speed of the liquid phase. In the experiment, four states of bubbles in the flow channel were captured. The author pointed out that increasing the speed can alleviate the phenomenon of blockage of the flow channel in the gas phase caused by the increase in liquid viscosity [2,3]. Barrios et al. [4] studied the gas–liquid two-phase flow in a submersible electric pump from both theoretical and experimental perspectives, analyzed the flow pattern and cavitation behavior in the pump, and made a visual measurement of cavitation diameter and internal flow. The authors found that under surge conditions, the pump’s air inlet would form a large air pocket. Experimental research can visually observe the evolution process and evolution law of bubbles in the flow channel of the ESP, and observe the changes in the shape and position of the bubbles, but it cannot accurately reveal the changes in the internal flow field and obtain the transient load changes of the blades. Salman et al. [5] studied the two-phase flow of the pump at fixed speed and different gas volume fractions, and found that the lower the gas volume fraction, the better the pump performance.

With the application of CFD technology in the research on the characteristics of ESPs, Zhu et al. [1] used 3D-CFD code with a frozen rotor interface model to simulate the flow inside the ESP, including velocity and pressure fields, as well as the recirculation and separation of the flow in 2016. Two supplementary models for bubble size prediction and drag coefficient calculation were proposed. It was found that the in situ prediction results of the mechanism model were in good agreement with the numerical simulation results. Stel et al. [6] pointed out the CFD simulation results of a multistage ESP. Pineda et al. [7] obtained the distribution and concentration of the dispersed phase in the rotary centrifugal pump by combining the realizable turbulence model and the VOF multiphase model, and found that the average voidage increased at a higher gas flow rate and a lower pressure. The rotating speed had no effect on the average porosity, but it increased the variation in the porosity with time, indicating that the higher the rotating speed, the more cavitation and the more dispersed the gas phase. Asad et al. [8] concluded in their study of the performance of gas–liquid multiphase flow in centrifugal pumps that increasing the speed will reduce the diameter of bubbles, which makes the impeller channel of the pump more stable when pumping gas–liquid two-phase flow, improving the pump performance. Michael et al. [9] conducted experimental research on gas–liquid two-phase flow in centrifugal pumps and supplemented the internal flow details using single-phase numerical simulation, further investigating the impact of rotational speed on pump performance. The final conclusion is that in gas–liquid two-phase flow, an increase in rotational speed will enhance the mixing of the two items and increase the turbulence of the flow inside the pump. In 2017, CFD simulated the influence of free gas entrainment flow on the pump [10], verifying the reliability of the bubble size model of impeller passage of ESPs proposed by Zhu, J., and proving that CFD simulation is an effective method to study multiphase flow. Unlike single-phase simulation, two-phase simulation requires solving the conservation equations of mass, momentum, and energy in the continuous and dispersed phases, as well as solving the interfacial momentum and heat transfer. There is not much research on CFD technology in the simulation of ESP s, especially the difficult transient two-phase flow, which requires continuous exploration and research. In 2019, Zhu et al. [11] used the hexahedral grid generated by ANSYS ICEM to simulate the gas–liquid two-phase flow of an ESP, and compared the simulation results with the corresponding visualization experiments of Barrios (2007). The authors found that the transient Eulerian-Eulerian model is better than the VOF model in studying the gas–liquid two-phase flow and bubble dynamic behavior in the ESP. In Liang et al. [12], based on computational fluid dynamics, Liang et al. used high-speed camera technology and CFD modeling technology to analyze the changes in the free surface of the aeration tank and the evolution of the internal flow field and flow pattern of the inverted umbrella aerator. The high-speed photography results are consistent with the numerical simulation results, which verifies the effectiveness of the CFD model in simulating two-phase flow and lays the foundation for the selection of corresponding methods in this article. In 2020, Li et al. [13] analyzed the quantitative relationship between the local Euler head distribution and internal flow of a centrifugal impeller. The study found that the local Euler head at the entrance was mainly affected by the clockwise vortex on the suction side of the blade. At the exit, it is affected by the relative motion of the clockwise and counterclockwise vortices. In 2021, Li et al. [14] in order to adapt to the turbulence in the pump, improved upon the Drag coefficient model studied by their predecessors, which improved the simulation prediction accuracy of pump performance and was more consistent with the experimental results. Li et al. [15] established a predictive model that helps guide the transient hydraulic design and transient energy characteristics of pumps by combining numerical simulation with experiments. This method was also used to analyze the impact of cavitation and its deterioration on the flow field structure inside the impeller and the overall performance of the pump. The simulation results were validated through experiments, proving that the deterioration of cavitation can reduce the output power of the impeller and reduce the overall performance of the pump [16]. Luo et al. [17] validated the numerical simulation results by numerically simulating the unsteady flow process inside the jet pump and establishing corresponding experiments. The experimental results proved the credibility of the simulation method, laying a theoretical foundation for the subsequent optimization design of the jet pump, which is conducive to improving and improving the overall performance of the pump. It can be seen that the simulation of centrifugal pumps using CFD technology in this article is feasible and there is not much difference compared to the experimental results. In the first part of reference [18], multiple researchers have conducted much research on the flow characteristics of pumps. Based on the conclusions of these scholars, this article conducts unsteady simulation of gas–liquid two-phase flow in the pump under the most widely used variable frequency regulation conditions, and studies the transient impact of rotational speed on the gas–liquid two-phase flow performance of ESPs. This further improves the understanding of gas–liquid two-phase flow in ESPs, provides guidance for the application of ESPs, and provides a theoretical basis for improving or designing ESPs with the ability to transport high-gas-content mixed liquids with a wider range of applications.

2. Structure Size and Grid Division of ESPs

This article takes the Q10 ESP impeller as an example (Figure 1), and the structural parameters are shown in

Table 1. Main parameters of ESP.

Parameter	Numerical Value	Unit
Rate of flow (Q)	100	m3/d
Head of delivery (H)	6.95	m
Rated speed (ne)	2900	r/min
Impeller inlet diameter (D1)	25.8	mm
Outer diameter of impeller (D2)	35.8	mm
Impeller outlet width (b1)	8	mm
Outlet diameter of diffuser (b2)	8	mm
Number of impeller blades	7
Number of diffuser blades	10

.

In this paper, TurboGrid is used to divide the single flow channel of the ESP. Considering the reliability of the calculation results and the calculation economy, the flow channel model is divided into five grids with different density degrees for grid independence analysis. Meshes with different density degrees were selected to simulate the design conditions, and the model calculation results with different mesh numbers are shown in

Table 2. The impact of different grid levels on the performance of ESP.

Impeller Grid Number	Number of Diffuser Grids	Head/m	Power/W	Efficiency
56,900	48,900	4.71	114	0.465
118,232	127,242	4.8	115.5	0.475
153,560	137,677	4.92	116.2	0.49
195,854	173,160	4.91	116.1	0.485
202,889	189,663	4.92	116.2	0.484

.

It can be seen from the results of head, power, and efficiency in Table 2 that when there are 195,854 impellers in a grid single-flow channel and 173,160 grids in the diffuser, the simulation results of head, power, and efficiency tend to be stable. Continuing to refine the grid has little effect on the accuracy of the calculation results. It can be considered that the number of grids is suitable for the solution requirements of this paper. The use of this level of grid can not only ensure the accuracy of the solution but also improve the efficiency of the solution. (Figure 2). It is found that there is no negative grid in the divided grid. According to the requirements using CFX software, the orthogonality range should be greater than 20 degrees, the grid expansion factor should be less than 20, and the aspect ratio should be less than 100. The minimum grid angle is 42°, the orthogonality range is 46.6–89.9°, the aspect ratio range is 1–26, and the extension ratio range is 1–1.79, which satisfies the 2021R2 CFX software’s requirements for mesh quality.

3. Simulation Result Verification

It can be seen from Figure 3 that the numerical simulation results and the experimental results are completely consistent in the same flow range. Among them, the calculation of efficiency and head are within 5% of the experimental error range. It can be seen that the software can predict the external characteristics of the pump accurately and also provides a strong guarantee for further predictive analysis.

4. CFD Calculation Method and Boundary Conditions

Based on ANSYS CFX, the Eulerian-Eulerian non-uniform phase flow model and the unsteady Reynolds time-averaged N-S equation are selected. When compared with traditional technologies, this method is faster, more accurate, and reduces spatial and temporal resolution, reducing computational workload. The liquid phase uses the standard k-ε turbulence model, the turbulence intensity is 5%, the incompressible fluid, and the liquid medium uses water at room temperature; the gas phase uses the unsteady Reynolds time-averaged N-S equation, the incompressible gas phase, and the gas medium uses air at room temperature. The liquid phase is the continuous phase, and the gas phase is the dispersed phase. Considering the slip velocity between the phases, the SIMPLEC algorithm is used to solve the pressure–velocity coupling equations, the discrete difference equation adopts the second-order upwind style, and the diffusion phase and the source phase adopt the second-order central difference scheme.

The inlet and outlet, respectively, define the velocity boundary and static pressure boundary, and the reference pressure is 1 atm. The walls are set to be adiabatic and standard wall functions are used. The liquid phase is a non-slip wall, and the gas phase is a free-slip wall. The wall roughness is set to 12.5. The boundary of the interface is set as the transient rotor stator to connect the impeller domain and the guide wheel domain. The interfaces on both sides of the single runner are set to rotational periodicity, and the pitch changes are 51.429 and 36, respectively.

The calculation accuracy is set to 10^–4. In order to ensure the reliability of the results, the transient solution is solved with the result of the steady-state solution as the initial condition. The total time is the time for the impeller to rotate 40 times, a total of 0.8276 s, and each time the impeller rotates 3° is set as a time step, and the step time is about 1.724 × 10⁻⁴ s.

5. Calculation Results and Analysis of Variable Speed Two-Phase Flow of ESPs

The gas phase volume fraction α = 30%. Taking the rotating speed of 0.8 times rated speed (0.8 n_e), rated speed (1.0 n_e), and 1.2 times rated speed (1.2 n_e) as examples, the distribution diagrams of gas phase volume fraction, pressure field, velocity field, and blade load in the middle section of the impeller flow passage were intersected. The flow mechanism and the dynamic change rule of flow spectrum in the pump were compared and analyzed when the rotation speed was compared with the two-phase flow.

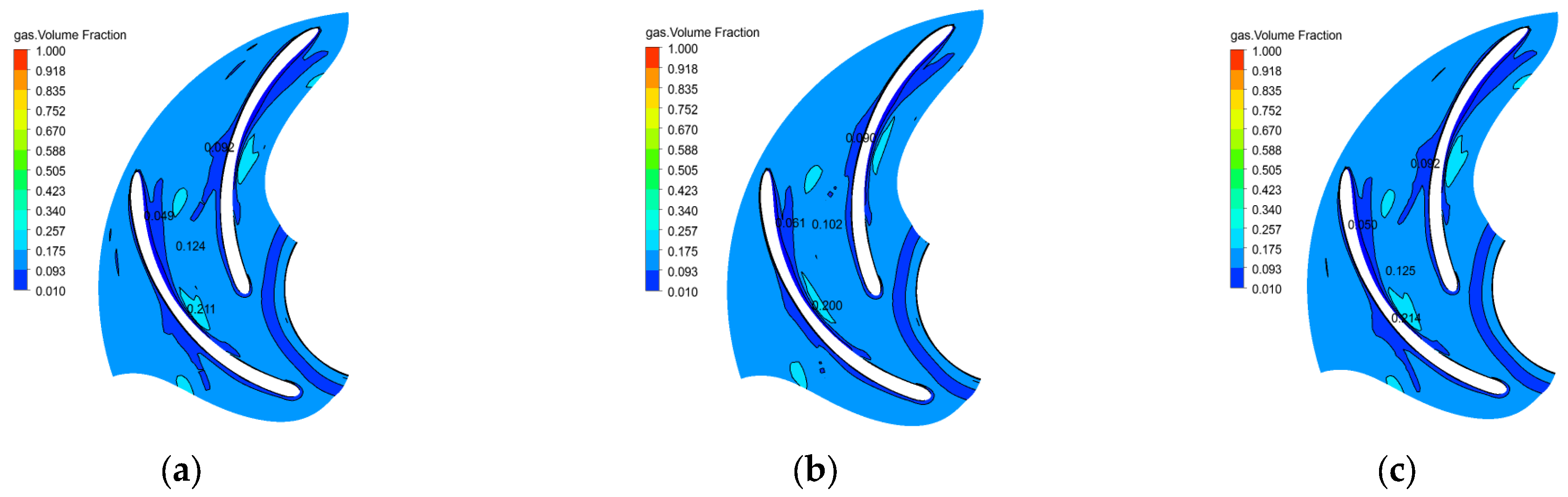
5.1. Transient Law of Gas Volume Fraction Distribution in the Pump

At the same speed, analyzing the cloud chart of the gas volume fraction distribution in the cross-section of the impeller at different times within 40 revolutions, the internal flow of the impeller is obviously periodic. Taking the two recent distributions of the same gas phase volume fraction as a single period judgment standard, the periods of the impeller at 0.8 n_e, 1.0 n_e, and 1.2 n_e speeds correspond to 186°, 174°, and 144°, respectively.

The gas phase volume fraction distribution cloud diagram in the next cycle at 0.8 n_e, 1.0 n_e, and 1.2 n_e speeds is selected for comparison and analysis. As shown in Figure 4, Figure 5 and Figure 6, the gas phase is mainly concentrated on the side of the suction surface of the blade, starting from the distance from the leading edge of the blade at the 0.2 chord length position, and it extends to the trailing edge of the blade and disappears in the three-dimensional wake area, and the air pockets present a non-uniform three-dimensional distribution state in the flow channel. The area with the highest gas concentration in the cross-section of the impeller flow channel is located on the side of the suction surface of the sheet and in a small area 40% chord length away from the leading edge, which becomes the gas core of the long and narrow air bag, where the gas fraction reaches 71%.

In the rotating motion of the impeller, due to the centrifugal force, the density of gas and liquid are different. The liquid gathers on the pressure surface side of the blade, while the gas is squeezed to the suction surface side of the blade by the liquid. As the blade rotates, the air pocket is not stable in one position, and will move back and forth along the blade profile line along the suction side of the blade, and the size of the air core inside will change. The size, shape, and gas phase fraction of the air pockets all show obvious periodicity, starting at a distance of 1/5 from the leading edge, and disappearing in the wake area of the trailing edge, and the gas volume fraction gradually decreases from the gas core to the long tail.

At different speeds, the morphology of gas phase accumulation and diffusion is similar, but the range of convergence is different. As the rotation speed increases, the volume of the air bag becomes smaller, and it is easy to separate and break into small air bags; instead, the gas fraction of the air core becomes smaller. Higher speeds have higher centrifugal force. Due to the large density difference between the gas phase and the liquid phase, the gas phase receives a small centrifugal force and is subjected to a large squeezing force from the liquid phase. The stability of the air bag is poor, and it is difficult for the gas to be concentrated at a high concentration.

When the rotation speeds are 0.8 n_e, 1.0 n_e, and 1.2 n_e, the maximum gas concentrations are 71%, 62%, and 59%, respectively. The starting position of the air pocket from the leading edge is 19%, 23%, and 20% of the chord length, respectively, and all disappear at the tail edge. The periods are 186°, 174°, and 144°, respectively.

Figure 7, Figure 8 and Figure 9 correspond to the mid-section pressure cloud diagrams with impeller speeds of 0.8 n_e, 1.0 n_e, and 1.2 n_e, respectively. At three different speeds, the pressure distributions are similar, and the pressure contours on the cross-section of the flow channel are relatively uniform and have a two-dimensional shape, indicating that at the three speeds, the main flow channel of the impeller flow channel is mainly laminar flow. Laminar flow is not conducive to the breakage of air bags. Excessive air bags can easily cause an air lock of the centrifugal pump and seriously deteriorate the lifting performance of the pump.

As the speed increases, the pressure difference from the inlet to the outlet of the impeller increases, indicating that a higher speed provides a higher head. There is a small lower pressure area at the leading edge of the blade. When the mixed liquid enters the flow channel, it impacts on the leading edge. It is easy to produce negative pressure in a small area on the suction side of the leading edge of the blade, resulting in a lower pressure area. The lower pressure area is also where gas converges. At the starting point, the centrifugal force along the chord length gradually increases, which is also a favorable environment for the formation of air pockets. The lower pressure area at the leading edge also has obvious periodicity. As the impeller speed increases, the lower pressure area decreases, and the pressure difference between the pressure surface and the suction surface increases.

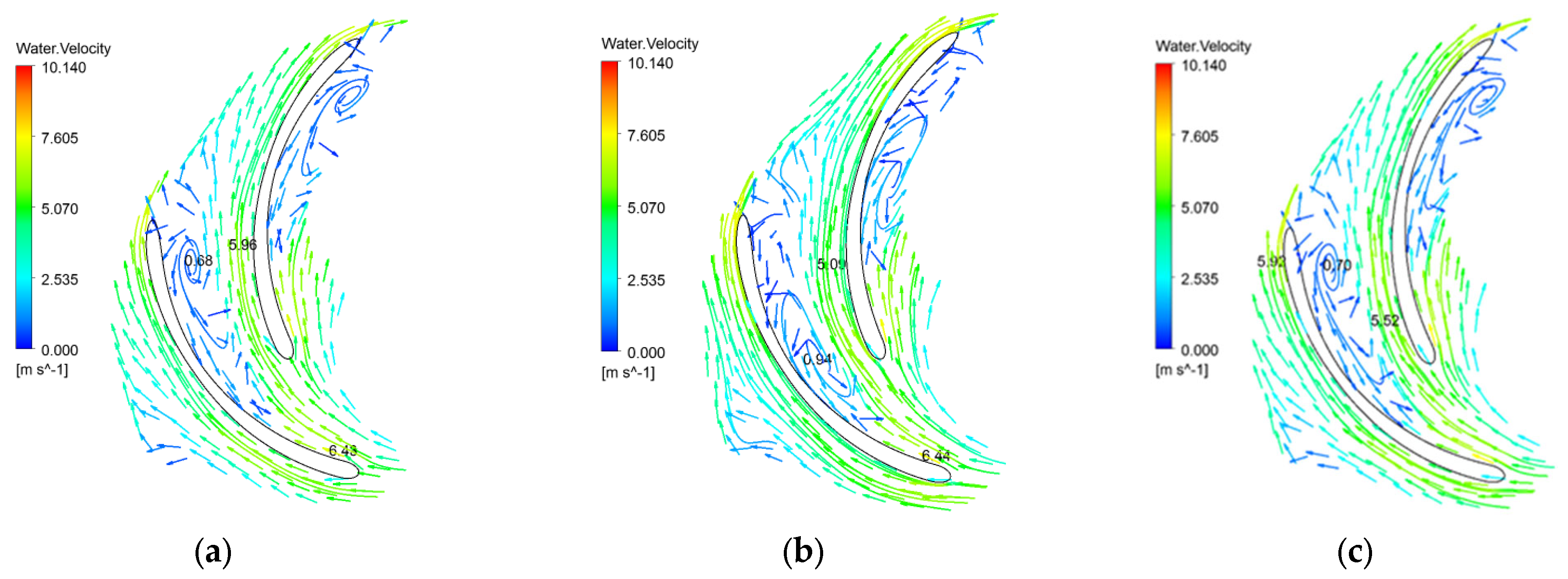
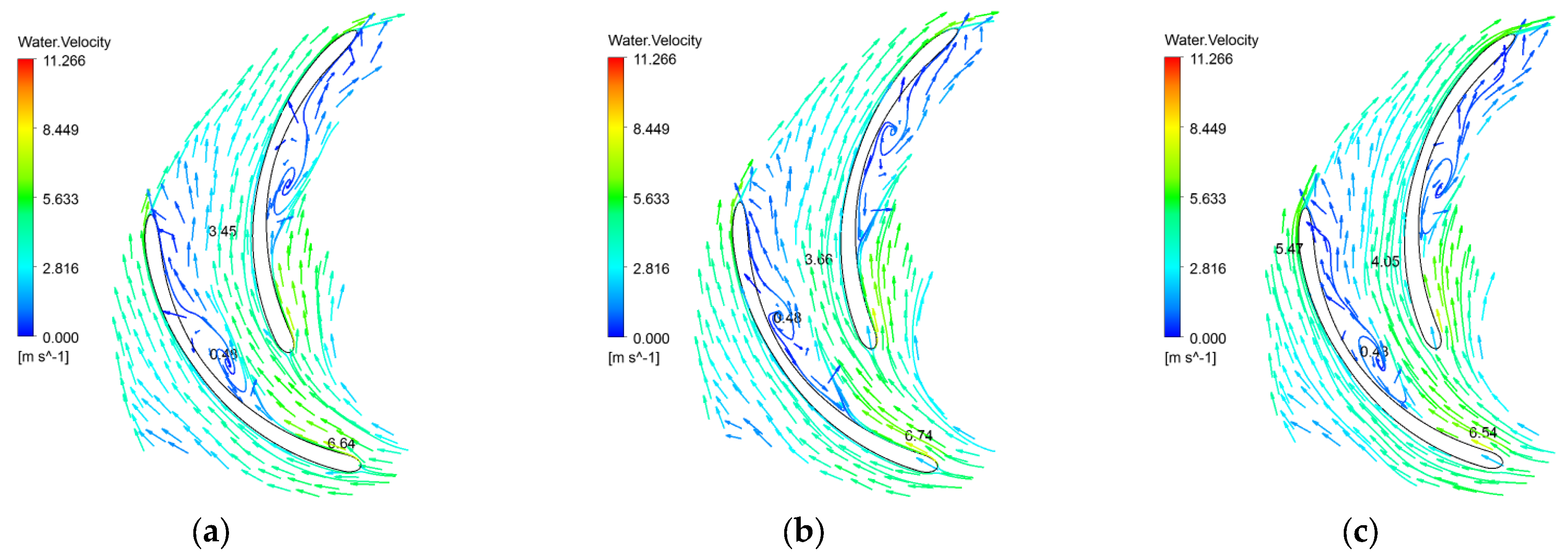
5.2. Transient Distribution of Velocity Field in the Pump

Figure 10, Figure 11 and Figure 12 represent, respectively, 0.8 n_e, 1.0 n_e, and 1.2 n_e, taking the periodic accumulation and diffusion period of the gas phase as a reference, and extracting the velocity vector diagrams at three moments of the cross-section of the middle position of the impeller blade in one period. Through comparative analysis, it is found that when the rotating speed of the impeller increases, the liquid flow velocity in the impeller increases. Along the pressure surface profile of the impeller, the liquid flow from the inlet to the outlet is smooth, showing laminar flow characteristics, and occupying nearly 1/2 of the flow channel. On the suction side of the blade, the liquid flow presents a three-dimensional flow state, and there is an obvious liquid vortex moving continuously up and down the flow passage. The three-dimensional flow region is consistent with the position and range occupied by the air bag. The complexity of liquid phase flow also represents the complexity of gas phase aggregation, separation, and re-aggregation, as well as the constant mixing, separation, and other exchange processes between liquid phase and gas phase. Under the three impeller speeds, the minimum velocity of the liquid phase vortex varies in a small range, between 0.6 and 1 m/s, and the vortex speed gradually decreases when moving from upstream to downstream along the chord direction. From the perspective of the three speed vector diagrams, the main location and range of influence of the vortex are not greatly affected by the change in speed.

5.3. Transient Analysis of Blade Load under Variable Speed Conditions

When the gas volume fraction α = 30% and the rotating speeds are 0.8 n_e and 1.2 n_e, taking the periodic accumulation and diffusion period of the gas phase as a reference, the pressure distribution in the impeller channel at three moments in a period is extracted along the blade profile of the middle section of the blade (see Figure 13 and Figure 14). Along the flow direction of the blade surface (that is, the blade chord direction), the relative chord length of the blade is taken as the abscissa, and the leading edge and trailing edge of the blade correspond to the abscissas of 0 and 1, respectively. The ordinate represents the pressure value on the section profile of the blade. The blade profile refers to the contour line of the blade section. The pressure value is selected from the leading edge, along the pressure surface to the trailing edge, and then back to the leading edge of the blade along the suction surface to form a closed blade load curve (Figure 13 and Figure 14).

When the ESP is carrying out gas–liquid two-phase mixing, the trailing edge of the blade presents a reverse pressure gradient phenomenon where the blade pressure surface pressure is less than the blade suction surface pressure. The high concentration of gas phase in the flow passage forms a low-speed air bag, which “squeezes” the flow passage and reduces the flow area of the flow passage. As a result, the flow velocity of liquid dominated by liquid at the side of the pressure surface in the flow passage increases, especially the velocity near the blade pressure surface, so the pressure on the pressure surface changes greatly. Moreover, the decreasing value near the relative positions of 0.09 and 0.95 at the front segment of the blade were the largest. When the impeller speed increases, the amplitude of the pressure fluctuation at the leading edge of the blade increases, resulting in a greater impact on the leading edge of the blade. At the same time, the fluid will turn abruptly, resulting in significant changes in the amplitude of the local high-pressure and low-pressure areas of the blade head.

The increase in the impeller speed increases the pressure difference between the two sides of the blade, the pressure difference between the inlet and outlet of the blade increases, and the load on the blade also increases. As the impeller rotates, the gas phase presents regular periodic fluctuations in the flow channel, causing regular fluctuations in the load on both sides of the blade. The pressure difference on both sides of the blade fluctuates with small amplitude, and the pressure difference in the front section of the blade fluctuates more obviously. The frequency of the alternating load acting on the blade is about 5.8 × 10³ Hz, which is likely to cause low-cycle fatigue damage of the blade.

6. Calculation Results and Analysis of Two-Phase Flow with Different Gas Content in ESPs

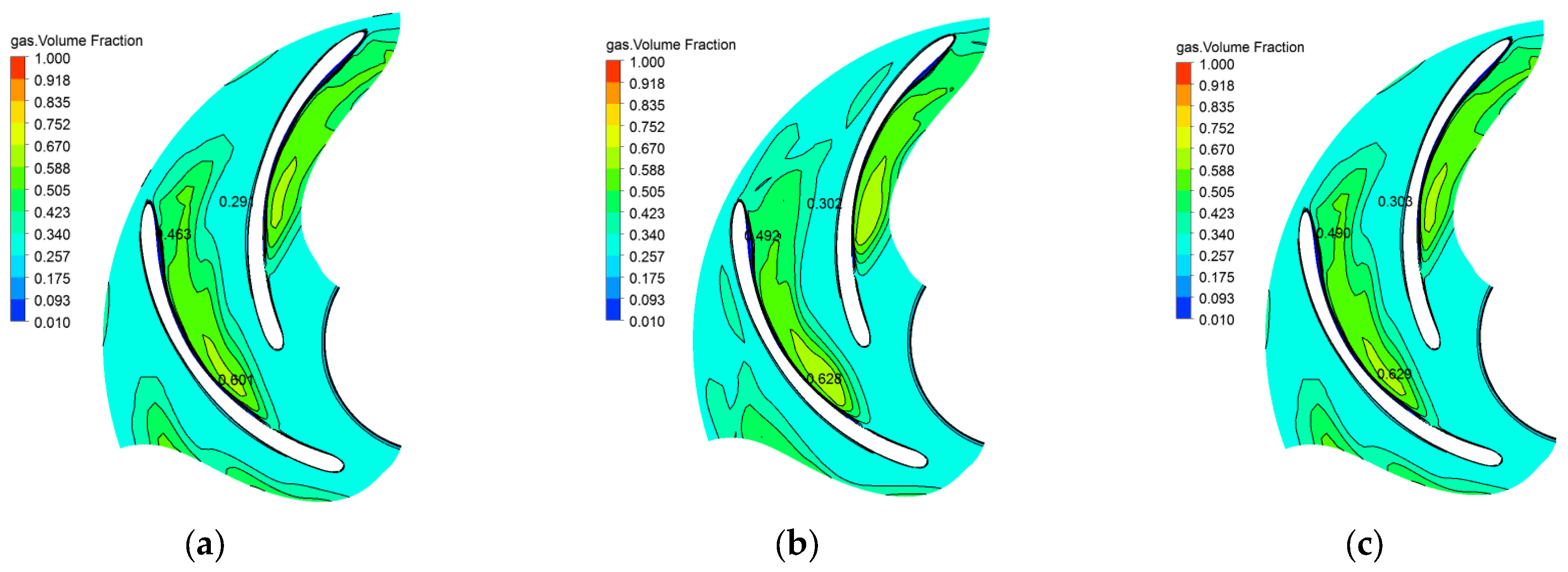
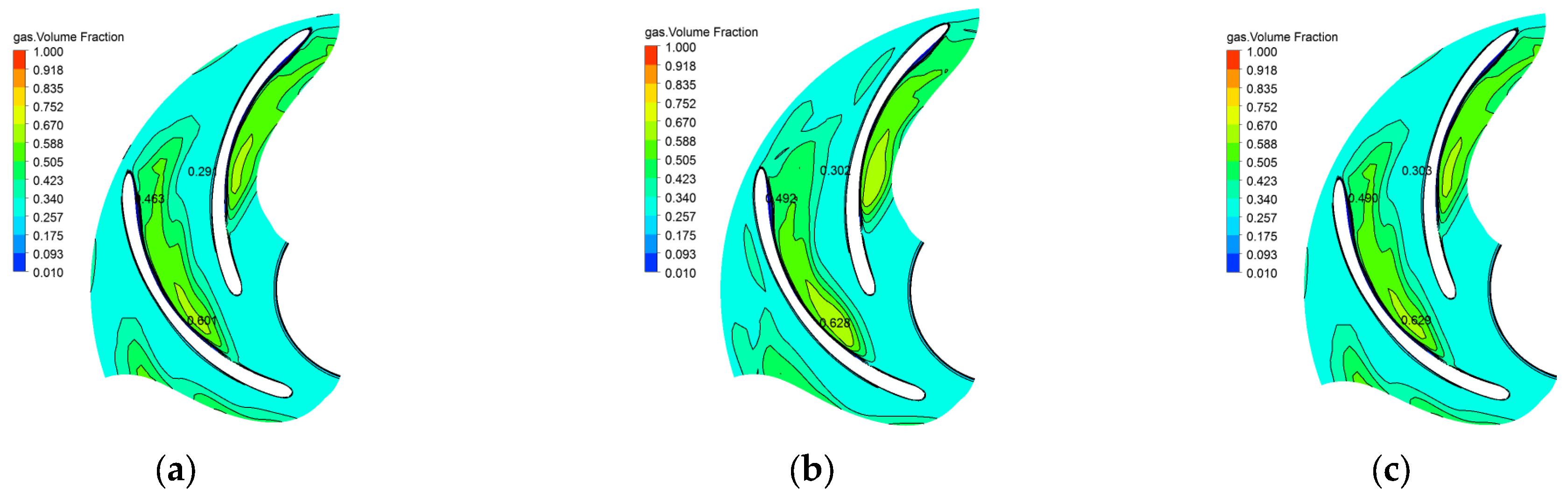
6.1. Transient Law of the Gas Volume Fraction Distribution in the Pump

Under the same gas content, the cloud diagram of the gas volume fraction distribution in the cross-section of the impeller was analyzed at different times within 40 circles, and the internal flow of the impeller was obviously periodic. Taking the two recent distribution diagrams of the same gas phase volume fraction as a single period judgment standard, when the gas content α is 10%, 30%, and 40%, the periods of the impeller correspond to 90°, 174°, and 132°, respectively.

The gas phase volume fraction distribution cloud diagram during a period when the gas content α is 10%, 30%, and 40% are selected for comparison and analysis. As shown in Figure 15, Figure 16 and Figure 17, the gas phase is mainly concentrated on the back side of the blade. When α is 10%, the gas phase is slightly distributed on the working surface, and the gas phase starts at the position of 0.2 chord from the leading edge of the blade on the back and extends to the trailing edge of the blade. When α is 30% and 40%, the gas phase starts at the position of 0.2 chord length from the leading edge of the blade on the working face and extends to the trailing edge of the blade, disappearing in the three-dimensional wake region, and the air bag presents a non-uniform three-dimensional distribution state in the flow passage. When α is 10%, most of the area with the highest concentration of gas phase in the cross-section of the impeller flow path is located on the suction side of the blade, and the area of low-concentration gas phase is mainly located at the front edge of the pressure and the trailing edge of the suction surface. When α is 30% and 40%, the highest concentration of gas phase in the section of the impeller flow passage is located in the small area at the suction surface side of the piece and 0.3 chord length away from the leading edge, which becomes the gas core of the irregular narrow and long air bag, and the gas fraction here reaches 78%.

In the rotating motion of the impeller, due to the centrifugal force, the density of gas and liquid are different. The liquid gathers on the pressure surface side of the blade, while the gas is squeezed to the suction surface side of the blade by the liquid. As the blade rotates, the air pocket is not stable in one position and will move back and forth along the blade profile line along the suction side of the blade, and the size of the air core inside will change. The size, shape, and gas fraction of the air pockets all show obvious periodicity, starting at 1/5 from the leading edge and disappearing in the wake area of the trailing edge. The gas volume fraction gradually decreases from the gas core to the long tail.

As α gradually increases, the morphology of gas phase aggregation and diffusion is similar, but the scope of aggregation is different. As the air content increases, the volume of the air bag increases, the head of the air bag extends to the front edge, and the tail of the air bag gradually extends into the wake area. The gas fraction of the gas core becomes larger, the area occupied by the back area becomes larger, and the gas accumulates to form a gas pocket with a high gas integral. It can be considered that the flow channel is blocked by the gas phase at this time, there is no obvious gas–liquid separation zone in the flow channel, and the gas phase concentration in the flow channel is not less than the gas phase concentration of the inlet. When the gas contents are 10%, 30%, and 40%, the maximum concentrations of gas phase are 21%, 62%, and 78%, respectively. The initial positions of the air bag from the leading edge are 20%, 18%, and 13% of the chord length, respectively, and all of them disappear at the trailing edge. The periods are 90°, 174°, and 132° respectively.

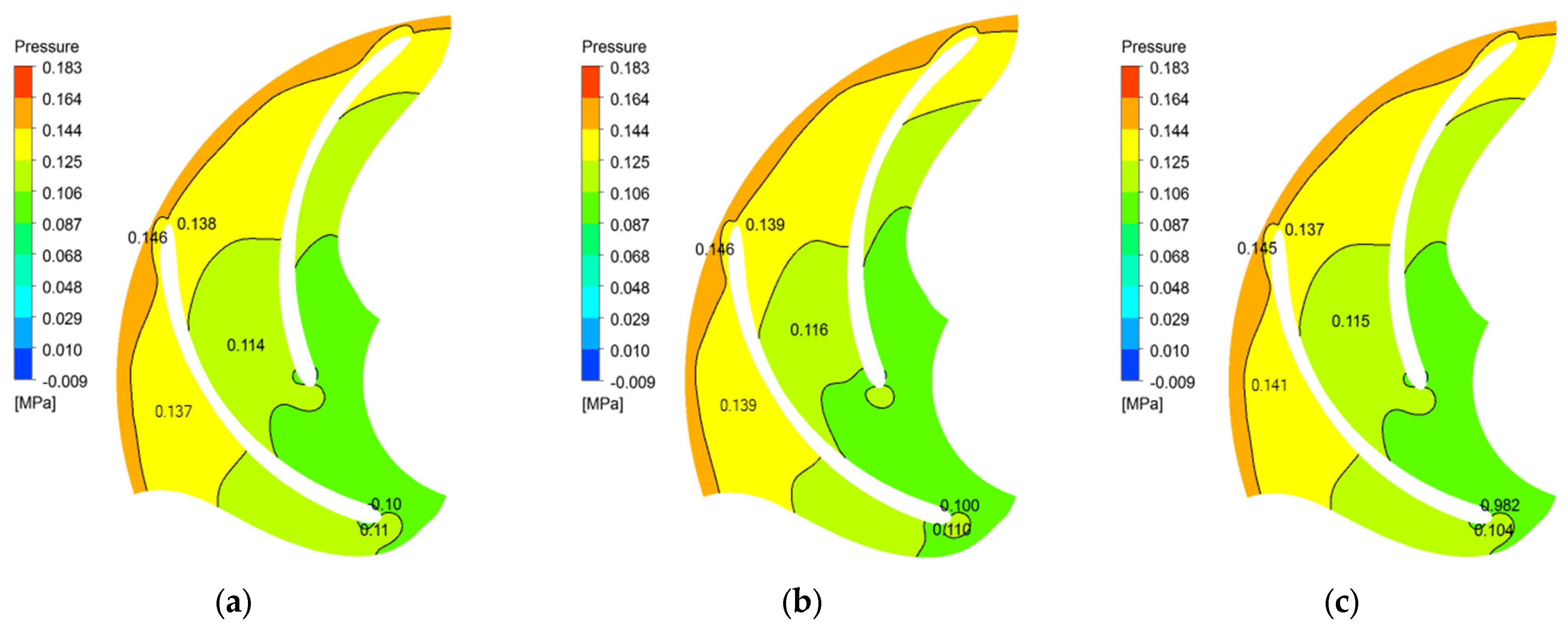
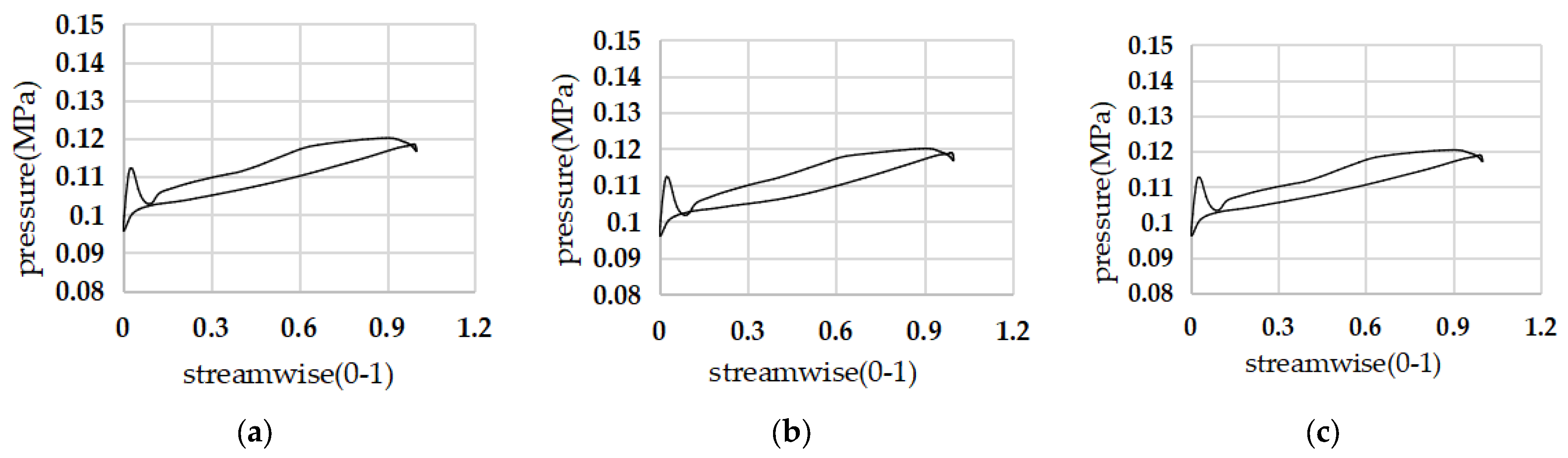
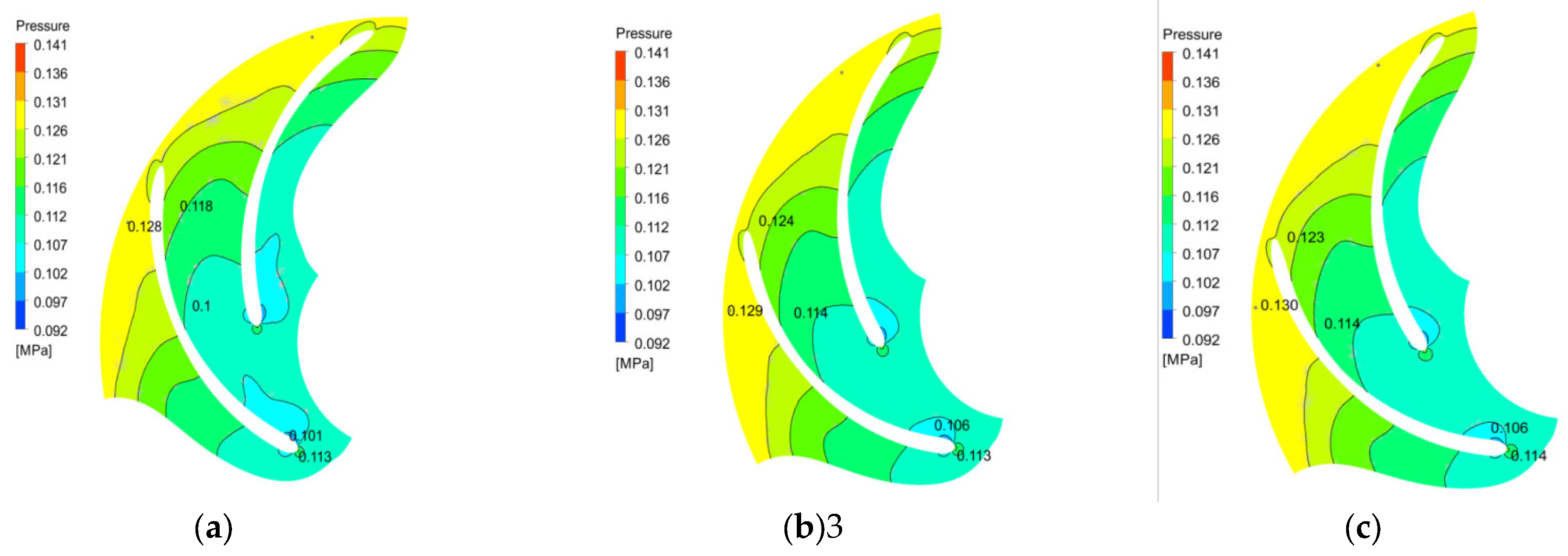
6.2. Transient Law of Pressure Feld in the Pump

Figure 18, Figure 19 and Figure 20 correspond to the mid-section pressure cloud diagrams with gas contents of 10%, 30%, and 40%, respectively. The three different gas contents have similar pressure distributions, and the pressure contours on the cross-section of the flow channel are relatively uniform and have a two-dimensional shape, indicating that under the three gas contents, the main flow channel of the impeller flow channel is mainly a laminar flow. Laminar flow is not conducive to the breakage of air bags. Excessive air bags can easily cause air lock of the centrifugal pump and seriously deteriorate the lifting performance of the pump. The pressure field of the two-phase flow is not obvious in the small high-pressure area on the working surface side of the blade head, and is only obvious in the section of the rear cover. There is no obvious lower pressure area at the trailing edge of the blade in the two-phase flow, that is, the position where the “wake” phenomenon occurs in the single-phase flow. Only a small lower pressure area at the rear cover position is observed when α = 30%.

Comparing and analyzing the pressure cloud diagrams at different times with the same gas content, it is found that the pressure field in the cross-section at all positions does not change significantly with the rotation of the impeller, the pressure value at the same position does not change significantly, and the pressure contour distribution at different times is similar. When the air content is high, the pressure in the lower pressure area of the blade head in all sections is greater than the pressure in the lower pressure area when the air content is low. Except for the lower pressure area at the blade head, the overall pressure in the flow channel is slightly lower when the air content is high than when the air content is low. As the air content increases, the local lower pressure area on the back of the blade expands.

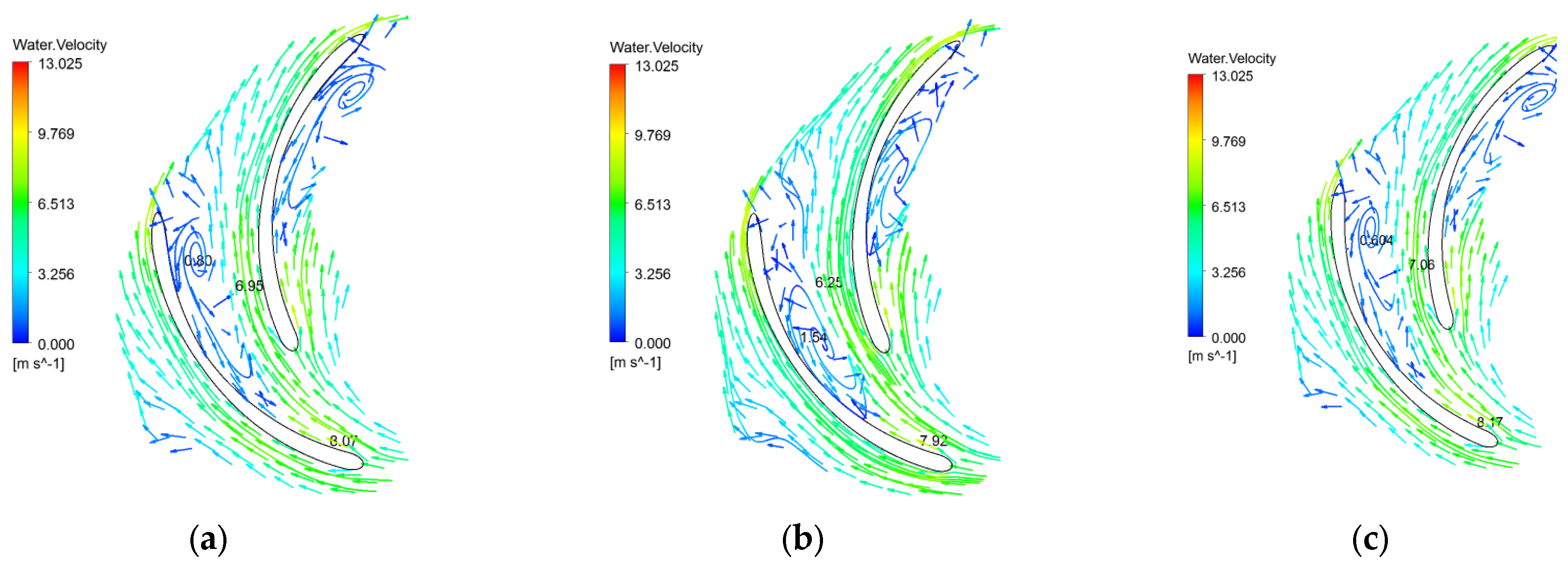
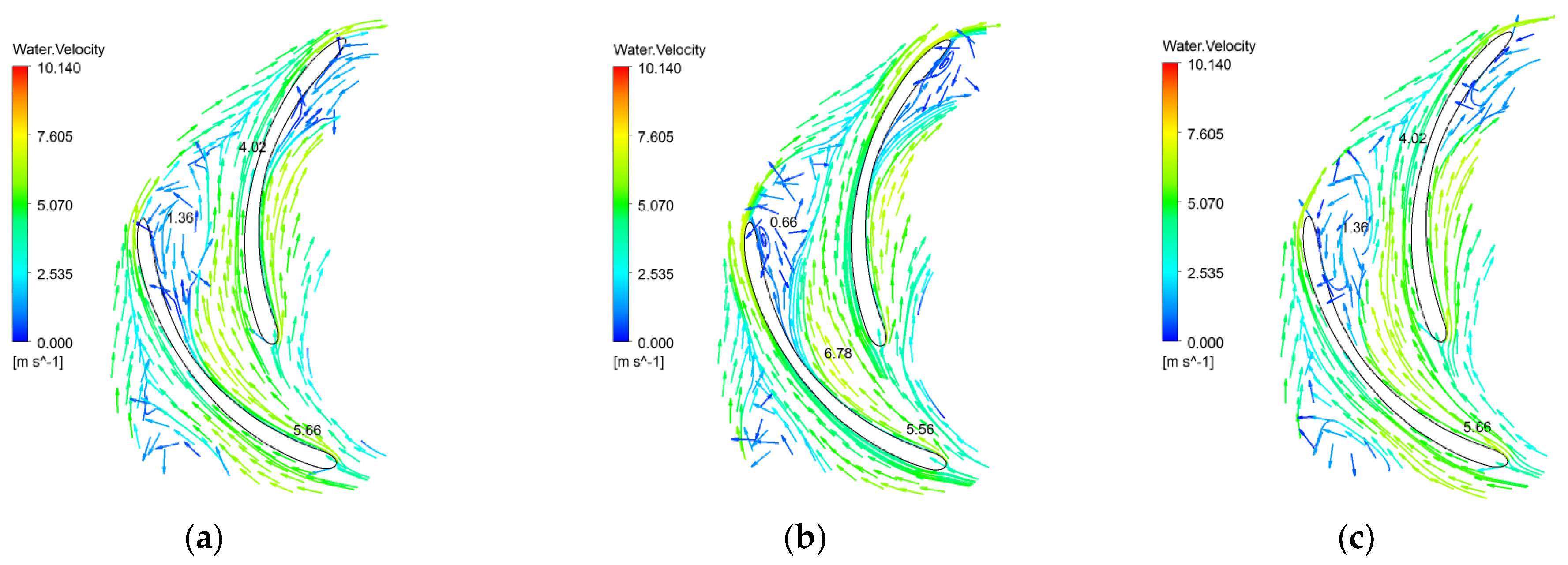
6.3. Transient Law of the Velocity Field in the Pump

Figure 21, Figure 22 and Figure 23 show the velocity vector diagrams at three moments of the cross-section of the impeller blade at the middle position of the impeller blade in periods when the gas contents are 10%, 30%, and 40%, taking the periodic accumulation and diffusion period of the gas as a reference. After comparative analysis, when the gas content of the inlet gas increases, except for the low-velocity zone affected by the vortex, the flow velocity of the main flow in the flow passage increases, and the range of influence of the vortex increases. Due to the increase in the content of the gas phase introduced, the concentration of the gas phase increases, the range of the gas phase concentration increases, and the flow channel narrows, resulting in an increase in the liquid phase flow rate in the flow channel. There are vortices in the high concentration accumulation area of gas phase, and the center of the vortex is the position where the concentration of gas phase is the highest. When the gas phase concentration reaches a certain value, the gas phase “occupies” the flow channel in the form of bubbles, resulting in a small liquid phase velocity in this area. There is a secondary flow phenomenon in the gas–liquid two-phase separation zone with very low concentration, which is a typical flow characteristic of a single-liquid phase flow. As the impeller rotates, the velocity vector in the flow channel also shows periodic changes. The middle position of the flow channel and the position of the back cover are the most periodic, and the period is the same as the reciprocating period of gas phase accumulation and diffusion.

7. Conclusions

On the basis of previous research results, this article conducts transient simulation of two-phase flow in an ESP under various gas contents and speed conditions, studies the transient impact of gas content and speed on pump performance, and compares external characteristics such as head, efficiency, and power of the ESP with experimental results. It further verifies the reliability of the simulation method and ultimately draws the following conclusions:

(1)

In the gas–liquid two-phase flow, the gas phase is unevenly distributed in the flow channel. Along the axial direction, the range of gas phase accumulation in the impeller is shown as extending from the entrance of the front cover to the exit of the rear cover. The concentration of gas phase accumulation decreases from the entrance of the front cover to the exit of the flow channel.

(2)

The gas phase accumulation form in the channel is not affected, and the gas phase accumulation and the diffusion period are shortened; the gas phase accumulation concentration in the impeller decreases with the increase in speed.

(3)

Due to the regular and periodic accumulation and diffusion of gas in the flow channel, the load on both sides of the blade changes regularly, and the pressure difference on both sides of the blade fluctuates with a small amplitude during the change period. The increase in the impeller speed results in the increase in the pressure difference between the two sides of the blade, the increase in the load of the blade, and the increase in the pressure difference between the inlet and outlet.

(4)

Gas mixing has little effect on the pressure field in the pump, and the pressure value in the flow field increases slightly. The velocity value of the gas mixed into the flow channel increased slightly. The range of the vortex in the impeller expands to the pressure surface of the blade, and the center of the vortex corresponds to the position of the maximum concentration of gas phase. As the flow rate increases, the pressure in the two-phase flow field increases and the flow velocity increases.

(5)

When the gas content in the inlet increases, the gas phase distribution in the flow channel does not change significantly, and the gas phase is mainly concentrated on the back of the blades on the side of the front corner. With the increase in the gas content in the inlet, the maximum concentration of gas phase in the flow channel increases, the area of the flow channel occupied by the high concentration gas phase increases, the period of periodic accumulation and diffusion increases, and the range of the gas–liquid separation zone shrinks toward the front cover. The gas content in the inlet increases, the pressure in the pump increases slightly, the flow rate of the mainstream increases, and the range of vortex action increases.

These conclusions provide a theoretical basis for the future application of ESPs in gas–liquid mixed transportation. In practical applications, based on the research results of this article, the speed of the ESP can be adjusted in a timely manner under the working condition of gas–liquid two-phase flow, thereby maintaining the impeller blade load within a stable range and avoiding an excessive pressure difference between the inlet and outlet of the ESP, which may cause the pump to tilt. The increase in gas content will slow down the periodic diffusion rate of gas and prolong the cycle. This may lead to a decrease in pump performance, which is detrimental to the production efficiency of oil wells. This can be further analyzed and verified in future research.