An Adaptive Model-Based Approach to the Diagnosis and Prognosis of Rotor-Bearing Unbalance
Abstract
:1. Introduction
2. Model-Based Unbalance Analysis of the Turbine Rotor-Bearing System
2.1. Rotor-Bearing Model
2.2. Mathematical Derivation of the Physical Model
2.3. Parameter Identification
2.4. Analysis of Individual Feature Errors
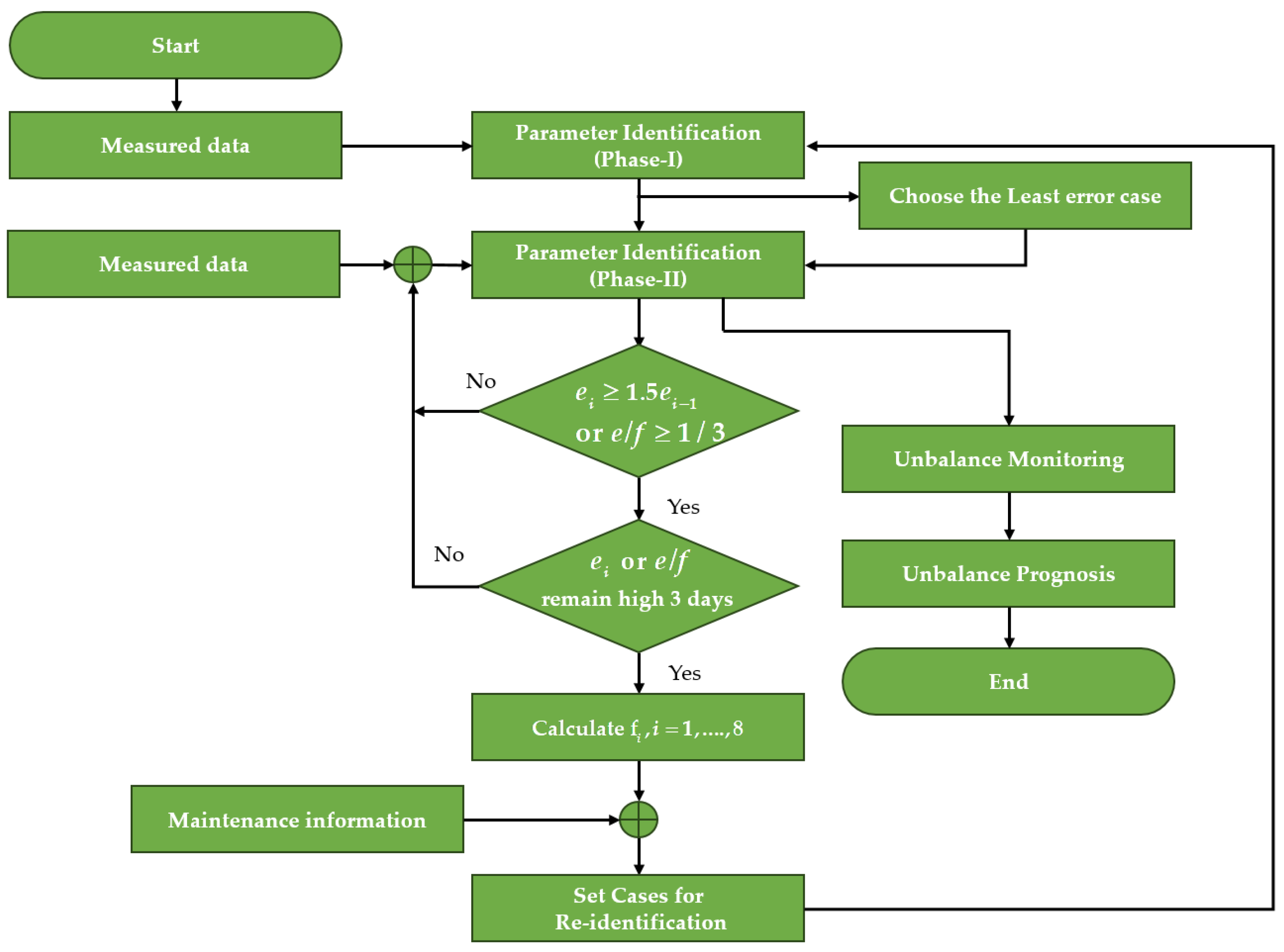
3. Adaptive Methodology
4. Prognostic Methodology
4.1. Auto Regressive Integrated Moving Average (ARIMA)
4.2. Long Short Term Memory (LSTM)
4.3. Numerical Evaluation
5. Results and Discussion
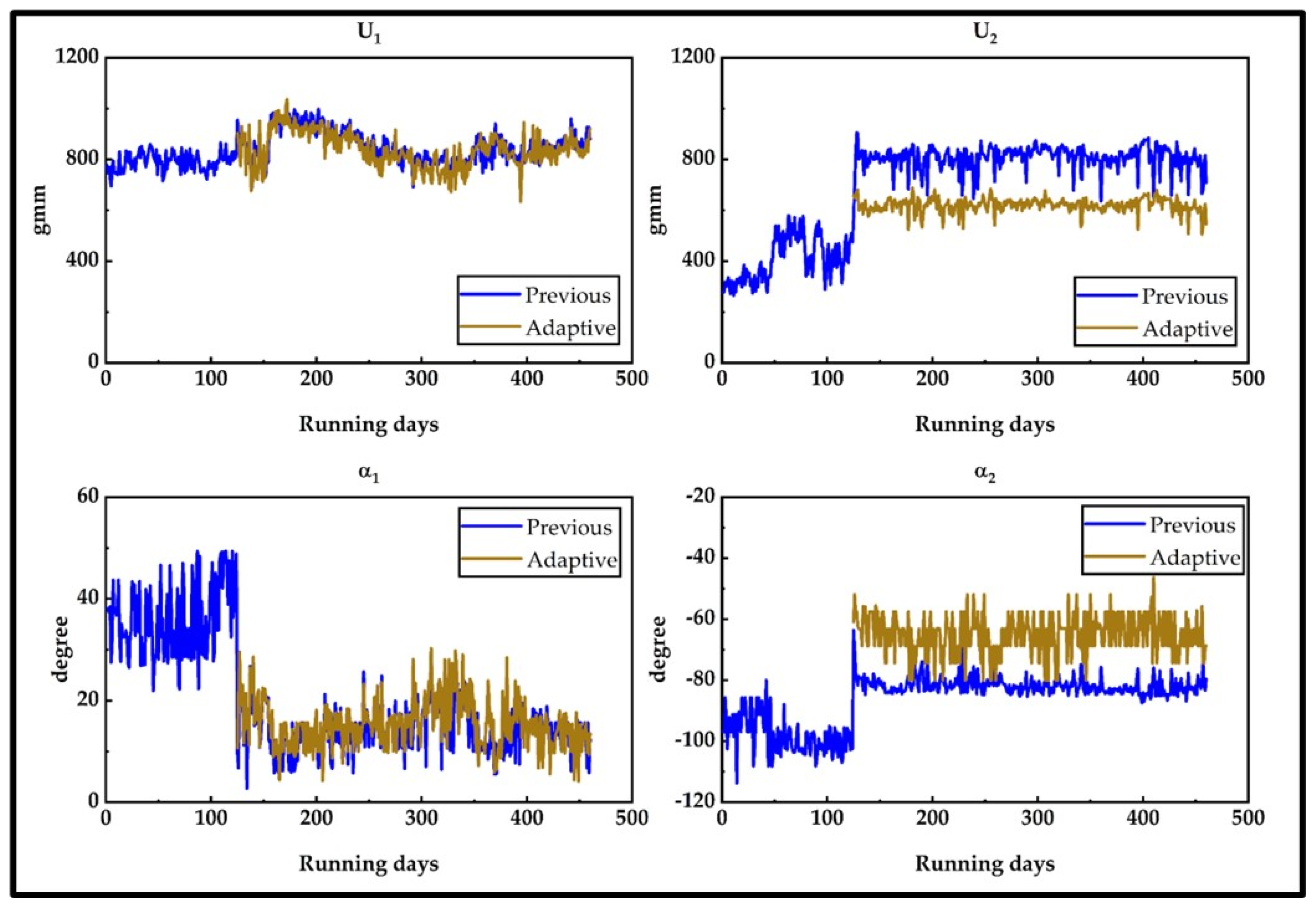
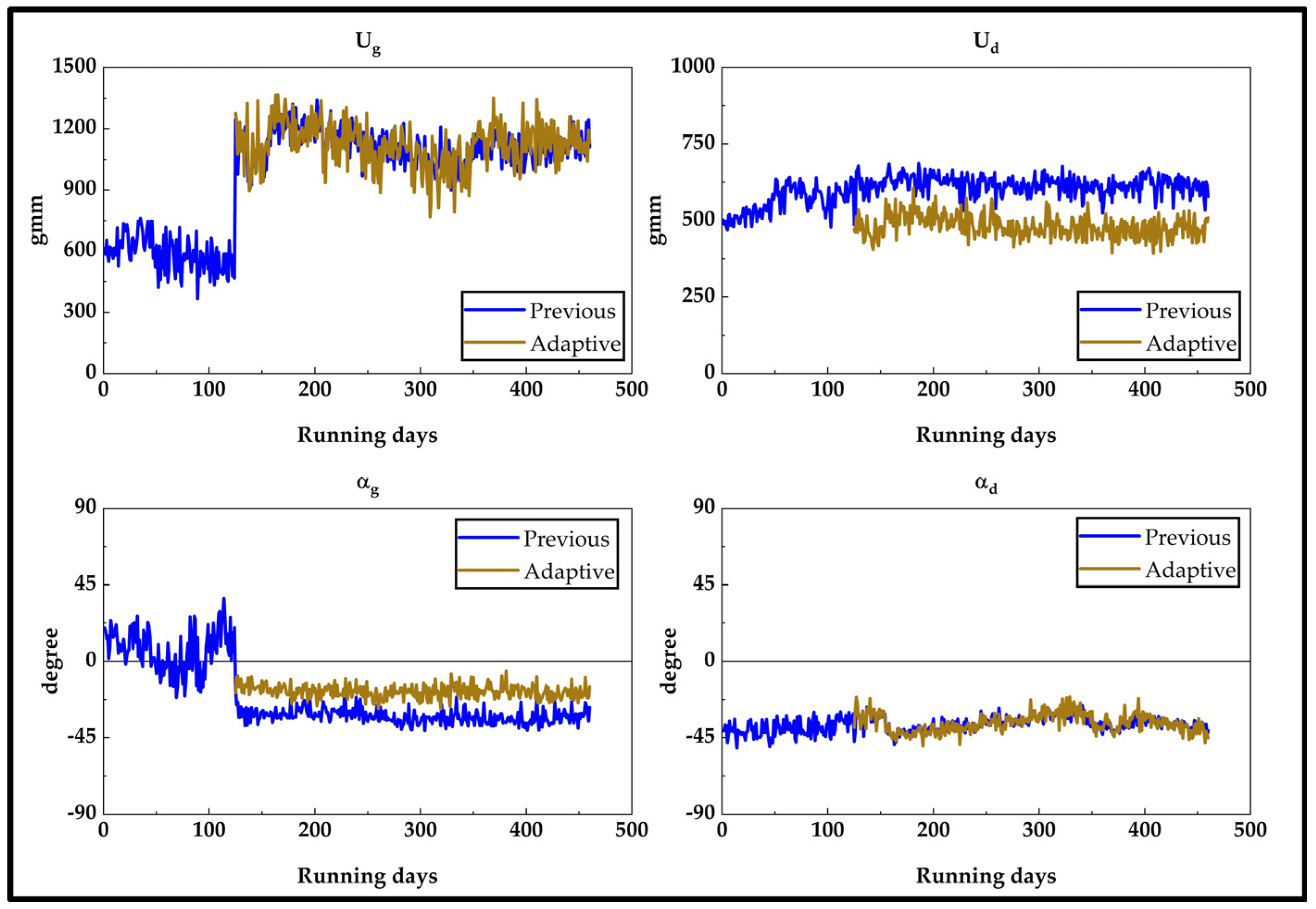
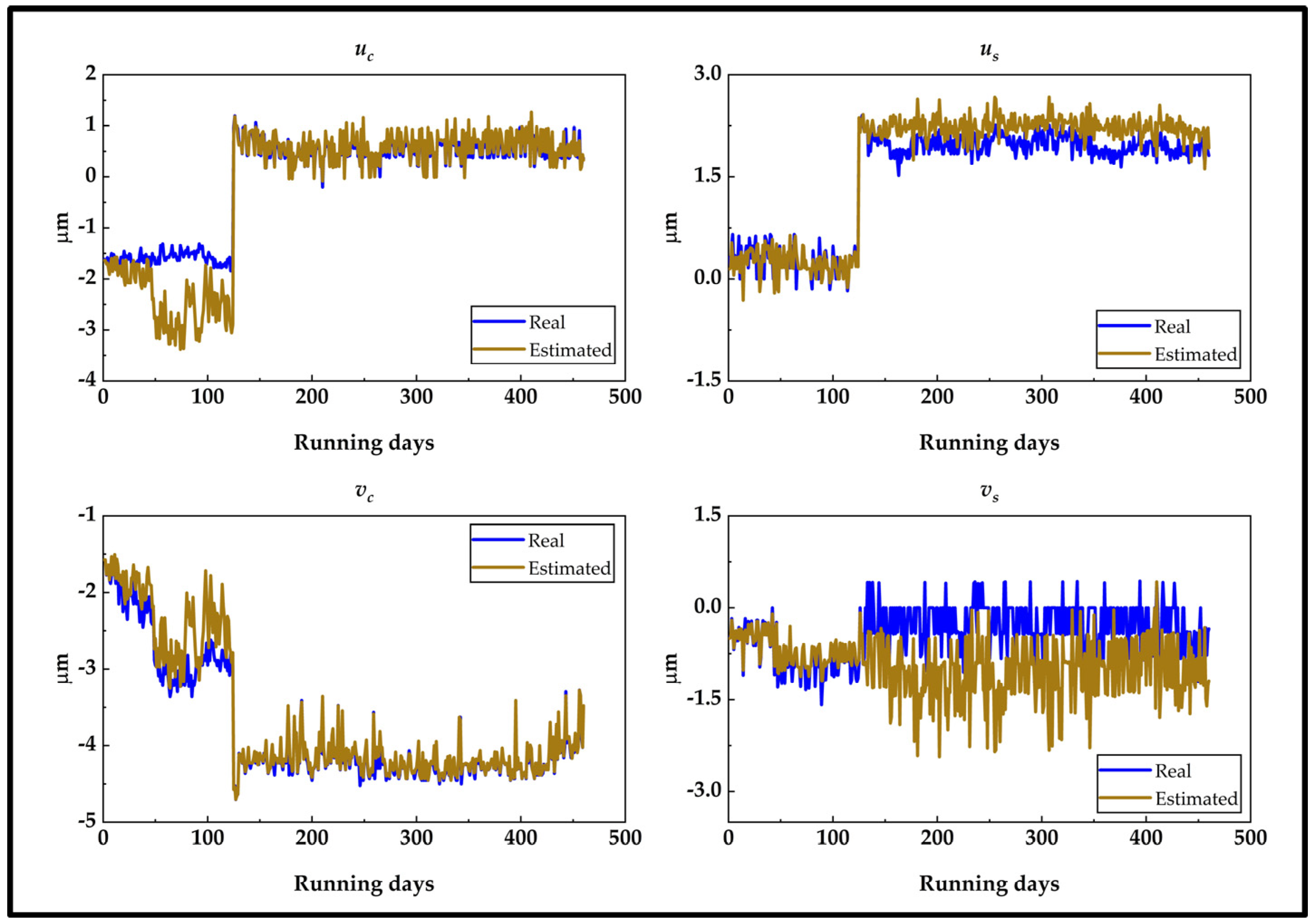
5.1. Unbalance Diagnosis and Monitoring
5.2. Monitoring and Prognostics
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, B.; Yuan, Q. Improved generative adversarial network for vibration-based fault diagnosis with imbalanced data. Measurement 2021, 169, 108522. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Sidar, R.; Sen, P.K.; Sahu, G. Review of vibration based fault diagnosis in rolling element bearing and vibration analysis techniques. Int. J. Sci. Res. Eng. Technol. 2015, 4, 998–1003. [Google Scholar]
- Elbhbah, K.; Sinha, J.K. Vibration-based condition monitoring of rotating machines using a machine composite spectrum. J. Sound Vib. 2013, 332, 2831–2845. [Google Scholar] [CrossRef]
- Lees, A.; Sinha, J.; Friswell, M. Model-based identification of rotating machines. Mech. Syst. Signal Process. 2009, 23, 1884–1893. [Google Scholar] [CrossRef]
- Jalan, A.K.; Mohanty, A. Model based fault diagnosis of a rotor–bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Devendiran, S.; Manivannan, K. Vibration based condition monitoring and fault diagnosis technologies for bearing and gear components-a review. Int. J. Appl. Eng. Res. 2016, 11, 3966–3975. [Google Scholar]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Peng, Z.; Peter, W.T.; Chu, F. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Seshadrinath, J.; Singh, B.; Panigrahi, B.K. Vibration analysis based interturn fault diagnosis in induction machines. IEEE Trans. Ind. Inform. 2013, 10, 340–350. [Google Scholar] [CrossRef]
- Casimir, R.; Boutleux, E.; Clerc, G.; Yahoui, A. The use of features selection and nearest neighbors rule for faults diagnostic in induction motors. Eng. Appl. Artif. Intell. 2006, 19, 169–177. [Google Scholar] [CrossRef]
- Sun, W.; Shao, S.; Zhao, R.; Yan, R.; Zhang, X.; Chen, X. A sparse auto-encoder-based deep neural network approach for induction motor faults classification. Measurement 2016, 89, 171–178. [Google Scholar] [CrossRef]
- Han, T.; Yang, B.-S.; Choi, W.-H.; Kim, J.-S. Fault diagnosis system of induction motors based on neural network and genetic algorithm using stator current signals. Int. J. Rotating Mach. 2006, 2006, 061690 . [Google Scholar] [CrossRef]
- Su, H.; Chong, K.T. Induction machine condition monitoring using neural network modeling. IEEE Trans. Ind. Electron. 2007, 54, 241–249. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Kumar, P.; Hati, A.S. Review on machine learning algorithm based fault detection in induction motors. Arch. Comput. Methods Eng. 2021, 28, 1929–1940. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Lin, C.-L.; Liang, J.-W.; Huang, Y.-M.; Huang, S.-C. A novel model-based unbalance monitoring and prognostics for rotor-bearing systems. Adv. Mech. Eng. 2023, 15, 16878132221148019. [Google Scholar] [CrossRef]
- Markert, R.; Platz, R.; Seidler, M. Model based fault identification in rotor systems by least squares fitting. Int. J. Rotating Mach. 2001, 7, 311–321. [Google Scholar] [CrossRef]
- Platz, R.; Markert, R.; Seidler, M. Validation of online diagnostics of malfunctions in rotor systems. IMECHE Conf. Trans. 2000, 6, 581–590. [Google Scholar]
- Platz, R. Fault models for online identification of malfunctions in rotor systems. In Proceedings of the Survelliance 4-Acoustical and Vibratory Surveillance Methods and Diagnostic Techniques, Compiegne, France, 16–18 October 2001. [Google Scholar]
- Sekhar, A. Identification of unbalance and crack acting simultaneously in a rotor system: Modal expansion versus reduced basis dynamic expansion. J. Vib. Control 2005, 11, 1125–1145. [Google Scholar] [CrossRef]
- Jain, J.; Kundra, T. Model based online diagnosis of unbalance and transverse fatigue crack in rotor systems. Mech. Res. Commun. 2004, 31, 557–568. [Google Scholar] [CrossRef]
- Isermann, R. Model base fault detection and diagnosis methods. In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995; Volume 3, pp. 1605–1609. [Google Scholar]
- Bachschmid, N.; PENNACCHI, P.; Vania, A. Identification of multiple faults in rotor systems. J. Sound Vib. 2002, 254, 327–366. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P. Accuracy of fault detection in real rotating machinery using model based diagnostic techniques. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2003, 46, 1026–1034. [Google Scholar] [CrossRef]
- Bently, D.E.; Hatch’Charles, T. Fundamentals of rotating machinery diagnostics. Mech. Eng. CIME 2003, 125, 53–54. [Google Scholar]
- Zhang, J.H.; Ma, L.; Lin, J.W.; Zhang, G.C. Dynamic analysis of flexible rotor-ball bearings system with unbalance-misalignment-rubbing coupling faults. Appl. Mech. Mater. 2012, 105, 448–453. [Google Scholar] [CrossRef]
- Ganeriwala, S.N.; Schwarz, B.; Richardson, M.H. Operating deflection shapes detect unbalance in rotating equipment. Sound Vib. 2009, 43, 11–13. [Google Scholar]
- Edwards, S.; Lees, A.; Friswell, M. Estimating rotor unbalance from a single run-down. IMeche Conf. Trans. 2000, 6, 323–334. [Google Scholar]
- Randall, R.B. State of the art in monitoring rotating machinery-part 1. Sound Vib. 2004, 38, 14–21. [Google Scholar]
- Walker, R.; Perinpanayagam, S.; Jennions, I.K. Physics-based simulation for health management of rotating machinery. In Proceedings of the 8th International Conference on Condition Monitoring and Machinery Failure Prevention Technologies, Cardiff Bay, UK, 20–22 June 2011; pp. 647–658. [Google Scholar]
- Sudhakar, G.; Sekhar, A. Identification of unbalance in a rotor bearing system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Tiwari, R.; Chakravarthy, V. Simultaneous estimation of the residual unbalance and bearing dynamic parameters from the experimental data in a rotor-bearing system. Mech. Mach. Theory 2009, 44, 792–812. [Google Scholar] [CrossRef]
- Mutra, R.R. An optimized bearing parameter identification approach from vibration response spectra. J. Vibroengineering 2019, 21, 1519–1532. [Google Scholar] [CrossRef]
- Lv, Y.; Zhao, W.; Zhao, Z.; Li, W.; Ng, K.K. Vibration signal-based early fault prognosis: Status quo and applications. Adv. Eng. Inform. 2022, 52, 101609. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Bera, B.; Lin, C.-L.; Huang, S.-C.; Liang, J.-W.; Lin, P.T. Establishing a Real-Time Multi-Step Ahead Forecasting Model of Unbalance Fault in a Rotor-Bearing System. Electronics 2023, 12, 312. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Shao, S.; Niu, T.; Yang, X. Attention-based LSTM network for rotatory machine remaining useful life prediction. IEEE Access 2020, 8, 132188–132199. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Bera, B.; Huang, S.-C.; Ling, C.-L.; Lian, J.-W.; Lin, P.T. Online Real-Time Rotating Unbalance Forecast Incorporating Model-Based with Machine Learning Techniques. In Proceedings of the 2023 9th International Conference on Applied System Innovation (ICASI), Chiba, Japan, 21–25 April 2023; pp. 86–88. [Google Scholar] [CrossRef]






| Cases | Cx1 | Cy1 | kx1 | ky1 | U1 | α1 | Cx2 | Cy2 | kx2 | ky2 | U2 | α2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | - | - | - | - | 2 × 103 | 7.7 × 104 | 3.5 × 108 | 1.9 × 108 | - | - |
| 2 | - | - | - | - | - | - | 2.7 × 104 | 8 × 104 | 3.5 × 108 | 1.9 × 108 | 650 | −57 |
| 3 | 2 × 105 | 7.86 × 104 | 1.89 × 108 | 3.5 × 108 | - | - | 2 × 103 | 2 × 103 | 1.6 × 108 | 1.2 × 108 | - | - |
| 4 | 1.4 × 105 | 5.57 × 104 | 1.32 × 108 | 2.6 × 108 | 502. | 35.0 | 2 × 103 | 6.4 × 104 | 3.1 × 108 | 1.8 × 108 | 600 | −62 |
| Cases | Average Residual (μm) | Absolute Sum of Total Residual (μm) | Percentage Residual Reduction (%) |
|---|---|---|---|
| 1 | 2.0926 | 703.12 | 53.95 |
| 2 | 2.0174 | 677.84 | 55.12 |
| 3 | 2.7382 | 920.02 | 43.82 |
| 4 | 2.9015 | 974.92 | 41.04 |
| Forecast | Model | RMSE Values | |||
|---|---|---|---|---|---|
| Ug | αg | Ud | αd | ||
| Daily | ARIMA (3,1,3) | 13.4639 | 0.5299 | 3.4743 | 0.3886 |
| LSTM (50) | 17.5981 | 1.0907 | 6.1918 | 0.8012 | |
| LSTM (55) | 14.9406 | 1.0627 | 5.0965 | 0.8186 | |
| LSTM (64) | 16.2910 | 1.2851 | 5.2719 | 0.8432 | |
| One Week | ARIMA (3,1,3) | 24.5688 | 1.9026 | 10.8808 | 1.3376 |
| LSTM (50) | 28.4997 | 1.5144 | 11.5623 | 1.6051 | |
| LSTM (55) | 30.8223 | 1.6213 | 11.78062 | 1.6285 | |
| LSTM (64) | 30.7599 | 1.5775 | 11.7438 | 1.5777 | |
| One Month | ARIMA (3,1,3) | 88.0832 | 8.1978 | 50.0537 | 5.8823 |
| LSTM (50) | 100.4109 | 5.9453 | 49.9060 | 6.1574 | |
| LSTM (55) | 92.8987 | 6.2579 | 50.8300 | 6.0797 | |
| LSTM (64) | 96.1129 | 5.9020 | 49.1724 | 6.1431 | |
| Two Months | ARIMA (3,1,3) | 130.2160 | 9.7533 | 66.8236 | 8.0524 |
| LSTM (64) | 131.9359 | 6.1146 | 59.9396 | 9.0648 | |
| LSTM (55) | 126.3275 | 6.0103 | 62.2515 | 8.6632 | |
| LSTM (50) | 129.7200 | 6.1129 | 56.6076 | 8.3724 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bera, B.; Huang, S.-C.; Najibullah, M.; Lin, C.-L. An Adaptive Model-Based Approach to the Diagnosis and Prognosis of Rotor-Bearing Unbalance. Machines 2023, 11, 976. https://doi.org/10.3390/machines11100976
Bera B, Huang S-C, Najibullah M, Lin C-L. An Adaptive Model-Based Approach to the Diagnosis and Prognosis of Rotor-Bearing Unbalance. Machines. 2023; 11(10):976. https://doi.org/10.3390/machines11100976
Chicago/Turabian StyleBera, Banalata, Shyh-Chin Huang, Mohammad Najibullah, and Chun-Ling Lin. 2023. "An Adaptive Model-Based Approach to the Diagnosis and Prognosis of Rotor-Bearing Unbalance" Machines 11, no. 10: 976. https://doi.org/10.3390/machines11100976
APA StyleBera, B., Huang, S.-C., Najibullah, M., & Lin, C.-L. (2023). An Adaptive Model-Based Approach to the Diagnosis and Prognosis of Rotor-Bearing Unbalance. Machines, 11(10), 976. https://doi.org/10.3390/machines11100976







