Evaluation of the Supporting Mounts of a Three-in-One Electric Drive Unit Using a Hybrid Simulation Model
Abstract
:1. Introduction
2. Theoretical Background
3. Dynamic Mechanical Property Test of Support Mounts
4. Hybrid Simulation Model of 3-in-1 Electric Drive Unit
4.1. Experimental Modal Test of 3-in-1 EDU
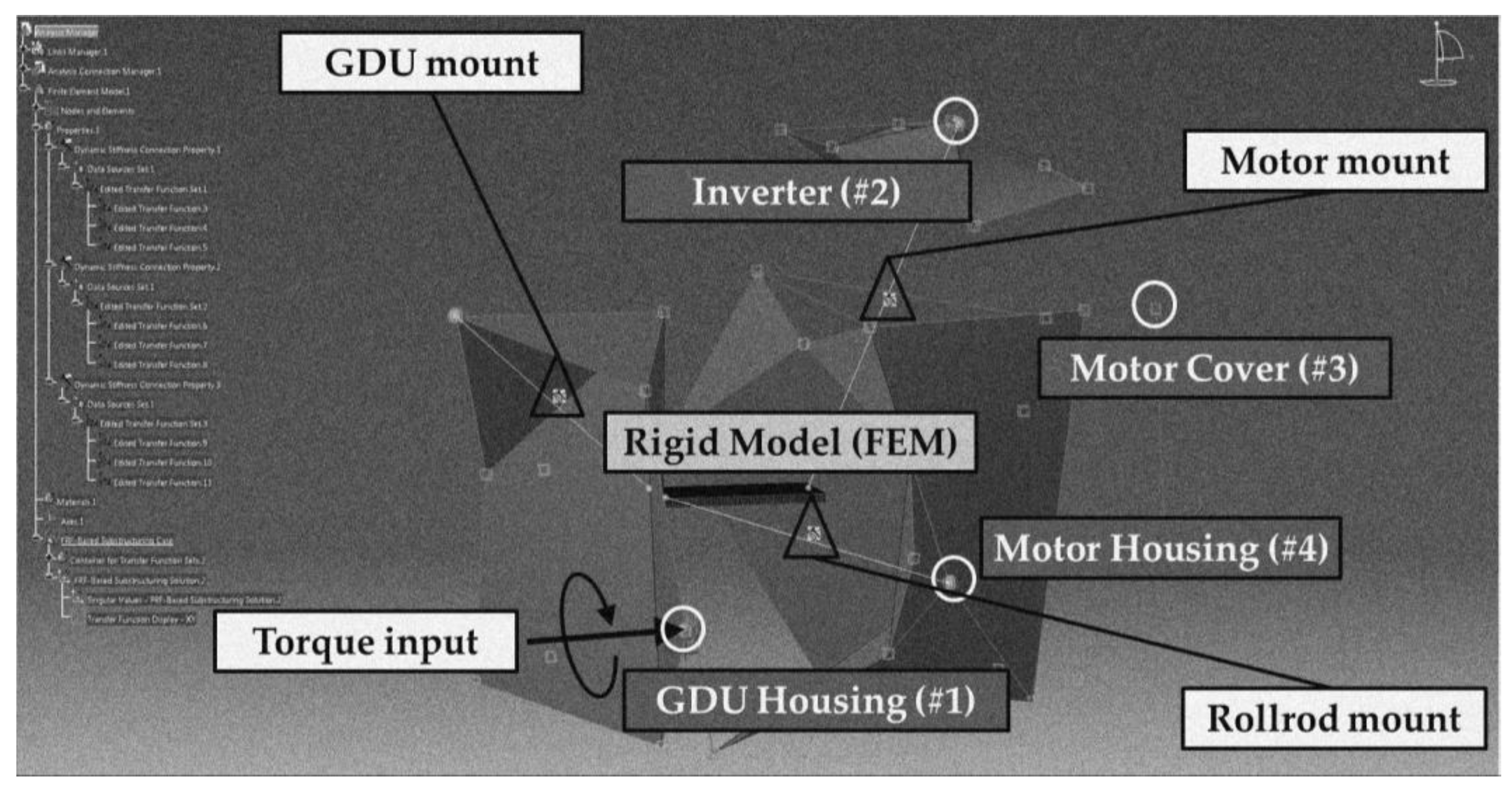
4.2. Hybrid Simulation Model of 3-in-1 EDU including a Rigid Finite Element Model
4.3. Verification of Hybrid Simulation Model of 3-in-1 EDU
5. Evaluation of Dynamic Characteristics of Supporting Mounts
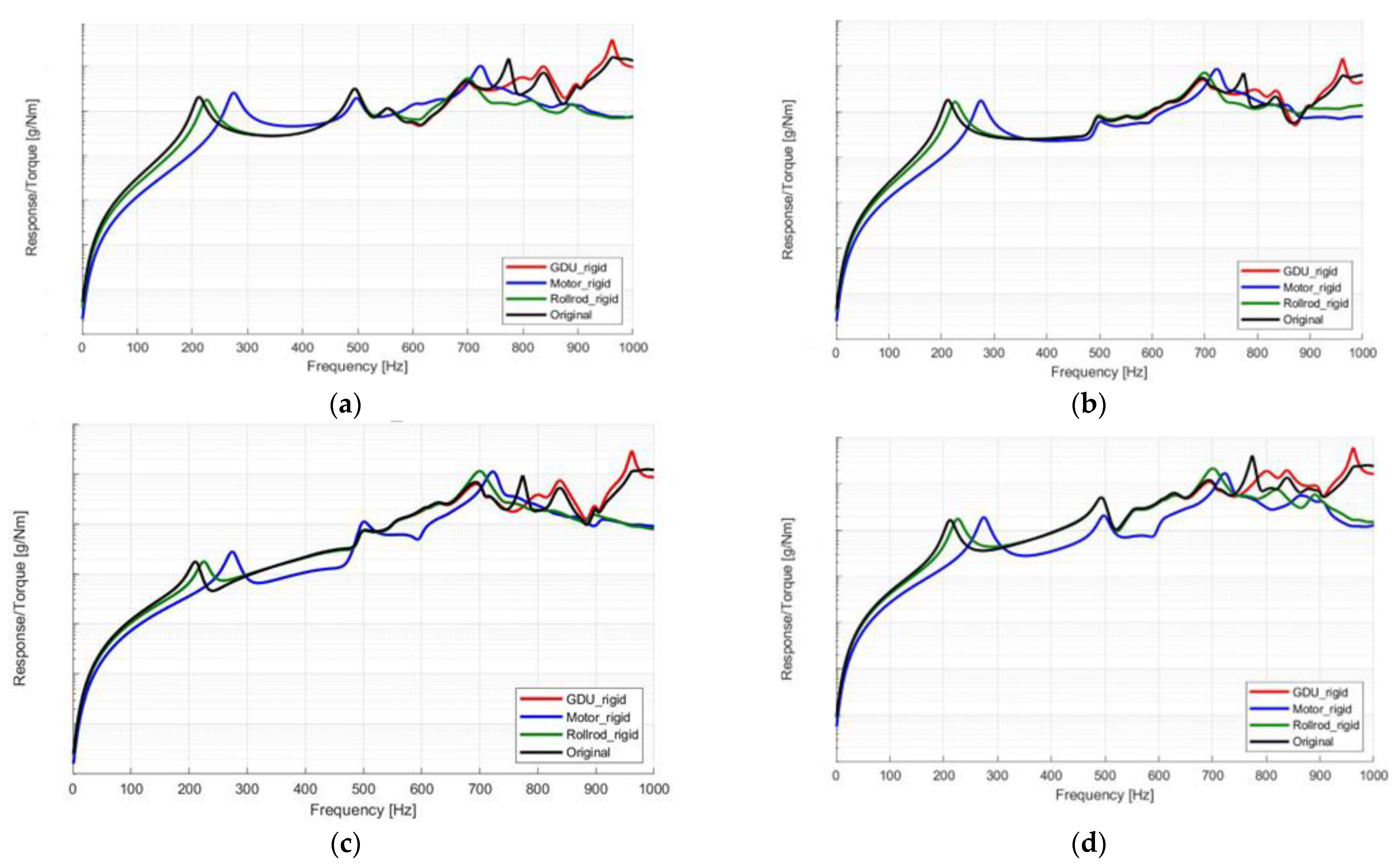
5.1. Dynamic Response from Hybrid 3-in-1 EDU Model
5.2. Dynamic Response from Powertrain Dynamometer Test of 3-in-1 EDU
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alujevic, N.; Cakmak, D.; Wolf, H.; Jokic, M. Passive and active vibration isolation system using inerter. J. Sound Vib. 2018, 418, 163–183. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Shuai, C.G.; Wang, C.Y. Improved hybrid isolator with maglev actuator integrated in air spring for active-passive isolation of ship machinery vibration. J. Sound Vib. 2017, 407, 226–239. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q. Recent Advances in Quasi-Zero Stiffness Vibration Isolation Systems: An Overview and Future Possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Ling, Y.; Wu, S.; Gu, J.; Lai, H. A Novel Ring Spring Vibration Isolator for Metro Superstructure. Appl. Sci. 2021, 11, 8422. [Google Scholar] [CrossRef]
- Yang, J.-H.; Yang, X.-D.; Han, Q.-K.; Liu, J.-G. Post-Buckling Spring Vibration Isolator Using Silicone Gel Column: A Theoretical and Experimental Study. Appl. Sci. 2021, 11, 10559. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, X.; Mu, D.; Huang, X.; Tong, W. Performance and Optimization of a Dual-Stage Vibration Isolation System Using Bio-Inspired Vibration Isolators. Appl. Sci. 2022, 12, 11387. [Google Scholar] [CrossRef]
- Choi, Y.; Wereley, N.M. Vibration Isolation Performance of an Adaptive Magnetorheological Elastomer-Based Dynamic Vibration Absorber. Actuators 2022, 11, 157. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Lu, C.; Liu, K.; Song, B. Influence of Road Traffic Vibration on Micro-Dynamic Response of Precision Instrument Vibration Isolation Platforms. Eng. Proc. 2023, 36, 48. [Google Scholar] [CrossRef]
- Kim, C.-J. Design criterion of damper component of passive-type mount module without using base mass-block. Energies 2018, 11, 1548. [Google Scholar] [CrossRef]
- Park, Y.W.; Kim, T.-W.; Kim, C.-J. Compromised vibration isolator of electric power generator considering self-excitation and basement input. Inventions 2023, 8, 40. [Google Scholar] [CrossRef]
- Kim, C.; Kim, C.-J. Tuning of Two Sub-Mounts in Mass-Block Integrated Mount Module over Self-Excitation and Basement Input. Appl. Sci. 2023, 13, 10159. [Google Scholar] [CrossRef]
- Oh, H.U.; Lee, K.J.; Jo, M.S. A passive launch and on-orbit vibration isolation system for the spaceborne cryocooler. Aerosp. Sci. Technol. 2013, 28, 324–331. [Google Scholar] [CrossRef]
- Lee, J.; Okwudire, C.E. Reduction of vibrations of passively-isolated ultra-precision manufacturing machines using mode coupling. Precis. Eng. 2016, 43, 164–177. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Sun, B.; Li, F. A 6DOF passive vibration isolator using X-shape supporting structures. J. Sound Vib. 2016, 380, 90–111. [Google Scholar] [CrossRef]
- Ribeiro, E.A.; Lopes, E.M.O.; Bavastri, C.A. A numerical and experimental study on optimal design of multi-DOF viscoelastic supports for passive vibration control in rotating machinery. J. Sound Vib. 2017, 411, 346–361. [Google Scholar] [CrossRef]
- Siami, A.; Karimi, H.R.; Cigada, A.; Zappa, E.; Sabbioni, E. Parameter optimization of an inerter-based isolator for passive vibration control of Michelangelo’s Rondanini Pieta. Mech. Syst. Signal Process. 2018, 98, 667–683. [Google Scholar] [CrossRef]
- Gu, X.; Yu, Y.; Li, J.; Li, Y. Semi-active control of magnetorheological elastomer base isolation system utilizing learning-based inverse model. J. Sound Vib. 2017, 406, 346–362. [Google Scholar] [CrossRef]
- Santos, M.B.; Coelho, H.T.; Neto, F.P.L.; Mafhoud, J. Assessment of semi-active friction dampers. Mech. Syst. Signal Process. 2017, 94, 33–56. [Google Scholar] [CrossRef]
- Oh, H.U.; Choi, Y.J. Enhancement of pointing performance by semi-active variable damping isolator with strategies for attenuating chattering effects. Sens. Actuators A Phys. 2011, 165, 385–391. [Google Scholar] [CrossRef]
- Azadi, M.; Behzadipour, S.; Faulkner, G. Performance analysis of a semi-active mount made by a new variable stiffness spring. J. Sound Vib. 2011, 330, 2733–2746. [Google Scholar] [CrossRef]
- Pingzhang, Z.; Jianbin, D.; Zhenhua, L. Simultaneous topology optimization of supporting structure and loci of isolators in an active vibration isolation system. Comput. Struct. 2018, 194, 74–85. [Google Scholar]
- Beijen, M.A.; Tjepkema, D.; Dijk, J. Two-sensor control in active vibration isolation using hard mounts. Control Eng. Pract. 2014, 26, 82–90. [Google Scholar] [CrossRef]
- Yang, X.L.; Wu, H.T.; Li, Y.; Chen, B. Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart platform. Mech. Mach. Theory 2017, 117, 244–252. [Google Scholar] [CrossRef]
- Wang, Z.; Mak, C.M. Application of a movable active vibration control system on a floating raft. J. Sound Vib. 2018, 414, 233–244. [Google Scholar] [CrossRef]
- Chi, W.; Cao, D.; Wang, D.; Tang, J.; Nie, Y.; Huang, W. Design and experimental study of a VCM-based stewart parallel mechanism used for active vibration isolation. Energies 2015, 8, 8001–8019. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibration, 5th ed.; Pearson: Singapore, 2011. [Google Scholar]
- Inman, D.J. Engineering Vibration, 4th ed.; Pearson: Singapore, 2013. [Google Scholar]
- Tsai, J.-S.; Chou, Y.-F. The identification of dynamic characteristics of a single bolt joint. J. Sound Vib. 1998, 125, 487–502. [Google Scholar] [CrossRef]
- Ren, Y.; Beards, C.F. On structure synthesis with FRF data. J. Sound Vib. 1995, 185, 845–866. [Google Scholar] [CrossRef]
- Lee, D.-H.; Hwang, W.-S.; Kim, C.-M. Design sensitivity analysis and optimization of an engine mount system using an FRF-based structuring method. J. Sound Vib. 2002, 255, 383–397. [Google Scholar] [CrossRef]
- Nicgorski, D.; Avitabile, P. Conditioning of FRF measurements for use with frequency based structuring. Mech. Syst. Singal Process. 2010, 24, 340–351. [Google Scholar] [CrossRef]
- Noh, H.-M. Prediction and reduction in vehicle noise by frequency response function-based substructuring. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Mayes, R.L.; Ross, M.R. Advancements in hybrid dynamic models combining experimental and finite element substructures. Mech. Syst. Singal Process. 2012, 31, 56–66. [Google Scholar] [CrossRef]
- Yang, G.; Wu, B.; Ou, G.; Wang, Z.; Dyke, S. HyTest: Platform for structural hybrid simulations with finite element model updating. Adv. Eng. Softw. 2017, 112, 200–210. [Google Scholar] [CrossRef]
- Ou, G.; Yang, G.; Dyke, S.; Wu, B. Investigation of hybrid simulation with model updating compared to an experimental shake table test. Front. Built Environ. 2020, 6, 103. [Google Scholar] [CrossRef]
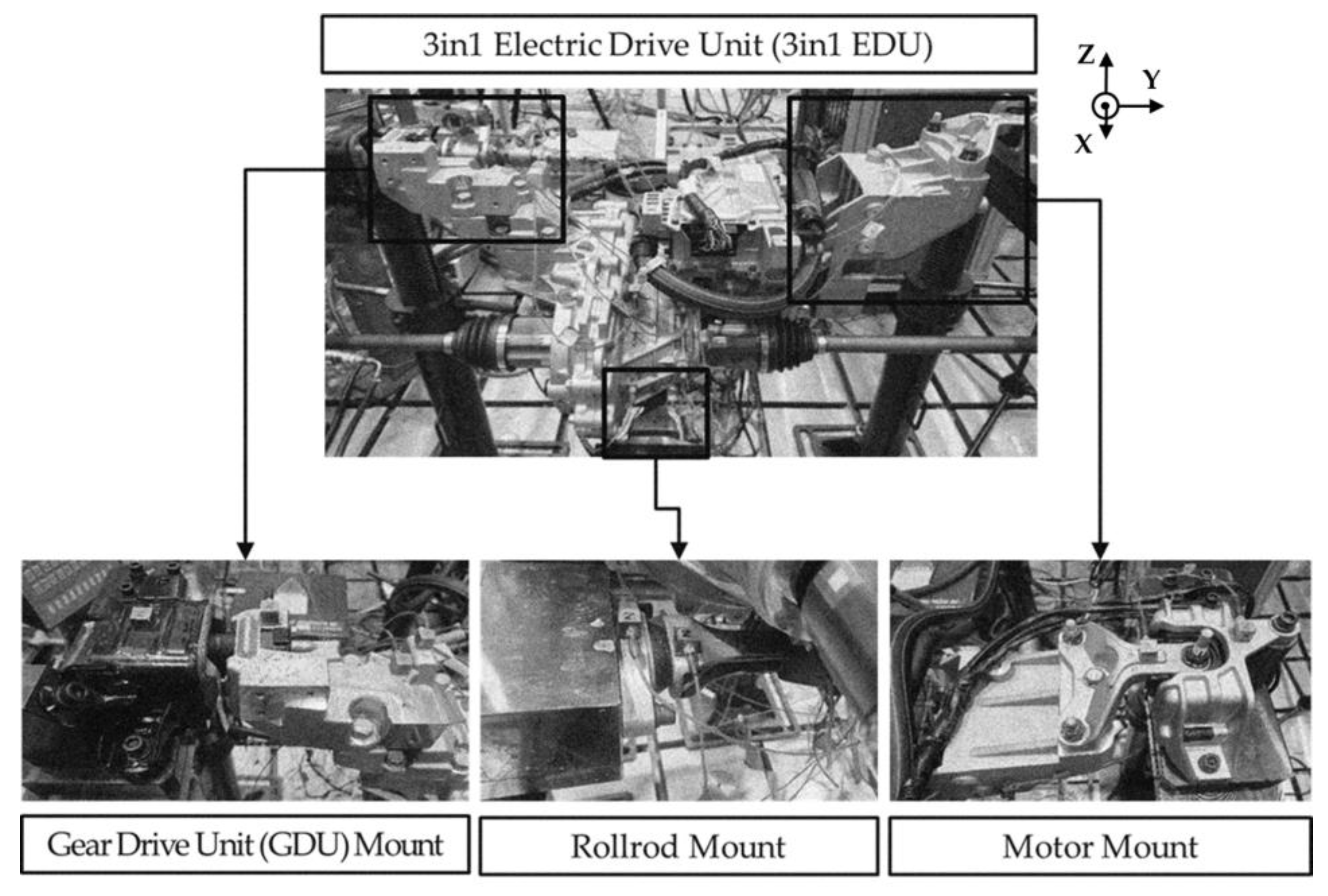
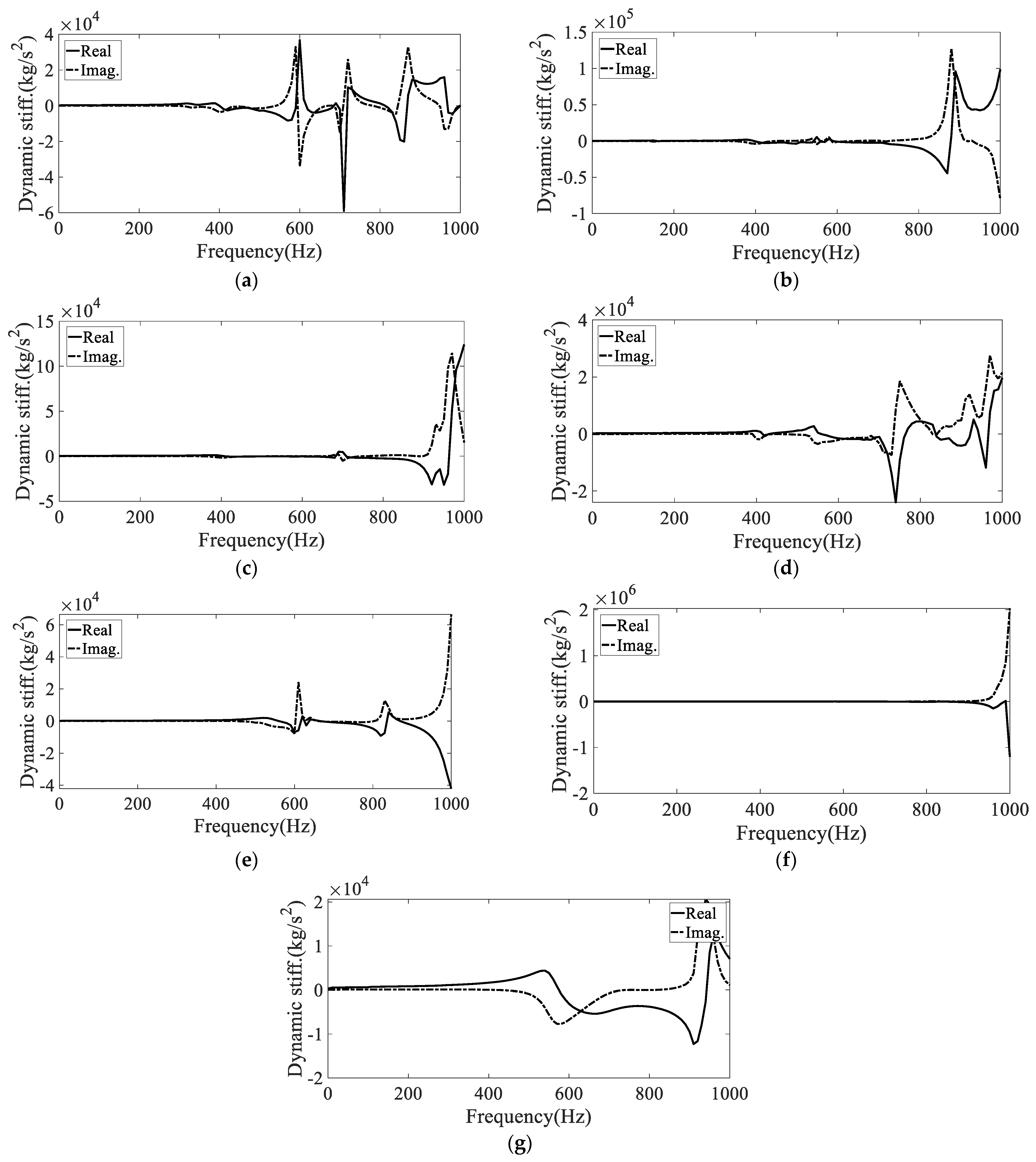





| Mount Type | Frequency (Hz) | Step (Hz) | Disp. (mm, p-p) | Direction | Preload (Static) |
|---|---|---|---|---|---|
| Rollrod | 10~100 | 2 | 0.2 | X | 0 kgf |
| 100~280 | 10 | 0.05 | |||
| 280~1000 | 10 | 0.01 | |||
| GDU | 10~100 | 2 | 0.2 | X, Y, Z | 0 kgf (X, Y) 75 kgf (Z) |
| 100~280 | 10 | 0.05 | |||
| 280~1000 | 10 | 0.005 | |||
| Motor | 10~100 | 2 | 0.2 | X, Y, Z | 0 kgf (X, Y) 70 kgf (Z) |
| 100~280 | 10 | 0.005 |
| Experiment | Simulation | Error (%) |
|---|---|---|
| 205.6 | 206.9 | 0.6 |
| 495.2 | 495.2 | 0.0 |
| 552.5 | 553.8 | 0.2 |
| 629.3 | 629.7 | 0.1 |
| 691.9 | 693.7 | 0.3 |
| 785.8 | 790.1 | 0.5 |
| 832.6 | 834.8 | 0.3 |
| 902.6 | 907.9 | 0.6 |
| Mount Condition | Location | Low Frequency Range (10–400 Hz) | High Frequency Range (400–1000 Hz) | Total | Rank |
|---|---|---|---|---|---|
| Original | #1 | 0.705 | 0.211 | 4.222 | 3 |
| #2 | 0.136 | 0.337 | |||
| #3 | 0.768 | 0.846 | |||
| #4 | 0.793 | 0.427 | |||
| Rigid GDU Mount | #1 | 0.705 | 0.245 | 4.667 | 4 (worst) |
| #2 | 0.135 | 0.441 | |||
| #3 | 0.768 | 1.000 (worst) | |||
| #4 | 0.793 | 0.579 | |||
| Rigid motor Mount | #1 | 0.675 | 0.162 | 3.415 | 2 |
| #2 | 0.120 | 0.206 | |||
| #3 | 0.726 | 0.334 | |||
| #4 | 1.000 (worst) | 0.193 | |||
| Rigid Rollrod mount | #1 | 0.668 | 0.152 | 3.324 | 1 (best) |
| #2 | 0.138 | 0.230 | |||
| #3 | 0.820 | 0.473 | |||
| #4 | 0.713 | 0.129 |
| Mount Condition | Location | Low Frequency Range (10–400 Hz) | High Frequency Range (400–1000 Hz) | Total | Rank |
|---|---|---|---|---|---|
| Original | #1 | 0.558 | 0.512 | 4.556 | 3 |
| #2 | 0.674 | 0.861 | |||
| #3 | 0.499 | 0.509 | |||
| #4 | 0.592 | 0.351 | |||
| Rigid GDU Mount (steel) | #1 | 0.674 | 0.563 | 4.932 | 4 |
| #2 | 0.664 | 0.928 | |||
| #3 | 0.520 | 0.585 | |||
| #4 | 0.626 | 0.372 | |||
| Rigid motor Mount (aluminum) | #1 | 0.776 | 0.524 | 5.826 | 5 (worst) |
| #2 | 1.000 (worst) | 1.000 (worst) | |||
| #3 | 0.981 | 0.500 | |||
| #4 | 0.678 | 0.367 | |||
| Rigid Rollrod Mount (steel) | #1 | 0.473 | 0.494 | 4.070 | 1 (best) |
| #2 | 0.576 | 0.794 | |||
| #3 | 0.456 | 0.481 | |||
| #4 | 0.460 | 0.336 | |||
| Rigid Rollrod Mount (aluminum) | #1 | 0.483 | 0.535 | 4.120 | 2 |
| #2 | 0.560 | 0.763 | |||
| #3 | 0.441 | 0.508 | |||
| #4 | 0.466 | 0.364 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Kim, C.-J.; Kang, Y. Evaluation of the Supporting Mounts of a Three-in-One Electric Drive Unit Using a Hybrid Simulation Model. Machines 2023, 11, 1026. https://doi.org/10.3390/machines11111026
Park S-H, Kim C-J, Kang Y. Evaluation of the Supporting Mounts of a Three-in-One Electric Drive Unit Using a Hybrid Simulation Model. Machines. 2023; 11(11):1026. https://doi.org/10.3390/machines11111026
Chicago/Turabian StylePark, So-Hee, Chan-Jung Kim, and Yeonjune Kang. 2023. "Evaluation of the Supporting Mounts of a Three-in-One Electric Drive Unit Using a Hybrid Simulation Model" Machines 11, no. 11: 1026. https://doi.org/10.3390/machines11111026
APA StylePark, S.-H., Kim, C.-J., & Kang, Y. (2023). Evaluation of the Supporting Mounts of a Three-in-One Electric Drive Unit Using a Hybrid Simulation Model. Machines, 11(11), 1026. https://doi.org/10.3390/machines11111026








