Feature-Based Bearing Fault Classification Using Taylor–Fourier Transform
Abstract
:1. Introduction
2. Fundamentals
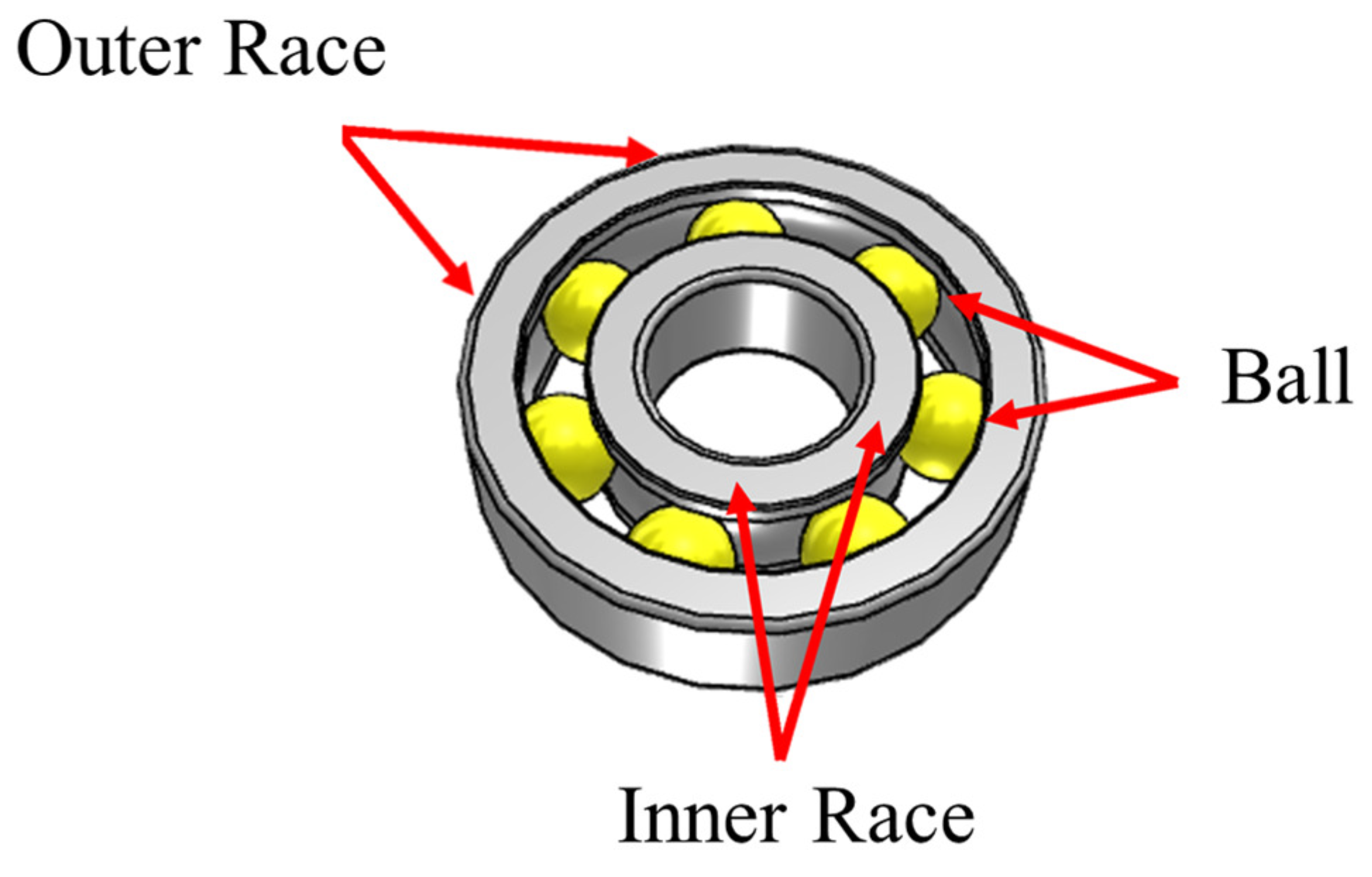
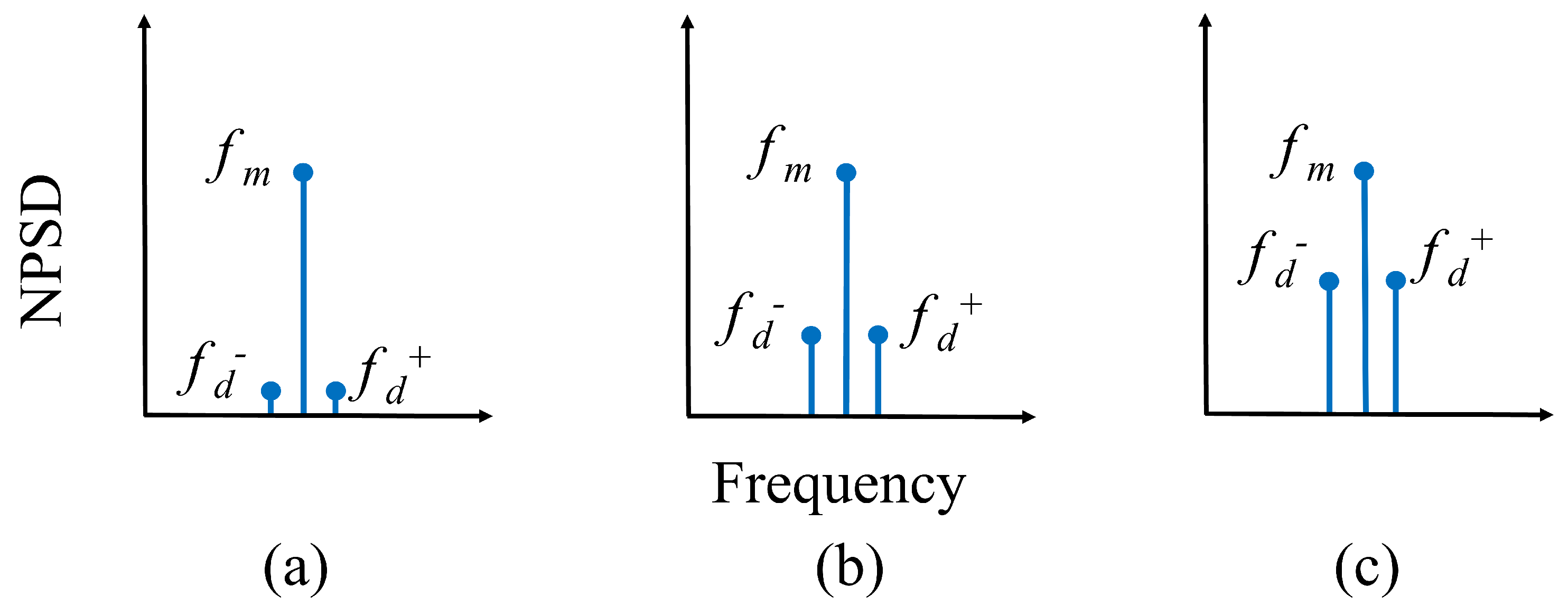
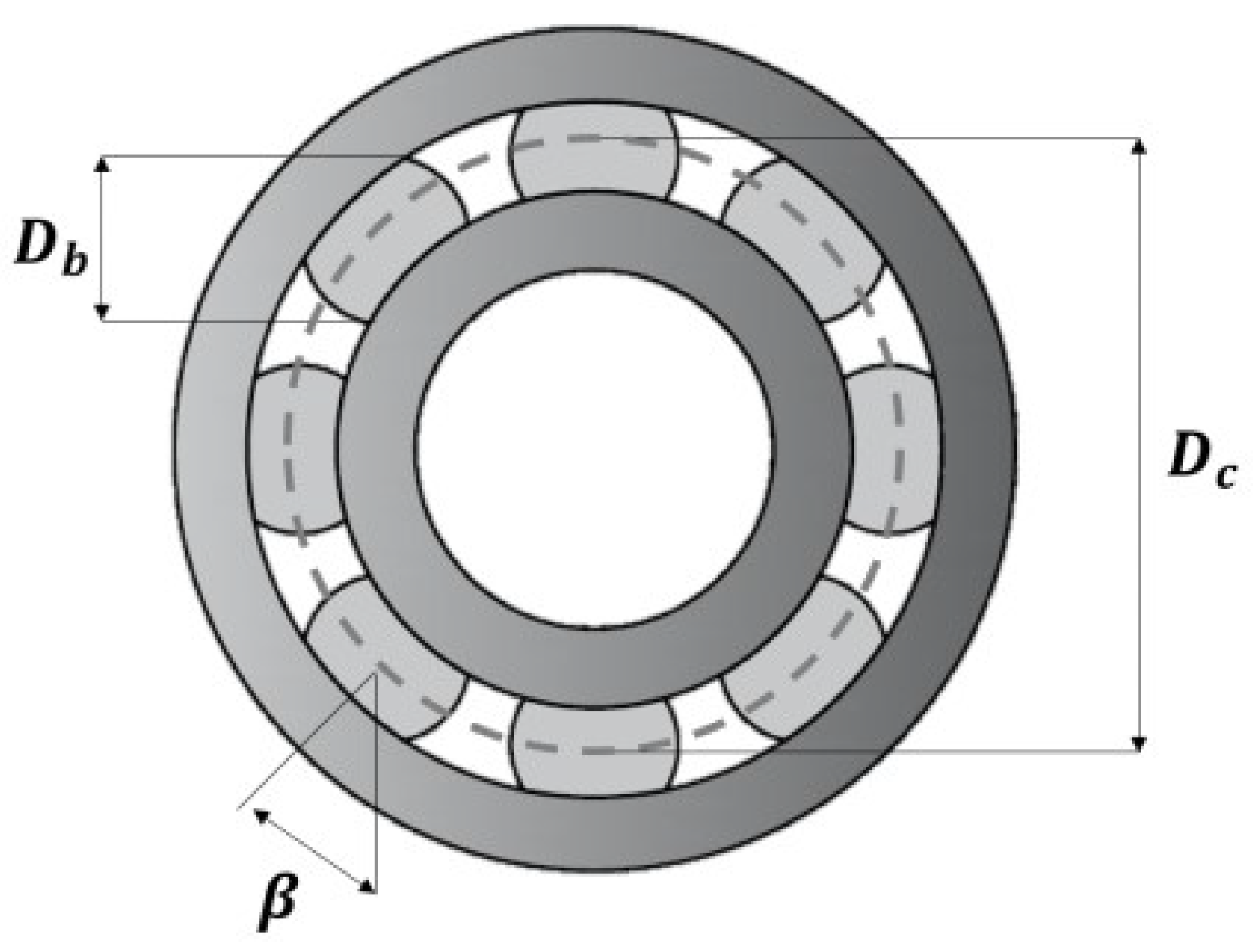
2.1. Bearing Damage Signature
2.1.1. Localized Defects
2.1.2. Nonlocalized Defects
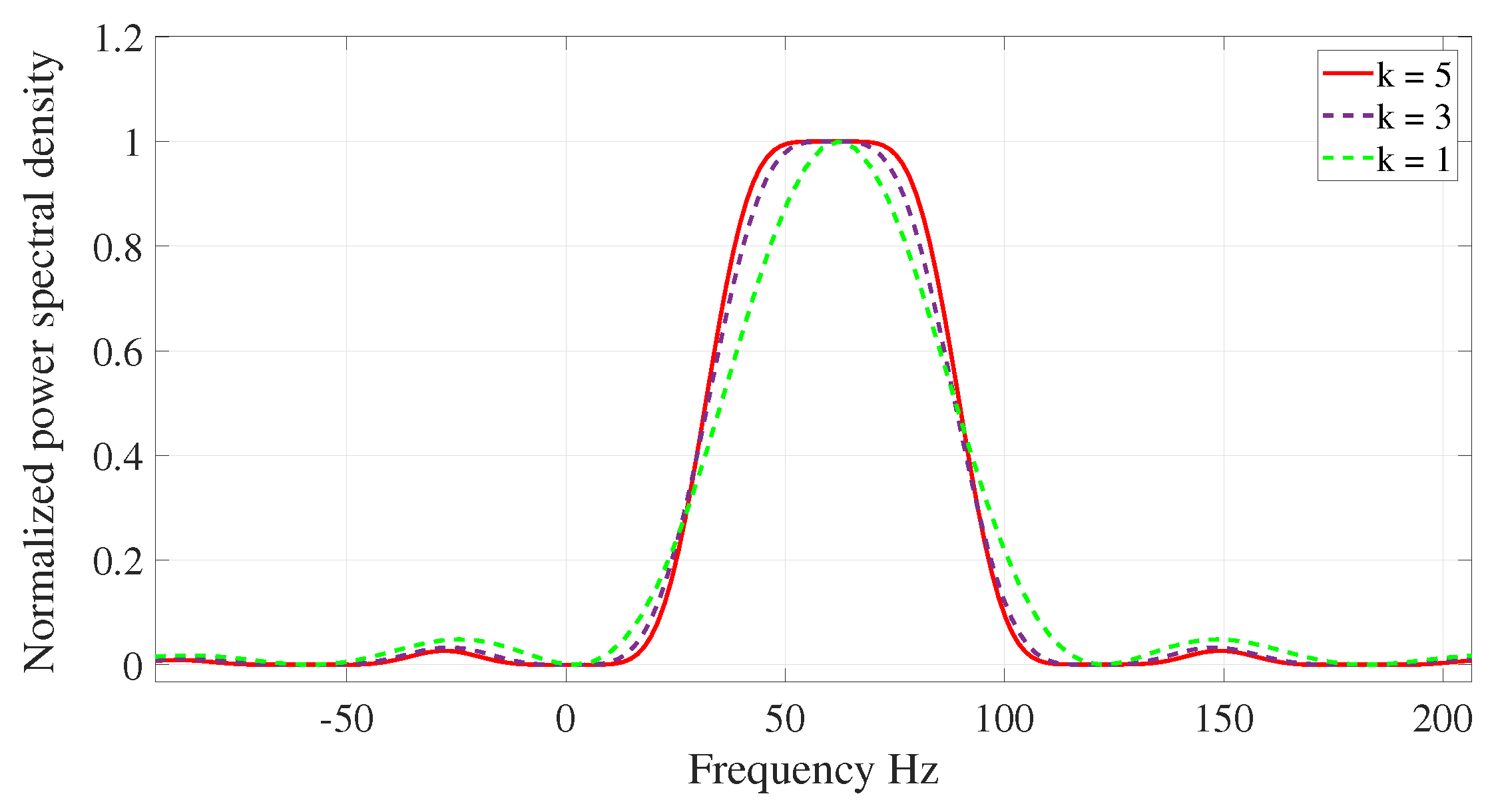
2.2. Digital Taylor–Fourier Transform
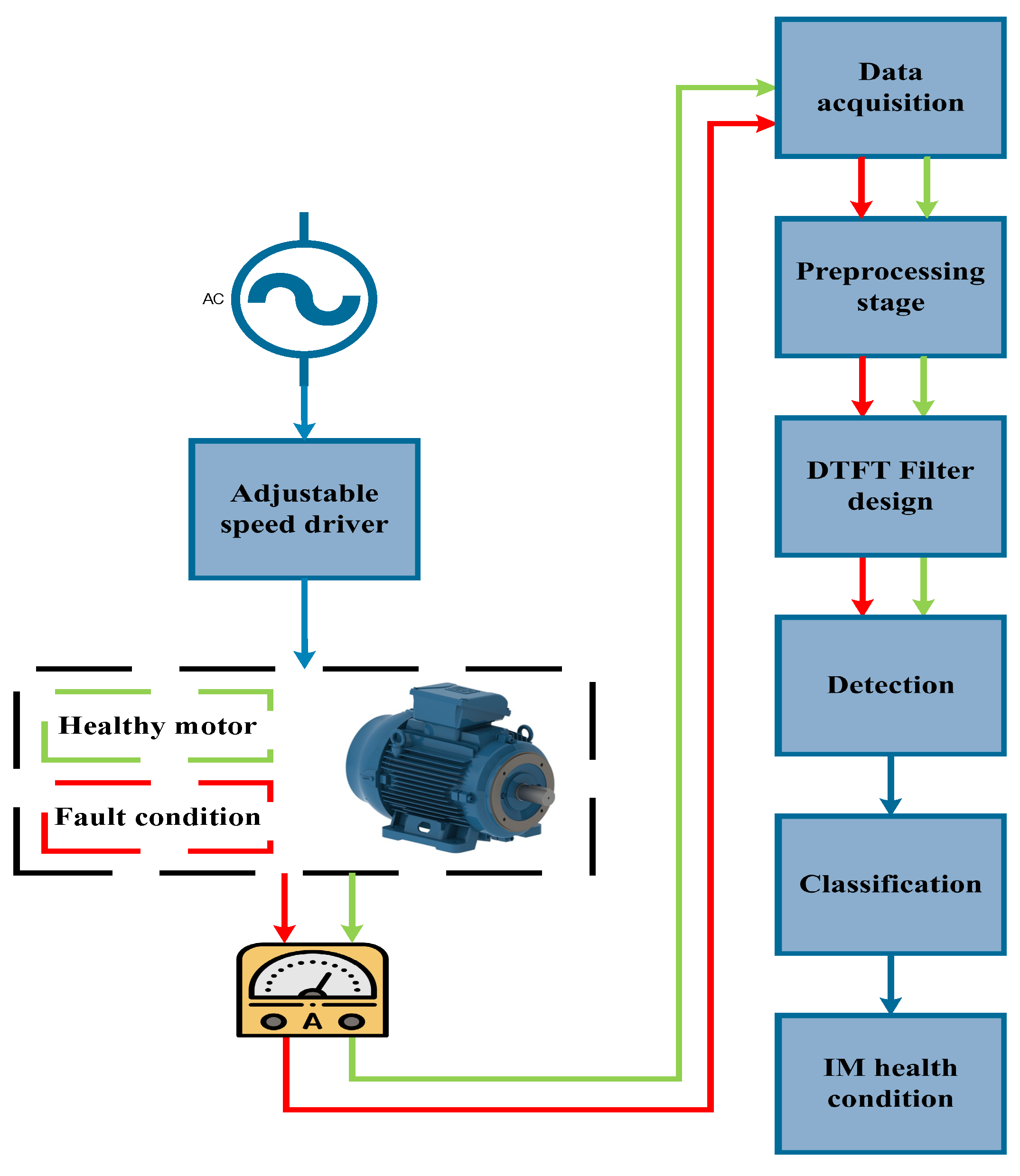
3. Methodology
4. Results
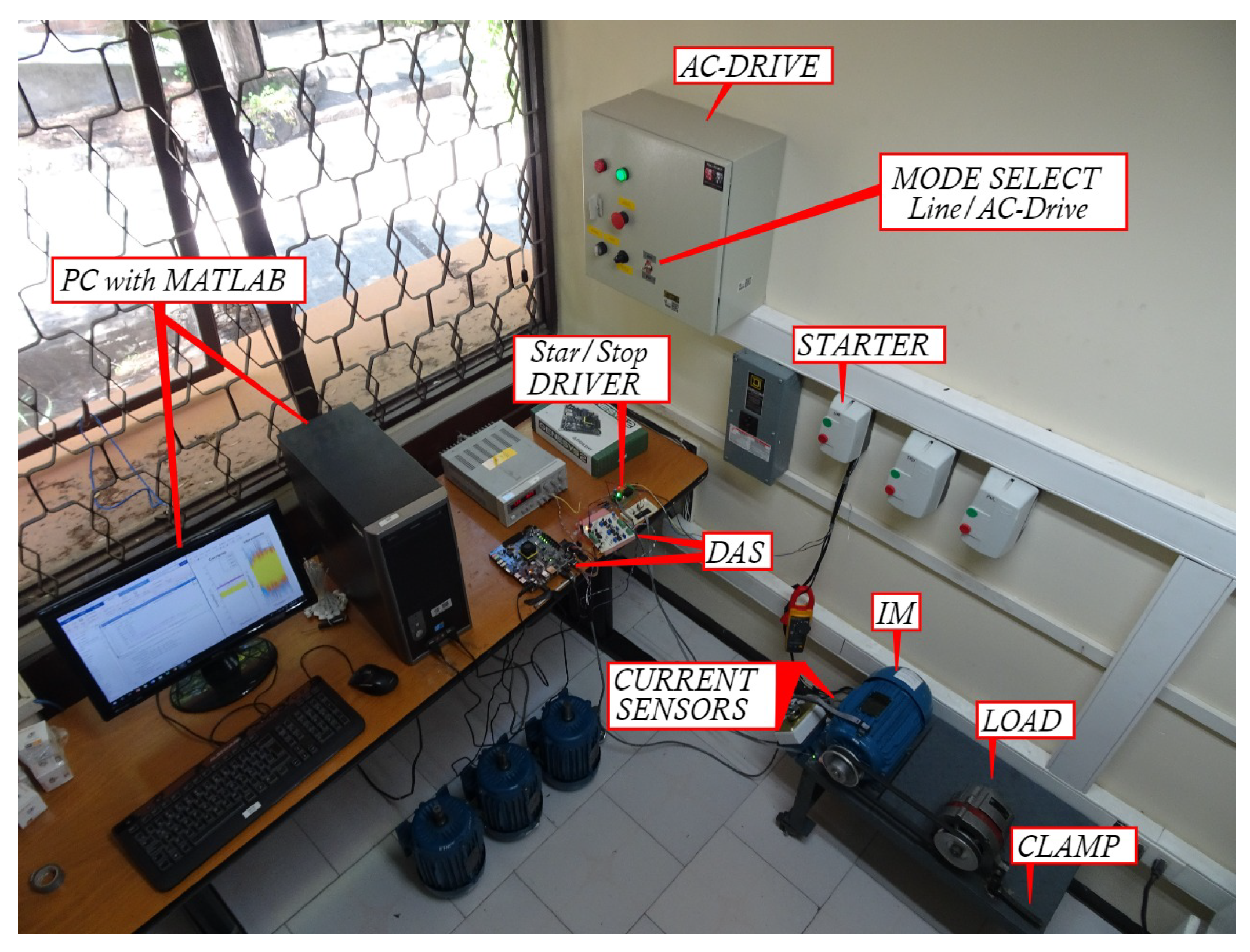
4.1. Experimental Setup
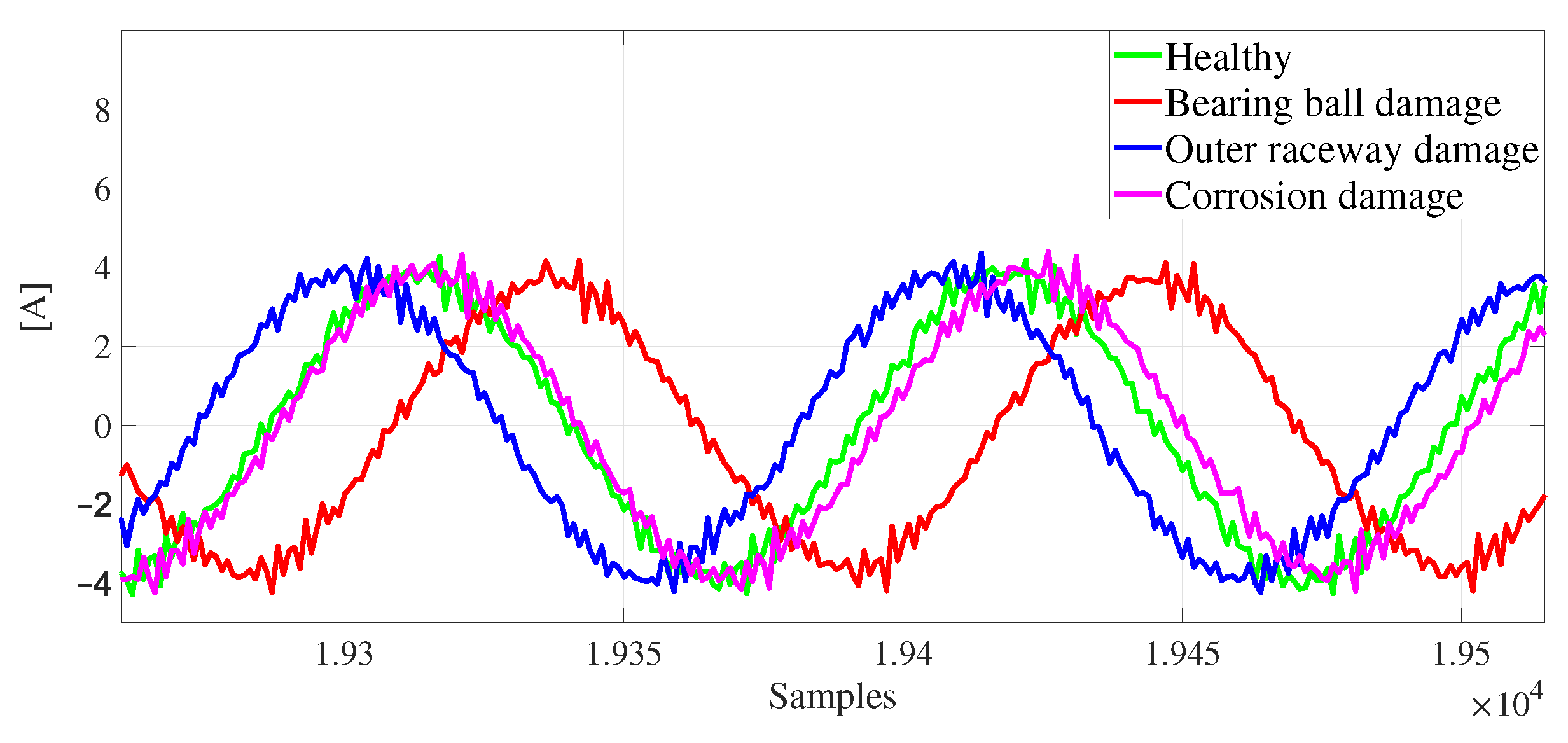
4.2. Experimental Results
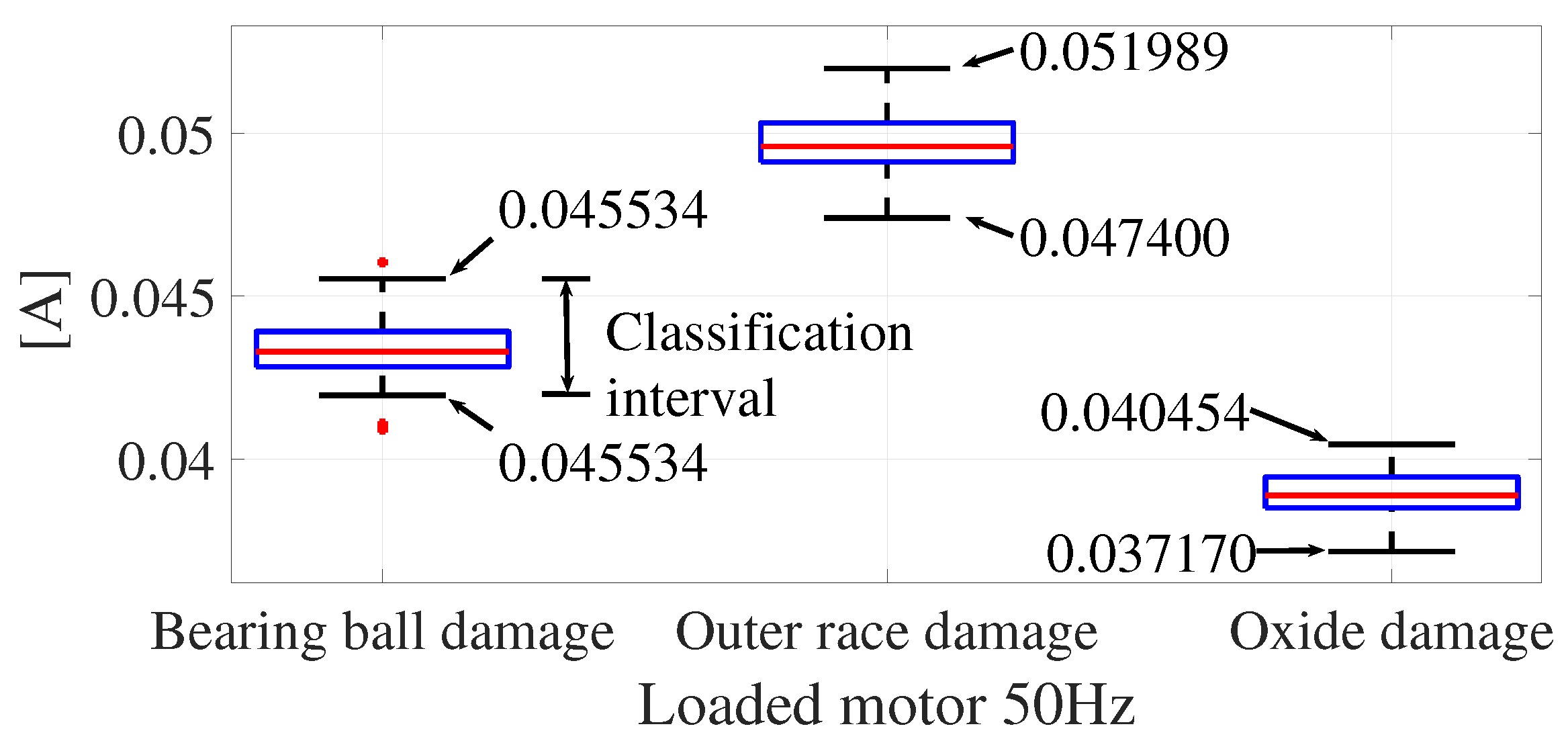
4.3. Bearing Ball Damage (BBD)
4.4. Outer-Race Damage (ORD)
4.5. Corrosion Damage (OD)
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peeters, C.; Guillaume, P.; Helsen, J. Vibration-based bearing fault detection for operations and maintenance cost reduction in wind energy. Renew. Energy 2017, 116, 74–87. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Lin, J.; Chen, Y.; Liu, J. Train axle bearing fault detection using a feature selection scheme based multi-scale morphological filter. Mech. Syst. Signal Process. 2018, 101, 435–448. [Google Scholar] [CrossRef]
- Chen, J.; Pan, J.; Li, Z.; Zi, Y.; Chen, X. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous Reluctance Motor vs. Induction Motor at Low-Power Industrial Applications: Design and Comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef]
- Kumar, S.; Mukherjee, D.; Guchhait, P.K.; Banerjee, R.; Srivastava, A.K.; Vishwakarma, D.N.; Saket, R.K. A Comprehensive Review of Condition Based Prognostic Maintenance (CBPM) for Induction Motor. IEEE Access 2019, 7, 90690–90704. [Google Scholar] [CrossRef]
- Blodt, M.; Granjon, P.; Raison, B.; Rostaing, G. Models for Bearing Damage Detection in Induction Motors Using Stator Current Monitoring. IEEE Trans. Ind. Electron. 2008, 55, 1813–1822. [Google Scholar] [CrossRef]
- Irgat, E.; Çinar, E.; Ünsal, A. The detection of bearing faults for induction motors by using vibration signals and machine learning. In Proceedings of the 2021 IEEE 13th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Dallas, TX, USA, 22–25 August 2021; Volume 1, pp. 447–453. [Google Scholar] [CrossRef]
- Jawad, S.; Jaber, A. Rolling Bearing Fault Detection Based on Vibration Signal Analysis and Cumulative Sum Control Chart. FME Trans. 2021, 49, 684–695. [Google Scholar] [CrossRef]
- Barusu, M.R.; Deivasigamani, M. Non-Invasive Vibration Measurement for Diagnosis of Bearing Faults in 3-Phase Squirrel Cage Induction Motor Using Microwave Sensor. IEEE Sens. J. 2021, 21, 1026–1039. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Antonino-Daviu, J.A.; Cureño-Osornio, J.; Saucedo-Dorantes, J.J. Gradual Wear Diagnosis of Outer-Race Rolling Bearing Faults through Artificial Intelligence Methods and Stray Flux Signals. Electronics 2021, 10, 1486. [Google Scholar] [CrossRef]
- Luo, G.; Habetler, T.G.; Hurwitz, J. Stray Flux-Based Incipient Stage Bearing Fault Detection for Induction Machines via Noise Cancellation Techniques. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 764–768. [Google Scholar] [CrossRef]
- Ramirez-Nunez, J.A.; Antonino-Daviu, J.A.; Climente-Alarcón, V.; Quijano-López, A.; Razik, H.; Osornio-Rios, R.A.; Romero-Troncoso, R.d.J. Evaluation of the Detectability of Electromechanical Faults in Induction Motors Via Transient Analysis of the Stray Flux. IEEE Trans. Ind. Appl. 2018, 54, 4324–4332. [Google Scholar] [CrossRef]
- Song, X.; Wang, Z.; Hu, J. Detection of Bearing Outer Race Fault in Induction Motors using Motor Current Signature Analysis. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Tang, H.; Dai, H.L.; Du, Y. Bearing Fault Detection for Doubly fed Induction Generator Based on Stator Current. IEEE Trans. Ind. Electron. 2022, 69, 5267–5276. [Google Scholar] [CrossRef]
- de Jesús Rangel-Magdaleno, J. Induction Machines Fault Detection: An Overview. IEEE Instrum. Meas. Mag. 2021, 24, 63–71. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Liang, X.; Zhang, Y.; Hu, T. Machine Learning-Based Fault Diagnosis for Single- and Multi-Faults in Induction Motors Using Measured Stator Currents and Vibration Signals. IEEE Trans. Ind. Appl. 2019, 55, 2378–2391. [Google Scholar] [CrossRef]
- Choudhary, A.; Goyal, D.; Letha, S.S. Infrared Thermography-Based Fault Diagnosis of Induction Motor Bearings Using Machine Learning. IEEE Sens. J. 2021, 21, 1727–1734. [Google Scholar] [CrossRef]
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A Motor Current Signal-Based Bearing Fault Diagnosis Using Deep Learning and Information Fusion. IEEE Trans. Instrum. Meas. 2020, 69, 3325–3333. [Google Scholar] [CrossRef]
- Mao, W.; Chen, J.; Liang, X.; Zhang, X. A New Online Detection Approach for Rolling Bearing Incipient Fault via Self-Adaptive Deep Feature Matching. IEEE Trans. Instrum. Meas. 2020, 69, 443–456. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, B.; Kanemaru, M.; Lin, C.; Liu, D.; Miyoshi, M.; Teo, K.H.; Habetler, T.G. Model-Based Analysis and Quantification of Bearing Faults in Induction Machines. IEEE Trans. Ind. Appl. 2020, 56, 2158–2170. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, H.; Miao, H.; Hao, J.; Li, C.; Song, W.; Yao, G.; Zhang, Y. Model-based vibration response analysis and experimental verification of lathe spindle-housing-belt system with rubbing. Mech. Syst. Signal Process. 2023, 186, 109841. [Google Scholar] [CrossRef]
- Pandarakone, S.E.; Mizuno, Y.; Nakamura, H. Distinct Fault Analysis of Induction Motor Bearing Using Frequency Spectrum Determination and Support Vector Machine. IEEE Trans. Ind. Appl. 2017, 53, 3049–3056. [Google Scholar] [CrossRef]
- Noureddine, B.; Remus, P.; Raphael, R.; Salim, S. Rolling Bearing Failure Detection in Induction Motors using Stator Current, Vibration and Stray Flux Analysis Techniques. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 1088–1095. [Google Scholar] [CrossRef]
- Nath, S.; Wu, J.; Zhao, Y.; Qiao, W. Low Latency Bearing Fault Detection of Direct-Drive Wind Turbines Using Stator Current. IEEE Access 2020, 8, 44163–44174. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic Phasor Estimates for Power System Oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- de la O Serna, J.A.; Ramirez, J.M.; Zamora Mendez, A.; Paternina, M.R.A. Identification of Electromechanical Modes Based on the Digital Taylor–Fourier Transform. IEEE Trans. Power Syst. 2016, 31, 206–215. [Google Scholar] [CrossRef]
- Aguayo-Tapia, S.; Ávalos Almazán, G.; Rangel-Magdaleno, J.; Paternina, M.R. Broken Rotor Bar Detection in Induction Motors using Digital Taylor–Fourier Transform. In Proceedings of the 2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 November 2022; Volume 6, pp. 1–6. [Google Scholar] [CrossRef]
- de la O Serna, J.A.; Paternina, M.R.A.; Zamora-Méndez, A.; Tripathy, R.K.; Pachori, R.B. EEG-Rhythm Specific Taylor–Fourier Filter Bank Implemented With O-Splines for the Detection of Epilepsy Using EEG Signals. IEEE Sens. J. 2020, 20, 6542–6551. [Google Scholar] [CrossRef]
- Avalos, G.; Aguayo, S.; Rangel-Magdaleno, J.; Paternina, M. Bearing fault detection in induction motors using digital Taylor–Fourier transform. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 1830–1835. [Google Scholar] [CrossRef]
- Serna, J.A.d.l.O. Dynamic Harmonic Analysis with FIR Filters Designed with O-Splines. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 5092–5100. [Google Scholar] [CrossRef]
- Aguayo-Tapia, S.; Avalos-Almazan, G.; Rangel-Magdaleno, J.d.J.; Ramirez-Cortes, J.M. Physical Variable Measurement Techniques for Fault Detection in Electric Motors. Energies 2023, 16, 4780. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Francq, P.; Shu, L.; Huang, J. Incipient Fault Diagnosis of Roller Bearing Using Optimized Wavelet Transform Based Multi-Speed Vibration Signatures. IEEE Access 2017, 5, 19442–19456. [Google Scholar] [CrossRef]
- Nishat Toma, R.; Kim, J.M. Bearing Fault Classification of Induction Motors Using Discrete Wavelet Transform and Ensemble Machine Learning Algorithms. Appl. Sci. 2020, 10, 5251. [Google Scholar] [CrossRef]
- Rostaghi, M.; Khatibi, M.M.; Ashory, M.R.; Azami, H. Bearing Fault Diagnosis Using Refined Composite Generalized Multiscale Dispersion Entropy-Based Skewness and Variance and Multiclass FCM-ANFIS. Entropy 2021, 23, 1510. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, Y.; Ge, M. A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy 2021, 23, 191. [Google Scholar] [CrossRef]





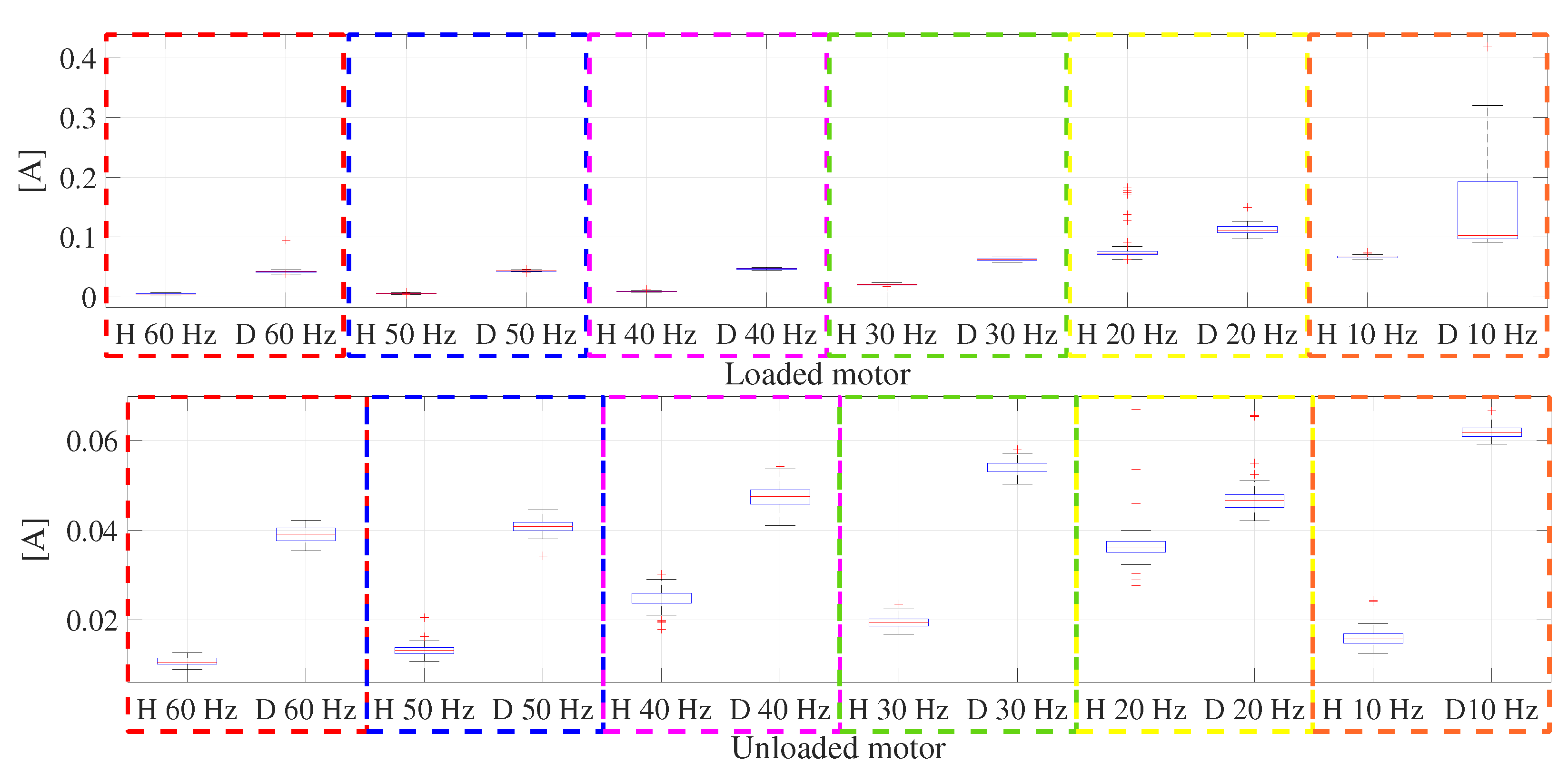
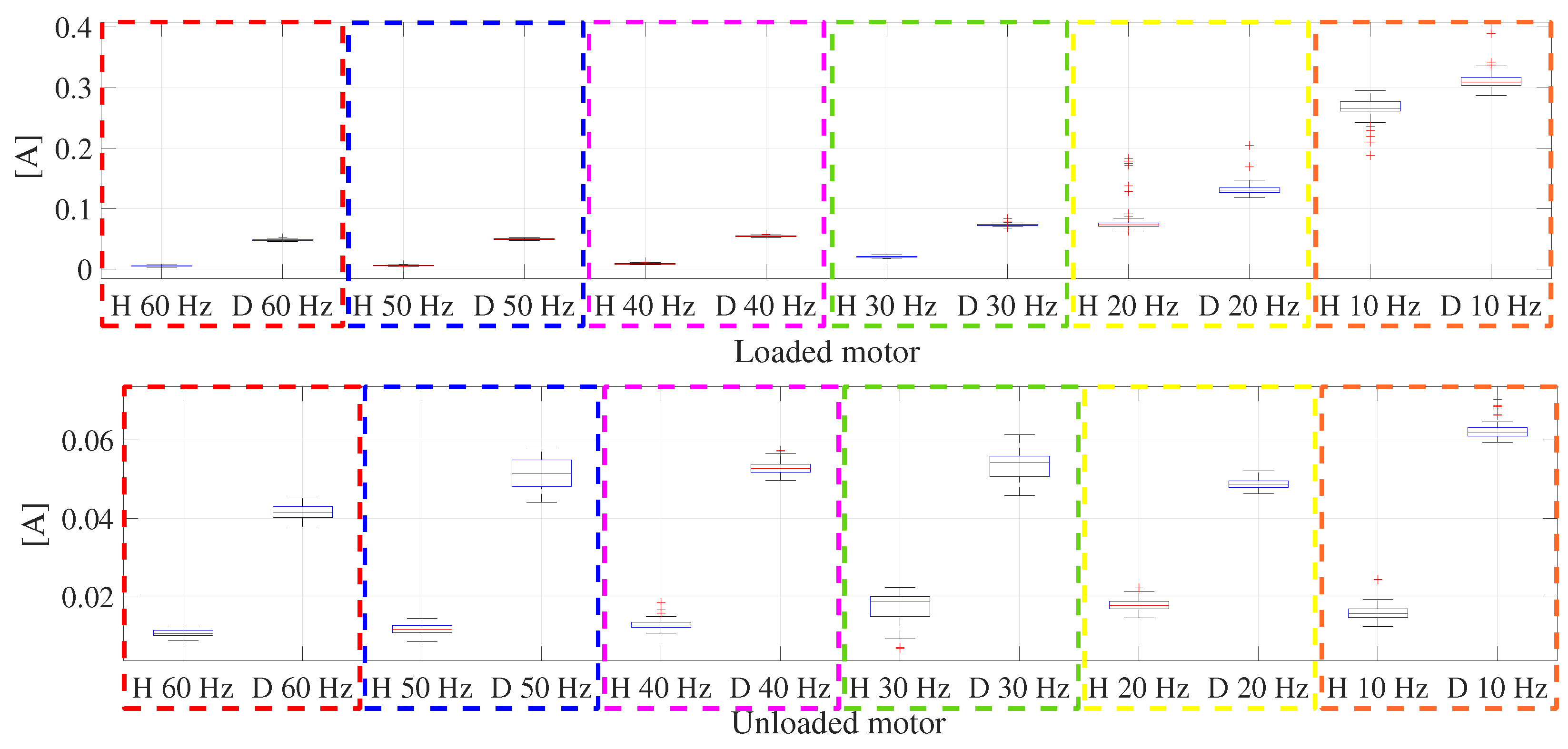
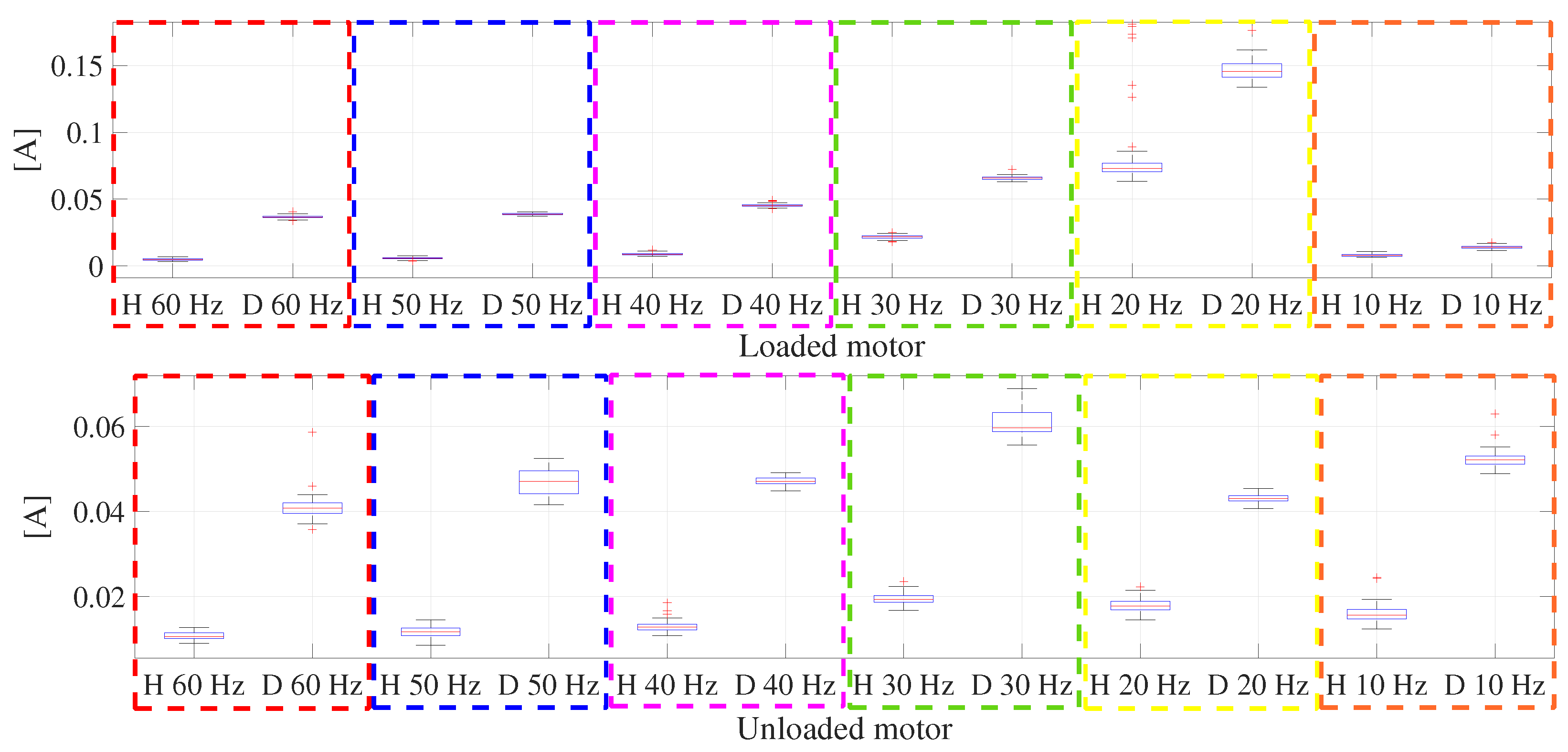
| Loaded Motor | |||||
|---|---|---|---|---|---|
| Frequency | BBD | ORD | OD | Out of Class Range | |
| BBD | 96% | 0% | 3% | 1% | |
| ORD | 60 Hz | 0% | 98% | 0% | 2% |
| OD | 4% | 0% | 95% | 1% | |
| BBD | 95% | 0% | 0% | 5% | |
| ORD | 50 Hz | 0% | 100% | 0% | 0% |
| OD | 0% | 0% | 99% | 1% | |
| BBD | 99% | 0% | 0% | 1% | |
| ORD | 40 Hz | 0% | 99% | 0% | 1% |
| OD | 0% | 0% | 100% | 0% | |
| BBD | 99% | 0% | 0% | 1% | |
| ORD | 30 Hz | 0% | 95% | 1% | 4% |
| OD | 0% | 1% | 97% | 2% | |
| BBD | 97% | 0% | 0% | 3% | |
| ORD | 20 Hz | 0% | 98% | 1% | 1% |
| OD | 0% | 0% | 94% | 6% | |
| BBD | 93% | 5% | 0% | 2% | |
| ORD | 10 Hz | 0% | 97% | 0% | 3% |
| OD | 0% | 0% | 98% | 2% | |
| Unloaded Motor | |||||
|---|---|---|---|---|---|
| Frequency | BBD | ORD | OD | Out of Class Range | |
| BBD | 97% | 0% | 0% | 3% | |
| ORD | 60 Hz | 0% | 98% | 0% | 2% |
| OD | 0% | 0% | 98% | 2% | |
| BBD | 98% | 0% | 0% | 2% | |
| ORD | 50 Hz | 0% | 100% | 0% | 0% |
| OD | 0% | 0% | 98% | 0% | |
| BBD | 97% | 0% | 0% | 3% | |
| ORD | 40 Hz | 0% | 97% | 0% | 3% |
| OD | 0% | 0% | 99% | 1% | |
| BBD | 99 | 0% | 0% | 1% | |
| ORD | 30 Hz | 0% | 95% | 0% | 5% |
| OD | 0% | 0% | 100% | 0% | |
| BBD | 97% | 0% | 0% | 3% | |
| ORD | 20 Hz | 0% | 98% | 0% | 2% |
| OD | 0% | 0% | 98% | 2% | |
| BBD | 98% | 0% | 0% | 2% | |
| ORD | 10 Hz | 0% | 91% | 0% | 9% |
| OD | 0% | 1% | 98% | 1% | |
| Year | Technique for Feature Extraction | Type of Fault | Classifier | Classifier Accuracy |
|---|---|---|---|---|
| 2017 [35] | Adaptative impulse modelling based wavelet | Ball, inner and outer race | Statistical analysis with neural network-based classifier | 100% |
| 2020 [36] | Discrete Wavelet transform | Inner and outer race | Random forest and extreme gradient boosting | 99.3% |
| 2021 [37] | Refined composite generalized multiscale dispersion entropy | Ball, inner and outer race | Multiclass adaptative neuro-fuzzy classifier | 89.62–99.27% |
| 2021 [38] | k-optimized adaptive local iterative filtering and improved multiscale permutation entropy | Ball, inner and outer race | Back-propagation neural network | 91.57–99.98% |
| 2021 [19] | Continuous Wavelet transform | Ball, inner and outer race | Convolutional neural network and support vector machine | 98.75–98.89% |
| This work | Amplitude estimation based on the Taylor–Fourier transform | Ball, inner and outer race and corrosion | Statistical analysis | 93–100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avalos-Almazan, G.; Aguayo-Tapia, S.; de Jesus Rangel-Magdaleno, J.; Arrieta-Paternina, M.R. Feature-Based Bearing Fault Classification Using Taylor–Fourier Transform. Machines 2023, 11, 999. https://doi.org/10.3390/machines11110999
Avalos-Almazan G, Aguayo-Tapia S, de Jesus Rangel-Magdaleno J, Arrieta-Paternina MR. Feature-Based Bearing Fault Classification Using Taylor–Fourier Transform. Machines. 2023; 11(11):999. https://doi.org/10.3390/machines11110999
Chicago/Turabian StyleAvalos-Almazan, Gerardo, Sarahi Aguayo-Tapia, Jose de Jesus Rangel-Magdaleno, and Mario R. Arrieta-Paternina. 2023. "Feature-Based Bearing Fault Classification Using Taylor–Fourier Transform" Machines 11, no. 11: 999. https://doi.org/10.3390/machines11110999
APA StyleAvalos-Almazan, G., Aguayo-Tapia, S., de Jesus Rangel-Magdaleno, J., & Arrieta-Paternina, M. R. (2023). Feature-Based Bearing Fault Classification Using Taylor–Fourier Transform. Machines, 11(11), 999. https://doi.org/10.3390/machines11110999







