A New Direct and Inexpensive Method and the Associated Device for the Inspection of Spur Gears

Abstract

This paper proposes a new rapid and straightforward method along with a related device for finding the three basic parameters of an actual external involute spur gear. The number of teeth is easily counted, but the other two parameters—the module and the coefficient of profile shift—are difficult to identify. The method is based on the principle of inspection of the precision of gear teeth, using the dimension over pins, when the maximum distance is measured between the lateral surfaces of two cylindrical rollers of well-controlled dimensions, placed into the spaces between teeth. The dimension over pins is applied as a function of the number of teeth (odd or even) and requires experience (and this is the main disadvantage of the method) for finding the correct maximum distance between pins. The new method eliminates this drawback as it proposes a measuring scheme where four identical rollers are used in a designed inspection device. The system is statically determinate and, therefore, the dimension to be measured is unequivocally found. A new relation for the dimension to be measured is deduced and allows for finding the module and the coefficient of profile shift. The inspection device is described and a concrete case is presented for exemplifying the methodology. A further application permits finding the centre distance for an external spur gearing. Unlike the classical technique where the centre distance is obtained based on the centring surfaces of the wheels, the new method implies only dimensions measured through flank measurements, thus eliminating errors introduced by the deviations between the flanks and the centring surfaces of the wheels.

1. Introduction

1.1. Structural Solutions for Coupling Two Shafts with Crossed Axes

One of the major tasks of the theory of mechanisms is the transmission of rotational motion between two shafts with stipulated directions, capable of ensuring a certain law of motion for the driven shaft when the motion of the driving shaft is imposed [1,2]. There are numerous solutions presented in the technical literature, but recent articles propose new coupling solutions.

Considerations regarding the costs, dimensions, and efficiency impose that the coupling kinematical chain between the two shafts has a structure that is as simple as possible. Two cases arise: first, the shafts have crossed directions in space [3,4] and therefore the transmission is a mechanism of family 0; secondly, the shafts have coplanar axes and so the mechanism of the transmission has family 3 (with the possibility of a spherical mechanism when the shafts have crossing axes or a parallel mechanism when the shafts have parallel axes). For the spatial case, a simple structural calculus [5] shows that the expected solution is with direct contact between the shafts, when a higher class 1 pair is formed between the shafts; for the mechanisms of family 3, the contact is completed by a class 4 pair [5]. For both situations, the pair occurring between the two shafts is a higher pair [6,7,8], so it concerns mechanisms transmitting the rotational motion from an element to another through a higher pair. This permits the extension of the definition of cam mechanisms to all types of mechanisms with direct contact between the driving and driven elements.

Discussing the spatial case, the most comprehensive situation arises when the higher pair through which the motion between the shafts is transmitted is completed by means of two surfaces ${\Sigma }_1$ and ${\Sigma }_2$, as shown in Figure 1. The two surfaces realise a Hertzian point contact in [8]. During the motion, on the two surfaces, the contact point M describes two curves ${\Gamma }_1,{ \Gamma }_2$, which are permanently tangent [9,10,11]. The transmission mechanism presents particular cases when one or both surfaces are replaced by curves or/and points. In [12], the principles of kinematic analysis are presented for the situation when the kinematic pair is made by a point and a surface, and [13,14] present the case when the kinematical pair is made by two curves. Another possible situation is the contact between a curve and a surface [15].

1.2. Structural Solutions for the Coupling of Two Shafts with Parallel Axes

In the case of planar mechanisms, the possible structural solutions for the transmission of rotational motion through direct coupling (higher pair) are:

• Mechanism with rotating cam and oscillating curved face follower [16]—the contact point moves on the follower (Figure 2);
• Mechanism with rotating cam and oscillating tip follower [16]—the contact point is immobile on the follower and describes an arc of circle while running (Figure 3).

1.3. Gears

A particular but frequently encountered case in technical applications concerns the mechanisms ensuring a constant transmission ratio:

$$i_{12}=\frac{{\omega }_1}{{\omega }_2}$$

(1)

The mechanisms that meet this requirement are gear mechanisms [17,18,19,20]. For the planar mechanisms, the centroids of relative motion are represented by the pitch circles $c_{w1}$ and $c_{w2}$ that roll without slipping over each other. The main geometric parameters are [21] the transmission ratio $i_{\mathrm{1,2}}$, the radii of the pitch circles $r_{w\mathrm{1,2}}$, and the centre distance, defined as

$$a_w=r_{w1}+r_{w2}.$$

(2)

As seen in Figure 4, the rotational motion is transmitted between the two toothed wheels by means of the higher pair formed between the profiles ${\gamma }_1$ and ${\gamma }_2$ of the two wheels. The first remark is that during gearing, the two flanks are reciprocally enveloping.

This principle is represented in Figure 5 for elliptical profile gears [22] and in Figure 6 for a circular arc profile [23].

The first section therefore shows that the simplest manner of transmitting the motion between two shafts consists of completing a direct point contact between them. The actual solution is materialised by the spatial cam mechanisms. When the constant transmission ratio is imposed, the cam mechanism becomes a particular case: the gear mechanism. For the case of gears with parallel axes, the majority is represented by the involute tooth profiles. For a spur gear with an involute tooth profile, the relations for the calculus of constructive parameters are presented. The conclusion that the entire geometry of the wheel is characterised by three parameters (number of teeth, module, and the coefficient of profile shift) is highlighted in the second section, Materials and Methods. One of the methods of the inspection of the involute profile of gears is the dimension over pins. This presents the disadvantage of different approaches, as a function of the number of the teeth of the wheel—odd or even—and also the fact that the dimension to be measured represents the maximum distance between two parallel cylinders. Based on the dimension over pins method, a new method for finding the module and the coefficient of profile shift for a spur gear is proposed in the Materials and Methods section. This method eliminates the drawbacks of the dimension over pins method. The section dedicated to the Results and Discussions shows the schematics of the laboratory test-rig for applying the proposed method, and then the actual device, followed by an exemplification for a concrete case. Next, another claim of the proposed device and method is presented, measurement of the centre distance for external spur gears, using only the flanks of the teeth as measuring surfaces and therefore eliminating the errors introduced in the classic case, when the centre distance is found through the centring dimensions of the two wheels.

2. Materials and Methods

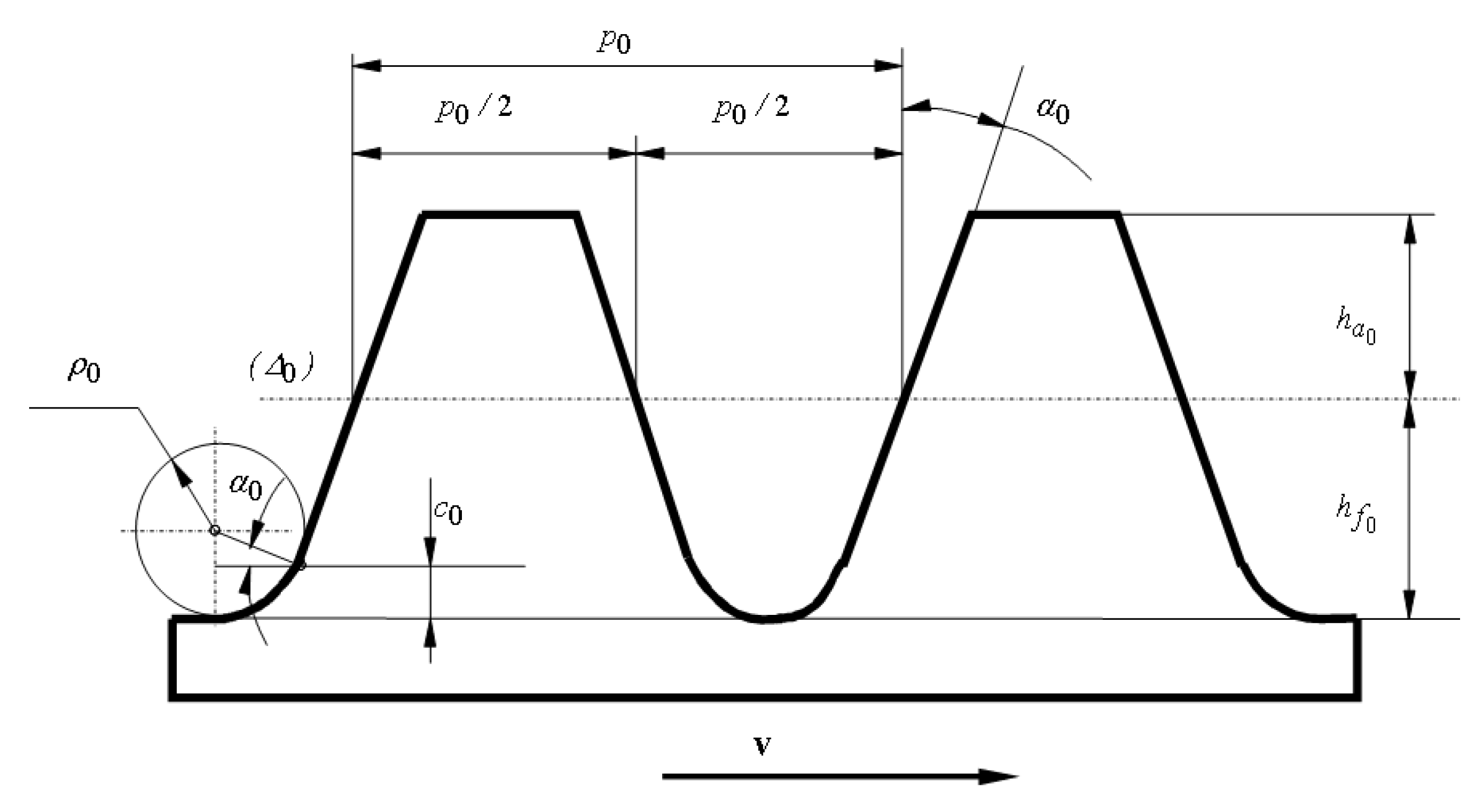
2.1. Cylindrical Gear with Involute Teeth

2.1.1. The Involute Curve, Definition, and Properties

There are conditions that must be obeyed by the two surfaces ${\Sigma }_1$, ${\Sigma }_2$ in order to ensure the transmission of motion with a constant transmission ratio. For the spatial mechanism case, in [18], three theorems are presented that stipulate the conditions required by a constant transmission ratio. For planar mechanisms, the condition to be satisfied by the two profile curves ${\gamma }_1$ and ${\gamma }_2$ is stipulated by the basic law of gearing [5] that affirms the following: what is necessary and sufficient for transmitting rotational motion with a constant transmission ratio between two profiles is that the common normal in the point of contact permanently passes through a fixed point (the gearing pole) situated on the centre line. Founded on the base law of gearing, the profile of the conjugate profile can be obtained when the radii of the pitch circles, the relative motion between the two wheels, and the profile of one of the gears are stipulated. Additionally, the method permits finding the trajectory of the contact point—the line of contact.

From the above considerations, with known pitch radii $r_{w\mathrm{1,2}}$ and transmission ratio $i_{12}$, one can choose an infinity of pairs of curves ${\gamma }_1$ and ${\gamma }_2$ that can transmit the rotational motion with constant ratio. In the general case, as it can be observed from Figure 5 and Figure 6, the curves ${\gamma }_1$ and ${\gamma }_2$ are different and, therefore, different manufacturing and inspection technologies are required for the two wheels of the gear mechanism. From technological and economical points of view, the ideal situation is when the two profiles have similar curves [21]. The curve that satisfies this condition is the involute of the circle, defined as in Figure 7, where the geometrical loci are described by a point of a mobile straight line $\Delta$ that rolls without slipping over a fixed circle, named the base circle.

From the definition of the involute and based on Figure 7, the following properties emerge:

• The normals to the involute are tangent to the base circle;
• The current point of tangency T between the mobile straight line $\Delta$ and the base circle $c_b$ is the curvature centre of the involute, and the curvature radius of the involute in the point M is $\rho =TM$.

The straight line $\Delta$ envelopes the involute, and the consequence of this observation is the possibility of manufacturing the involute profile with straight-edge gear-cutting tools with relatively low cost. For $r_b\to \infty$ and $\rho \to \infty$, the involute degenerates into a straight line and the geared wheel becomes a basic rack. The basic rack is a fictive part that allows for defining any wheel with which it can gear. In order to obtain the equations of the involute curve, the polar parametric coordinates $\left(r,\theta \right)$ are used:

$$\left\{\begin{array}{c}r=OM=r_b/\mathit{cos}\alpha \\ \theta =M_{0}OM=\mathit{tan}\alpha -\alpha =inv\alpha \end{array}\right.$$

(3)

In the relations of (3), the angle $\alpha$ is the pressure angle, which is the angle made by the vector radius $OM$ with the tangent to the involute curve—the straight line $\Delta$ in the point M. One must emphasise that in the theory of gearing, the current technique is to define a circle using the pressure angle of the involute profile generated with the base circle $c_b$. That is, the circle must be concentric to the base circle and its radius is according to the first relation from Equation (3).

2.1.2. The Basic Rack for Spur Gear

The basic rack is the fictive part used to define the cylindrical gears. Figure 8 represents the standard basic rack for a spur gear. The shape and relative dimensions of the basic rack are standardised by STAS 822-82 [24].

The characteristic parameters of the basic rack are:

• $p_0$—the rack pitch;
• ${\alpha }_0=20°$—the pressure angle corresponding to pitch circle (the angle of inclination of the profile with respect to the normal to reference line);
• $h_{a_0}$—the addendum of the tooth;
• $h_{f_0}$—the dedendum of the tooth;
• m—the module.

The module is used for expressing all parameters with the dimension of length. The values of the module are standardised:

$$p_0=\pi m$$

(4)

$$h_{a0}=h_{a0}^{\mathrm{*}}m;\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{h}_{a0}^{\mathrm{*}}=1\left(standard\right)$$

(5)

$$h_{f0}=\left(h_{ao}^{\mathrm{*}}+c_0^{\mathrm{*}}\right)m; c_0^{\mathrm{*}}=0.25\left(standard\right)$$

(6)

where $h_{a0}^{*}$ is the coefficient of the reference addendum and $c_0^{*}$ is the coefficient of bottom clearance. For the basic rack, the bottom clearance is filleted to the flanks using two arcs of a circle of radius ${\rho }_0$. The value of the radius ${\rho }_0$ is found from the condition that the filleted region has a height equal to the standard bottom clearance $c_0$. From this condition, based on Figure 8, we write

$${\rho }_0=\frac{c_0}{1-\mathit{sin}({\alpha }_0)}=0.38 \mathrm{m} (standard)$$

(7)

2.1.3. The Definition of the Cylindrical Gear Using the Standard Basic Rack for Spur Gear

The toothed wheel is defined according to Figure 9 [21]. The rolling circle that allows the definition of the gear is named the pitch circle $\left(c_d\right)$. The pitch circle and the pitch line are permanently tangent. The distance between the pitch line and the reference line, denoted as X, is the profile shift. The signum of the profile shift is:

• $x=0$: the reference line and the pitch circle are tangent;
• $x<0$: the reference line and the pitch circle are intersecting;
• $x>0$: the reference line and the pitch circle have no common points.

The shift of the profile X is expressed using the module and the profile shift coefficient x:

$$X=mx$$

(8)

The circular pitch on the pitch circle is

$$p=p_w=p_0$$

(9)

The pitch diameter is

$$d=\frac{zp}{\pi }=\frac{z\pi m}{\pi }=mz$$

(10)

The addendum of the spur gear:

$$h_a=h_{f0}-c_0+X=h_{a_0}+X=m(h_{a_0}^{\mathrm{*}}+x)$$

(11)

The dedendum of the spur gear:

$$h_f=h_{a_0}+c_0-X=(h_{a_0}^{\mathrm{*}}+c_0^{\mathrm{*}}-x)m$$

(12)

The addendum diameter:

$$d_a=d+2h_a=m\left(z+2h_{a_0}^{\mathrm{*}}+2x\right)$$

(13)

The dedendum diameter:

$$d_f=d-2h_f=m\left(z-2h_{a_0}^{\mathrm{*}}-2c_0^{\mathrm{*}}+2x\right)$$

(14)

From Figure 10, where, in the ABC triangle, $BC=X\mathit{tan}({\alpha }_0)$, the arc tooth thickness at pitch circle s is found with the following relation:

$$s=e_{w_0}=\frac{p_0}{2}+2Xtan({\alpha }_0)=\left[\frac{\pi }{2}+2xtan({\alpha }_0)\right]m$$

(15)

The space width between two teeth on the pitch circle e is calculated using the following relation:

$$e=p-s_{w_0}=\pi m-\left[\frac{\pi }{2}+2xtan({\alpha }_0)\right]m=\frac{\pi }{2}-2xtan({\alpha }_0)m$$

(16)

The base diameter does not depend on the coefficient of profile shift:

$$d_b=d\mathit{cos}({\alpha }_0)=mz\mathit{cos}({\alpha }_0)$$

(17)

From the above considerations, one can state that the whole geometry of a spur gear is expressed as function of:

• The number of teeth, z;
• The module, m;
• The coefficient of profile shift, x.

2.2. Inspection Dimensions for Spur Gears with External Teeth

An extremely large number of manual and automatic inspection techniques exist due to the variety of gears and parameters to be measured. The first classification is in analytical and functional measurements, depending on the quantitative or qualitative aspects envisaged [25]. From the analytical methods, the simplest are the manual techniques carried out with instruments like callipers and micrometres [26], while the most cutting-edge techniques are performed with coordinate measuring machines or dedicated high-precision measuring instruments that can perform automatic and continuous inspection. The modern methods developed using precision measurement techniques are non-contact, requiring sophisticated equipment that uses, for example, optical measurements [27,28], laser sensors [29], moiré interferometry [30], or coordinate-measuring machines (CMMs) [31,32]. The methods should cover the size domain from small gears [33] to large gears [29]. Even if specific machines exist, new measuring devices are still developed [33,34], confirming the need for low-cost measuring apparatuses, comparable in precision with modern dedicated measuring apparatuses. Two classical inspection methods with direct contact are used for the control of the tooth of spur gears with an involute profile: the span over teeth and the dimension over pins [25,26]. We propose a simple, direct, low-cost method, applicable for small- and medium-sized gears.

2.2.1. The Surfaces Used in the Inspection of the Precision of the Teeth of Spur Gears

As shown previously, the entire geometry of the spur gear with the involute profile is fully defined by three parameters: number of teeth z, module m, and coefficient of shift profile x [31]. The number of teeth is found by simply counting them. The module of the spur gear is a standard value, a fact that is a major advantage. So, when the module is found by any method, the exact value is that from the list of standard modules, STAS 822-82. Then, the most difficult task is finding the coefficient of profile shift.

All characteristic phenomena of gearing are directly influenced by the values of the profile shift coefficients. Based on this, the block contour diagrams were traced. This permits a rapid selection of the coefficients of profile shift, aiming towards the result that the gear will respond to numerous functional requirements like interference, covering degree, and undercutting. Energy efficiency is highly important, since sliding and friction exist [35,36,37] between the flanks of the wheels (except the pitch point).

The geometry of a spur gear with external teeth (Figure 11) has the following as boundary surfaces:

• The addendum (outside) cylinder $S_a$;
• The dedendum cylinder $S_f$(root cylinder);
• Axial face $S_t$;
• Cylindrical hole for shaft assembly $S_c;$
• Keyway surface $S_p$;
• Involute flank surface $S_e.$

The shift is a characteristic of the involute flank surface.

From the boundary surfaces, the addendum cylinder, the dedendum cylinder, and the axial faces are free surfaces, being manufactured with large tolerances, and it is not recommended to use them in the measurements for finding the coefficient of profile shift. The keyway surface cannot be used, since there is no condition between it and the flank of the spur gear. The use of the cylindrical hole for shaft assembly is restricted by the error introduced by the radial runout of the gear. As a conclusion, in order to determine the coefficient of profile shift, it is recommended to perform the inspection measurements using only the flank surface.

2.2.2. Inspection Dimensions for Spur Gears

• Span over teeth.

This is the distance between the tangents to the anti-homologous profiles for a number N of teeth. The number of teeth N is found from the condition that the two tangents should be parallel and be materialised by the flanks of a measuring instrument, such as callipers (Figure 12).

The relations for the calculus of the number of teeth N and the value of the span over these $W_N$ are presented in the technical literature [21].

2.

The dimension over pins.

This represents the distance between the generatrixes of two pins introduced in the spaces between teeth. Two situations can occur, as a function of the odd or even number of teeth, presented in Figure 13. The diameter of the pins must be chosen to satisfy the condition that the pin–tooth contact is made on the involute domain of the tooth flank, preferably in the following range:

$$r_u<r<r_a$$

(18)

where $r_u$ is the radius of the circle demarcating the involute profile from the non-involute one.

The advantage of this method is that it is applicable in measurements for both external and internal gears. Compared to the span over teeth method, the drawback of dimension over pins is the dependence of this dimension on the position of the contact points and on the size of the pins (Figure 13). For the system presented in Figure 14, a simple calculus of mobility is made using the following relation:

$$M_3=3(n-1)-c_4-2c_5=3·(5-1)-6-2·1=4$$

(19)

where $n$ is the number of elements:

$$n(\mathrm{0,1},\mathrm{2,3},4)=5$$

(20)

The number of higher pairs $c_4$ is

$$c_4(B,C,D,E,F)=5$$

(21)

and the number of lower pairs $c_5$ is

$$c_5\left(A\right)=1$$

(22)

Of the four degrees of freedom, two are represented by the rotations of the pins about their axes, motions that do not modify the geometry of the system; therefore, they can be cancelled. The other two degrees of freedom are represented by the translations from the pairs B and C; if these are dissimilar motions, they will cause the displacement of the mobile arm of the callipers and so they will alter the value of the measured dimension.

2.3. Proposed New Method for Measuring the Dimension over Pins

2.3.1. Principle of the Method

The present paper proposes the removal of this drawback by applying a new measuring scheme (Figure 15) with three pins or four pins (placed symmetrically with respect to the direction of measurement).

For the measuring scheme presented in Figure 15a, the mobility is

$$M_3=3·(n-1)-c_4-2·c_5=3·(6-1)-9-2·1=4$$

(23)

Three degrees of freedom are passive ones, represented by the rotations of the pins about their axes. The remaining degree of freedom represents the displacement of the points of contact between the pins and the arms of the callipers, which is normal on the measuring direction, and thus does not affect the precision of the measurement.

For Figure 15b, the mobility is

$$M_3=3·(n-1)-c_4-2·c_5=3·(7-1)-12-2·1=4$$

(24)

The four degrees of freedom now represent the rotations of the pins about their axes and, thus, when the scheme from Figure 15b is used, an over-constrained system is obtained (one of the pins is a passive element).

2.3.2. The Algorithm for the Calculus of Module and the Coefficient of Flank Shift

The verifying algorithm is based on the pin’s diameter, which is adopted according to STAS 12222-84 [38], and Figure 16.

$$d_R\cong 1.8 \mathrm{m}$$

(25)

In order to apply the new method, the relation for the calculus of the radius of the centre of the pin $r_R$ is required. Towards this purpose, the pressure angle of the involute profile on the circle of $r_R$ radius is necessary. From Figure 17, we see that

$$\mathrm{\angle }{B}_{R}OB={\theta }_R+\frac{{\varphi }_B}{2}$$

(26)

where

$${\theta }_R=inv{\alpha }_R$$

(27)

The relation for the calculus of the width of the space between two teeth on an arbitrary circle of radius $r_y$ [21], with the pressure angle ${\alpha }_y$, is

$$e_y=\frac{mz\mathit{cos}{\alpha }_0}{\mathit{cos}{\alpha }_y}\left[\frac{\pi }{2z}-\frac{2x\mathit{tan}{\alpha }_0}{z}+inv{\alpha }_y-in{v}_0\right]$$

(28)

The relation, applied for the base circle, ${\alpha }_y=0$, becomes

$$e_b=mz\mathit{cos}{\alpha }_0\left[\frac{\pi }{2z}-\frac{2x\mathit{tan}{\alpha }_0}{z}-in{v}_0\right]$$

(29)

Now, the angle ${\varphi }_b$ can be found:

$${\varphi }_b=\frac{e_b/2}{d_b/2}=\frac{\pi }{2z}-\frac{2x\mathit{tan}{\alpha }_0}{z}-in{v}_0$$

(30)

Let us examine the process of generation of involutes passing both through the centre of the pin $O_R$ and through the contact point T between the pin and the profile; the segment $O_{R}T$ lies over the arc $B_{R}B$ from the base circle. Based on this remark, one can write

$$length\left(arc{B}_{R}B\right)=length\left(\overline{O_{R}T}\right)=\frac{d_R}{2}$$

(31)

On the base circle,

$$\mathrm{\angle }{B}_{R}OB=\frac{d_R/2}{d_B/2}=\frac{d_R}{mz{\alpha }_0}$$

(32)

From the above relations, an equation of unknown ${\alpha }_r$ results in the following:

$$\frac{d_R}{mz{\alpha }_0}=inv{\alpha }_R+\frac{\pi }{2z}-\frac{2x\mathit{tan}{\alpha }_0}{z}-in{v}_0$$

(33)

The pressure angle is thus found:

$$inv{\alpha }_R=in{v}_0-\frac{\pi }{2z}+\frac{2x\mathit{tan}{\alpha }_0}{z}+\frac{d_R}{mz{\alpha }_0}$$

(34)

or

$${\alpha }_R=\mathit{arg}(inv{\alpha }_R)$$

(35)

where ${\alpha }_0=20^o$ is the pressure angle of the profile on the pitch circle of the wheel. Equation (35) is a transcendental expression and is solved using the Root function from Mathcad software (7) [39]. The radius of the circle where the centres of the pins are placed is found:

$$r_R=\frac{d_b}{2\mathit{cos}{\alpha }_R}=\frac{mz}{2}\frac{\mathit{cos}{\alpha }_0}{\mathit{cos}{\alpha }_R}$$

(36)

The dimension over pins with the newly proposed scheme is

$$D=D_1+D_2=r_R(\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2)+d_R$$

(37)

where the angles ${\psi }_1$ and ${\psi }_2$ are found according to Figure 16. In order to apply relation (37), the following conditions must be fulfilled:

$$\left\{\begin{array}{c}{D}_1>r_a\\ D_2>r_a\end{array}\right.$$

(38)

The corroboration of the conditions in (38) is necessary to avoid the situation when the active surface of the callipers touches the addendum of teeth.

In the case where the module of the gear is not known, the hypothesis is accepted where the values of the coefficient of flank shift do not significantly affect the external dimensions of the wheel. Therefore, it is considered that the gear is unshifted:

$$x=0$$

(39)

and the dimension over pins D is measured. The radius $r_R$ is found from the following relation:

$$r_R=\frac{D-d_R}{\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2}$$

(40)

and then the pressure angle ${\alpha }_R$ is calculated:

$${\alpha }_R=\mathit{acos}\frac{mz\mathit{cos}{\alpha }_0}{2r_R}=\mathit{acos}\frac{\mathit{mzcos}{\alpha }_0}{2(D-d_r)}\left(\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2\right)$$

(41)

With ${\alpha }_R$, from relation (34), the following results:

$$inv\left\{\mathit{acos}\left[\frac{\mathit{mzcos}{\alpha }_0}{2(D-d_r)}\left(\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2\right)\right]\right\}=inv{\alpha }_0-\frac{\pi }{2z}+\frac{2x\mathit{tan}{\alpha }_0}{z}+\frac{d_R}{mz{\alpha }_0}$$

(42)

Equation (42) has the two parameters of the gear as unknowns: the module $m$ and the coefficient of flank shift $x$. A supplementary equation is required for finding the two parameters, which is obtained using two remarks:

• The change in the coefficient of flank shift does not significantly alter the geometry of the gear;
• The module of the gear must have a standard value.

Based on the above considerations, the two parameters are found following the methodology below:

• For the unshifted flank profile gear $x=0$, Equation (42) becomes

$$inv\left\{\mathit{acos}\left[\frac{\mathit{mzcos}{\alpha }_0}{2(D-d_r)}\left(\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2\right)\right]\right\}=inv{\alpha }_0-\frac{\pi }{2z}+\frac{d_R}{mz{\alpha }_0}$$

(43)

The unknown is the value of the module. The resulting equation is a transcendental expression and it is solved numerically [39].

• Next, the module m_std is adopted as the closest value from the standard STAS 822-82. This value is then introduced in relation (42), which becomes

$$inv\left\{\mathit{acos}\left[\frac{m_{\mathit{std}}\mathit{zcos}{\alpha }_0}{2(D-d_r)}\left(\mathit{cos}{\psi }_1+\mathit{cos}{\psi }_2\right)\right]\right\}=inv{\alpha }_0-\frac{\pi }{2z}+\frac{2x\mathit{tan}{\alpha }_0}{z}+\frac{d_R}{m_{std}z{\alpha }_0}$$

(44)

This is an algebraic equation that allows for finding the coefficient of profile shift.

3. Results and Discussions

3.1. The Experimental Test-Rig

Based on the scheme from Figure 16, the device was designed as presented in Figure 18. The main parts are the metallic base plate 1, on top of which a parallelepipedal part 2 is mounted. On the plate 1, four mounting brackets 6 are fixed, which ensure the support of two parallel cylindrical rods 8. A mobile parallelepipedal part 3 glides on these rods. Two ball bushings 7 are used for reducing friction between the rods and the mobile part and also for avoiding self-locking. The measurement procedure follows the next steps:

• Positioning the gear 5 to be measured with the front face on the surface of the base plate 1.
• Two identical pins 4 are introduced in the spaces between teeth; afterwards, through gliding, the two pins are brought into contact with the active face of the fixed prism.
• Diametrically opposite to the first two pins, one or two other pins are introduced in the spaces between the teeth (as in Figure 18).
• The mobile prism 3 is translated along the rods 8 and the face of the mobile prism 3 is brought into contact with the pins; a firm contact must be achieved between all the pins and the mating prismatic parts.
• A calliper is used for measuring the distance between the active faces of the two prisms. A correct measurement requires symmetrical placement of the pins with respect to the measuring direction.
• The actual test-rig, assembled in the laboratory, is presented in Figure 19.

Figure 19 shows that the mobile prism is kept in a stable position by a screw 9 and a threaded nut 10, fixed on the base plate. The precision of the device must be carefully obtained, and ensuring the tight controlled parallelism between the active faces of the two prisms is an essential condition. Towards this purpose, the fixed prism was precisely positioned on the base plate via two cylindrical bolts 11, of diameter $\varphi 10h7$. The mating holes (diameter $\varphi 10H7$) were manufactured simultaneously, by the same grip of the plate and mobile prism; then, the prism was assembled with the plate with the screws 12. Next, the ball bushings 7 were assembled with the mobile prism using spring-retaining rings. The rods 8 were introduced into the bushings and into the brackets 6. The brackets were placed on top of the plate. The mobile prism was brought into contact with the fixed prism and centred symmetrically with respect to the plate. By maintaining the contact between the prisms, the rods and the mounting brackets were allowed to glide to the desired position. Next, mating holes for the brackets 6 were drilled into the plate 1 and subsequently the brackets were fixed using the screws 12.

3.2. Example of Application of the New Method for Establishing the Characteristics of a Spur Gear

Next, a practical example of using the device is presented. The initial parameters required are:

• The number of teeth of the wheel, z;
• The diameter of the pins d_R;
• The polar angles of the centres of the wheels with respect to the measuring direction ${\psi }_1$, ${\psi }_2$;
• The distance between the active faces of the prisms, D;

The spur gear to be measured for finding its parameters is presented in Figure 20, with the following known initial parameters:

• The pressure angle of the basic rack is ${\alpha }_0=20^{\mathrm{o}}$;
• The diameter of the pins d_R = 12 mm;
• The number of teeth z = 25,

The position angles of the centres of the pins with respect to the measuring direction ${\psi }_1=\pi /z{, \psi }_2=2\pi /z$ can be obtained. Then, the module is obtained by solving Equation (43).

For these values, the solution of the transcendental equation (Equation (43)) is $m=4.93$(mm), and then $m_{std}=5 \left(\mathrm{m}\mathrm{m}\right)$ is adopted. Using the standard values of the module, Equation (44) gives the coefficient of profile shift $x=-0.121$.

3.3. Applying the New Method for Centre Distance

Another application of the device is finding the distance between centres for a spur gear with involute teeth (Figure 21). The classic methodology uses the centring surfaces of the two wheels (holes or shafts).

The centre distance is found by measuring the maximum and minimum distances, $L_{max}$ and $L_{min}$, respectively (Figure 21), of the centring surfaces, and the following relation is applied:

$$a_w=(L_{max}+L_{min})/2$$

(45)

The inconvenience of the method is that for a gearing, the centre distance is entirely determined by the flanks of the involute teeth. The employment of any surfaces other than the ones fully defining the respective dimension in the measurement of a dimension makes it so the positioning errors (for the present case, the radial runout of the gear) of the definition surfaces and measuring surfaces will be appreciated as deviations in the dimension to be measured.

The proposed arrangement presents a new method for tooth measurements that implies only the flank surfaces of the teeth. The measuring scheme is presented in Figure 22. The standard module $m_{std}$ is found, as well as the coefficients of profile shift for the two spur gears, $x_1$ and $x_2$. Next, the distance D between the active surfaces of the prisms and the four pins is measured, according to Figure 23. Each wheel makes two contacts: with the mating gear and with two of the four identical pins.

Based on notations from Figure 23, we can write

$$D=r_{R1}\mathit{cos}\psi {\mathrm{’}}_1+a_w+r_{R2}\mathit{cos}\psi {″}_2+d_R$$

(46)

and it results in the centre distance:

$$a_w=D-r_{R1}\mathit{cos}\psi {\mathrm{’}}_1-r_{R2}\mathit{cos}\psi {″}_2-d_R$$

(47)

Apart from the surface of involute flanks, the unique surfaces involved in the measuring process are the cylindrical surface of the four pins, and it is recognised that the pins (cylindrical rollers of bearings) are high-precision manufactured parts. The value obtained for the centre distance $a_w$ can now be used for verifying the precision of finding the profile shift coefficients of the gears. Thus, the pitch circle pressure angle ${\alpha }_w$ is found:

$${\alpha }_w=\mathit{acos}(a_w/a_0)$$

(48)

where $a_0$ is the reference centre distance (when $x_1+x_2=0$):

$$a_0=m\frac{z_1+z_2}{2}$$

(49)

The value obtained for the pitch angle is now introduced into the fundamental equation of gearing:

$$inv{\alpha }_w=inv{\alpha }_0+2\frac{x_1+x_2}{z_1+z_2}\mathit{tan}{\alpha }_0$$

(50)

From the obtained results from the equation, the sum of profile shift coefficients is ${x(x}_1+x_2)$, which is compared to the value obtained by the newly proposed method.

4. Conclusions

This work proposes a method and device for finding the parameters of an involute tooth profile.

Most of the spur gears are teethed wheels with an involute tooth profile. The surfaces of the teeth transmitting the motion between the flanks of the two wheels are involute cylinders, of intricate geometry, and additionally, the dimensions of the active regions of the teeth are reduced. These remarks allow for the affirmation that the task of controlling and measuring the parameters of a gear is difficult. It must also be added that the precision of finding the control parameters of a gear must be high, since the shape and position deviations of the flank geometry cause inappropriate running of the mechanism and, therefore, an alteration of the law of motion of the driven element.

From the three parameters of a spur gear, the number of teeth, the module, and the shift profile coefficient, only the first one can be directly found, by counting. The other two parameters are estimated by means of other geometric characteristics, which, in turn, are directly influenced by the three fundamental parameters. For the inspection of the spur gear precision, the span over teeth and the dimension over pins are the used as parameters.

The span over teeth method is applicable only for external gearing. The dimension over pins method removes this inconvenience but requires expertise in applying it: firstly, it refers to the dimension representing the maximum distance between two cylindrical rollers placed in spaces diametrically or quasi-diametrically opposite; secondly, it is applied differently according to the odd/even number of teeth.

This paper proposes a new measuring method using two pairs of identical pins placed symmetrically with respect to the measuring direction. The main advantage of the method resides in the fact that the wheel contacting the pins, and which contact the measuring surfaces of the device, represent a statically determinate system. Therefore, the dimension to be measured is unambiguously found.

The designed and built measuring device is presented, along with the relation between the basic parameters of the gear, the diameter of the pin, and the measured distance. This relation allows for finding the module of the gear under the assumption of the unshifted profile. The actual module is then adopted as the closest value to standards.

With the standard module value, the shift profile coefficient is next calculated from the relation. The method is exemplified for an actual situation. The accuracy of finding the module and the profile shift coefficient is directly influenced by the measuring precision of the inspection dimension.

Another useful application of the device is finding the centre distance of spur gears with high precision. The difference between the classical method and the proposed one is the fact that the new method supposes the use of only the flanks of the two wheels, while the traditional method uses the cylindrical centring surfaces of the wheels (holes or shafts). The obtained value of the centre distance is a parameter employing the estimation of the precision of valuation of the shift profile coefficients.

For further research, we aim to apply the method in the case of helical gears. For these gears, besides the three parameters—number of teeth z, module m, and the coefficient of profile shift x—the helix angle β also defines the geometry of the wheel. The gear is defined in a normal section on the flank line, but the entire gearing process can be studied in the frontal section of the wheel. In a frontal section, the wheel also has an involute profile but is defined with the rack obtained by sectioning the standard rack gear with a frontal plane. Therefore, the method proposed in the present paper can be applied in the case of helical gears obeying the following observation: the rollers should be replaced by balls having the centres positioned in the same plane, normal to the axis of the wheel. The rollers cannot be used, since (although the flank surfaces are ruled surfaces and may achieve a linear contact flank-roller) the two straight lines of the contact flank-roller are not parallel as in the spur gear case.

Possible future research directions could include the following: adapting the measuring procedure for internal spur gears and employing an electronic device capable of automatic measurement of the distance, in order to diminish human errors.