An Investigation into the Multi-Pass Radial-Mode Micro Abrasive Air Jet Turning of Fused-Silica Rods
Abstract
1. Introduction
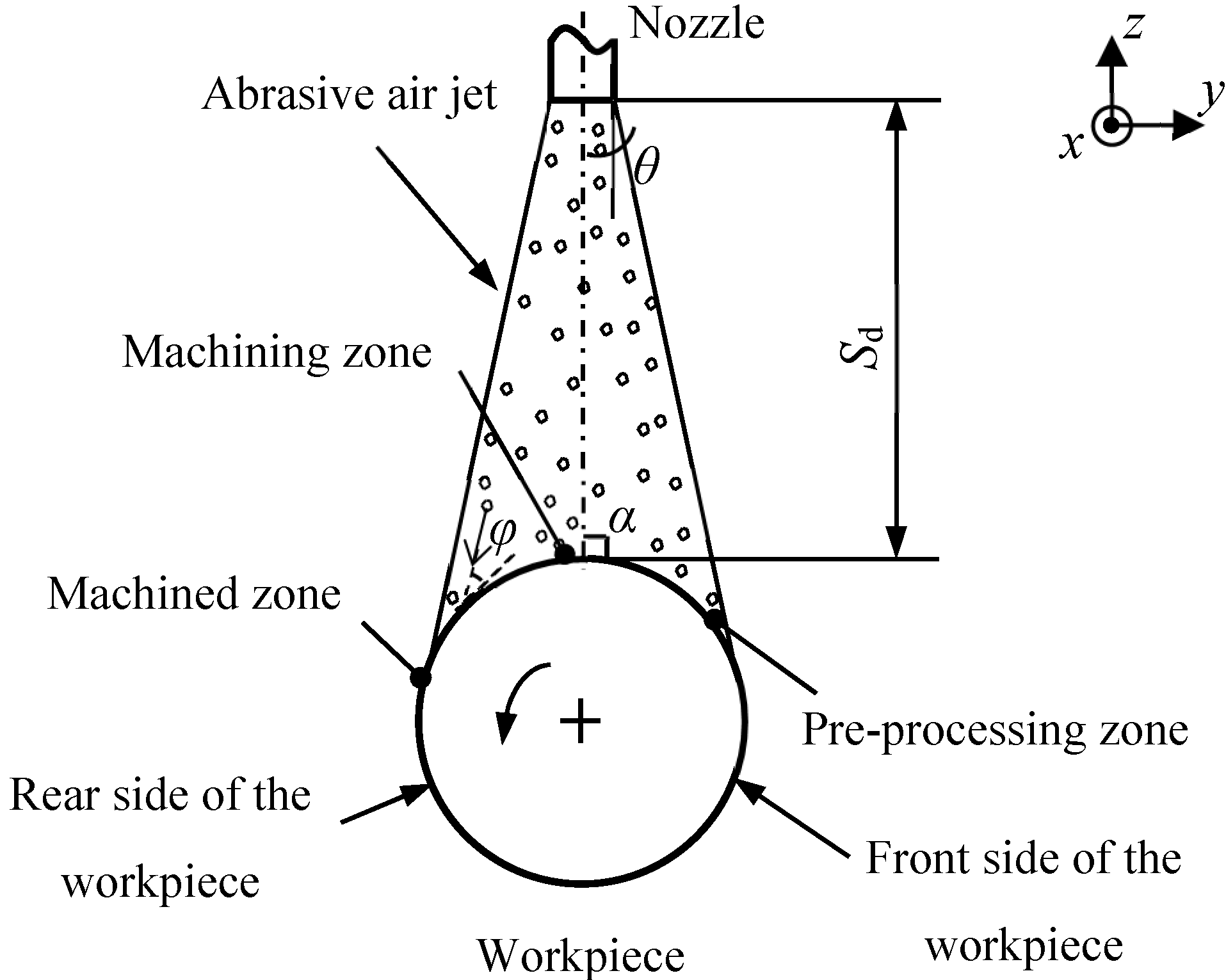
2. Experimental Set-Up and Procedure
3. Results and Discussion
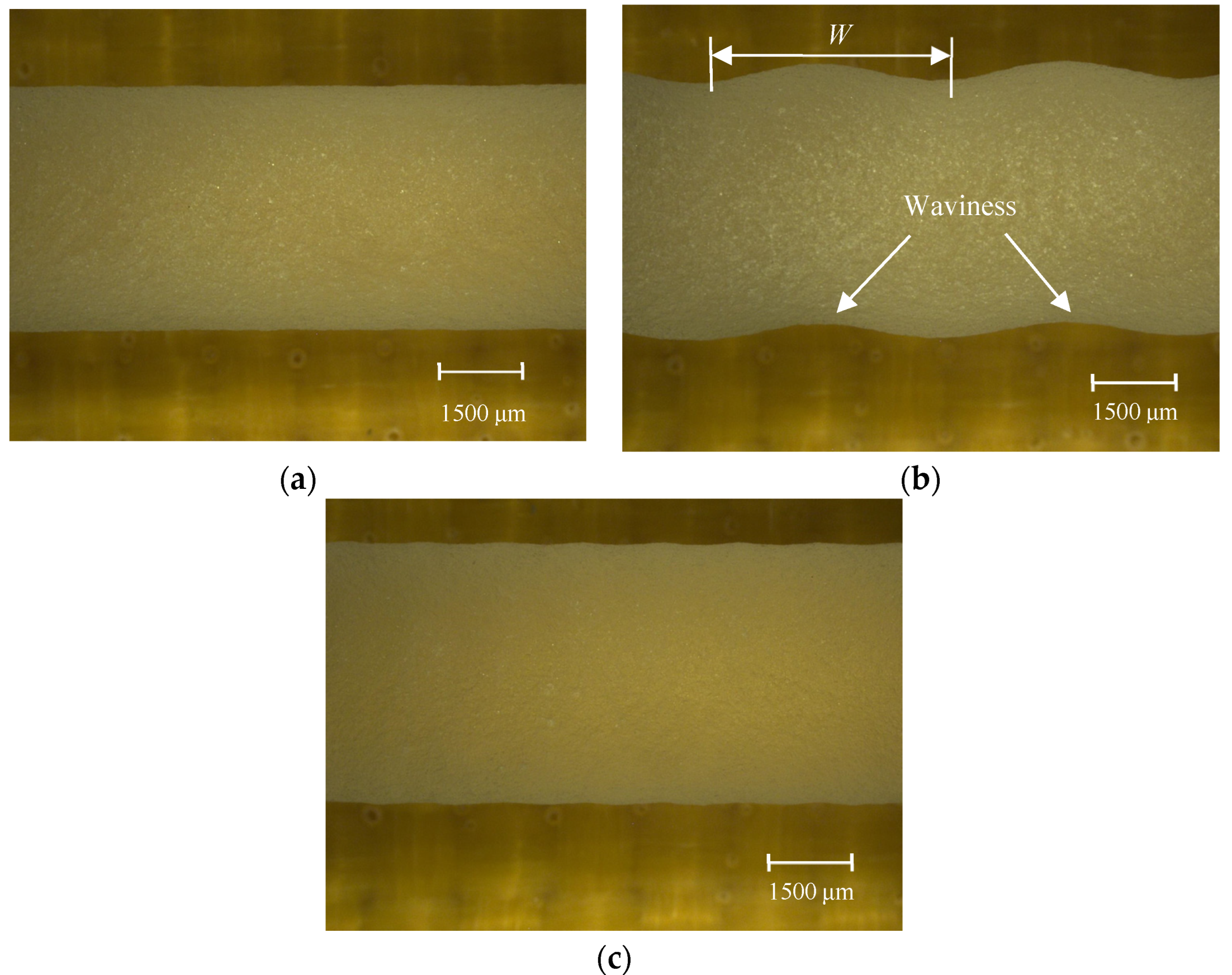
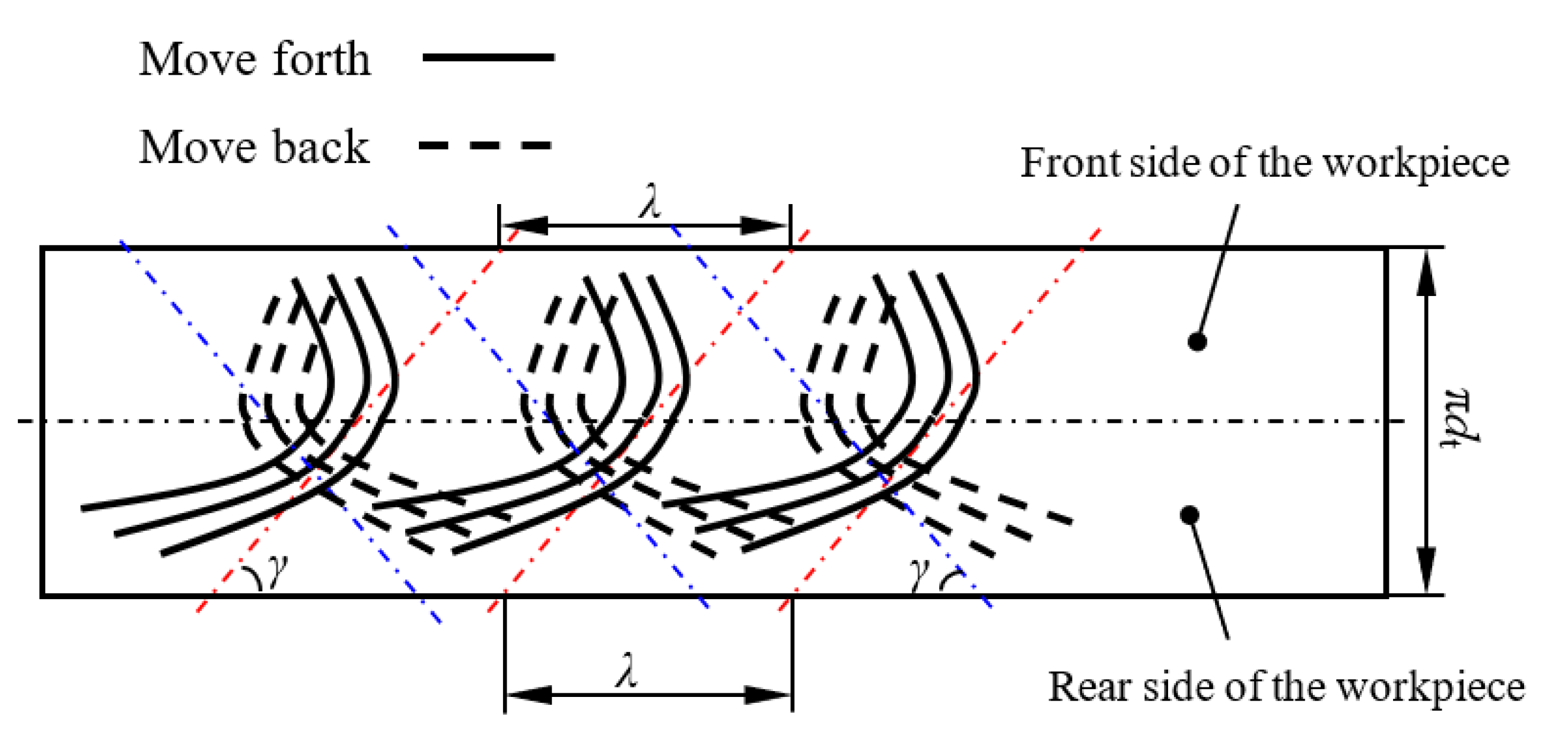
3.1. Waviness on Surface Generated by MAAJ Turning
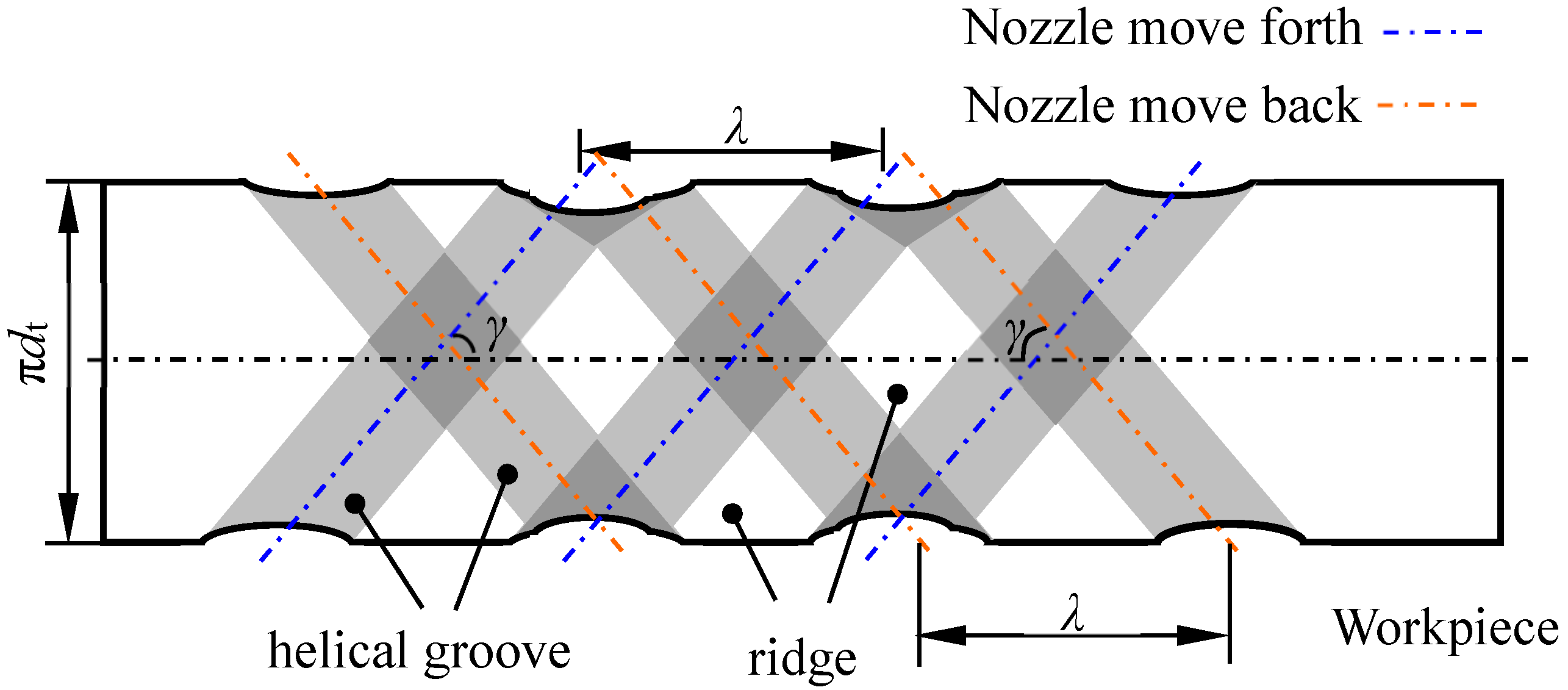
3.2. Striation on Surface Generated by MAAJ Turning
3.3. Analysis of Variance for h and MRR
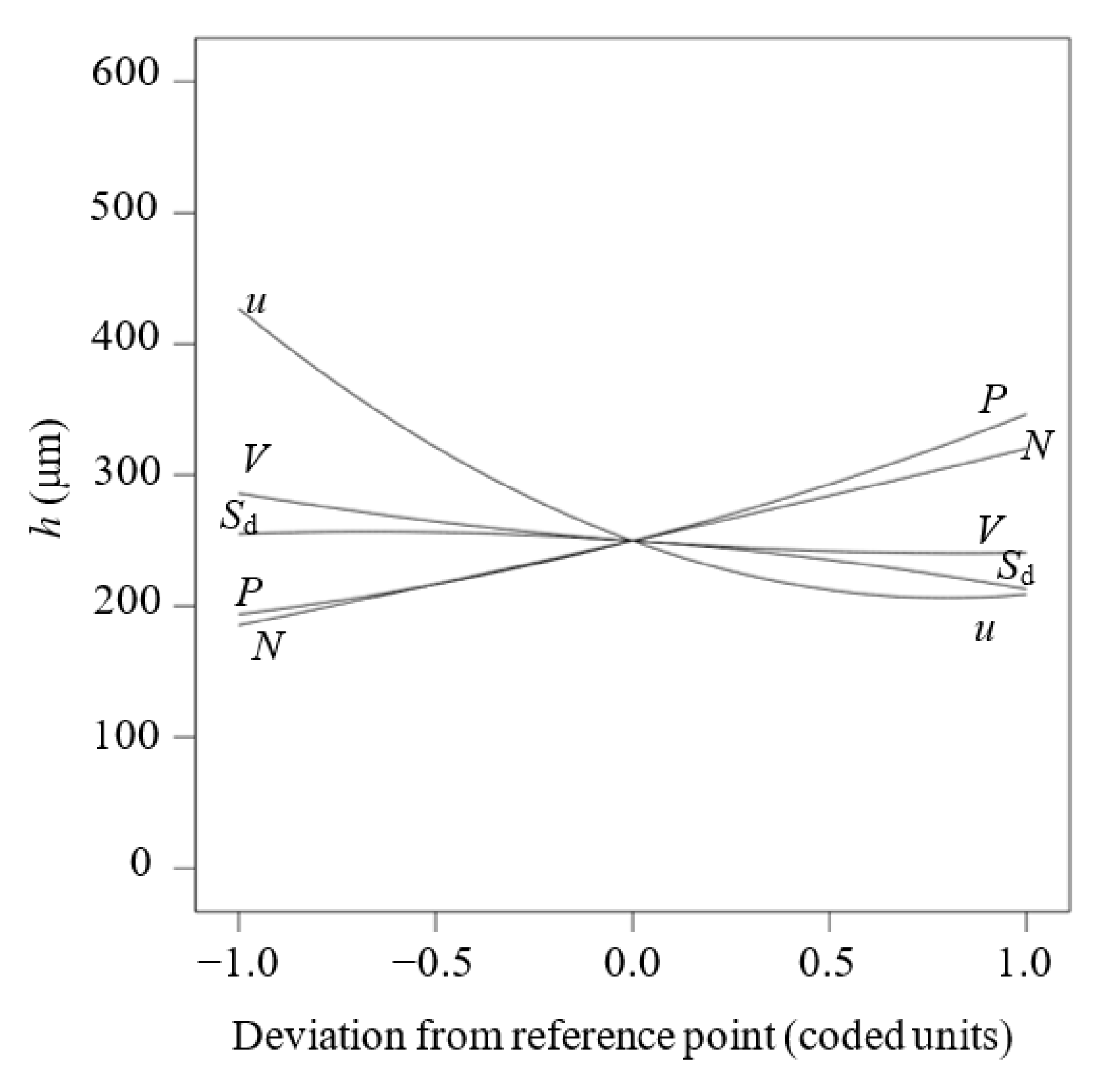
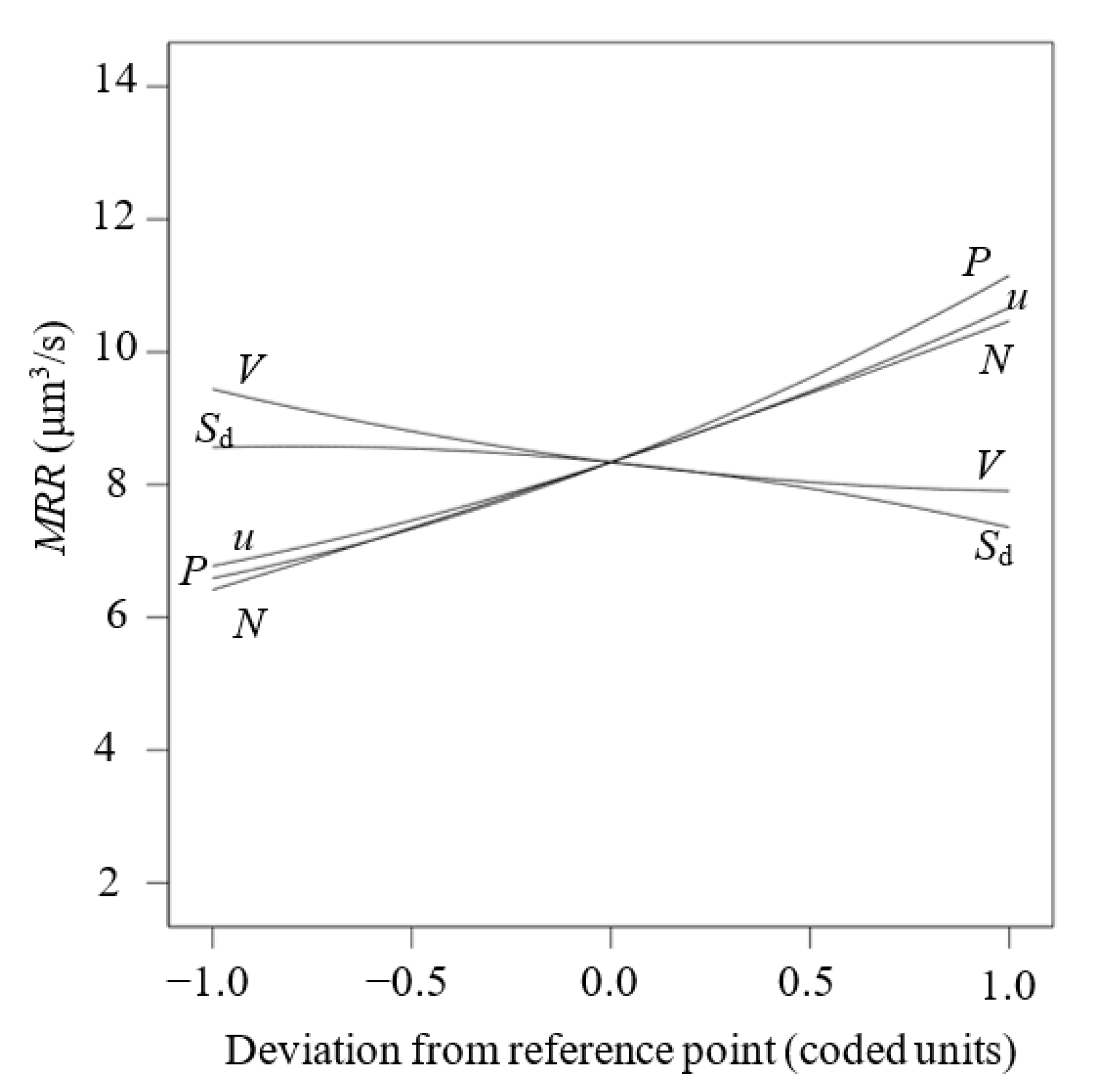
3.4. The Effect of Machining Parameters on h and MRR
3.4.1. The Main Effect of Machining Parameters
3.4.2. The Interactive Effect of Machining Parameters
4. Dimensional Analysis Model of MRR
5. Conclusions
- h increases with an increase in P, while h increases with a decrease in u. h increases slightly firstly and then decreases with an increase in Sd. MRR increases with an increase in P and u. MRR almost remains constant at first and then decreases significantly as the Sd increases. Increasing N significantly increases h and MRR. h and MRR significantly increase with a decrease in V.
- The machined surfaces, with waviness as the primary surface irregular characteristic, were found. The formation of the wavy surface may be attributed to the intersection and overlap of the adjoint jet footprint. The flat machined surfaces, without waviness characteristics, can be obtained by selecting the machining parameters appropriately.
- The striations were formed on the surface of hard and brittle material under MAAJ turning. The drag angle of the striation is different from the helix angle of the helical groove. The intersection of striations was found, which may lead to the elimination of the striation.
- The predictive model of MRR was developed using the dimensional analysis method. The model was assessed and shown to be able to give adequate predictions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| C1, C2,C3 | contants |
| d | jet diameter (mm) |
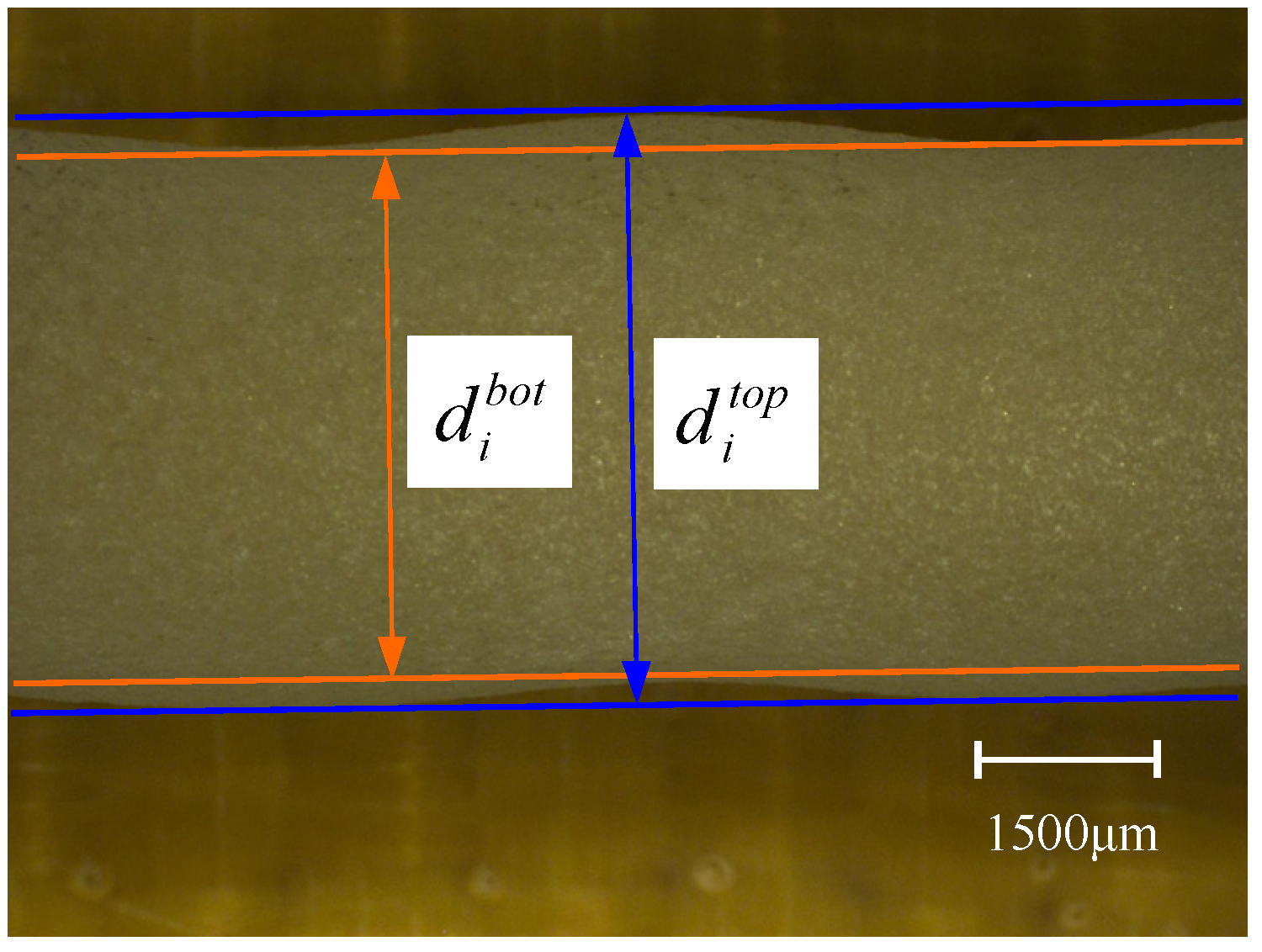
| di | workpiece diameter of the ith measured position (mm) |
| maximum diameter of the ith measured position (mm) | |
| minimum diameter of the ith measured position (mm) | |
| dnozzle | nozzle diameter (mm) |
| dt | initial diameter of workpiece (mm) |
| Ek | kinetic energy of abrasive jet (J) |
| Hd | particle hardness (GPa) |
| Ht | workpiece hardness (GPa) |
| h | depth of cut (μm) |
| hi | depth of cut for the ith measured position after MAAJ turning (mm) |
| K1C | workpiece fracture toughness (MPa·m1/2) |
| MRR | material removal rate (mm3/s) |
| ma | abrasive flow rate (g/min) |
| N | number of passes |
| n | workpiece rotation speed (rpm) |
| P | air pressure (MPa) |
| S | jet ejection distance (mm) |
| Sd | standoff distance (mm) |
| T | time required for one rotation of the workpiece (s) |
| u | feed speed (mm/s) |
| V | workpiece surface speed (mm/s) |
| α | jet impact angle (radians) |
| αi(i=1…m) | contants |
| β | drag angle (radians) |
| γ | helix angle (radians) |
| θ | jet divergence angle (degrees) |
| φ | particle impact angle (radians) |
| λ | pitch of helical groove (μm) |
References
- Nouhi, A.; Spelt, J.K.; Papini, M. Abrasive jet turning of glass and PMMA rods and the micro-machining of helical channels. Precis. Eng. J. Int. Soc. Precis. Eng. Nanotechnol. 2018, 53, 151–162. [Google Scholar]
- Park, D.S.; Cho, M.W.; Lee, H.; Cho, W.S. Micro-grooving of glass using micro-abrasive jet machining. J. Mater. Process. Technol. 2004, 146, 234–240. [Google Scholar]
- Aurich, J.C.; Kirsch, B.; Setti, D.; Axinte, D.; Beaucamp, A.; Butler-Smith, P.; Yamaguchi, H. Abrasive processes for micro parts and structures. Cirp. Ann. Manuf. Technol. 2019, 68, 653–676. [Google Scholar]
- Wang, J.; Moridi, A.; Mathew, P. Micro-grooving on quartz crystals by an abrasive air jet. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2161–2173. [Google Scholar] [CrossRef]
- Li, Q.L.; Deng, Y.F.; Li, J.; Shi, W.T. Roughness characterization and formation mechanism of abrasive air jet micromachining surface studied by power spectral density. J. Manuf. Process. 2020, 57, 737–747. [Google Scholar]
- Li, H.Z.; Wang, J.; Kwok, N.; Nguyen, T.; Yeoh, G.H. A study of the micro-hole geometry evolution on glass by abrasive air-jet micromachining. J. Manuf. Process. 2018, 31, 156–161. [Google Scholar] [CrossRef]
- Li, W.Y.; Zhu, H.T.; Wang, J.; Ali, Y.M.; Huang, C.Z. An investigation into the radial-mode abrasive waterjet turning process on high tensile steels. Int. J. Mech. Sci. 2013, 77, 365–376. [Google Scholar] [CrossRef]
- Liu, D.; Huang, C.Z.; Wang, J.; Zhu, H.T.; Yao, P.; Liu, Z.W. Modeling and optimization of operating parameters for abrasive waterjet turning alumina ceramics using response surface methodology combined with Box-Behnken design. Ceram. Int. 2014, 40, 7899–7908. [Google Scholar]
- Zohourkari, I.; Zohoor, M.; Annoni, M. Investigation of the effects of machining parameters on material removal rate in abrasive waterjet turning. Adv. Mech. Eng. 2014, 2014, 624203. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, H.T.; Huang, C.Z.; Wang, J.; Yao, P. Prediction model of depth of penetration for alumina ceramics turned by abrasive waterjet-finite element method and experimental study. Int. J. Adv. Manuf. Technol. 2016, 87, 2673–2682. [Google Scholar]
- Yue, Z.B.; Huang, C.Z.; Zhu, H.T.; Wang, J.; Yao, P.; Liu, Z.W. Optimization of machining parameters in the abrasive waterjet turning of alumina ceramic based on the response surface methodology. Int. J. Adv. Manuf. Technol. 2014, 71, 2107–2114. [Google Scholar] [CrossRef]
- Kowsari, K.; Nouhi, A.; Hadavi, V.; Spelt, J.K.; Papini, M. Prediction of the erosive footprint in the abrasive jet micro-machining of flat and curved glass. Tribol. Int. 2017, 106, 101–108. [Google Scholar] [CrossRef]
- Chen, F.L.; Wang, J.; Lemma, E.; Siores, E. Striation formation mechanisms on the jet cutting surface. J. Mater. Process. Technol. 2003, 141, 213–218. [Google Scholar] [CrossRef]
- Zhang, G.G.; Sun, Y.L.; Gao, H.; Zuo, D.W.; Liu, X. A theoretical and experimental investigation of particle embedding and erosion behaviour of PDMS in micro-abrasive air-jet machining. Wear 2021, 486–487, 204118. [Google Scholar]
- Li, Q.L.; Wang, J.; Huang, C.Z. Erosion mechanisms of monocrystalline silicon under a microparticle laden air jet. J. Appl. Phys. 2008, 104, 034903. [Google Scholar]
- Qi, H.; Fan, J.M.; Wang, J.; Li, H.Z. Impact erosion by high velocity micro-particles on a quartz crystal. Tribol. Int. 2015, 82, 200–210. [Google Scholar] [CrossRef]
- Li, H.Z.; Wang, J.; Fan, J.M. Analysis and modelling of particle velocities in micro-abrasive air jet. Int. J. Mach. Tools Manuf. 2009, 49, 850–858. [Google Scholar]
- Li, H.Z.; Lee, A.; Fan, J.M.; Yeoh, G.H.; Wang, J. On DEM-CFD study of the dynamic characteristics of high speed micro-abrasive air jet. Powder Technol. 2014, 267, 161–179. [Google Scholar] [CrossRef]
- Jafar, R.H.M.; Spelt, J.K.; Papini, M. Numerical simulation of surface roughness and erosion rate of abrasive jet micro-machined channels. Wear 2013, 303, 302–312. [Google Scholar]
- Rodriguez, A.; Lopez de Lacalle, L.N.; Pereira, O.; Fernanez, A.; Ayesta, I. Isotropic finishing of austempered iron casting cylindrical parts by roller burnishing. J. Adv. Manuf. Technol. 2022, 110, 753–761. [Google Scholar]
- Zhang, G.G.; Sun, Y.L.; Gao, H.; Liu, X.; Zuo, D.W. Characteristics of cryogenic abrasive air-jet direct-write machining: A comparison with abrasive air-jet direct-write machining at oblique angles. J. Mater. Process. Technol. 2022, 299, 19. [Google Scholar] [CrossRef]
- Gonzalez, H.; Calleja, A.; Pereira, O.; Ortega, N.; Norberto Lopez de Lacalle, L.; Barton, M. Super Abrasive Machining of Integral Rotary Components Using Grinding Flank Tool. Metals 2018, 8, 24. [Google Scholar]







| Shape: round bar | Density: 2.2 g/cm3 | Elastic modulus: 70.56 GPa |
| Diameter: 5 mm | Compressive strength: 9.23 GPa | Poisson’s ratio: 0.16 |
| Length: 10 mm | Fracture toughness: 0.753 MPa·m1/2 |
| Machining Parameters | Symbol | Units | Factor Level | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| Air pressure | P | MPa | 0.3 | 0.4 | 0.5 |
| Standoff distance | Sd | mm | 15 | 20 | 25 |
| Feed speed | u | mm/s | 1.12 | 2.24 | 3.36 |
| Surface speed | V | mm/s | 3.93 | 7.85 | 11.78 |
| Number of passes | N | 2 | 3 | 4 | |
| Source | DF | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| P | 1 | 92,948 | 92,948 | 68.89 | 0.00 |
| Sd | 1 | 7070 | 7070 | 5.24 | 0.03 |
| V | 1 | 8248 | 8248 | 6.11 | 0.02 |
| N | 1 | 72,590 | 72,590 | 53.80 | 0.00 |
| u | 1 | 189,625 | 189,625 | 140.54 | 0.00 |
| u2 | 1 | 44,128 | 44,128 | 32.71 | 0.00 |
| V × N | 1 | 6258 | 6258 | 4.64 | 0.04 |
| Error | 38 | 51,272 | 1349 | ||
| Total | 45 | 472,140 |
| Source | DF | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| P | 1 | 83.16 | 83.16 | 77.77 | 0.00 |
| Sd | 1 | 5.80 | 5.80 | 5.42 | 0.03 |
| V | 1 | 9.41 | 9.41 | 8.80 | 0.01 |
| N | 1 | 65.56 | 65.56 | 61.31 | 0.00 |
| u | 1 | 60.56 | 60.56 | 56.63 | 0.00 |
| V × N | 1 | 6.64 | 6.64 | 6.21 | 0.02 |
| Error | 39 | 41.70 | 1.07 | ||
| Total | 45 | 272.82 |
| No. | P (MPa) | Sd (mm) | u (mm/s) | V (mm/s) | N | MRR (mm3/s) | MRRpre (mm3/s) | Error (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.35 | 17 | 2.52 | 11.52 | 2.5 | 3.86 | 4.58 | 18.65 |
| 2 | 0.45 | 19 | 2.52 | 10.47 | 3.5 | 6.43 | 7.67 | 19.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Li, Q.; Zhang, W.; Deng, Y.; Li, J. An Investigation into the Multi-Pass Radial-Mode Micro Abrasive Air Jet Turning of Fused-Silica Rods. Machines 2023, 11, 164. https://doi.org/10.3390/machines11020164
Yang R, Li Q, Zhang W, Deng Y, Li J. An Investigation into the Multi-Pass Radial-Mode Micro Abrasive Air Jet Turning of Fused-Silica Rods. Machines. 2023; 11(2):164. https://doi.org/10.3390/machines11020164
Chicago/Turabian StyleYang, Ruibo, Quanlai Li, Weipeng Zhang, Yafeng Deng, and Jialin Li. 2023. "An Investigation into the Multi-Pass Radial-Mode Micro Abrasive Air Jet Turning of Fused-Silica Rods" Machines 11, no. 2: 164. https://doi.org/10.3390/machines11020164
APA StyleYang, R., Li, Q., Zhang, W., Deng, Y., & Li, J. (2023). An Investigation into the Multi-Pass Radial-Mode Micro Abrasive Air Jet Turning of Fused-Silica Rods. Machines, 11(2), 164. https://doi.org/10.3390/machines11020164







