Dynamic Launch Trajectory Planning of a Cable-Suspended Translational Parallel Robot Using Point-to-Point Motions
Abstract
:1. Introduction
1.1. Cable-Suspended Parallel Robots: Kinematics, Dynamics and Design
1.2. CSPRs for Throwing Motions
1.3. A Novel Concept of a CSPR for Throwing Operations
2. Design, Kinematic and Dynamic Model
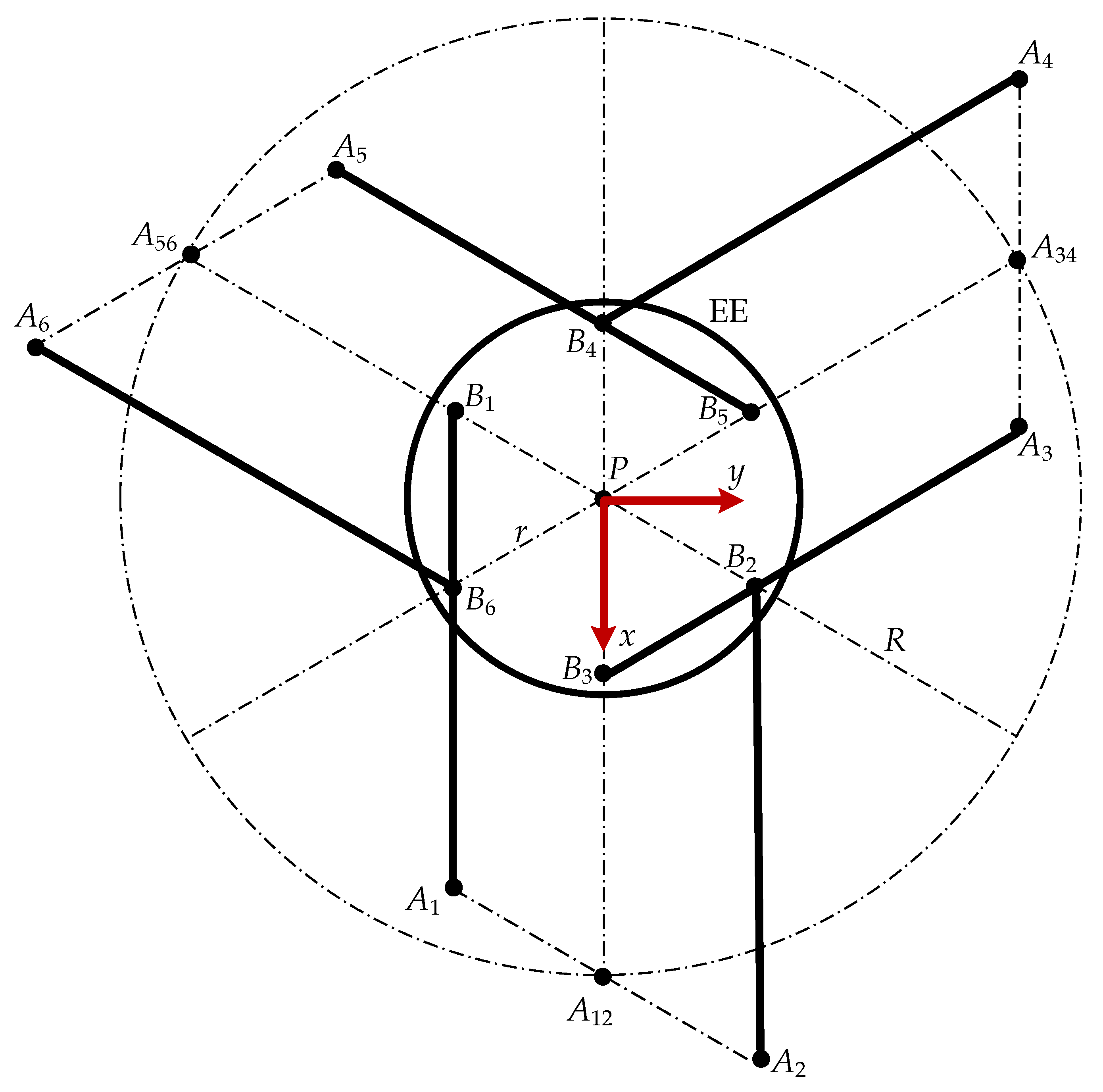
2.1. Robot Architecture
2.2. Kinematic and Dynamic Model
2.3. Jacobian Matrix and Sensitivity Indexes
3. Point-to-Point Trajectory Planning
3.1. Parametric Equation of the Trajectory
3.2. Cable Tension Constraints
- When , Equation (20) has two coincident roots, namelyAgain, always has the same sign, except at the repeated root (where it becomes zero): this corresponds to an inflection point for , which is otherwise monotonic. Therefore, we fall back to case 1 above, and it is sufficient to verify that Equation (22) holds.
- When , has two distinct roots, namelywhere one root corresponds to a local minimum of and the other to a maximum. If is positive at these two local extrema, at the beginning of the trajectory segment, and at its end, then Equation (19) is always satisfied. The following conditions then need to be verified:
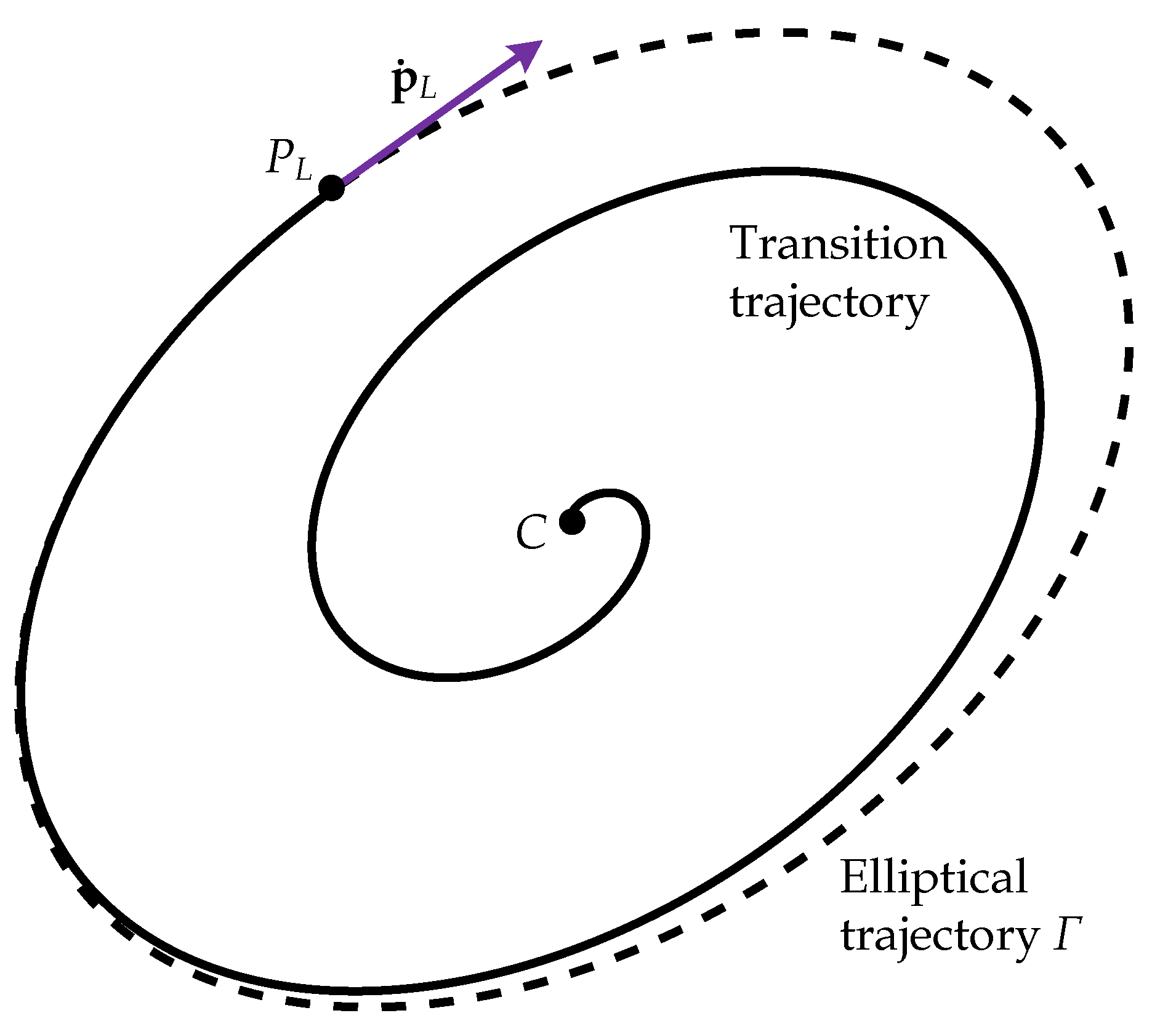
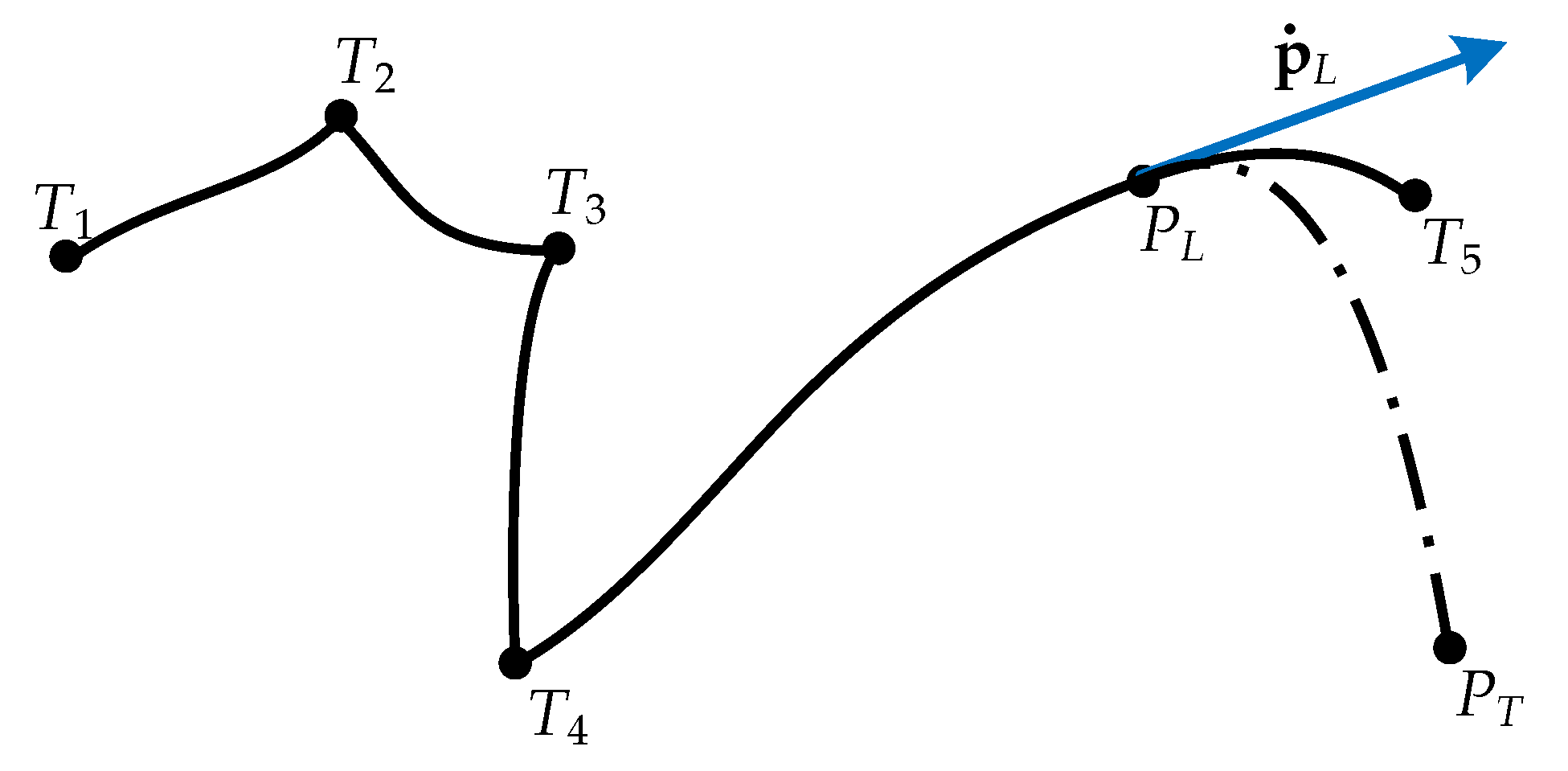
4. Launch Trajectory Planning
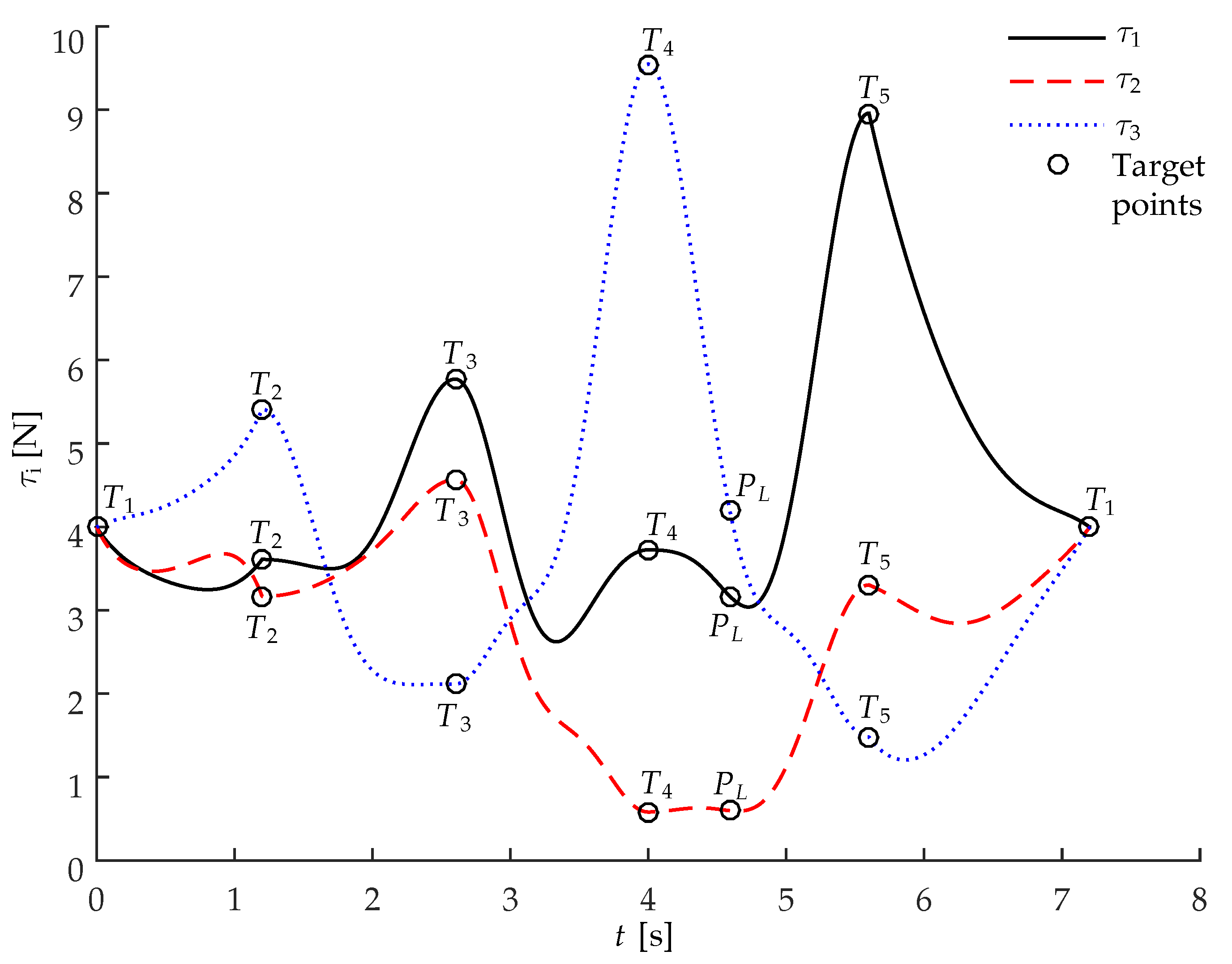
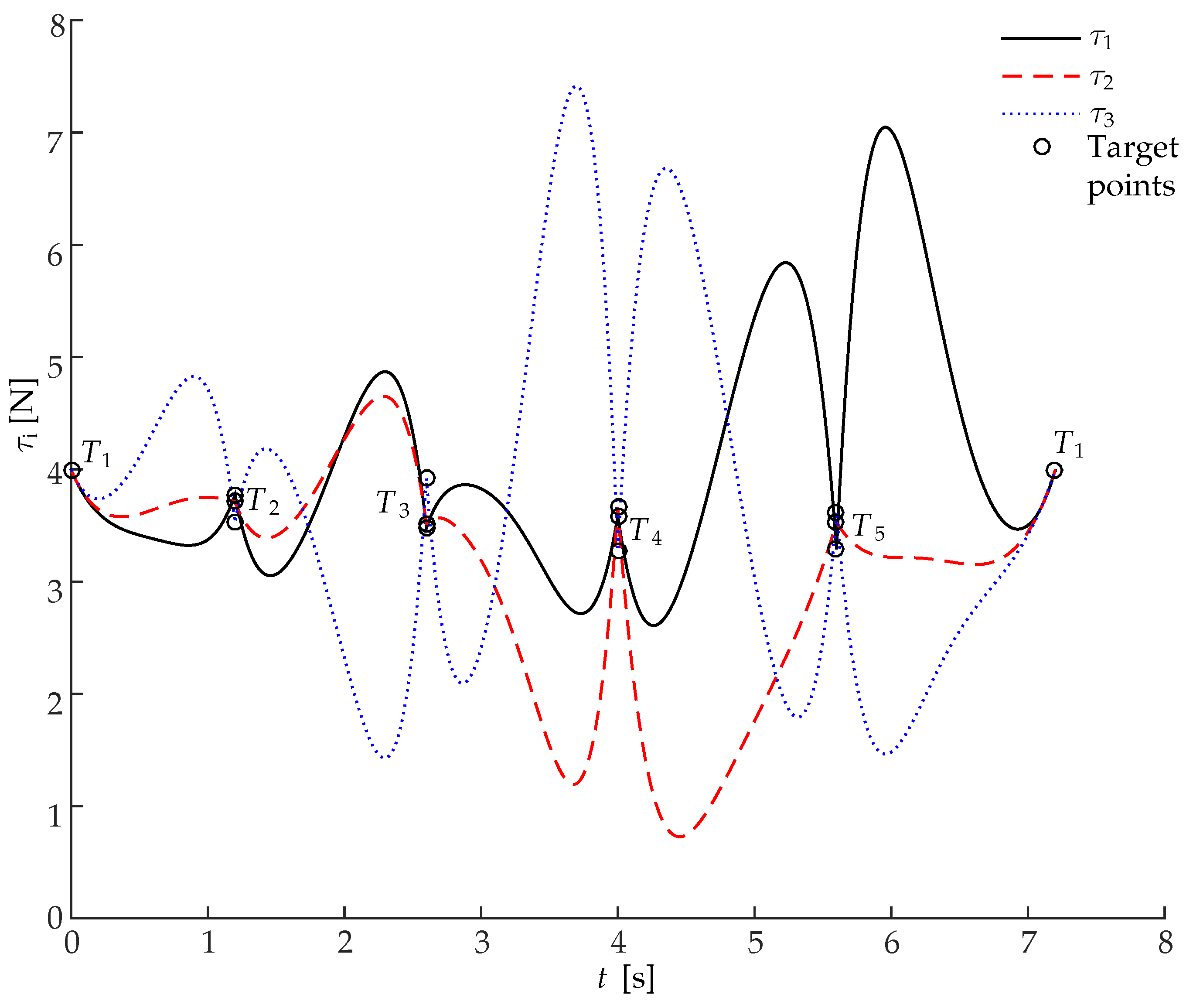
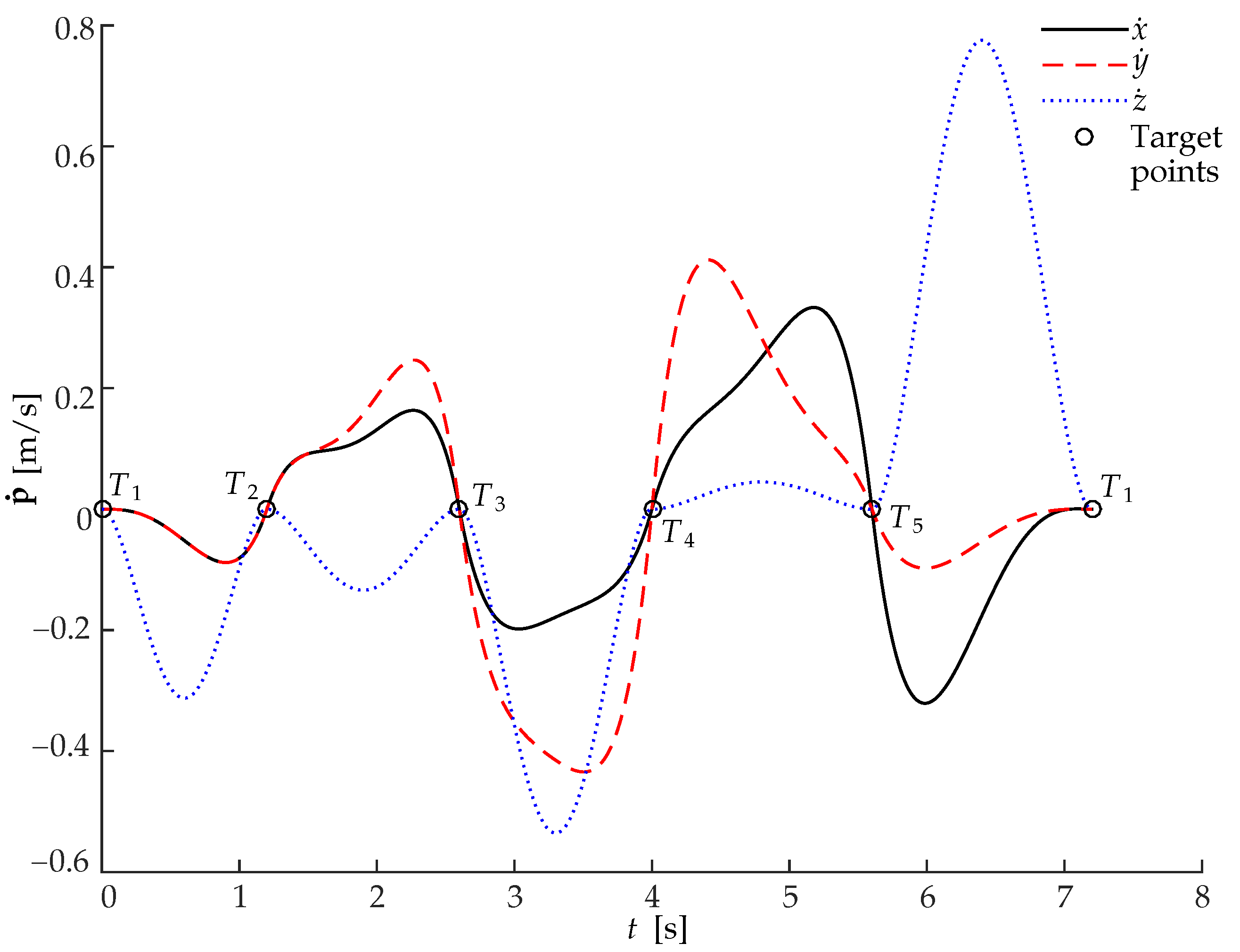
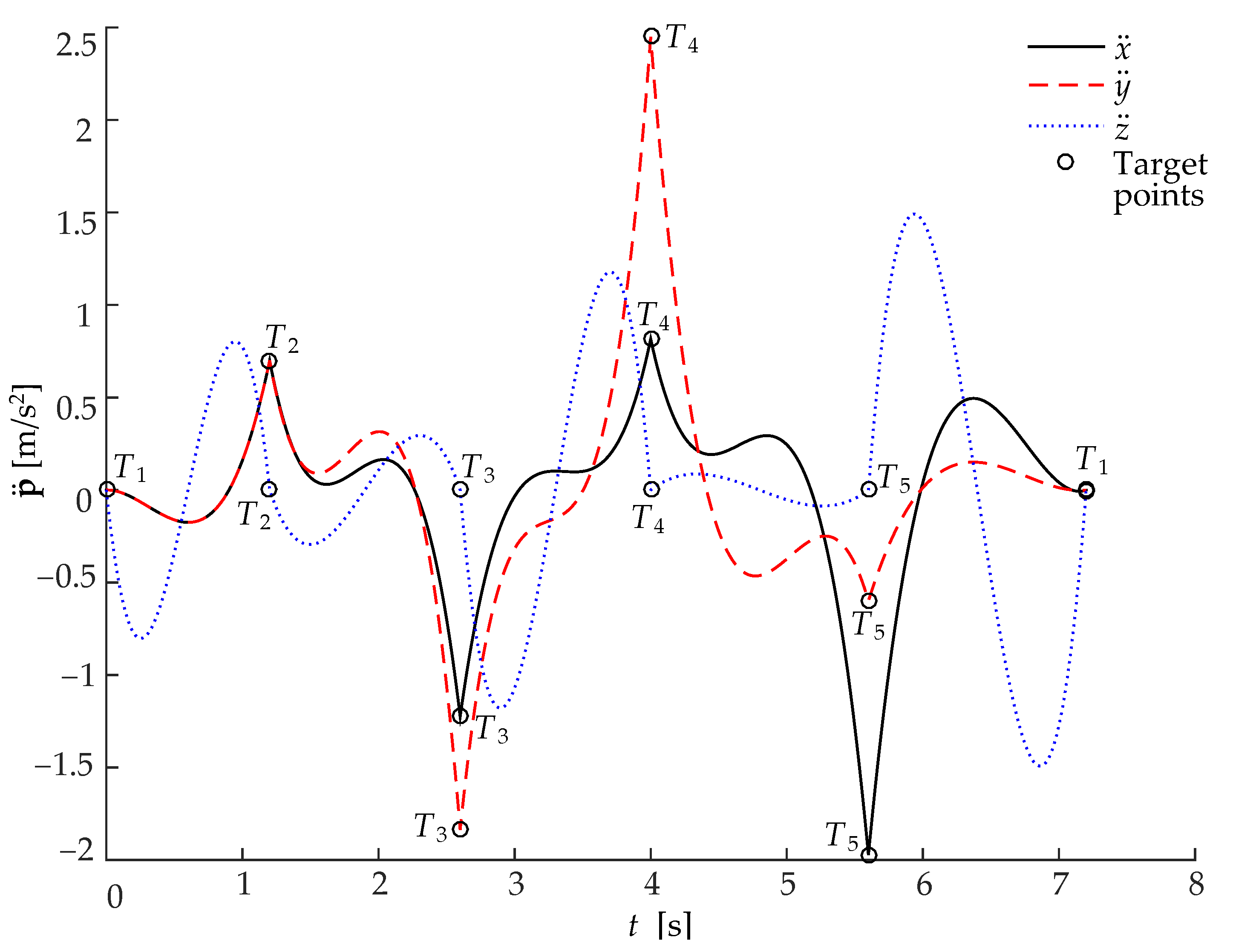
5. Simulations and Experimental Verification
5.1. Final Design
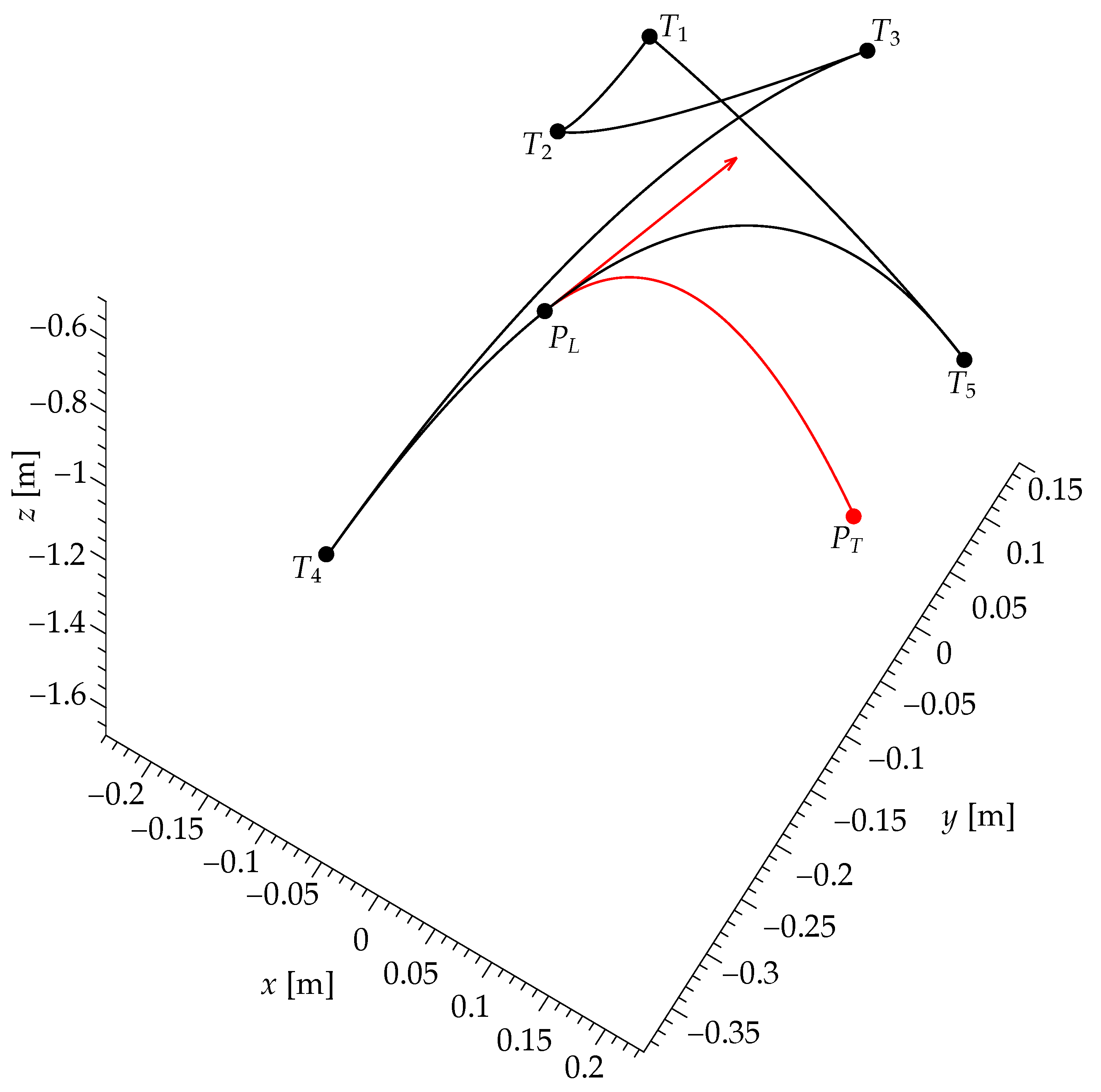
5.2. Simulations and Comparisons
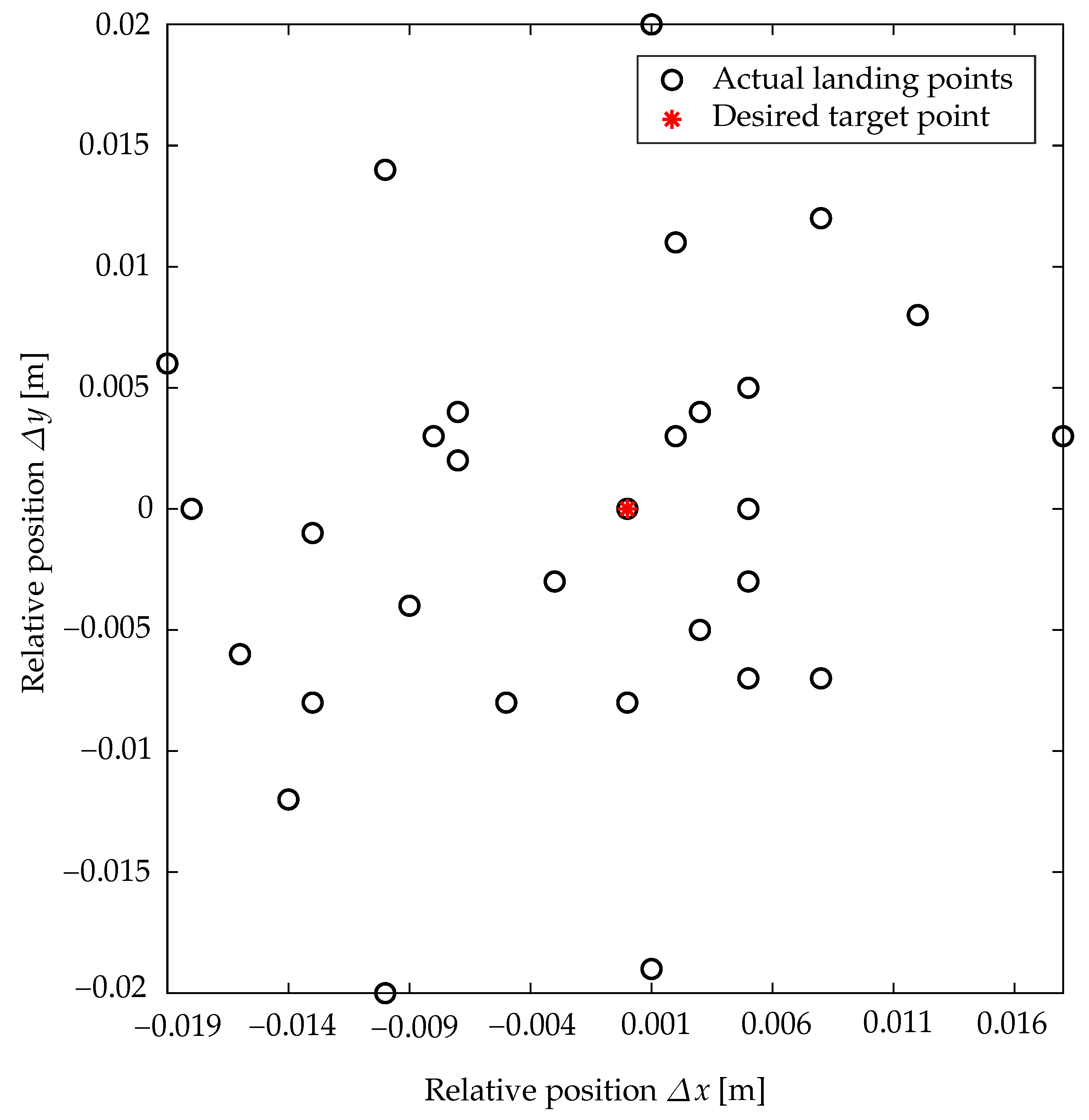
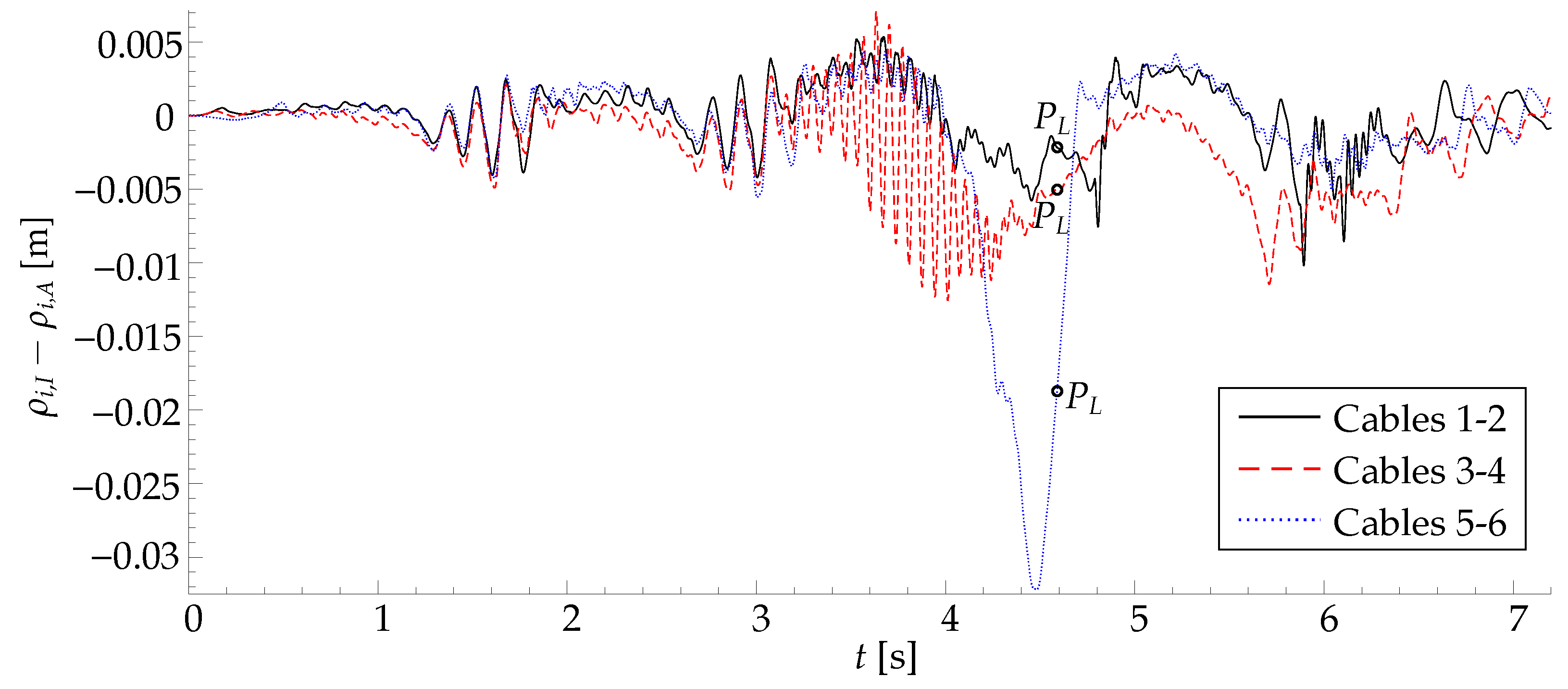
5.3. Experiments
6. Discussion
7. Conclusions
- In our tests, for simplicity, we used PD control for the cable winches. This, however, was found to have limited performance in the compensation for external disturbances and lower tracking accuracy. Introducing improved control algorithms may significantly increase the repeatability of the launch motions;
- The gripper on the EE is currently connected through a wire to the control system on the frame; this wire, however, may interfere with the robot cables. A wireless control system for the gripper will increase performance;
- Improve the method used for measuring the motion of the launched object; a computer-vision-based system will be used, to avoid interference with the ballistic motion;
- Our tests indicate that discontinuities in the cable tensions will occur after the launch, which may lead to losing control of the robot, especially if the mass of the launched object is not negligible with respect to that of the EE. Optimizing the trajectory planning to minimize said discontinuities appears to be a promising option.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Expressions
References
- Lawrence, L.C. Skycam: An aerial robotic camera system. Byte 1985, 10, 122–132. [Google Scholar]
- Lamaury, J.; Gouttefarde, M. Control of a large redundantly actuated cable-suspended parallel robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar] [CrossRef]
- Nan, R.; Li, D.; Jin, C.; Wang, Q.; Zhu, L.; Zhu, W.; Zhang, H.; Yue, Y.; Qian, L. The five-hundred-meter aperture spherical radio telescope (FAST) project. Int. J. Mod. Phys. D 2011, 20, 989–1024. [Google Scholar] [CrossRef]
- Riechel, A.T.; Ebert-Uphoff, I. Force-feasible workspace analysis for underconstrained, point-mass cable robots. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4956–4962. [Google Scholar] [CrossRef]
- Gosselin, C.M. Global planning of dynamically feasible trajectories for three-DOF spatial cable-suspended parallel robots. In 1st International Conference on Cable-Driven Parallel Robots; Gouttefarde, M., Bruckmann, T., Pott, A., Eds.; Springer: Stuttgart, Germany, 2013; pp. 3–22. [Google Scholar] [CrossRef]
- Jiang, X.; Barnett, E.; Gosselin, C.M. Dynamic point-to-point trajectory planning beyond the static workspace for six-DOF cable-suspended parallel robots. IEEE Trans. Robot. 2018, 34, 1–13. [Google Scholar] [CrossRef]
- Mattioni, V.; Idà, E.; Carricato, M. Design of a planar cable-driven parallel robot for non-contact tasks. Appl. Sci. 2021, 20, 9491. [Google Scholar] [CrossRef]
- Vu, D.S.; Barnett, E.; Zaccarin, A.; Gosselin, C.M. On the design of a three-DOF cable-suspended parallel robot based on a parallelogram arrangement of the cables. In 3rd International Conference on Cable-Driven Parallel Robots; Gosselin, C.M., Cardou, P., Bruckmann, T., Pott, A., Eds.; Springer: Québec, QC, Canada, 2018; pp. 319–330. [Google Scholar] [CrossRef]
- Bosscher, P.; Williams, R.; Tummino, M. A concept for rapidly-deployable cable robot search and rescue systems. In Proceedings of the ASME 2005 IDETC/CIE, Long Beach, CA, USA, 24–28 September 2005; pp. 589–598. [Google Scholar] [CrossRef]
- Barnett, E.; Gosselin, C.M. Large-scale 3D printing with a cable-suspended robot. Addit. Manuf. 2015, 7, 27–44. [Google Scholar] [CrossRef]
- Mottola, G.; Gosselin, C.M.; Carricato, M. Dynamically feasible motions of a class of purely-translational cable-suspended parallel robots. Mech. Mach. Theory. 2019, 132, 193–206. [Google Scholar] [CrossRef]
- Bosscher, P.; Williams, R.; Bryson, L.; Castro-Lacouture, D. Cable-suspended robotic contour crafting system. Autom. Constr. 2007, 17, 45–55. [Google Scholar] [CrossRef]
- Castelli, G.; Ottaviano, E.; Rea, P. A Cartesian cable-suspended robot for improving end-users’ mobility in an urban environment. Robot. Comput. Integr. Manuf. 2014, 30, 335–343. [Google Scholar] [CrossRef]
- Idà, E.; Nanetti, F.; Mottola, G. An alternative parallel mechanism for horizontal positioning of a nozzle in an FDM 3D printer. Machines 2022, 7, 542. [Google Scholar] [CrossRef]
- Alikhani, A.; Behzadipour, S.; Alasty, A.; Vanini, S. Design of a large-scale cable-driven robot with translational motion. Robot. Comput. Integr. Manuf. 2011, 27, 357–366. [Google Scholar] [CrossRef]
- Saber, O. A spatial translational cable robot. ASME J. Mech. Rob. 2015, 7, 031006. [Google Scholar] [CrossRef]
- Sciarra, G.; Rasheed, T.; Mattioni, V.; Cardou, P.; Caro, S. Design and kinetostatic modeling of a cable-driven Schönflies-motion generator. In Proceedings of the ASME 2022 IDETC/CIE, St. Louis, MO, USA, 14–17 August 2022; p. V007T07A020. [Google Scholar] [CrossRef]
- Wang, R.; Li, S.; Li, Y. A suspended cable-driven parallel robot with articulated reconfigurable moving platform for Schönflies motions. IEEE/ASME Trans. Mechatron. 2022, 27, 5173–5184. [Google Scholar] [CrossRef]
- Behzadipour, S.; Khajepour, A. A new cable-based parallel robot with three degrees of freedom. Multibody Syst. Dyn. 2005, 13, 371–383. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; Wang, L. Optimization and implementation of a high-speed 3-DOFs translational cable-driven parallel robot. Mech. Mach. Theory. 2020, 145, 103693. [Google Scholar] [CrossRef]
- Barrette, G.; Gosselin, C.M. Determination of the dynamic workspace of cable-driven planar parallel mechanisms. ASME J. Mech. Des. 2005, 127, 242–248. [Google Scholar] [CrossRef]
- Idà, E.; Briot, S.; Carricato, M. Robust trajectory planning of under-actuated cable-driven parallel robot with 3 cables. In Advances in Robot Kinematics; Lenarčič, J., Siciliano, B., Eds.; Springer International Publishing: Ljubljana, Slovenia, 2020; pp. 65–72. [Google Scholar] [CrossRef]
- Mottola, G.; Gosselin, C.M.; Carricato, M. Dynamically feasible periodic trajectories for generic spatial three-degree-of-freedom cable-suspended parallel robots. ASME J. Mech. Rob. 2018, 10, 031004. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, D.; Li, Q. Dynamically feasible transition trajectory planning for three-dof cable-suspended parallel robots. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 789–794. [Google Scholar] [CrossRef]
- Lefrançois, S.; Gosselin, C.M. Point-to-point motion control of a pendulum-like 3-DOF underactuated cable-driven robot. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 5187–5193. [Google Scholar] [CrossRef]
- Zanotto, D.; Rosati, G.; Agrawal, S.K. Modeling and control of a 3-DOF pendulum-like manipulator. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3964–3969. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Foucault, S. Dynamic point-to-point trajectory planning of a two-DOF cable-suspended parallel robot. IEEE Trans. Robot. 2014, 30, 728–736. [Google Scholar] [CrossRef]
- Jiang, X.; Gosselin, C.M. Dynamic point-to-point trajectory planning of a three-DOF cable-suspended parallel robot. IEEE Trans. Robot. 2016, 32, 1550–1557. [Google Scholar] [CrossRef]
- Zhang, N.; Shang, W.; Cong, S. Geometry-based trajectory planning of a 3-3 cable-suspended parallel robot. IEEE Trans. Robot. 2016, 33, 484–491. [Google Scholar] [CrossRef]
- Dion-Gauvin, P.; Gosselin, C.M. Dynamic point-to-point trajectory planning of a three-DOF cable-suspended mechanism using the hypocycloid curve. IEEE/ASME Trans. Mechatron. 2018, 23, 1964–1972. [Google Scholar] [CrossRef]
- Mottola, G.; Gosselin, C.M.; Carricato, M. Dynamically-feasible elliptical trajectories for fully constrained 3-DOF cable-suspended parallel robots. In 3rd International Conference on Cable-Driven Parallel Robots; Gosselin, C.M., Cardou, P., Bruckmann, T., Pott, A., Eds.; Springer: Québec, QC, Canada, 2018; pp. 219–230. [Google Scholar] [CrossRef]
- Zhang, N.; Shang, W. Dynamic trajectory planning of a 3-DOF under-constrained cable-driven parallel robot. Mech. Mach. Theory. 2016, 98, 21–35. [Google Scholar] [CrossRef]
- Dion-Gauvin, P.; Gosselin, C.M. Beyond-the-static-workspace point-to-point trajectory planning of a 6-DoF cable-suspended mechanism using oscillating SLERP. Mech. Mach. Theory. 2022, 174, 104894. [Google Scholar] [CrossRef]
- Raptopoulos, F.; Koskinopoulou, M.; Maniadakis, M. Robotic pick-and-toss facilitates urban waste sorting. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1149–1154. [Google Scholar] [CrossRef]
- Reist, P.; D’Andrea, R. Design and analysis of a blind juggling robot. IEEE Trans. Robot. 2012, 28, 1228–1243. [Google Scholar] [CrossRef]
- Fagiolini, A.; Torelli, A.; Bicchi, A. Casting robotic end-effectors to reach far objects in space and planetary missions. In Proceedings of the 9th ESA Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands, November 28–30 2006. [Google Scholar]
- Arisumi, H.; Otsuki, M.; Nishida, S. Launching penetrator by casting manipulator system. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5052–5058. [Google Scholar] [CrossRef]
- Hatakeyama, T.; Mochiyama, H. Shooting manipulation inspired by chameleon. IEEE/ASME Trans. Mechatron. 2013, 18, 527–535. [Google Scholar] [CrossRef]
- Asgari, M.; Nikoobin, A. A variational approach to determination of maximum throw-able workspace of robotic manipulators in optimal ball pitching motion. Trans. Inst. Meas. Control 2021, 43, 2378–2391. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Lee, J.; Rodriguez, A.; Funkhouser, T. TossingBot: Learning to throw arbitrary objects with residual physics. IEEE Trans. Robot. 2020, 36, 1307–1319. [Google Scholar] [CrossRef]
- Hassan, G.; Chemori, A.; Gouttefarde, M.; El Rafei, M.; Francis, C.; Hervé, P.E.; Sallé, D. A novel extended desired compensation adaptive law for high-speed pick-and-throw with PKMs. In Proceedings of the 14th IFAC International Workshop on Adaptation and Learning in Control and Signal Processing, Casablanca, Morocco, 29 June–1 July 2022; pp. 627–633. [Google Scholar] [CrossRef]
- Hassan, G.; Gouttefarde, M.; Chemori, A.; Hervé, P.E.; El Rafei, M.; Francis, C.; Sallé, D. Time-optimal pick-and-throw S-curve trajectories for fast parallel robots. IEEE/ASME Trans. Mechatron. 2022, 27, 4707–4717. [Google Scholar] [CrossRef]
- Frank, H.; Wellerdick-Wojtasik, N.; Hagebeuker, B.; Novak, G.; Mahlknecht, S. Throwing objects—A bio-inspired approach for the transportation of parts. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 91–96. [Google Scholar] [CrossRef]
- Frank, T.; Janoske, U.; Mittnacht, A.; Schroedter, C. Automated throwing and capturing of cylinder-shaped objects. In Proceedings of the IEEE 2012 ICRA, Saint Paul, MN, USA, 14–18 May 2012; pp. 5264–5270. [Google Scholar] [CrossRef]
- Fischer, O.; Toshimitsu, Y.; Kazemipour, A.; Katzschmann, R.K. Dynamic control of soft manipulators to perform real-world tasks. arXiv 2022, arXiv:2201.02151. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Siciliano, B. Nonprehensile dynamic manipulation: A survey. IEEE Robot. Autom. Lett. 2018, 3, 1711–1718. [Google Scholar] [CrossRef]
- Lin, D.; Mottola, G.; Carricato, M.; Jiang, X. Modeling and control of a cable-suspended sling-like parallel robot for throwing operations. Appl. Sci. 2020, 10, 9067. [Google Scholar] [CrossRef]
- Lin, D.; Mottola, G.; Carricato, M.; Jiang, X.; Li, Q. Dynamically-feasible trajectories for a cable-suspended robot performing throwing operations. In Proceedings of the ROMANSY 23 Symposium on Robot Design, Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2020; pp. 547–555. [Google Scholar] [CrossRef]
- Mottola, G.; Gosselin, C.M.; Carricato, M. Effect of actuation errors on a purely-translational spatial cable-driven parallel robot. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 701–707. [Google Scholar] [CrossRef]
- Salisbury, J. Active stiffness control of a manipulator in Cartesian coordinates. In Proceedings of the 1980 IEEE Conference on Decision and Control, Albuquerque, NM, USA, 10–12 December 1980; pp. 95–100. [Google Scholar] [CrossRef]
- Yoshikawa, T. Analysis and control of robot manipulators with redundancy. In Proceedings of the 1st International Symposium on Robotics Research, Bretton Woods, NH, USA, 25 August–2 September 1983. [Google Scholar]
- Cardou, P.; Bouchard, S.; Gosselin, C.M. Kinematic-sensitivity indices for dimensionally nonhomogeneous Jacobian matrices. IEEE Trans. Robot. 2010, 26, 166–173. [Google Scholar] [CrossRef]
- Merlet, J.P. Jacobian, manipulability, condition number, and accuracy of parallel robots. ASME J. Mech. Rob. 2006, 128, 199–206. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator performance measures-a comprehensive literature survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Bernstein, D.S. Matrix Mathematics: Theory, Facts, and Formulas; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Monographs in Visual Communication; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Zhang, N.; Shang, W.; Cong, S. Dynamic trajectory planning for a spatial 3-DoF cable-suspended parallel robot. Mech. Mach. Theory. 2018, 122, 177–196. [Google Scholar] [CrossRef]
- Qian, S.; Bao, K.; Zi, B.; Zhu, W.D. Dynamic trajectory planning for a three degrees-of-freedom cable-driven parallel robot using quintic B-splines. ASME J. Mech. Des. 2020, 142, 073301. [Google Scholar] [CrossRef]
- Tempel, P.; Schnelle, F.; Pott, A.; Eberhard, P. Design and programming for cable-driven parallel robots in the German Pavilion at the EXPO 2015. Machines 2015, 3, 223–241. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Mottola, G. Dynamic Launch Trajectory Planning of a Cable-Suspended Translational Parallel Robot Using Point-to-Point Motions. Machines 2023, 11, 224. https://doi.org/10.3390/machines11020224
Lin D, Mottola G. Dynamic Launch Trajectory Planning of a Cable-Suspended Translational Parallel Robot Using Point-to-Point Motions. Machines. 2023; 11(2):224. https://doi.org/10.3390/machines11020224
Chicago/Turabian StyleLin, Deng, and Giovanni Mottola. 2023. "Dynamic Launch Trajectory Planning of a Cable-Suspended Translational Parallel Robot Using Point-to-Point Motions" Machines 11, no. 2: 224. https://doi.org/10.3390/machines11020224
APA StyleLin, D., & Mottola, G. (2023). Dynamic Launch Trajectory Planning of a Cable-Suspended Translational Parallel Robot Using Point-to-Point Motions. Machines, 11(2), 224. https://doi.org/10.3390/machines11020224





