Minimum Dynamic Cable Tension Workspace Generation Techniques and Cable Tension Sensitivity Analysis Methods for Cable-Suspended Gangue-Sorting Robots

Abstract

The separation of gangues from coals with robots is an effective and practicable means. Therefore, a cable-suspended gangue-sorting robot (CSGSR) with an end-grab was developed in our early work. Due to the unidirectional characteristic, the flexibility of cables, and the dynamic impact of pick-and-place gangues, one of the significant issues with the robots is robustness under internal and external disturbances. Cable tensions, being the end-grab’s constraints, have a crucial effect on the robustness of the CSGSR while disturbances are on. Two main issues related to the CSGSR, as a result, are addressed in the present paper: minimum dynamic cable tension workspace generation and a sensitivity analysis method for the dynamic cable tensions. Firstly, the four cable tensions and minimum dynamic cable tension while the end-grab was located at an arbitrary position of the task space were obtained with the dynamics of the CSGSR. In addition, with the dynamics of the CSGSR, a minimum dynamic cable tension workspace (MDCTW) generating approach is presented, where the minimum dynamic cable tensions are greater than a preset value, therefore ensuring the robustness of the end-grab under the disturbances. Secondly, a method for dynamic cable tension sensitivity (DCTS) of the robots is proposed with grey relational analysis, by which the influence degree of the end-grab’s positions on the four dynamic cable tensions and the minimum dynamic cable tensions was considered. Finally, the effectiveness of the proposed MDCTW generation algorithm and the DCTS analysis method were examined through simulation on the CSGSR, and it was indicated that the proposed MDCTW generation algorithm and the DCTS analysis method were able to provide theoretical guidance for pick-and-place trajectory planning and generation of the end-grab in practice.

1. Introduction

1.1. Background and Motivation

Coals are an essential and fundamental energy source in China, especially in the current international situation. Nonetheless, the direct utilization of raw coals has brought on serious environmental concerns because coals are inevitably mixed with gangues. Therefore, the separation of gangues from coals must be enforced to realize the clean utilization of coals. Automatic separation of coals and gangues is an effective and practicable means to solve this problem. Cable robots, which show several promising advantages over rigid-link robots, have been employed in various fields which require high load-carrying capacity, larger workspaces, and high accelerations [1,2,3,4,5]. Under the given situation, a cable-suspended gangue-sorting robot (CSGSR) with an end-grab has been developed [6,7]. With cables in the CSGSR, there are many advantages over rigid-link manipulators. However, the unidirectional forces of the cables and the dynamic impact while picking and placing gangues introduce many new challenges in the research of the CSGSR. One of the essential points with the CSGSR is robustness under internal and external disturbances [8,9]. Cable tensions, being the constraint of the end-grab for the robots, have a crucial effect on the robustness of the CSGSR while the disturbances are on [10]. The CSGSR is disturbed along the direction of the weakest constraint while the disturbances act on the end-grab, namely the direction of the cable possessing the minimum cable tension among the cables. Note that cable tensions highly depend on the end-grab’s positions. Additionally, therefore, cable tensions may have significant fluctuations when there are slight deviations of the end-grab’s positions with the disturbances, even leading to the violation of constraint conditions for cable tensions. Due to the unidirectional characteristic, the flexibility of cables, and the dynamic impact, ensuring the robustness of the CSGSR under internal and external disturbances is a major challenge. One of the significant issues with the CSGSR is generating a workspace where the robots maintain specific robustness under dynamic impacts and disturbances. Another major issue in the robustness of the CSGSR is the reduction of the fluctuation of cable tensions caused by the deviation of the positions of the end-grab with a suitable controller. Specifically, two main issues related to the CSGSR, in this regard, are addressed in the present paper: minimum dynamic cable tension workspace generation and a sensitivity analysis method for cable tensions.

1.2. Literature Review and Comments

The research on the workspace and cable tension sensitivity for cable robots is reviewed from two following aspects in this section. On the one hand, the research on defining and solving the workspaces of the robots is presented. The investigations related to the cable tension sensitivity for cable robots, on the other hand, are reviewed.

The workspace for cable robots is a collection of spatial positions that the end-effector can approach with different constraints, such as the condition of cable tensions, the kinematic state of the end-effector, and so on [11,12,13,14]. Moreover, their workspace is complex due to the unidirectional constraint characteristic of cables. Note that the combinations of different conditions and the workspace generation can create multiple workspaces, such as static workspace, dynamic workspace, and so on [15,16,17,18,19,20,21,22]. An analytical method for generating the wrench-feasible workspace was presented for the cable robots [8,9]. The influence of the end-effector’s payload and dimensions on the static equilibrium workspace for cable robots was presented in [23]. A general approach to generating the force-closure workspace for the cable robots was presented in [24]. An analytical approach to generating the boundaries of the wrench-feasible workspace was proposed, and complete analytical expressions for the boundaries were depicted for two types of cable robots, respectively [25]. A control stability workspace, which can determine whether the controller of the robots can guide the cable robot to a desired pose, is presented and investigated [22]. The improved dynamic feasible workspace was proposed in [15], which took the end-effector’s inertia, external wrenches, and centrifugal and Coriolis forces into account. The dynamic and workspace classification of cable robots were investigated, and a qualitative comparison of different types of workspaces was implemented [26]. The minimum cable tension workspace of cable robots was proposed, which the end-effector of the robots can reach statically [27,28]. Nevertheless, the proposed minimum cable tensions and the presented workspace were in the static sense, and in more detail, the workspace was a subset of the static equilibrium workspace. Concerning cable robots, the workspace is a highly critical issue, especially for the CSGSRs by which the moving gangues can be picked and placed with the end-grab. Cable tensions are the essential issues to constrain the end-grab of the CSGSR, so cable tensions affect dynamic robustness to disturbances for the CSGSR. In addition, minimum dynamic cable tensions inevitably affect the dynamic robustness of the CSGSR. As a result, the workspace generation and analysis of the CSGSR, with consideration of the minimum dynamic cable tensions, are critical issues in maintaining a certain robustness under internal and external disturbances for the robots. For the pick-and-place operation of gangues with the CSGSR, it is required to maintain a certain robustness to the disturbances for the end-grab, and the MDCTW represents a usable workspace of the CSGSR. Furthermore, the functional workspace of the end-grab for CSGSRs is essential for pick-and-place trajectory planning and generating, as well as the configuration design of the CSGSR. For this reason, one of the crucial subjects in the development and application of the CSGSR is generating the MDCTW so that the end-grab can maintain a certain robustness along the direction of the weakest constraint while the disturbances act on the end-grab, as it directly affects the reliability and stability of picking and placing gangues with the robot. Thus, we focused on the MDCTW because the end-grab would be disturbed along the direction of the cable possessing the minimum cable tension among four cables during motion.

As mentioned above, the DCTS is a primary concern of the CSGSR. It is well-known that cable tensions and minimum dynamic cable tensions of the CSGSR are highly dependent on the end-grab’s position. Furthermore, the relationship between cable tensions and end-grab positions is not directly expressed by functions because cable tensions are obtained by optimization. Note that the end-grab can be operated with a certain robustness to the disturbances within the MDCTW for the CSGSR; cable tensions and minimum dynamic cable tensions, however, may have significant fluctuations with minor deviations of the end-grab’s positions caused by a suitable controller under the disturbances. This may lead to the consequence that the original desired MDCTW is changed, and the end-grab is outside the MDCTW when it is located at the workspace’s boundaries. Therefore, the other one of the essential problems in the development and application of CSGSRs is investigating the influence mechanism of the end-grab’s positions on the four cable tensions and minimum dynamic cable tensions and developing a DCTS analysis method. This is because cable tensions may have significant fluctuations when there is slight deviation of the end-grab’s positions with the disturbances, even leading to the violation of constraint conditions for cable tensions and the structural destruction of robots. As far as the author knows, the influence mechanism of the end-grab’s positions on the four cable tensions and the minimum dynamic cable tensions for the CSGSR can be analyzed with DCTS, and the importance of each influencing factor can be obtained. The grey relational analysis method has been employed to the robotic system [29,30,31], especially to investigate the dynamic stability sensitivity and the cable tension sensitivity for cable robots [10,32,33]. A grey relational analysis method for investigating the stability sensitivity of a cable-suspended gangue-sorting cable robot was proposed in [6]. In addition, a grey relational analysis method for the cable tension sensitivity of camera robots with a large-dimension workspace was investigated in [10]. It can be seen that the grey relational analysis can discuss the sensitivity of each influencing factor relative to the main factors, and their sequences of the influencing factors can be ranked [34,35,36,37,38,39]. Thus, an analysis method for investigating DCTS for the CSGSR is developed with grey relational analysis in this paper.

1.3. Contribution and Paper Organization

It is essential to investigate the robustness of the end-grab under disturbances with the cable robots to accomplish the separation of gangues from coals. As a result, the issues of the MDCTW generation and the DCTS analysis method are two of the most critical issues for the CSGSR. However, the existing literature, to the best of the author’s knowledge, does not adequately address the two issues. In addition, completing the operation of gangues from coals with the CSGSR is also affected by dynamic phenomena associated with internal and external disturbances. For this reason, the innovation of this paper is presented as follows:

(i) Compared with Refs. [27,28], the dynamic minimum cable tensions are proposed with the dynamic model of the CSGSR, and, moreover, a methodology for generating the DMCTW for the robots is proposed.

(ii) The influence degree of the end-grab’s positions on the four cable tensions and dynamic minimum cable tensions was investigated, and an approach to investigating dynamic cable tension sensitivity, inspired by Refs. [6,10], is presented with grey relational analysis.

The remainder of this paper is structured as follows. The next section investigates the kinematics and dynamics of the CSGSR. The minimum dynamic cable tensions while the end-grab is located at an arbitrary position are determined with the dynamic model of the CSGSR. Section 3 addresses the issue of MDCTW generation. Section 4 presents an analysis method for DCTS of the CSGSR with grey relational analysis. Section 5 presents several numerical examples of the MDCTW generation algorithm and DCTS analysis method for the CSGSR. Lastly, Section 6 concludes this paper, discusses the contributions of this work, and presents the research directions for the future.

2. Modeling of a Cable-Suspended Gangue-Sorting Robot (CSGSR)

Kinematics and dynamics are the basis of computing cable tensions and analyzing workspaces for cable robots. This section, as a result, aims to present the kinematics and dynamics for the CSGSR. The four cable tensions and the minimum dynamic cable tension while the end-grab is located at an arbitrary position of the task space for the CSGSR are determined with the dynamic model.

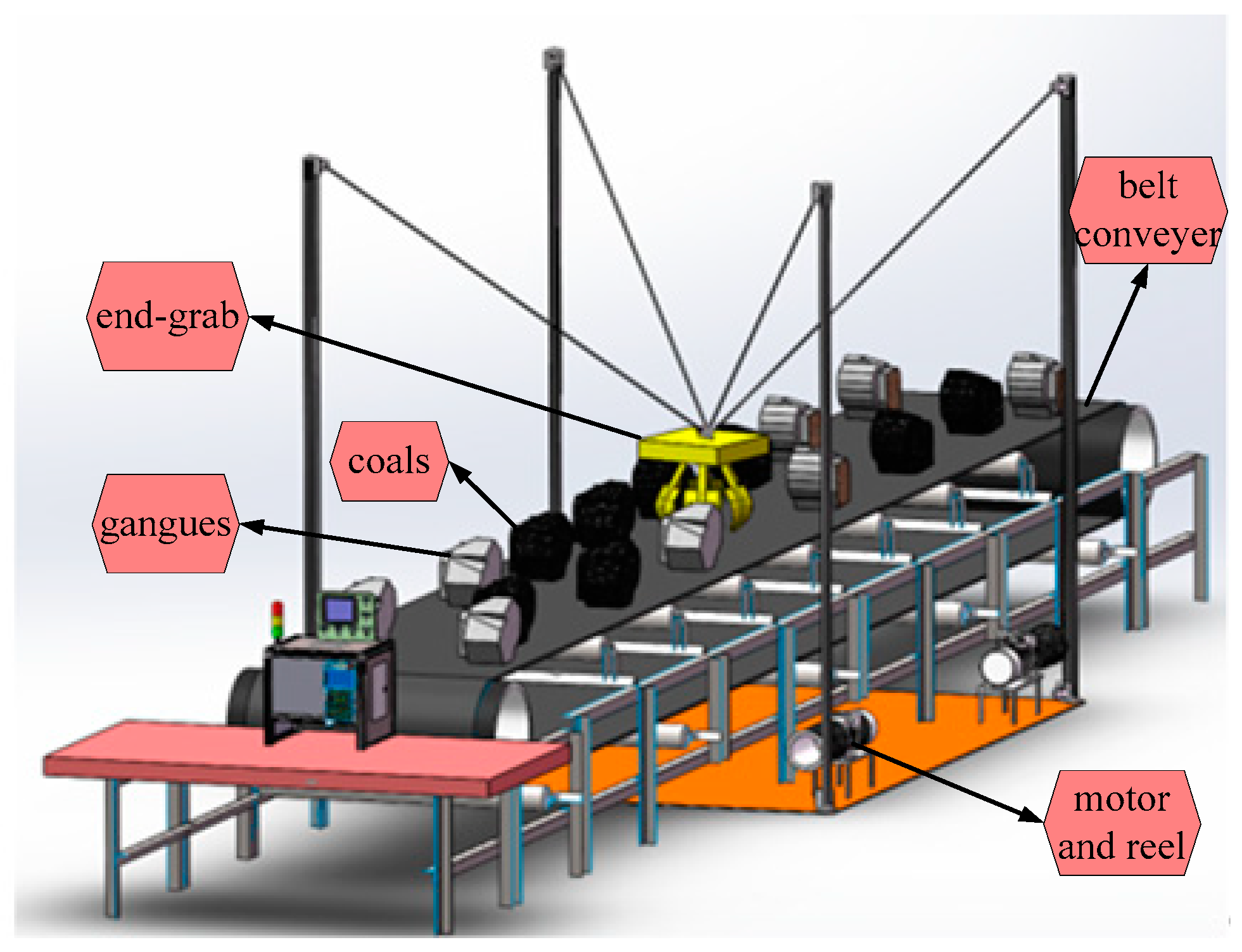
As shown in Figure 1, the proposed CSGSR is a cable robot driven by four cables with an end-grab [7], in which the pick-and-place trajectory planning and trajectory tracking control of the robot in the operation space were investigated. As an extension of our previous work [7], minimum dynamic cable tension workspace generation techniques and cable tension sensitivity analysis methods will be investigated for the proposed CSGSR in this paper because dynamic cable tensions are the basis of pick-and-place trajectory planning and generating, as well as the motion control. Note that the four cables are connected to the end-grab at the same point, and thus the end-grab’s position can be achieved by four cables, while the end-grab can adjust its posture because there is a certain degree of freedom and drivers for the end-grab. Additionally, therefore, it is essential to note that the CSGSR is regarded as a cable robot with a point mass. The translation-only motion of the end-grab can be achieved by the four cables. Meanwhile, the CSGSR operates the end-grab to pick and place the gangues, and thus, considering the belt conveyor’s dimensions, the space dimensions of the CSGSR are selected as 3.7 m × 4.0 m × 2.3 m in this paper. As a result, the following assumptions can be made for the proposed CSGSR in this paper: (i) the mass and the elasticity of the cables can be ignored; (ii) cables do not stretch or sag during motion; (iii) the locations of the cables’ attachments to the end-grab and the motors are known.

Note that it is exceptionally conclusive to maintain positive cable tension to completely constrain the end-grab during motion. However, the cables can only pull, and not push, on the end-grab, and therefore there are four cables for the CSGSR. Additionally, as is shown in Figure 2, the dynamic model of the CSGSR is obtained with Newton–Euler’s law as follows:

At + Q = 0

(1)

where t represents the four cable tensions, and t = [t₁, t₂, t₃, t₄]^T; A denotes the general structure matrix, which is expressed as A = [a₁, a₂, a₃, a₄] for the CSGSR, and a_𝑖 is a unit vector along the four cables, respectively; Q can be expressed as follows:

$$\mathit{Q}=\mathit{G}+\left[\begin{array}{c}m\ddot{x}\\ m\ddot{y}\\ m\ddot{z}\end{array}\right]$$

(2)

where $\ddot{x}$, $\ddot{y}$, and $\ddot{z}$ are acceleration components of the end-grab along the x-axis, y-axis, and z-axis, respectively.

Moreover, Equation (1) can be rewritten as follows:

$$\mathit{M}\left(\mathit{X}\right)\ddot{\mathit{X}}+\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)+\mathit{G}\left(\mathit{X}\right)=-\mathit{A}\mathit{t}$$

(3)

where X = [x, y, z]^T represents the end-grab’s position; $\dot{\mathit{X}}$ denotes linear velocities of the end-grab; $\ddot{\mathit{X}}$ represents the end-grab’s acceleration; M(X) = mI_3×3 is the mass inertia matrix of the end-grab, and I_3×3 is the identity matrix; $\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)$ is the matrix of Coriolis and centripetal terms, and note that $\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)=\mathbf{0}$ for the CSGSR; G(X) = [0, 0, mg]^T represents gravity term, and m is the end-grab’s mass.

It is worth noting that Equations (1) and (3) are valid only if the cable tensions meet ${\mathit{t}}_{\mathrm{s},\min }\le \mathit{t}\le {\mathit{t}}_{\mathrm{s},\max }$, in which the lower boundary of the cable tension denoted by t_s,min = [t_1,min, t_2,min, t_3,min, t_4,min ]^T is necessary to maintain the taut cables, while the upper boundary of the vector t denoted by t_s,max = [t_1,max, t_2,max, t_3,max, t_4,max]^T is determined by the motor’s torques and maximum allowable cable tensions.

For a given pick-and-place trajectory and load of the end-grab, Equation (3) of the CSGSR is a non-homogeneous linear equation. There will be multiple solutions to the four cable tensions. To solve Equation (3), with the introduction of Moore–Penrose pseudoinverse matrix A⁺, t can be determined as follows [40,41,42]:

$$\mathit{t}={\mathit{t}}_h+{\mathit{t}}_n$$

(4)

It can be seen that there are two parts in Equation (4), where ${\mathit{t}}_h=-{\mathit{A}}^{+}\left(\mathit{M}\left(\mathit{X}\right)\ddot{\mathit{X}}+\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)+\mathit{G}\left(\mathit{X}\right)\right)$ depicts the particular solution to the cable tension t and ${\mathit{t}}_n=\mathit{N}\lambda$ denotes its homogeneous solution.

The CSGSR employs four cables to operate the end-grab to accomplish the separation of gangues from coals with three translation-only motions of the end-grab. Therefore, ensuring the positive cable tensions can be realized by choosing an appropriate $\lambda$ as an arbitrary scalar for the CSGSR. To obtain the cable tensions with Equation (4) and to maintain cable tensions for the cable robots, many cable tension distribution algorithms have been proposed [43,44,45,46,47]. In this section, the determination of the four cable tensions can be achieved through the following model:

$$\begin{array}{c}\mathrm{Objective}:min\left(\frac{1}{4}\left[{\displaystyle \sum _{i=1}^4{\left(t_i-E\left(\mathit{t}\right)\right)}^2}\right]\right)\\ \begin{array}{cc}\mathrm{subject}& \mathrm{to}\end{array}:\mathit{M}\left(\mathit{X}\right)\ddot{\mathit{X}}+\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)+\mathit{G}\left(\mathit{X}\right)=-\mathit{A}\mathit{t}\\ \mathrm{and}{\mathit{t}}_{\mathrm{s},\min }\le \mathit{t}\le {\mathit{t}}_{\mathrm{s},\max }\end{array}$$

(5)

where E(t) is the average value of the vector t.

Minimum cable tensions for cable robots were presented based on the static equilibrium of the end-effector in Refs. [27,28]. Contrary to the above literature, the minimum dynamic cable tension t_min while the end-grab of the CSGSR is located at an arbitrary position of the task space is calculated after obtaining the four dynamic cable tensions with the dynamic model of the CSGSR, and t_min can be acquired through the following equation:

$$t_{\min }\left(\mathit{X}\right)=min\left(\mathit{t}\left(\mathit{X}\right)\right)$$

(6)

where $min(•)$ is the most minor component of the cable tension, and X denotes the position of the end-grab.

It can be seen from Equation (6) that the minimum dynamic cable tension is depicted as a function of the end-grab’s positions, and, thus, t_min is dependent on the end-grab’s position. Meanwhile, with the greater cable tensions and minimum dynamic cable tensions, the CSGSR possesses a stronger robustness to resist disturbances. As a result, it is of interest to obtain a workspace where the minimum dynamic cable tensions meet or exceed a given value for the CSGSR.

3. Minimum Dynamic Cable Tension Workspace (MDCTW) Generation Algorithm

Concerning cable robots, the workspace is the most critical issue, especially for CSGSRs, because it is the basis of pick-and-place trajectory planning and generating of the end-grab. Generally speaking, a workspace of cable robots is defined as the set of all poses of the end-effector for which any given wrenches can act on the end-effector [48,49]. It indicates the end-effector could reach the workspace while all cable tensions are positive and the constraints of the desired motions and/or cable tensions are satisfied. As mentioned above, the combinations of different conditions and workspace generation for the robots can generate different workspaces. The difference from the above workspace is that the CSGSR must possess a particular ability to resist internal and external disturbances, and to maintain robustness under disturbances, because of the unidirectional characteristic and the flexibility of cables and the dynamic impact of picking and placing gangues. Given the results of the minimum dynamic cable tensions, we can measure the robustness of the CSGSR to the disturbances at that position of the end-grab. For a given pick-and-place operation of gangues, the CSGSR might be required to maintain a certain amount of robustness to disturbances during the whole motions. The end-grab of the CSGSR is disturbed along the direction of the cable possessing the minimum cable tension among four cables while the disturbances act on the end-grab. Meanwhile, the minimum dynamic cable tensions for the robots are dependent on the end-grab’s position. Therefore, it is of interest to obtain the set of all end-grab positions where the CSGSR meets or exceeds this specified value of minimum dynamic cable tensions. Consequently, the concepts of minimum dynamic cable tensions and workspace generation are combined to put forward the MDCTW, which is a new and valuable workspace for the CSGSR. The MDCTW for the robot is composed of all positions of the end-grab exceeding the preset value of minimum dynamic cable tensions. Indeed, the proposed MDCTW for the CSGSR is not only dependent on the end-grab’s kinematic state (e.g., the position, velocity, and acceleration), but is also dependent on the minimum dynamic cable tension. Indeed, the MDCTW is a subset of the dynamic workspace of the CSGSR. This section, as a result, aims to address the issue of MDCTW generation, and a pointwise method is presented for generating the MDCTW for the CSGSR.

Definition 1.

The proposed MDCTW for the CSGSR is defined as the set of all positions that the end-grab can reach with at least one kinematic state where the four cable tensions remain within the prescribed range, and more importantly, the minimum dynamic cable tensions are greater than or equal to a required value.

The above definition indicates that the MDCTW for the CSGSR is a mixed space of the end-grab’s position and kinematic state. The CSGSR can be controlled dynamically within the MDCTW. For the CSGSR, which is a cable robot with a point mass, it is required to exert a particular set of forces without considering the associated moments on the end-grab. There is no corresponding moment on the end-grab. In this case, the conditions of the MDCTW for the CSGSR are expressed as follows:

$$\begin{array}{l}\mathit{M}\left(\mathit{X}\right)\ddot{\mathit{X}}+\mathit{C}\left(\mathit{X},\dot{\mathit{X}}\right)+\mathit{G}\left(\mathit{X}\right)=-\mathit{A}\mathit{t}\left({\mathit{t}}_{\mathrm{s},\min }\le \mathit{t}\le {\mathit{t}}_{\mathrm{s},\max }\right),i=1,2,3,4\\ t_{\min }\left(\mathit{X}\right)\ge t_{\min ,g}\end{array}$$

(7)

where t_min,g represents the given allowable minimum dynamic cable tension.

The proposed MDCTW for the CSGSR can be generated by judging whether a position of the end-grab X meets the conditions described in Equation (7) or not. For cable robots, there are three methods employed to generate the workspace. Additionally, in detail, the first one is a pointwise method that discretizes the task space and further investigates whether or not each discrete position of the end-grab is within the investigated workspace by the given constraint condition [40]. Additionally, the second one is a continuous method, such as the interval analysis [21]. The last one is an analytical method that can generate the boundary equations of the investigated workspace [8]. In most studies of cable robots, the numerical approach is employed to figure out the corresponding workspace, with which the entire task space of the robots is discretized, and to search for the predefined workspace. The pointwise method, as a result, is employed to generate the MDCTW for the CSGSR in this section. The search space for the end-grab’s position X is mainly determined by the pulley’s positions, and therefore it is a cuboid for the CSGSR. Based on the proposed definition of the DMCTW, the generation algorithm of the DMCTW for the CSGSR can be summarized as the presented Algorithm 1.

Algorithm 1. MDCTW generation algorithm for the CSGSRs.

4. Analysis Methods for Dynamic Cable Tension Sensitivity (DCTS)

The four cable tensions and minimum dynamic cable tensions are dependent on the end-grab’s position, and thus they highly depend on the end-grab’s positions for the CSGSRs. There may be significant fluctuations in the four cable tensions and the minimum dynamic cable tensions when the end-grab’s positions have slight deviations under the disturbances. Consequently, this section focuses on the influencing degree of the end-grab’s positions on the four cable tensions and the minimum dynamic cable tensions for the CSGSRs, and the most sensitive influencing factor can be identified and obtained through the importance degree of the influencing factors. There is a reduction of the fluctuation of cable tensions caused by the deviation of the positions of the end-grab while the most sensitive influencing factor is controlled preferentially. Up to now, a DCTS analysis method for the CSGSRs is presented with grey relational analysis, and it can be described as follows:

(1) Determination of the sequences

In this paper, the numerical values of four cable tensions and the minimum dynamic cable tensions are chosen as the reference sequence, respectively, and a total of five reference sequences of the cable tensions can be obtained, while the end-grab’s position components are chosen as the comparison sequences. Additionally, in detail, the reference sequences of the cable tensions are, respectively, denoted as ${\mathit{P}}_{0j}={\left[P_{0j}\left(1\right),P_{0j}\left(2\right),\cdots ,P_{0j}\left(k\right)\right]}^{\mathrm{T}},j=1,2,3,4,5$, where j indicates the above five reference sequences; and the shared comparable sequences are expressed as ${\mathit{P}}_l={\left[P_l\left(1\right),P_l\left(2\right),\cdots ,P_l\left(k\right)\right]}^{\mathrm{T}},l=1,2,3$, where l represents the end-grab’s position components, and k is the change number of the cable tensions and the end-grab’s positions for the robots. Therefore, there are five groups of data on cable tensions and end-grab positions, and they can be denoted as ${\mathit{T}}_1=\left[{\mathit{P}}_{01},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]$, ${\mathit{T}}_2=\left[{\mathit{P}}_{02},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]$, ${\mathit{T}}_3=\left[{\mathit{P}}_{03},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]$, ${\mathit{T}}_4=\left[{\mathit{P}}_{04},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]$, and ${\mathit{T}}_5=\left[{\mathit{P}}_{05},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]$, respectively.

(2) Normalization of the above five groups of data

It should be pointed out that the raw data of five reference sequences of the cable tensions and three comparison sequences of the end-grab’s position component are different from the others, so this may lead to an incorrect conclusion. As a result, a normalization treatment on the five groups of initial data must be implemented first. Take a set of data as an example to illustrate the normalization treatment. Additionally, a group of data is denoted as ${\mathit{T}}_1=\left[{\mathit{P}}_{01},{\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3\right]=\left[\begin{array}{cccc}{P}_{01}\left(1\right)& P_1\left(1\right)& P_2\left(1\right)& P_3\left(1\right)\\ P_{01}\left(2\right)& P_1\left(2\right)& P_2\left(2\right)& P_3\left(2\right)\\ ⋮& ⋮& ⋮& ⋮\\ P_{01}\left(k\right)& P_1\left(k\right)& P_2\left(k\right)& P_3\left(k\right)\end{array}\right]$, then the data are addressed with a normalization treatment, and they can be transformed with the following equations:

$$P_{01}^{\prime }\left(m\right)=\frac{P_{01}\left(m\right)-\min P_{01}}{\max P_{01}-\min P_{01}},\left(m=1,2,\cdots ,k\right)$$

(8)

$$P_l^{\prime }\left(m\right)=\frac{P_l\left(m\right)-\min P_l}{\max P_l-\min P_l},\left(l=1,2,3;m=1,2,\cdots ,k\right)$$

(9)

Note that Equation (8) is derived with the first column of the matrix, while Equation (9) is deduced using the remaining three columns.

(3) Calculation of grey relational coefficient

Furthermore, the absolute difference between the selected reference sequence among the above five and the three shared comparison sequences ${\varpi }_{01,l}=|P_{01}^{\prime }\left(m\right)-P_l^{\prime }\left(m\right)|$ is obtained. Based on these results, the maximum difference and minimum difference are obtained, respectively, and they are expressed as follows:

$${\varpi }_{\max }=\underset{1\le l\le 3}{{\displaystyle \max }}\underset{1\le m\le k}{{\displaystyle \max }}|P_{01}^{\prime }\left(m\right)-P_l^{\prime }\left(m\right)|$$

(10)

$${\varpi }_{\min }=\underset{1\le l\le 3}{{\displaystyle \min }}\underset{1\le m\le k}{{\displaystyle \min }}|P_{01}^{\prime }\left(m\right)-P_l^{\prime }\left(m\right)|$$

(11)

Consequently, grey relation coefficients for the end-grab’s position component with regard to the selected reference sequence can be obtained as follows:

$$R_l\left(m\right)=\frac{{\varpi }_{\min }+\mu {\varpi }_{\max }}{{\varpi }_{01,l}\left(m\right)+\mu {\varpi }_{\max }}$$

(12)

where $\mu$ is the distinguishing coefficient, which is located in the interval [0, 1], and the distinguishing coefficient, generally speaking, is chosen as 0.5 [50,51].

(4) Determination of the grey relational degree

The correlation between the selected reference sequence and the three end-grab position components can be characterized using the grey relational degree. The grey relational degree can be used to describe the influence degree of the end-grab’s position components on four cable tensions and minimum dynamic cable tensions. Then, the maximum and minimum influencing factors can be obtained with the grey relational degrees, respectively. In consequence, a DCTS analysis method for the CSGSR is presented, and an analysis index for the DCTS is obtained through the following equation:

$$D_l=\frac{1}{k}{\displaystyle \sum _{m=1}^k{R}_l}\left(m\right)$$

(13)

It should be pointed out that three analysis indices can be calculated for one of the five reference sequences (four cable tensions and minimum dynamic cable tensions), and they denote the influence degree of the end-grab’s position components on the cable tensions, respectively. Consequently, the three analysis indices could describe the sensitivity of the end-grab’s position components on the corresponding reference sequence and rank their sequences. Moreover, the most sensitive influencing factor can be recognized and controlled preferentially in practice. As a consequence, there is a reduction of fluctuations of the four cable tensions and the minimum dynamic cable tensions caused by the deviation of the end-grab’s positions because the most sensitive influencing factor is controlled preferentially.

5. Results and Discussion

In this section, the proposed MDCTW generation algorithm and DCTS analysis method are examined on a CSGSR with some simulation studies. The system parameters of the selected CSGSR are as follows: the end-grab’s mass is set as 10 kg; the lower boundary and the upper boundary of the cable tension t are chosen as 10 N and 300 N, respectively. Furthermore, the dimensions of the CSGSR, as mentioned in Section 2, are set as 3.7 m × 4.0 m × 2.3 m. Consequently, the task space of the selected CSGSR is a cuboid with the above dimensions.

On the one hand, the proposed MDCTW generation algorithm for the CSGSR was examined, and the entire task space of the robot was discretized and exhaustively searched to figure out the MDCTW. Additionally, as mentioned above, the MDCTW of the CSGSR is not only dependent on the end-grab’s kinematic state, but is also dependent on the minimum dynamic cable tension. Consequently, the variation law of MDCTW with the minimum dynamic cable tension is studied first, and the obtained results are depicted in Figure 3. Additionally, in more detail, Figure 3a–d depict the MDCTW of the CSGSR with t_min,g = 10 N, 15 N, 20 N, and the three situations together, respectively, while the end-grab’s acceleration is set to zero. It can be seen that with the increase in the given allowable minimum dynamic cable tension t_min,g, the corresponding MDCTW decreases. In other words, the higher the permissible conditions for the minimum dynamic cable tension, the smaller the set of the end-grab’s positions that meets the given requirement.

Meanwhile, the variation law of the MDCTW with the end-grab’s kinematic state is then studied, and the obtained results are shown in Figure 4. In more detail, Figure 4a,c,e depict the MDCTW of the CSGSR with $\ddot{\mathit{X}}={[0,0,0]}^{\mathrm{T}}$, $\ddot{\mathit{X}}={[5,5,5]}^{\mathrm{T}}$, and $\ddot{\mathit{X}}={[10,10,10]}^{\mathrm{T}}$, respectively, while the allowable minimum dynamic cable tension is set to 10 N. Furthermore, Figure 4b,d,f are the top views of Figure 4a,c,f, respectively. It is obvious from the figure that with the increase in the end-grab’s acceleration, the generating MDCTW for the robot decreases. There are accelerations along the x- and y-directions for the end-grab, so the positions that initially met the conditions of the MDCTW are missing. Moreover, as the end-grab’s acceleration increases, the missing volume of the MDCTW increases. It can be seen from the above results that the MDCTW of the CSGSR is not only dependent on the end-grab’s kinematic state, but is also dependent on the minimum dynamic cable tension.

On the other hand, the presented DCTS analysis method for the robots was investigated in this section. In detail, a spiral trajectory within the MDCTW was selected for the robot to discuss the influence of the end-grab’s position components on four cable tensions and minimum dynamic cable tensions. The radius of the spiral trajectory is R = 1 m; the speed along the z-direction of the end-grab v = 0.2; the total running time is 10 s; the starting point of the spiral trajectory is (2.85, 2, 0); and the end point of the spiral trajectory is (2.85, 2, 2). As shown in Figure 5, the selected spatial spiral marked with the red line within the MDCTW of the CSGSR with t_min,g = 10 N is depicted. It should be pointed out that the surface is the lower boundary of the MDCTW. Observing the results, it can be seen that the selected spatial spiral is entirely within the MDCTW, and therefore the CSGSR will possess a preset robustness to the disturbances while carrying out the pick-and-place operation of the moving gangues.

As mentioned above, the four dynamic cable tensions and the minimum dynamic cable tensions for the CSGSR can be achieved using the cable tension optimization distribution model, and thus only discrete values of the four dynamic cable tensions and minimum dynamic cable tensions, as well as the end-grab’s positions, can be obtained by simulation. Additionally, in more detail, eleven sets of data when the end-grab of the CSGSR was located on the spiral trajectory were obtained and are shown in

Table 1. Original data of the cable tensions and the end-grab’s positions.

The Five Reference Sequences					The Three Comparison Sequences
t1(N)	t2(N)	t3(N)	t4(N)	tmin(N)	x(m)	y(m)	z(m)
131.128	275.996	275.996	131.128	131.128	2.850	2.000	2.000
85.490	131.385	172.379	98.609	85.490	2.659	2.588	1.800
62.059	68.187	122.756	104.108	62.059	2.159	2.951	1.600
54.103	48.451	83.273	99.051	48.451	1.541	2.951	1.400
64.358	38.660	48.324	88.134	38.660	1.041	2.588	1.200
73.521	32.181	32.181	73.520	32.181	0.850	2.000	1.000
71.447	38.058	28.283	50.670	28.283	1.041	1.412	0.800
63.212	51.398	26.350	32.082	26.350	1.541	1.049	0.600
48.071	59.491	29.695	23.813	23.813	2.159	1.049	0.400
30.757	59.687	40.938	20.254	20.254	2.659	1.412	0.200
20.423	51.926	51.926	20.423	20.423	2.850	2.000	0.000

. Observing the results, it can be seen that the obtained cable tensions satisfy the limit condition of cable tensions, and the eleven t_min are the smallest among the four cables. This proves the correctness of the obtained cable tensions.

For one cable tension, three grey relational degrees can be obtained with regard to the end-grab’s position components, and the sensitivity of each position component for the cable tension can be obtained by comparing the three grey relational degrees. As is shown in

Table 2. Grey relational degree and ranking of the end-grab’s position components.

Grey Relational Degree and Ranking	Influencing Factors
	x-Component	y-Component	z-Component
Grey relational degree of t1	0.644	0.617	0.821
Ranking	2	3	1
Grey relational degree of t2	0.649	0.577	0.651
Ranking	2	3	1
Grey relational degree of t3	0.675	0.617	0.647
Ranking	1	3	2
Grey relational degree of t4	0.607	0.742	0.878
Ranking	3	2	1
Grey relational degree of tmin	0.684	0.628	0.694
Ranking	2	3	1

, the grey relational degree and ranking of the end-grab’s position components relative to the four dynamic cable tensions and minimum dynamic cable tensions are calculated using Equations (8)–(13). Observing the results, it is obvious that the grey relational degrees of the cable tensions are greater than 0.5, so the end-grab’s displacement components have a significant influence on the four dynamic cable tensions and minimum dynamic cable tensions. Compared with t₁, t₂, and t_min, the orders of the end-grab’s position components relative to t₃ and t₄ are slightly different. On the whole, the influence laws of the end-grab’s position components on the four cable tensions and the minimum dynamic cable tensions are basically consistent with each other, and the sensitivity of the three end-grab position components on the cable tensions are, in an ascending order: the end-grab’s position component along the y-axis < the end-grab’s position component along the x-axis < the end-grab’s position component along the z-axis. Consequently, it is more effective to control the deviation of the end-grab’s position component along the z-axis to limit the fluctuation of cable tensions.

Moreover, the grey relational degrees of the end-grab’s position components relative to the cable tensions are depicted in Figure 6. We can intuitively compare the sensitivity of the end-grab’s position components to the cable tensions. It should be noted that the effects of distinguishing coefficient $\mu$ on the analysis index for DCTS for the CSGSR are investigated, and the results are depicted in Figure 6f while $\mu =0.6$. It can be seen that the influence laws of the end-grab’s position components on t_min coincide with each other while $\mu =0.5$ and $\mu =0.6$.

From the above analysis, we can see that the DCTS for the CSGSR, which investigates the influence law of the end-grab’s position components relative to the dynamic cable tensions and minimum dynamic cable tensions, can be reported with the grey relational degrees, and the most sensitive influencing factor can be recognized in practice. In detail, the end-grab’s position component along the x-axis has the minimal impact on the cable tensions, and conversely, the end-grab’s position component along the z-axis has the greatest impact on cable tensions. Furthermore, compared with t₁, t₂, and t_min, the orders of the end-grab’s position components relative to t₃ and t₄ are slightly different. Thus, our future work will further investigate an evaluation methodology that can unify the influence laws of the end-grab’s position components on four cable tensions and minimum dynamic cable tensions for the CSGSR.

6. Conclusions and Future Works

This work aimed to address the main issues related to the CSGSR in two key areas: MDCTW generation techniques and DCTS analysis methods, and the following conclusions can be drawn:

(i) Firstly, the dynamic cable tensions were presented based on the dynamics model of the CSGSRs. Combining the concepts of minimum dynamic cable tensions and workspace generation, a new and valuable workspace for the CSGSRs, namely the MDCTW, was proposed in this paper, and, moreover, the generation algorithm for the proposed DMCTW of the CSGSR was presented. It was shown that the method for generating the MDCTW for the CSGSR can be used to construct a set of the end-grab’s positions where the robot can maintain predetermined robustness to the disturbances.

(ii) Secondly, a quantitative analysis method for the DCTS of the CSGSRs was developed with grey relational analysis; furthermore, an analysis index for DCTS was proposed. The influence mechanism of the end-grab’s positions on the four cable tensions and minimum dynamic cable tensions was investigated, respectively.

(iii) Finally, some simulations were presented to confirm the proposed MDCTW generation algorithm and the DCTS analysis method for CSGSRs. On the one hand, the presented MDCTW of the CSGSR was analyzed at various kinematic states and different predetermined conditions of the minimum dynamic cable tension. The simulation results show that with the increase in the given allowable minimum dynamic cable tension and the end-grab’s acceleration, the generating MDCTW both decrease. On the other hand, the sensitivity of the end-grab’s position components on the four cable tensions and the minimum dynamic cable tensions was investigated, and their sequences were ranked with the obtained grey correlation degrees, respectively. Additionally, the simulation results show that the influence laws of the end-grab’s position components on the four cable tensions and the minimum dynamic cable tensions are basically consistent with each other. The sensitivity of three end-grab’s position components on the cable tensions are, in ascending order: the end-grab’s position component along the y-axis < the end-grab’s position component along the x-axis < the end-grab’s position component along the z-axis.

In addition, there are several topics for future work that can be executed in the investigation of the CSGSR. One possibility is to investigate an analytical method for generating a complete description of the continuous boundaries of the MDCTW, similar to what was performed for point-mass cable robots in Refs. [8,9]. Another potential area of future work is to plan and generate a pick-and-place trajectory of the end-grab, insensitive to the deviations of the end-grab’s positions, on which the deviations of the end-grab’s positions will not produce significant fluctuation of the cable tensions.