Design and Verification of Adaptive Adjustable Output Control on Micro Spray Gun †
Abstract
:1. Introduction
2. Materials and Methods
2.1. DC Motor Drive Module
2.2. PID Control Unit
- Kp: proportional gain adjustable parameter,
- Ki: integral gain adjustable parameter,
- Kd: differential gain adjustable parameter,
- t: current time,
- τ: variable of integration, with the number from 0 to current time .
2.3. Experimental Design
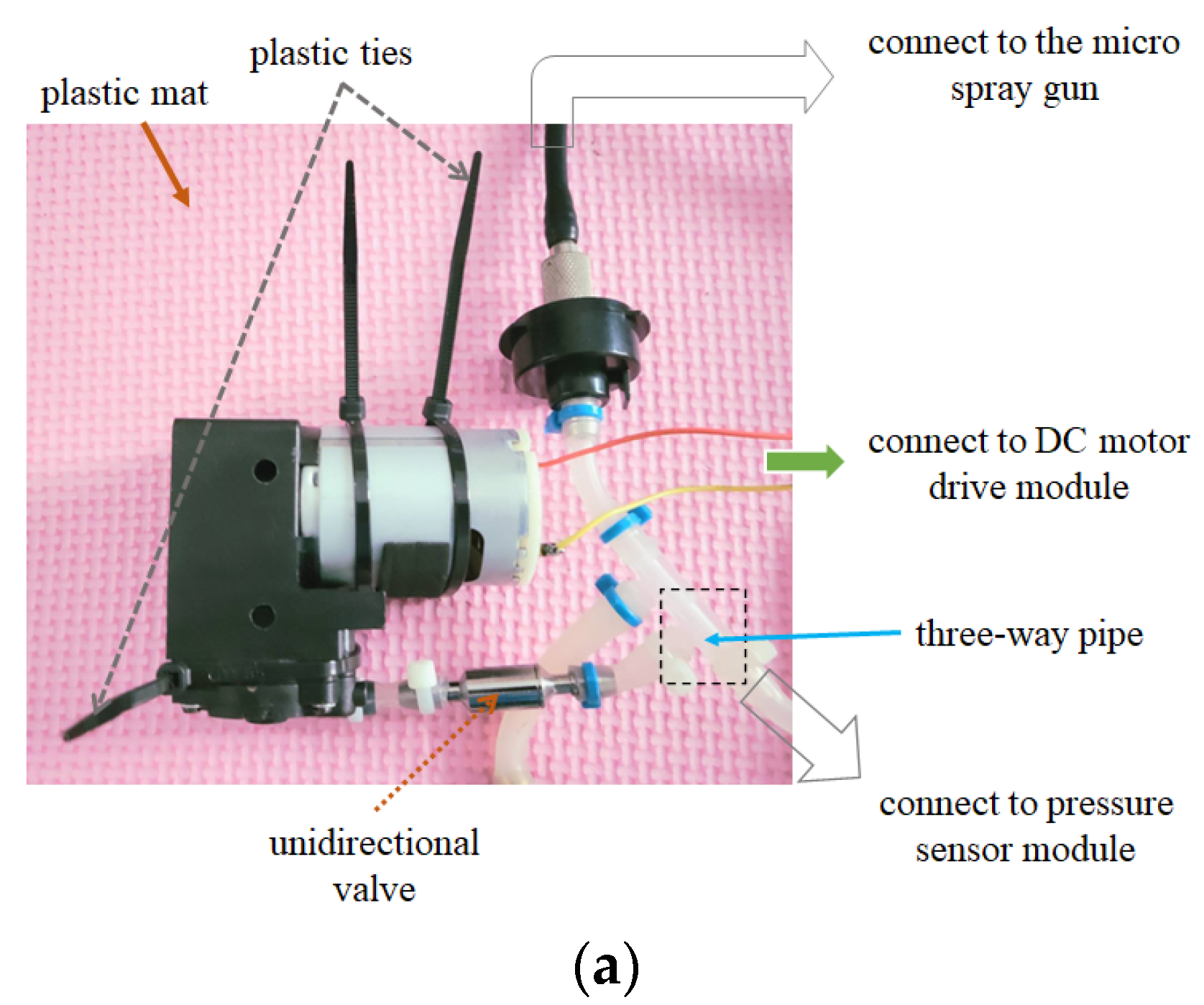
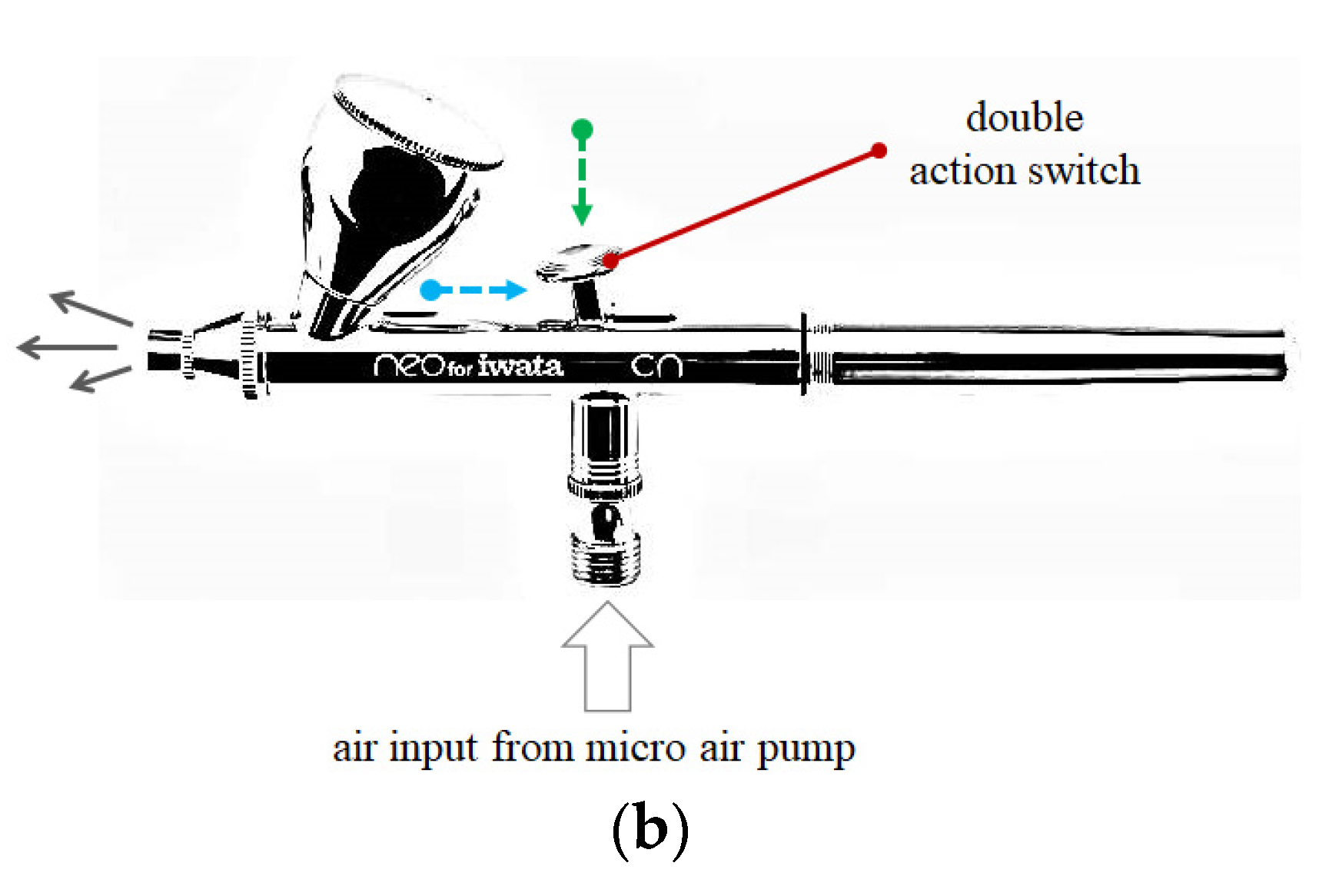
2.3.1. System Architecture
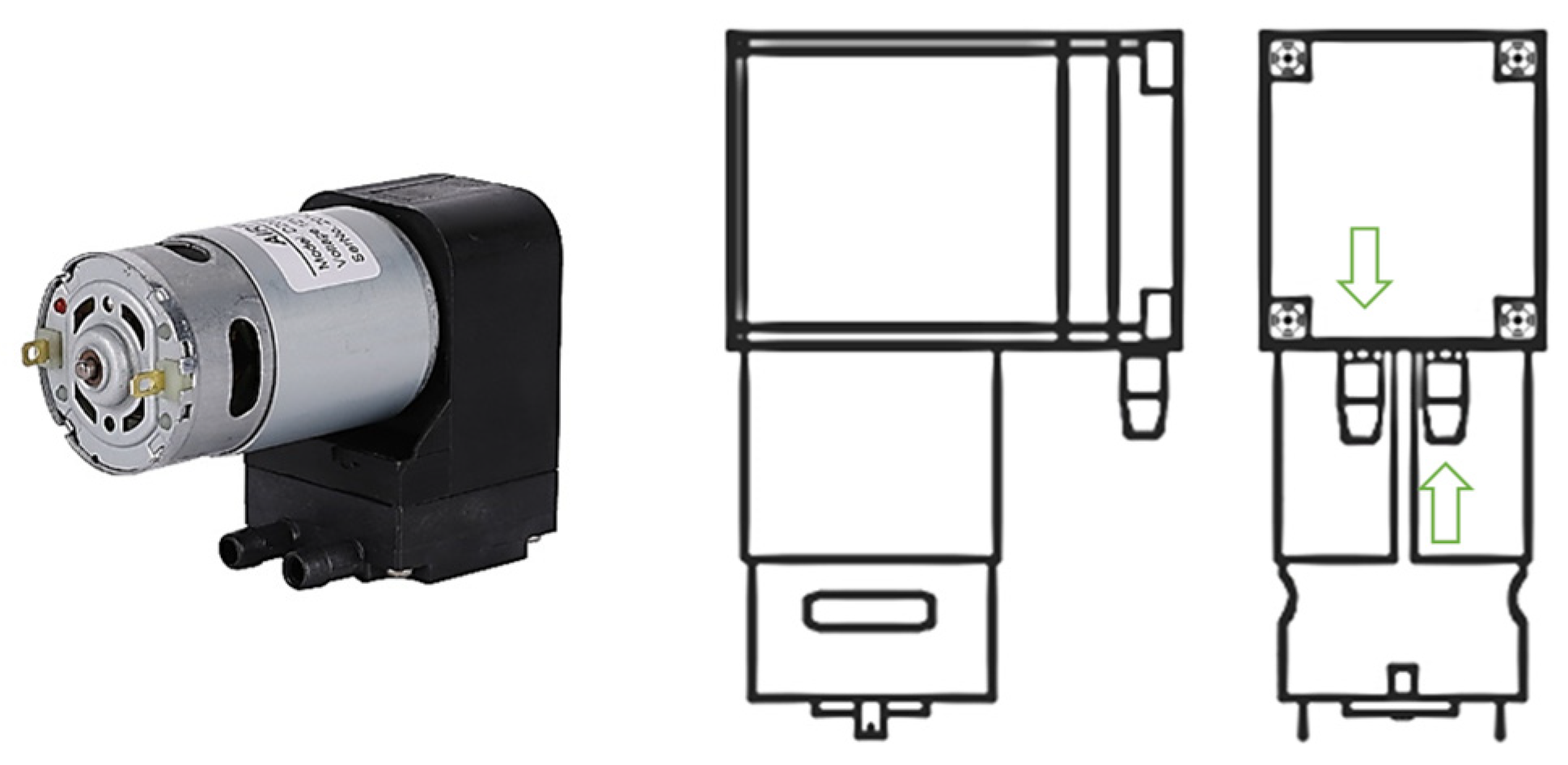
2.3.2. Characteristics of the Micro Air Pump
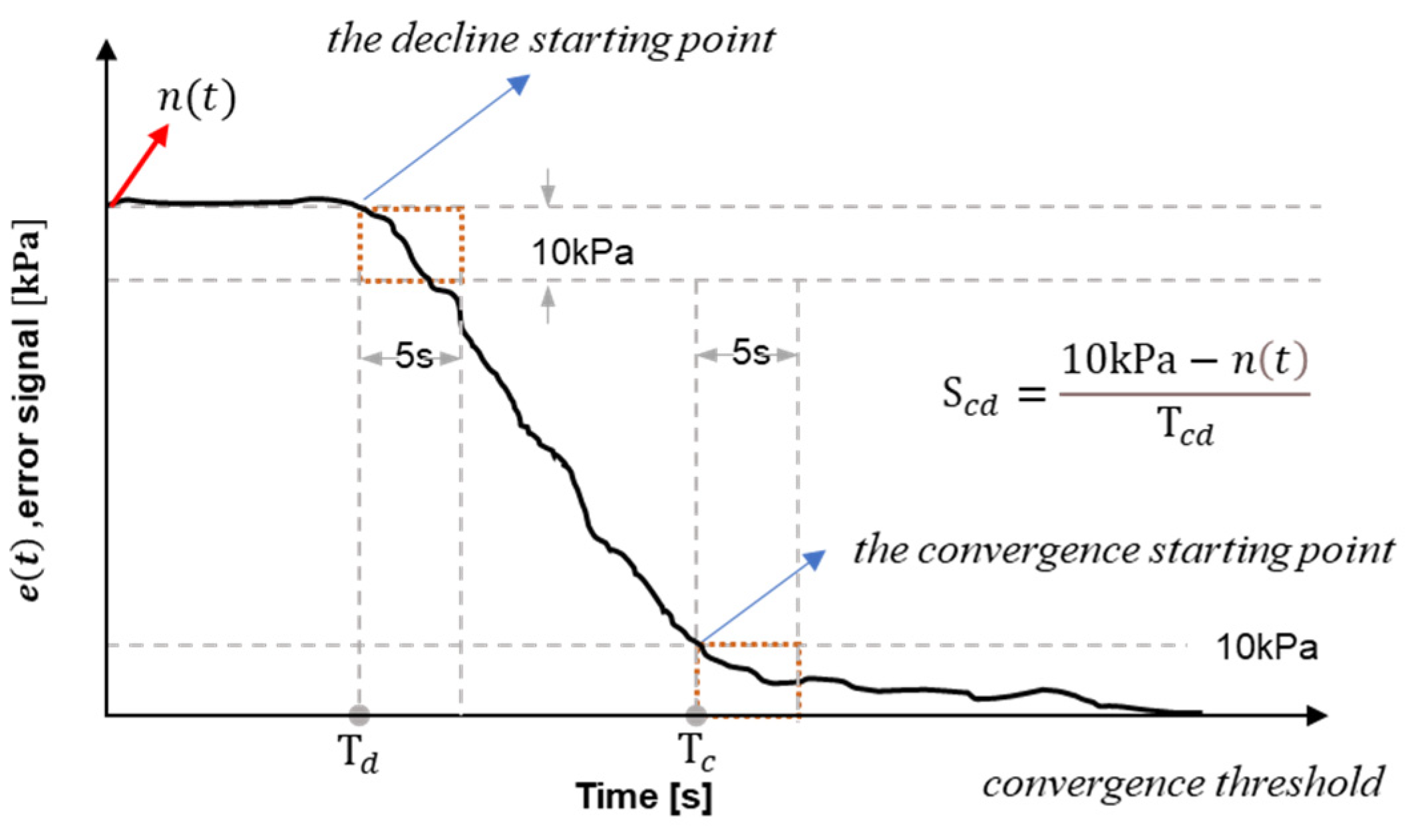
2.3.3. Convergence Condition
3. Results
3.1. Effects under Different Target Values
3.2. Effects under Pulse-like Variables
3.3. Effects of PID Convergence
4. Discussions
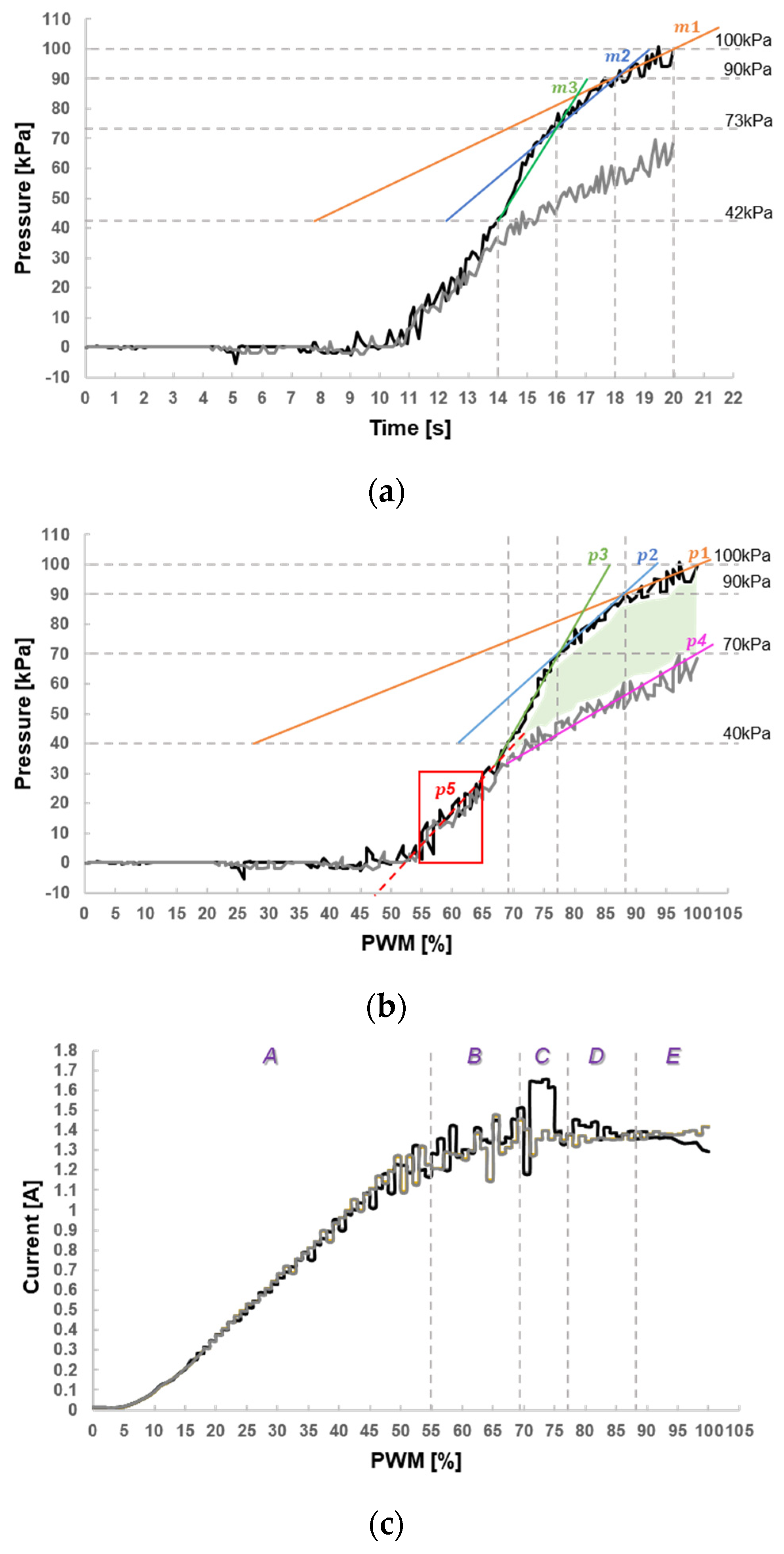
- The experimental data reveal that the internal structure of the micro air pump presents certain effects on the control response, rather than simply a linear state. Consequently, the experiment results shown in Figure 5a could verify the better pressure output range of the micro air pump above 40 kPa. The exhaust, when the spray gun is pressed, results in dropping pressure in the pipe to influence the overall pressure output. In this case, the maximal pressure sensed is about 70 kPa when PWM is modulated to the maximal 100%, with the difference of about 30 kPa from the spray gun not being pressed. In the experiment in Section 3.3, the preset target value of 65 kPa would drop down to 40 kPa after pressing the spray gun. The low pressure during paint spray would affect the spray quality and result in the irregular operation of the motor, due to the unstable air pump, damaging the life. Automatic control technology could effectively change the exhaust output volume and stabilize the operation of the air pump. This study verifies the driving module and algorithm control technology of the automatic system. The experiment results after pressing the spray gun proves that proper parameter modulation allows the system design to return the target pressure within a specified period.
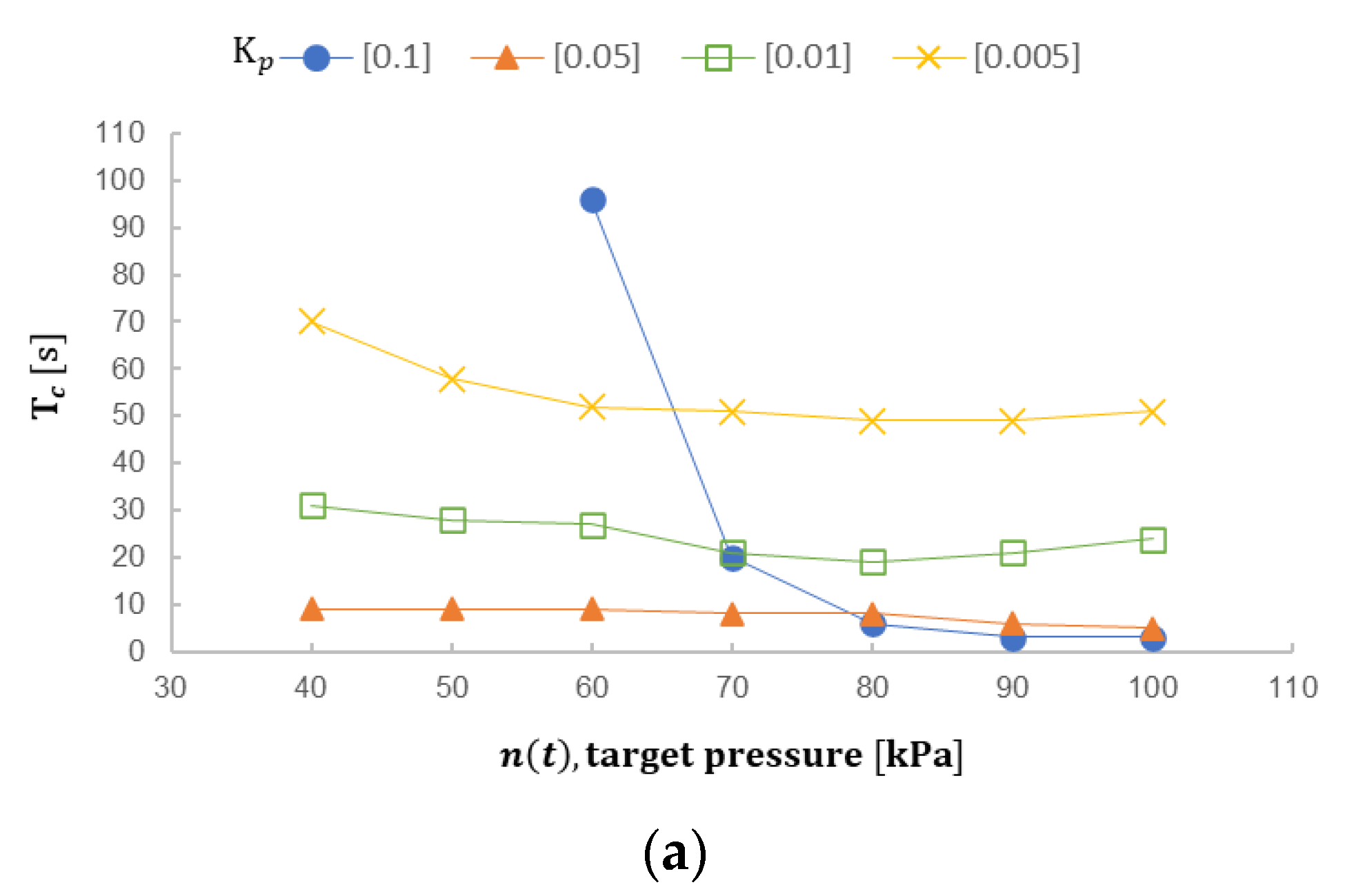
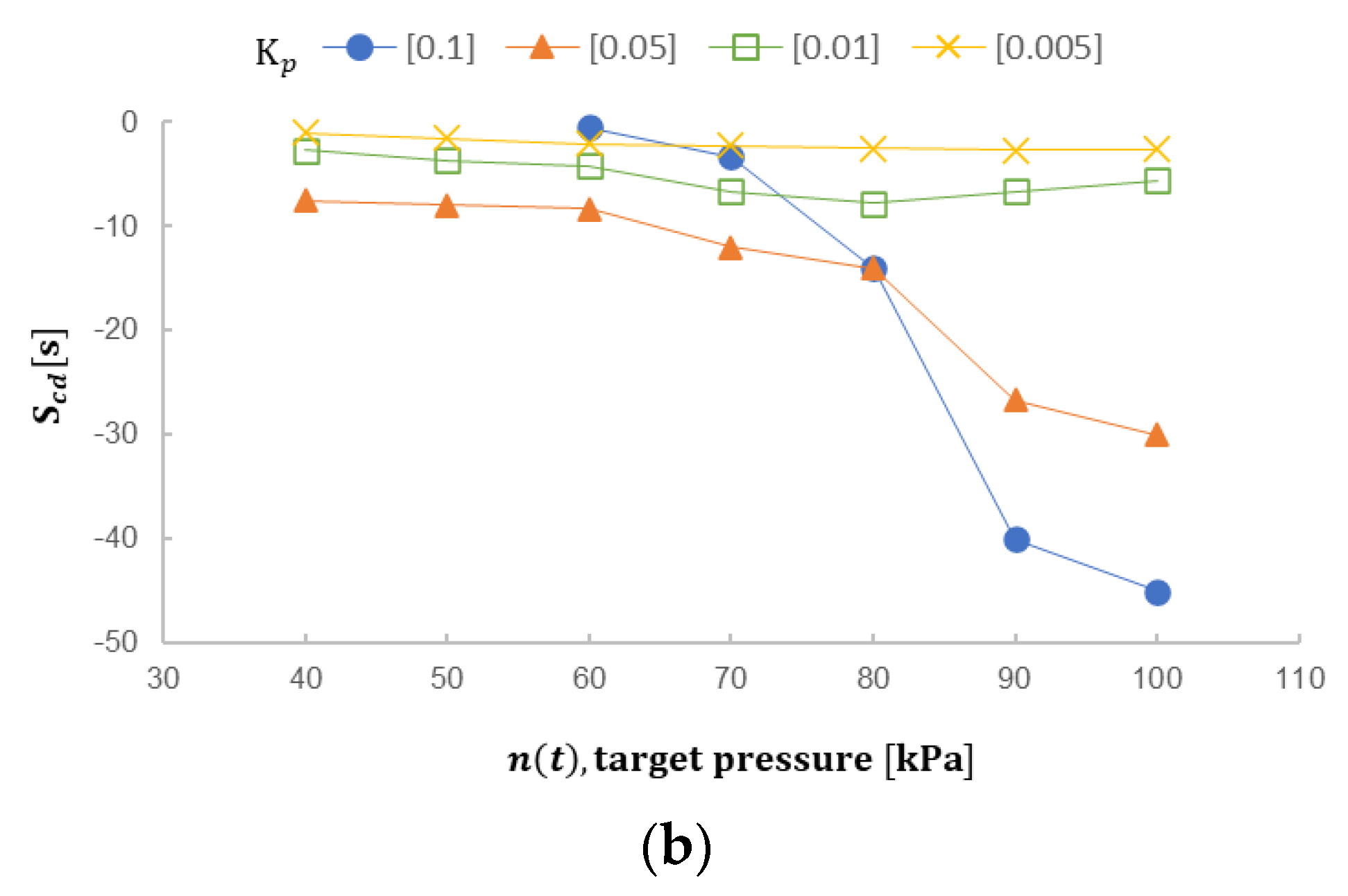
- The proportional gain adjustable parameter Kp determines the ratio of the output response to the error signal. In general, increasing Kp will increase the responsiveness of the control system, but if the proportional gain is too large, the process variable will start to oscillate. If Kp is increased further, the vibration will become larger and larger, and the system will become unstable, and even uncontrollable vibration may occur. As the result in Figure 7, Kp = 0.1 is obviously a larger value in this experiment; under the same target value n(t), the error is comparatively difficulty to be controlled in the convergence range. Perhaps, Kp appears faster convergence time and convergence speed when n(t) is above 80 kPa with several larger target values n(t), as in Figure 8a. Nevertheless, the higher instability results in n(t) being 60 and 70 kPa, the convergence time being largely prolonged, and the convergence time, with n(t) being 60 kPa, is even longer than it when Kp is 0.005. Particularly, it could not get into the convergence condition when n(t) is 40 kPa and 50 kPa. Such applications would cause several unpredictable errors and even non-practical ones.When smaller Kp is selected, the error signal is less sensitive and the response to the target signal being suddenly interfered with or appearing larger variable would be too slow and the output control signal is not large enough to catch up with the variable quantity. As in Figure 9, the target value n(t) in the moment of conversion at 65 kPa and 95 kPa, when Kp is 0.01, does not cause system instability or divergence, but the speed to catch up with the target value is indeed slower. In real applications, it is difficult to predict or limit users to stably press the spray gun so that the pressure variable would happen at any time. The pulse-like target variable experiment planned in Section 3.2 is used for coping with such pressure variables with proper parameter settings so that the micro spray gun system could be normally operated.
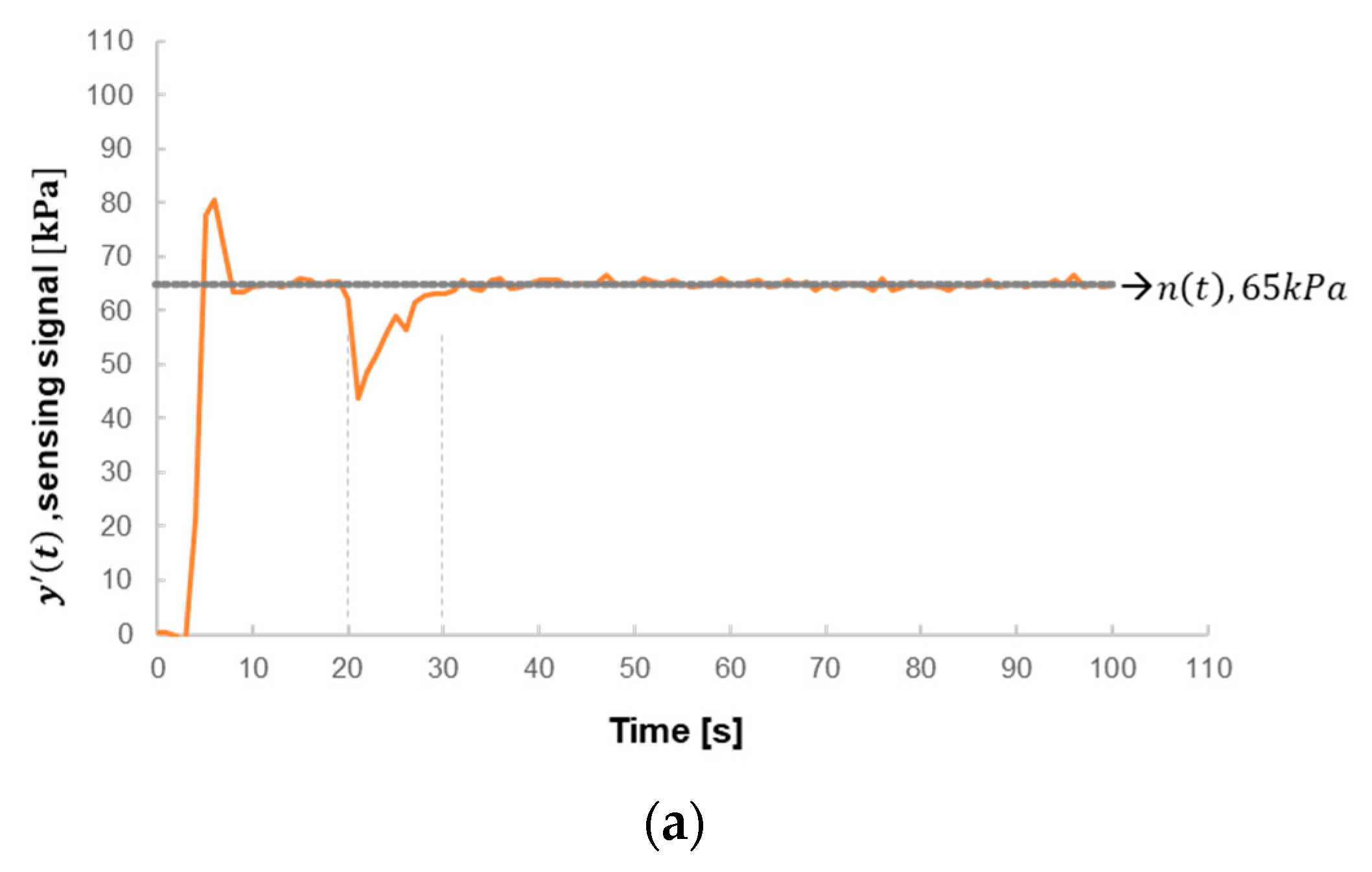
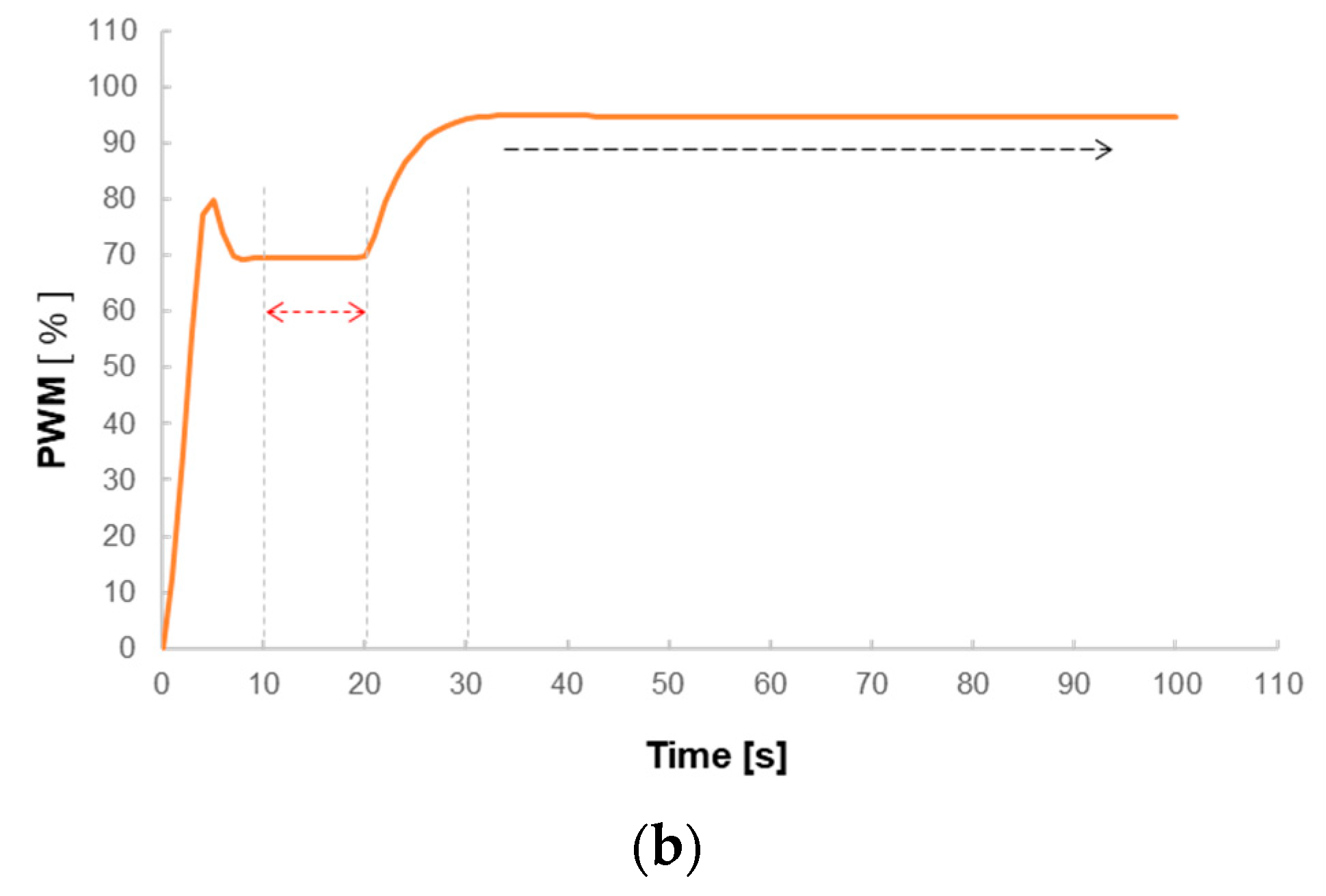
- After pressing the micro spray gun, the pressure of the feedback signal immediately drops to have the PID system make larger output modulation. It reveals the same operation idea of pulse-like variable target value; but the pressure disturbance in the pipe, after pressing the spray gun, cannot be predicted. Figure 10a shows that y′(t), after returning the target value, still appears slight fluctuation. However, the PID output control could have the PWM stably increase, without overshoot of the system, Figure 10b. It is therefore considered that Kp being set to 0.05 could effectively catch up with the target within a short period, and selecting proper Ki could accelerate the system approaching the target and eliminate the steady state error on Kp.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sudduth, K.A.; Borgelt, S.C.; Hou, J. Performance of a chemical injection sprayer system. Appl. Eng. Agric. 1995, 11, 343–348. [Google Scholar] [CrossRef] [Green Version]
- Erkan, U.; Huseyin, G.; First, K. A review of electrostatic spraying for agricultural applications. J. Agric. Mach. Sci. 2016, 12, 229–233. [Google Scholar]
- Liu, Z.B. High-Precision Spray Gun Spraying Control System Based on Linear Regulation. China Patent CN113019732A, 2021. [Google Scholar]
- Giles, D.K.; Bensalem, E. Spray droplet velocity and energy in intermittent flow from hydraulic nozzles. J. Agric. Eng. Res. 1992, 51, 101–112. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, C.; Chen, L.; Wang, X. Comparison of spray characteristics for three types of variable spray. J. Agric. Eng. Res. 2016, XLVII 512, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Grella, M.; Gioelli, F.; Marucco, P.; Zwertvaegher, I.; Mozzanini, E.; Mylonas, N.; Nuyttens, D.; Balsari, P. Field assessment of a pulse width modulation (PWM) spray system applying different spray volumes: Duty cycle and forward speed effects on vines spray coverage. Precis. Agric. 2022, 23, 219–252. [Google Scholar] [CrossRef]
- Orti, E.; Cuenca, A.; Perez, M.; Torregrosa, A.; Ortiz, C.; Rovira-Mas, F. Preliminary evaluation of a blast sprayer controlled by pulse-width-modulated nozzles. Sensors 2022, 22, 4924. [Google Scholar] [CrossRef] [PubMed]
- Maski, D.; Durairaj, D. Effects of electrode voltage, liquid flow rate, and liquid properties on spray chargeability of an air-assisted electrostatic-induction spray-charging system. J. Electrost. 2010, 68, 152–158. [Google Scholar] [CrossRef]
- Chen, S.; Yin, D.; Wei, X.; Pei, W. Design and simulation of variable weed spraying controller based on adaptive neural fuzzy inference system. J. Drain. Irrig. Mach. Eng. 2011, 29, 272–276. [Google Scholar]
- Patel, M.K.; Ghanshyam, C.; Kapur, P. Characterization of electrode material for electrostatic spray charging: Theoretical and engineering practices. J. Electrost. 2013, 71, 55–60. [Google Scholar] [CrossRef]
- Sasaki, R.S.; Teixeira, M.M.; Fernandes, H.C.; Paulo, M.; Denílson, E.R.; Cleyton, B. Parameters of electrostatic spraying and its influence on the application efficiency. Rev. Ceres 2013, 60, 474–479. [Google Scholar] [CrossRef]
- Shilkrot, R.; Maes, P.; Paradiso, J.A.; Zoran, A. Augmented airbrush for computer aided painting. ACM Trans. Graph. 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Mohamed, A.A.S. An Investigation into the History of the Airbrush and the Impact of the Conservation Treatment of Airbrushed Canvas Paintings. Ph.D. Thesis, Northumbria University, Newcastle upon Tyne, UK, 2016. [Google Scholar]
- Chen, Y.C. Study on the Airbrush Makeup Applied to the Whole Fashion Design Combining with the Concept of Multi-Media. Master’s Thesis, Department of Cosmetics Science, Vanung University, Taoyuan, Taiwan, 2022. [Google Scholar]
- Lin, J.H.; Tang, S.T.; Chen, C.H.; Cheng, Y.T.; Tai, C.C.; Lin, M.H. The Prototype Design and Verification of Intelligent Variable Output Control Apply on Micro-spray Gun Simulation Platform. In Proceedings of the 2022 International Conference on Fuzzy Theory and Its Applications (iFUZZY), Garden Villa, Kaohsiung, Taiwan, 3–5 November 2022. [Google Scholar]
- Yan, H. Diaphragm Air Pump. China Patent CN201714643U, 2011. [Google Scholar]
- Jalnekar, R.M.; Jog, K.S. Pulse-width-modulation techniques: A review. IETE J. Res. 2020, 46, 175–183. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. Patents, software and hardware for PID control—An overview and analysis of the current art. IEEE Control Syst. Mag. 2006, 26, 42–54. [Google Scholar]
- Lopez-Gomez, J.; Vargas-Trevino, M.A.D.; Vergara-Limon, S.; Vargas-Trevino, M.; Gutierrez-Gutierrez, J.; Palomino-Merino, A.D.; Martinez-Solis, F.; Felix-Beltran, O. Influence of PWM torque control frequency in DC motors by means of an optimum design method. IEEE Access 2020, 8, 80691–80706. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, L.X. Research on motor control and simulation based on PID and internet of things system. Microprocess. Microsyst. 2021, 80, 103602. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.-H.; Chen, C.-H.; Tang, S.-T. Design and Verification of Adaptive Adjustable Output Control on Micro Spray Gun. Machines 2023, 11, 354. https://doi.org/10.3390/machines11030354
Lin J-H, Chen C-H, Tang S-T. Design and Verification of Adaptive Adjustable Output Control on Micro Spray Gun. Machines. 2023; 11(3):354. https://doi.org/10.3390/machines11030354
Chicago/Turabian StyleLin, Jiun-Hung, Chih-Hong Chen, and Shih-Tsang Tang. 2023. "Design and Verification of Adaptive Adjustable Output Control on Micro Spray Gun" Machines 11, no. 3: 354. https://doi.org/10.3390/machines11030354
APA StyleLin, J.-H., Chen, C.-H., & Tang, S.-T. (2023). Design and Verification of Adaptive Adjustable Output Control on Micro Spray Gun. Machines, 11(3), 354. https://doi.org/10.3390/machines11030354





