A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts
Abstract
:1. Introduction
2. Dynamic Characteristics of Thin−Walled Machining System
2.1. Dynamics Identification of In−Process Workpiece
2.1.1. Experimental Modal Analysis
2.1.2. Analytical/Semi−Analytical Methods
2.1.3. Finite Element Modal Analysis (FEMA)
2.2. Dynamics Identification of the Slender Cutting Tool
2.2.1. Modal Impact Testing
2.2.2. Theoretical Simulation Methods
2.2.3. Data−Driven Prediction Methods
3. Chatter Stability Modeling and Analysis
3.1. Dynamic Models under Different Stiffness Conditions
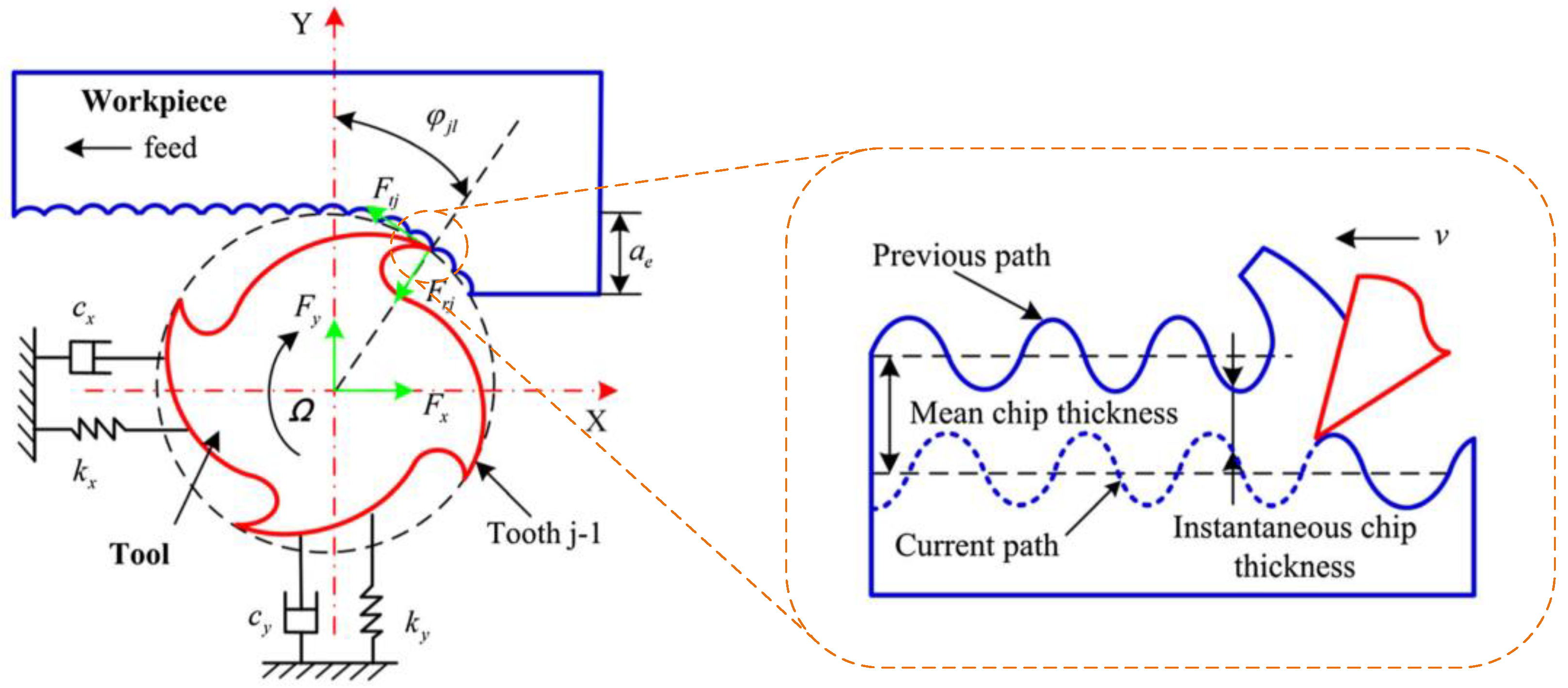
3.2. Research on Dynamic Cutting Force Modeling
3.2.1. Calibration of CFCs
| Calibration Methods | Average Force Method | Instantaneous Force Method | Optimization Method |
|---|---|---|---|
| Merits |
|
|
|
| Limitations |
|
|
|
| Identification image |  |  |  |
| Principle | linear regression | fitting | optimization |
| Formula |
3.2.2. The Extraction of Cutter–Workpiece Engagement
3.3. Tool Wear and Process Damping
3.4. Stability Prediction Algorithm
3.4.1. Frequency Domain Method
3.4.2. Time Domain Method
3.4.3. Discrete Time Domain Method
4. Chatter Avoidance/Suppression Methods and Devices
4.1. Machining Parameters Optimization
4.2. Variable−Pitch Cutting Tools
4.3. Spindle Speed Variation
4.4. Damping/Stiffness Enhancement
4.5. Active Chatter Control

5. Discussion and Future Prospects
5.1. Identification of System Dynamic Characteristics
5.2. Modeling and Prediction of Chatter Stability
5.3. Chatter Avoidance/Suppression Methods and Devices
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herranz, S.; Campa, F.J.; De Lacalle, L.N.L.; Rivero, A.; Lamikiz, A.; Ukar, E.; Sánchez, J.A.; Bravo, U. The Milling of Airframe Components with Low Rigidity: A General Approach to Avoid Static and Dynamic Problems. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 789–801. [Google Scholar] [CrossRef]
- Izamshah, R.A.R.; Mo, J.P.T.; Ding, S. Finite Element Analysis of Machining Thin-Wall Parts. Key Eng. Mater. 2011, 458, 283–288. [Google Scholar] [CrossRef]
- Taylor, F.W. On the Art of Cutting Metals; American Society of Mechanical Engineers: New York, NY, USA, 1906; Volume 23. [Google Scholar]
- Quintana, G.; Ciurana, J. Chatter in Machining Processes: A Review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter Suppression Techniques in Metal Cutting. CIRP Ann. Manuf. Technol. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Y.; Guo, D. Chatter Prediction Utilizing Stability Lobes with Process Damping in Finish Milling of Titanium Alloy Thin-Walled Workpiece. Int. J. Adv. Manuf. Technol. 2017, 89, 2663–2674. [Google Scholar] [CrossRef]
- Altintas, Y.; Weck, M. Chatter Stability of Metal Cutting and Grinding. CIRP Ann. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Altintas, Y.; Stépán, G.; Budak, E.; Schmitz, T.; Kilic, Z.M. Chatter Stability of Machining Operations. ASME J. Manuf. Sci. Eng. 2020, 142, 110801. [Google Scholar] [CrossRef]
- Siddhpura, M.; Paurobally, R. A Review of Chatter Vibration Research in Turning. Int. J. Mach. Tools Manuf. 2012, 61, 27–47. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, C. Recent Progress of Chatter Prediction, Detection and Suppression in Milling. Mech. Syst. Signal Process. 2020, 143, 106840. [Google Scholar] [CrossRef]
- Ismail, F.; Ziaei, R. Chatter Suppression in Five-Axis Machining of Flexible Parts. Int. J. Mach. Tools Manuf. 2002, 42, 115–122. [Google Scholar] [CrossRef]
- Bravo, U.; Altuzarra, O.; López De Lacalle, L.N.; Sánchez, J.A.; Campa, F.J. Stability Limits of Milling Considering the Flexibility of the Workpiece and the Machine. Int. J. Mach. Tools Manuf. 2005, 45, 1669–1680. [Google Scholar] [CrossRef]
- Nikolaev, S.; Kiselev, I.; Kuts, V.; Voronov, S. Optimal Milling Modes Identification of a Jet-Engine Blade Using Time-Domain Technique. Int. J. Adv. Manuf. Technol. 2020, 107, 1983–1992. [Google Scholar] [CrossRef]
- Meshreki, M.; Kövecses, J.; Attia, H.; Tounsi, N. Dynamics Modeling and Analysis of Thin-Walled Aerospace Structures for Fixture Design in Multiaxis Milling. J. Manuf. Sci. Eng. 2008, 130, 310111–3101112. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Honeycutt, A. Analytical Solutions for Fixed-Free Beam Dynamics in Thin Rib Machining. J. Manuf. Process. 2017, 30, 41–50. [Google Scholar] [CrossRef]
- Song, Q.; Shi, J.; Liu, Z.; Wan, Y. A Time-Space Discretization Method in Milling Stability Prediction of Thin-Walled Component. Int. J. Adv. Manuf. Technol. 2017, 89, 2675–2689. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Yan, S.; Ding, M.; Zhang, X.; Zhang, J.; Lan, J. Theoretical Prediction and Experimental Validation of Dynamic Deformation during Machining of Thin-Walled Structure. ASME Int. Mech. Eng. Congr. Expo. Proc. 2017, 2, V002T02A004. [Google Scholar] [CrossRef]
- Shi, J.; Song, Q.; Liu, Z.; Wan, Y. Formulating a Numerically Low-Cost Method of a Constrained Layer Damper for Vibration Suppression in Thin-Walled Component Milling and Experimental Validation. Int. J. Mech. Sci. 2017, 128–129, 294–311. [Google Scholar] [CrossRef]
- Shi, J.; Song, Q.; Liu, Z.; Ai, X. A Novel Stability Prediction Approach for Thin-Walled Component Milling Considering Material Removing Process. Chin. J. Aeronaut. 2017, 30, 1789–1798. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, B.; Luo, M.; Zhang, D. Modeling and Cutting Path Optimization of Shallow Shell Considering Its Varying Dynamics During Machining. Procedia CIRP 2015, 31, 521–526. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, K. Finite Strip Modeling of the Varying Dynamics of Thin-Walled Pocket Structures during Machining. Int. J. Adv. Manuf. Technol. 2017, 89, 2691–2699. [Google Scholar] [CrossRef]
- Baker, J.R.; Rouch, K.E. Use of Finite Element Structural Models in Analyzing Machine Tool Chatter. Finite Elem. Anal. Des. 2002, 38, 1029–1046. [Google Scholar] [CrossRef]
- Elbestawi, M.A.; Sagherian, R. Dynamic modeling for the prediction of surface errors in the milling of thin-walled sections. J. Mater. Process. Technol. 1991, 25, 215–228. [Google Scholar] [CrossRef]
- Altintas, Y.; Montgomery, D.; Budak, E. Dynamic Peripheral Milling of Flexible Structures. J. Eng. Ind. 1992, 114, 137–145. [Google Scholar] [CrossRef]
- Seguy, S.; Dessein, G.; Arnaud, L. Surface Roughness Variation of Thin Wall Milling, Related to Modal Interactions. Int. J. Mach. Tools Manuf. 2008, 48, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Mañé, I.; Gagnol, V.; Bouzgarrou, B.C.; Ray, P. Stability-Based Spindle Speed Control during Flexible Workpiece High-Speed Milling. Int. J. Mach. Tools Manuf. 2008, 48, 184–194. [Google Scholar] [CrossRef]
- Thevenot, V.; Arnaud, L.; Dessein, G.; Cazenave-Larroche, G. Integration of Dynamic Behaviour Variations in the Stability Lobes Method: 3D Lobes Construction and Application to Thin-Walled Structure Milling. Int. J. Adv. Manuf. Technol. 2006, 27, 638–644. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.J.; Xiong, C.H.; Ding, Y.; Zhang, X.M. Stability Analysis in Milling of Thin-Walled Workpieces with Emphasis on the Structural Effect. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 589–608. [Google Scholar] [CrossRef]
- Jin, X.; Sun, Y.; Guo, Q.; Guo, D. 3D Stability Lobe Considering the Helix Angle Effect in Thin-Wall Milling. Int. J. Adv. Manuf. Technol. 2016, 82, 2123–2136. [Google Scholar] [CrossRef]
- Campa, F.J.; Lopez de Lacalle, L.N.; Celaya, A. Chatter Avoidance in the Milling of Thin Floors with Bull-Nose End Mills: Model and Stability Diagrams. Int. J. Mach. Tools Manuf. 2011, 51, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Thevenot, V.; Arnaud, L.; Dessein, G.; Cazenave-Larroche, G. Influence of Material Removal on the Dynamic Behavior of Thin-Walled Structures in Peripheral Milling. Mach. Sci. Technol. 2006, 10, 275–287. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L. Investigation on Chatter Stability of Thin-Walled Parts Considering Its Flexibility Based on Finite Element Analysis. Int. J. Adv. Manuf. Technol. 2018, 94, 3173–3187. [Google Scholar] [CrossRef]
- Budak, E.; Tunç, L.T.; Alan, S.; Özgüven, H.N. Prediction of Workpiece Dynamics and Its Effects on Chatter Stability in Milling. CIRP Ann. Manuf. Technol. 2012, 61, 339–342. [Google Scholar] [CrossRef]
- Yue, C.; Gao, H.; Liu, X.; Wang, L.; Liang, S.Y. Analytical Prediction of Part Dynamics and Process Damping for Machining Stability Analysis. In 51st Cirp Conference on Manufacturing Systems; Wang, L., Ed.; Procedia CIRP: Stockholm, Sweden, 16–18 May 2018; Volume 72, pp. 1463–1468.
- Song, Q.; Liu, Z.; Wan, Y.; Ju, G.; Shi, J. Application of Sherman-Morrison-Woodbury Formulas in Instantaneous Dynamic of Peripheral Milling for Thin-Walled Component. Int. J. Mech. Sci. 2015, 96–97, 79–90. [Google Scholar] [CrossRef]
- Wang, X.; Song, Q.; Liu, Z. Position-Dependent Stability Prediction for Multi-Axis Milling of the Thin-Walled Component with a Curved Surface. Appl. Sci. 2020, 10, 8779. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.H.; Ma, Y.C.; Wan, M. Chatter Prediction for the Peripheral Milling of Thin-Walled Workpieces with Curved Surfaces. Int. J. Mach. Tools Manuf. 2016, 109, 36–48. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Frequency Domain Updating of Thin-Walled Workpiece Dynamics Using Reduced Order Substructuring Method in Machining. J. Manuf. Sci. Eng. 2017, 139, 071013. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Time-Domain Modeling of Varying Dynamic Characteristics in Thin-Wall Machining Using Perturbation and Reduced-Order Substructuring Methods. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 011015. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.H.; Ma, Y.C.; Wan, M.; Dang, X. Bin. An Efficient Decomposition-Condensation Method for Chatter Prediction in Milling Large-Scale Thin-Walled Structures. Mech. Syst. Signal Process. 2019, 121, 58–76. [Google Scholar] [CrossRef]
- Tian, W.; Ren, J.; Zhou, J.; Wang, D. Dynamic Modal Prediction and Experimental Study of Thin-Walled Workpiece Removal Based on Perturbation Method. Int. J. Adv. Manuf. Technol. 2018, 94, 2099–2113. [Google Scholar] [CrossRef]
- Zhao, L.; Jin, D.; Wang, H.; Liu, C. Modal Parameter Identification of Time-Varying Systems via Wavelet-Based Frequency Response Function. Arch. Appl. Mech. 2020, 90, 2529–2542. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G.; Wang, D. Time-Varying Dynamics Updating Method for Chatter Prediction in Thin-Walled Part Milling Process. Mech. Syst. Signal Process. 2021, 159, 107840. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, J.; Zhang, H.; Zhao, W.; Liu, H. Generalized Equivalent Method for Dynamics of Multipocket Thin-Walled Parts. Int. J. Adv. Manuf. Technol. 2022, 120, 2731–2745. [Google Scholar] [CrossRef]
- Dang, X.B.; Wan, M.; Yang, Y.; Zhang, W.H. Efficient Prediction of Varying Dynamic Characteristics in Thin-Wall Milling Using Freedom and Mode Reduction Methods. Int. J. Mech. Sci. 2019, 150, 202–216. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Chen, X.; Cao, H. Time-Varying Chatter Frequency Characteristics in Thin-Walled Workpiece Milling with B-Spline Wavelet on Interval Finite Element Method. J. Manuf. Sci. Eng. 2019, 141, 51008. [Google Scholar] [CrossRef]
- Wang, D.; Ren, J.; Tian, W.; Shi, K.; Zhang, B. Predicting the Dynamics of Thin-Walled Parts with Curved Surfaces in Milling Based on FEM and Taylor Series. Int. J. Adv. Manuf. Technol. 2019, 103, 927–942. [Google Scholar] [CrossRef]
- Kiss, A.K.; Hajdu, D.; Bachrathy, D.; Stepan, G. Operational Stability Prediction in Milling Based on Impact Tests. Mech. Syst. Signal Process. 2018, 103, 327–339. [Google Scholar] [CrossRef] [Green Version]
- Gradišek, J.; Kalveram, M.; Insperger, T.; Weinert, K.; Stépán, G.; Govekar, E.; Grabec, I. On Stability Prediction for Milling. Int. J. Mach. Tools Manuf. 2005, 45, 769–781. [Google Scholar] [CrossRef]
- Zhang, X.J.; Xiong, C.H.; Ding, Y.; Feng, M.J.; Xiong, Y.L. Milling Stability Analysis with Simultaneously Considering the Structural Mode Coupling Effect and Regenerative Effect. Int. J. Mach. Tools Manuf. 2012, 53, 127–140. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. A Comprehensive Dynamic End Milling Simulation Model. J. Manuf. Sci. Eng. 2006, 128, 86–95. [Google Scholar] [CrossRef]
- Eksioglu, C.; Kilic, Z.M.; Altintas, Y. Discrete-Time Prediction of Chatter Stability, Cutting Forces, and Surface Location Errors in Flexible Milling Systems. J. Manuf. Sci. Eng. ASME 2012, 134, 061006. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y. Stability Analysis for a Milling System Considering Multi-Point-Contact Cross-Axis Mode Coupling and Cutter Run-out Effects. Mech. Syst. Signal Process. 2020, 141, 106452. [Google Scholar] [CrossRef]
- Faassen, R.P.H.; Van de Wouw, N.; Oosterling, J.A.J.; Nijmeijer, H. Prediction of Regenerative Chatter by Modelling and Analysis of High-Speed Milling. Int. J. Mach. Tools Manuf. 2003, 43, 1437–1446. [Google Scholar] [CrossRef]
- Rantatalo, M.; Aidanpää, J.O.; Göransson, B.; Norman, P. Milling Machine Spindle Analysis Using FEM and Non-Contact Spindle Excitation and Response Measurement. Int. J. Mach. Tools Manuf. 2007, 47, 1034–1045. [Google Scholar] [CrossRef]
- Tatar, K.; Gren, P. Measurement of Milling Tool Vibrations during Cutting Using Laser Vibrometry. Int. J. Mach. Tools Manuf. 2008, 48, 380–387. [Google Scholar] [CrossRef]
- Tatar, K.; Rantatalo, M.; Gren, P. Laser Vibrometry Measurements of an Optically Smooth Rotating Spindle. Mech. Syst. Signal Process. 2007, 21, 1739–1745. [Google Scholar] [CrossRef]
- Zaghbani, I.; Songmene, V. Estimation of Machine-Tool Dynamic Parameters during Machining Operation through Operational Modal Analysis. Int. J. Mach. Tools Manuf. 2009, 49, 947–957. [Google Scholar] [CrossRef]
- Gagnol, V.; Le, T.P.; Ray, P. Modal Identification of Spindle-Tool Unit in High-Speed Machining. Mech. Syst. Signal Process. 2011, 25, 2388–2398. [Google Scholar] [CrossRef]
- Li, B.; Cai, H.; Mao, X.; Huang, J.; Luo, B. Estimation of CNC Machine-Tool Dynamic Parameters Based on Random Cutting Excitation through Operational Modal Analysis. Int. J. Mach. Tools Manuf. 2013, 71, 26–40. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Davies, M.A.; Kennedy, M.D. Tool Point Frequency Response Prediction for High-Speed Machining by Rcsa. J. Manuf. Sci. Eng. Trans. ASME 2001, 123, 700–707. [Google Scholar] [CrossRef]
- Schmitz, T.; Betters, E.; Budak, E.; Yüksel, E.; Park, S.; Altintas, Y. Review and Status of Tool Tip Frequency Response Function Prediction Using Receptance Coupling. Precis. Eng. 2022, 79, 60–77. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Powell, K.; Won, D.; Scott Duncan, G.; Gregory Sawyer, W.; Ziegert, J.C. Shrink Fit Tool Holder Connection Stiffness/damping Modeling for Frequency Response Prediction in Milling. Int. J. Mach. Tools Manuf. 2007, 47, 1368–1380. [Google Scholar] [CrossRef]
- Ealo, J.A.; Garitaonandia, I.; Fernandes, M.H.; Hernandez-Vazquez, J.M.; Muñoa, J. A Practical Study of Joints in Three-Dimensional Inverse Receptance Coupling Substructure Analysis Method in a Horizontal Milling Machine. Int. J. Mach. Tools Manuf. 2018, 128, 41–51. [Google Scholar] [CrossRef]
- Yang, Y.; Wan, M.; Ma, Y.C.; Zhang, W.H. An Improved Method for Tool Point Dynamics Analysis Using a Bi-Distributed Joint Interface Model. Int. J. Mech. Sci. 2016, 105, 239–252. [Google Scholar] [CrossRef]
- Du, C.; Lu, D.; Zhang, J.; Zhang, H.; Zhao, W. Pose-dependent dynamic modeling and analysis of BI-rotary milling head. In Proceedings of the Asme 11th International Manufacturing Science and Engineering Conference, Blacksburg, VA, USA, 27 June–1 July 2016; Volume 2. [Google Scholar]
- Zhang, J.; Li, J.; Xie, Z.; Du, C.; Gui, L.; Zhao, W. Rapid Dynamics Prediction of Tool Point for Bi-Rotary Head Five-Axis Machine Tool. Precis. Eng. 2017, 48, 203–215. [Google Scholar] [CrossRef]
- Ertürk, A.; Özgüven, H.N.; Budak, E. Analytical Modeling of Spindle-Tool Dynamics on Machine Tools Using Timoshenko Beam Model and Receptance Coupling for the Prediction of Tool Point FRF. Int. J. Mach. Tools Manuf. 2006, 46, 1901–1912. [Google Scholar] [CrossRef]
- Ertürk, A.; Özgüven, H.N.; Budak, E. Effect Analysis of Bearing and Interface Dynamics on Tool Point FRF for Chatter Stability in Machine Tools by Using a New Analytical Model for Spindle-Tool Assemblies. Int. J. Mach. Tools Manuf. 2007, 47, 23–32. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Li, B.; He, Z. Chatter Stability of Milling with Speed-Varying Dynamics of Spindles. Int. J. Mach. Tools Manuf. 2012, 52, 50–58. [Google Scholar] [CrossRef]
- Yang, Y.; Wan, M.; Ma, Y.C.; Zhang, W.H. A New Method Using Double Distributed Joint Interface Model for Three-Dimensional Dynamics Prediction of Spindle-Holder-Tool System. Int. J. Adv. Manuf. Technol. 2018, 95, 2729–2745. [Google Scholar] [CrossRef]
- Xi, S.; Cao, H.; Chen, X. Dynamic Modeling of Spindle Bearing System and Vibration Response Investigation. Mech. Syst. Signal Process. 2019, 114, 486–511. [Google Scholar] [CrossRef]
- Brecher, C.; Altstädter, H.; Daniels, M. Axis Position Dependent Dynamics of Multi-Axis Milling Machines. Procedia CIRP 2015, 31, 508–514. [Google Scholar] [CrossRef] [Green Version]
- Deng, C.; Liu, Y.; Zhao, J.; Wei, B.; Yin, G. Analysis of the Machine Tool Dynamic Characteristics in Manufacturing Space Based on the Generalized Dynamic Response Model. Int. J. Adv. Manuf. Technol. 2017, 92, 1411–1424. [Google Scholar] [CrossRef]
- Deng, C.; Miao, J.; Wei, B.; Feng, Y.; Zhao, Y. Evaluation of Machine Tools with Position-Dependent Milling Stability Based on Kriging Model. Int. J. Mach. Tools Manuf. 2018, 124, 33–42. [Google Scholar] [CrossRef]
- Chen, G.; Li, Y.; Liu, X. Pose-Dependent Tool Tip Dynamics Prediction Using Transfer Learning. Int. J. Mach. Tools Manuf. 2019, 137, 30–41. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Chen, G. Multimode Tool Tip Dynamics Prediction Based on Transfer Learning. Robot. Comput. Integr. Manuf. 2019, 57, 146–154. [Google Scholar] [CrossRef]
- Nguyen, V.; Cvitanic, T.; Melkote, S. Data-Driven Modeling of the Modal Properties of a Six-Degrees-of-Freedom Industrial Robot and Its Application to Robotic Milling. J. Manuf. Sci. Eng. Trans. ASME 2019, 141, 121006. [Google Scholar] [CrossRef]
- Nguyen, V.; Johnson, J.; Melkote, S. Active Vibration Suppression in Robotic Milling Using Optimal Control. Int. J. Mach. Tools Manuf. 2020, 152, 103541. [Google Scholar] [CrossRef]
- Wang, R.; Li, F.; Niu, J.; Sun, Y. Prediction of Pose-Dependent Modal Properties and Stability Limits in Robotic Ball-End Milling. Robot. Comput. Integr. Manuf. 2022, 75, 102370. [Google Scholar] [CrossRef]
- Mahnama, M.; Movahhedy, M.R. Prediction of Machining Chatter Based on FEM Simulation of Chip Formation under Dynamic Conditions. Int. J. Mach. Tools Manuf. 2010, 50, 611–620. [Google Scholar] [CrossRef]
- Wan, M.; Ma, Y.-C.; Zhang, W.-H.; Yang, Y. Study on the Construction Mechanism of Stability Lobes in Milling Process with Multiple Modes. Int. J. Adv. Manuf. Technol. 2015, 79, 589–603. [Google Scholar] [CrossRef]
- Tang, X.; Peng, F.; Yan, R.; Gong, Y.; Li, X. An Effective Time Domain Model for Milling Stability Prediction Simultaneously Considering Multiple Modes and Cross-Frequency Response Function Effect. Int. J. Adv. Manuf. Technol. 2016, 86, 1037–1054. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, C. Chatter Stability Prediction of Ball-End Milling Considering Multi-Mode Regenerations. Int. J. Adv. Manuf. Technol. 2019, 100, 131–142. [Google Scholar] [CrossRef]
- Ahmadi, K.; Ahmadian, H. Modelling Machine Tool Dynamics Using a Distributed Parameter Tool-Holder Joint Interface. Int. J. Mach. Tools Manuf. 2007, 47, 1916–1928. [Google Scholar] [CrossRef]
- Badiola, X.; Iturrospe, A.; Abete, J.M.; Arrazola, P.J. State-Space Analysis of Mode-Coupling Workpiece Chatter. Int. J. Adv. Manuf. Technol. 2019, 103, 2773–2781. [Google Scholar] [CrossRef]
- Kolluru, K.; Axinte, D.; Becker, A. A Solution for Minimising Vibrations in Milling of Thin Walled Casings by Applying Dampers to Workpiece Surface. CIRP Ann. 2013, 62, 415–418. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Song, Q.; Liu, Z. Dynamic Model and Stability Prediction of Thin-Walled Component Milling with Multi-Modes Coupling Effect. J. Mater. Process. Technol. 2021, 288, 116869. [Google Scholar] [CrossRef]
- Zhu, L.; Ding, Y.; Liu, C.; Xu, Z. Investigation on Chatter Stability of Thin-Walled Parts in High-Speed Milling Based on Relative Transfer Functions. J. Vibroeng. 2016, 18, 3459–3472. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Zhu, L.; Dun, Y.; Liu, C. Investigation on Chatter Stability of Thin-Walled Parts in Milling Based on Process Damping with Relative Transfer Functions. Int. J. Adv. Manuf. Technol. 2017, 89, 2701–2711. [Google Scholar] [CrossRef]
- Jia, Z.; Lu, X.; Yang, K.; Sun, X.; Liang, S.Y. Stability of Micro-Milling Thin-Walled Part Process. Int. J. Adv. Manuf. Technol. 2021, 112, 1529–1544. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Yan, S.; Zhang, X.; Lan, J.; Dai, S. Chatter Prediction for Milling of Flexible Pocket-Structure. Int. J. Adv. Manuf. Technol. 2017, 89, 2721–2730. [Google Scholar] [CrossRef]
- Siddhpura, M.; Siddhpura, A.; Paurobally, R. Chatter Stability Prediction for a Flexible Tool-Workpiece System in a Turning Process. Int. J. Adv. Manuf. Technol. 2017, 92, 881–896. [Google Scholar] [CrossRef]
- Gerasimenko, A.; Guskov, M.; Gouskov, A.; Lorong, P.; Shokhin, A. Analytical Modeling of a Thin-Walled Cylindrical Workpiece during the Turning Process. Stability Analysis of a Cutting Process. J. Vibroeng. 2017, 19, 5825–5841. [Google Scholar] [CrossRef] [Green Version]
- Lu, K.; Wang, Y.; Gu, F.; Pang, X.; Ball, A. Dynamic Modeling and Chatter Analysis of a Spindle-Workpiece-Tailstock System for the Turning of Flexible Parts. Int. J. Adv. Manuf. Technol. 2019, 104, 3007–3015. [Google Scholar] [CrossRef]
- Sun, Y.; Yan, S. Dynamics Identification and Stability Analysis in Turning of Slender Workpieces with Flexible Boundary Constraints. Mech. Syst. Signal Process. 2022, 177, 109245. [Google Scholar] [CrossRef]
- Yan, S.; Kong, J.; Sun, Y. Continuum Model Based Chatter Stability Prediction for Highly Flexible Parts in Turning Process with Accurate Dynamic Force Modeling. J. Manuf. Process. 2021, 62, 221–233. [Google Scholar] [CrossRef]
- Tang, A.; Liu, Z. Three-Dimensional Stability Lobe and Maximum Material Removal Rate in End Milling of Thin-Walled Plate. Int. J. Adv. Manuf. Technol. 2009, 43, 33–39. [Google Scholar] [CrossRef]
- Song, Q.; Liu, Z.; Ai, X. Influence of Chatter on Machining Distortion for Thin-Walled Component Peripheral Milling. Adv. Mech. Eng. 2014, 6, 1–7. [Google Scholar] [CrossRef]
- Otto, A.; Khasawneh, F.A.; Radons, G. Position-Dependent Stability Analysis of Turning with Tool and Workpiece Compliance. Int. J. Adv. Manuf. Technol. 2015, 79, 1453–1463. [Google Scholar] [CrossRef]
- Akhtar, M.M.; Huang, X.; Wenliang, C.; Lin, Z. Multi-Level Dynamics in Deep Milling of Flexible Workpiece; Advanced Materials Research, Trans Tech Publications, Ltd.: Bäch, Switzerland, 2012; Volume 482–484, pp. 2234–2237. [Google Scholar]
- Khoshdarregi, M.R.; Altintas, Y. Dynamics of Multipoint Thread Turning-Part I: General Formulation. J. Manuf. Sci. Eng. ASME 2018, 140, 061003. [Google Scholar] [CrossRef]
- Khoshdarregi, M.R.; Altintas, Y. Dynamics of Multipoint Thread Turning-Part II: Application to Thin-Walled Oil Pipes. J. Manuf. Sci. Eng. ASME 2018, 140, 041016. [Google Scholar] [CrossRef]
- Jiang, S.; Zhan, D.; Liu, Y.; Sun, Y.; Xu, J. Modeling of Variable-Pitch/helix Milling System Considering Axially Varying Dynamics with Cutter Runout Offset and Tilt Effects. Mech. Syst. Signal Process. 2022, 168, 108674. [Google Scholar] [CrossRef]
- Ozsoy, M.; Sims, N.D.; Ozturk, E. Robotically Assisted Active Vibration Control in Milling: A Feasibility Study. Mech. Syst. Signal Process. 2022, 177, 109152. [Google Scholar] [CrossRef]
- Wang, W.; Lin, B.; Guo, Y.; Li, L. Dynamic Simulation of Mirror Cutting. Int. J. Adv. Manuf. Technol. 2019, 103, 4331–4340. [Google Scholar] [CrossRef]
- Bo, Q.; Liu, H.; Lian, M.; Wang, Y.; Liu, K. The Influence of Supporting Force on Machining Stability during Mirror Milling of Thin-Walled Parts. Int. J. Adv. Manuf. Technol. 2019, 101, 2341–2353. [Google Scholar] [CrossRef]
- Yuwen, S.; Shanglei, J. Cross-Axis and Cross-Point Modal Testing and Parameter Identification Method for Predicting the Cutting Stability. U.S. Patent No. 11,426,833, 30 August 2022. [Google Scholar]
- Jayaram, S.; Kapoor, S.G.; DeVor, R.E. Estimation of the Specific Cutting Pressures for Mechanistic Cutting Force Models. Int. J. Mach. Tools Manuf. 2001, 41, 265–281. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y.; Armarego, E. Prediction of Milling Force Coefficients from Orthogonal Cutting Data. J. Manuf. Sci. Eng. ASME 1996, 118, 216–224. [Google Scholar] [CrossRef]
- Shin, Y.C.; Waters, A.J. A New Procedure to Determine Instantaneous Cutting Force Coefficients for Machining Force Prediction. Int. J. Mach. Tools Manuf. 1997, 37, 1337–1351. [Google Scholar] [CrossRef]
- Gonzalo, O.; Beristain, J.; Jauregi, H.; Sanz, C. A Method for the Identification of the Specific Force Coefficients for Mechanistic Milling Simulation. Int. J. Mach. Tools Manuf. 2010, 50, 765–774. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H.; Qin, G.H.; Tan, G. Efficient Calibration of Instantaneous Cutting Force Coefficients and Runout Parameters for General End Mills. Int. J. Mach. Tools Manuf. 2007, 47, 1767–1776. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H.; Tan, G.; Qin, G.H. New Algorithm for Calibration of Instantaneous Cutting-Force Coefficients and Radial Run-out Parameters in Flat End Milling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 1007–1019. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H.; Tan, G.; Qin, G.H. An in-Depth Analysis of the Synchronization between the Measured and Predicted Cutting Forces for Developing Instantaneous Milling Force Model. Int. J. Mach. Tools Manuf. 2007, 47, 2018–2030. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.-H.; Dang, J.-W.; Yang, Y. A Novel Cutting Force Modelling Method for Cylindrical End Mill. Appl. Math. Model. 2010, 34, 823–836. [Google Scholar] [CrossRef]
- Wan, M.; Lu, M.-S.; Zhang, W.-H.; Yang, Y. A New Ternary-Mechanism Model for the Prediction of Cutting Forces in Flat End Milling. Int. J. Mach. Tools Manuf. 2012, 57, 34–45. [Google Scholar] [CrossRef]
- Zhang, D.; Mo, R.; Chang, Z.; Sun, H.; Li, C. A Study of Computing Accuracy of Calibrating Cutting Force Coefficients and Run-out Parameters in Flat-End Milling. Int. J. Adv. Manuf. Technol. 2016, 84, 621–630. [Google Scholar] [CrossRef]
- Rivière-Lorphèvre, E.; Letot, C.; Ducobu, F.; Dehombreux, P.; Filippi, E. Dynamic Simulation of Milling Operations with Small Diameter Milling Cutters: Effect of Material Heterogeneity on the Cutting Force Model. Meccanica 2017, 52, 35–44. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Zhang, J.; Pang, B.; Zhao, W. General Modeling and Calibration Method for Cutting Force Prediction With Flat-End Cutter. J. Manuf. Sci. Eng. 2018, 140, 21007. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.-H.; Dang, J.-W.; Yang, Y. New Procedures for Calibration of Instantaneous Cutting Force Coefficients and Cutter Runout Parameters in Peripheral Milling. Int. J. Mach. Tools Manuf. 2009, 49, 1144–1151. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, X.; Xie, Y.; Ding, H. Precise Estimation of Cutting Force Coefficients and Cutter Runout in Milling Using Differential Evolution Algorithm. Procedia CIRP 2018, 77, 283–286. [Google Scholar] [CrossRef]
- Grossi, N.; Sallese, L.; Scippa, A.; Campatelli, G. Speed-Varying Cutting Force Coefficient Identification in Milling. Precis. Eng. 2015, 42, 321–334. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Meng, G.; Ren, S.; Zhou, J. A New Procedure for the Prediction of the Cutting Forces in Peripheral Milling. Int. J. Adv. Manuf. Technol. 2017, 89, 1709–1715. [Google Scholar] [CrossRef]
- Yao, Q.; Luo, M.; Zhang, D.; Wu, B. Identification of Cutting Force Coefficients in Machining Process Considering Cutter Vibration. Mech. Syst. Signal Process. 2018, 103, 39–59. [Google Scholar] [CrossRef]
- Rubeo, M.A.; Schmitz, T.L. Mechanistic Force Model Coefficients: A Comparison of Linear Regression and Nonlinear Optimization. Precis. Eng. Int. Soc. Precis. Eng. Nanotechnol. 2016, 45, 311–321. [Google Scholar] [CrossRef]
- Schwenzer, M.; Auerbach, T.; Döbbeler, B.; Bergs, T. Comparative Study on Optimization Algorithms for Online Identification of an Instantaneous Force Model in Milling. Int. J. Adv. Manuf. Technol. 2018, 101, 2249–2257. [Google Scholar] [CrossRef]
- Grossi, N. Accurate and Fast Measurement of Specific Cutting Force Coefficients Changing with Spindle Speed. Int. J. Precis. Eng. Manuf. 2017, 18, 1173–1180. [Google Scholar] [CrossRef]
- Wan, M.; Yin, W.; Zhang, W. Study on the Correction of Cutting Force Measurement with Table Dynamometer. Procedia CIRP 2016, 56, 119–123. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Gao, H.; Yue, C.; Li, R.; Jiang, N.; Yang, L. Investigation of the Milling Stability Based on Modified Variable Cutting Force Coefficients. Int. J. Adv. Manuf. Technol. 2018, 96, 2991–3002. [Google Scholar] [CrossRef]
- Zhan, D.; Li, S.; Jiang, S.; Sun, Y. Optimal Pitch Angles Determination of Ball-End Cutter for Improving Five-Axis Milling Stability. J. Manuf. Process. 2022, 84, 832–846. [Google Scholar] [CrossRef]
- Sun, Y.; Jia, J.; Xu, J.; Chen, M.; Niu, J. Path, Feedrate and Trajectory Planning for Free-Form Surface Machining: A State-of-the-Art Review. Chin. J. Aeronaut. 2022, 35, 12–29. [Google Scholar] [CrossRef]
- Wei, Z.C.; Wang, M.J.; Zhu, J.N.; Gu, L.Y. Cutting Force Prediction in Ball End Milling of Sculptured Surface with Z-Level Contouring Tool Path. Int. J. Mach. Tools Manuf. 2011, 51, 428–432. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, S. Predictive Modeling of Chatter Stability Considering Force-Induced Deformation Effect in Milling Thin-Walled Parts. Int. J. Mach. Tools Manuf. 2018, 135, 38–52. [Google Scholar] [CrossRef]
- Kim, G.M.; Cho, P.J.; Chu, C.N. Cutting Force Prediction of Sculptured Surface Ball-End Milling Using Z-Map. Int. J. Mach. Tools Manuf. 2000, 40, 277–291. [Google Scholar] [CrossRef]
- Zhu, R.; Kapoor, S.G.; DeVor, R.E. Mechanistic Modeling of the Ball End Milling Process for Multi-Axis Machining of Free-Form Surfaces. J. Manuf. Sci. Eng. 2001, 123, 369–379. [Google Scholar] [CrossRef]
- Fussell, B.K.; Jerard, R.B.; Hemmett, J.G. Modeling of Cutting Geometry and Forces for 5-Axis Sculptured Surface Machining. Comput. Des. 2003, 35, 333–346. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Zheng, X.; Pang, B.; Zhao, W. Tool Orientation Optimization of 5-Axis Ball-End Milling Based on an Accurate Cutter/workpiece Engagement Model. CIRP J. Manuf. Sci. Technol. 2017, 19, 106–116. [Google Scholar] [CrossRef]
- Taner, T.L.; Ömer, Ö.; Erhan, B. Generalized Cutting Force Model in Multi-Axis Milling Using a New Engagement Boundary Determination Approach. Int. J. Adv. Manuf. Technol. 2015, 77, 341–355. [Google Scholar] [CrossRef]
- Sun, C.; Altintas, Y. Chatter Free Tool Orientations in 5-Axis Ball-End Milling. Int. J. Mach. Tools Manuf. 2016, 106, 89–97. [Google Scholar] [CrossRef]
- Larue, A.; Altintas, Y. Simulation of Flank Milling Processes. Int. J. Mach. Tools Manuf. 2005, 45, 549–559. [Google Scholar] [CrossRef] [Green Version]
- Ferry, W.B.; Altintas, Y. Virtual Five-Axis Flank Milling of Jet Engine Impellers—Part I: Mechanics of Five-Axis Flank Milling. J. Manuf. Sci. Eng. 2008, 130, 011005. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Wan, M.; Ma, Y. A Solid Trimming Method to Extract Cutter–workpiece Engagement Maps for Multi-Axis Milling. Int. J. Adv. Manuf. Technol. 2013, 68, 2801–2813. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wang, X.-Z.; Zhu, L.-M. Arc–surface Intersection Method to Calculate Cutter–workpiece Engagements for Generic Cutter in Five-Axis Milling. Comput. Des. 2016, 73, 1–10. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. Chatter Prediction in Flank Milling of Thin-Walled Parts Considering Force-Induced Deformation. Mech. Syst. Signal Process. 2022, 165, 108314. [Google Scholar] [CrossRef]
- Totis, G.; Insperger, T.; Sortino, M.; Stépán, G. Symmetry Breaking in Milling Dynamics. Int. J. Mach. Tools Manuf. 2019, 139, 37–59. [Google Scholar] [CrossRef]
- Niu, J.; Jia, J.; Wang, R.; Xu, J.; Sun, Y.; Guo, D. State Dependent Regenerative Stability and Surface Location Error in Peripheral Milling of Thin-Walled Parts. Int. J. Mech. Sci. 2021, 196, 106294. [Google Scholar] [CrossRef]
- Sarıkaya, M.; Gupta, M.K.; Tomaz, I.; Pimenov, D.Y.; Kuntoğlu, M.; Khanna, N.; Yıldırım, Ç.V.; Krolczyk, G.M. A State-of-the-Art Review on Tool Wear and Surface Integrity Characteristics in Machining of Superalloys. CIRP J. Manuf. Sci. Technol. 2021, 35, 624–658. [Google Scholar] [CrossRef]
- Mahmood, J.; Mustafa, G.; Ali, M. Accurate Estimation of Tool Wear Levels during Milling, Drilling and Turning Operations by Designing Novel Hyperparameter Tuned Models Based on LightGBM and Stacking. Measurement 2022, 190, 110722. [Google Scholar] [CrossRef]
- Lins, R.G.; Guerreiro, B.; Marques de Araujo, P.R.; Schmitt, R. In-Process Tool Wear Measurement System Based on Image Analysis for CNC Drilling Machines. IEEE Trans. Instrum. Meas. 2020, 69, 5579–5588. [Google Scholar] [CrossRef]
- Miao, H.; Zhao, Z.; Sun, C.; Li, B.; Yan, R. A U-Net-Based Approach for Tool Wear Area Detection and Identification. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Ånmark, N.; Björk, T.; Ganea, A.; Ölund, P.; Hogmark, S.; Karasev, A.; Jönsson, P.G. The Effect of Inclusion Composition on Tool Wear in Hard Part Turning Using PCBN Cutting Tools. Wear 2015, 334–335, 13–22. [Google Scholar] [CrossRef]
- Fan, Y.H.; Hao, Z.P.; Lin, J.Q. Tribological Characteristics and Wear Mechanism of Cemented Carbide Tool in Dry Machining Ti-6Al-4V. Int. J. Mater. Prod. Technol. 2017, 54, 275–290. [Google Scholar] [CrossRef]
- Ambhore, N.; Kamble, D.; Chinchanikar, S.; Wayal, V. Tool Condition Monitoring System: A Review. Mater. Today Proc. 2015, 2, 3419–3428. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Sağlam, H. Investigation of Progressive Tool Wear for Determining of Optimized Machining Parameters in Turning. Measurement 2019, 140, 427–436. [Google Scholar] [CrossRef]
- Yu, W.; Mechefske, C.; Kim, I.Y. Identifying Optimal Features for Cutting Tool Condition Monitoring Using Recurrent Neural Networks. Adv. Mech. Eng. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Sisson, T.R.; Kegg, R.L. An Explanation of Low-Speed Chatter Effects. J. Eng. Ind. 1969, 91, 951–958. [Google Scholar] [CrossRef]
- Wu, D.W. A New Approach of Formulating the Transfer Function for Dynamic Cutting Processes. J. Eng. Ind. 1989, 111, 37–47. [Google Scholar] [CrossRef]
- Ahmadi, K.; Altintas, Y. Identification of Machining Process Damping Using Output-Only Modal Analysis. J. Manuf. Sci. Eng. 2014, 136, 51017. [Google Scholar] [CrossRef]
- Budak, E.; Tunc, L.T. Identification and Modeling of Process Damping in Turning and Milling Using a New Approach. CIRP Ann. 2010, 59, 403–408. [Google Scholar] [CrossRef]
- Tunc, L.T.; Budak, E. Identification and Modeling of Process Damping in Milling. J. Manuf. Sci. Eng. 2013, 135, 21001. [Google Scholar] [CrossRef]
- Li, X.; Zhao, W.; Li, L.; He, N.; Chi, S. Modeling and Application of Process Damping in Milling of Thin-Walled Workpiece Made of Titanium Alloy. Shock Vib. 2015, 2015, 431476. [Google Scholar] [CrossRef] [Green Version]
- Wan, M.; Feng, J.; Ma, Y.-C.; Zhang, W.-H. Identification of Milling Process Damping Using Operational Modal Analysis. Int. J. Mach. Tools Manuf. 2017, 122, 120–131. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Analytical Modeling of Process Damping in Machining. J. Manuf. Sci. Eng. ASME 2019, 141, 061006. [Google Scholar] [CrossRef]
- Denkena, B.; Grabowski, R.; Krödel, A.; Ellersiek, L. Time-Domain Simulation of Milling Processes Including Process Damping. CIRP J. Manuf. Sci. Technol. 2020, 30, 149–156. [Google Scholar] [CrossRef]
- Li, M.; Zhao, W.; Li, L.; He, N.; Jamil, M. Study the Effect of Anti-Vibration Edge Length on Process Stability of Milling Thin-Walled Ti-6Al-4V Alloy. Int. J. Adv. Manuf. Technol. 2021, 113, 2563–2574. [Google Scholar] [CrossRef]
- Das, M.K.; Tobias, S.A. The Relation between the Static and the Dynamic Cutting of Metals. Int. J. Mach. Tool Des. Res. 1967, 7, 63–89. [Google Scholar] [CrossRef]
- Molnár, T.G.; Insperger, T.; Bachrathy, D.; Stépán, G. Extension of Process Damping to Milling with Low Radial Immersion. Int. J. Adv. Manuf. Technol. 2017, 89, 2545–2556. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Wan, M.; Gao, T.-Q.; Zhang, W.-H. Mechanism of Process Damping in Milling of Thin-Walled Workpiece. Int. J. Mach. Tools Manuf. 2018, 134, 1–19. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Altintas, Y.; Stepan, G.; Merdol, D.; Dombovari, Z. Chatter Stability of Milling in Frequency and Discrete Time Domain. CIRP J. Manuf. Sci. Technol. 2008, 1, 35–44. [Google Scholar] [CrossRef]
- Budak, E.; Altintas¸, Y. Analytical Prediction of Chatter Stability in Milling-Part I: General Formulation. J. Dyn. Syst. Meas. Control 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Multi Frequency Solution of Chatter Stability for Low Immersion Milling. J. Manuf. Sci. Eng. 2004, 126, 459–466. [Google Scholar] [CrossRef]
- Altintas, Y.; Shamoto, E.; Lee, P.; Budak, E. Analytical Prediction of Stability Lobes in Ball End Milling. J. Manuf. Sci. Eng. ASME 1999, 121, 586–592. [Google Scholar] [CrossRef]
- Altmtaş, Y.; Engin, S.; Budak, E. Analytical Stability Prediction and Design of Variable Pitch Cutters. J. Manuf. Sci. Eng. Trans. ASME 1999, 121, 173–178. [Google Scholar] [CrossRef]
- Turner, S.; Merdol, D.; Altintas, Y.; Ridgway, K. Modelling of the Stability of Variable Helix End Mills. Int. J. Mach. Tools Manuf. 2007, 47, 1410–1416. [Google Scholar] [CrossRef]
- Ozlu, E.; Budak, E. Analytical Modeling of Chatter Stability in Turning and Boring Operations-Part I: Model Development. J. Manuf. Sci. Eng. 2007, 129, 726–732. [Google Scholar] [CrossRef]
- Yan, B.; Zhu, L. Research on Milling Stability of Thin-Walled Parts Based on Improved Multi-Frequency Solution. Int. J. Adv. Manuf. Technol. 2019, 102, 431–441. [Google Scholar] [CrossRef]
- Sanz-Calle, M.; Munoa, J.; Iglesias, A.; Lopez de Lacalle, L.; Dombovari, Z. Semi-analytical period-doubling chatter analysis in thin wall milling. MM Sci. J. 2021, 2021, 5126–5133. [Google Scholar] [CrossRef]
- Montgomery, D.; Altintas, Y. Mechanism of Cutting Force and Surface Generation in Dynamic Milling. J. Eng. Ind. 1991, 113, 160–168. [Google Scholar] [CrossRef]
- Qu, S.; Zhao, J.; Wang, T. Three-Dimensional Stability Prediction and Chatter Analysis in Milling of Thin-Walled Plate. Int. J. Adv. Manuf. Technol. 2016, 86, 2291–2300. [Google Scholar] [CrossRef]
- Rubeo, M.A.; Schmitz, T.L. Global Stability Predictions for Flexible Workpiece Milling Using Time Domain Simulation. J. Manuf. Syst. 2016, 40, 8–14. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Semi-Discretization Method for Delayed Systems: Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated Semi-Discretization Method for Periodic Delay-Differential Equations with Discrete Delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Bayly, P.V.; Halley, E.; Mann, B.P.; Davies, M.A. Stability of Interrupted Cutting by Temporal Finite Element Analysis. J. Manuf. Sci. Eng. 2003, 125, 220–225. [Google Scholar] [CrossRef]
- Olgac, N.; Sipahi, R. A Unique Methodology for Chatter Stability Mapping in Simultaneous Machining. J. Manuf. Sci. Eng. 2005, 127, 791–800. [Google Scholar] [CrossRef]
- Butcher, E.A.; Nindujarla, P.; Bueler, E. Stability of Up- and Down-Milling Using Chebyshev Collocation Method. In Proceedings of the ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers Digital Collection, Long Beach, CA, USA, October 2008; pp. 841–850. [Google Scholar]
- Compeán, F.I.; Olvera, D.; Campa, F.J.; López de Lacalle, L.N.; Elías-Zúñiga, A.; Rodríguez, C.A. Characterization and Stability Analysis of a Multivariable Milling Tool by the Enhanced Multistage Homotopy Perturbation Method. Int. J. Mach. Tools Manuf. 2012, 57, 27–33. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A Full-Discretization Method for Prediction of Milling Stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-Order Full-Discretization Method for Milling Stability Prediction. Int. J. Mach. Tools Manuf. 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Numerical Integration Method for Prediction of Milling Stability. J. Manuf. Sci. Eng. 2011, 133, 031005. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Zhu, L.; Ding, H. Runge-Kutta Methods for a Semi-Analytical Prediction of Milling Stability. Nonlinear Dyn. 2014, 76, 289–304. [Google Scholar] [CrossRef]
- Ozoegwu, C.G.; Omenyi, S.N.; Ofochebe, S.M. Hyper-Third Order Full-Discretization Methods in Milling Stability Prediction. Int. J. Mach. Tools Manuf. 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y.; Yuan, X.; Liu, W. A Second-Order Semi-Discretization Method for the Efficient and Accurate Stability Prediction of Milling Process. Int. J. Adv. Manuf. Technol. 2017, 92, 583–595. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y. A Multi-Order Method for Predicting Stability of a Multi-Delay Milling System Considering Helix Angle and Run-out Effects. Chin. J. Aeronaut. 2018, 31, 1375–1387. [Google Scholar] [CrossRef]
- Zhan, D.; Jiang, S.; Li, S.; Sun, Y. A Hybrid Multi-Step Method Based on 1/3 and 3/8 Simpson Formulas for Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2022, 120, 265–277. [Google Scholar] [CrossRef]
- Wu, Y.; You, Y.; Liu, A.; Deng, B.; Liu, W. An Implicit Exponentially Fitted Method for Chatter Stability Prediction of Milling Processes. Int. J. Adv. Manuf. Technol. 2020, 106, 2189–2204. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A predictor-corrector-based holistic-discretization method for accurate and efficient milling stability analysis. Int. J. Adv. Manuf. Technol. 2018, 96, 2043–2054. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A novel stability prediction method for milling operations using the holistic-interpolation scheme. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4463–4475. [Google Scholar] [CrossRef]
- Zhi, H.Y.; Zhang, T.S.; Du, J.; Yan, X. An Efficient Full-Discretization Method for Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2020, 107, 4955–4967. [Google Scholar] [CrossRef]
- Wang, L.; Li, W.; Yu, G. Time Domain Study on the Construction Mechanism of Milling Stability Lobe Diagrams with Multiple Modes. J. Manuf. Sci. Eng. 2021, 144, 021007. [Google Scholar] [CrossRef]
- Xia, Y.; Wan, Y.; Luo, X.; Liu, Z.; Song, Q. An Improved Numerical Integration Method to Predict the Milling Stability Based on the Lagrange Interpolation Scheme. Int. J. Adv. Manuf. Technol. 2021, 116, 2111–2123. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Y.; Gao, X.; Yang, W.; Sun, W.; Dai, F. Improved Semi-Discretization Method Based on Predictor-Corrector Scheme for Milling Stability Analysis. Int. J. Adv. Manuf. Technol. 2021, 114, 3377–3389. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, X.; Ding, H. A Novel Chebyshev-Gauss Pseudospectral Method for Accurate Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2021, 117, 2867–2881. [Google Scholar] [CrossRef]
- Zhang, C. Numerical Integration Scheme–based Semi-Discretization Methods for Stability Prediction in Milling. Int. J. Adv. Manuf. Technol. 2021, 115, 397–411. [Google Scholar] [CrossRef]
- Jin, G.; Li, W.; Han, J.; Li, Z.; Hu, G.; Sun, G. An Updated Method for Stability Analysis of Milling Process with Multiple and Distributed Time Delays and Its Application. Appl. Sci. 2021, 11, 4203. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Jia, J.; Ma, B.; Jiang, X.; Wang, D.; Zhu, T. High-Order Semi-Discretization Methods for Stability Analysis in Milling Based on Precise Integration. Precis. Eng. 2022, 73, 71–92. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, J.-W.; Tie, D.; Wan, M.; Zhang, W.-H. An Efficient and Accurate Chatter Prediction Method of Milling Processes with a Transition Matrix Reduction Scheme. Mech. Syst. Signal Process. 2023, 182, 109535. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W.; Ehmann, K.F. Three-Dimensional Process Stability Prediction of Thin-Walled Workpiece in Milling Operation. Mach. Sci. Technol. 2016, 20, 406–424. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, M.; Wu, B.; Zhang, D. Dynamic Modeling and Stability Prediction in Milling Process of Thin-Walled Workpiece with Multiple Structural Modes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 2205–2218. [Google Scholar] [CrossRef]
- Ma, S.-L.; Huang, T.; Zhang, X.-M.; Wiercigroch, M.; Chen, D.; Ding, H. Effect of State-Dependent Time Delay on Dynamics of Trimming of Thin-Walled Structures. Int. J. Mech. Sci. 2022, 233, 107651. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, H. Note on a Novel Method for Machining Parameters Optimization in a Chatter-Free Milling Process. Int. J. Mach. Tools Manuf. 2013, 72, 11–15. [Google Scholar] [CrossRef]
- Germashev, A.; Logominov, V.; Anpilogov, D.; Vnukov, Y.; Khristal, V. Optimal Cutting Condition Determination for Milling Thin-Walled Details. Adv. Manuf. 2018, 6, 280–290. [Google Scholar] [CrossRef]
- Orak, S.; Arapoğlu, R.A.; Sofuoğlu, M.A. Development of an ANN-Based Decision-Making Method for Determining Optimum Parameters in Turning Operation. Soft Comput. 2018, 22, 6157–6170. [Google Scholar] [CrossRef]
- Sofuoglu, M.A.; Orak, S. A Hybrid Decision Making Approach to Prevent Chatter Vibrations. Appl. Soft Comput. 2015, 37, 180–195. [Google Scholar] [CrossRef]
- Wang, S.; Geng, L.; Zhang, Y.; Liu, K.; Ng, T. Chatter-Free Cutter Postures in Five-Axis Machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 1428–1439. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Wang, H.; Wang, K.; Wang, D. Stability Prediction of Five-Axis Ball-End Finishing Milling by Considering Multiple Interaction Effects between the Tool and Workpiece. Mech. Syst. Signal Process. 2019, 131, 261–287. [Google Scholar] [CrossRef]
- Lu, Y. Dynamics and Stability Prediction of Five-Axis Flat-End Milling. J. Manuf. Sci. Eng. 2017, 139, 061015. [Google Scholar] [CrossRef]
- Tang, X.; Zhu, Z.; Yan, R.; Chen, C.; Peng, F.; Zhang, M.; Li, Y. Stability Prediction Based Effect Analysis of Tool Orientation on Machining Efficiency for Five-Axis Bull-Nose End Milling. J. Manuf. Sci. Eng. 2018, 140, 121015. [Google Scholar] [CrossRef]
- Tang, X.; Peng, F.; Yan, R.; Zhu, Z.; Li, Z.; Xin, S. Nonlinear Process Damping Identification Using Finite Amplitude Stability and the Influence Analysis on Five-Axis Milling Stability. Int. J. Mech. Sci. 2021, 190, 106008. [Google Scholar] [CrossRef]
- Ozturk, E.; Tunc, L.T.; Budak, E. Investigation of Lead and Tilt Angle Effects in 5-Axis Ball-End Milling Processes. Int. J. Mach. Tools Manuf. 2009, 49, 1053–1062. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, E.; Budak, E. Dynamics and Stability of Five-Axis Ball-End Milling. J. Manuf. Sci. Eng. Trans. ASME 2010, 132, 210031–2100313. [Google Scholar] [CrossRef]
- Shamoto, E.; Akazawa, K. Analytical Prediction of Chatter Stability in Ball End Milling with Tool Inclination. CIRP Ann. 2009, 58, 351–354. [Google Scholar] [CrossRef]
- Shamoto, E.; Fujimaki, S.; Sencer, B.; Suzuki, N.; Kato, T.; Hino, R. A Novel Tool Path/posture Optimization Concept to Avoid Chatter Vibration in Machining-Proposed Concept and Its Verification in Turning. CIRP Ann. 2012, 61, 331–334. [Google Scholar] [CrossRef]
- Tunc, L.T.; Budak, E.; Bilgen, S.; Zatarain, M. Process Simulation Integrated Tool Axis Selection for 5-Axis Tool Path Generation. CIRP Ann.-Manuf. Technol. 2016, 65, 381–384. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, X.-M.; Ding, H. Tool Orientation Optimization for Reduction of Vibration and Deformation in Ball-End Milling of Thin-Walled Impeller Blades. Procedia CIRP 2017, 58, 210–215. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, S.; Wang, Z.; Liu, N.; Wang, S.; Ma, C.; Yang, B. Interference- and Chatter-Free Cutter Posture Optimization towards Minimal Surface Roughness in Five-Axis Machining. Int. J. Mech. Sci. 2020, 171, 105395. [Google Scholar] [CrossRef]
- Habibi, M.; Kilic, Z.M.; Altintas, Y. Minimizing Flute Engagement to Adjust Tool Orientation for Reducing Surface Errors in Five-Axis Ball End Milling Operations. J. Manuf. Sci. Eng. 2020, 143, 021009. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; de Lacalle, L.N.L. Stability Contour Maps with Barrel Cutters Considering the Tool Orientation. Int. J. Adv. Manuf. Technol. 2017, 89, 2491–2501. [Google Scholar] [CrossRef]
- Zhan, D.; Jiang, S.; Niu, J.; Sun, Y. Dynamics Modeling and Stability Analysis of Five-Axis Ball-End Milling System with Variable Pitch Tools. Int. J. Mech. Sci. 2020, 182, 105774. [Google Scholar] [CrossRef]
- Hahn, R.S. Metal-Cutting Chatter & Its Elimination. Trans. ASME 1952, 74, 1073–1080. [Google Scholar]
- Slavicek, J. The Effect of Irregular Tooth Pitch on Stability of Milling. In Proceedings of the 6th MTDR Conference; Pergamon Press: London, UK, 1965; Volume 1, pp. 15–22. [Google Scholar]
- Budak, E. An Analytical Design Method for Milling Cutters With Nonconstant Pitch to Increase Stability, Part I: Theory. J. Manuf. Sci. Eng. 2003, 125, 29–34. [Google Scholar] [CrossRef]
- Budak, E. An Analytical Design Method for Milling Cutters with Nonconstant Pitch to Increase Stability, Part 2: Application. J. Manuf. Sci. Eng. Trans. ASME 2003, 125, 35–38. [Google Scholar] [CrossRef] [Green Version]
- Olgac, N.; Sipahi, R. Dynamics and Stability of Variable-Pitch Milling. J. Vib. Control 2007, 13, 1031–1043. [Google Scholar] [CrossRef]
- Stepan, G.; Hajdu, D.; Iglesias, A.; Takacs, D.; Dombovari, Z. Ultimate Capability of Variable Pitch Milling Cutters. CIRP Ann. 2018, 67, 373–376. [Google Scholar] [CrossRef]
- Yusoff, A.R.; Sims, N.D. Optimisation of Variable Helix Tool Geometry for Regenerative Chatter Mitigation. Int. J. Mach. Tools Manuf. 2011, 51, 133–141. [Google Scholar] [CrossRef] [Green Version]
- Takuya, K.; Suzuki, N.; Hino, R.; Shamoto, E. A Novel Design Method of Variable Helix Cutters to Attain Robust Regeneration Suppression. Procedia CIRP 2013, 8, 363–367. [Google Scholar] [CrossRef] [Green Version]
- Hayasaka, T.; Ito, A.; Shamoto, E. Generalized Design Method of Highly-Varied-Helix End Mills for Suppression of Regenerative Chatter in Peripheral Milling. Precis. Eng. 2017, 48, 45–59. [Google Scholar] [CrossRef]
- Comak, A.; Budak, E. Modeling Dynamics and Stability of Variable Pitch and Helix Milling Tools for Development of a Design Method to Maximize Chatter Stability. Precis. Eng. 2017, 47, 459–468. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, W.; Jiang, Y.; Sun, Y. 3D Surface Topography Prediction in the Five-Axis Milling of Plexiglas and Metal Using Cutters with Non-Uniform Helix and Pitch Angles Combining Runout. J. Mater. Process. Technol. 2023, 314, 117885. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Mechanics and Dynamics of Serrated Cylindrical and Tapered End Mills. J. Manuf. Sci. Eng. 2004, 126, 317–326. [Google Scholar] [CrossRef]
- Bari, P.; Kilic, Z.M.; Law, M.; Wahi, P. Rapid Stability Analysis of Serrated End Mills Using Graphical-Frequency Domain Methods. Int. J. Mach. Tools Manuf. 2021, 171, 103805. [Google Scholar] [CrossRef]
- Tehranizadeh, F.; Koca, R.; Budak, E. Investigating Effects of Serration Geometry on Milling Forces and Chatter Stability for Their Optimal Selection. Int. J. Mach. Tools Manuf. 2019, 144, 103425. [Google Scholar] [CrossRef]
- Dombovari, Z.; Stepan, G. The Effect of Helix Angle Variation on Milling Stability. J. Manuf. Sci. Eng. 2012, 134, 051015. [Google Scholar] [CrossRef]
- Tehranizadeh, F.; Berenji, K.R.; Yıldız, S.; Budak, E. Chatter Stability of Thin-Walled Part Machining Using Special End Mills. CIRP Ann. 2022, 71, 365–368. [Google Scholar] [CrossRef]
- Tehranizadeh, F.; Rahimzadeh Berenji, K.; Budak, E. Dynamics and Chatter Stability of Crest-Cut End Mills. Int. J. Mach. Tools Manuf. 2021, 171, 103813. [Google Scholar] [CrossRef]
- Farahani, N.D.; Altintas, Y. Chatter Stability of Serrated Milling Tools in Frequency Domain. J. Manuf. Sci. Eng. 2022, 144, 031013. [Google Scholar] [CrossRef]
- Smith, S.; Tlusty, J. Stabilizing Chatter by Automatic Spindle Speed Regulation. CIRP Ann. 1992, 41, 433–436. [Google Scholar] [CrossRef]
- Smith, S.; Delio, T. Sensor-Based Chatter Detection and Avoidance by Spindle Speed Selection. J. Dyn. Syst. Meas. Control 1992, 114, 486–492. [Google Scholar] [CrossRef]
- Liao, Y.S.; Young, Y.C. A New on-Line Spindle Speed Regulation Strategy for Chatter Control. Int. J. Mach. Tools Manuf. 1996, 36, 651–660. [Google Scholar] [CrossRef]
- Tsai, N.-C.; Chen, D.-C.; Lee, R.-M. Chatter Prevention for Milling Process by Acoustic Signal Feedback. Int. J. Adv. Manuf. Technol. 2010, 47, 1013–1021. [Google Scholar] [CrossRef]
- Tsai, N.-C.; Chen, D.-C.; Lee, R.-M. Chatter Prevention and Improved Finish of Workpiece for a Milling Process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 224, 579–588. [Google Scholar] [CrossRef]
- Sastry, S.; Kapoor, S.G.; DeVor, R.E. Floquet Theory Based Approach for Stability Analysis of the Variable Speed Face-Milling Process. J. Manuf. Sci. Eng. 2001, 124, 10–17. [Google Scholar] [CrossRef]
- Al-Regib, E.; Ni, J.; Lee, S.H. Programming Spindle Speed Variation for Machine Tool Chatter Suppression. Int. J. Mach. Tools Manuf. 2003, 43, 1229–1240. [Google Scholar] [CrossRef]
- Bediaga, I.; Zatarain, M.; Muñoa, J.; Lizarralde, R. Application of Continuous Spindle Speed Variation for Chatter Avoidance in Roughing Milling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 631–640. [Google Scholar] [CrossRef]
- Seguy, S.; Insperger, T.; Arnaud, L.; Dessein, G.; Peigné, G. On the Stability of High-Speed Milling with Spindle Speed Variation. Int. J. Adv. Manuf. Technol. 2010, 48, 883–895. [Google Scholar] [CrossRef] [Green Version]
- Sexton, J.S.; Stone, B. The Stability of Machining with Continuously Varying Spindle Speed. CIRP Ann. -Manuf. Technol. 1978, 27, 321–326. [Google Scholar]
- Zatarain, M.; Bediaga, I.; Muñoa, J.; Lizarralde, R. Stability of Milling Processes with Continuous Spindle Speed Variation: Analysis in the Frequency and Time Domains, and Experimental Correlation. CIRP Ann. 2008, 57, 379–384. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Zhu, L.; Ding, H. Stability Analysis of Milling Processes With Periodic Spindle Speed Variation Via the Variable-Step Numerical Integration Method. J. Manuf. Sci. Eng. 2016, 138, 114501. [Google Scholar] [CrossRef]
- Yamato, S.; Ito, T.; Matsuzaki, H.; Fujita, J.; Kakinuma, Y. Self-Acting Optimal Design of Spindle Speed Variation for Regenerative Chatter Suppression Based on Novel Analysis of Internal Process Energy Behavior. Int. J. Mach. Tools Manuf. 2020, 159, 103639. [Google Scholar] [CrossRef]
- Aoyama, T.; Kakinuma, Y. Development of Fixture Devices for Thin and Compliant Workpieces. CIRP Ann. 2005, 54, 325–328. [Google Scholar] [CrossRef]
- Kolluru, K.; Axinte, D. Novel Ancillary Device for Minimising Machining Vibrations in Thin Wall Assemblies. Int. J. Mach. Tools Manuf. 2014, 85, 79–86. [Google Scholar] [CrossRef]
- Wang, X.; Ma, P.; Peng, X.; Ning, S. Study on Vibration Suppression Performance of a Flexible Fixture for a Thin-Walled Casing. Int. J. Adv. Manuf. Technol. 2020, 106, 4281–4291. [Google Scholar] [CrossRef]
- Zeng, S.; Wan, X.; Li, W.; Yin, Z.; Xiong, Y. A Novel Approach to Fixture Design on Suppressing Machining Vibration of Flexible Workpiece. Int. J. Mach. Tools Manuf. 2012, 58, 29–43. [Google Scholar] [CrossRef]
- Wan, M.; Dang, X.-B.; Zhang, W.-H.; Yang, Y. Chatter Suppression in the Milling Process of the Weakly-Rigid Workpiece through a Moving Fixture. J. Mater. Process. Technol. 2022, 299, 117293. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Xiao, J.; Ding, M.; Yan, S.; Zhang, X.; Zhang, J. Investigation of Moving Fixture on Deformation Suppression during Milling Process of Thin-Walled Structures. J. Manuf. Process. 2018, 32, 403–411. [Google Scholar] [CrossRef]
- Fu, R.; Curley, P.; Higgins, C.; Kilic, Z.M.; Sun, D.; Murphy, A.; Jin, Y. Double-Sided Milling of Thin-Walled Parts by Dual Collaborative Parallel Kinematic Machines. J. Mater. Process. Technol. 2022, 299, 117395. [Google Scholar] [CrossRef]
- Shamoto, E.; Mori, T.; Nishimura, K.; Hiramatsu, T.; Kurata, Y. Suppression of Regenerative Chatter Vibration in Simultaneous Double-Sided Milling of Flexible Plates by Speed Difference. CIRP Ann. 2010, 59, 387–390. [Google Scholar] [CrossRef]
- Matsubara, A.; Taniyama, Y.; Wang, J.; Kono, D. Design of a Support System with a Pivot Mechanism for Suppressing Vibrations in Thin-Wall Milling. CIRP Ann. 2017, 66, 381–384. [Google Scholar] [CrossRef]
- Fei, J.; Lin, B.; Yan, S.; Ding, M.; Xiao, J.; Zhang, J.; Zhang, X.; Ji, C.; Sui, T. Chatter Mitigation Using Moving Damper. J. Sound Vib. 2017, 410, 49–63. [Google Scholar] [CrossRef]
- Mori, T.; Hiramatsu, T.; Shamoto, E. Simultaneous Double-Sided Milling of Flexible Plates with High Accuracy and High efficiency—Suppression of Forced Chatter Vibration with Synchronized Single-Tooth Cutters. Precis. Eng. 2011, 35, 416–423. [Google Scholar] [CrossRef]
- Smith, S.; Wilhelm, R.; Dutterer, B.; Cherukuri, H.; Goel, G. Sacrificial Structure Preforms for Thin Part Machining. CIRP Ann. 2012, 61, 379–382. [Google Scholar] [CrossRef] [Green Version]
- Alan, S.; Budak, E.; Özgüven, H.N. Analytical Prediction of Part Dynamics for Machining Stability Analysis. Int. J. Autom. Technol. 2010, 4, 259–267. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, D.H.; Wu, B.H.; Zhou, X. Material Removal Process Optimization for Milling of Flexible Workpiece Considering Machining Stability. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1263–1272. [Google Scholar] [CrossRef]
- Tunc, L.T.; Zatarain, M. Stability Optimal Selection of Stock Shape and Tool Axis in Finishing of Thin-Wall Parts. CIRP Ann. 2019, 68, 401–404. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, K.; Zheng, G.; Lv, B.; He, Y. Experimental and Simulation Study on Chatter Stability Region of Integral Impeller with Non-Uniform Allowance. Sci. Prog. 2020, 103, 1–16. [Google Scholar] [CrossRef]
- Bolsunovsky, S.; Vermel, V.; Gubanov, G.; Leontiev, A. Reduction of Flexible Workpiece Vibrations with Dynamic Support Realized as Tuned Mass Damper. Procedia CIRP 2013, 8, 230–234. [Google Scholar] [CrossRef] [Green Version]
- Moradi, H.; Vossoughi, G.; Behzad, M.; Movahhedy, M.R. Vibration Absorber Design to Suppress Regenerative Chatter in Nonlinear Milling Process: Application for Machining of Cantilever Plates. Appl. Math. Model. 2015, 39, 600–620. [Google Scholar] [CrossRef]
- Yuan, H.; Wan, M.; Yang, Y. Design of a Tunable Mass Damper for Mitigating Vibrations in Milling of Cylindrical Parts. Chin. J. Aeronaut. 2019, 32, 748–758. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, R.; Liu, Q. Design of a Passive Damper with Tunable Stiffness and Its Application in Thin-Walled Part Milling. Int. J. Adv. Manuf. Technol. 2017, 89, 2713–2720. [Google Scholar] [CrossRef]
- Yuan, H.; Wan, M.; Yang, Y.; Zhang, W.H. A Tunable Passive Damper for Suppressing Chatters in Thin-Wall Milling by Considering the Varying Modal Parameters of the Workpiece. Int. J. Adv. Manuf. Technol. 2019, 104, 4605–4616. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, W.; Liu, Q. Design and Implementation of Two-Degree-of-Freedom Tuned Mass Damper in Milling Vibration Mitigation. J. Sound Vib. 2015, 335, 78–88. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, W.; Liu, Q. Design and Machining Application of a Two-DOF Magnetic Tuned Mass Damper. Int. J. Adv. Manuf. Technol. 2017, 89, 1635–1643. [Google Scholar] [CrossRef]
- Wan, M.; Dang, X.-B.; Zhang, W.-H.; Yang, Y. Optimization and Improvement of Stable Processing Condition by Attaching Additional Masses for Milling of Thin-Walled Workpiece. Mech. Syst. Signal Process. 2018, 103, 196–215. [Google Scholar] [CrossRef]
- Nakano, Y.; Kishi, T.; Takahara, H. Experimental Study on Application of Tuned Mass Dampers for Chatter in Turning of a Thin-Walled Cylinder. Appl. Sci. 2021, 11, 12070. [Google Scholar] [CrossRef]
- Shi, J.; Song, Q.; Liu, Z.; Ai, X. Partial Surface Damper to Suppress Vibration for Thin Walled Plate Milling. Chin. J. Mech. Eng. 2017, 30, 632–643. [Google Scholar] [CrossRef]
- Scalzo, F.; Totis, G.; Vaglio, E.; Sortino, M. Passive Chatter Suppression of Thin-Walled Parts by Means of High-Damping Lattice Structures Obtained from Selective Laser Melting. J. Manuf. Mater. Process. 2020, 4, 117. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Meng, G.; Ren, S. Milling Chatter Suppression in Viscous Fluid: A Feasibility Study. Int. J. Mach. Tools Manuf. 2017, 120, 20–26. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Liu, X.; Zhang, W.; Meng, G. Chatter Mitigation for the Milling of Thin-Walled Workpiece. Int. J. Mech. Sci. 2018, 138–139, 262–271. [Google Scholar] [CrossRef]
- Dang, X.B.; Wan, M.; Zhang, W.H.; Yang, Y. Chatter Analysis and Mitigation of Milling of the Pocket-Shaped Thin-Walled Workpieces with Viscous Fluid. Int. J. Mech. Sci. 2021, 194, 106214. [Google Scholar] [CrossRef]
- Monnin, J.; Kuster, F.; Wegener, K. Optimal Control for Chatter Mitigation in Milling-Part 1: Modeling and Control Design. Control Eng. Pract. 2014, 24, 156–166. [Google Scholar] [CrossRef]
- Denkena, B.; Gümmer, O. Process Stabilization with an Adaptronic Spindle System. Prod. Eng. 2012, 6, 485–492. [Google Scholar] [CrossRef]
- van Dijk, N.J.M.; van de Wouw, N.; Doppenberg, E.J.J.; Oosterling, H.A.J.; Nijmeijer, H. Robust Active Chatter Control in the High-Speed Milling Process. IEEE Trans. Control Syst. Technol. 2012, 20, 901–917. [Google Scholar] [CrossRef]
- van de Wouw, N.; van Dijk, N.J.M.; Schiffler, A.; Nijmeijer, H.; Abele, E. Experimental Validation of Robust Chatter Control for High-Speed Milling Processes BT-Time Delay Systems: Theory, Numerics, Applications and Experiments; Insperger, T., Ersal, T., Orosz, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 315–331. ISBN 978-3-319-53426-8. [Google Scholar]
- Wan, S.; Li, X.; Su, W.; Yuan, J.; Hong, J. Active Chatter Suppression for Milling Process with Sliding Mode Control and Electromagnetic Actuator. Mech. Syst. Signal Process. 2020, 136, 106528. [Google Scholar] [CrossRef]
- Li, X.; Wan, S.; Yuan, J.; Yin, Y.; Hong, J. Active Suppression of Milling Chatter with LMI-Based Robust Controller and Electromagnetic Actuator. J. Mater. Process. Technol. 2021, 297, 117238. [Google Scholar] [CrossRef]
- Li, D.; Cao, H.; Chen, X. Active Control of Milling Chatter Considering the Coupling Effect of Spindle-Tool and Workpiece Systems. Mech. Syst. Signal Process. 2022, 169, 108769. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Liu, Y.; Cao, H.; Chen, X. Stiffness Variation Method for Milling Chatter Suppression via Piezoelectric Stack Actuators. Int. J. Mach. Tools Manuf. 2018, 124, 53–66. [Google Scholar] [CrossRef]
- Vashisht, R.K.; Peng, Q. Efficient Active Chatter Mitigation for Boring Operation by Electromagnetic Actuator Using Optimal Fractional Order PDλ Controller. J. Mater. Process. Technol. 2020, 276, 116423. [Google Scholar] [CrossRef]
- Bahador, A.; Du, C.; Jin, Y. Piezoelectric Active Damper for Surface Roughness Improvement in Hard Turning Processes. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 156. [Google Scholar] [CrossRef]
- Saleh, M.K.A.; Nejatpour, M.; Yagci Acar, H.; Lazoglu, I. A New Magnetorheological Damper for Chatter Stability of Boring Tools. J. Mater. Process. Technol. 2021, 289, 116931. [Google Scholar] [CrossRef]
- Saleh, M.K.A.; Ulasyar, A.; Lazoglu, I. Active Damping of Chatter in the Boring Process via Variable Gain Sliding Mode Control of a Magnetorheological Damper. CIRP Ann. 2021, 70, 337–340. [Google Scholar] [CrossRef]
- Basovich, S.; Arogeti, S. Identification and Robust Control for Regenerative Chatter in Internal Turning with Simultaneous Compensation of Machining Error. Mech. Syst. Signal Process. 2021, 149, 107208. [Google Scholar] [CrossRef]
- Zhang, Y.; Sims, N.D. Milling Workpiece Chatter Avoidance Using Piezoelectric Active Damping: A Feasibility Study. Smart Mater. Struct. 2005, 14, N65–N70. [Google Scholar] [CrossRef]
- Parus, A.; Powałka, B.; Marchelek, K.; Domek, S.; Hoffmann, M. Active Vibration Control in Milling Flexible Workpieces. J. Vib. Control 2012, 19, 1103–1120. [Google Scholar] [CrossRef]
- Jia, J.; Niu, J.; Sun, Y. Dynamics Modeling and Stability Improvement in the Machining of Thin-Walled Workpiece with Force-Tunable Pneumatic Fixture. Int. J. Adv. Manuf. Technol. 2021, 117, 1029–1043. [Google Scholar] [CrossRef]
- Ozturk, E.; Barrios, A.; Sun, C.; Rajabi, S.; Munoa, J. Robotic Assisted Milling for Increased Productivity. CIRP Ann. 2018, 67, 427–430. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.; Yang, Z.; Jiang, Y.; Xu, J. A State-of-the-Art Review on Robotic Milling of Complex Parts with High Efficiency and Precision. Robot. Comput. Integr. Manuf. 2023, 79, 102436. [Google Scholar] [CrossRef]
- Beudaert, X.; Erkorkmaz, K.; Munoa, J. Portable Damping System for Chatter Suppression on Flexible Workpieces. CIRP Ann. 2019, 68, 423–426. [Google Scholar] [CrossRef]
- Xiaohui, J.; Yong, Z.; Weiwei, L.; Shan, G.; Ling, L.; Xiao, L. Characteristics of Shear Stress Based on Magnetorheological Fluid Flexible Fixture during Milling of the Thin-Walled Part. Int. J. Adv. Manuf. Technol. 2020, 108, 2607–2619. [Google Scholar] [CrossRef]
- Paul, S.; Morales-Menendez, R. Active Control of Chatter in Milling Process Using Intelligent PD/PID Control. IEEE Access 2018, 6, 72698–72713. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Liu, J.; Cao, H.; Chen, X. Adaptive Vibration Reshaping Based Milling Chatter Suppression. Int. J. Mach. Tools Manuf. 2019, 141, 30–35. [Google Scholar] [CrossRef]
- Mizrachi, E.; Basovich, S.; Arogeti, S. Robust Time-Delayed H∞ Synthesis for Active Control of Chatter in Internal Turning. Int. J. Mach. Tools Manuf. 2020, 158, 103612. [Google Scholar] [CrossRef]
- Feng, J.; Wan, M.; Dong, Z.-Y.; Zhang, W.-H. A Unified Process Damping Model Considering the Varying Stiffness of the Milling System. Int. J. Mach. Tools Manuf. 2019, 147, 103470. [Google Scholar] [CrossRef]


















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zheng, M.; Jiang, S.; Zhan, D.; Wang, R. A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts. Machines 2023, 11, 359. https://doi.org/10.3390/machines11030359
Sun Y, Zheng M, Jiang S, Zhan D, Wang R. A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts. Machines. 2023; 11(3):359. https://doi.org/10.3390/machines11030359
Chicago/Turabian StyleSun, Yuwen, Meng Zheng, Shanglei Jiang, Danian Zhan, and Ruoqi Wang. 2023. "A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts" Machines 11, no. 3: 359. https://doi.org/10.3390/machines11030359
APA StyleSun, Y., Zheng, M., Jiang, S., Zhan, D., & Wang, R. (2023). A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts. Machines, 11(3), 359. https://doi.org/10.3390/machines11030359









