Kinematic Calibration of a Space Manipulator Based on Visual Measurement System with Extended Kalman Filter
Abstract
1. Introduction
2. Materials and Methods
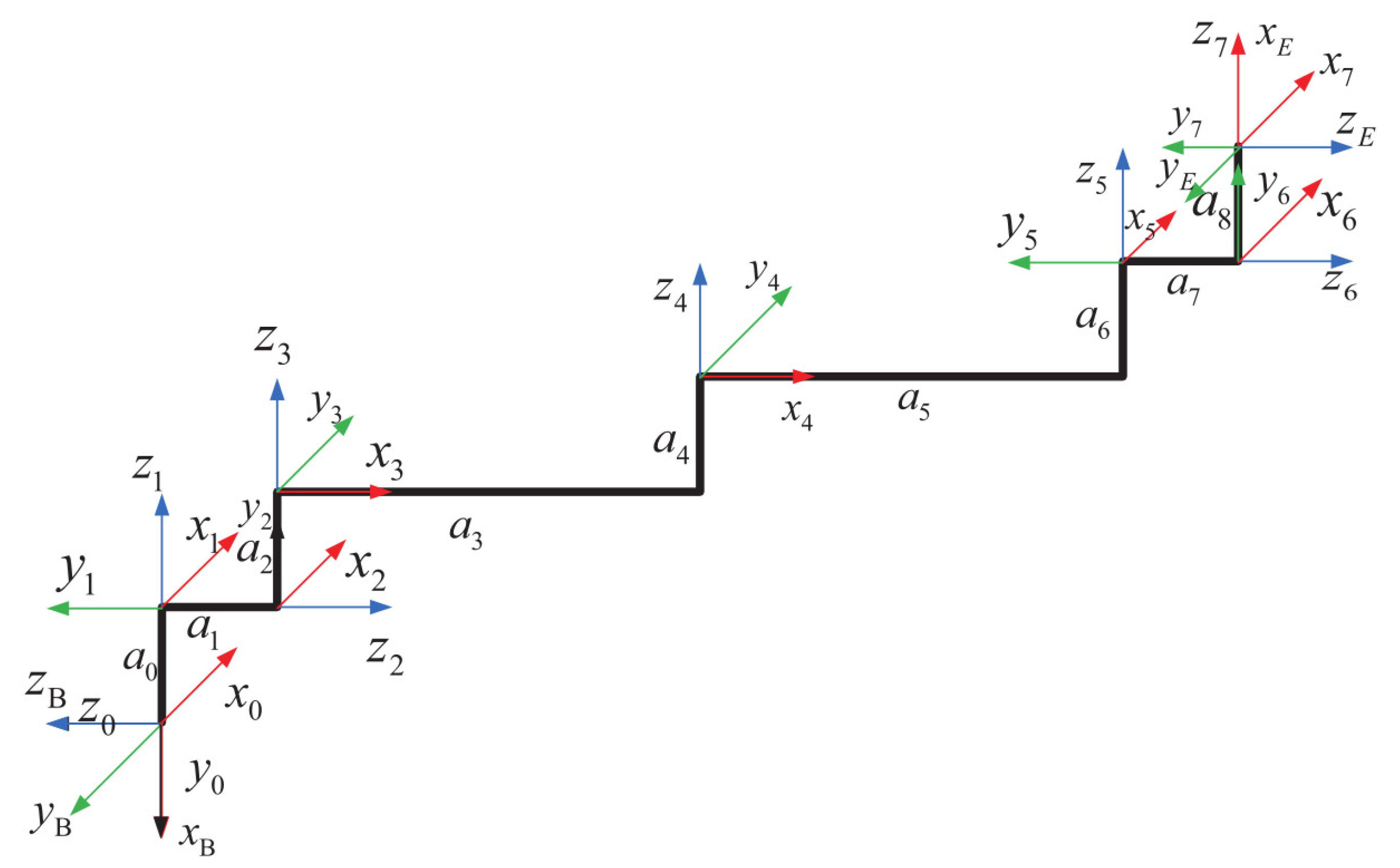
2.1. DH Coordinate System
2.2. Forward and Inverse Kinematic Model
2.3. Identification Model
3. Identification of Kinematic Errors
3.1. End-Effector Pose Acquisition
3.2. Identification Algorithm
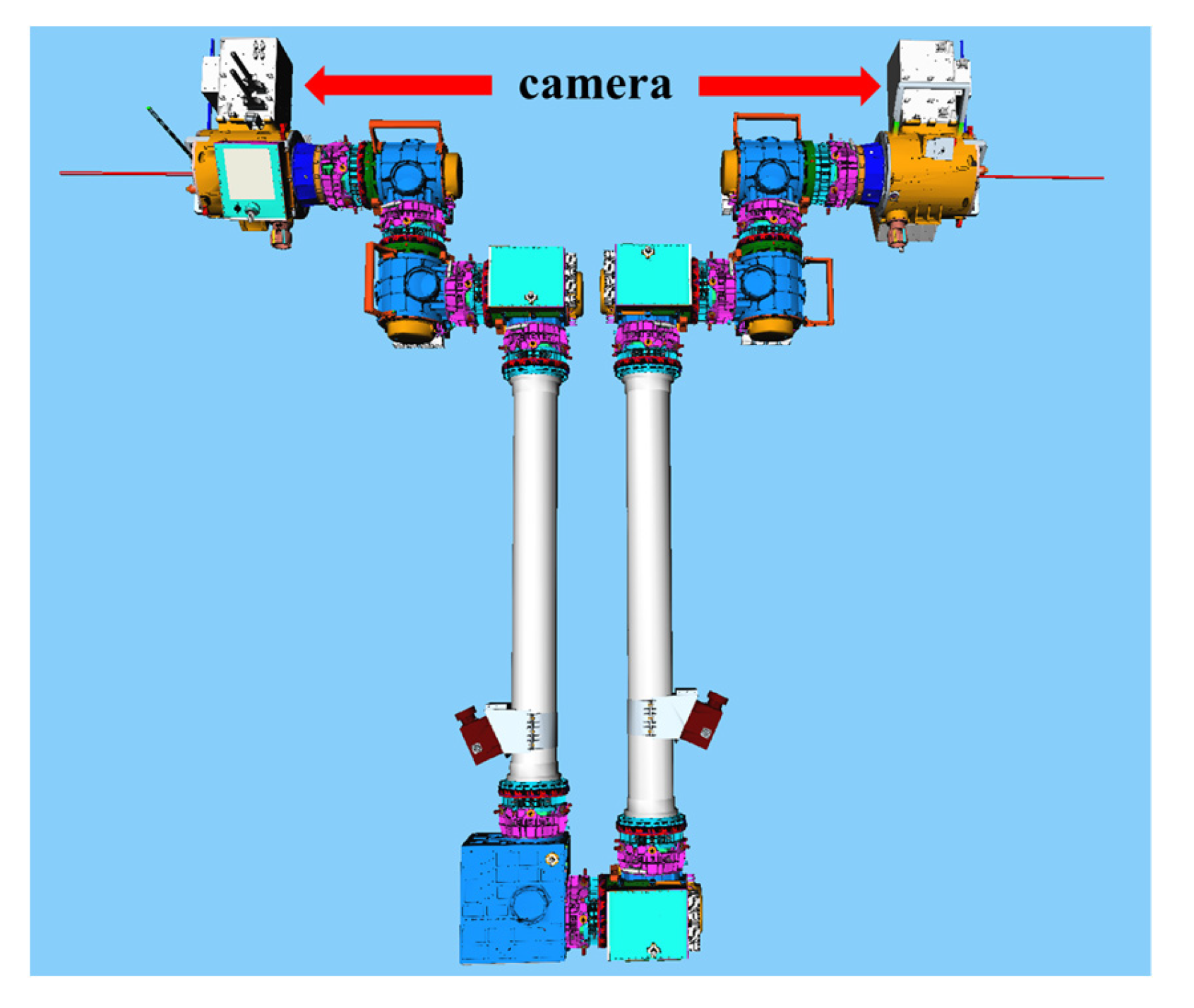
4. Experiment
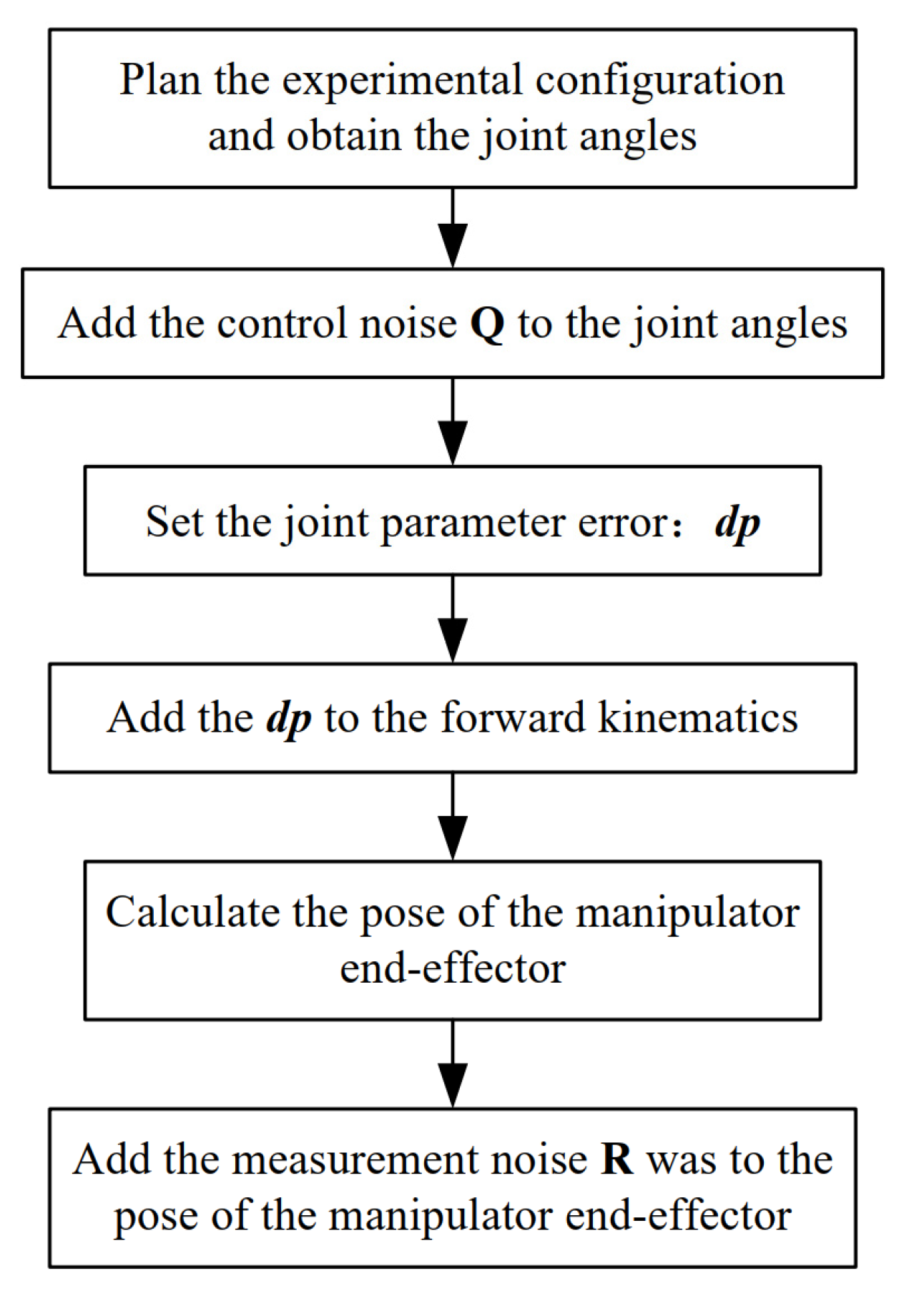
4.1. Simulation Process of a Calibration Experiment
4.2. Contrast Test of Calibration Effect
4.3. Comparative Test of Calibration Efficiency
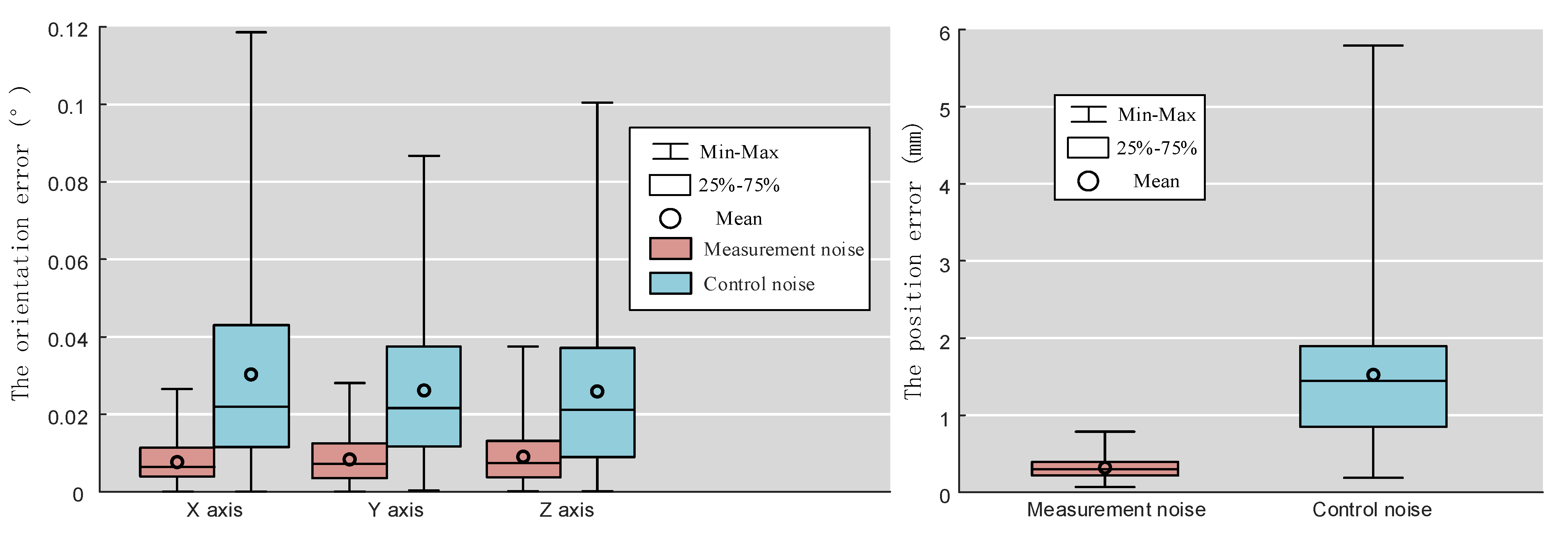
4.4. Comparative Experiment of Different Noise
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variables | |
| The length of the link. | |
| The camera intrinsic matrix. | |
| The offset distance of the i-th link. | |
| The error matrix (4 × 4) of the homogeneous transformation matrix of coordinate system relative to coordinate system . | |
| The offset from the theoretical position of the coordinate system with respect to the coordinate system . | |
| The offset from the theoretical attitude of the coordinate system with respect to the coordinate system . | |
| Differential coefficient matrix of four kinematic parameters of the i-th link. | |
| Offset vector (6 × 1) of the theoretical position and attitude of the end-effector with respect to the coordinate system . | |
| Offset vector (6 × 1) of the theoretical position and attitude of the coordinate system with respect to the coordinate system . | |
| The transformation matrix (6 × 6) from the coordinate system to the coordinate system . | |
| Coefficient matrix (6 × 4) of differential motion of the coordinate system with respect to the coordinate system . | |
| The end-effector pose error (6 × 1) of the k-th configuration. | |
| The unit matrix (28 × 28). | |
| The Jacobi matrix corresponding to the k-th configuration. | |
| The Kalman gain in round k iteration. | |
| Two-dimensional coordinates on the picture, . | |
| Augmented matrix of m. | |
| The coordinate of a point in the Cartesian space, . | |
| Augmented matrix of M, . | |
| Number of test configurations. | |
| The noise covariance matrix (28 × 28) in round k iteration. | |
| The noise covariance matrix (28 × 28) of the prediction in round k + 1 iteration. | |
| The initial noise covariance matrix (28 × 28). | |
| The rotation parameter which relates the world coordinate system to the camera coordinate system. | |
| A scale factor of the camera. | |
| The translation parameter which relates the world coordinate system to the camera coordinate system. | |
| The actual homogeneous transformation matrix (4 × 4) of coordinate system relative to coordinate system . | |
| Theoretical homogeneous transformation matrix (4 × 4) of coordinate system relative to coordinate system . | |
| The homogeneous transformation matrix (4 × 4) of coordinate system relative to coordinate system . | |
| Fixed joint angle. In the text, . | |
| Joint vector (1 × 7), . | |
| Initial joint vector. | |
| Kinematic parameter error of the i-th link, . | |
| Kinematic parameters for all joints, . | |
| The estimation result (28 × 1) of the system state in round k iteration. | |
| The prediction state (28 × 1) of the system state in round k + 1 iteration based on the result of round k iteration. | |
| The end-effector pose (6 × 1) of the k-th configuration. | |
| The torsion angle of the i-th link. | |
| The rotation angle of the i-th link. | |
| The offset vector (4 × 1) of the kinematic parameters of the i-th link, . | |
| Slight changes in the four kinematic parameters of the i-th link. | |
| Micromovement rate (4 × 4) of the transformation matrix of coordinate system relative to coordinate system . | |
| Coordinate system of the manipulator. |
References
- Ma, B.; Xie, Z.; Jiang, Z.; Liu, H. Precise Semi-Analytical Inverse Kinematic Solution for 7-DOF Offset Manipulator with Arm Angle Optimization. Front. Mech. Eng. 2021, 16, 435–450. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, Z.; Liu, Y. Review of Space Manipulator Technology. Manned Spacefl. 2015, 21, 435–443. [Google Scholar] [CrossRef]
- Meng, G.; Han, L.; Zhang, C. Research progress and technical challenges of space robot. Acta Aeronaut. Et Astronaut. Sin. 2021, 42, 8–32. [Google Scholar]
- Liu, H.; Liu, Y.; Jiang, L. Space Robot and Teleoperation; Harbin Institute of Technology Press: Harbin, China, 2012; ISBN 978-7-5603-3806-4. (In Chinese) [Google Scholar]
- Chen, G.; Li, T.; Chu, M.; Xuan, J.-Q.; Xu, S.-H. Review on Kinematics Calibration Technology of Serial Robots. Int. J. Precis. Eng. Manuf. 2014, 15, 1759–1774. [Google Scholar] [CrossRef]
- Schröer, K.; Albright, S.L.; Grethlein, M. Complete, Minimal and Model-Continuous Kinematic Models for Robot Calibration. Robot. Comput. -Integr. Manuf. 1997, 13, 73–85. [Google Scholar] [CrossRef]
- Hayati, S.A. Robot Arm Geometric Link Parameter Estimation. In Proceedings of the 22nd IEEE Conference on Decision and Control, San Antonio, TX, USA, December 1983; pp. 1477–1483. [Google Scholar] [CrossRef]
- Veitschegger, W.K.; Wu, C.-H. Robot Calibration and Compensation. IEEE J. Robot. Automat. 1988, 4, 643–656. [Google Scholar] [CrossRef]
- Okamura, K.; Park, F.C. Kinematic Calibration Using the Product of Exponentials Formula. Robotica 1996, 14, 415–421. [Google Scholar] [CrossRef]
- He, R.; Zhao, Y.; Yang, S.; Yang, S. Kinematic-Parameter Identification for Serial-Robot Calibration Based on POE Formula. IEEE Trans. Robot. 2010, 26, 411–423. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Li, J.; Chen, K. A Minimal Kinematic Model for Serial Robot Calibration Using POE Formula. Robot. Comput. -Integr. Manuf. 2014, 30, 326–334. [Google Scholar] [CrossRef]
- Chen, I.-M.; Yang, G.; Tan, C.T.; Yeo, S.H. Local POE Model for Robot Kinematic Calibration. Mech. Mach. Theory 2001, 36, 1215–1239. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Löwe, H.; Li, Z. POE-Based Robot Kinematic Calibration Using Axis Configuration Space and the Adjoint Error Model. IEEE Trans. Robot. 2016, 32, 1264–1279. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Lin, Z. Determination of the Identifiable Parameters in Robot Calibration Based on the POE Formula. IEEE Trans. Robot. 2014, 30, 1066–1077. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Dubowsky, S. An Analytical Method to Eliminate the Redundant Parameters in Robot Calibration. In Proceedings of the IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), 2000 ICRA, Millennium Conference, San Francisco, CA, USA, 24–28 April 2000; Volume 4, pp. 3609–3615. [Google Scholar] [CrossRef]
- Gan, Y.; Duan, J.; Dai, X. A Calibration Method of Robot Kinematic Parameters by Drawstring Displacement Sensor. Int. J. Adv. Robot. Syst. 2019, 16, 172988141988307. [Google Scholar] [CrossRef]
- Jang, J.H.; Kim, S.H.; Kwak, Y.K. Calibration of Geometric and Non-Geometric Errors of an Industrial Robot. Robotica 2001, 19, 311–321. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute Calibration of an ABB IRB 1600 Robot Using a Laser Tracker. Robot. Comput.-Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Fachinotti, V.D.; Anca, A.A.; Cardona, A. A Method for the Solution of Certain Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Zhu, Q.; Xie, X.; Li, C.; Xia, G.; Liu, Q. Kinematic Self-Calibration Method for Dual-Manipulators Based on Optical Axis Constraint. IEEE Access 2019, 7, 7768–7782. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P. Online Serial Manipulator Calibration Based on Multisensory Process via Extended Kalman and Particle Filters. IEEE Trans. Ind. Electron. 2014, 61, 6852–6859. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P.; Li, D. Online Robot Calibration Based on Hybrid Sensors Using Kalman Filters. Robot. Comput. -Integr. Manuf. 2015, 31, 91–100. [Google Scholar] [CrossRef]
- Du, G.; Shao, H.; Chen, Y.; Zhang, P.; Liu, X. An Online Method for Serial Robot Self-Calibration with CMAC and UKF. Robot. Comput.-Integr. Manuf. 2016, 42, 39–48. [Google Scholar] [CrossRef]
- Yang, C.; Shi, W.; Chen, W. Comparison of Unscented and Extended Kalman Filters with Application in Vehicle Navigation. J. Navig. 2017, 70, 411–431. [Google Scholar] [CrossRef]
- Bonyan Khamseh, H.; Ghorbani, S.; Janabi-Sharifi, F. Unscented Kalman Filter State Estimation for Manipulating Unmanned Aerial Vehicles. Aerosp. Sci. Technol. 2019, 92, 446–463. [Google Scholar] [CrossRef]
- Moghaddam, B.M.; Chhabra, R. On the Guidance, Navigation and Control of in-Orbit Space Robotic Missions: A Survey and Prospective Vision. Acta Astronaut. 2021, 184, 70–100. [Google Scholar] [CrossRef]
- Zheng, Z.; Shirong, L.; Botao, Z. An Improved Sage-Husa Adaptive Filtering Algorithm. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 5113–5117. [Google Scholar]
- Song, K.; Cong, S.; Deng, K.; Shang, W.; Kong, D.; Shen, H. Design of Adaptive Strong Tracking and Robust Kalman Filter. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 6626–6631. [Google Scholar] [CrossRef]
- Ma, L.; Bazzoli, P.; Sammons, P.M.; Landers, R.G.; Bristow, D.A. Modeling and Calibration of High-Order Joint-Dependent Kinematic Errors for Industrial Robots. Robot. Comput.-Integr. Manuf. 2018, 50, 153–167. [Google Scholar] [CrossRef]
- Sun, T.; Lian, B.; Zhang, J.; Song, Y. Kinematic Calibration of a 2-DoF Over-Constrained Parallel Mechanism Using Real Inverse Kinematics. IEEE Access 2018, 6, 67752–67761. [Google Scholar] [CrossRef]
- Alıcı, G.; Jagielski, R.; Ahmet Şekercioğlu, Y.; Shirinzadeh, B. Prediction of Geometric Errors of Robot Manipulators with Particle Swarm Optimisation Method. Robot. Auton. Syst. 2006, 54, 956–966. [Google Scholar] [CrossRef]
- Fang, L.; Dang, P. A Step Identification Method of Joint Parameters of Robots Based on the Measured Pose of End-Effector. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 3218–3233. [Google Scholar] [CrossRef]
- Cao, H.Q.; Nguyen, H.X.; Tran, T.N.-C.; Tran, H.N.; Jeon, J.W. A Robot Calibration Method Using a Neural Network Based on a Butterfly and Flower Pollination Algorithm. IEEE Trans. Ind. Electron. 2022, 69, 3865–3875. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Mao, C.; Zhang, X. An ANN-Based Precision Compensation Method for Industrial Manipulators via Optimization of Point Selection. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Jing, W.; Tao, P.Y.; Yang, G.; Shimada, K. Calibration of Industry Robots with Consideration of Loading Effects Using Product-Of-Exponential (POE) and Gaussian Process (GP). In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4380–4385. [Google Scholar] [CrossRef]
- Shi, S.; Wang, D.; Ruan, S.; Li, R.; Jin, M.; Liu, H. High Integrated Modular Joint for Chinese Space Station Experiment Module Manipulator. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 1195–1200. [Google Scholar] [CrossRef]
- Ma, B.; Jiang, Z.; Liu, Y.; Xie, Z. Advances in Space Robots for On-Orbit Servicing: A Comprehensive Review. Adv. Intell. Syst. 2023. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Zhang, Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 1, pp. 666–673. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Kalman Filtering Principle and Application MATLAB Simulation; Publishing House of Electronics Industry: Beijing, China, 2015; ISBN 978-7-121-26310-1. (In Chinese) [Google Scholar]
- Wang, G.; Shi, Z.; Shang, Y.; Sun, X.; Zhang, W.; Yu, Q. Precise Monocular Vision-Based Pose Measurement System for Lunar Surface Sampling Manipulator. Sci. China Technol. Sci. 2019, 62, 1783–1794. [Google Scholar] [CrossRef]
- Joubair, A.; Bonev, I.A. Comparison of the Efficiency of Five Observability Indices for Robot Calibration. Mech. Mach. Theory 2013, 70, 254–265. [Google Scholar] [CrossRef]




| Algorithm | Advantage | Disadvantage | Reference |
|---|---|---|---|
| LSE | Simple structure; widely used. | It is sensitive to measurement noise and requires sensors with high precision. | [16,17,18] |
| LM | It is friendly to the user and could circumvent the singularity problem of the D-H model. | It is prone to generating suboptimal results. | [19,20,21] |
| EKF | The calculation speed is fast, the effect is obvious, and the measurement noise can be filtered. | The effect is unstable and the statistical property of noise needs to be known. | [22,23] |
| UKF | The effect is obvious, fewer original data may be required, and the measurement noise can be filtered. | The effect is unstable and the statistical property of noise needs to be known. | [24,25,26,27] |
| Sage–Husa AKF | It can deal with time-varying noise problem. | The calculation is complex and the effect is unstable. | [28,29] |
| MLE | It is intuitive and straightforward in practice. | A large quantity of experimental data is required. | [30] |
| GA | It is reliable, numerically precise, and the kinematic model of the manipulator is not required. | It is very sensitive to parameter change and computations are huge. | [31] |
| PSO | It has simple structure, and it is easy to implement. | It can fall into a local optimum with slow convergence. | [32] |
| QPSO | It has simple structure, and it is easy to implement. | It can fall into a local optimum with slow convergence. | [33] |
| ANN | It is a powerful tool for treating mathematically ill-defined systems, and the kinematic model of the manipulator is not required. | Suffers from dependency on procedure and excessive tuning of adaptive gains. | [34,35,36] |
| Link i | ||||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | −90 |
| 1 | 0 | 90 | l0 | 0 |
| 2 | 0 | 90 | l1 | 0 |
| 3 | 0 | −90 | l2 | −90 |
| 4 | l3 | 0 | l4 | 0 |
| 5 | l5 | 0 | l6 | 90 |
| 6 | 0 | 90 | l7 | 0 |
| 7 | 0 | −90 | l8 | 0 |
| E | 0 | 90 | 0 | 90 |
| Joint | (°) | (°) | (mm) | (mm) |
|---|---|---|---|---|
| 1 | 0.3 | 0.2 | 0.5 | −0.9 |
| 2 | −0.2 | 0.3 | 0.8 | 0.8 |
| 3 | 0.2 | −0.25 | −0.6 | −1 |
| 4 | 0.3 | 0.3 | −0.9 | 0.8 |
| 5 | 0.2 | −0.3 | 1 | 0.8 |
| 6 | 0.2 | −0.2 | −0.8 | 0.75 |
| 7 | −0.3 | 0.25 | 0.9 | 0.6 |
| Initial | LSE | EKF | ||||
|---|---|---|---|---|---|---|
| Value | Value | Optimization Ratio | Value | Optimization Ratio | ||
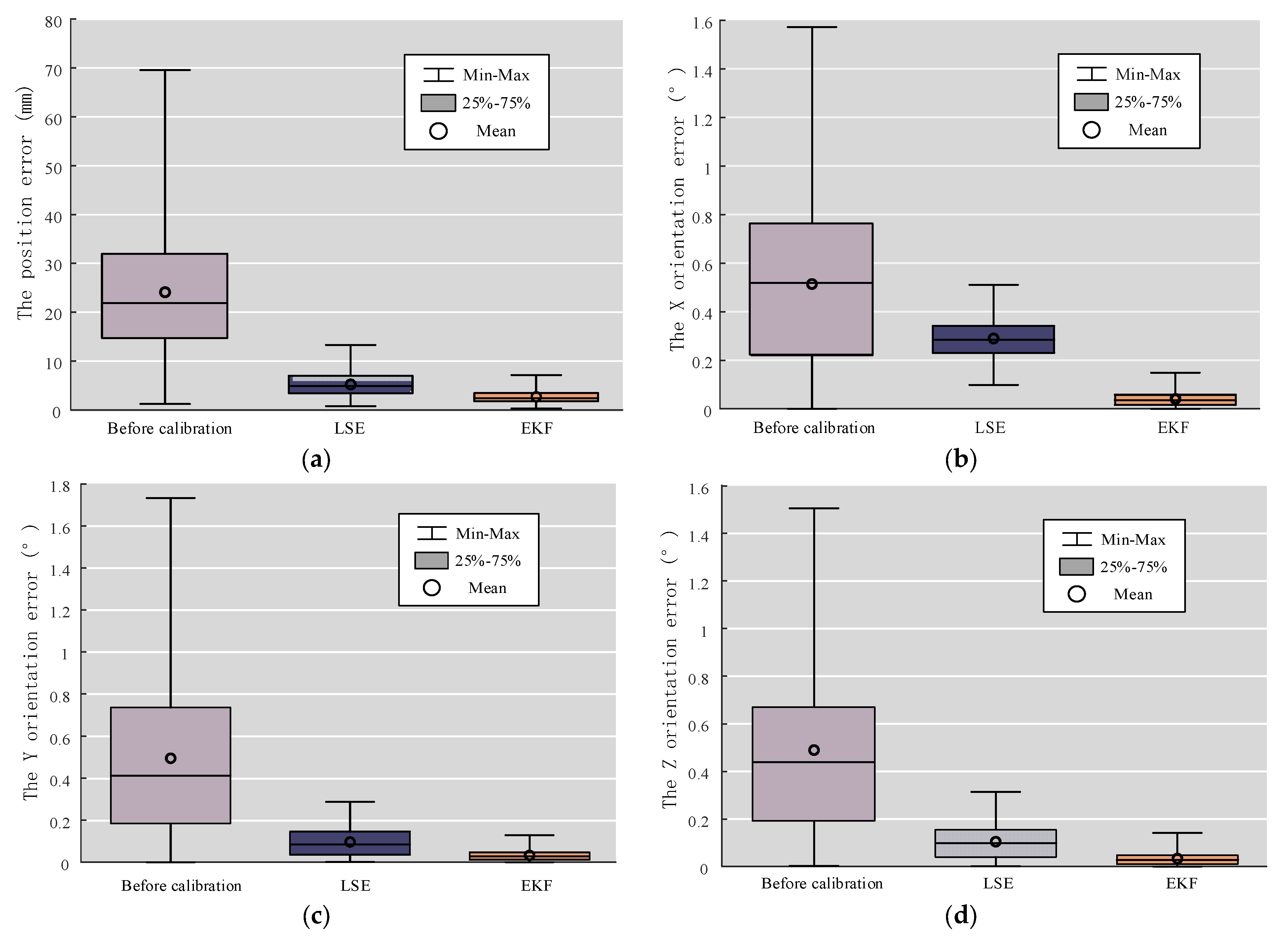
| Position (mm) | Extreme values | 69.9453 | 12.7133 | 81.8240% | 7.3965 | 89.4253% |
| Average value | 24.2930 | 5.2593 | 78.3506% | 2.3335 | 90.3944% | |
| X axis orientation (°) | Extreme values | 1.5867 | 0.5163 | 67.4608% | 0.1473 | 90.7166% |
| Average value | 0.5188 | 0.2836 | 45.3354% | 0.0467 | 90.9985% | |
| Y axis orientation (°) | Extreme values | 1.7236 | 0.2933 | 82.9833% | 0.1432 | 91.6918% |
| Average value | 0.4951 | 0.1082 | 78.1458% | 0.0237 | 95.2131% | |
| Z axis orientation (°) | Extreme values | 1.5012 | 0.3266 | 78.2441% | 0.1147 | 92.3594% |
| Average value | 0.4802 | 0.1345 | 71.9908% | 0.0335 | 93.0237% | |
| 0.01 mm/0.01° | 0.01 mm/0.5° | 0.3 mm/0.01° | 0.3 mm/0.5° | |||||
|---|---|---|---|---|---|---|---|---|
| Average | Extremum | Average | Extremum | Average | Extremum | Average | Extremum | |
| LSE (mm) | 1.9356 | 5.8736 | 3.1832 | 8.3625 | 1.4362 | 6.0831 | 4.7239 | 13.5341 |
| EKF (mm) | 1.9463 | 5.9541 | 1.9687 | 6.0528 | 1.8125 | 6.6727 | 2.4368 | 7.3659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cao, B.; Xie, Z.; Ma, B.; Sun, K.; Liu, Y. Kinematic Calibration of a Space Manipulator Based on Visual Measurement System with Extended Kalman Filter. Machines 2023, 11, 409. https://doi.org/10.3390/machines11030409
Wang Z, Cao B, Xie Z, Ma B, Sun K, Liu Y. Kinematic Calibration of a Space Manipulator Based on Visual Measurement System with Extended Kalman Filter. Machines. 2023; 11(3):409. https://doi.org/10.3390/machines11030409
Chicago/Turabian StyleWang, Zhengpu, Baoshi Cao, Zongwu Xie, Boyu Ma, Kui Sun, and Yang Liu. 2023. "Kinematic Calibration of a Space Manipulator Based on Visual Measurement System with Extended Kalman Filter" Machines 11, no. 3: 409. https://doi.org/10.3390/machines11030409
APA StyleWang, Z., Cao, B., Xie, Z., Ma, B., Sun, K., & Liu, Y. (2023). Kinematic Calibration of a Space Manipulator Based on Visual Measurement System with Extended Kalman Filter. Machines, 11(3), 409. https://doi.org/10.3390/machines11030409







