Research on the Optimal Control Strategy for the Maximum Torque per Ampere of Brushless Doubly Fed Machines
Abstract
:1. Introduction
2. Reduced-Order State-Space Equations for BDFM
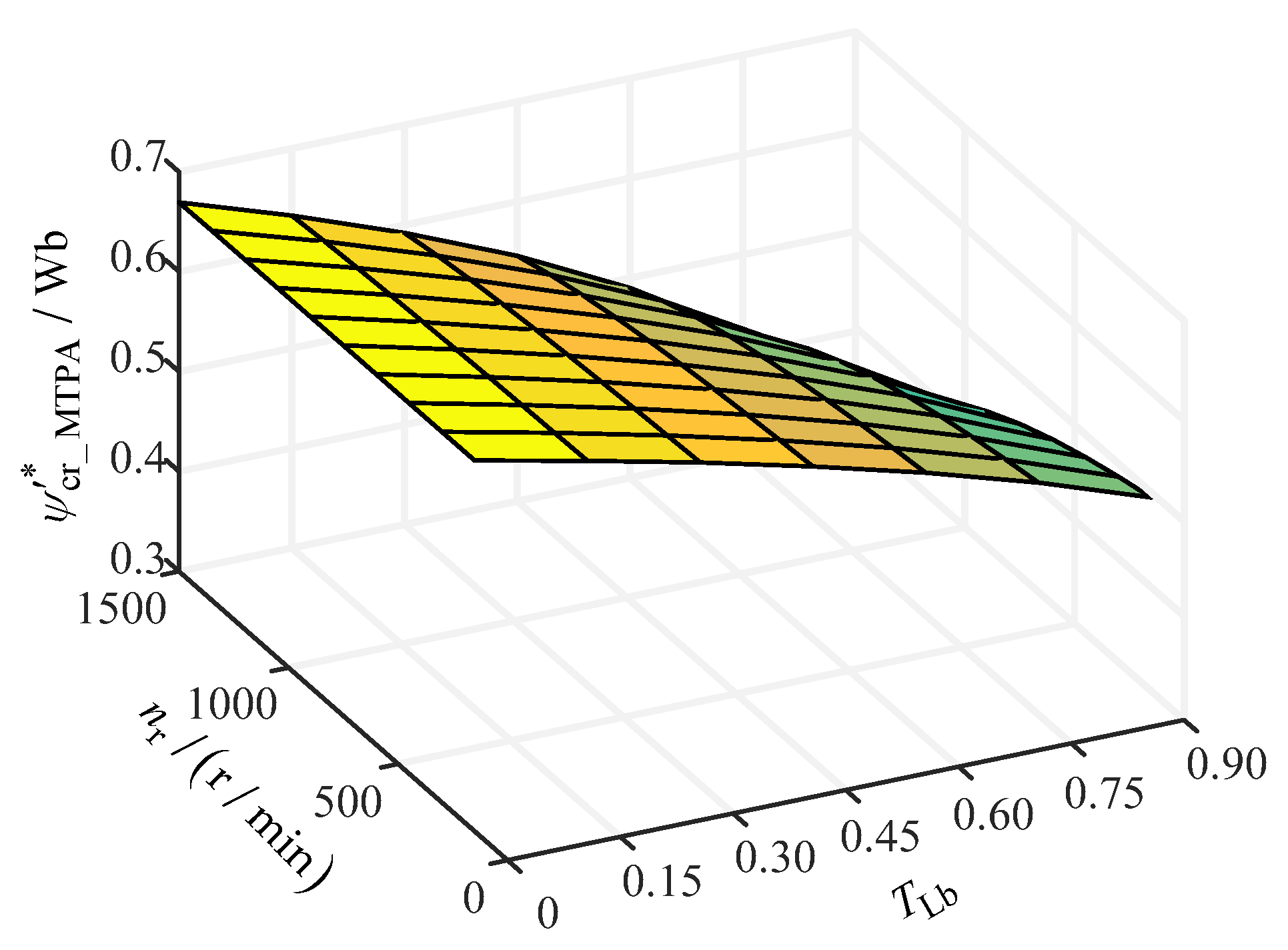
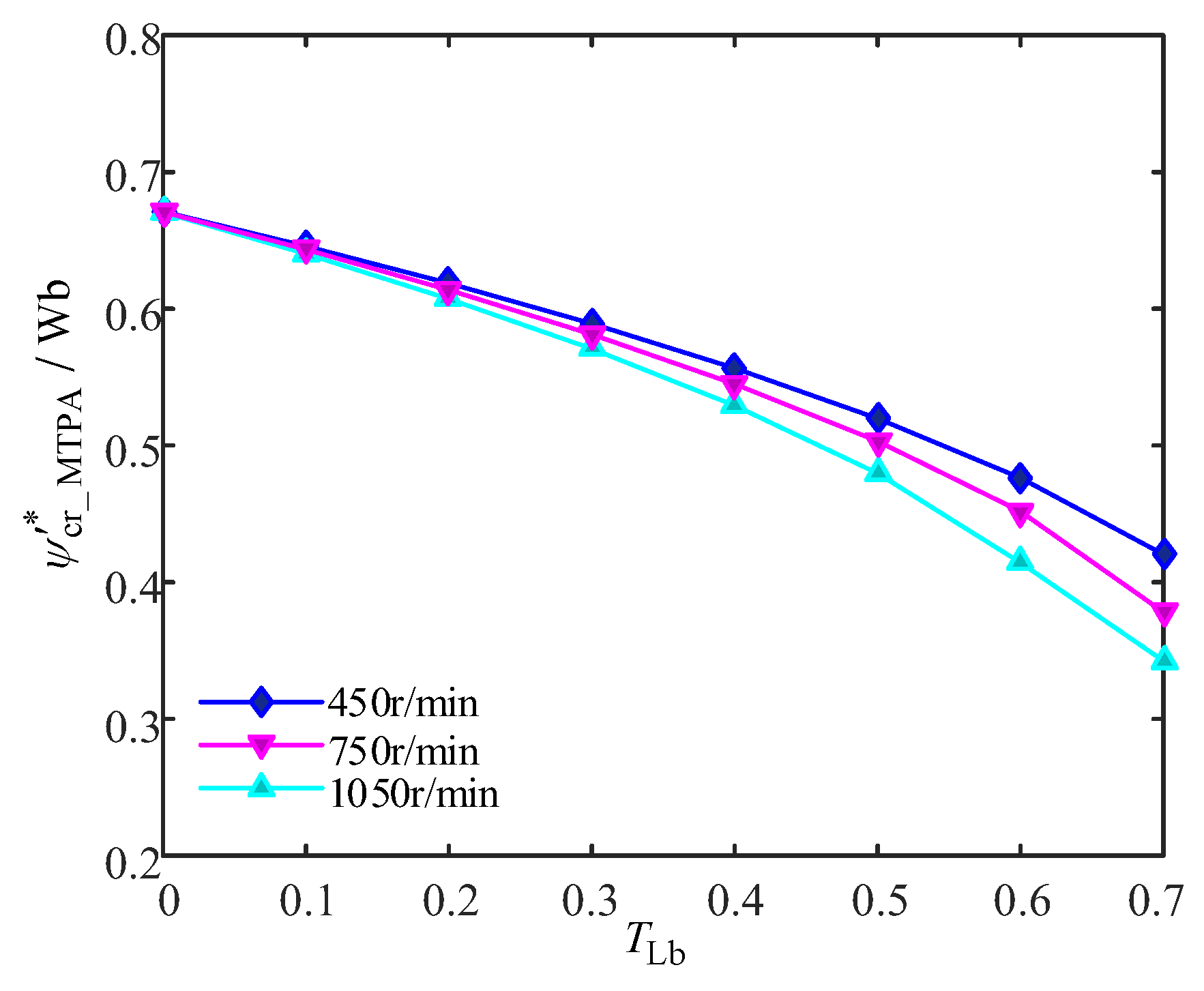
3. Description of MTPA-(SFV-FLC) Optimal Control Strategy
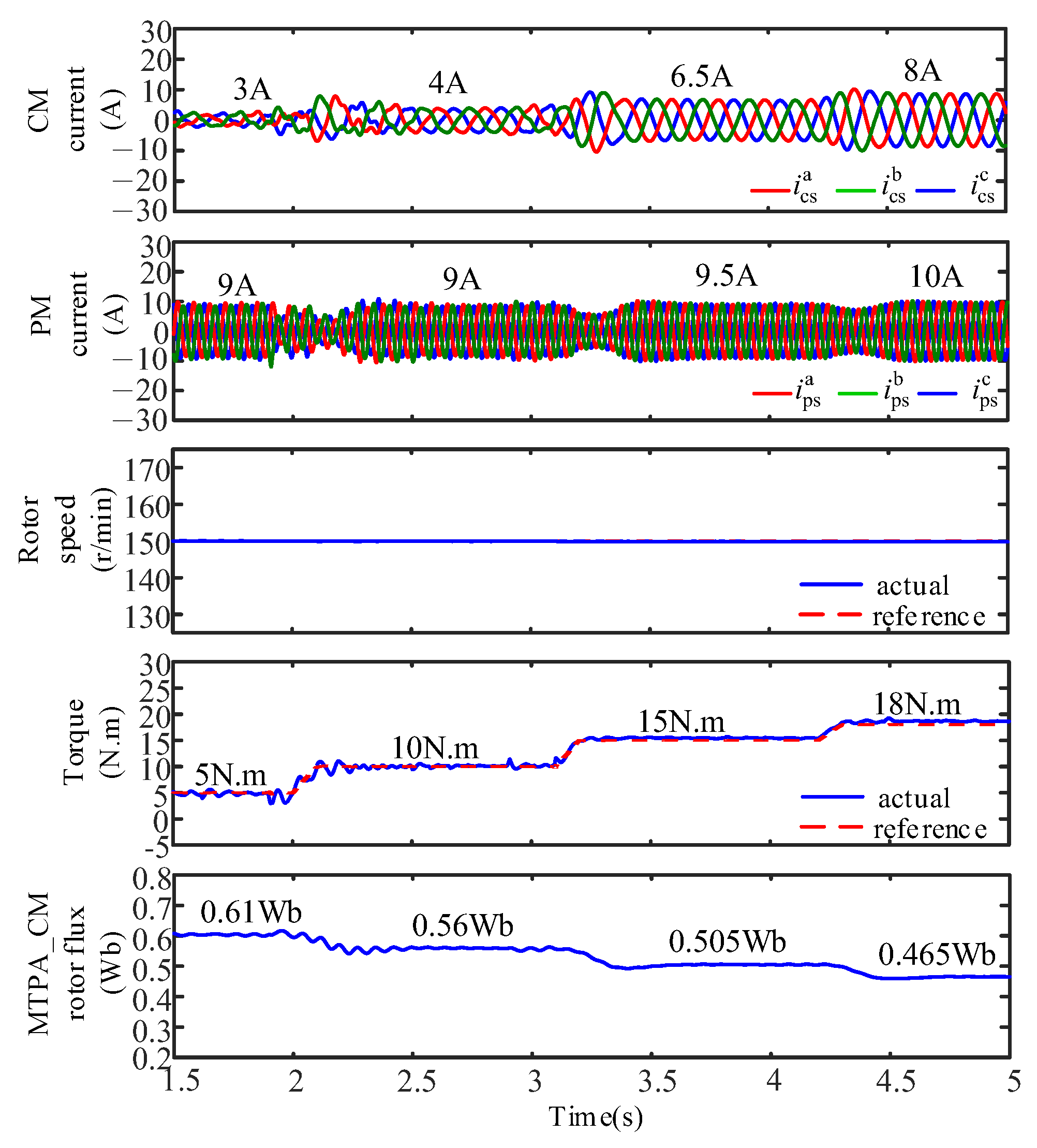
4. Simulation Experiment Results
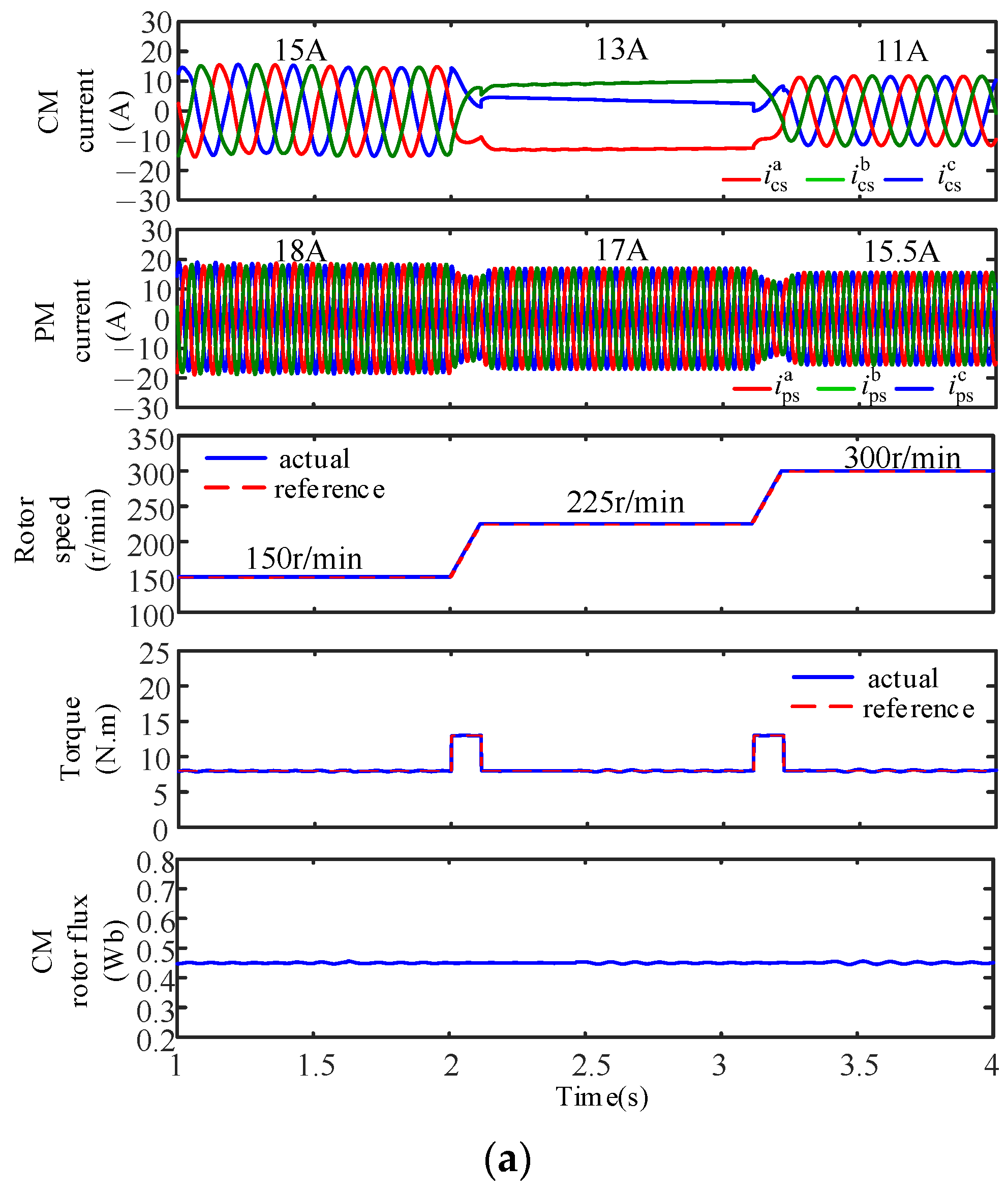
4.1. Verification of Dynamic Tracking Performance
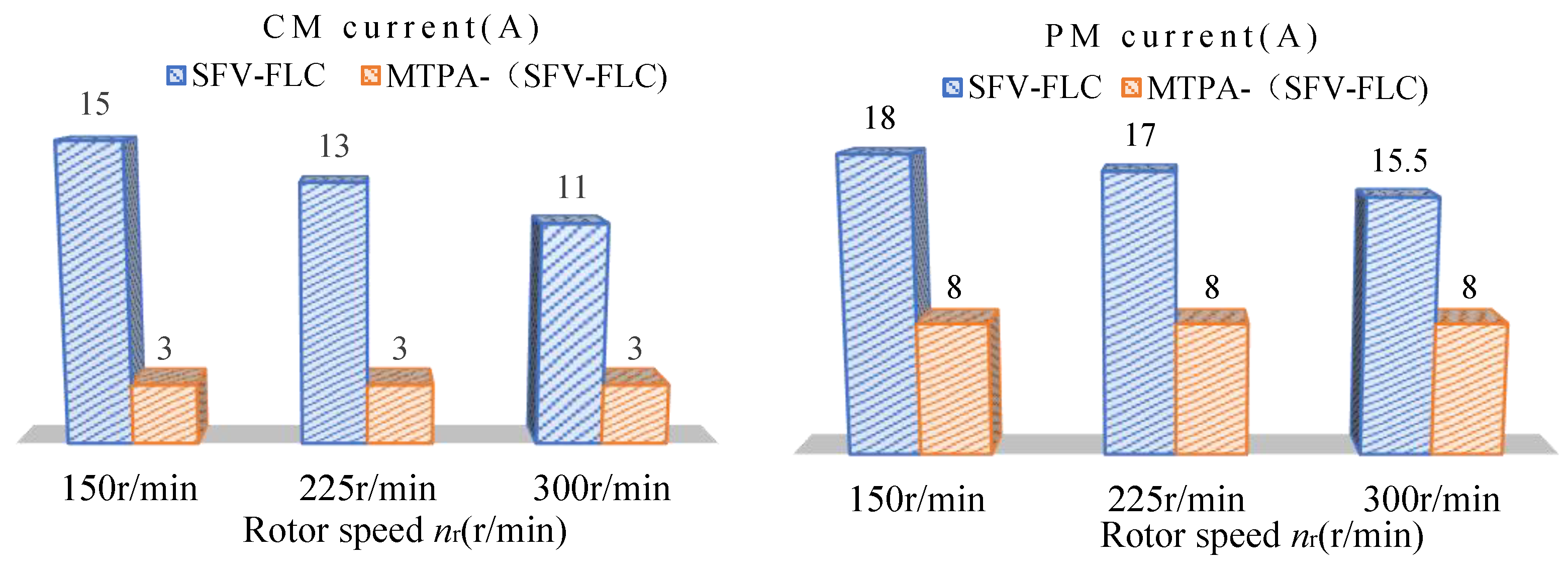
4.2. Verification of Robust Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Agha Kashkooli, M.R.; Ademi, S. Super-Twisting Sliding Mode Direct Power Control of a Brushless Doubly Fed Induction Generator. IEEE Trans. Ind. Electron. 2018, 65, 9147–9156. [Google Scholar] [CrossRef]
- Wei, X.; Cheng, M.; Zhu, J.; Yang, H.; Luo, R. Finite-Set Model Predictive Power Control of Brushless Doubly Fed Twin Stator Induction Generator. IEEE Trans. Power Electron. 2019, 34, 2300–2311. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, M.; Wei, X.; Yan, X.; Zeng, Y. Dual Synchronous Rotating Frame Current Control of Brushless Doubly Fed Induction Generator Under Unbalanced Network. IEEE Trans. Power Electron. 2021, 36, 6712–6724. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-Driven Fault Diagnosis for Traction Systems in High-Speed Trains: A Survey, Challenges, and Perspectives. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1700–1716. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Lu, N.; Jiang, B.; Zio, E. Data-Driven Optimal Test Selection Design for Fault Detection and Isolation Based on CCVKL Method and PSO. IEEE Trans. Instrum. Meas. 2022, 71, 3512310. [Google Scholar] [CrossRef]
- Bing, L.; Shi, L.; Teng, L.; Jia, Z. Duty Ratio Modulation Direct Torque Control of Brushless Doubly-Fed Machines. Automatika 2017, 58, 479–486. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.; Hou, X. Study on the Static Load Capacity and Synthetic Vector Direct Torque Control of Brushless Doubly Fed Machines. Energies 2016, 9, 966. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Yang, M.Y. Vector Control Study for Cascade Brushless Doubly-Fed Machine. Adv. Mater. Res. 2012, 433–440, 7247–7252. [Google Scholar] [CrossRef]
- Shao, S.; Abdi, E.; Barati, F.; McMahon, R. Stator-Flux-Oriented Vector Control for Brushless Doubly Fed Induction Generator. IEEE Trans. Ind. Electron. 2009, 56, 4220–4228. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, J.; Sun, Y.; Su, M.; Tang, W.; Zhu, Q.; Wang, H. A Robust Control Scheme Based on ISMC for the Brushless Doubly Fed Induction Machine. IEEE Trans. Power Electron. 2018, 33, 3129–3140. [Google Scholar] [CrossRef]
- Hopfensperger, B.; Atkinson, D.J.; Lakin, R.A. Stator Flux Oriented Control of a Cascaded Doubly-Fed Induction Machine. IEE Proc.—Electr. Power Appl. 1999, 146, 597. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Xu, S.; Chen, H.; Jia, L.; Ma, K. A General Degradation Process of Useful Life Analysis Under Unreliable Signals for Accelerated Degradation Testing. IEEE Trans. Ind. Inform. 2022, 1–9. [Google Scholar] [CrossRef]
- Wang, N.N. Performance Analysis of Vector Control of Brushless Doubly-Fed Machine in Double Synchronous Reference Frame. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022. [Google Scholar] [CrossRef]
- Xia, C.; Guo, H. Feedback Linearization Control Approach for Brushless Doubly-Fed Machine. Int. J. Precis. Eng. Manuf. 2015, 16, 1699–1709. [Google Scholar] [CrossRef]
- Wei, X.; Cheng, M.; Wang, W.; Han, P.; Luo, R. Direct Voltage Control of Dual-Stator Brushless Doubly Fed Induction Generator for Stand-Alone Wind Energy Conversion Systems. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Sun, T.; Long, L.; Yang, R.; Li, K.; Liang, J. Extended Virtual Signal Injection Control for MTPA Operation of IPMSM Drives with Online Derivative Term Estimation. IEEE Trans. Power Electron. 2021, 36, 10602–10611. [Google Scholar] [CrossRef]
- Khazaee, A.; Zarchi, H.A.; Markadeh, G.A.; Mosaddegh Hesar, H. MTPA Strategy for Direct Torque Control of Brushless DC Motor Drive. IEEE Trans. Ind. Electron. 2021, 68, 6692–6700. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Z.; Alippi, C.; Huang, B.; Liu, D. Explainable Intelligent Fault Diagnosis for Nonlinear Dynamic Systems: From Unsupervised to Supervised Learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, X.; Lu, N.; Jiang, B. Conditional Joint Distribution-Based Test Selection for Fault Detection and Isolation. IEEE Trans. Cybern. 2022, 52, 13168–13180. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.N.; Xia, C.Y. Feedback Linearization and Maximum Torque per Ampere Control Methods of Cup Rotor Permanent-Magnet Doubly Fed Machine. Energies 2021, 14, 6402. [Google Scholar] [CrossRef]
- Lee, K.; Han, Y. Reactive-Power-Based Robust MTPA Control for v/f Scalar-Controlled Induction Motor Drives. IEEE Trans. Ind. Electron. 2022, 69, 169–178. [Google Scholar] [CrossRef]
- Mosaddegh Hesar, H.; Abootorabi Zarchi, H.; Arab Markadeh, G. Online MTPTA and MTPIA Control of Brushless Doubly Fed Induction Motor Drives. IEEE Trans. Power Electron. 2021, 36, 691–701. [Google Scholar] [CrossRef]
- Ahmadian, M.; Jandaghi, B.; Oraee, H. Maximun Torque per Ampere Operation of Brushless Doubly Fed Induction Machines. Renew. Energy Power Qual. J. 2011, 1, 981–985. [Google Scholar] [CrossRef]
- Chen, H.; Li, L.; Shang, C.; Huang, B. Fault Detection for Nonlinear Dynamic Systems with Consideration of Modeling Errors: A Data-Driven Approach. IEEE Trans. Cybern. 2022, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Wang, N. Research and Analysis of the Characteristics of the Brushless Doubly-Fed Machine with High-Performance Decoupling Control. Machines 2023, 11, 313. [Google Scholar] [CrossRef]
- Li, Y.; Lu, N.; Shi, J.; Jiang, B. A Quantitative Causal Diagram Based Optimal Sensor Allocation Strategy Considering the Propagation of Fault Risk. J. Frankl. Inst. 2021, 358, 1021–1043. [Google Scholar] [CrossRef]





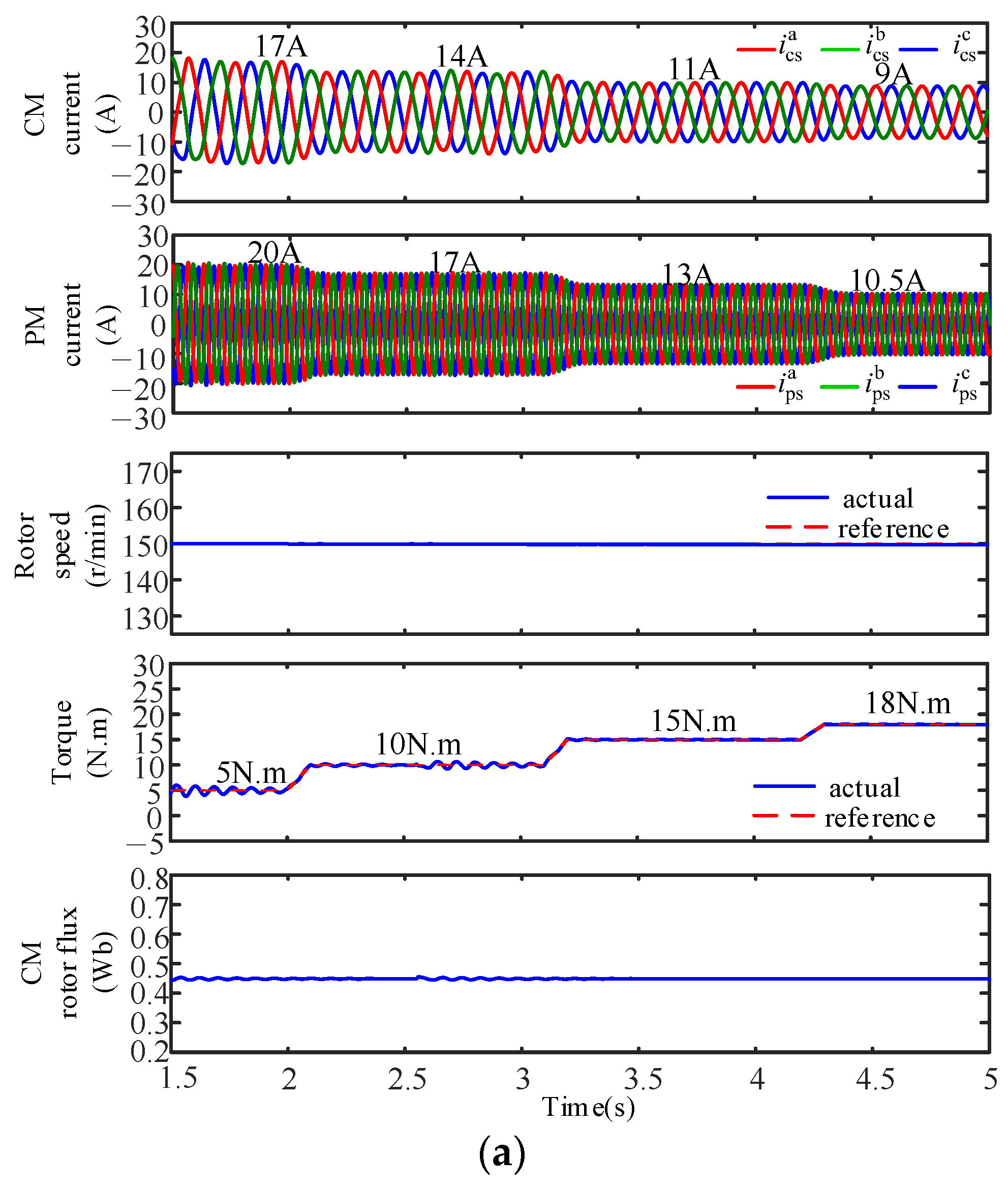
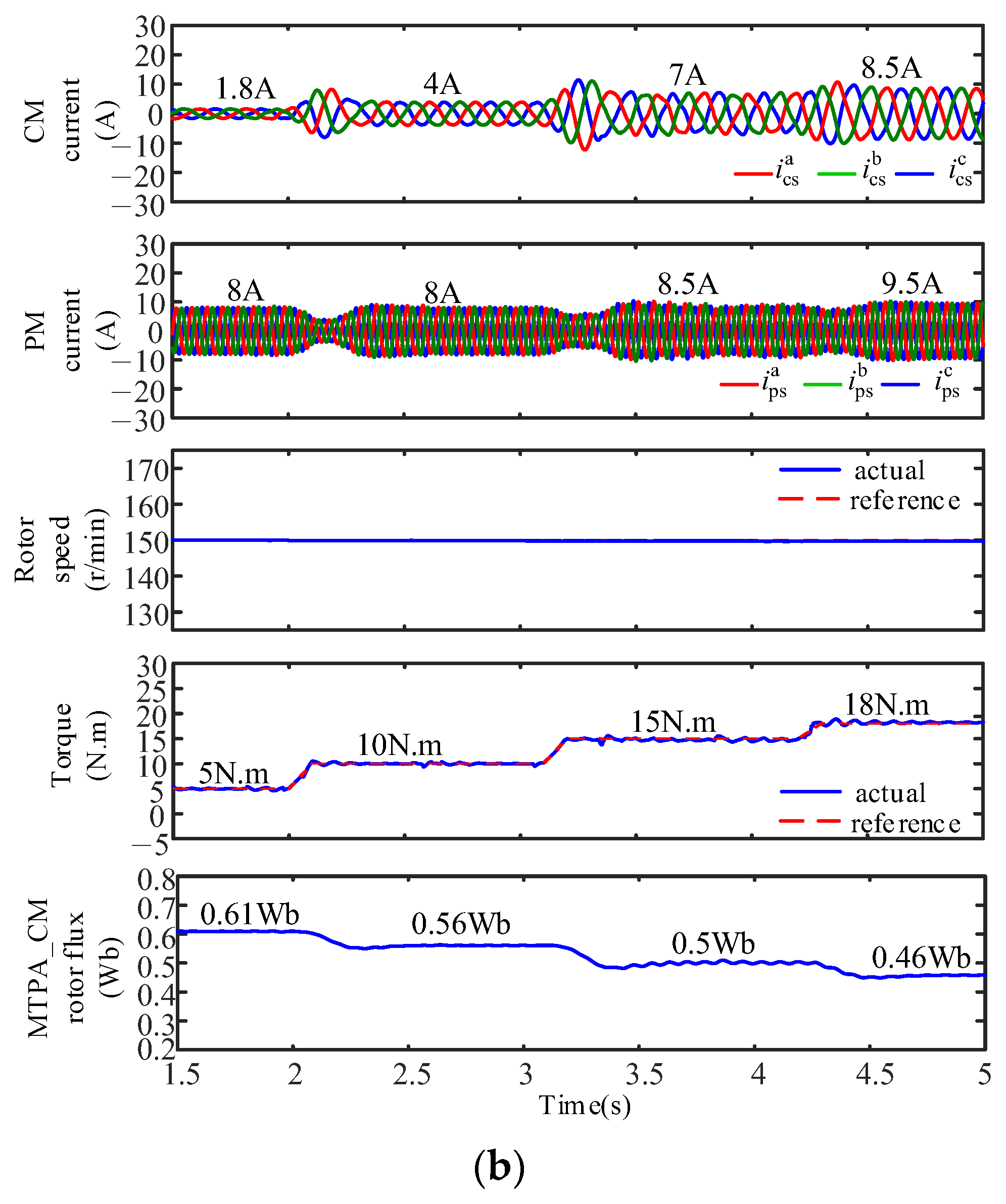
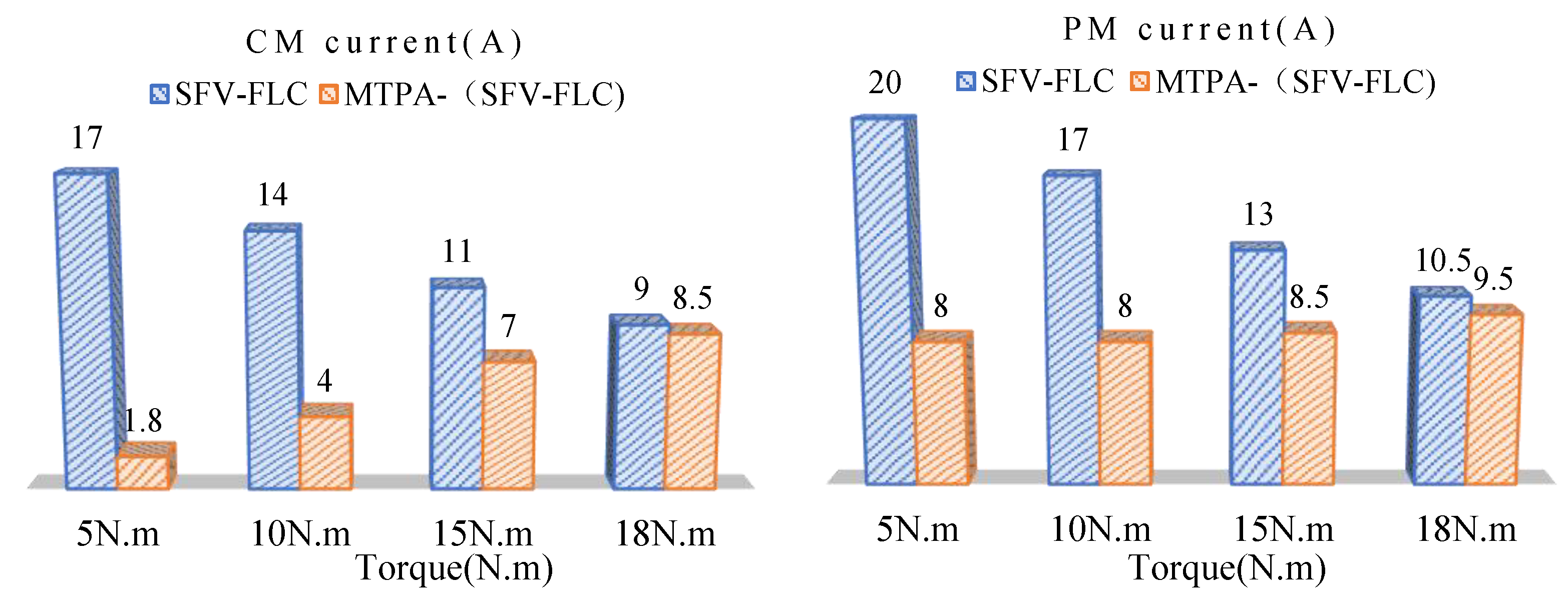
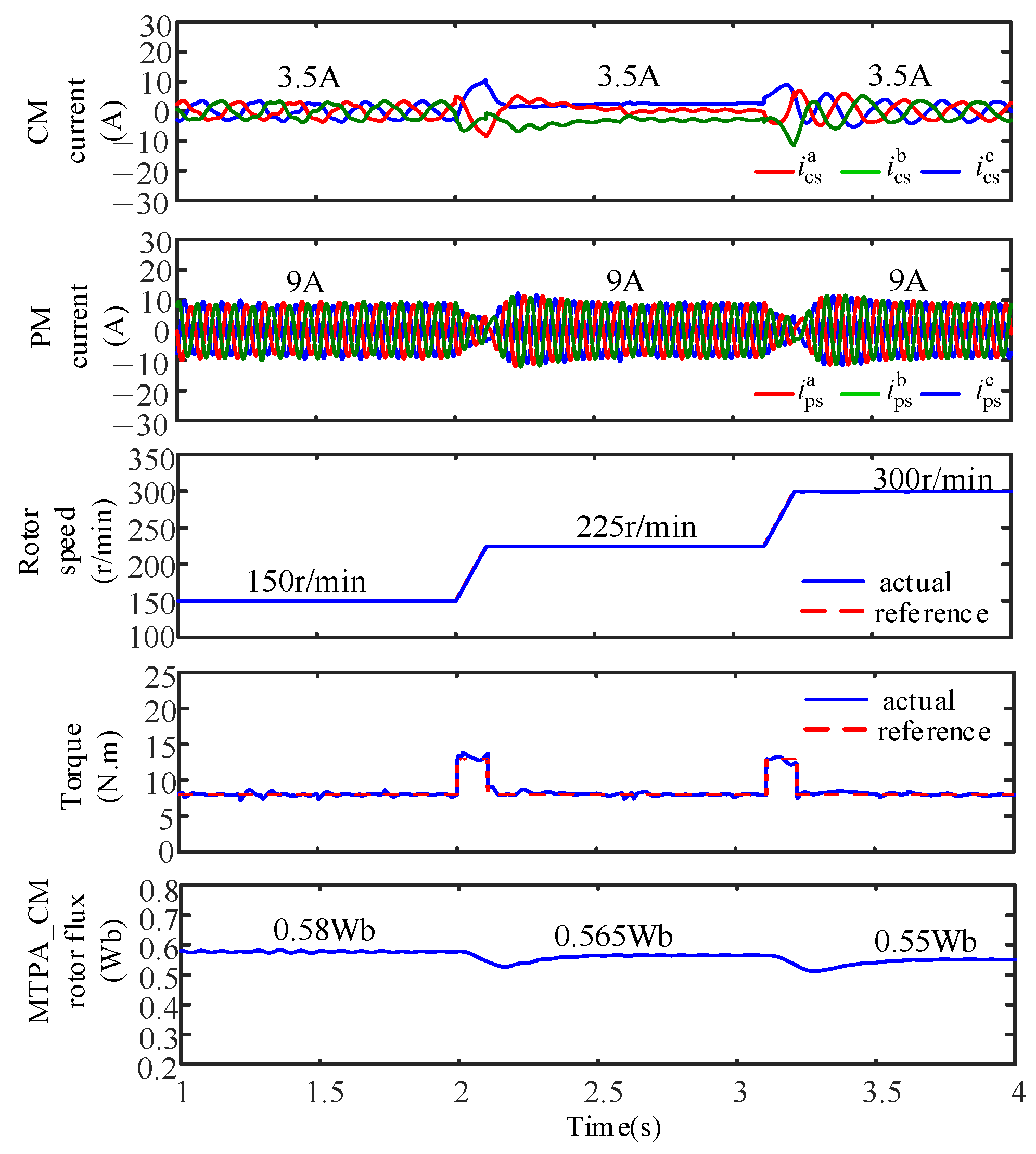


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| P (kW) | 8 | ups (V/Hz) | 220/50 |
| TN/(N·m) | 50 | rps/rcs (Ω) | 0.813/0.533 |
| pp | 1 | rpr/rcr (Ω) | 0.6/0.493 |
| pc | 3 | lps/lcs (H) | 0.372/0.0649 |
| nr (r/min) | 1500 | lpm/lcm (H) | 0.367/0.0636 |
| nr (r/min) | ||
|---|---|---|
| 150 | −80% | −56% |
| 225 | −76% | −53% |
| 300 | −72% | −48.3% |
| Te (N.m) | ||
|---|---|---|
| 5 | −89.4% | −60% |
| 10 | −71% | −53% |
| 15 | −36.3% | −35% |
| 18 | −6% | −9% |
| nr (r/min) | ||
|---|---|---|
| 150 | −76% | −50% |
| 225 | −73% | −47% |
| 300 | −68% | −42% |
| Te (N.m) | ||
|---|---|---|
| 5 | −82.3% | −55% |
| 10 | −71% | −47% |
| 15 | −41% | −27% |
| 18 | −8% | −5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Xia, C. Research on the Optimal Control Strategy for the Maximum Torque per Ampere of Brushless Doubly Fed Machines. Machines 2023, 11, 422. https://doi.org/10.3390/machines11040422
Wang N, Xia C. Research on the Optimal Control Strategy for the Maximum Torque per Ampere of Brushless Doubly Fed Machines. Machines. 2023; 11(4):422. https://doi.org/10.3390/machines11040422
Chicago/Turabian StyleWang, Nannan, and Chaoying Xia. 2023. "Research on the Optimal Control Strategy for the Maximum Torque per Ampere of Brushless Doubly Fed Machines" Machines 11, no. 4: 422. https://doi.org/10.3390/machines11040422
APA StyleWang, N., & Xia, C. (2023). Research on the Optimal Control Strategy for the Maximum Torque per Ampere of Brushless Doubly Fed Machines. Machines, 11(4), 422. https://doi.org/10.3390/machines11040422









