Enhancing Positional Accuracy of the XY-Linear Stage Using Laser Tracker Feedback and IT2FLS
Abstract
:1. Introduction
2. Interval Type-2 Fuzzy Systems Structure
- Find the interval type-2 fuzzy membership functions are as follows
- Calculate and , j = 1, …, M as follows
- Calculate , and as in (7) and (9), where is as defined as in (2).
- Calculate , and as in (6) and (8).
- Calculate as in (10).


3. Experimental Setup
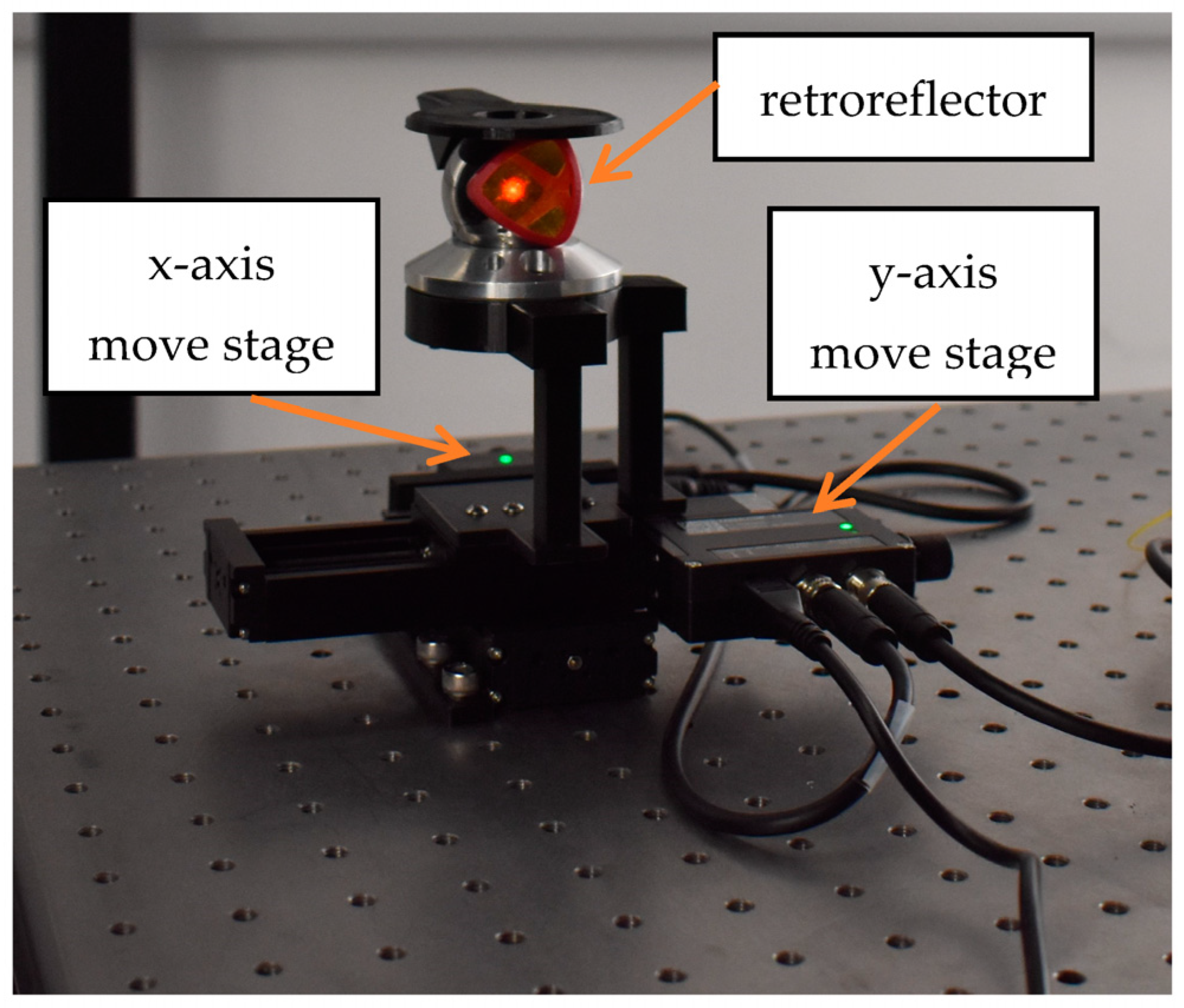
3.1. Hardware Setup
3.1.1. Laser Tracker
3.1.2. XY-Linear Stage
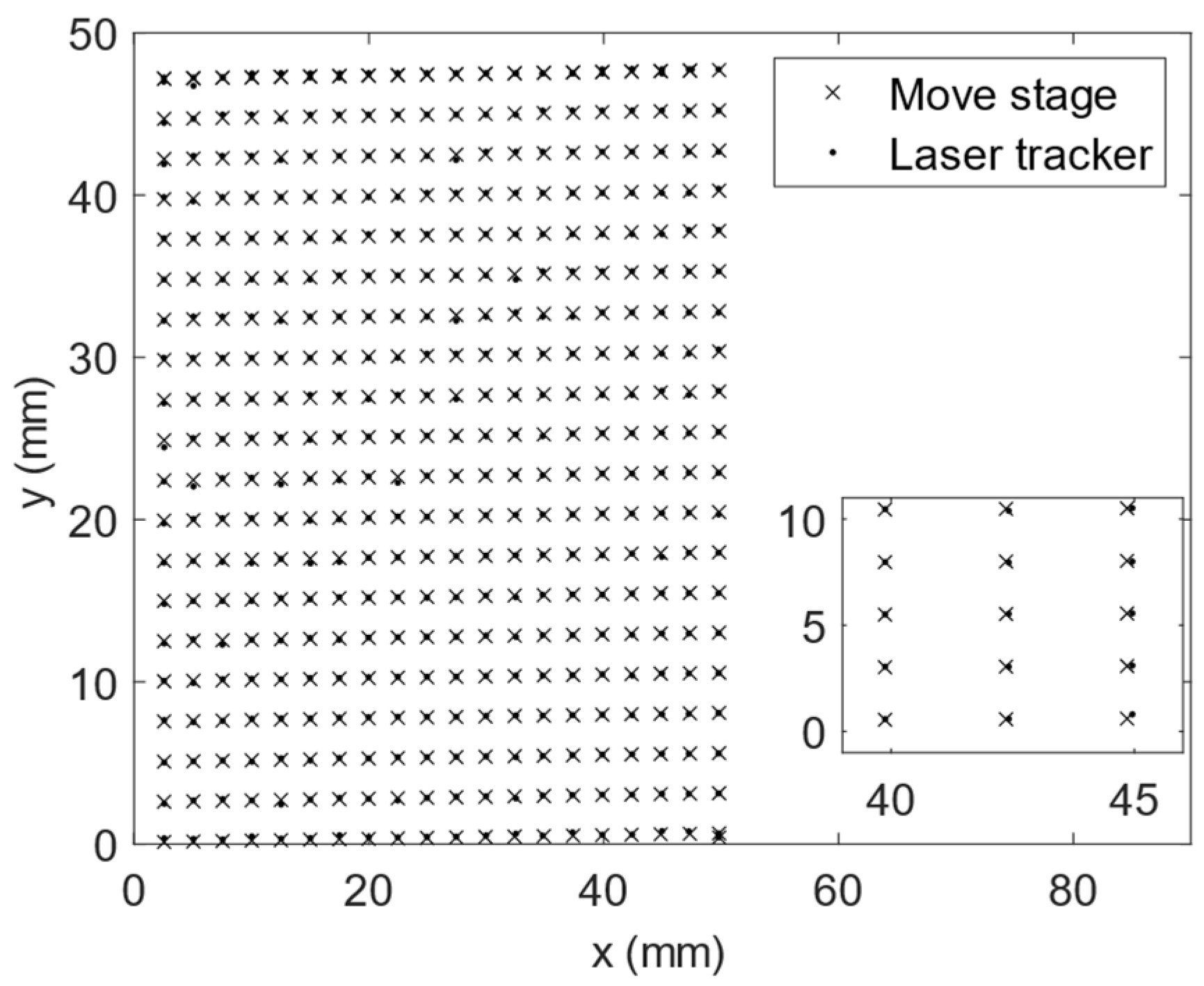
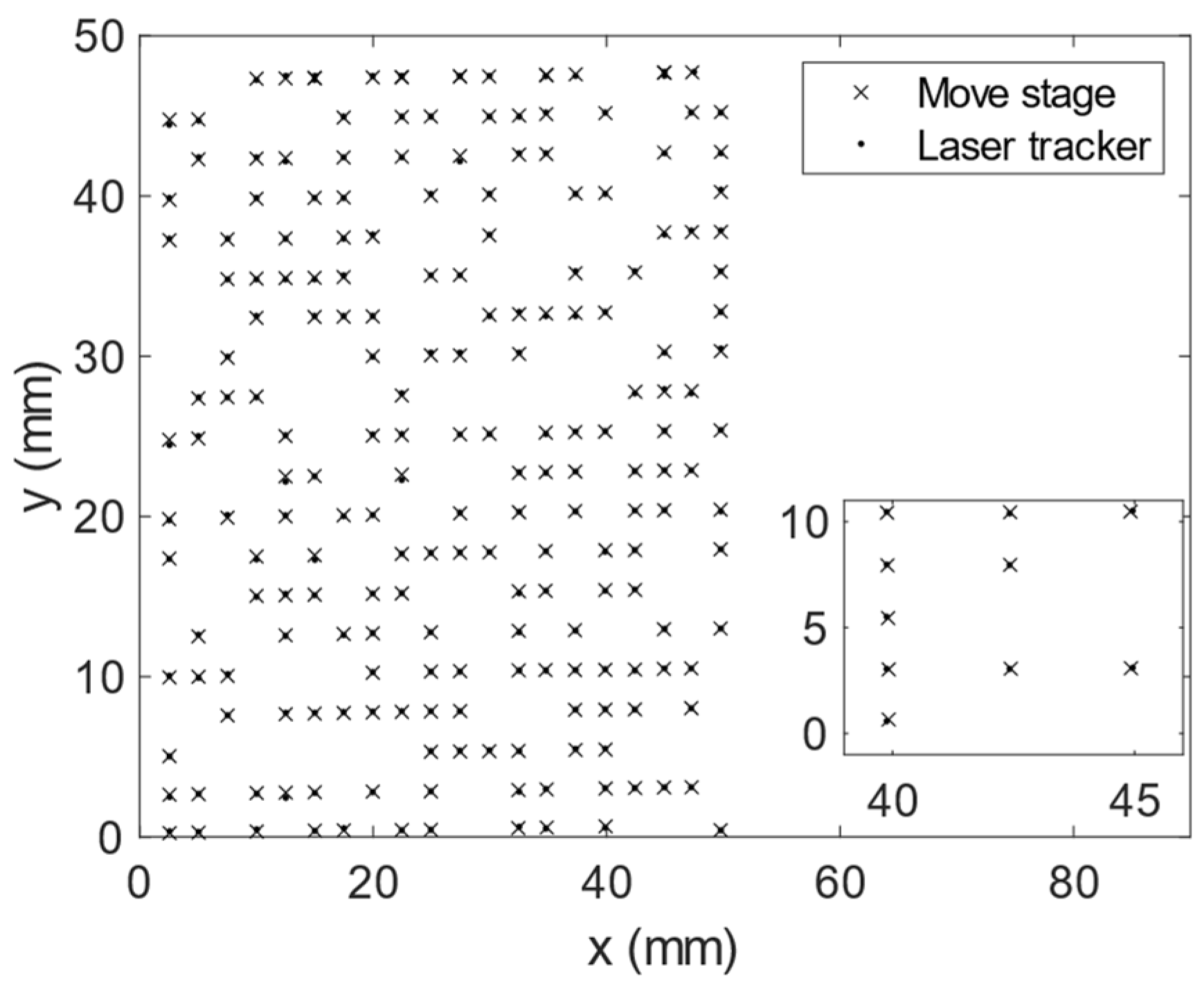
3.2. Data Resampling and Synchronization
3.3. Change in Coordinates
4. Methodology
4.1. Particle Swarm Optimization
4.2. Training IT2FLS
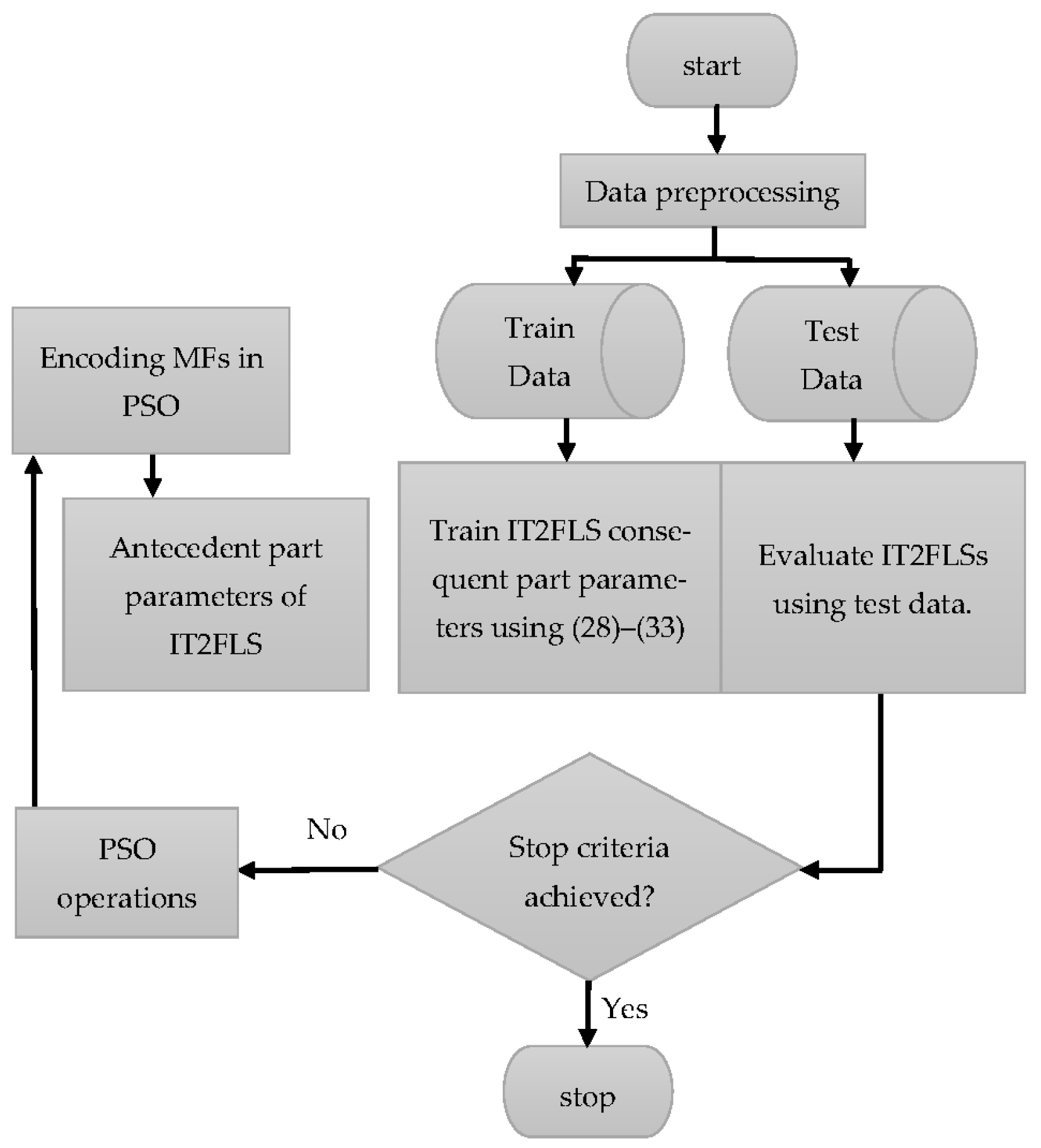
4.3. Overall Hybrid Training Algorithm for IT2FLS
4.4. Overall Calibration Algorithm
5. Experimental Results
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, P.; Takamura, T.; Takahashi, S.; Takamasu, K.; Sato, O.; Osawa, S.; Takatsuji, T. Development of high-precision micro-coordinate measuring machine: Multi-probe measurement system for measuring yaw and straightness motion error of XY linear stage. Precis. Eng. 2011, 35, 424–430. [Google Scholar] [CrossRef]
- Jeong, Y.; Dong, J.; Ferreira, P. Self-calibration of dual-actuated single-axis nanopositioners. Meas. Sci. Technol. 2008, 19, 045203. [Google Scholar] [CrossRef]
- Yoo, S.; Kim, S.-W. Self-calibration algorithm for testing out-of-plane errors of two-dimensional profiling stages. Int. J. Mach. Tools Manuf. 2004, 44, 767–774. [Google Scholar] [CrossRef]
- Korpelainen, V.; Lassila, A. Calibration of a commercial AFM: Traceability for a coordinate system. Meas. Sci. Technol. 2007, 18, 395. [Google Scholar] [CrossRef]
- Xu, M.; Dziomba, T.; Dai, G.; Koenders, L. Self-calibration of scanning probe microscope: Mapping the errors of the instrument. Meas. Sci. Technol. 2008, 19, 025105. [Google Scholar] [CrossRef]
- Dang, Q.; Yoo, S.; Kim, S.-W. Complete 3-D self-calibration of coordinate measuring machines. CIRP Ann. 2006, 55, 527–530. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Phillips, S.; Sawyer, D. Laser trackers for large-scale dimensional metrology: A review. Precis. Eng. 2016, 44, 13–28. [Google Scholar] [CrossRef]
- Mei, B.; Zhu, W. Accurate positioning of a drilling and riveting cell for aircraft assembly. Robot. Comput.-Integr. Manuf. 2021, 69, 102112. [Google Scholar] [CrossRef]
- Guo, F.; Wang, Z.; Kang, Y.; Li, X.; Chang, Z.; Wang, B. Positioning method and assembly precision for aircraft wing skin. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 317–327. [Google Scholar] [CrossRef]
- Gale, D.M. Experience of primary surface alignment for the LMT using a laser tracker in a non-metrology environment. In Proceedings of the Ground-Based and Airborne Telescopes IV, Amsterdam, The Netherlands, 1–6 July 2012; Volume 8444, pp. 1649–1664. [Google Scholar]
- Rakich, A.; Bugonovic, D. A laser-tracker-target fiducialized alignment telescope for astronomical telescope alignment. In Proceedings of the Ground-Based and Airborne Telescopes IX, Montreal, QC, Canada, 17–22 July 2022; Volume 12182, p. 1218202. [Google Scholar]
- Burge, J.H.; Su, P.; Zhao, C.; Zobrist, T. Use of a commercial laser tracker for optical alignment. In Proceedings of the Optical System Alignment and Tolerancing, San Diego, CA, USA, 26–27 August 2007; Volume 6676, pp. 132–143. [Google Scholar]
- Lou, Z.; Zhang, J.; Gao, R.; Xu, L.; Fan, K.-C.; Wang, X. A 3D Passive Laser Tracker for Accuracy Calibration of Robots. IEEE/ASME Trans. Mechatron. 2022, 27, 5803–5811. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, R.; Keogh, P. Real-time laser tracker compensation of robotic drilling and machining. J. Manuf. Mater. Process. 2020, 4, 79. [Google Scholar] [CrossRef]
- Nguyen, V.; Cvitanic, T.; Baxter, M.; Ahlin, K.; Johnson, J.; Freeman, P.; Balakirsky, S.; Brown, A.; Melkote, S. Precision robotic milling of fiberglass shims in aircraft wing assembly using laser tracker feedback. SAE Int. J. Aerosp. 2022, 15, 87–97. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Piano, S.; Branson, D. Improving the Positional Accuracy of Industrial Robots by Forward Kinematic Calibration Using Laser Tracker System. In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics, Lisbon, Portugal, 14–16 July 2022. [Google Scholar]
- Xu, S.; An, X.; Qiao, X.; Zhu, L.; Li, L. Multi-output least-squares support vector regression machines. Pattern Recognit. Lett. 2013, 34, 1078–1084. [Google Scholar] [CrossRef]
- Wu, D. An overview of alternative type-reduction approaches for reducing the computational cost of interval type-2 fuzzy logic controllers. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Chen, C.; Wu, D.; Garibaldi, J.M.; John, R.I.; Twycross, J.; Mendel, J.M. A comprehensive study of the efficiency of type-reduction algorithms. IEEE Trans. Fuzzy Syst. 2020, 29, 1556–1566. [Google Scholar] [CrossRef]
- Mendel, J.M. Interval type-2 fuzzy systems. In Uncertain Rule-Based Fuzzy Systems: Introduction and New Directions, 2nd ed.; Springer: Cham, Switzerland, 2017; pp. 449–527. [Google Scholar]
- Wu, D.; Mendel, J.M. Enhanced karnik–mendel algorithms. IEEE Trans. Fuzzy Syst. 2008, 17, 923–934. [Google Scholar]
- Wu, D.; Mendel, J.M. Enhanced Karnik-Mendel algorithms for Interval Type-2 fuzzy sets and systems. In Proceedings of the NAFIPS 2007—2007 Annual Meeting of the North American Fuzzy Information Processing Society, San Diego, CA, USA, 24–27 June 2007; pp. 184–189. [Google Scholar]
- Greenfield, S.; Chiclana, F. Accuracy and complexity evaluation of defuzzification strategies for the discretised interval type-2 fuzzy set. Int. J. Approx. Reason. 2013, 54, 1013–1033. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.; Mendel, J. On the robustness of type-1 and interval type-2 fuzzy logic systems in modeling. Inf. Sci. 2011, 181, 1325–1347. [Google Scholar] [CrossRef]
- Nie, M.; Tan, W.W. Towards an efficient type-reduction method for interval type-2 fuzzy logic systems. In Proceedings of the 2008 IEEE International Conference on Fuzzy Systems (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1425–1432. [Google Scholar]
- Li, J.; John, R.; Coupland, S.; Kendall, G. On Nie-Tan operator and type-reduction of interval type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 26, 1036–1039. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Mendel, J.M. Maclaurin series expansion complexity-reduced center of sets type-reduction+ defuzzification for interval type-2 fuzzy systems. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 1224–1231. [Google Scholar]
- Khanesar, M.; Branson, D.T. Prediction interval identification using interval type-2 fuzzy logic systems: Lake water level prediction using remote sensing data. IEEE Sens. J. 2021, 21, 13815–13827. [Google Scholar] [CrossRef]
- Kyle, S. Operational features of the Leica laser tracker. In Proceedings of the IEE Seminar on Business Improvement through Measurement, Birmingham, UK, 8 June 1999. [Google Scholar]
- Dusek, J.E.; Triantafyllou, M.S.; Lang, J.H. Piezoresistive foam sensor arrays for marine applications. Sens. Actuators A Phys. 2016, 248, 173–183. [Google Scholar] [CrossRef]
- Castellanos-Ramos, J.; Navas-González, R.; Fernández, I.; Vidal-Verdú, F. Insights into the mechanical behaviour of a layered flexible tactile sensor. Sensors 2015, 15, 25433–25462. [Google Scholar] [CrossRef]
- Arrington, C.B.; Rau, D.A.; Williams, C.B.; Long, T.E. UV-assisted direct ink write printing of fully aromatic Poly (amide imide) s: Elucidating the influence of an acrylic scaffold. Polymer 2021, 212, 123306. [Google Scholar] [CrossRef]
- Fotiou, A.; Kaltsikis, C. Computationally efficient methods and solutions with least squares similarity transformation models. Living GIS 2016, 2, 2018. [Google Scholar]
- Yang, X.-S.; Deb, S.; Zhao, Y.-X.; Fong, S.; He, X. Swarm intelligence: Past, present and future. Soft Comput. 2018, 22, 5923–5933. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kar, A.K. Swarm intelligence: A review of algorithms. In Nature-Inspired Computing and Optimization: Theory and Applications; Springer: Cham, Switzerland, 2017; pp. 475–494. [Google Scholar]
- Dong, W.Y.; Zhang, R.R. Order-3 stability analysis of particle swarm optimization. Inf. Sci. 2019, 503, 508–520. [Google Scholar] [CrossRef]
- Kadirkamanathan, V.; Selvarajah, K.; Fleming, P.J. Stability analysis of the particle dynamics in particle swarm optimizer. IEEE Trans. Evol. Comput. 2006, 10, 245–255. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Zhou, A. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput. 2021, 60, 100808. [Google Scholar] [CrossRef]
- Hassan, S.; Khanesar, M.A.; Hussein, N.K.; Belhaouari, S.B.; Amjad, U.; Mashwani, W.K. Optimization of interval type-2 fuzzy logic system using grasshopper optimization algorithm. Comput. Mater. Contin. 2022, 71, 3513–3531. [Google Scholar] [CrossRef]



| Environmental Working Conditions | IP54: The IEC-Certified Sealed Unit Guarantees Ingress Protection against Dust and Other Contaminants |
|---|---|
| Operating temperature | Wide operating temperature range of −15 to 45 degrees Celsius |
| Temperature compensation | MeteoStation: Integrated environmental unit monitors conditions including temperature, pressure, and humidity to compensate for changes |
| ISO certification | ISO 17025 |
| Connectivity | Wifi and LAN |
| Detector features | Red ring reflector—1.5” radius: 19.05 mm ± 0.0025 mm, centring of optics: < ±0.003 mm, ball roundness: ≤0.003 mm, acceptance angle: ±30°, weight: 170 g |
| Data output rate | Measurement rate of up to 1000 points per second |
| Distance accuracy | 40 m in diameter and a 6DoF measuring volume of up to 20 m |
| Laser safety | Laser class 2 |
| Performance Indexes | Percentage Improvement of IT2FLS vs. Raw Data | ||||
| MAE | Train | 41.6 | 50.4 | 52.4 | 20.6% |
| 68.8 | 68.3 | 79.1 | 13.0% | ||
| MAE | Test | 34.2 | 49.7 | 58.2 | 41.2% |
| 55.9 | 69.8 | 86.1 | 35.1% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanesar, M.A.; Yan, M.; Isa, M.; Piano, S.; Ayoubi, M.A.; Branson, D.T. Enhancing Positional Accuracy of the XY-Linear Stage Using Laser Tracker Feedback and IT2FLS. Machines 2023, 11, 497. https://doi.org/10.3390/machines11040497
Khanesar MA, Yan M, Isa M, Piano S, Ayoubi MA, Branson DT. Enhancing Positional Accuracy of the XY-Linear Stage Using Laser Tracker Feedback and IT2FLS. Machines. 2023; 11(4):497. https://doi.org/10.3390/machines11040497
Chicago/Turabian StyleKhanesar, Mojtaba A., Minrui Yan, Mohammed Isa, Samanta Piano, Mohammad A. Ayoubi, and David T. Branson. 2023. "Enhancing Positional Accuracy of the XY-Linear Stage Using Laser Tracker Feedback and IT2FLS" Machines 11, no. 4: 497. https://doi.org/10.3390/machines11040497
APA StyleKhanesar, M. A., Yan, M., Isa, M., Piano, S., Ayoubi, M. A., & Branson, D. T. (2023). Enhancing Positional Accuracy of the XY-Linear Stage Using Laser Tracker Feedback and IT2FLS. Machines, 11(4), 497. https://doi.org/10.3390/machines11040497







