Modeling and Optimization of the Blade Structural Parameters for a Turbomolecular Pump
Abstract
1. Introduction
2. Theoretical Model
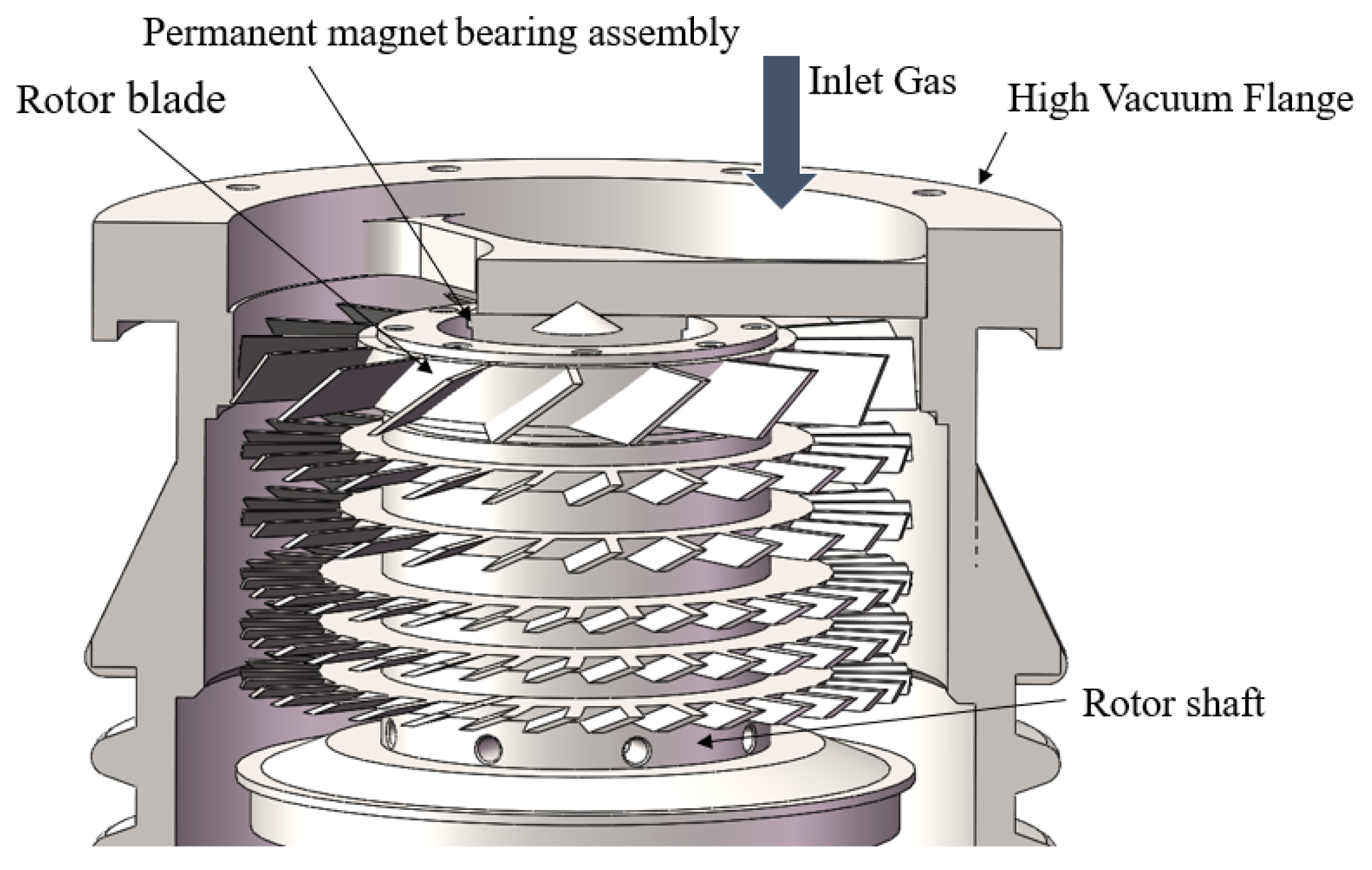
2.1. Working Principle of Turbomolecular Pump
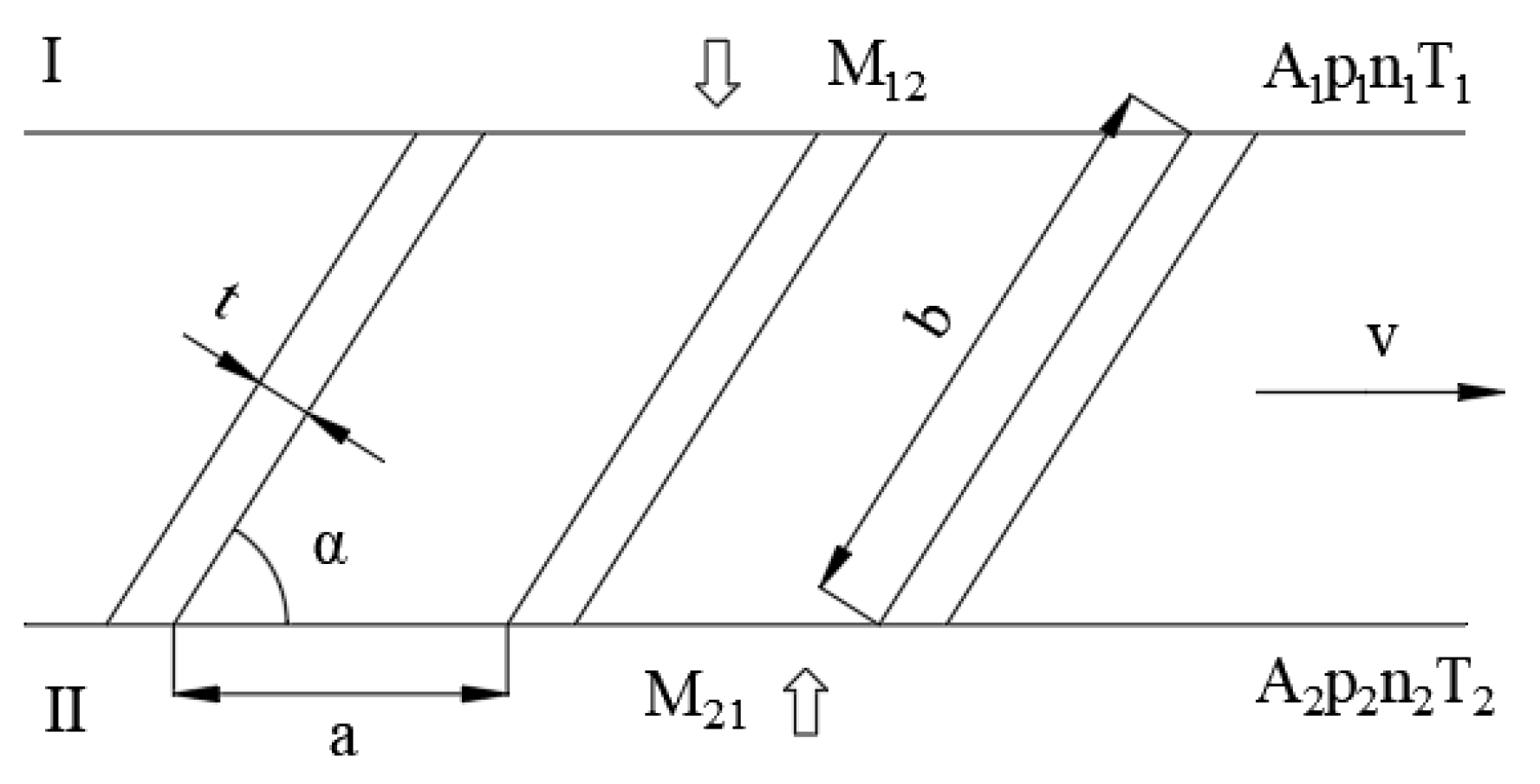
2.2. Aerodynamic Modeling of Turbomolecular Pump
3. Structure Design of a Single-Stage Blade Row with a Curved Surface
3.1. Design of Blade Row Structure
3.2. Simulation Analysis of the Pumping Performance of Blade Rows
4. Structure Parameter Optimization of Blade Rows with Quadratic Surfaces
4.1. Experiment Design
4.2. Simulation Experiment Results and Discussion
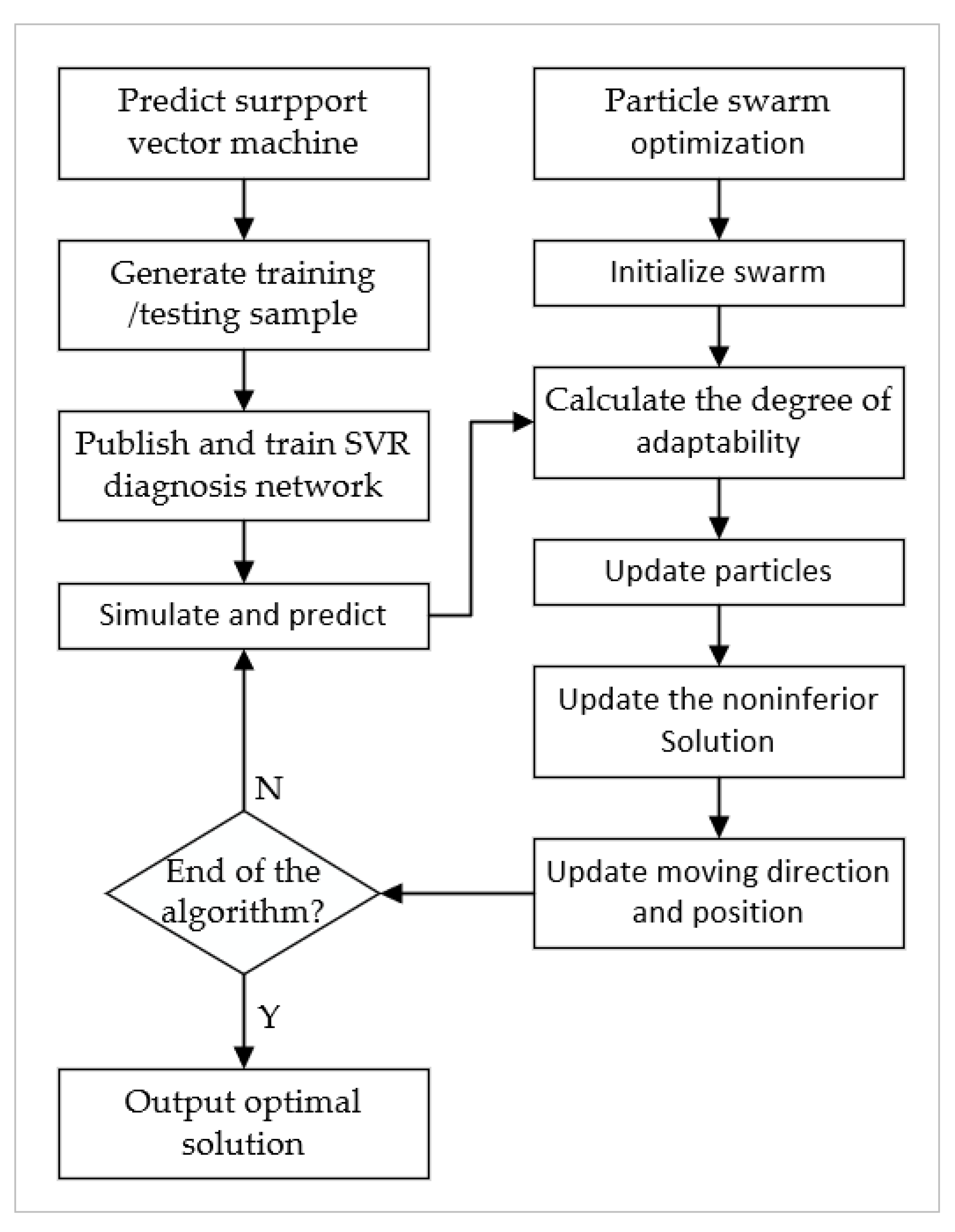
4.3. SVR-PSO Multi-Objective Optimization Algorithm and Optimized Results
4.4. Optimization of Turbine-Stage and Intermediate-Stage Blade Rows
5. Verification of the Model
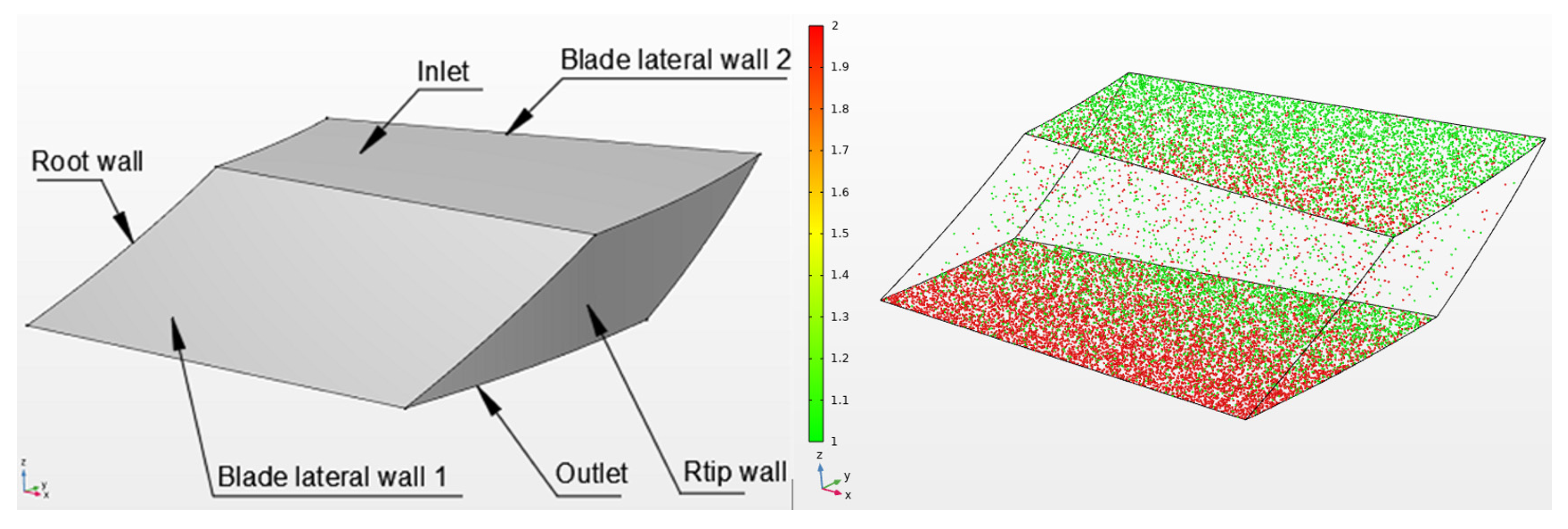
5.1. Test Method
5.2. Performance Testing of TMP Rotor
6. Conclusions
- Several types of curved blade were presented with the ability to improve the pumping performance of TMP. Compared with parallel blades and other curved blades, the positive quadratic surface blades showed better pumping performances, with good promotion and application value for practical engineering.
- The hybrid optimization SVR-PSO method was proposed in order to obtain the structural parameters of the rotor blade for the highest pumping speed and maximum compression ratio. This increased the maximum compression ratio by 10.35% and the maximum pumping speed factor by 4.61%.
- The relative errors of the maximum pumping speed factor and the maximum compression ratio between the results of the aerodynamic model simulation and the experimental data were 2.47–4.83% and 2.47–4.79%, respectively. This means that the thin gas aerodynamic model showed good precision. Therefore, the model can also be utilized to develop new molecular pumps with different pumping performance requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gordeeva, U.S. Efficiency of the Drag Stage Application in the Multistage Turbomolecular Vacuum Pump. In Proceedings of the Oil and Gas Engineering (OGE) Conference, Omsk, Russia, 26–29 February 2020. [Google Scholar]
- Han, B.; Huang, Z.; Le, Y. Design aspects of a large scale turbomolecular pump with active magnetic bearings. Vacuum 2017, 142, 96–105. [Google Scholar] [CrossRef]
- Schopphoff, A.; Braunschweig, F. Generation of UHV with Turbomolecular Pump and Dry Backing Pump Meeting the demand for completely hydrocarbon-free vacuum. Vak. Forsch. Prax. 2017, 29, 22–25. [Google Scholar] [CrossRef]
- Zhang, X.; Han, B.; Liu, X.; Chen, Y.; Zhai, L. Prediction and experiment of DC- bias iron loss in radial magnetic bearing for a small scale turbomolecular pump. Vacuum 2019, 163, 224–235. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Ge, S.; Qian, J.; Miao, W. Portable linear ion trap mass spectrometer with compact multistage vacuum system and continuous atmospheric pressure interface. Analyst 2019, 144, 5127–5135. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-H.; Lu, I.C. Novel ion source for a portable mass spectrometer. Rapid Commun. Mass Spectrom. 2021, 35, e8503. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.; Xu, X.; Huang, Z. Optimal design of magnetically suspended high-speed rotor in turbo-molecular pump. Vacuum 2021, 193, 110510. [Google Scholar] [CrossRef]
- Mao, K.; Liu, G. An improved braking control method for the magnetically levitated TMP with a fast transient response. Vacuum 2018, 148, 312–318. [Google Scholar] [CrossRef]
- Huang, Z.; Han, B.; Mao, K.; Peng, C.; Fang, J. Mechanical stress and thermal aspects of the rotor assembly for turbomolecular pumps. Vacuum 2016, 129, 55–62. [Google Scholar] [CrossRef]
- Hsu, C.N. Experimental and performance analyses of a turbomolecular pump rotor system. Vacuum 2015, 121, 260–273. [Google Scholar] [CrossRef]
- Ge, M.; Petkovsek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Huang, Z.; Han, B.; Le, Y. Modeling method of the modal analysis for turbomolecular pump rotor blades. Vacuum 2017, 144, 145–151. [Google Scholar] [CrossRef]
- Barfuss, H. The Development of the Turbomolecular Pump within the last three Decades Enabler of digital Technologies and High Vacuum Workhorse. Vak. Forsch. Prax. 2018, 30, 20–24. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, S.W.; Han, F.; Zhao, F.; Zhang, Z.J.; Han, J. A New Modeling Method to Reveal Pumping Mechanism of Turbomolecular Pump. J. Appl. Fluid Mech. 2021, 14, 165–173. [Google Scholar] [CrossRef]
- Huang, Z.; Han, B.; Le, Y. Multidisciplinary Design Strategies for Turbomolecular Pumps with Ultrahigh Vacuum Performance. IEEE Trans. Ind. Electron. 2019, 66, 9549–9558. [Google Scholar] [CrossRef]
- Wang, S.; Ninokata, H.; Merzari, E.; Lei, K.; Luo, X.; Lu, L.; Kase, K. Numerical study of a single blade row in turbomolecular pump. Vacuum 2009, 83, 1106–1117. [Google Scholar] [CrossRef]
- Funke, R.; Schnacke, E.; Voss, G. A novel turbomolecular pump for R&D and analytical applications: General remarks on development and applications. Vak. Forsch. Prax. 2015, 27, 30–35. [Google Scholar] [CrossRef]
- Sharipov, F. Numerical simulation of turbomolecular pump over a wide range of gas rarefaction. J. Vac. Sci. Technol. A 2010, 28, 1312–1315. [Google Scholar] [CrossRef]
- Versluis, R.; Dorsman, R.; Thielen, L.; Roos, M.E. Numerical investigation of turbomolecular pumps using the direct simulation Monte Carlo method with moving surfaces. J. Vac. Sci. Technol. A 2009, 27, 543–547. [Google Scholar] [CrossRef]
- Sengil, N.; Edis, F.O. Fast cell determination of the DSMC molecules in multi-stage turbo molecular pump design. Comput. Fluids 2011, 45, 202–206. [Google Scholar] [CrossRef]
- Shams, M.; Sheykhzadeh, H.; Taghavi, M. Mathematical Simulation of Free Molecular Flow in a Three-Dimensional Turbomolecular Pump with Nonparallel Blades. J. Dispers. Sci. Technol. 2010, 31, 299–306. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, S.W.; Li, Y.J.; Zhang, Z.J.; Li, H.T.; Mu, R.Y. Monte Carlo simulation of gas free molecular flow in turbo molecular pump’s inlet tube. Mol. Simul. 2018, 44, 1261–1269. [Google Scholar] [CrossRef]
- Bird, G.A. Effect of inlet guide vanes and sharp blades on the performance of a turbomolecular pump. J. Vac. Sci. Technol. A Vac. Surf. Film. 2011, 29, 011016. [Google Scholar] [CrossRef]
- Sengil, N. Performance increase in turbomolecular pumps with curved type blades. Vacuum 2012, 86, 1764–1769. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Jia, Y.; Liu, M.; Wang, Z. Numerical investigation of three turbomolecular pump models in the free molecular flow range. Vacuum 2014, 101, 337–344. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Guo, W.; Li, D.; Wang, Q.; Feng, K. Accurate simulation of turbomolecular pumps with modified algorithm by 3D direct simulation Monte Carlo method. Vacuum 2014, 109, 354–359. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, H.; Yan, Z.; Han, F.; Yan, H. Machining characteristics of 65 vol.% SiCp/Al composite in micro-WEDM. Ceram. Int. 2021, 47, 13533–13543. [Google Scholar] [CrossRef]
- Ghazvinian, H.; Mousavi, S.-F.; Karami, H.; Farzin, S.; Ehteram, M.; Hossain, M.S.; Fai, C.M.; Bin Hashim, H.; Singh, V.P.; Ros, F.C.; et al. Integrated support vector regression and an improved particle swarm optimization-based model for solar radiation prediction. PLoS ONE 2019, 14, e0217634. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, Z.P.; Adenutsi, C.D.; Zhang, L.; Lai, F.P.; Wang, K.J. A novel multi-objective optimization method for well control parameters based on PSO-LSSVR proxy model and NSGA-II algorithm. J. Pet. Sci. Eng. 2021, 196, 107694. [Google Scholar] [CrossRef]
- Sawada, T.; Murakami, K. The Axial Flow Molecular Pump (I). Shinku 1971, 14, 33–41. [Google Scholar] [CrossRef]

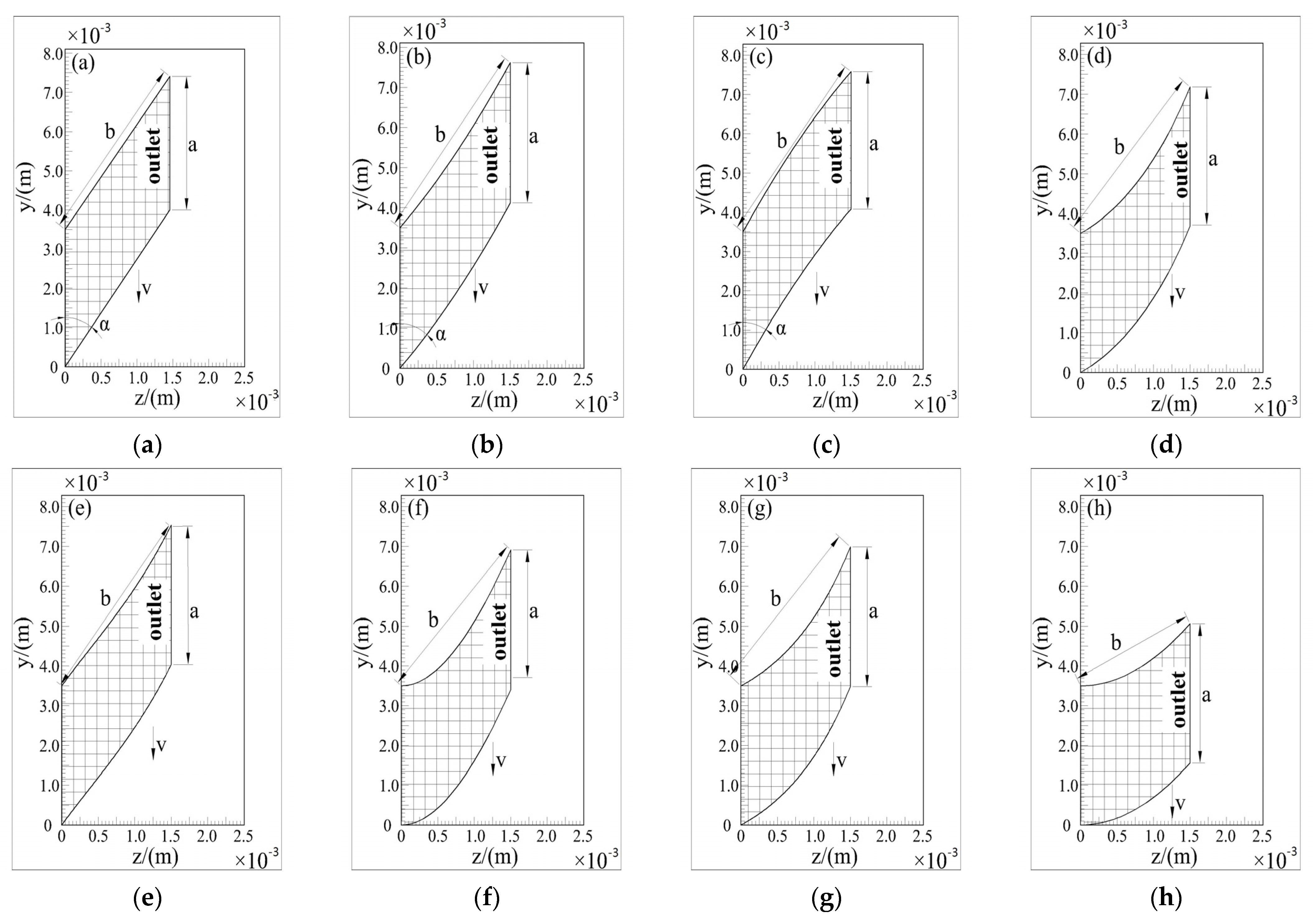




| Turbine Stage | Intermediate Stage | Compression Stage | |
|---|---|---|---|
| No. of blades, N | 16 | 24 | 32 |
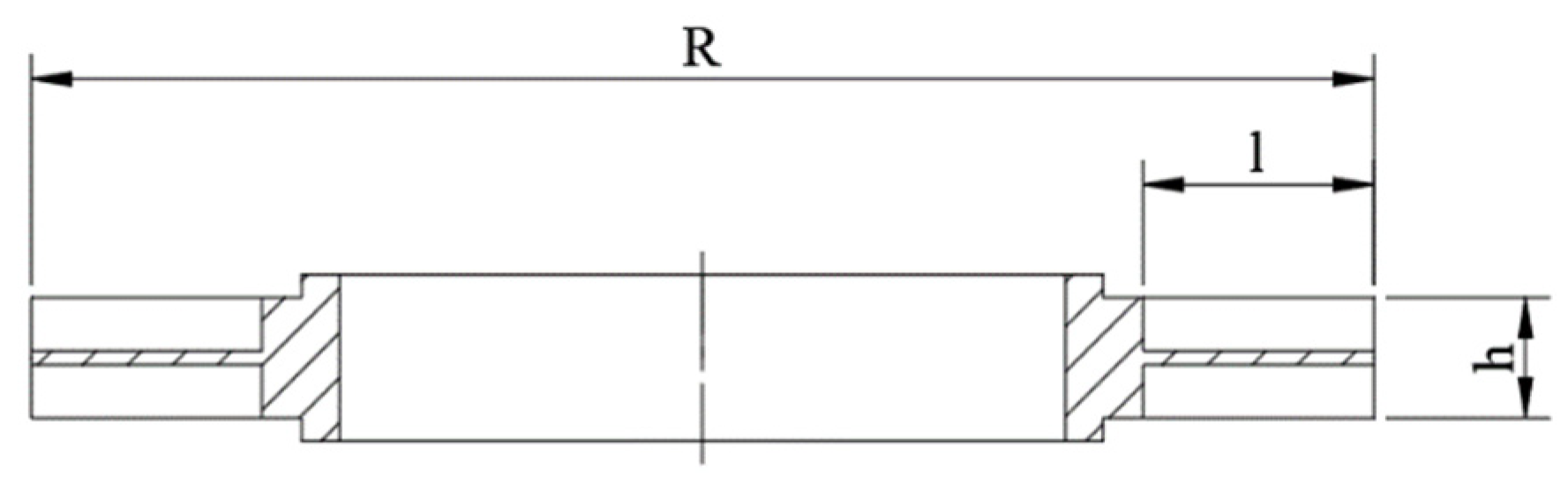
| R (mm) | 67 | 67 | 67 |
| l (mm) | 11.5 | 9.75 | 7.75 |
| α (°) | 36 | 25.5 | 20 |
| h (mm) | 6 | 2 | 1.5 |
| t (mm) | 0.55 | 0.55 | 0.55 |
| Blade Shape | Upper Wall | Lower Wall | Average Angle/(°) |
|---|---|---|---|
| Parallel | y = 2.7475z + 0.0035 | y = 2.7475z | 20 |
| Positive quadratic surfaces | y = 2.1445z + 400z2 + 0.0035 | y = 2.1445z + 400z2 | 19.765 |
| Reverse quadratic surfaces | y = 3.32z − 400z2 + 0.0035 | y = 3.32z − 400z2 | 19.925 |
| Elliptical surface | y = (h2 × 82 − 82/22 × z2)1/2 + 0.0035 | y = (h2 × 82 − 82/22 × z2)1/2 | 19.808 |
| Cubic surface I | y = 2.5z − 400z2 + 3.6 × 105 × z3 + 0.0035 | y = 2.5z − 400z2 + 3.6 * 105 × z3 | 19.903 |
| Cubic surface II | y = 1800z2 − 1.9 × 105 × z3 + 0.0035 | y = 1800z2 − 1.9 × 105 × z3 | 20.018 |
| Exponential surface | y = 0.001 × exp(1000 * z) + 0.0035 | y = 0.001 × exp(1000 * z) | 20.536 |
| Hyperbola surface | y = (0.452 + 0.452 × z2/(h2 * 122))1/2 + 0.0035 | y = (0.452 + 0.452 × z2/(h2 × 122))1/2 | 39.846 |
| Indicator | Parallel | Positive Quadratic | Reverse Quadratic | Elliptical Surface | |||
|---|---|---|---|---|---|---|---|
| Result | Improvement | Result | Improvement | Result | Improvement | ||
| M12 | 0.3606 | 0.3635 | 0.804% | 0.3694 | 2.440% | 0.4048 | 12.26% |
| M21 | 0.1436 | 0.1447 | 0.766% | 0.1482 | 3.203% | 0.1724 | 20.06% |
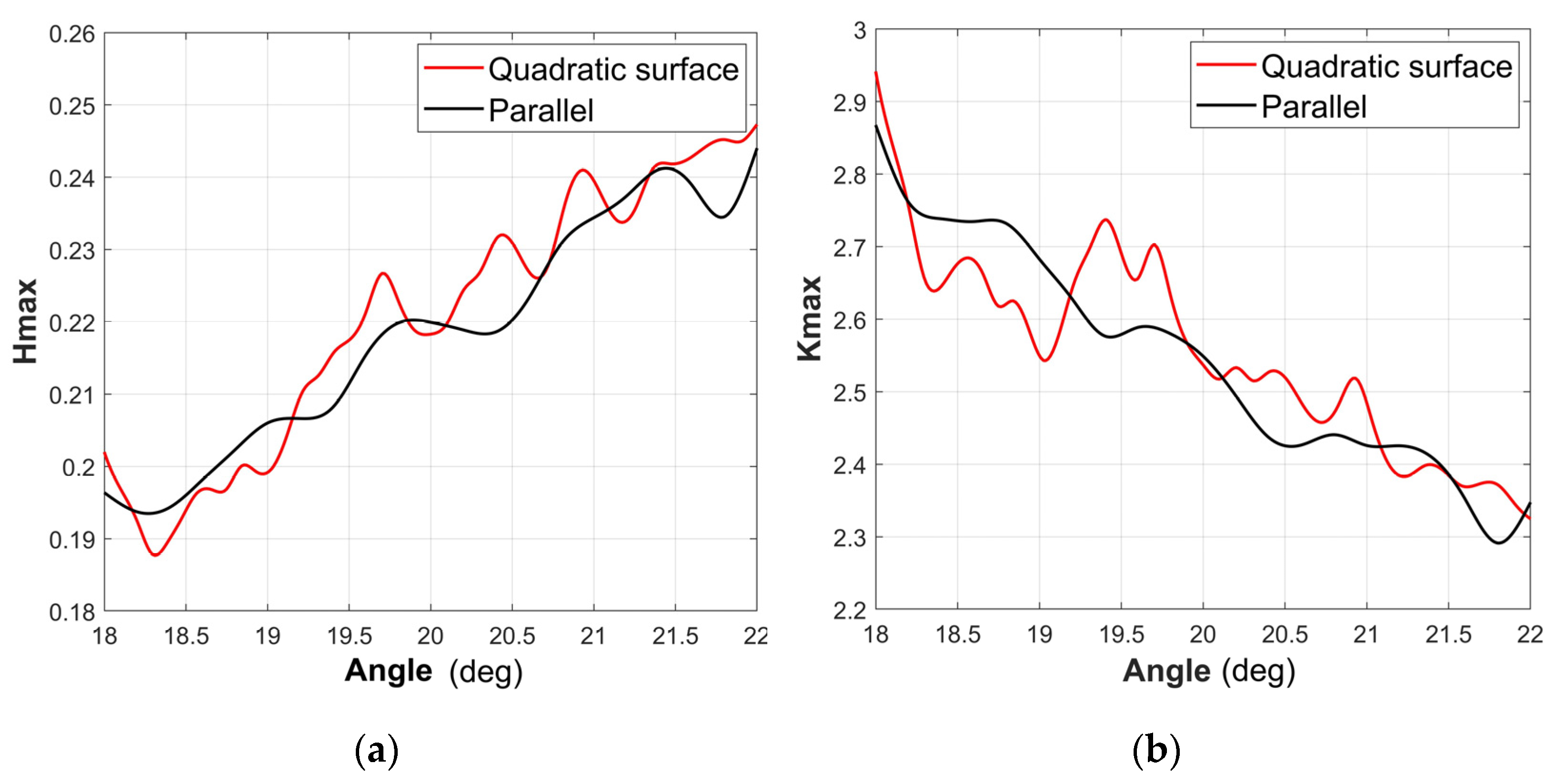
| Hmax | 0.2170 | 0.2188 | 0.829% | 0.2212 | 1.936% | 0.2324 | 7.097% |
| Kmax | 2.5111 | 2.5121 | 0.040% | 2.4926 | −0.737% | 2.3480 | −6.495% |
| Cubic Surface I | Cubic Surface II | Exponential Surface | Hyperbola Surface | ||||
| Result | Improvement | Result | Improvement | Result | Improvement | Result | Improvement |
| 0.3712 | 2.940% | 0.4346 | 20.52% | 0.4320 | 2.440% | 0.3468 | −3.980% |
| 0.1437 | 0.070% | 0.1948 | 35.66% | 0.1964 | 3.203% | 0.1409 | −1.916% |
| 0.2275 | 4.839% | 0.2498 | 15.12% | 0.2356 | 1.936% | 0.2059 | −5.391% |
| 2.5832 | 2.871% | 2.2310 | −11.15% | 2.1996 | −0.737% | 2.4613 | −2.023% |
| m | n | Average Angle/(°) | Hmax | Kmax |
|---|---|---|---|---|
| 2.7475 | −60 | 20.615 | 0.2262 | 2.4775 |
| 2.7475 | −40 | 20.407 | 0.2340 | 2.5425 |
| 2.7475 | −20 | 20.202 | 0.2272 | 2.5691 |
| 2.7475 | 20 | 19.8 | 0.2212 | 2.5994 |
| 2.7475 | 40 | 19.603 | 0.2185 | 2.5937 |
| 2.7475 | 60 | 19.408 | 0.2177 | 2.78 |
| Factor | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
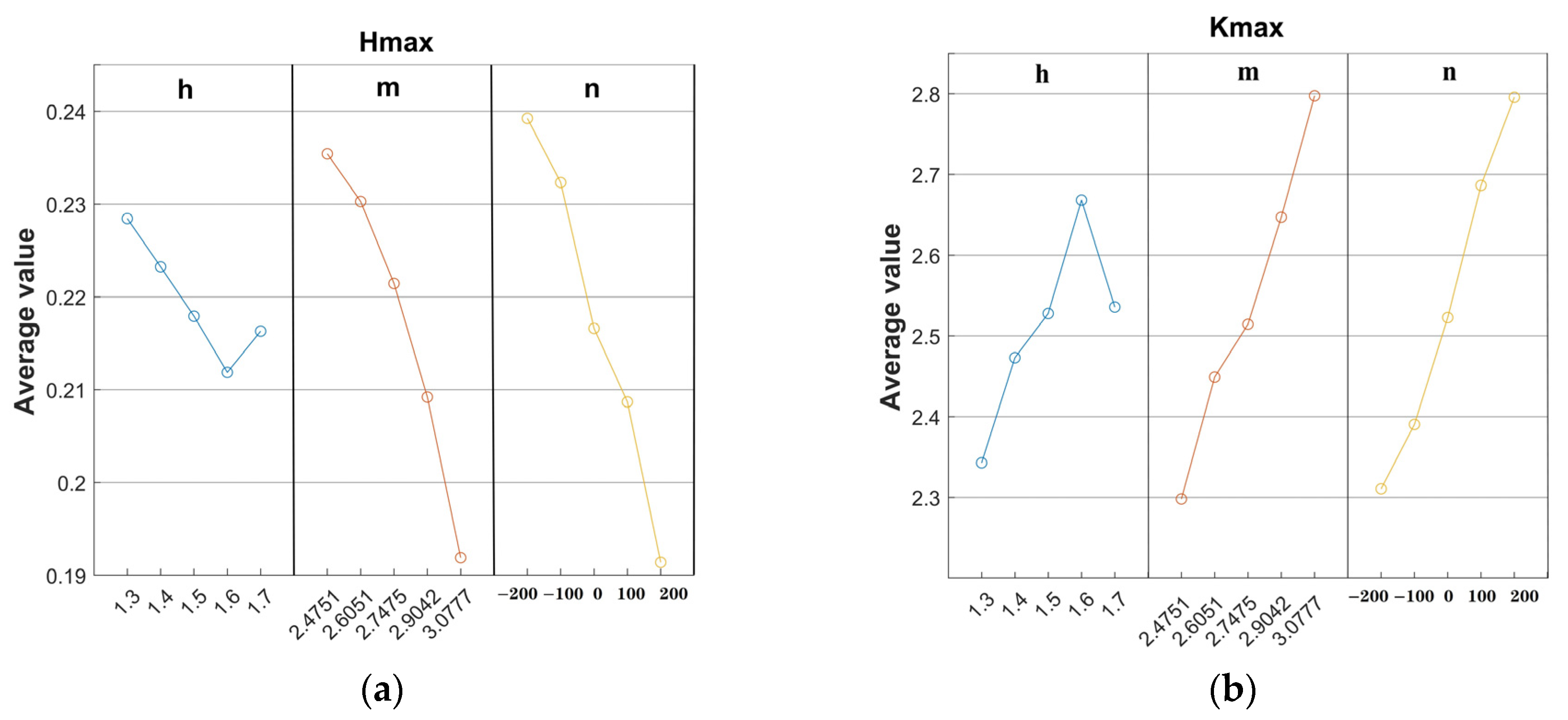
| h | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 |
| m | 2.4751 | 2.6051 | 2.7475 | 2.9042 | 3.0777 |
| n | −200 | −100 | 0 | 100 | 200 |
| No. | h (mm) | m | n | Hmax | Kmax |
|---|---|---|---|---|---|
| 1 | 1.3 | 2.4751 | −200 | 0.251 | 1.86 |
| 2 | 1.3 | 2.6051 | −100 | 0.259 | 2.15 |
| 3 | 1.3 | 2.7475 | 0 | 0.232 | 2.27 |
| 4 | 1.3 | 2.9042 | 100 | 0.216 | 2.61 |
| 5 | 1.3 | 3.0777 | 200 | 0.185 | 2.87 |
| 6 | 1.4 | 2.4751 | −100 | 0.251 | 2.07 |
| 7 | 1.4 | 2.6051 | 0 | 0.239 | 2.34 |
| 8 | 1.4 | 2.7475 | 100 | 0.215 | 2.54 |
| 9 | 1.4 | 2.9042 | 200 | 0.19 | 2.89 |
| 10 | 1.4 | 3.0777 | −200 | 0.220 | 2.50 |
| 11 | 1.5 | 2.4751 | 0 | 0.239 | 2.29 |
| 12 | 1.5 | 2.6051 | 100 | 0.221 | 2.58 |
| 13 | 1.5 | 2.7475 | 200 | 0.189 | 2.71 |
| 14 | 1.5 | 2.9042 | −200 | 0.234 | 2.45 |
| 15 | 1.5 | 3.0777 | −100 | 0.206 | 2.69 |
| 16 | 1.6 | 2.4751 | 100 | 0.230 | 2.64 |
| 17 | 1.6 | 2.6051 | 200 | 0.184 | 2.59 |
| 18 | 1.6 | 2.7475 | −200 | 0.244 | 2.40 |
| 19 | 1.6 | 2.9042 | −100 | 0.216 | 2.66 |
| 20 | 1.6 | 3.0777 | 0 | 0.186 | 3.03 |
| 21 | 1.7 | 2.4751 | 200 | 0.207 | 2.91 |
| 22 | 1.7 | 2.6051 | −200 | 0.249 | 2.33 |
| 23 | 1.7 | 2.7475 | −100 | 0.229 | 2.66 |
| 24 | 1.7 | 2.9042 | 0 | 0.188 | 2.69 |
| 25 | 1.7 | 3.0777 | 100 | 0.162 | 3.12 |
| No. | Parameters | Hmax | Kmax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| h (mm) | m | n | Experimental Data | Predicted Data | Relative Error% | Experimental Data | Predicted Data | Relative Error% | |
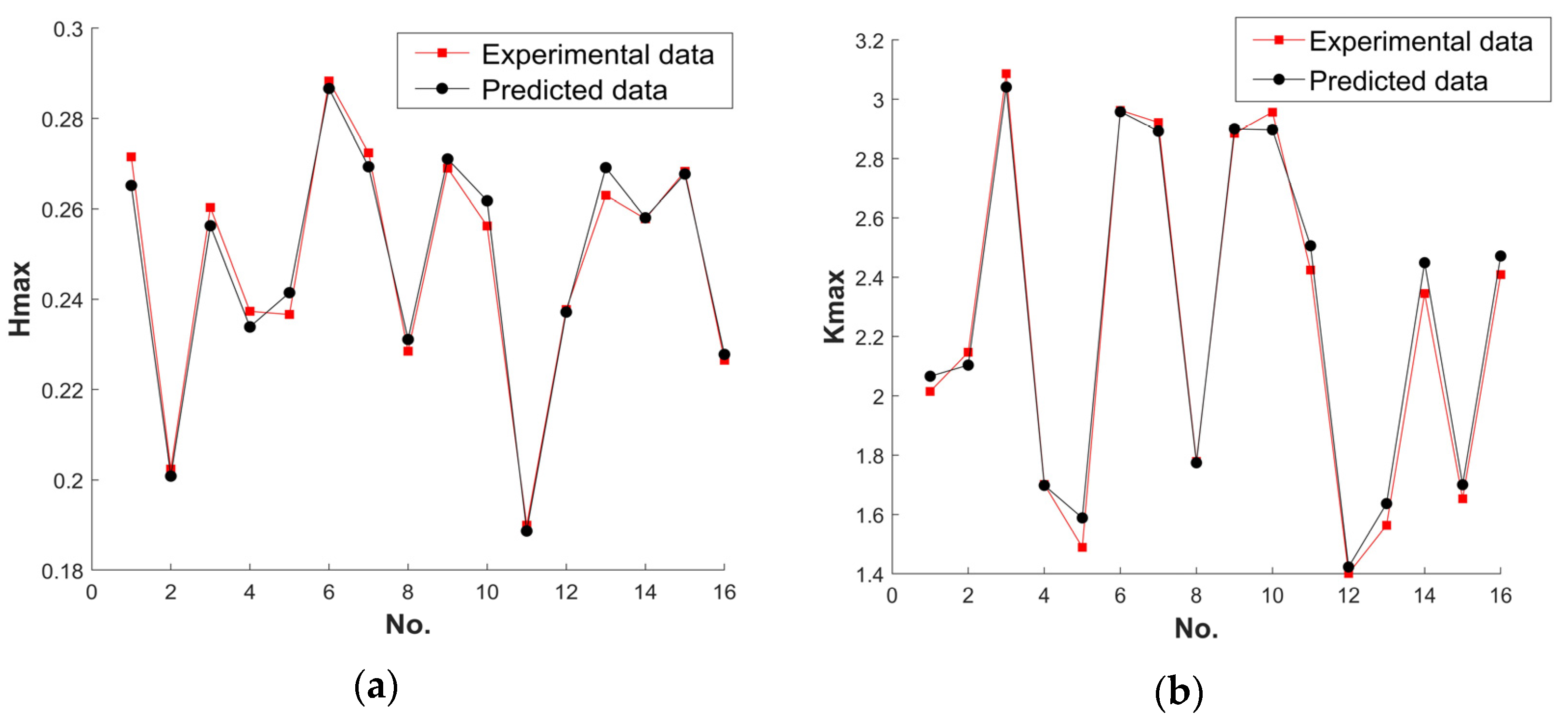
| 1 | 1.693 | 2.761 | −79.9 | 0.222 | 0.227 | 2.20 | 2.657 | 2.771 | 4.11 |
| 2 | 1.700 | 2.628 | −26.6 | 0.225 | 0.220 | 2.27 | 2.649 | 2.555 | 3.70 |
| 3 | 1.700 | 2.685 | −29.2 | 0.218 | 0.217 | 0.46 | 2.687 | 2.584 | 3.99 |
| 4 | 1.697 | 2.687 | −65.4 | 0.227 | 0.232 | 2.16 | 2.628 | 2.700 | 2.67 |
| 5 | 1.662 | 2.709 | −115.7 | 0.235 | 0.238 | 1.26 | 2.529 | 2.619 | 3.44 |
| 6 | 1.668 | 2.930 | −101.8 | 0.214 | 0.211 | 1.42 | 2.721 | 2.779 | 2.09 |
| No. | Pre-Optimization Data | Optimized Data | Improvement | |||
|---|---|---|---|---|---|---|
| Hmax | Kmax | Hmax | Kmax | Hmax | Kmax | |
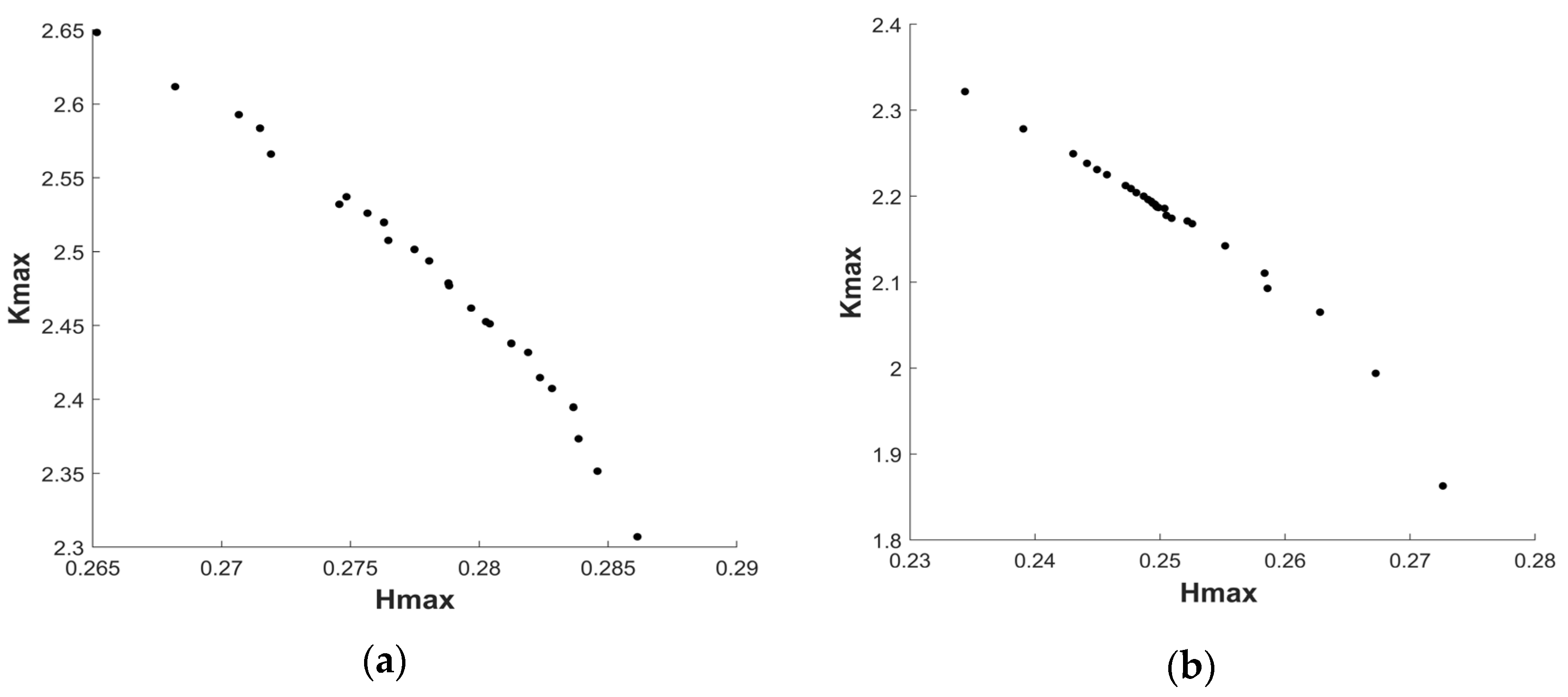
| 1 | 0.2170 | 2.5111 | 0.222 | 2.657 | 4.6% | 10.35% |
| 2 | 0.214 | 2.721 | 6.91% | 7.53% | ||
| Hmax | Kmax | |
|---|---|---|
| Turbine stage | 0.2849 | 2.2196 |
| Intermediate stage | 0.2565 | 1.9277 |
| Factor | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| h | 5.4 | 5.7 | 6.0 | 6.3 | 6.6 |
| m | 1.1918 | 1.2799 | 1.3764 | 1.4826 | 1.6003 |
| n | −400 | −200 | 0 | 200 | 400 |
| Factor | Level | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| h | 1.8 | 1.9 | 2.0 | 2.1 | 2.2 |
| m | 1.8418 | 1.9626 | 2.0965 | 2.246 | 2.4142 |
| n | −200 | −100 | 0 | 100 | 200 |
| No. | Parameters | Hmax | Kmax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| h (mm) | m | n | Experimental Data | Predicted Data | Relative Error% | Experimental Data | Predicted Data | Relative Error% | |
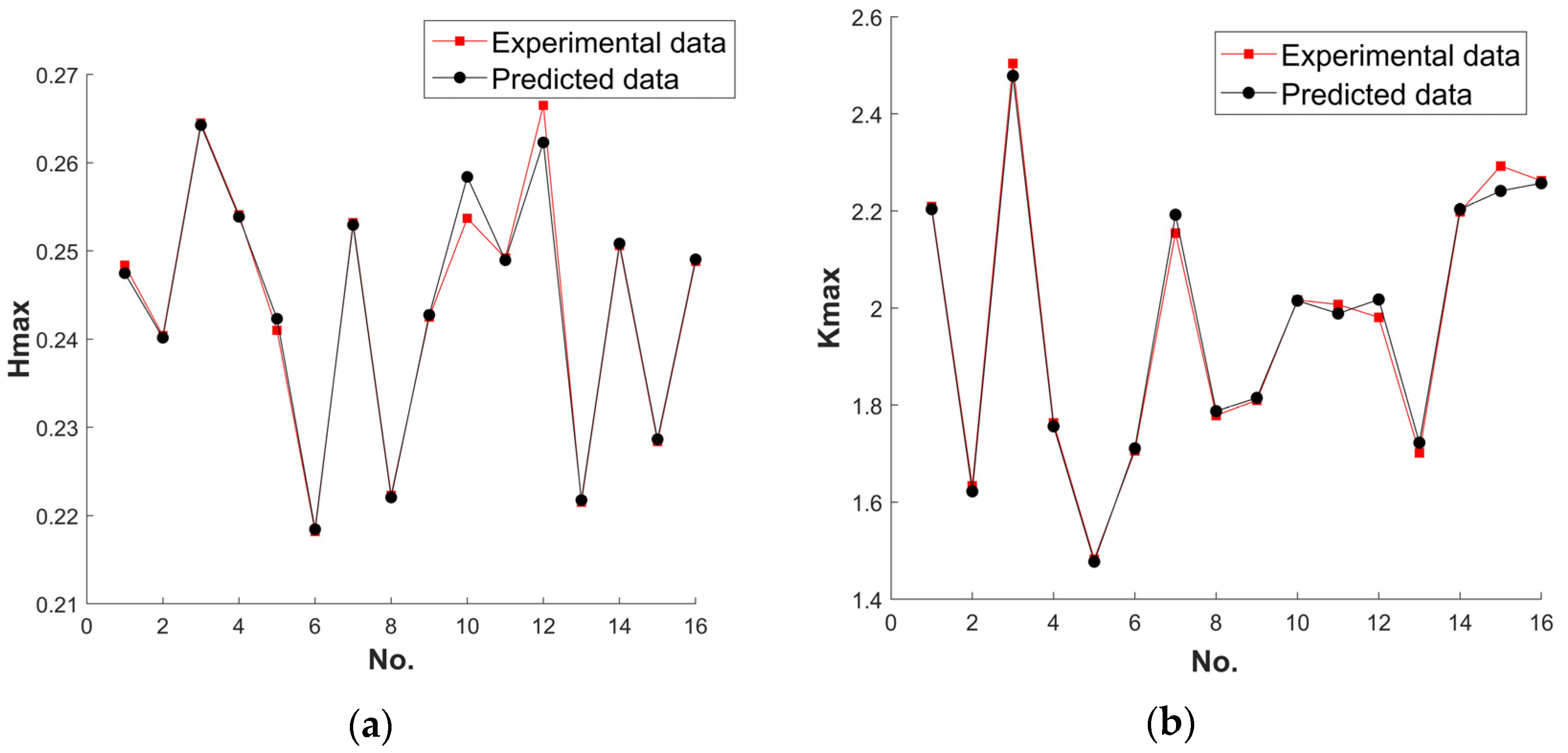
| 1 | 5.667 | 1.537 | 0.646 | 0.286 | 0.2741 | 4.34 | 2.307 | 2.286 | 0.92 |
| 2 | 5.677 | 1.539 | 6.913 | 0.285 | 0.2647 | 7.67 | 2.352 | 2.293 | 2.57 |
| 3 | 5.652 | 1.558 | 11.517 | 0.284 | 0.2714 | 4.64 | 2.395 | 2.400 | 0.21 |
| 4 | 5.665 | 1.559 | 12.756 | 0.283 | 0.2585 | 9.48 | 2.407 | 2.335 | 0.31 |
| 5 | 5.664 | 1.532 | 11.958 | 0.284 | 0.2751 | 3.24 | 2.373 | 2.399 | 0.11 |
| No. | Parameters | Hmax | Kmax | ||||||
|---|---|---|---|---|---|---|---|---|---|
| h (mm) | m | n | Experimental Data | Predicted Data | Relative Error% | Experimental Data | Predicted Data | Relative Error% | |
| 1 | 2.180 | 1.990 | 49.103 | 0.263 | 0.263 | 0 | 2.065 | 2.104 | 1.85 |
| 2 | 2.179 | 2.082 | 26.672 | 0.259 | 0.251 | 3.19 | 2.093 | 2.056 | 1.80 |
| 3 | 2.192 | 2.065 | 39.033 | 0.258 | 0.241 | 7.05 | 2.110 | 2.006 | 5.18 |
| 4 | 2.192 | 2.033 | −24.982 | 0.267 | 0.254 | 5.12 | 1.994 | 1.918 | 3.96 |
| 5 | 2.195 | 2.082 | 50.771 | 0.255 | 0.249 | 2.41 | 2.142 | 2.104 | 1.81 |
| Blade No. 1 | Blade No. 2 | Blade No. 3 | |
|---|---|---|---|
| No. of blades, N | 24 | 36 | 48 |
| R (mm) | 90 | 90 | 90 |
| l (mm) | 18 | 18 | 18 |
| α (°) | 20 | 30 | 40 |
| h (mm) | 8 | 8 | 8 |
| t (mm) | 3.17 | 3.10 | 2.94 |
| Blade No. 1 | Blade No. 2 | Blade No. 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Experiment | Simulation | Experiment | Simulation | Experiment | Simulation | ||||||
| Kmax | Hmax | Kmax | Hmax | Kmax | Hmax | Kmax | Hmax | Kmax | Hmax | Kmax | Hmax | |
| C1 | 1.506 | 0.046 | 1.416 | 0.042 | 1.464 | 0.062 | 1.322 | 0.058 | 1.297 | 0.071 | 1.300 | 0.074 |
| C2 | 1.786 | 0.073 | 1.761 | 0.069 | 1.672 | 0.090 | 1.550 | 0.090 | 1.496 | 0.112 | 1.466 | 0.110 |
| C3 | 2.087 | 0.093 | 2.126 | 0.093 | 1.801 | 0.118 | 1.789 | 0.118 | 1.672 | 0.143 | 1.639 | 0.140 |
| C4 | 2.515 | 0.118 | 2.503 | 0.113 | 2.107 | 0.146 | 2.018 | 0.148 | 1.805 | 0.168 | 1.864 | 0.175 |
| C5 | 2.981 | 0.146 | 3.050 | 0.138 | 2.435 | 0.179 | 2.386 | 0.179 | 1.979 | 0.205 | 2.106 | 0.209 |
| No. | Average Relative Error (%) | |
|---|---|---|
| Kmax | Hmax | |
| Blade No.1 | 2.4663 | 4.8325 |
| Blade No.2 | 4.7943 | 2.4717 |
| Blade No.3 | 2.6949 | 2.9694 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, W.; Li, Z.; Yan, H. Modeling and Optimization of the Blade Structural Parameters for a Turbomolecular Pump. Machines 2023, 11, 517. https://doi.org/10.3390/machines11050517
Chen Z, Wang W, Li Z, Yan H. Modeling and Optimization of the Blade Structural Parameters for a Turbomolecular Pump. Machines. 2023; 11(5):517. https://doi.org/10.3390/machines11050517
Chicago/Turabian StyleChen, Zhi, Wenlong Wang, Zhizuo Li, and Hongzhi Yan. 2023. "Modeling and Optimization of the Blade Structural Parameters for a Turbomolecular Pump" Machines 11, no. 5: 517. https://doi.org/10.3390/machines11050517
APA StyleChen, Z., Wang, W., Li, Z., & Yan, H. (2023). Modeling and Optimization of the Blade Structural Parameters for a Turbomolecular Pump. Machines, 11(5), 517. https://doi.org/10.3390/machines11050517





