1. Introduction
The development of autonomous underwater vehicles (AUVs) over the past three decades has exhibited a high security, high controllability, and low cost [
1]. AUVs are utilized extensively in hydrological surveys, seabed surveys, environmental assessments, and other fields today. Due to the complexity of and variation in the circumstances, it is difficult for AUVs to avoid all faults caused by events or the AUV itself [
2]. As the primary source of motion control for AUVs, excluding the thrusters, the rudder is also the leading source of AUV malfunctions. In the event of rudder defects, the motion control of AUVs is compromised. Therefore, detecting rudder failure is critical to improving the safety of AUVs.
In recent years, the methods for detecting AUV faults have primarily incorporated three aspects: signal processing, an analytical model, and a data-driven model [
3]. Enhanced fractal features integrated with the wavelet decomposition identification method were proposed for AUVs with a thruster fault, and the time-domain and frequency-domain data were utilized to identify thruster malfunctions [
4]. In order to address the issue that there is no useful feature in the frequency domain, Yu et al. [
5] proposed a new method for calculating the weak fault severity of thrusters’ features. Maleki et al. [
6] devised the discrete wavelet transform as a method for monitoring machine vibrations and employed the DWT-FFT signal processing method to detect the fault of the rotating shaft. Signal processing techniques are widely utilized in rotating machinery fault detection [
7], but, for AUVs, the signal processing technique is impacted by random ocean currents and intense measurement noise [
8]. After signal processing, it is difficult to distinguish the fault feature from the disturbance feature for a weak fault [
9]. As a result, the issue of incorrect diagnosis arises.
The analytical model-based implementation is relatively simple. Sun et al. [
10] developed a fault diagnosis (FD) scheme based on a Gaussian particle filter (PF) and demonstrated the practicability and validity of the developed method for estimating the AUV failure model and motion state. In their study, Lv et al. [
11] proposed a fault-tolerant control (FTC) method integrated with thrust allocation based on the sliding mode theory to reduce the error caused by thruster faults when using a conventional sliding mode controller. In order to solve the unknown effects of multiple autonomous underwater vehicles (AUVs) system actuator failures, Xu et al. [
12] designed a fault-tolerant control method based on extended state observers (ESOs) and an adaptive strategy. Abdollahi [
13] established a method that decouples the entire system into two subsystems and designed two independent sliding mode observers (SMOs) to estimate sensor and actuator faults for corresponding subsystems. A particle filter (PF)-based robust navigation system with FD was designed for an underwater robot [
14]. A method for fault localization was proposed that calculated the pole-to-pole voltage as diagnostic variables and designed an error-based threshold [
15]. Chu et al. [
16] proposed an observer-based fault detection method for magnetically coupled undersea thrusters. Yin et al. [
17] designed an FD method based on the current observer that used fault residuals to detect and locate faults and an adaptive threshold to reduce error interference. Due to the complexity of the ocean environment and other factors, it is difficult to create an accurate model [
18]. In contrast, the model-based method is sensitive to system parameters and dependent on the traditional experience threshold, which reduces its robustness, and it also has stricter control system requirements [
19].
The data-driven fault diagnosis methods do not require models. Compared to traditional model-based diagnosis, this method significantly reduced the time required for diagnosis and increased efficiency. An example of using recurrent neural networks (RNNs) is given by Nascimento and Valdenegro-Toro [
20], who presented a data-driven fault detection and diagnosis scheme for underwater thrusters.
Fabiani et al. [
21] presented a method for fault detection and isolation on the thrusters of an over-actuated AUV based on non-linear principal component analysis (NLPCA) and an off-line artificial neural network (ANN). Combined with motor current signals, Li et al. [
22] proposed a new scheme based on a deep extreme learning machine for roller bearing fault diagnosis. Ji et al. [
23] investigated a novel fault diagnosis method based on convolutional neural networks (SeqCNN). Although the data-driven fault diagnosis methods are accurate, their adaptability is weak [
24].
Increasing numbers of FD studies employ a combination of signal processing and analytical model-based and data-driven approaches in order to ensure the accuracy of FD and improve the diagnostic feasibility. Chu et al. [
25] developed an RBF neural-network-based adaptive sliding mode control scheme. The state space equation was used to describe the dynamic model of ROVs. When the propeller is saturated, this hybrid model approach combines a neural network and sliding mode control to ensure the stability of the adaptive trajectory tracking system. Wang et al. [
26] designed a method for extracting features from raw vibration signals and used 1D-CNN-based networks for bearing FD, combining signal processing techniques with a data-driven approach. A fault-tolerant control method based on adaptive and radial basis function neural networks (RBFNN) was proposed by Wang et al. [
27] for autonomous underwater vehicles exposed to dynamic uncertainties and potential unknown thruster failures. Xu et al. [
28] designed a novel robust Gaussian approximation smoother based on the expectation–maximization (EM) algorithm, combining data-driven and model-building methods.
However, the majority of research on AUV FD has focused on thruster and sensor failures. Few studies have been conducted on the FD of AUV rudder systems, and the ones that have are frequently concerned with fault-tolerant control. Liu and Xu [
29] addressed the issue of fault localization (FL) and fault-tolerant control (FTC) for AUV rudders when deformation faults occur. Liu et al. [
30] were primarily concerned with the development of FTC based on active compensation in rudder fault mode. Che and Yu [
31] designed two neural network estimators to estimate rudder faults and ocean current disturbance, respectively, to solve the fault-tolerant tracking control problem. However, the aforementioned methods were only validated through simulation. A PF-based method for estimating rudder effect deduction and the unscented Kalman filter (UKF) were proposed for proposal distribution, respectively [
32]. By analyzing the pertinent indicators, the rudder’s fault type could be determined and experimentally confirmed; however, the current focus of this method is on the response of the AUV to the dynamics control under ideal conditions; the parameter error of the sensor was not considered, and the sensor’s usability must be enhanced.
This paper, inspired by prior research, presents a data-driven and hybrid-model FD scheme for the AUV rudder system. Given this, the following are the principal contributions of this paper.
- (1)
Aiming at the fault problem of an AUV rudder without feedback, a new rudder fault detection method combined with an AUV dynamic model is proposed in this paper. Considering the uncertainty of AUV dynamic model parameters, this paper proposes an RNN-based method for identifying the nonlinear parameters of an AUV dynamic model. At the same time, the singular value decomposition (SVD) method was used to denoise the original data. Compared with the parameter identification methods based on RLS and the traditional RNN, the proposed method has a higher identification accuracy.
- (2)
In order to reduce the influence of sensor parameter errors and prediction model errors on fault detection results, this paper developed an adaptive threshold for analyzing prediction results. Compared with the method of fault diagnosis based on an empirical threshold, the proposed method adapts to changes in environmental parameters and has a higher reliability, thereby reducing the incidence of misdiagnosis.
The remainder of the paper is structured as follows. In
Section 2, a description of the problems is provided.
Section 3 discusses the models and algorithms. The experiments and their results are presented in
Section 4. The conclusion is presented in
Section 5.
4. Experiments and Results Analysis
This section mainly introduces the experimental platform, model identification results, and fault detection results.
4.1. Experimental Platform
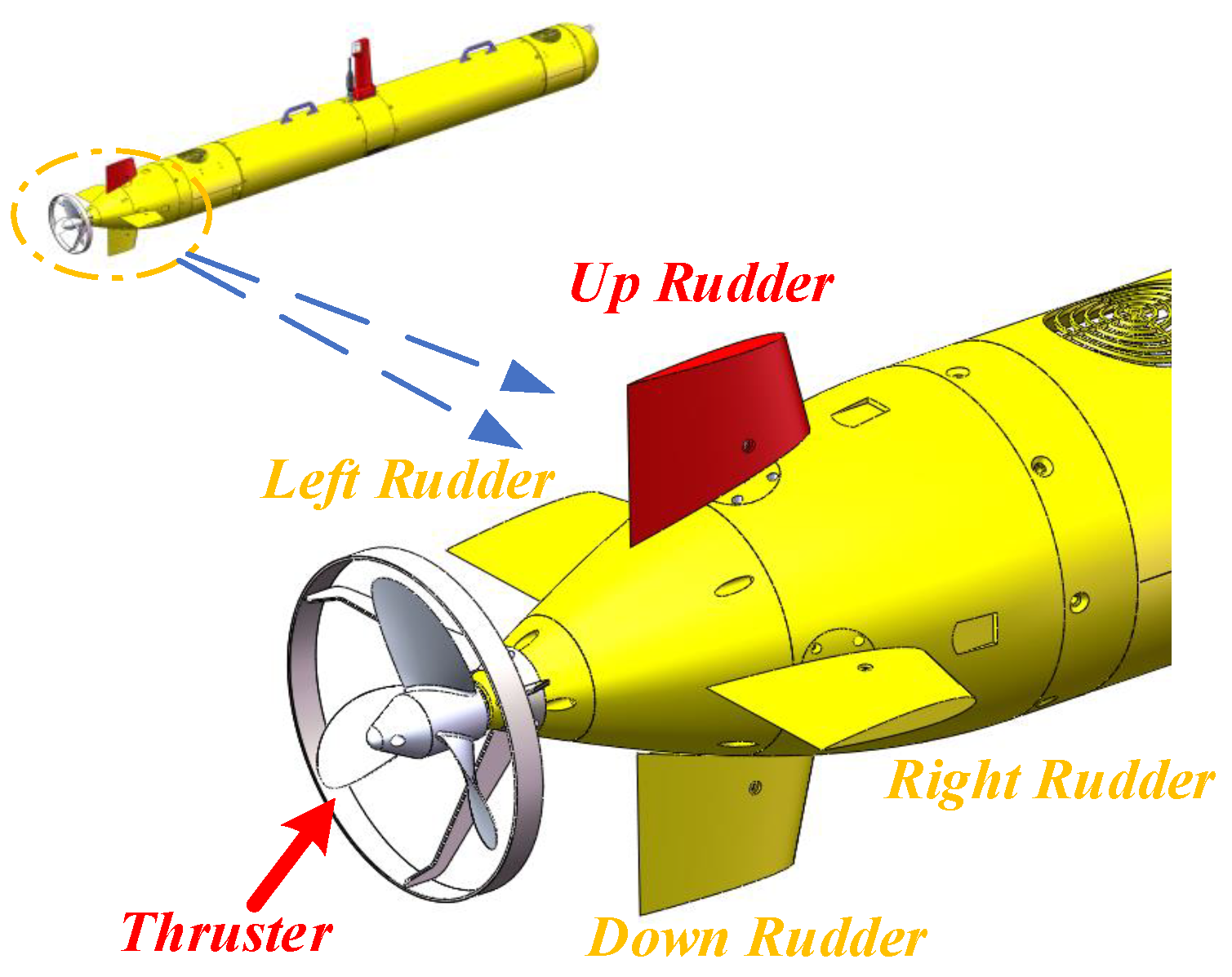
Experiments on the AUV Sailfish-210, which was independently designed by the Ocean University of China and depicted in
Figure 9a, were conducted to test the efficacy of the fault detection method proposed in this paper. Notably, although the algorithm is based on offline historical data, the data collected are real. All experimental data presented in this article originated from the Sailfish-210 AUV.
Figure 9b depicts the Sailfish-210 AUV conducting a sea test.
4.2. Model Identification Results
In order to obtain stable motion data of AUV and verify the accuracy of the proposed parameter identification method, sea areas with a small current and good sea conditions were selected for the experiment. Through neural network training, the predicted value was obtained. This model training used the data between 0 and 150 s as the training set and the data between 384 and 451 s as the test set.
Figure 10 depicts the predicted effects of pitch, roll, and yaw acceleration. The parameter-identified error prevents the convergence of the value of the prediction error to zero. For fault-free modes, the prediction error occasionally exceeds the range of the adaptive threshold. We employed a 5 s time-window approach and tended to disregard short-term outliers. After calculation, the determination coefficients of the three predictions based on this method are
,
, and
, respectively. This is a model with a high degree of dependability. The forecast error sequence has standard deviations of
,
, and
.
In order to further validate the efficacy of the proposed method, prediction results generated by recursive least squares (RLSs) and recurrent neural networks (RNNs) were compared with the proposed method. The RLS-based AUV model parameter identification method appeared earlier and has the advantages of fast and efficient identification, but it also has the problem of data saturation [
50]. The RLS parameter identification method often obtains unsatisfactory results for AUV nonlinear factors. Neural networks for parameter identification do not care about the size of the parameters while looking for a good fit. The RNN neural network is improved from the traditional BP neural network. In this problem, the RNN network was chosen because of the poor training effect of BP. The superiority of RNN is that the concept of a time sequence is added to the network, which can learn, and the training effect is improved. However, the disadvantage is that the traditional RNN has the phenomenon of gradient explosion and disappearance [
44].Therefore, an improved RNN method, LSTM, was adopted in this paper. Meanwhile, the singular value decomposition method deals with noise effects. As demonstrated in
Figure 11, the pitch angle prediction results based on SVD-RNN are closer to the sensor’s original values.
In this paper, in order to measure the performance of the prediction models, MAE and RMSE were selected as the evaluation indexes for the model’s prediction accuracy [
51]. The formulas of these indexes are as follows:
where
respects the actual values,
respects the predicted values, and
n is the amount of data forecasting.
Here, only the comparison of prediction effects of the pitch angle is listed in
Figure 11. The comparison of prediction results of different methods of the roll angle and yaw data are similar to it, and no further graphical comparison is made. After a large number of training tests, the comparison between the model prediction by different methods and the original model according to the evaluation indicators is shown in
Table 5.
As can be seen from the comparison results, for the pitch angle predicted by the proposed method, compared with the prediction results using RLS and RNN, MAE is reduced by and , respectively, and RMSE is reduced by and , respectively. For the roll angle, MAE decreases by and , respectively, and RMSE decreases by and , respectively. For the yaw data, MAE is reduced by and , respectively, and RMSE is reduced by and , respectively. It can be seen that the MAE and RMSE of the prediction error using the proposed method are significantly reduced compared with RLS and RNN.
The above results reveal that the identification model is convergent and bounded, indicating that the proposed identification method is effective.
4.3. Fault Detection Results
In this subsection, several cases relating to different faults are carried out in order to verify the proposed fault detection method.
4.3.1. Experiment of Rudder Jam Fault
Figure 12 reveals that, at 35 s, the rudder current is close to the locked-rotor current, and the duration exceeds the predetermined threshold of 2 s. This fault is referred to as a rudder jam fault.
4.3.2. Experiment of Rudder Blade Falling off Fault
Figure 13 shows that only at the rudder start time is there a large current, close to 1 A, whereas, for the rest of the time, the current is nearly zero. Consequently, this fault type is diagnosed as a rudder blade falling off.
The fault diagnosis method for the rudder blade falling off and rudder jamming is mainly used to collect current information through the current module designed in the AUV cabin. This method is unsuitable for diagnosing rudder blade deflection faults because this fault type has no prominent current characteristics. Therefore, this fault diagnosis must be combined with the model method described above.
4.3.3. Experiment of Rudder Blade Deflection Fault
In the deflection fault experiments, different deflection angles of the rudder blade will have different effects on the model prediction residual. The actual rudder angle range of the AUV is and, if the rudder blade deflection angle is less than 5° or even smaller, the predicted residual is indeed very small, which will make judging the occurrence of faults difficult. Therefore, in this experiment, combined with the actual fault situation of the AUV, the fault type was set as the deflection angle of 15°, which is obvious enough for realizing the diagnosis and location of the rudder deflection fault.
Figure 14 depicts the effect predicted by the model when the right rudder is deflected downward by 15°.
In this fault mode, the MAE and RMSE of the pitch angle prediction results are 2.237 and 2.918, and those of the roll angle prediction results are 5.286 and 6.849, respectively. The actual pitch value is greater than the value predicted by the model, the predicted roll value is obviously greater than the actual roll value (calculated in absolute value), and the error is significantly greater than the threshold value. In other words, the fault rudder produces undesirable roll and yaw torque and adversely affects the control process. As can be seen from
Figure 14b,d, the prediction error lies within the set adaptation range at the moment close to 1920 s. The actual set failure duration threshold is 5 s, so it is determined that this phenomenon cannot be diagnosed as a normal state of the AUV rudder. This phenomenon is often caused by anomalous phenomena, such as the AUV suddenly receiving wave interference. Considering that this phenomenon is transient and does not occur frequently, this abnormal prediction result can be ignored.
According to the results of adaptive threshold analysis, the pitch and roll angle prediction errors of
and
in the fault mode are outside the range of the adaptive threshold, respectively, which proves that the method has a high accuracy. In order to illustrate the superiority of the method, it was compared with the commonly used RLS with the empirical threshold method, as shown in
Figure 15. Based on historical experience reference, the threshold for this method was chosen to be 2°. The fault diagnosis accuracy of these two methods is shown in
Table 6.
Compared with the RLS with the empirical threshold method, the proposed method can improve the diagnostic accuracy by 18.1% and 40.7%, respectively, using the predicted pitch and roll results. Based on the results of the threshold analysis, the rudder is faulty. In order to diagnose this fault as a right rudder deflection fault, we refer to
Table 4. The left rudder’s fault detection method is similar to that of the right rudder, and other types of horizontal rudder deflection will not be described in detail.
Figure 16 depicts the effect predicted by the model when the down vertical rudder is deflected leftward. This fault test was also carried out under the condition that the deflection angle is set to 15°.
As shown in
Figure 16a,b, the predicted value of the roll angle by the model deviates significantly from the actual sensor value after 1885 s, and the error exceeds the adaptive threshold for an extended period.
Figure 16c,d reveal that the prediction error of the yaw angular acceleration tends to fluctuate frequently, which makes it difficult to depict the yaw effect caused by the defective rudder accurately. In order to represent the change in the yaw moment more accurately, the yaw angular acceleration was converted to the yaw angular velocity using the following formula:
where
represents the yaw angular acceleration and
denotes the corresponding initial yaw angular velocity. The yaw rate is shown in
Figure 16e,f. The actual yaw rate value is less than predicted by the model, and the error exceeds the adaptive threshold. In this failure case, the MAE and RMSE of the predicted results of the roll angle are 2.369 and 2.836, respectively; the MAE and RMSE of the predicted results of the yaw angular velocity are 3.240 and 4.037, respectively.
In this fault mode,
and
of roll and yaw angular velocity prediction errors are outside the adaptive threshold, respectively, which proves that the method has a high accuracy. Similar to the analysis of the left rudder fault results, in order to illustrate the superiority of the method, it was compared with the commonly used RLS with the empirical threshold method, as shown in
Figure 17. The fault diagnosis accuracy of these two methods is shown in
Table 7.
Compared with the RLS with the empirical threshold method, the proposed method can improve the diagnostic accuracy by 10.1% and 18.5%, respectively, using the predicted roll and yaw angular velocity results. This result shows that the proposed method has a specific advanced performance. According to the predicted results of the roll and yaw angular velocity, the down rudder is the type of fault that deflects to the left. It can be observed that the prediction error occasionally falls within the threshold range for the failure mode, and the AUV anomaly is responsible for this occurrence. Based on the sliding window method, it is determined that this phenomenon is typically brief and infrequent, so such anomalous prediction results can be disregarded. Other fault types of vertical rudders will not be discussed in detail.
In order to better support the effectiveness of the algorithm, we added a comparison of turning radius data under the AUV rudder fault mode, as shown in
Figure 18. This fault test occurs when a part of the rudder force is lost in the down vertical rudder. It is also the deflection fault experiment shown in
Figure 16. With the rudder angle set to 45° in normal mode, the fault deflection angle is set to −15°, which means that the down rudder angle after a fault is 30°. It can be seen from
Figure 18 that the turning motion of the AUV is not precisely circular, which is caused by the disturbance of waves and other factors. After an approximate calculation, the turning radius of the AUV in the fault-free mode is approximately 25 m, whereas, in the fault mode, the turning radius of the AUV is approximately 15 m. This result indicates that the turning radius in the fault mode is much larger than that in the fault-free mode. The result also shows the rationality of using the AUV yaw angular velocity prediction results for fault diagnosis in yaw fault experiments.
The above experimental results indicate that, in the mode of rudder failure, the error between the predicted value of the model and the actual value of the sensor exceeds the adaptive threshold range, indicating that the proposed method is effective.