Cutting Process Consideration in Dynamic Models of Machine Tool Spindle Units
Abstract
:1. Introduction
2. Materials and Methods
- The interaction of the cutting process with the elastic system of the machine tool is represented by a closed dynamic model;
- The elastic system of a machine tool is a set of coupled mechanical partial subsystems;
- In the closed dynamic model of the machine tool, the cutting process is taken into account as an elastic connection between the subsystems of the workpiece and tool;
- The elastic coupling is given with the stiffness coefficient equal to the ratio of the change in cutting force to the change in depth of cut;
- The coordinate relation between the workpiece and tool subsystems is defined by the condition of joint elastic deformations at the place of their contact. The dynamic vibrations coupling of the workpiece and tool is determined by the stiffness of the elastic coupling between them.
2.1. Materials
2.2. Methods
- The spindle unit is considered a linear dynamic system with distributed and concentrated parameters;
- The spindle bearings have radial, axial, and angular stiffness, with linear stiffness and damping characteristics;
- The elastic–inertial and damping properties of the spindle and its bearings do not change with the rotation angle, i.e., are isotropic in the plane perpendicular to the spindle rotation axis (axisymmetric problem).
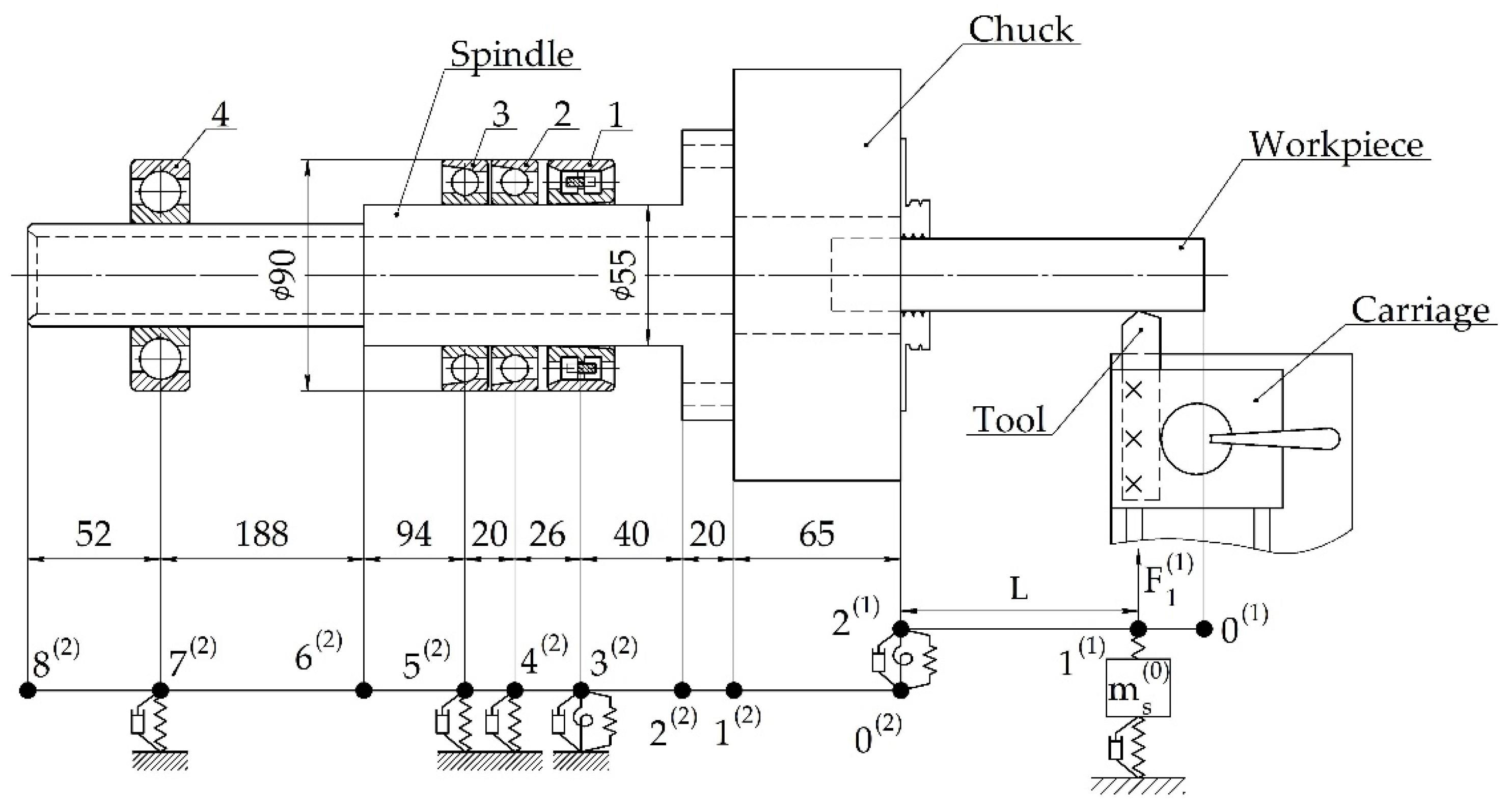
2.2.1. Model of the Spindle Unit System
2.2.2. Analytical Method
2.2.3. FEM
3. Results
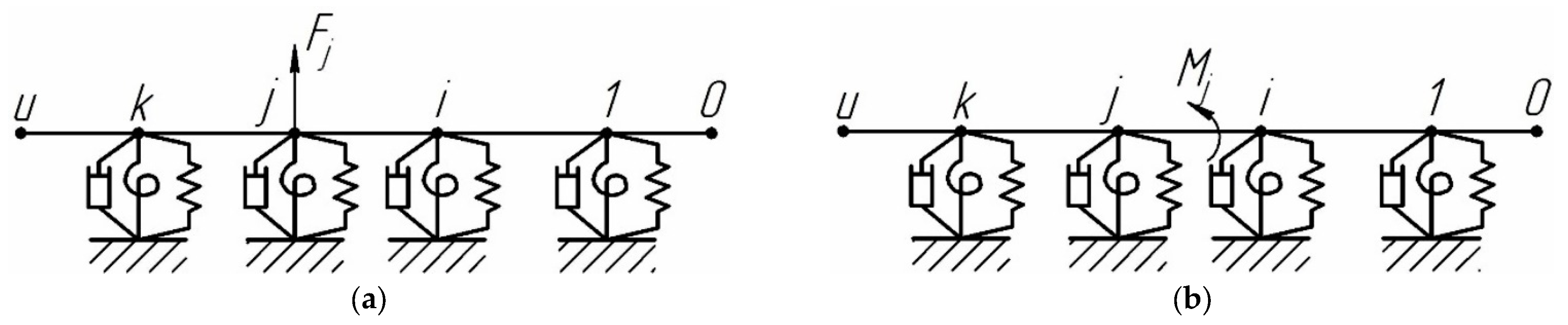
3.1. Dynamic Model of System “Spindle Unit”
- under the force action (open-loop system):
- when representing the cutting process by taking into account the elastic relationship with stiffness (closed system):
3.2. Stiffness Calculation of the Additional Elastic Coupling
3.3. Determination of Natural Frequencies Vibration of the Lathe Elastic System “Spindle–Workpiece–Tool”
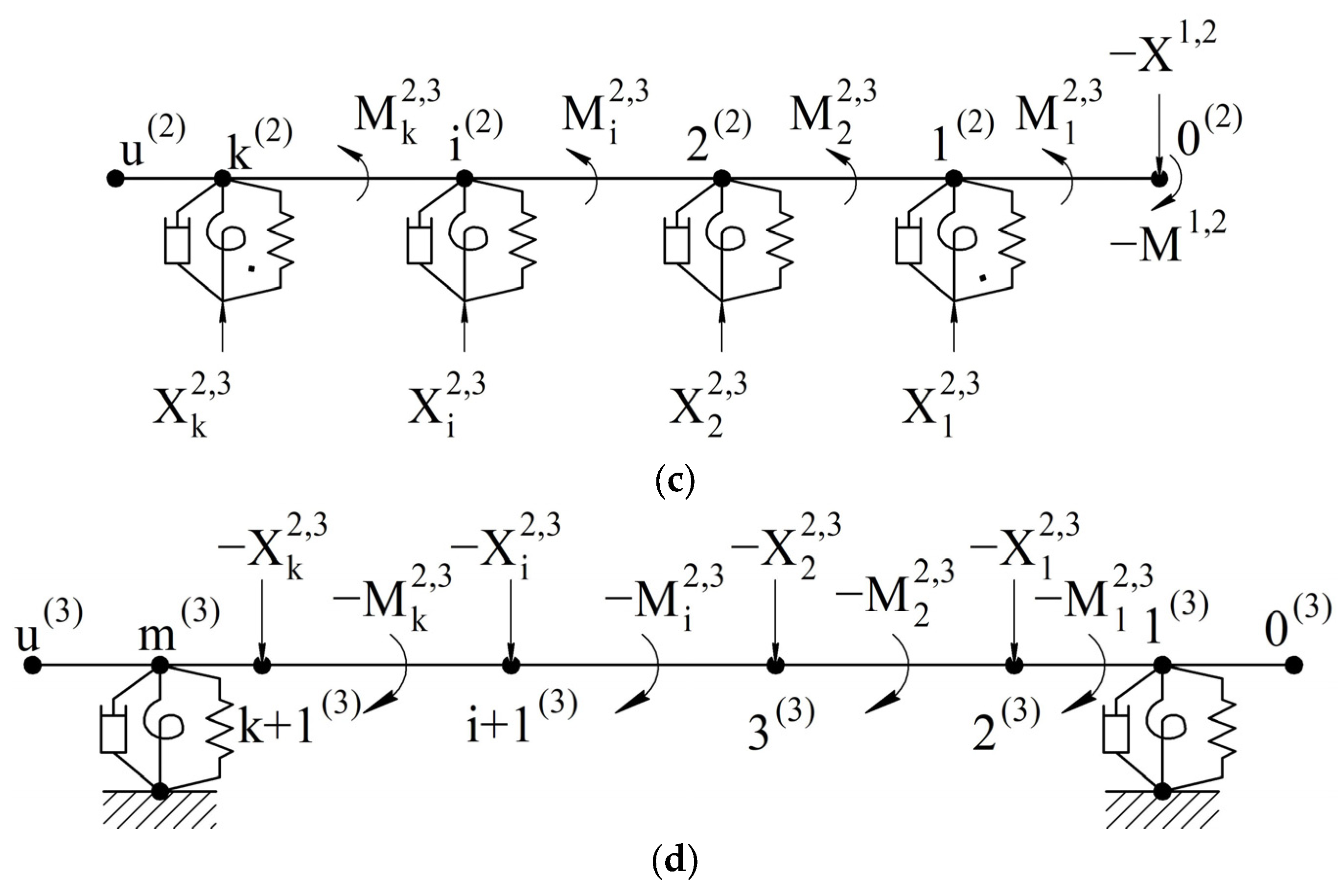
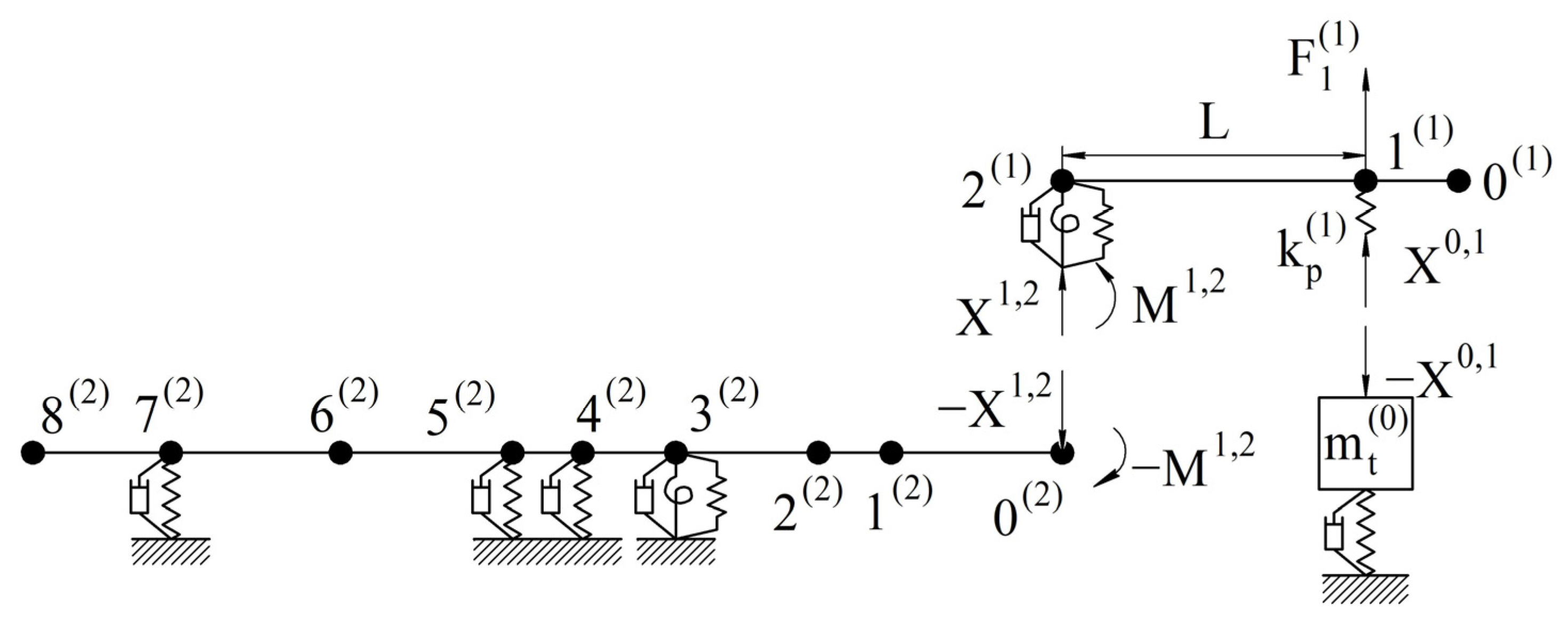
3.3.1. Dynamic Model of the Lathe “Spindle–Workpiece–Tool” System
- for the subsystems of the workpiece (s = 1) and tool (s = 0):
- ➢
- for the subsystems of the workpiece (s = 1) and the spindle with chuck (s = 2):4
- workpiece subsystem (s = 1):
- spindle chuck subsystem (s = 2):
- tool subsystem (s = 0):
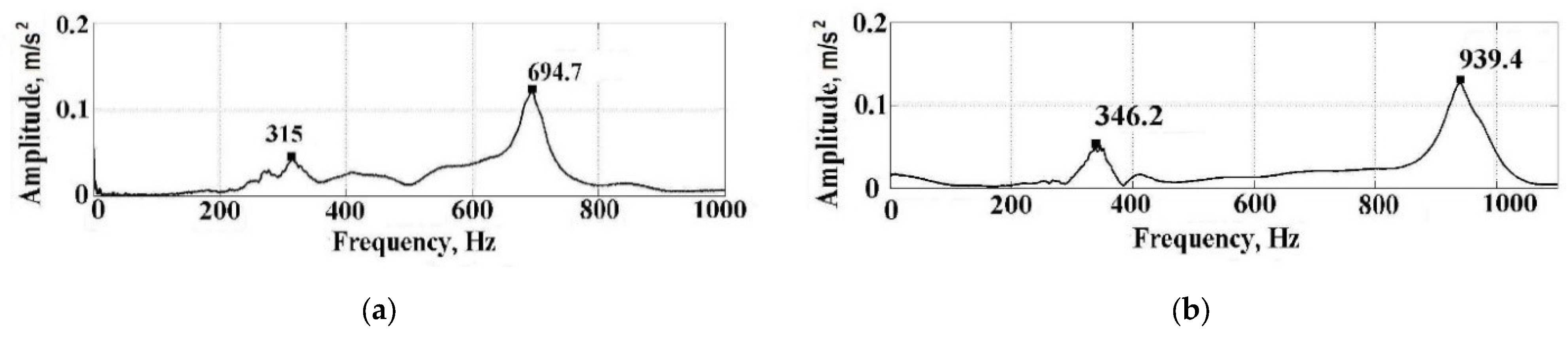
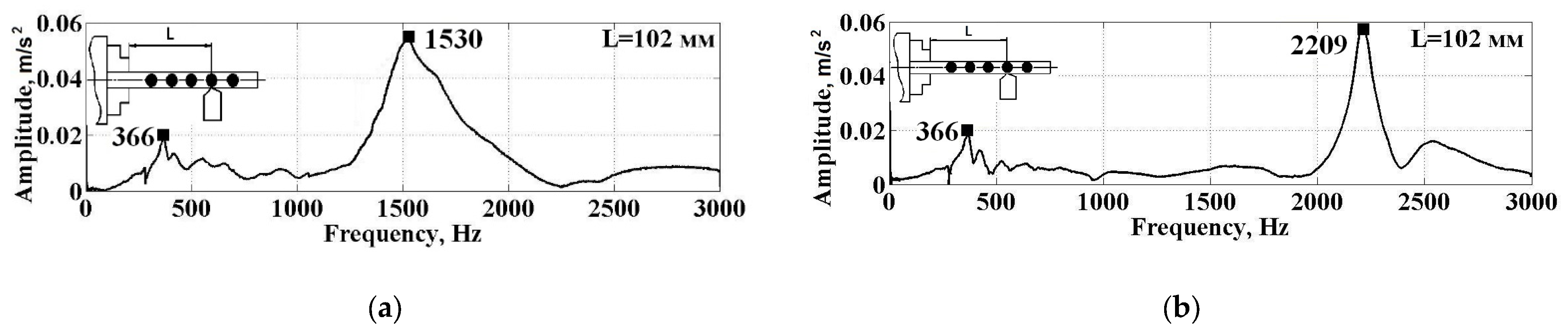
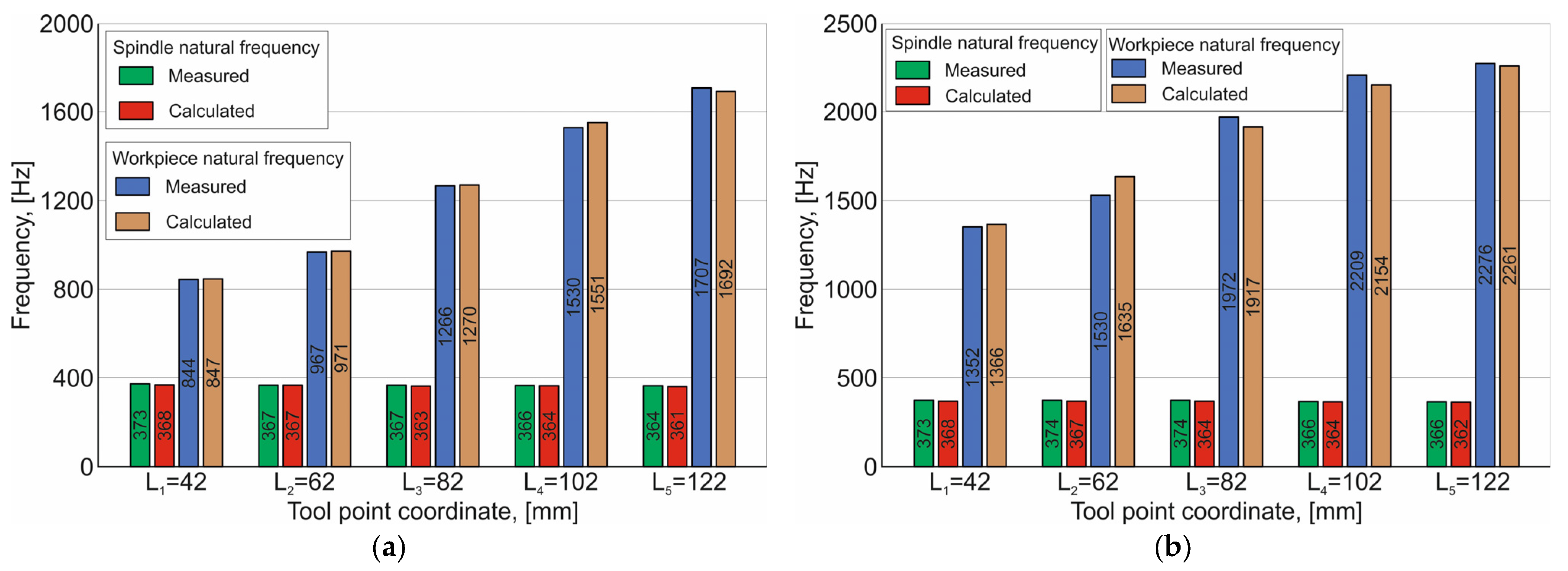
3.3.2. Experimental Determination of Natural Vibration Frequencies of the “Spindle–Workpiece–Tool” Elastic System
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| W(ω) | dynamic transfer function | θi | the slope of the subsystem in i-th section |
| cutting force in the form of polyharmonic functions with zero harmonic component | M | external bending moment in i-th section | |
| the static component of the | Q | external shear force in i-th section | |
| the dynamic component of the | {Y}i | subsystem parameters column vector | |
| a | chip width | [T] | general transfer matrix of a subsystem, which is equal to the product of section transfer matrices [T]i by order from beam end to its beginning |
| Kf | cutting coefficient | [T]i | transfer matrix of subsystem section (4 ∗ 4) between i-1 and i points |
| cutting process stiffness | [Tp]i | mass and inertia matrix of localized mass | |
| radial stiffness of subsystems linkage | [Tb]i | elastic support matrix with damping | |
| angular stiffness of subsystems linkage | [Tu]i | beam section matrix with distributed mass | |
| elastic linkage stiffness of the workpiece s = 1 and carriage s = 0 subsystems | [Ti],j | matrix, which is equal to the product of section transfer matrices [T]i, between i-th and j-th sections | |
| reactions of discarded bonds in the i-th point of subsystems s and s + 1 disconnection, forces, and moments | [Ti]0 | matrix, which is equal to the product of section transfer matrices [T]i, located between i-th and 0-th sections | |
| displacement-to-force and slope-to-force receptances in i-th section from the unit harmonic force in j-th section | P, S, R, T | functions | |
| displacement-to-moment and slope-to-moment receptances in i-th section from the unit harmonic moment in j-th section | mw | mass of the weight | |
| , | displacement-to-force and slope-to-moment receptances at separation points of s = 1 and s = 2 subsystems | J | transverse moment of inertia of localized mass |
| displacement-to-force receptance of the tool subsystem, represented as a 1-DOF (degree of freedom) system | [F]j | load column vector in j-th section [F]j= {0,0,0,Pj}T or [F]j= {0,0,Mj,0} | |
| [F] | block/partitioned matrix of discarded bonds generalized reaction amplitudes X (forces) and M (bending moments) from external harmonic loads | [T] matrix elements | |
| [D(ω)] | receptance block/partitioned matrix | Hs | specified cutting depth |
| [ΔF] | block/ partitioned matrix of generalized receptances from external harmonic load | Ha | actual cutting depth |
| X | column vectors of discarded bonds, forces | Cp, k | correction factors |
| M | bending moments amplitudes | S | feed |
| calculated transverse (radial) displacements function of subsystem s in the i-th point | V | cutting speed | |
| y | transverse displacement of the beam with x coordinate | x, y, n | indices |
| x | coordinate in the direction of the longitudinal axis of the beam | workpiece and tool elastic displacements in the cutting zone | |
| E Ii | the flexural stiffness of the beam section | generalized subsystems receptance | |
| mi | weight of the unit length of the beam section | ) | |
| t | time | tool natural frequency | |
| l | beam section length | first and second natural frequencies of the closed-loop dynamic system | |
| ω | the angular frequency of the bending vibration of the beam | s | subsystem index, s = 0,1,2,3 |
| Fj | external harmonic force in j-th section | u | number of subsystem sections |
| Mj | an external harmonic moment in j-th section | subsystem s damping coefficient in i-th cross-section | |
| yi | deflection of the subsystem in i-th section | localized mass of the tool subsystem s = 0 |
Appendix A
- for the k-th section:
- for the j-th section:
- for the i-th section:
- for the 1-st section:
Appendix B
| Harmonic Influence Coefficients of Type ,,, | Beam Section Number | Supporting Matrices | |||
|---|---|---|---|---|---|
| i | j | ||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| , | 0 | 1 | - | - | |
| , , , | 0 | 2 | - | - | |
| 1 | 1 | - | |||
| , | 2 | 1 | - | ||
| , | 1 | 2 | - | 0 | |
| , , , | 2 | 2 | - | ||
References
- Monostori, L. Cyber-Physical Systems. In CIRP Encyclopedia of Production Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Melesse, T.Y.; Pasquale, V.D.; Riemma, S. Digital Twin Models in Industrial Operations: A Systematic Literature Review. Procedia Manuf. 2020, 42, 267–272. [Google Scholar] [CrossRef]
- Ferry, N.; Terrazas, G.; Kalweit, P.; Solberg, A.; Ratchev, S.; Weinelt, D. Towards a big data platform for managing machine generated data in the cloud. In Proceedings of the IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 263–270. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Chen, J.; Hu, P.; Zhou, H.; Yang, J.; Xie, J.; Jiang, Y.; Gao, Z.; Zhang, C. Toward Intelligent Machine Tool. Engineering 2019, 5, 679–690. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, X.; Chen, X. The Concept and Progress of Intelligent Spindles: A Review. Int. J. Mach. Tools Manuf. 2017, 112, 21–52. [Google Scholar] [CrossRef]
- Abele, E.; Altintas, Y.; Brecher, C. Machine tool spindle units. CIRP Ann. 2010, 59, 781–802. [Google Scholar] [CrossRef]
- Altintas, Y.; Cao, Y. Virtual Design and Optimization of Machine Tool Spindles. CIRP Ann. Manuf. Technol. 2005, 54, 379–382. [Google Scholar] [CrossRef]
- Bach, P. Modelling of Milling Spindles for Optimizing the Spindle Cutting Performance. In Proceedings of the 34th International MATADOR Conference, Manchester, UK, 7–9 July 2004; Hinduja, S., Ed.; Springer: London, UK, 2004; pp. 453–458. [Google Scholar] [CrossRef]
- Zhang, X.J.; Xiong, C.H.; Ding, Y.; Feng, M.J.; Xiong, Y.L. Milling stability analysis with simultaneously considering the structural mode coupling effect and regenerative effect. Int. J. Mach. Tools Manuf. 2012, 53, 127–140. [Google Scholar] [CrossRef]
- Hentati, T.; Barkallah, M.; Bouaziz, S.; Haddar, M. Dynamic modeling of spindle-rolling bearings systems in peripheral milling operations. J. Vibroeng. 2016, 18, 1444–1458. [Google Scholar] [CrossRef]
- Hu, G.; Gao, W.; Chen, Y.; Zhang, D.; Tian, Y.; Qi, X.; Zhang, H. An experimental study on the rotational accuracy of variable preload spindle-bearing system. Adv. Mech. Eng. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical Prediction of Chatter Stability in Milling—Part II: Application of the General Formulation to Common Milling Systems. ASME J. Dyn. Syst. Meas. Control 1998, 120, 31–36. [Google Scholar] [CrossRef]
- Li, J.; Kilic, Z.M.; Altintas, Y. General Cutting Dynamics Model for Five-Axis Ball-End Milling Operations. J. Manuf. Sci. Eng. 2020, 142, 121003. [Google Scholar] [CrossRef]
- Kim, J.; Zverev, I.; Lee, K. Model of Rotation Accuracy of High-Speed Spindles on Ball Bearings. Engineering 2010, 2, 477–484. [Google Scholar] [CrossRef]
- Lin, C.W.; Lin, Y.K.; Chu, C.H. Dynamic models and design of spindle-bearing systems of machine tools: A review. Int. J. Precis. Eng. Manuf. 2013, 14, 513–521. [Google Scholar] [CrossRef]
- Zverev, I.; Pyoun, Y.-S.; Lee, K.-B.; Kim, J.-D.; Jo, I.; Combs, A. An elastic deformation model of high speed spindles built into ball bearings. J. Mater. Process. Technol. 2005, 170, 570–578. [Google Scholar] [CrossRef]
- Genta, G. Vibration Dynamics and Control; Springer: New York, NY, USA, 2008; 856p. [Google Scholar] [CrossRef]
- Abbas, L.K.; Zhou, Q.; Hendy, H.; Rui, X. Transfer matrix method for determination of the natural vibration characteristics of elastically coupled launch vehicle boosters. Acta Mech. Sin. 2015, 31, 570–580. [Google Scholar] [CrossRef]
- Myklestad, N.O. A New Method of Calculating Natural Modes of Uncoupled Bending Vibration of Airplane Wings and Other Types of Beams. J. Aeronaut. Sci. 1994, 11, 153–162. [Google Scholar] [CrossRef]
- Khomyakov, V.S.; Kochinev, N.A.; Sabirov, F.S. Dynamic characteristics of spindle components. Russ. Eng. Res. 2009, 29, 607–611. [Google Scholar] [CrossRef]
- Fedorynenko, D.; Kirigaya, R.; Nakao, Y. Dynamic characteristics of spindle with water-lubricated hydrostatic bearings for ultra-precision machine tools. Precis. Eng. 2020, 63, 187–196. [Google Scholar] [CrossRef]
- Demec, P. Simplified Dynamic Analysis of Grinders Spindle Node. Technol. Eng. 2014, 11, 11–15. [Google Scholar] [CrossRef]
- Rui, X.; Wang, X.; Zhou, Q.; Zhang, J. Transfer matrix method for multibody systems (Rui method) and its applications. Sci. China Technol. Sci. 2019, 62, 712–720. [Google Scholar] [CrossRef]
- Boiangiu, M.; Ceausu, V.; Untaroiu, C.D. A transfer matrix method for free vibration analysis of Euler-Bernoulli beams with variable cross section. J. Vib. Control 2016, 22, 2591–2602. [Google Scholar] [CrossRef]
- Chen, D.; Gu, C.; Li, M.; Sun, B.; Li, X. Natural vibration characteristics determination of elastic beam with attachments based on a transfer matrix method. J. Vib. Control 2022, 28, 637–651. [Google Scholar] [CrossRef]
- Rui, X.; Zhang, J.; Wang, X.; Rong, B.; He, B.; Jin, Z. Multibody system transfer matrix method: The past, the present, and the future. Int. J. Mech. Syst. Dyn. 2022, 2, 3–26. [Google Scholar] [CrossRef]
- Rui, X.; Wang, G.; Zhang, J. Transfer Matrix Method for Multibody Systems: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019; 768p, ISBN 978-1118724804. [Google Scholar]
- Rong, B.; Rui, X.T.; Yang, F.F. Discrete time transfer matrix method for dynamics of multibody system with real-time control. J. Sound Vib. 2010, 329, 627–643. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: Cambridge, UK, 2012; 382p, ISBN 978-0521172479. [Google Scholar]
- Sun, Y.; Zheng, M.; Jiang, S.; Zhan, D.; Wang, R. A State-of-the-Art Review on Chatter Stability in Machining Thin–Walled Parts. Machines 2023, 11, 359. [Google Scholar] [CrossRef]
- Yue, C.X.; Gao, H.; Liu, X.; Liang, S.Y.; Wang, L. A review of chatter vibration research in milling. Chin. J. Aeronaut. 2019, 32, 215–242. [Google Scholar] [CrossRef]
- Lu, K.; Wang, Y.; Gu, F.; Pang, X.; Ball, A. Dynamic modeling and chatter analysis of a spindle-workpiece-tailstock system for the turning of flexible parts. Int. J. Adv. Manuf. Technol. 2019, 104, 3007–3015. [Google Scholar] [CrossRef]
- Stepan, G.; Kiss, A.K.; Ghalamchi, B.; Sopanen, J.; Bachrathy, D. Chatter avoidance in cutting highly flexible workpieces. CIRP Ann. Manuf. Technol. 2017, 66, 1–4. [Google Scholar] [CrossRef]
- Otto, A.; Khasawneh, F.A.; Radons, G. Position-dependent stability analysis of turning with tool and workpiece compliance. Int. J. Adv. Manuf. Technol. 2015, 79, 1453–1463. [Google Scholar] [CrossRef]
- Sekar, M.; Srinivas, J.; Kotaiah, K.R.; Yang, S.H. Stability analysis of turning process with tailstock-supported workpiece. Int. J. Adv. Manuf. Technol. 2009, 43, 862–871. [Google Scholar] [CrossRef]
- Sun, Y.; Shuyang, Y. Dynamics identification and stability analysis in turning of slender workpieces with flexible boundary constraints. Mech. Syst. Signal Process. 2022, 177, 109245. [Google Scholar] [CrossRef]
- Schmitz, T.; Betters, E.; Budak, E.; Yüksel, E.; Park, S.; Altintas, Y. Review and status of tool tip frequency response function prediction using receptance couplin. Precis. Eng. 2023, 79, 60–77. [Google Scholar] [CrossRef]
- Ganguly, V.; Schmitz, T.L. Spindle dynamics identification using particle swarm optimization. J. Manuf. Process. 2013, 15, 444–451. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Donalson, R.R. Predicting High-Speed Machining Dynamics by Substructure Analysis. CIRP Ann. 2000, 49, 303–308. [Google Scholar] [CrossRef]
- Tsai, S.H.; Ouyang, H.; Chang, J.Y. A receptance-based method for frequency assignment via coupling of subsystems. Arch. Appl. Mech. 2020, 90, 449–465. [Google Scholar] [CrossRef]
- Honeycutt, A.; Schmitz, T. Receptance coupling model for variable dynamics in fixed-free thin rib machining. Procedia Manuf. 2018, 26, 173–180. [Google Scholar] [CrossRef]
- Iglesias, A.L.; Tunç, L.T.; Özsahin, O.; Franco, O.; Munoa, J.; Budak, E. Alternative experimental methods for machine tool dynamics identification: A review. Mech. Syst. Signal Process. 2022, 170, 108837. [Google Scholar] [CrossRef]
- Özşahin, O.; Ertürk, A.; Özgüven, H.N.; Budak, E. A closed-form approach for identification of dynamical contact parameters in spindle–holder–tool assemblies. Int. J. Mach. Tools Manuf. 2009, 49, 25–35. [Google Scholar] [CrossRef]
- Bisu, C.F.; K’nevez, J.Y.; Darnis, P.; Laheurte, R.; Gérard, A. New method to characterize a machining system: Application in turning. Int. J. Mater. Form. 2009, 2, 93–105. [Google Scholar] [CrossRef]
- Zapciu, M.; K’nevez, J.Y.; Gérard, A.; Cahuc, O.; Bisu, C.F. Dynamic characterization of machining systems. Int. Adv. Manuf. Technol. 2011, 57, 73–83. [Google Scholar] [CrossRef]
- Soleimanimehr, H.; Nategh, M.J.; Najafabadi, A.F.; Zarnani, A. The analysis of the Timoshenko transverse vibrations of workpiece in the ultrasonic vibration-assisted turning process and investigation of the machining error caused by this vibration. Precis. Eng. 2018, 54, 99–106. [Google Scholar] [CrossRef]
- Erturk, A.; Özgüven, H.N.; Budak, E. Analytical modeling of spindle-tool dynamics on machine tools using Tymoshenko beam model and receptance coupling for the prediction of tool point FRF. Int. J. Mach. Tools Manuf. 2006, 46, 1901–1912. [Google Scholar] [CrossRef]
- Hatter, D.J. Matrix Computer Methods of Vibration Analysis; Butterworth: London, UK, 1973; 206p, ISBN 0470359951. [Google Scholar]
- Merchant, M.E. Mechanics of the Metal Cutting Process. J. Appl. Phys. 1945, 16, 267–275. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford University Press: New York, NY, USA; Oxford, UK, 2005; 759p, ISBN 9780195142068. [Google Scholar]
- Tsekhanov, J.; Storchak, M. Development of analytical model for orthogonal cutting. Prod. Eng. Res. Dev. 2014, 9, 247–255. [Google Scholar] [CrossRef]
- Kushner, V.; Storchak, M. Determining mechanical characteristics of material resistance to deformation in machining. Prod. Eng. Res. Dev. 2014, 8, 679–688. [Google Scholar] [CrossRef]
- Storchak, M.; Möhring, H.-C.; Stehle, T. Improving the friction model for the simulation of cutting processes. Tribol. Int. 2021, 167, 107376. [Google Scholar] [CrossRef]
- Heisel, U.; Krivoruchko, D.V.; Zaloha, W.A.; Storchak, M.; Stehle, T. Thermomechanical exchange effects in machining. Z. Für Wirtsch. Fabr. ZWF 2009, 104, 263–272. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Bergs, T.; Hardt, M.; Schraknepper, D. Determination of Johnson-Cook material model parameters for AISI 1045 from orthogonal cutting tests using the Downhill-Simplex algorithm. Procedia Manuf. 2020, 48, 541–552. [Google Scholar] [CrossRef]
- Meng, X.; Lin, Y.; Mi, S. An Improved Johnson–Cook Constitutive Model and Its Experiment Validation on Cutting Force of ADC12 Aluminum Alloy during High-Speed Milling. Metals 2020, 10, 1038. [Google Scholar] [CrossRef]
- Heisel, U.; Krivoruchko, D.V.; Zaloha, W.A.; Storchak, M.; Stehle, T. Breakage models for the modeling of cutting processes. ZWF Z. Fuer Wirtsch. Fabr. 2009, 104, 330–339. [Google Scholar] [CrossRef]
- Storchak, M.; Jiang, L.; Xu, Y.; Li, X. Finite element modeling for the cutting process of the titanium alloy Ti10V2Fe3Al. Prod. Eng. Res. Dev. 2016, 10, 509–517. [Google Scholar] [CrossRef]
- Zorev, N.N. Metal Cutting Mechanics; Pergamon Press GmbH: Frankfurt, Germany, 1966; 526p, ISBN 978-0080107233. [Google Scholar]
- Oxley, P.L.B.; Shaw, M.C. Mechanics of Machining. In An Analytical Approach to Assessing Machinability; Ellis Horwood: Chichester, UK, 1989; 242p. [Google Scholar] [CrossRef]
- Fluhrer, J. Deform-User Manual Deform V12.0.; SFTC: Columbus, OH, USA, 2019. [Google Scholar]
- Danylchenko, Y.; Petryshyn, A.; Repinskyi, S.; Bandura, V.; Kalimoldayev, M.; Gromaszek, K.; Imanbek, B. Dynamic characteristics of “tool-workpiece” elastic system in the low stiffness parts milling process. In Mechatronic Systems 2: Applications in Material Handling Processes and Robotics; Routledge: London, UK, 2021; pp. 225–236. [Google Scholar] [CrossRef]
- Kushnir, E.; Portman, V.T. Geometric and Kinematic Contributors of Cutting Force Excursion. Procedia CIRP 2022, 112, 292–297. [Google Scholar] [CrossRef]
- Özşahin, O.; Ritou, M.; Budak, E.; Rabréau, C.; Le Loch, S. Identification of spindle dynamics by receptance coupling for non-contact excitation system. Procedia CIRP 2019, 82, 273–278. [Google Scholar] [CrossRef]
- Türkeş, E.; Neşeli, S. A simple approach to analyze process damping in chatter vibration. Int. J. Adv. Manuf. Technol. 2014, 70, 775–786. [Google Scholar] [CrossRef]
- Banakh, L.Y.; Kempner, M.L. Vibrations of Mechanical Systems with Regular Structure; Springer: Berlin/Heidelberg, Germany, 2010; 249p. [Google Scholar] [CrossRef]
- Schmitz, T.; Honeycutt, A.; Gomez, M.; Stokes, M.; Betters, E. Multi-point coupling for tool point receptance prediction. J. Manuf. Process. 2019, 43, 2–11. [Google Scholar] [CrossRef]
- Petrakov, Y.; Danylchenko, M.; Petryshyn, A. Prediction of chatter stability in turning. East. Eur. J. Enterp. Technol. 2019, 5, 58–64. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Azvar, M.; Budak, E. Suppressing vibration modes of spindle-holder-tool assembly through FRF modification for enhanced chatter stability. CIRP Ann. 2018, 67, 397–400. [Google Scholar] [CrossRef]
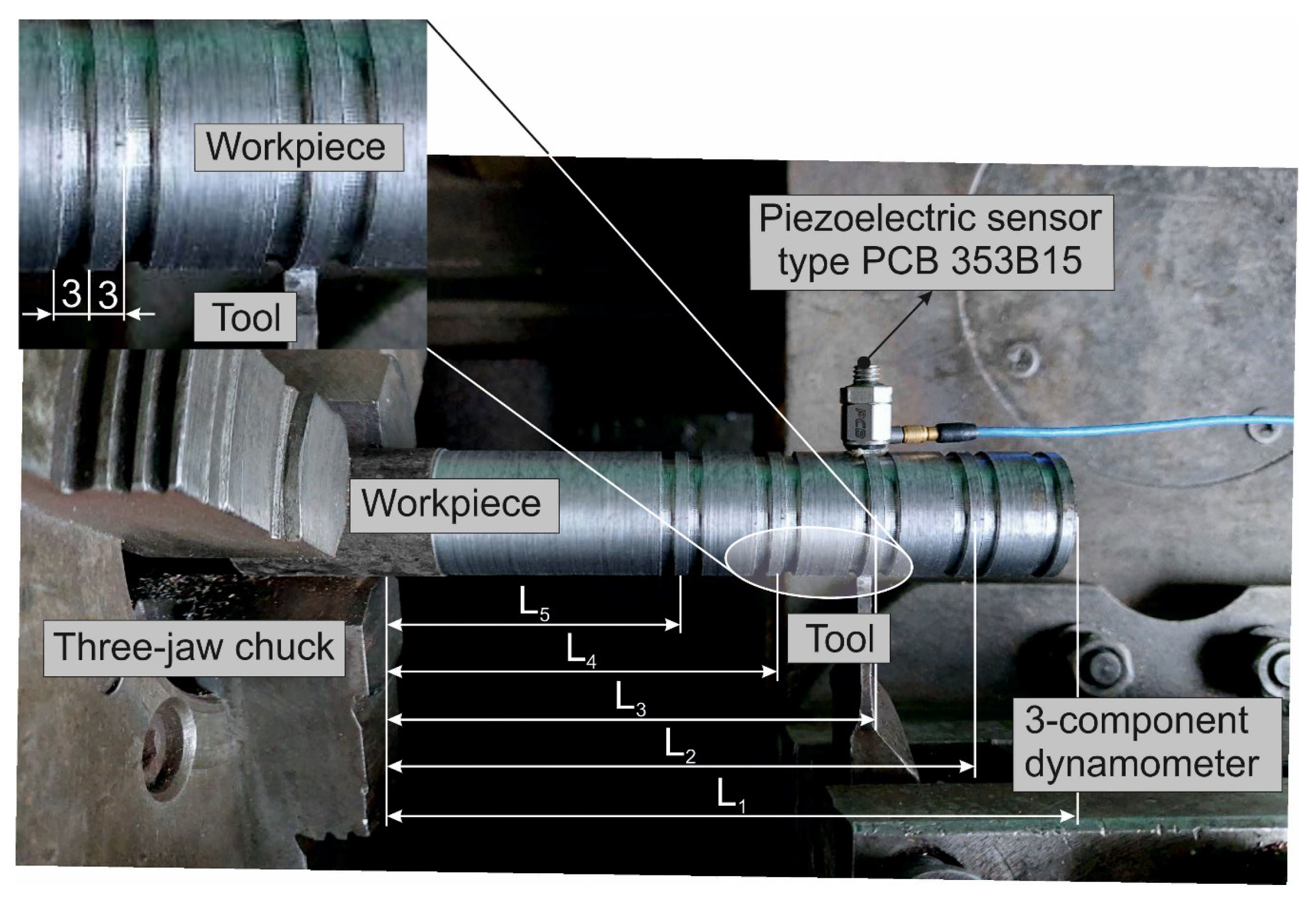

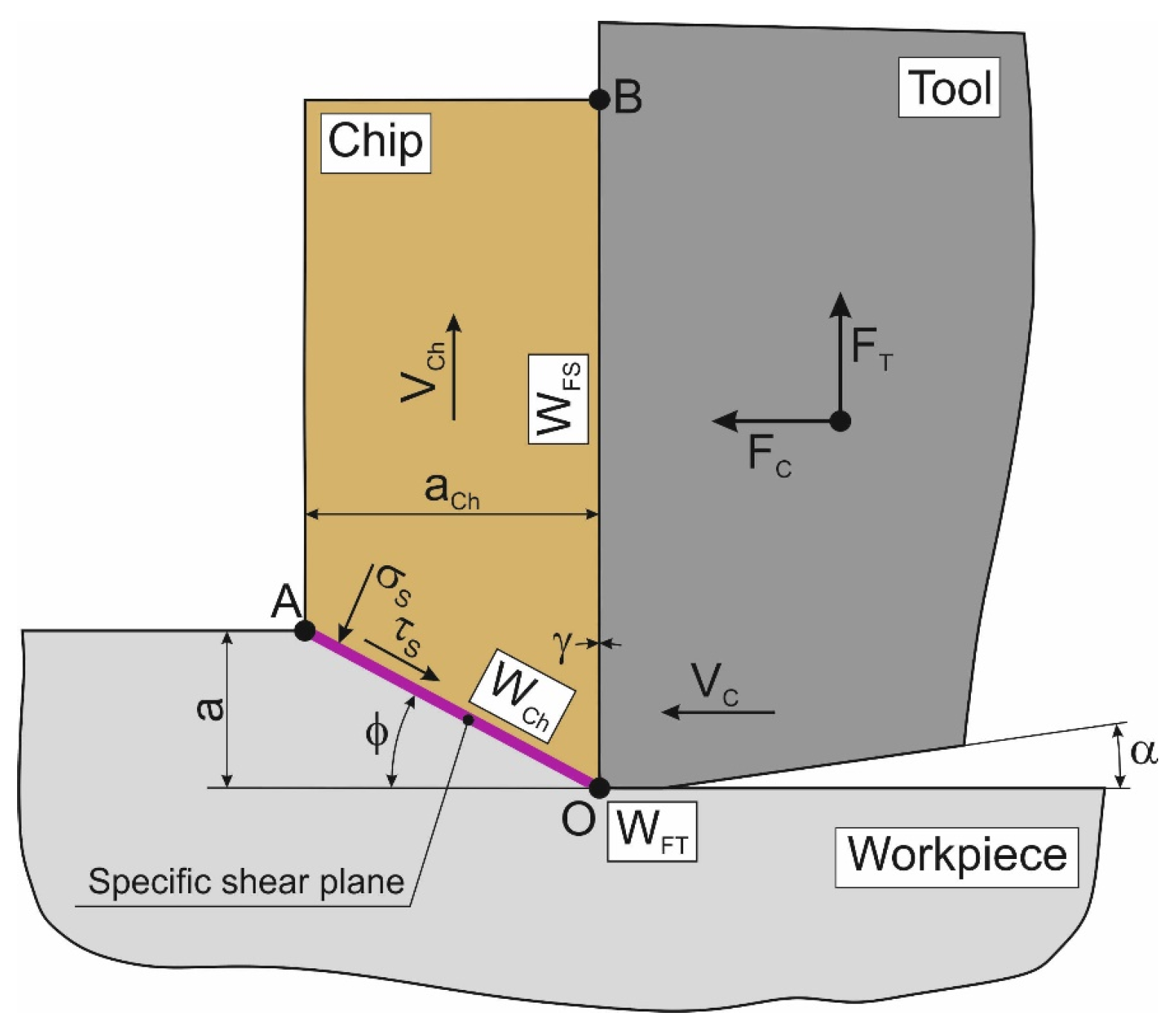
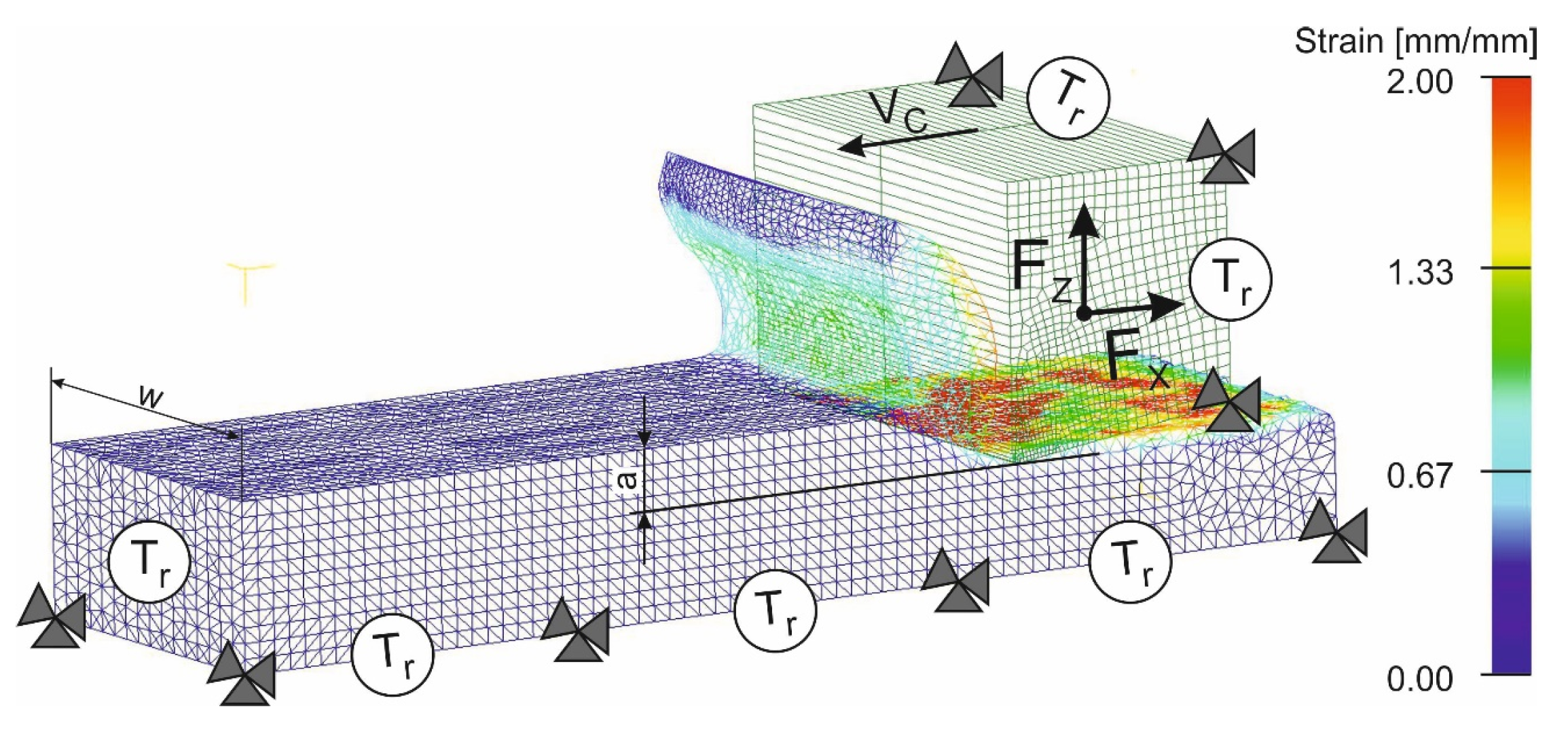

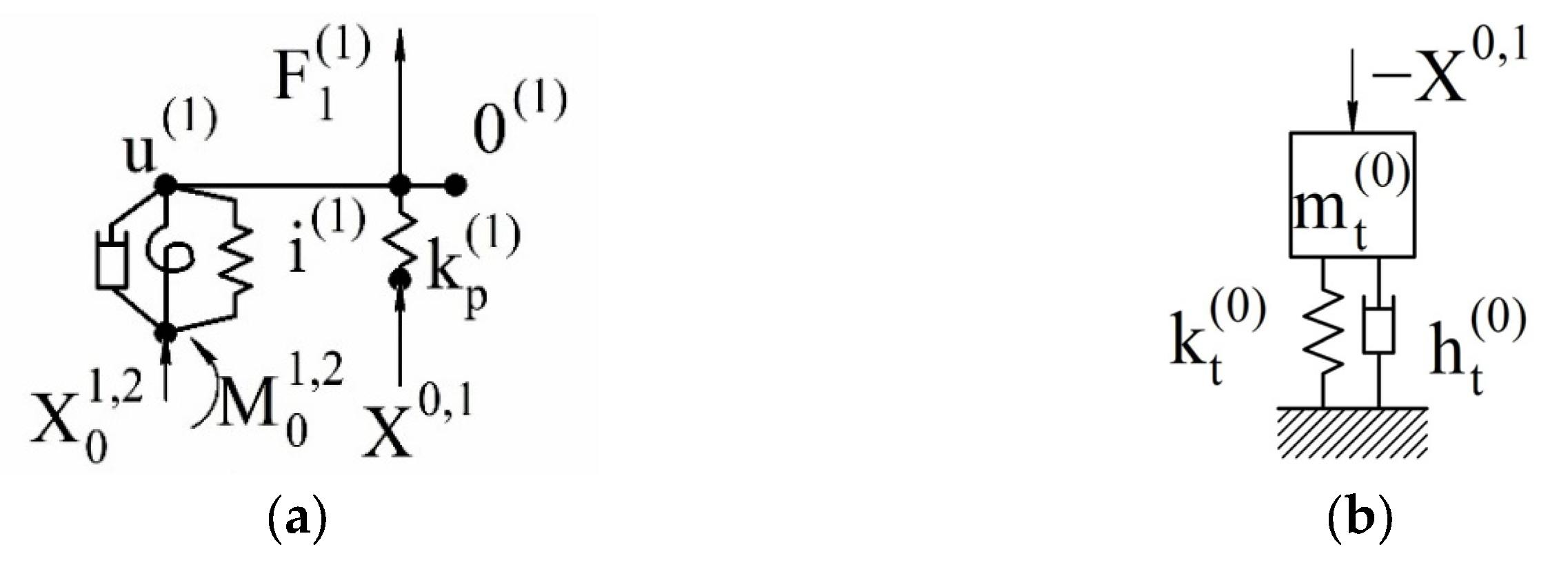


| Strength (MPa) | Elastic Modulus (GPa) | Elongation (%) | Hardness (HB) | Poisson′s Ratio | Specific Heat (J/kg·K) | Thermal Expansion (µm/m · °C) | Thermal Conductivity (W/m·K) | |
|---|---|---|---|---|---|---|---|---|
| Tensile | Yield | |||||||
| 690 | 620 | 206 | 12 | 180 | 0.29 | 486 | 14 | 49.8 |
| Dynamic Model Coefficients | Bearings | Tool–Holder–Chuck Joint | ||
|---|---|---|---|---|
| Double-Row Cylindrical Roller Bearing (Position 1) | Angular Contact Ball Bearing (Positions 2 and 3) | Radial Bearing (Position 4) | ||
| Radial stiffness, (N/µm) | 502 | 257 | 365 | 12 |
| Angular stiffness, (N·µm/rad) | 12,050 | - | - | 3.67 × 10−2 |
| Damping, hi (Ns/mm) | 2 | 2 | 2 | 0.3 |
| lathe carriage | ||||
| Equivalent mass, mc (kg) | 0.95 | |||
| Equivalent stiffness, kc (N/µm) | 242 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danylchenko, Y.; Storchak, M.; Danylchenko, M.; Petryshyn, A. Cutting Process Consideration in Dynamic Models of Machine Tool Spindle Units. Machines 2023, 11, 582. https://doi.org/10.3390/machines11060582
Danylchenko Y, Storchak M, Danylchenko M, Petryshyn A. Cutting Process Consideration in Dynamic Models of Machine Tool Spindle Units. Machines. 2023; 11(6):582. https://doi.org/10.3390/machines11060582
Chicago/Turabian StyleDanylchenko, Yurii, Michael Storchak, Mariia Danylchenko, and Andrii Petryshyn. 2023. "Cutting Process Consideration in Dynamic Models of Machine Tool Spindle Units" Machines 11, no. 6: 582. https://doi.org/10.3390/machines11060582






