Vibro-Acoustic Performance of a Fluid-Loaded Periodic Locally Resonant Plate
Abstract
:1. Introduction
2. Theoretical Models
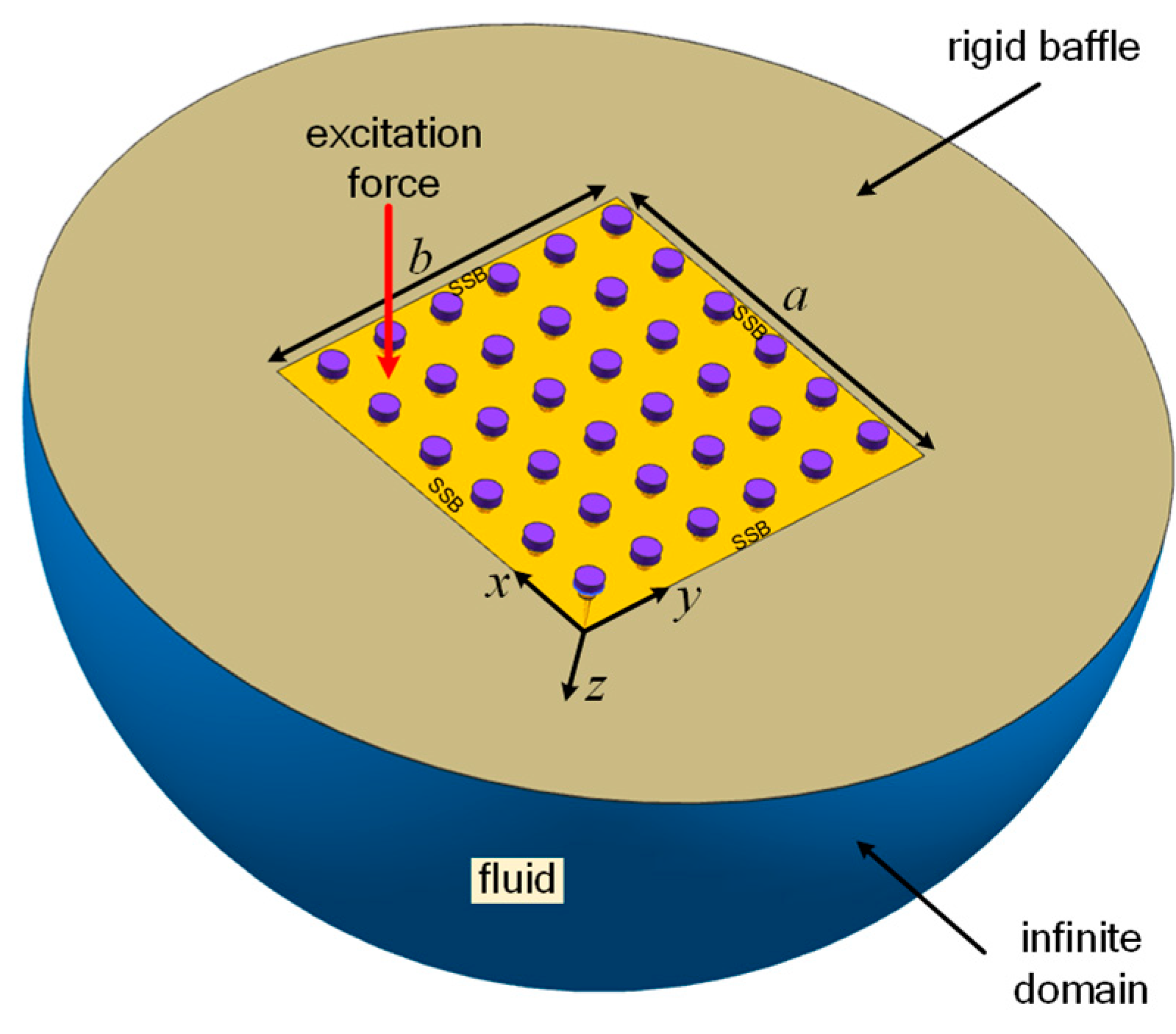
2.1. Structure Model and Basic Governing Equations
2.2. Band-Gap Formulations of an Infinite LR Plate
2.3. Vibration and Radiation Formulations of a Finite LR Plate
3. Results and Discussion
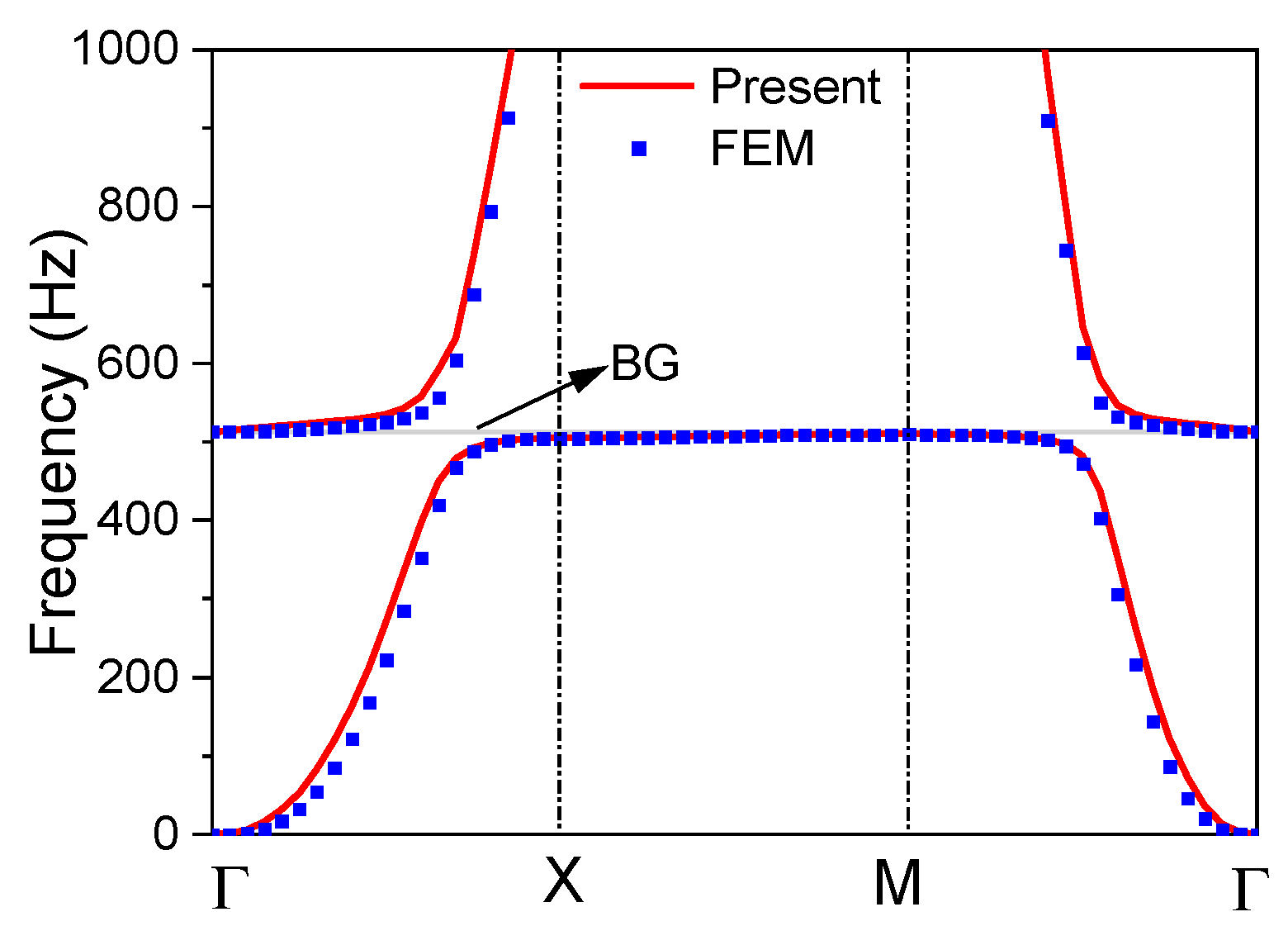
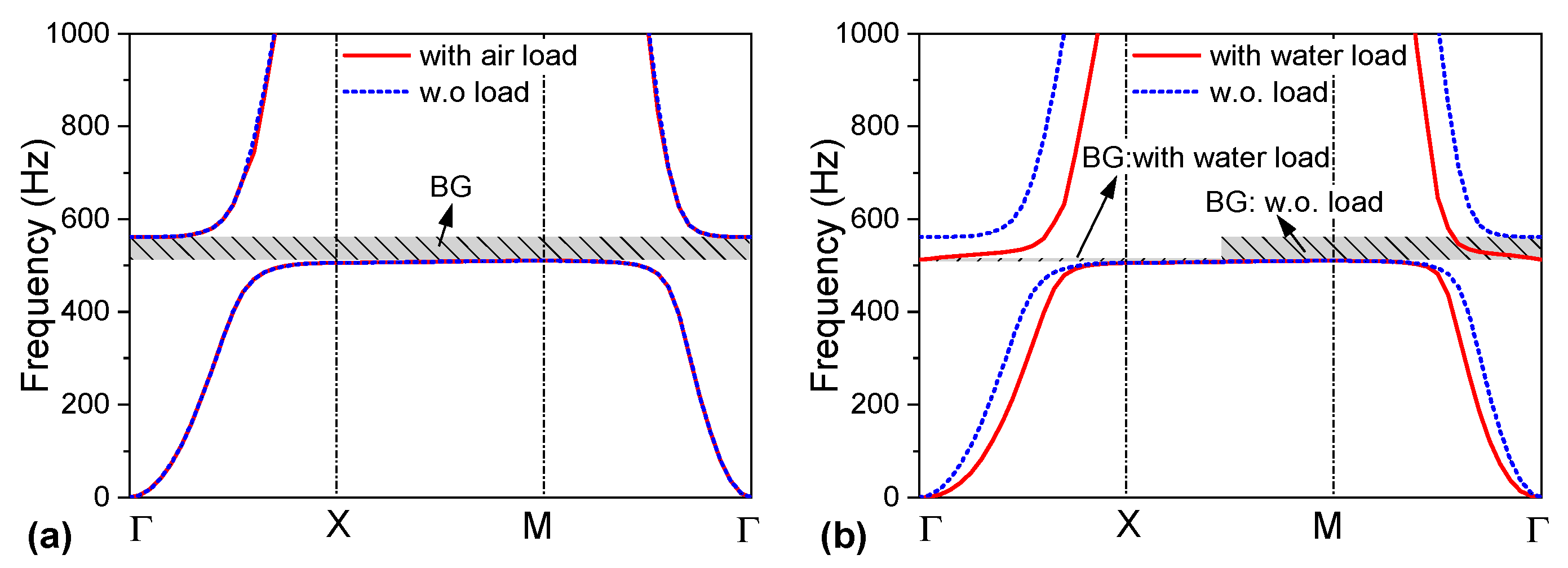
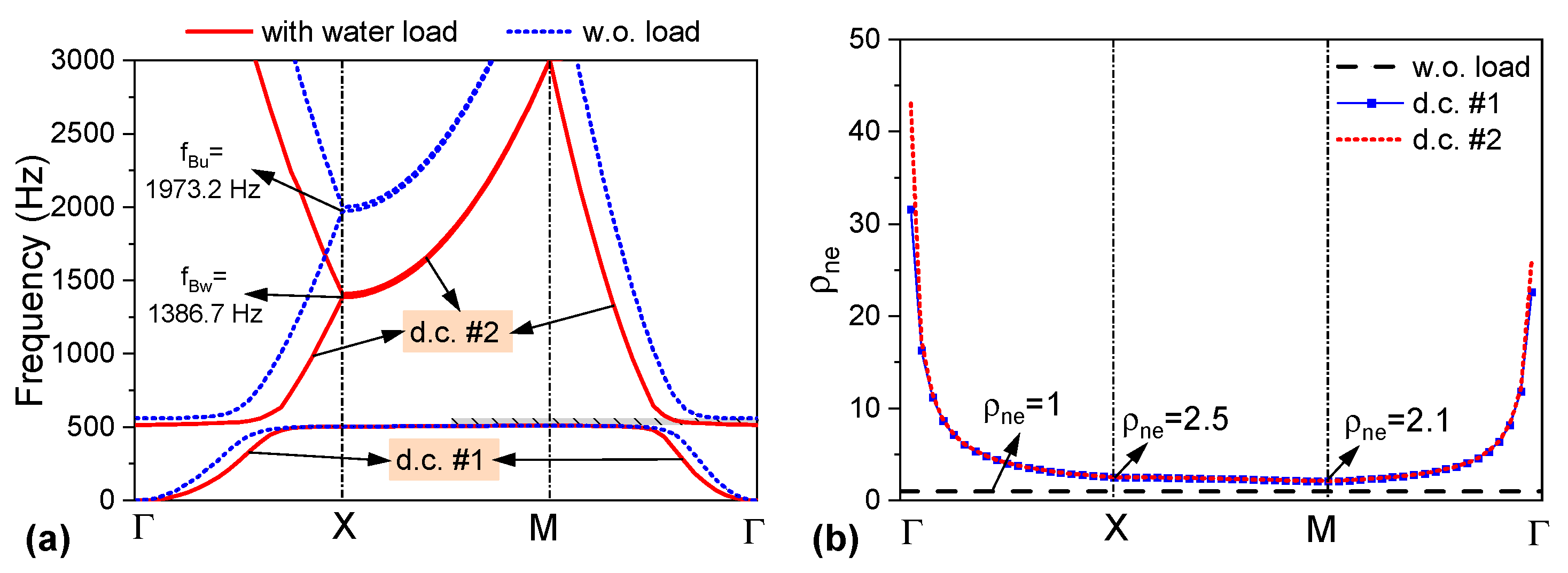
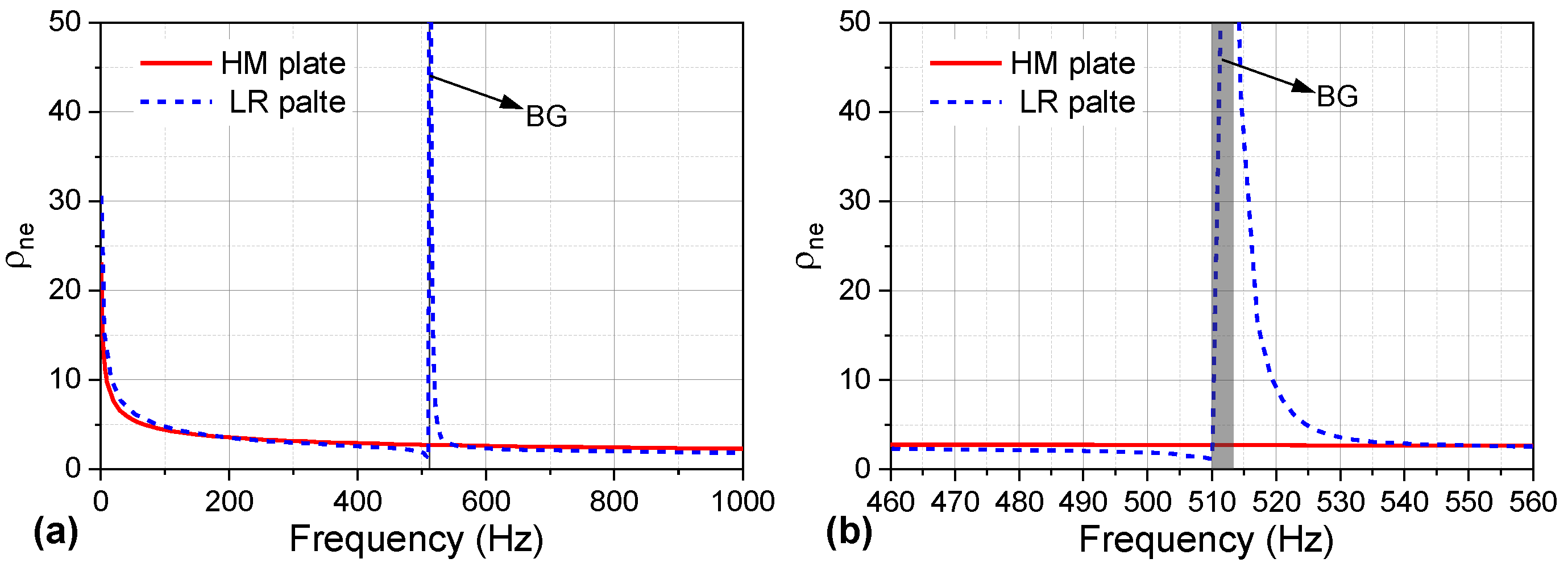
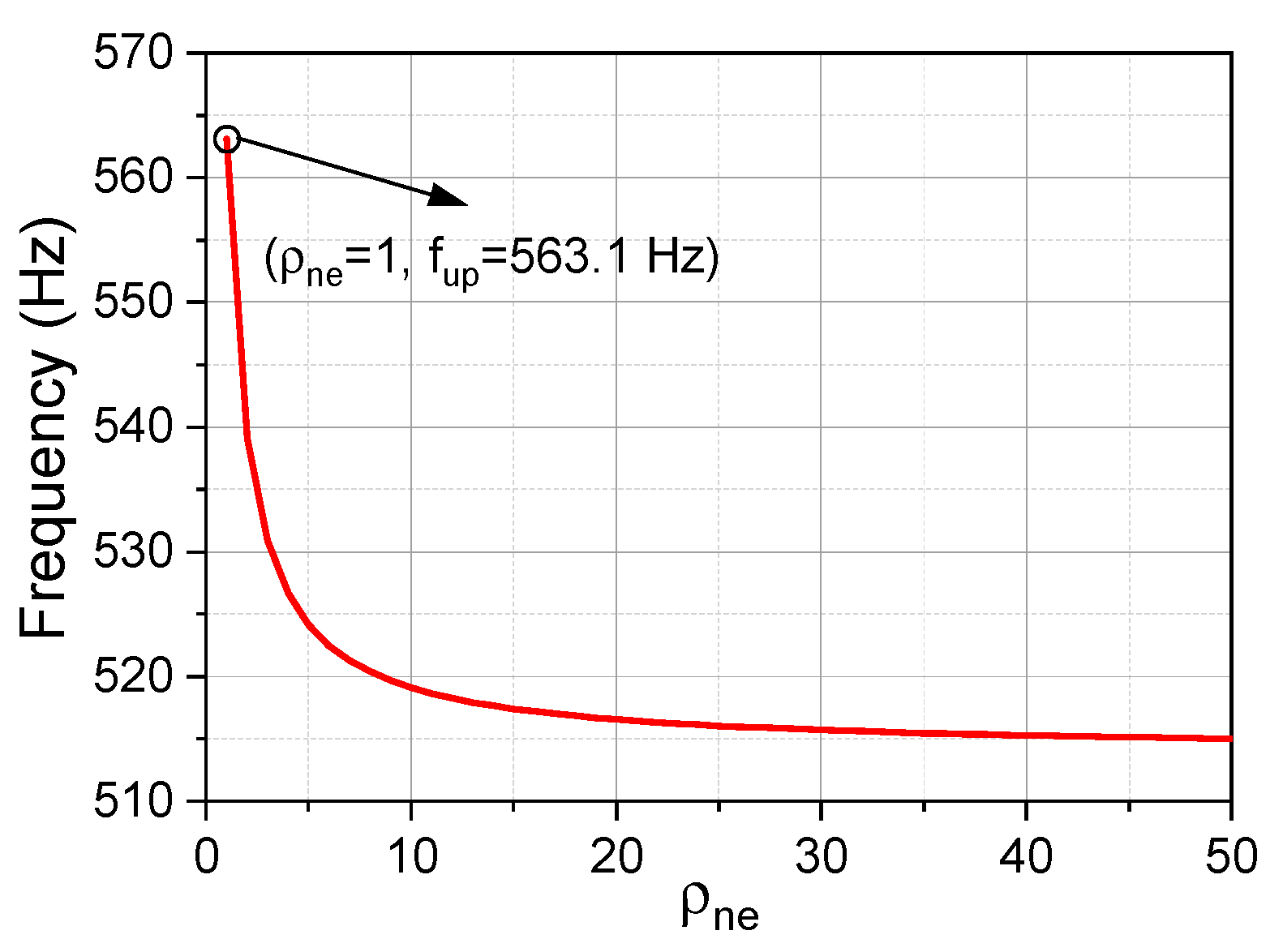
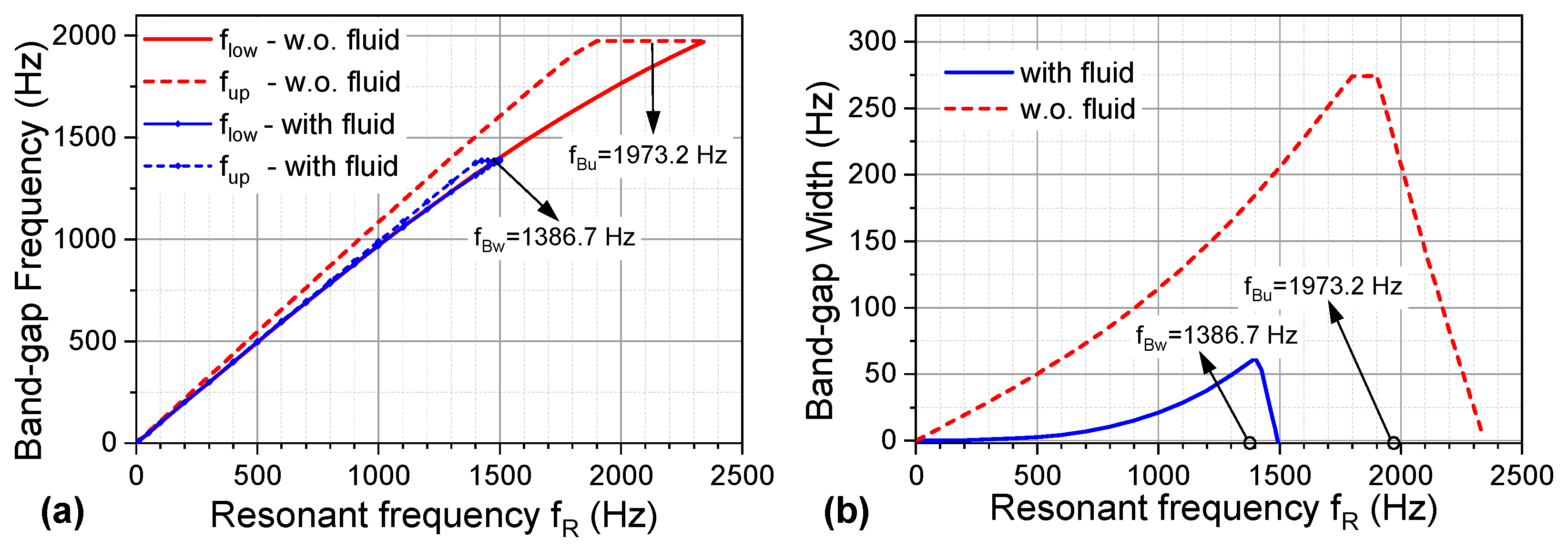
3.1. Band-Gap Properties
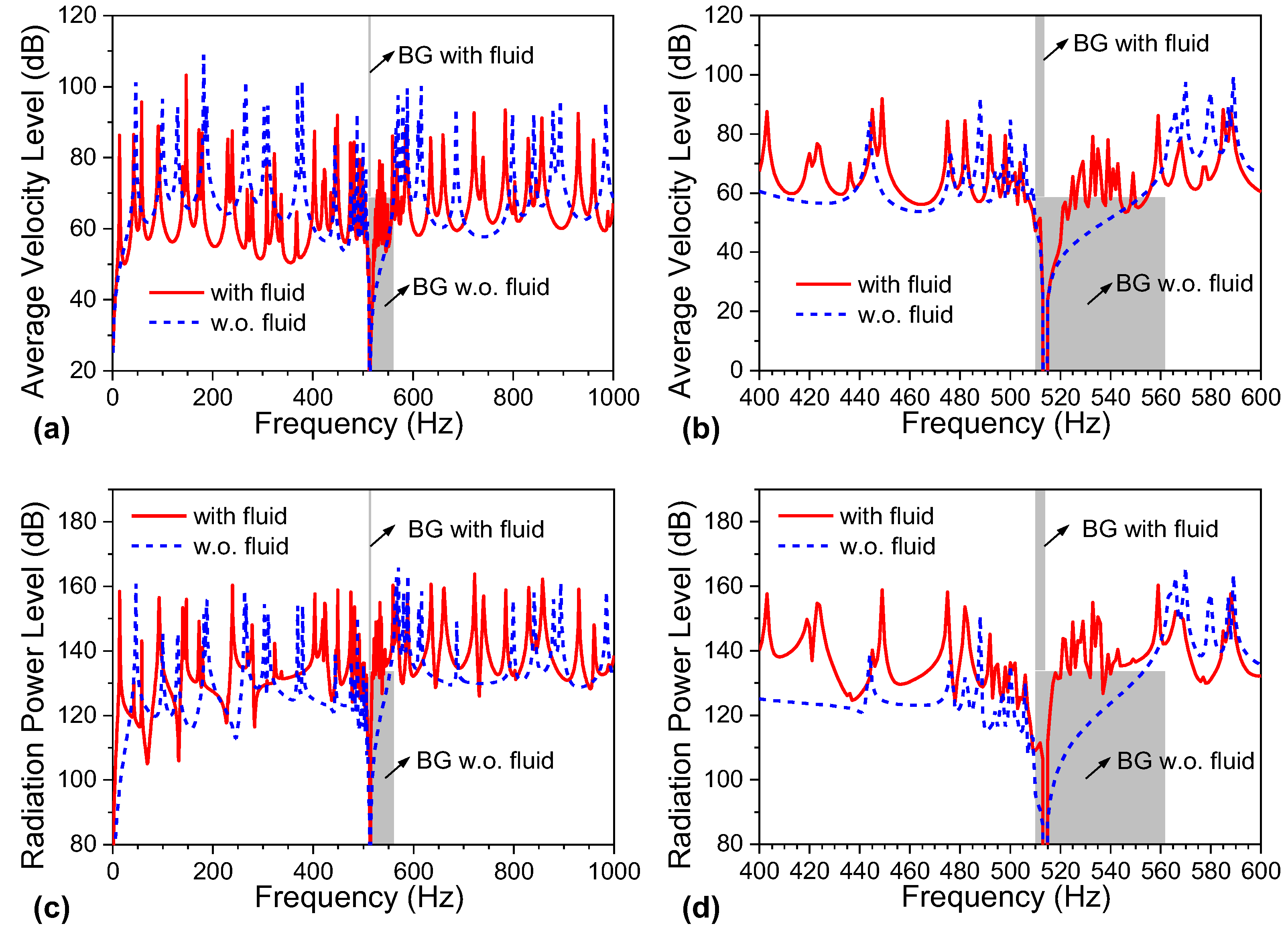
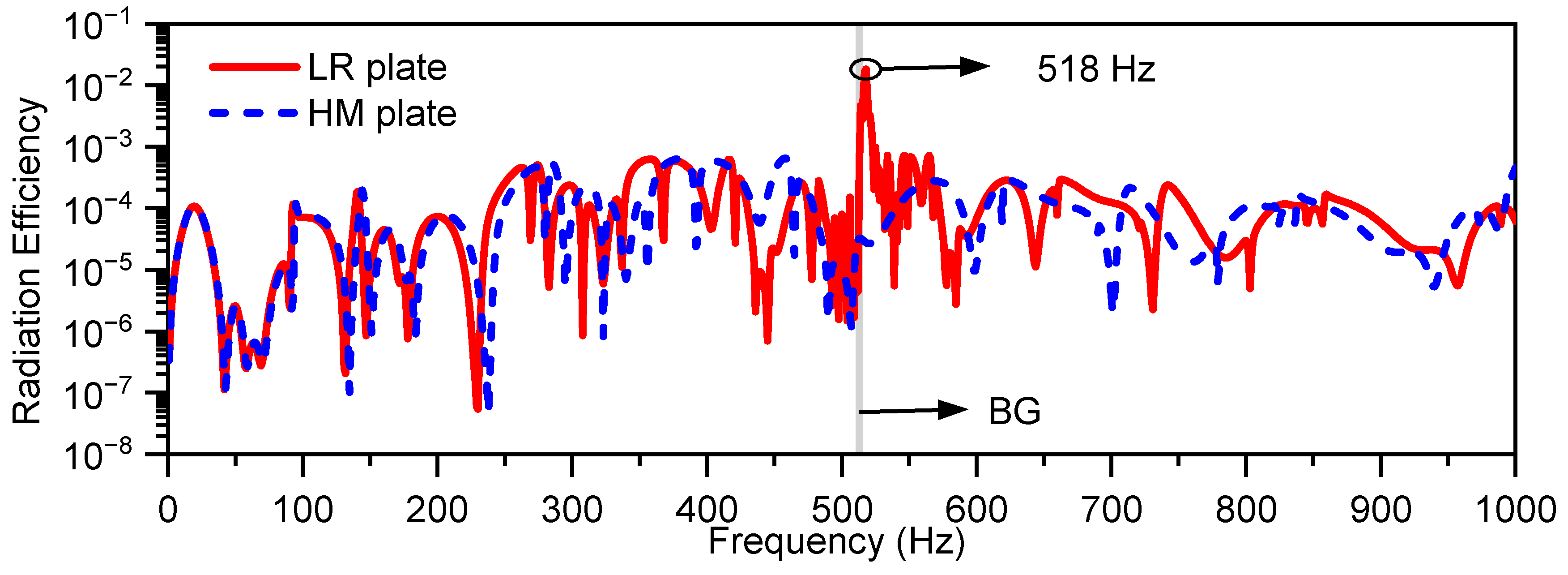
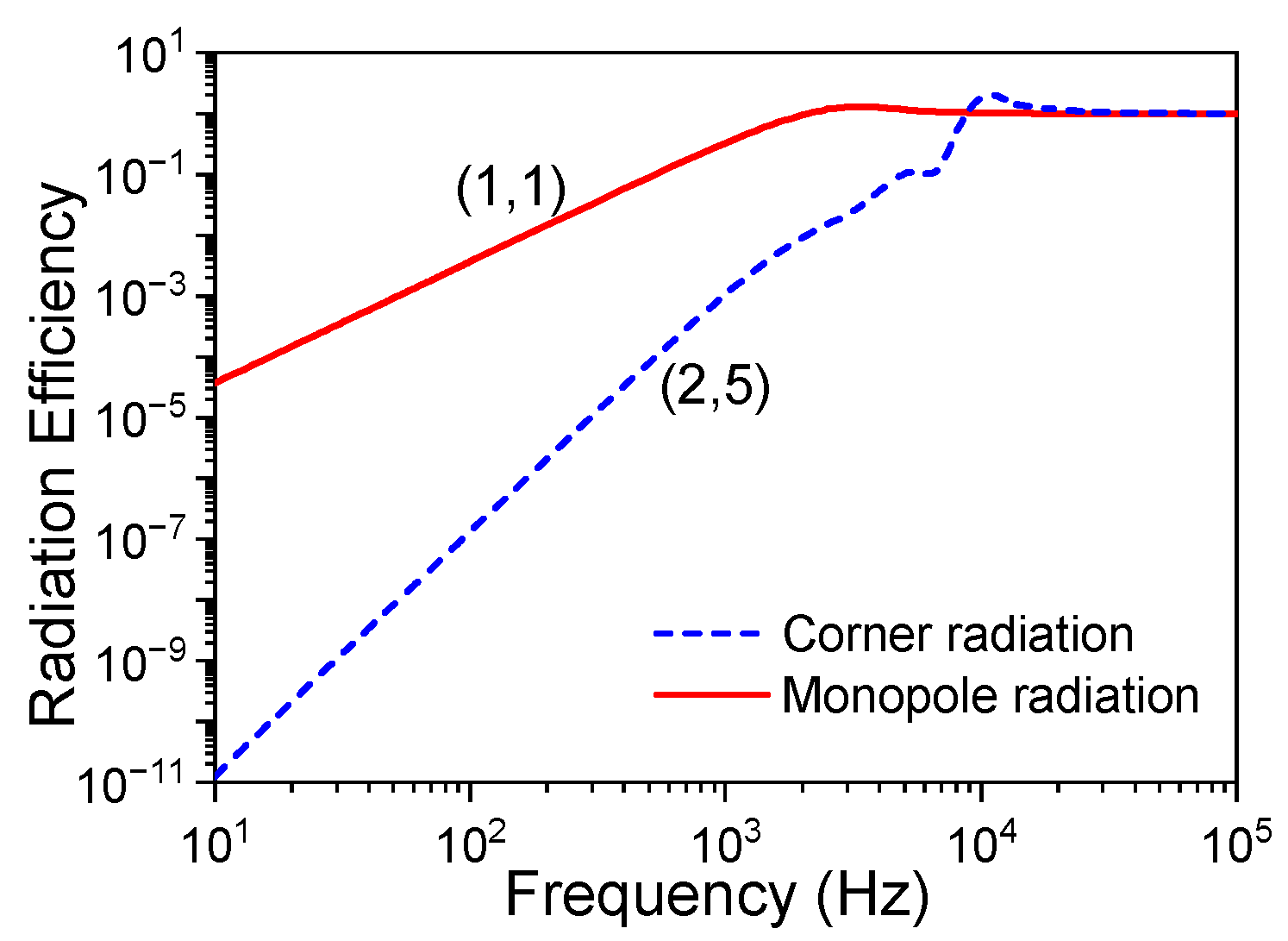
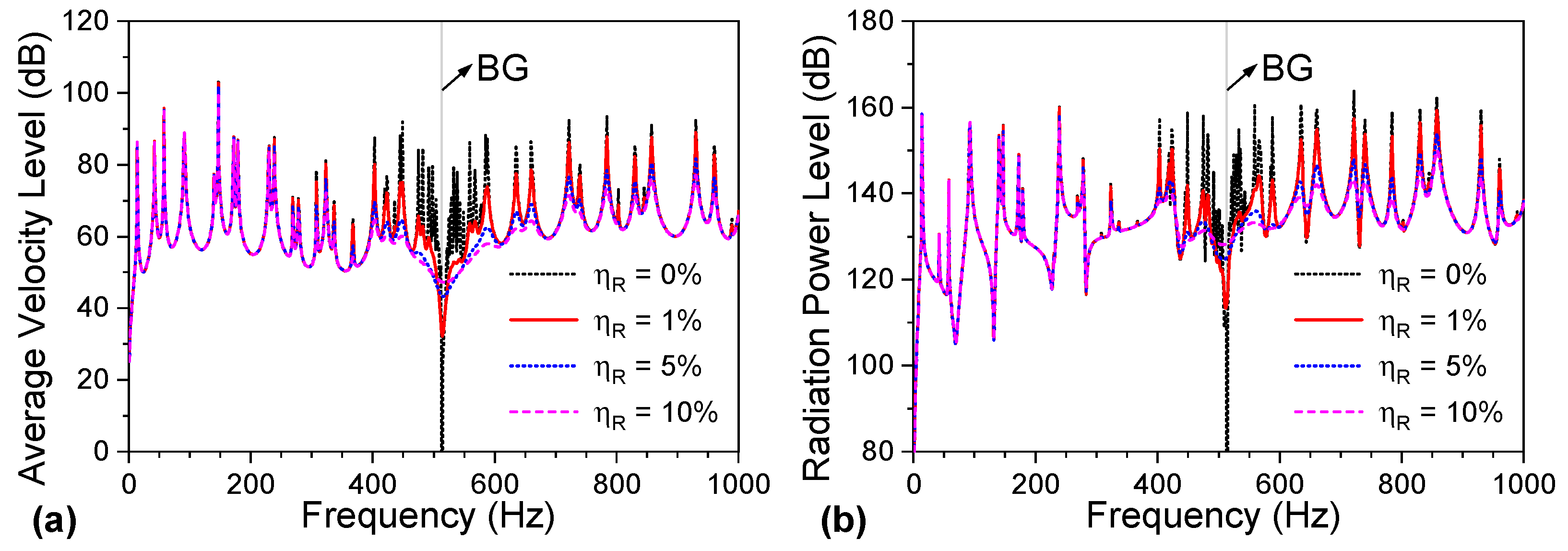
3.2. Vibration and Sound Radiation Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, N.S.; Zhang, Z.C.; Deng, J.; Guo, X.Y.; Cheng, B.Z.; Hou, H. Acoustic metamaterials for noise reduction: A review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Liao, G.X.; Luan, C.C.; Wang, Z.W.; Liu, J.P.; Yao, X.H.; Fu, J.Z. Acoustic metamaterials: A review of theories, structures, fabrication approaches, and applications. Adv. Mater. Technol. 2021, 6, 2000787. [Google Scholar] [CrossRef]
- Liu, J.Y.; Guo, H.B.; Wang, T. A review of acoustic metamaterials and phononic crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 1st ed.; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1946. [Google Scholar]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafarirouhani, B. Acoustic band-structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Y.; Zhang, X.X.; Mao, Y.W.; Zhu, Y.Y.; Yang, Z.Y.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Wen, X.; Wen, J.; Yu, D.; Wang, G.; Liu, Y.; Han, X. Phononic Crystals, 1st ed.; National Defence Industry Press: Beijing, China, 2009. [Google Scholar]
- Wen, Q.H.; Zuo, S.G.; Wei, H. Locally resonant elastic wave band gaps in flexural vibration of multi-oscillators beam. Acta Phys. Sin. 2012, 61, 034301. [Google Scholar]
- Wu, J.; Bai, X.C.; Xiao, Y.; Geng, M.X.; Yu, D.L.; Wen, J.H. Low frequency band gaps and vibration reduction properties of a multi-frequency locally resonant phononic plate. Acta Phys. Sin. 2016, 65, 064602. [Google Scholar]
- Xiao, Y.; Wen, J.H.; Wen, X.S. Broadband locally resonant beams containing multiple periodic arrays of attached resonators. Phys. Lett. A 2012, 376, 1384–1390. [Google Scholar] [CrossRef]
- Romero-Garcia, V.; Krynkin, A.; Garcia-Raffi, L.M.; Umnova, O.; Sanchez-Perez, J.V. Multi-resonant scatterers in sonic crystals: Locally multi-resonant acoustic metamaterial. J. Sound Vib. 2013, 332, 184–198. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.H.; Wen, X.S. Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators. J. Sound Vib. 2012, 331, 5408–5423. [Google Scholar] [CrossRef]
- Ma, J.G.; Sheng, M.P.; Guo, Z.W.; Qin, Q. Dynamic analysis of periodic vibration suppressors with multiple secondary oscillators. J. Sound Vib. 2018, 424, 94–111. [Google Scholar] [CrossRef]
- Qin, Q.; Sheng, M.P.; Guo, Z.W. Low-frequency vibration and radiation performance of a locally resonant plate attached with periodic multiple resonators. Appl. Sci. 2020, 10, 2843. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, H.; Wang, T. Vibro-acoustic performance of acoustic metamaterial plate with periodic lateral local resonator. Acta Phys. Sin. 2021, 70, 214301. [Google Scholar] [CrossRef]
- Deymierv, P.A. Acoustic Metamaterials and Phononic Crystals; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Spadoni, A.; Daraio, C.; Hurst, W.; Brown, M. Nonlinear phononic crystals based on chains of disks alternating with toroidal structures. Appl. Phys. Lett. 2011, 98, 161901. [Google Scholar] [CrossRef]
- Romeo, F.; Ruzzene, M. Wave Propagation in Linear and Nonlinear Periodic Media: Analysis and Applications; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Fang, X.; Wen, J.H.; Benisty, H.; Yu, D.L. Ultrabroad acoustical limiting in nonlinear metamaterials due to adaptive-broadening band-gap effect. Phys. Rev. B 2020, 101, 104304. [Google Scholar] [CrossRef]
- Sheng, P.; Fang, X.; Wen, J.H.; Yu, D.L. Vibration properties and optimized design of a nonlinear acoustic metamaterial beam. J. Sound Vib. 2021, 492, 115739. [Google Scholar] [CrossRef]
- Duhamel, D.; Mace, B.R.; Brennan, M.J. Finite element analysis of the vibrations of waveguides and periodic structures. J. Sound Vib. 2006, 294, 205–220. [Google Scholar] [CrossRef]
- Mead, D.J. The forced vibration of one-dimensional multi-coupled periodic structures: An application to finite element analysis. J. Sound Vib. 2009, 319, 282–304. [Google Scholar] [CrossRef]
- Manktelow, K.; Narisetti, R.K.; Leamy, M.J.; Ruzzene, M. Finite-element based perturbation analysis of wave propagation in nonlinear periodic structures. Mech. Syst. Signal Process. 2013, 39, 32–46. [Google Scholar] [CrossRef]
- Qiu, C.Y.; Liu, Z.Y.; Mei, J.; Ke, M.Z. The layer multiple-scattering method for calculating transmission coefficients of 2D phononic crystals. Solid State Commun. 2005, 134, 765–770. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.H.; Wen, X.S. Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap. Phys. Rev. B 2005, 71, 104302. [Google Scholar] [CrossRef]
- Cao, Y.J.; Hou, Z.L.; Liu, Y.Y. Finite difference time domain method for band-structure calculations of two-dimensional phononic crystals. Solid State Commun. 2004, 132, 539–543. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Jiao, Y. Vibration and bandgap behavior of sandwich pyramid lattice core plate with resonant rings. Materials 2023, 16, 2730. [Google Scholar] [CrossRef]
- Yu, D.L.; Liu, Y.Z.; Qiu, J.; Zhao, H.G.; Liu, Z.M. Experimental and theoretical research on the vibrational gaps in two-dimensional three-component composite thin plates. Chin. Phys. Lett. 2005, 22, 1958–1960. [Google Scholar]
- Zhao, H.G.; Wen, J.H.; Yu, D.L.; Wen, X.S. Low-frequency acoustic absorption of localized resonances: Experiment and theory. J. Appl. Phys. 2010, 107, 023519. [Google Scholar] [CrossRef]
- Meng, H.; Wen, J.H.; Zhao, H.G.; Wen, X.S. Optimization of locally resonant acoustic metamaterials on underwater sound absorption characteristics. J. Sound Vib. 2012, 331, 4406–4416. [Google Scholar] [CrossRef]
- Zhang, S.W.; Wu, J.H.; Hu, Z.P. Low-frequency locally resonant band-gaps in phononic crystal plates with periodic spiral resonators. J. Appl. Phys. 2013, 113, 163511. [Google Scholar] [CrossRef]
- Nouh, M.; Aldraihem, O.; Baz, A. Wave propagation in metamaterial plates with periodic local resonances. J. Sound Vib. 2015, 341, 53–73. [Google Scholar] [CrossRef]
- Hsu, J.C. Local resonances-induced low-frequency band gaps in two-dimensional phononic crystal slabs with periodic stepped resonators. J. Phys. D Appl. Phys. 2011, 44, 055401. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.H.; Yu, D.L.; Wen, X.S. Flexural wave propagation in beams with periodically attached vibration absorbers: Band-gap behavior and band formation mechanisms. J. Sound Vib. 2013, 332, 867–893. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.S. Complete bandgaps in two-dimensional phononic crystal slabs with resonators. J. Appl. Phys. 2013, 114, 043509. [Google Scholar] [CrossRef]
- Casadei, F.; Dozio, L.; Ruzzene, M.; Cunefare, K.A. Periodic shunted arrays for the control of noise radiation in an enclosure. J. Sound Vib. 2010, 329, 3632–3646. [Google Scholar] [CrossRef]
- Aladwani, A.; Almandeel, A.; Nouh, M. Fluid-structural coupling in metamaterial plates for vibration and noise mitigation in acoustic cavities. Int. J. Mech. Sci. 2019, 152, 151–166. [Google Scholar] [CrossRef]
- Claeys, C.C.; Sas, P.; Desmet, W. On the acoustic radiation efficiency of local resonance based stop band materials. J. Sound Vib. 2014, 333, 3203–3213. [Google Scholar] [CrossRef]
- Guo, Z.W.; Pan, J.; Sheng, M.P. Vibro-acoustic performance of a sandwich plate with periodically inserted resonators. Appl. Sci. 2019, 9, 3651. [Google Scholar] [CrossRef]
- Song, Y.B.; Wen, J.H.; Yu, D.L.; Liu, Y.Z.; Wen, X.S. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators. J. Sound Vib. 2014, 333, 3031–3043. [Google Scholar] [CrossRef]
- Jin, G.Y.; Shi, K.K.; Ye, T.G.; Zhou, J.L.; Yin, Y.W. Sound absorption behaviors of metamaterials with periodic multi-resonator and voids in water. Appl. Acoust. 2020, 166, 107351. [Google Scholar] [CrossRef]
- Zhong, H.B.; Tian, Y.J.; Gao, N.S.; Lu, K.; Wu, J.H. Ultra-thin composite underwater honeycomb-type acoustic metamaterial with broadband sound insulation and high hydrostatic pressure resistance. Compos. Struct. 2021, 277, 114603. [Google Scholar] [CrossRef]
- Li, W.L. An analytical solution for the self- and mutual radiation resistances of a rectangular plate. J. Sound Vib. 2001, 245, 1–16. [Google Scholar] [CrossRef]
- Sugino, C.; Xia, Y.; Leadenham, S.; Ruzzene, M.; Erturk, A. A general theory for bandgap estimation in locally resonant metastructures. J. Sound Vib. 2017, 406, 104–123. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.H.; Wen, X.S. Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators. J. Phys. D Appl. Phys. 2012, 45, 195401. [Google Scholar] [CrossRef]
- Fahy, F.; Gardonio, P. Sound and Structural Vibration: Radiation, Transmission and Response, 2nd ed.; Elsevier/Academic Press: Oxford, UK, 2007. [Google Scholar]





| Band-Gap Start Frequency | Band-Gap Cut-off Frequency | Band-Gap Width | |
|---|---|---|---|
| Present model | 510.1 Hz | 512.8 Hz | 2.7 Hz |
| FEM model | 510.0 Hz | 512.8 Hz | 2.8 Hz |
| Band-Gap Start Frequency | Band-Gap Cut-off Frequency | Band-Gap Width | |
|---|---|---|---|
| without fluid load | 510.1 Hz | 561.6 Hz | 51.5 Hz |
| with air load | 510.1 Hz | 561.6 Hz | 51.5 Hz |
| with water load | 510.1 Hz | 512.8 Hz | 2.7 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Sheng, M.; Zeng, H.; Wang, M.; Li, Q. Vibro-Acoustic Performance of a Fluid-Loaded Periodic Locally Resonant Plate. Machines 2023, 11, 590. https://doi.org/10.3390/machines11060590
Guo Z, Sheng M, Zeng H, Wang M, Li Q. Vibro-Acoustic Performance of a Fluid-Loaded Periodic Locally Resonant Plate. Machines. 2023; 11(6):590. https://doi.org/10.3390/machines11060590
Chicago/Turabian StyleGuo, Zhiwei, Meiping Sheng, Hao Zeng, Minqing Wang, and Qiaojiao Li. 2023. "Vibro-Acoustic Performance of a Fluid-Loaded Periodic Locally Resonant Plate" Machines 11, no. 6: 590. https://doi.org/10.3390/machines11060590
APA StyleGuo, Z., Sheng, M., Zeng, H., Wang, M., & Li, Q. (2023). Vibro-Acoustic Performance of a Fluid-Loaded Periodic Locally Resonant Plate. Machines, 11(6), 590. https://doi.org/10.3390/machines11060590







