Pose Determination System for a Serial Robot Manipulator Based on Artificial Neural Networks
Abstract
1. Introduction
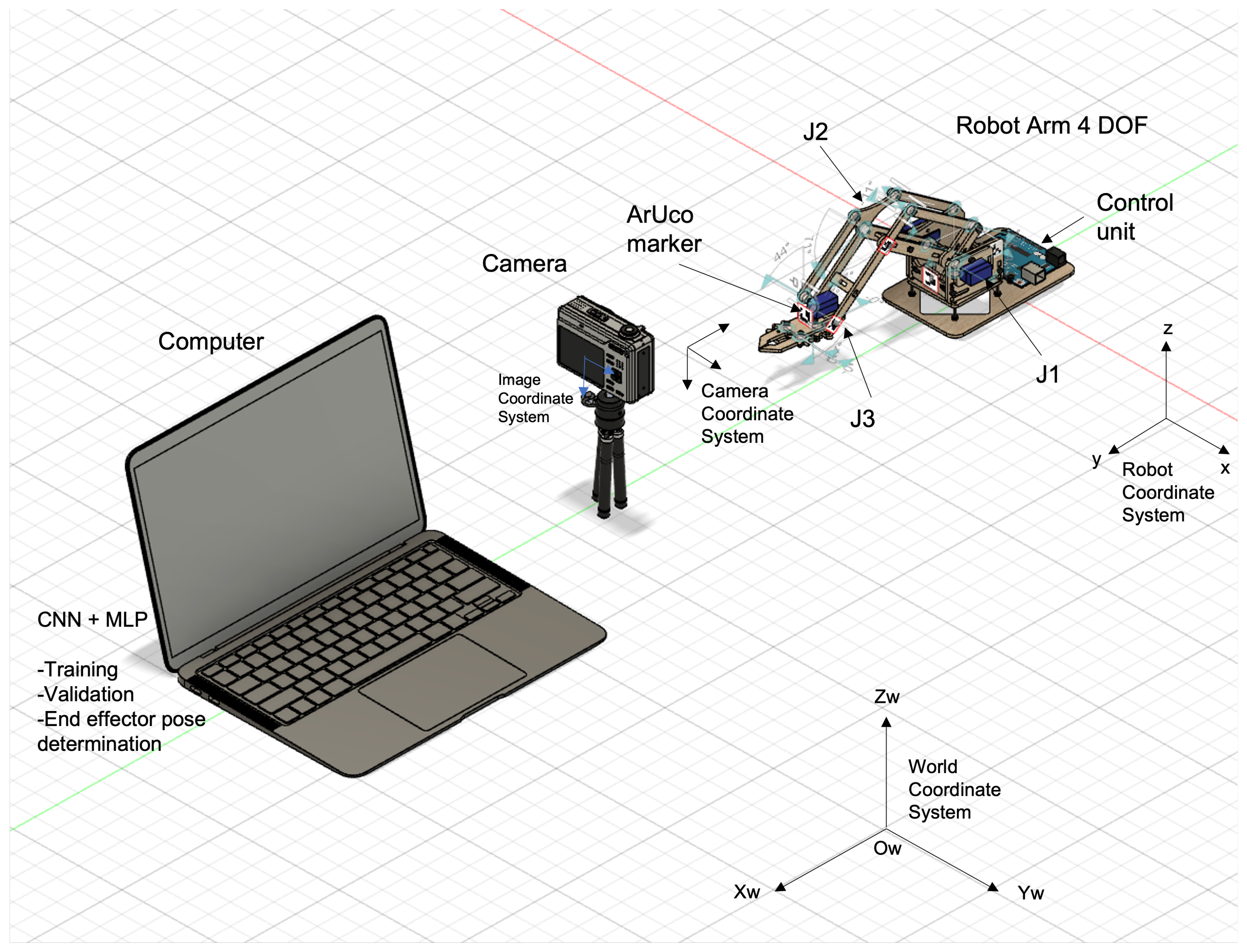
2. Proposed System Approach
2.1. Proposed Convolutional Neural Network
2.2. Proposed Linear Regression Model Based on Multilayer Perceptron Network
2.3. Proposed Pose-Recognition System (CNN + MLR)
2.4. Classes Generated by Joint Angles
2.4.1. Data Set for CNN Classification
2.4.2. Data Set for MLP Fitting as MLR
2.5. Evaluation Metrics for the Proposed System Evaluation
2.5.1. Performance Evaluation of CNN
2.5.2. Performance Evaluation of MLR
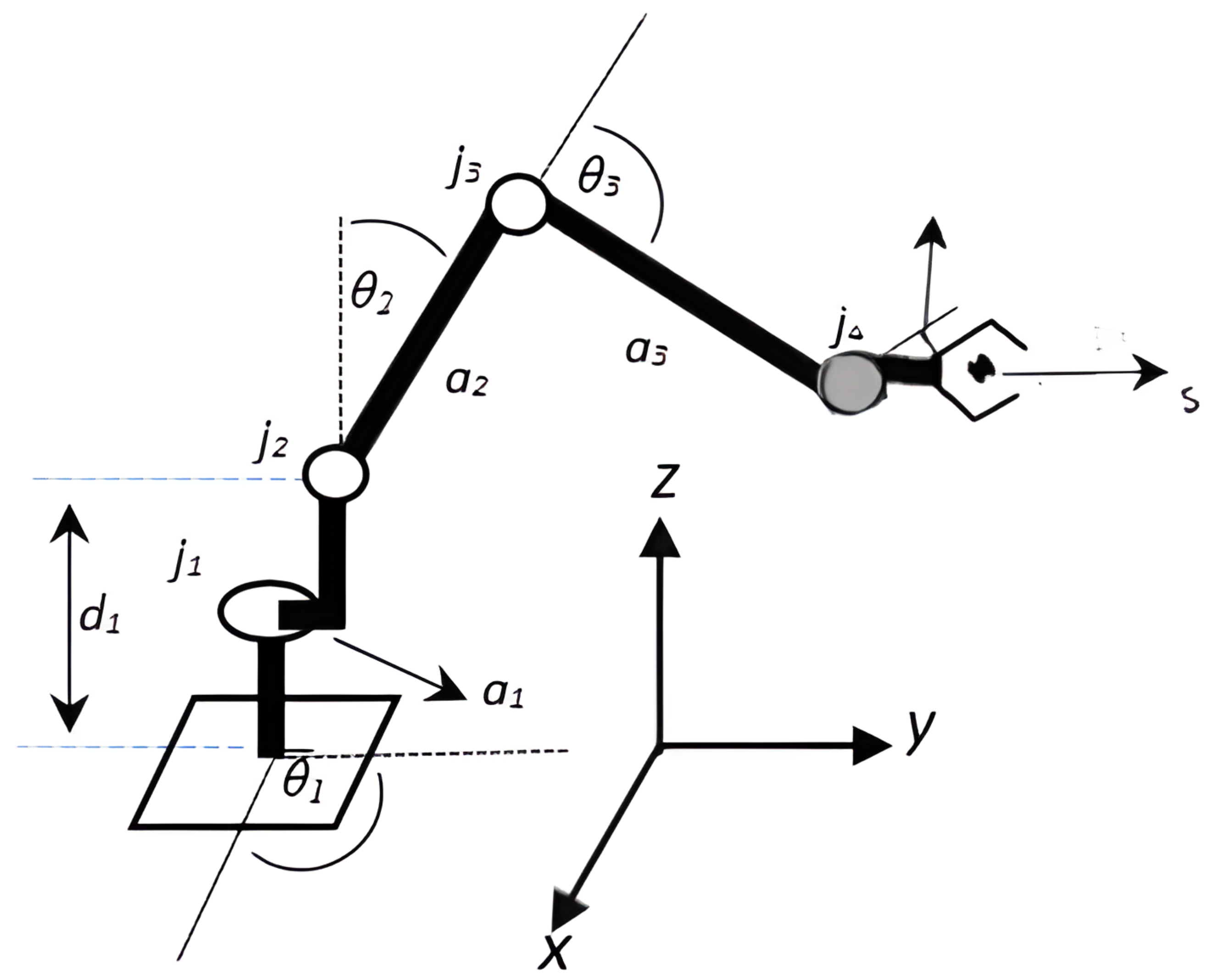
2.6. Manipulator Kinematics Analysis
3. Comparison with Pose Estimation by Perspective-n-Point (PnP)
3.1. Parameters for PnP Problem Solving
3.1.1. Camera Calibration
3.1.2. ArUco Markers
3.1.3. Solving PnP Pose Estimation
4. Results
4.1. Experimental Setup
4.1.1. Hyper Parameters for the CNN Training Process
4.1.2. Hyper Parameters for the MLP Training Process
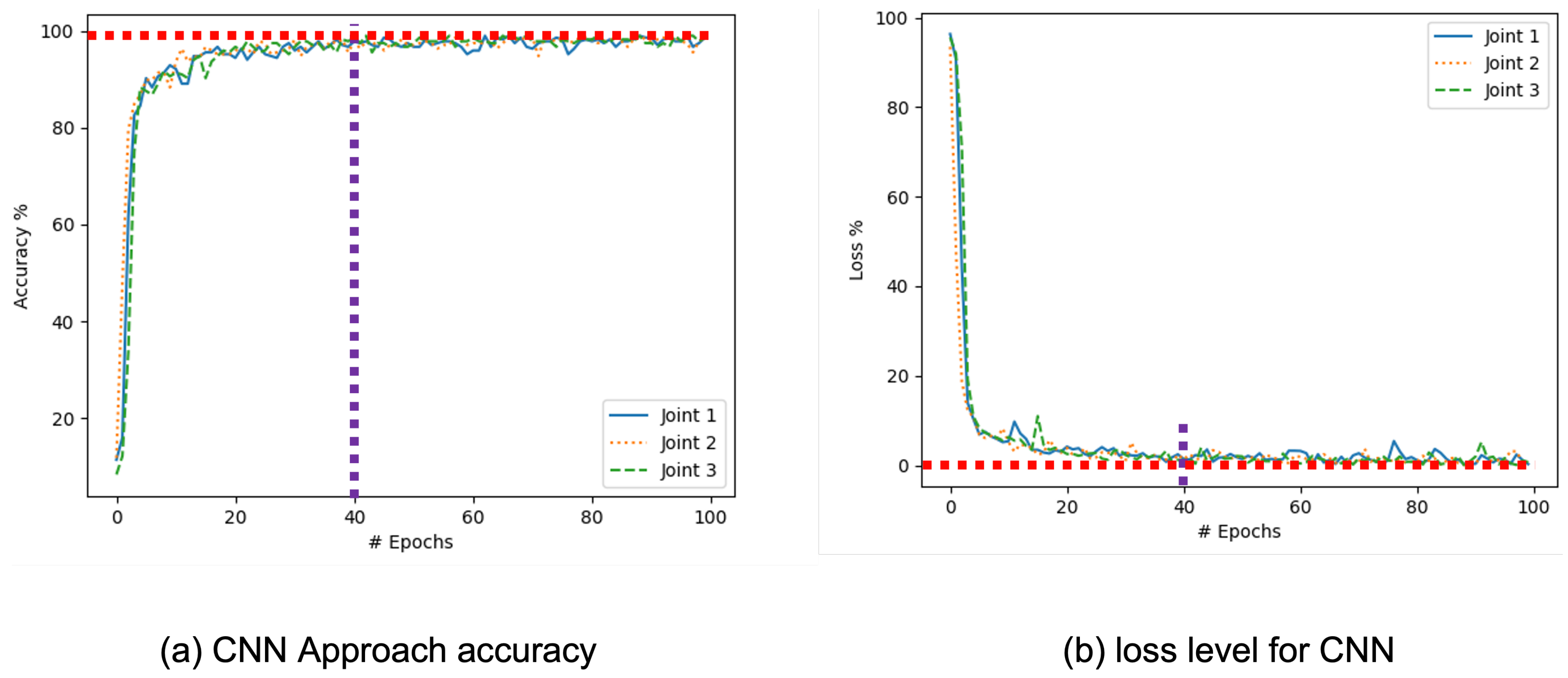
4.2. Training and Test Evaluation of Model Classification
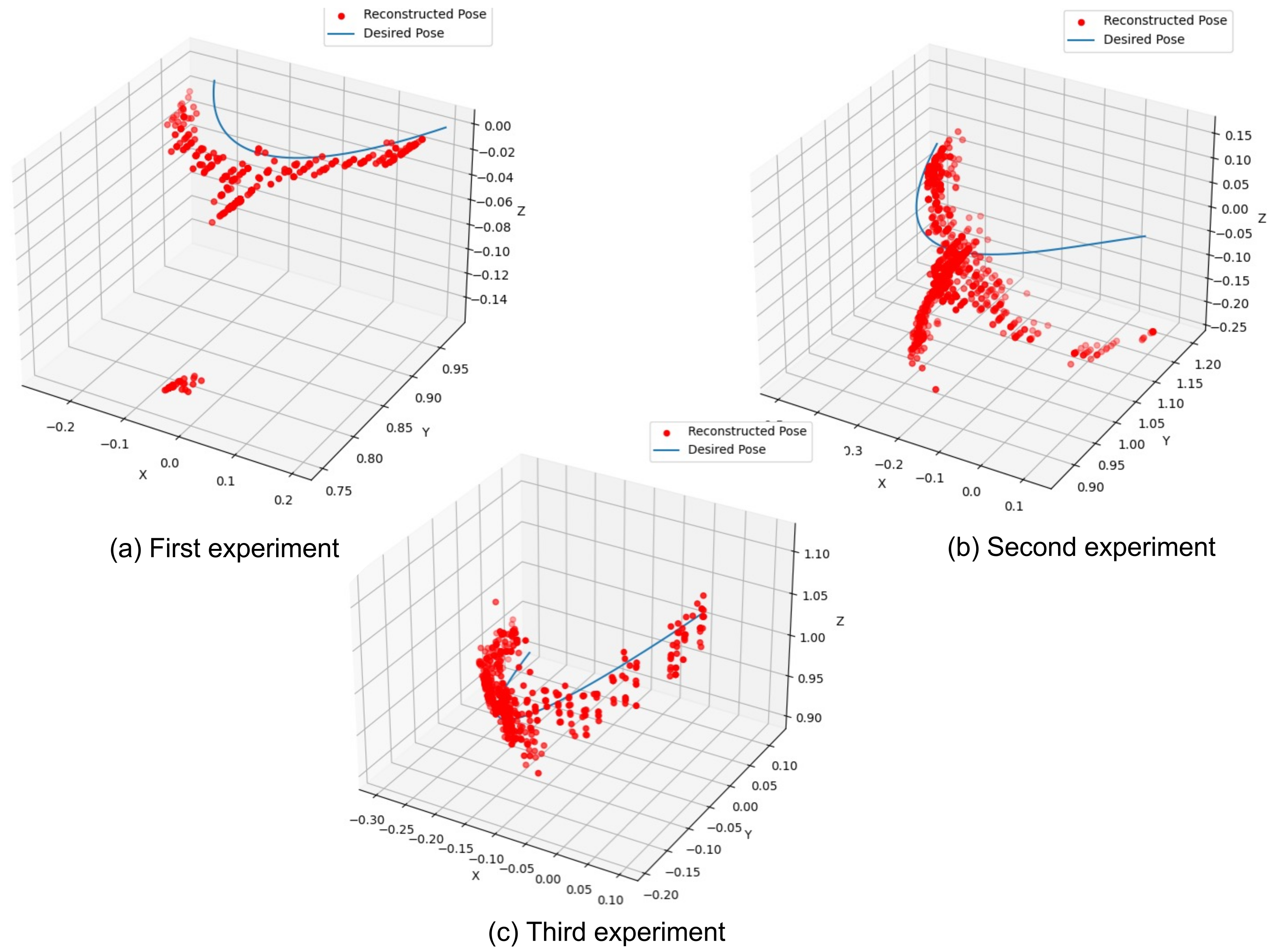
4.3. Error Evaluation
4.3.1. Solving PnP Problem
4.3.2. CNN + MLP: Classifier + MLR
4.3.3. Methods Comparison and Performance Metrics
5. Discussion
6. Conclusions and Future Work
- A novel combination of neural networks to obtain the joint angle values of a serial robot manipulator.
- A benchmark between other computer vision methods for pose estimation and the novel proposed system.
- A guide for application in serial robots with limited technological resources, which offers ease of implementation in more sophisticated systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bentaleb, T.; Iqbal, J. On the improvement of calibration accuracy of parallel robots–modeling and optimization. J. Theor. Appl. Mech. 2020, 58, 261–272. [Google Scholar] [CrossRef]
- Kuo, Y.L.; Liu, B.H.; Wu, C.Y. Pose determination of a robot manipulator based on monocular vision. IEEE Access 2016, 4, 8454–8464. [Google Scholar] [CrossRef]
- Tinoco, V.; Silva, M.F.; Santos, F.N.; Morais, R.; Filipe, V. SCARA Self Posture Recognition Using a Monocular Camera. IEEE Access 2022, 10, 25883–25891. [Google Scholar] [CrossRef]
- Bohigas, O.; Manubens, M.; Ros, L. A Complete Method for Workspace Boundary Determination on General Structure Manipulators. IEEE Trans. Robot. 2012, 28, 993–1006. [Google Scholar] [CrossRef]
- Diao, X.; Ma, O. Workspace Determination of General 6-d.o.f. Cable Manipulators. Adv. Robot. 2008, 22, 261–278. [Google Scholar] [CrossRef]
- Lin, C.C.; Gonzalez, P.; Cheng, M.Y.; Luo, G.Y.; Kao, T.Y. Vision based object grasping of industrial manipulator. In Proceedings of the 2016 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 31 August–2 September 2016. [Google Scholar] [CrossRef]
- Yu, J.; Weng, K.; Liang, G.; Xie, G. A vision-based robotic grasping system using deep learning for 3D object recognition and pose estimation. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013. [Google Scholar] [CrossRef]
- Wang, D.; Jia, W.; Yu, Y.; Wang, W. Recognition and Grasping of Target Position and Pose of Manipulator Based on Vision. In Proceedings of the 2018 5th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Hangzhou, China, 16–19 August 2018. [Google Scholar] [CrossRef]
- Hao, R.; Ozguner, O.; Cavusoglu, M.C. Vision-Based Surgical Tool Pose Estimation for the da Vinci® Robotic Surgical System. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar] [CrossRef]
- Taryudi.; Wang, M.S. 3D object pose estimation using stereo vision for object manipulation system. In Proceedings of the 2017 International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017. [Google Scholar] [CrossRef]
- Ka, H.W. Three Dimensional Computer Vision-Based Alternative Control Method For Assistive Robotic Manipulator. Symbiosis 2016, 1, 1–6. [Google Scholar] [CrossRef]
- Wong, A.K.C.; Mayorga, R.V.; Rong, A.; Liang, X. A vision based online motion planning of robot manipulators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Osaka, Japan, 8 November 1996. [Google Scholar] [CrossRef]
- Braun, G.; Nissler, C.; Krebs, F. Development of a vision-based 6D pose estimation end effector for industrial manipulators in lightweight production environments. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015. [Google Scholar] [CrossRef]
- Zhou, Z.; Cao, J.; Yang, H.; Fan, Y.; Huang, H.; Hu, G. Key technology research on monocular vision pose measurement under complex background. In Proceedings of the 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI), Xiamen, China, 29–31 March 2018. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, Z.H. Vision-based Pose and Motion Estimation of Non-cooperative Target for Space Robotic Manipulators. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.M.; Zeng, L.; Huang, Y.J. A monocular vision system for online pose measurement of a 3RRR planar parallel manipulator. J. Intell. Robot. Syst. 2018, 92, 3–17. [Google Scholar] [CrossRef]
- Peng, J.; Xu, W.; Liang, B. An Autonomous Pose Measurement Method of Civil Aviation Charging Port Based on Cumulative Natural Feature Data. IEEE Sens. J. 2019, 19, 11646–11655. [Google Scholar] [CrossRef]
- Cao, N.; Jiang, W.; Pei, Z.; Li, W.; Wang, Z.; Huo, Z. Monocular Vision-Based Pose Measurement Algorithm for Robotic Scraping System of Residual Propellant. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019. [Google Scholar] [CrossRef]
- Meng, J.; Wang, S.; Li, G.; Jiang, L.; Zhang, X.; Xie, Y. A Convenient Pose Measurement Method of Mobile Robot Using Scan Matching and Eye-in-Hand Vision System. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019. [Google Scholar] [CrossRef]
- Xu, L.; Cao, Z.; Liu, X. A monocular vision system for pose measurement in indoor environment. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016. [Google Scholar] [CrossRef]
- Liang, C.J.; Lundeen, K.M.; McGee, W.; Menassa, C.C.; Lee, S.; Kamat, V.R. A vision-based marker-less pose estimation system for articulated construction robots. Autom. Constr. 2019, 104, 80–94. [Google Scholar] [CrossRef]
- Katsuki, R.; Ota, J.; Arai, T.; Ueyama, T. Proposal of artificial mark to measure 3D pose by monocular vision. J. Adv. Mech. Des. Syst. Manuf. 2007, 1, 155–169. [Google Scholar] [CrossRef]
- Kuzdeuov, A.; Rubagotti, M.; Varol, H.A. Neural Network Augmented Sensor Fusion for Pose Estimation of Tensegrity Manipulators. IEEE Sens. J. 2020, 20, 3655–3666. [Google Scholar] [CrossRef]
- Driels, M.R.; Swayze, W.; Potter, S. Full-pose calibration of a robot manipulator using a coordinate-measuring machine. Int. J. Adv. Manuf. Technol. 1993, 8, 34–41. [Google Scholar] [CrossRef]
- Driels, M.R.; Swayze, W.E. Automated partial pose measurement system for manipulator calibration experiments. IEEE Trans. Robot. Autom. 1994, 10, 430–440. [Google Scholar] [CrossRef]
- Bai, S.; Teo, M.Y. Kinematic calibration and pose measurement of a medical parallel manipulator by optical position sensors. J. Robot. Syst. 2003, 20, 201–209. [Google Scholar] [CrossRef]
- Meng, Y.; Zhuang, H. Autonomous robot calibration using vision technology. Robot. Comput.-Integr. Manuf. 2007, 23, 436–446. [Google Scholar] [CrossRef]
- Liu, H.; Yan, Z.; Xiao, J. Pose error prediction and real-time compensation of a 5-DOF hybrid robot. Mech. Mach. Theory 2022, 170, 104737. [Google Scholar] [CrossRef]
- Yin, J.; Gao, Y. Pose accuracy calibration of a serial five dof robot. Energy Procedia 2012, 14, 977–982. [Google Scholar] [CrossRef]
- Taylor, C.J.; Ostrowski, J.P. Robust vision-based pose control. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar] [CrossRef]
- Tsay, T.I.J.; Chang, C.J. Pose control ofmobile manipulators with an uncalibrated eye-in-hand vision system. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004. [Google Scholar] [CrossRef]
- Tang, X.; Han, X.; Zhen, W.; Zhou, J.; Wu, P. Vision servo positioning control of robot manipulator for distribution line insulation wrapping. J. Phys. Conf. Ser. 2021, 1754, 012133. [Google Scholar] [CrossRef]
- Wu, B.; Wang, L.; Liu, X.; Wang, L.; Xu, K. Closed-Loop Pose Control and Automated Suturing of Continuum Surgical Manipulators With Customized Wrist Markers Under Stereo Vision. IEEE Robot. Autom. Lett. 2021, 6, 7137–7144. [Google Scholar] [CrossRef]
- Cvitanic, T.; Melkote, S.N. A new method for closed-loop stability prediction in industrial robots. Robot. Comput.-Integr. Manuf. 2022, 73, 102218. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, Y.; Tian, M. Pose Estimation of Excavator Manipulator Based on Monocular Vision Marker System. Sensors 2021, 21, 4478. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Betancur, D.; Moreno, I.; Guerrero-Mendez, C.; Saucedo-Anaya, T.; González, E.; Bautista-Capetillo, C.; González-Trinidad, J. Convolutional Neural Network for Measurement of Suspended Solids and Turbidity. Appl. Sci. 2022, 12, 6079. [Google Scholar] [CrossRef]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Educacion: Mexico City, Mexico, 2005. [Google Scholar]
- Dai, J.S. Euler–Rodrigues formula variations, quaternion conjugation and intrinsic connections. Mech. Mach. Theory 2015, 92, 144–152. [Google Scholar] [CrossRef]
- Rodriguez-Miranda, S.; Mendoza-Vazquez, F.; Yañez-Mendiola, J. Robot end effector positioning approach based on single-image 2D reconstruction. In Proceedings of the 2021 IEEE International Summer Power Meeting/International Meeting on Communications and Computing (RVP-AI/ROC&C), Acapulco, Mexico, 14–18 November 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Peng, K.; Hou, L.; Ren, R.; Ying, X.; Zha, H. Single view metrology along orthogonal directions. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1658–1661. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]




| Layer (Type) | Output Shape | Param # | |
|---|---|---|---|
| 2D-Convolutional-Layer-1 | (None, 126, 126, 16) | 448 | |
| (Conv2D) | |||
| 2D-MaxPool-Layer-1 | (None, 63, 63, 16) | 0 | |
| (MaxPooling2D) | |||
| Dropout-Layer-1 (Dropout) | (None, 63, 63, 16) | 0 | |
| 2D-Convolutional-Layer-2 | (None, 61, 61, 64) | 9280 | |
| (Conv2D) | |||
| 2D-MaxPool-Layer-2 | (None, 30, 30, 64) | 0 | |
| (MaxPooling2D) | |||
| CNN Model | Dropout-Layer-2 (Dropout) | (None, 30, 30, 64) | 0 |
| 2D-Convolutional-Layer-3 | (None, 30, 30, 64) | 36,928 | |
| (Conv2D) | |||
| 2D-MaxPool-Layer-3 | (None, 15, 15, 64) | 0 | |
| (MaxPooling2D) | |||
| Dropout-Layer-3 (Dropout) | (None, 15, 15, 64) | 0 | |
| Flatten-Layer (Flatten) | (None, 14,400) | 0 | |
| Hidden-Layer-1 (Dense) | (None, 64) | 921,664 | |
| Output-Layer (Dense) | (None, 12) | 780 | |
| Dense (Dense) | (None, 6) | 78 | |
| MLP Model | Dense_1 (Dense) | (None, 8) | 56 |
| Dense_2 (Dense) | (None, 1) | 9 | |
| Angle Size (Step) (Degrees) | Training Time (Min) | Error Estimation Compared with Encoder Signal | Number of Images in Data Set |
|---|---|---|---|
| 20 | 25.8 | 3.89 | 2925 |
| 15 | 32.1 | 1.30 | 3250 |
| 10 | 51.9 | 0.91 | 5525 |
| 5 | 96.6 | 0.75 | 7400 |
| Joint 1 | Joint 2 | Joint 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Class | Precision | Recall | F-Score | Precision | Recall | F-Score | Precision | Recall | F-Score | Support |
| 0 | 0.97 | 0.97 | 0.97 | 0.58 | 1.0 | 0.74 | 1.0 | 0.81 | 0.9 | |
| 1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 2 | 0.97 | 0.97 | 0.97 | 1.0 | 0.04 | 0.08 | 0.82 | 1.0 | 0.9 | |
| 3 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 4 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 5 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 6 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 7 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 8 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 9 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 10 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Accuracy | 0.99 | 0.91 | 0.98 | 2600 | ||||||
| Macro Avg. | 0.99 | 0.99 | 0.99 | 0.96 | 0.91 | 0.89 | 0.98 | 0.98 | 0.98 | 2600 |
| Weighted Avg. | 0.99 | 0.99 | 0.99 | 0.95 | 0.91 | 0.88 | 0.98 | 0.98 | 0.98 | 2600 |
| Training Time (min) | 32.12 | 27.12 | 22.56 |
| Joint 1 | Joint 2 | Joint 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Class | Precision | Recall | F-Score | Precision | Recall | F-Score | Precision | Recall | F-Score | Support per Joint |
| 0 | 0.88 | 0.88 | 0.88 | 0.38 | 1.0 | 0.56 | 1.0 | 0.81 | 0.9 | |
| 1 | 1.0 | 1.0 | 1.0 | 1.0 | 0.89 | 0.94 | 1.0 | 1.0 | 1.0 | |
| 2 | 0.5 | 0.5 | 0.5 | 1.0 | 0.12 | 0.22 | 0.82 | 1.0 | 0.9 | |
| 3 | 0.75 | 1.0 | 0.86 | 0.75 | 1.0 | 0.86 | 1.0 | 1.0 | 1.0 | |
| 4 | 1.0 | 0.83 | 0.91 | 1.0 | 0.9 | 0.95 | 1.0 | 1.0 | 1.0 | |
| 5 | 1.0 | 0.9 | 0.95 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 6 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 7 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 8 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 9 | 1.0 | 1.0 | 1.0 | 0.89 | 1.0 | 0.94 | 1.0 | 1.0 | 1.0 | |
| 10 | 1.0 | 1.0 | 1.0 | 1.0 | 0.89 | 0.94 | 1.0 | 1.0 | 1.0 | |
| Accuracy | 0.94 | 0.85 | 0.97 | 650 | ||||||
| Macro Avg. | 0.92 | 0.92 | 0.92 | 0.91 | 0.89 | 0.86 | 0.97 | 0.96 | 0.96 | 650 |
| Weighted Avg. | 0.95 | 0.94 | 0.94 | 0.93 | 0.85 | 0.83 | 0.98 | 0.97 | 0.97 | 650 |
| Sources | Sample 1 (Degrees) | Sample 2 (Degrees) | Sample 3 (Degrees) | MSE | MAE | |
|---|---|---|---|---|---|---|
| Joint 1 | ||||||
| Commanded value (Max.–Min. Values) | 15–90 | 90–130 | 130–150 | |||
| Encoder value | 14.99–89.97 | 89.97–129.90 | 129.90–150.01 | 1.89 | 1.37 | 0.999 |
| Method in [35] | 11.99–79.97 | 79.97–127.34 | 127.34–152.77 | 5.51 | 2.42 | 0.955 |
| Proposed approach (CNN + MLR) | 14.59–91.97 | 91.97–129.60 | 129.60–148.99 | 5.20 | 0.75 | 0.997 |
| Joint 2 | ||||||
| Commanded value (Max.–Min. Values) | 45–60 | 90–105 | 20–135 | |||
| Encoder value | 45.01–59.99 | 89.99–104.99 | 120–134.90 | 1.12 | 0.37 | 0.999 |
| Method in [35] | 44.93–58.92 | 90.10–105.70 | 118.20–137.98 | 4.23 | 3.22 | 0.932 |
| Proposed approach (CNN + MLR) | 14.98–89.97 | 89.97–105.12 | 119.95–134.95 | 2.28 | 0.69 | 0.998 |
| Joint 3 | ||||||
| Commanded value (Max.–Min. Values) | 0–15 | 45–75 | 150–165 | |||
| Encoder value | 0.01–15.01 | 45.02–75.01 | 150.01–165.1 | 1.09 | 0.44 | 0.999 |
| Method in [35] | 5.31–17.23 | 48.30–77.45 | 155.30–168.30 | 7.23 | 5.22 | 0.901 |
| Proposed approach (CNN + MLR) | 1.95–16.12 | 45.99–75.05 | 151.20–167.20 | 3.14 | 1.69 | 0.981 |
| Method in [35] | Proposed Approach | |||
|---|---|---|---|---|
| Mean (mm) | Std. (mm) | Mean (mm) | Std. (mm) | |
| Sample 1 | 5.34 | 10.91 | 2.45 | 7.12 |
| Sample 2 | 8.11 | 14.22 | 5.01 | 12.33 |
| Sample 3 | 12.34 | 14.99 | 5.62 | 9.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Miranda, S.; Yañez-Mendiola, J.; Calzada-Ledesma, V.; Villanueva-Jimenez, L.F.; De Anda-Suarez, J. Pose Determination System for a Serial Robot Manipulator Based on Artificial Neural Networks. Machines 2023, 11, 592. https://doi.org/10.3390/machines11060592
Rodríguez-Miranda S, Yañez-Mendiola J, Calzada-Ledesma V, Villanueva-Jimenez LF, De Anda-Suarez J. Pose Determination System for a Serial Robot Manipulator Based on Artificial Neural Networks. Machines. 2023; 11(6):592. https://doi.org/10.3390/machines11060592
Chicago/Turabian StyleRodríguez-Miranda, Sergio, Javier Yañez-Mendiola, Valentin Calzada-Ledesma, Luis Fernando Villanueva-Jimenez, and Juan De Anda-Suarez. 2023. "Pose Determination System for a Serial Robot Manipulator Based on Artificial Neural Networks" Machines 11, no. 6: 592. https://doi.org/10.3390/machines11060592
APA StyleRodríguez-Miranda, S., Yañez-Mendiola, J., Calzada-Ledesma, V., Villanueva-Jimenez, L. F., & De Anda-Suarez, J. (2023). Pose Determination System for a Serial Robot Manipulator Based on Artificial Neural Networks. Machines, 11(6), 592. https://doi.org/10.3390/machines11060592








