Tires and Vehicle Lateral Dynamic Performance: A Corrective Algorithm for the Influence of Temperature
Abstract
:1. Introduction
- To identify an analytical model able to capture the phenomenon accurately;
- To generalize and optimize the model identified. It has to become a ready-to-use tool for a large number of vehicle categories requiring, for every correction that has to be done, the smallest amount of data possible;
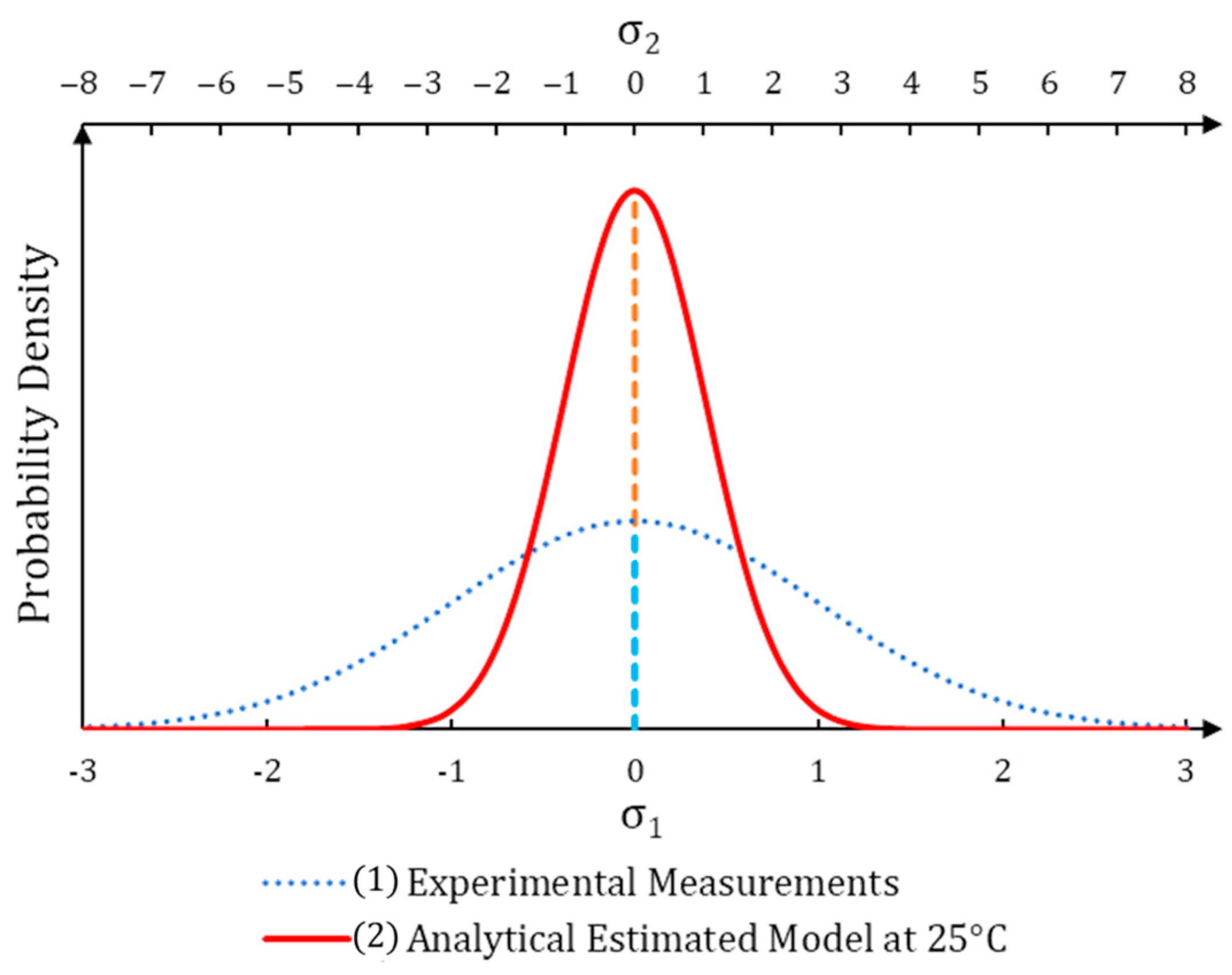
- To validate the analytical compensative tool from a statistical point of view;
- To implement it in a MATLAB bicycle model to update the measured values of the numerical transfer functions that describe the dynamic behavior of the vehicle during the maneuvers and compare the results with the original curves.
2. Model Definition
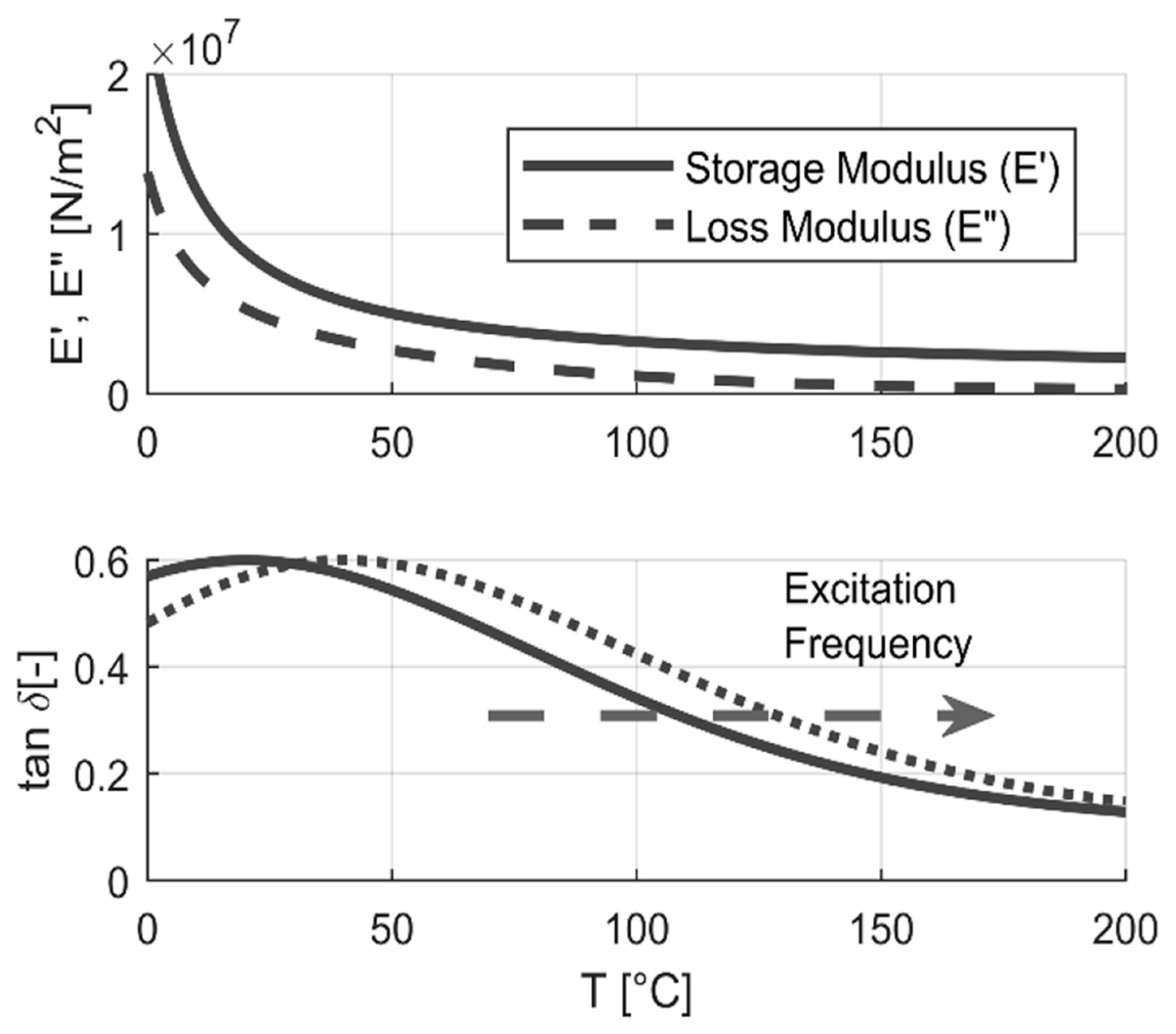
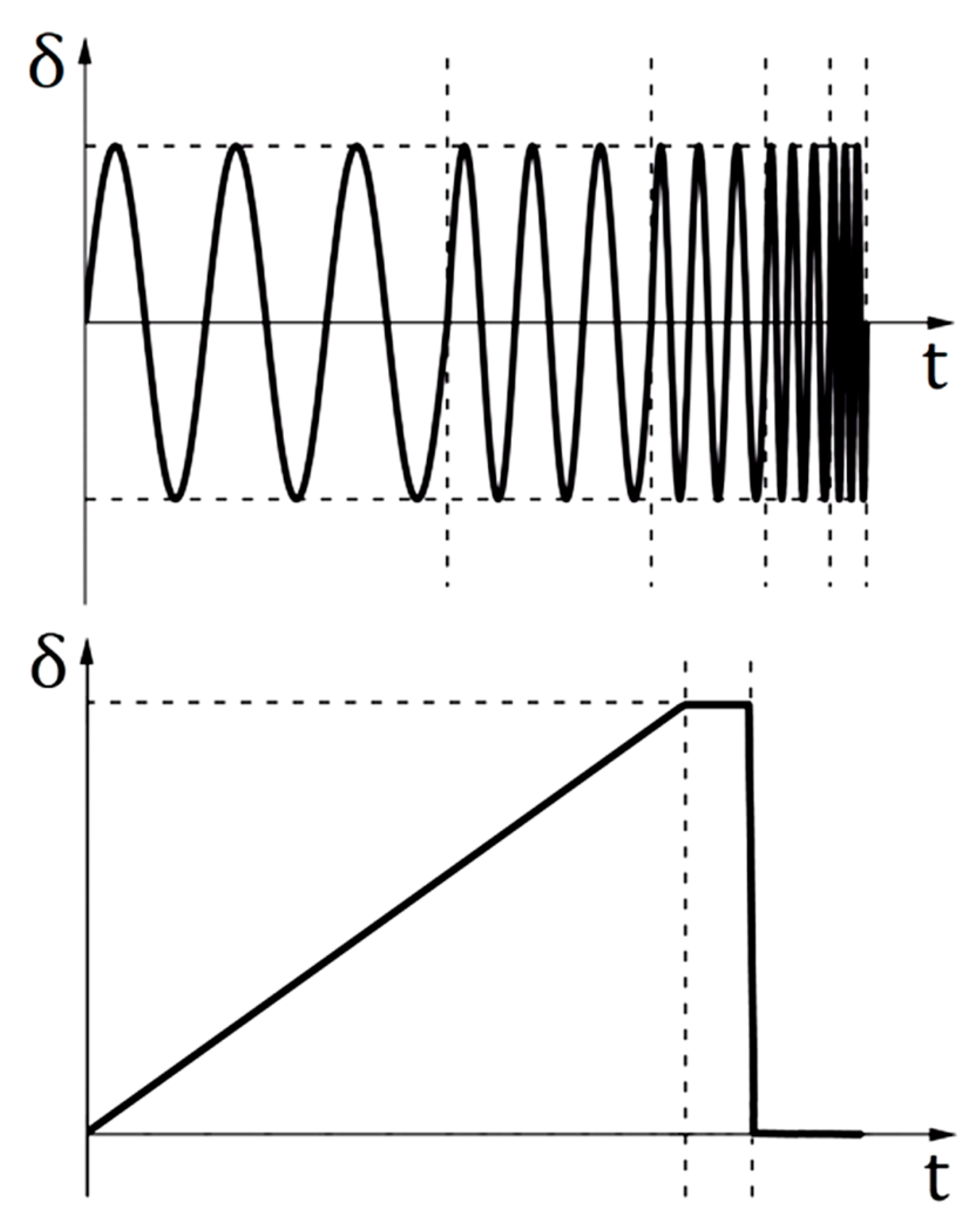
2.1. Database Acquired and Maneuvers
- All the parameters necessary to build a bicycle model that describe the vehicle and its dynamic behavior during the maneuver;
- A table indicating the numerical values assumed by a wide set of transfer functions in the frequency domain during the maneuver;
- Tables indicating the analytical values assumed by the same set of transfer functions mentioned at the previous point in the frequency domain during the maneuver. There are two different tables for two distinct approaches: in one case the relaxation length of the tires is considered, while in the other they are not.
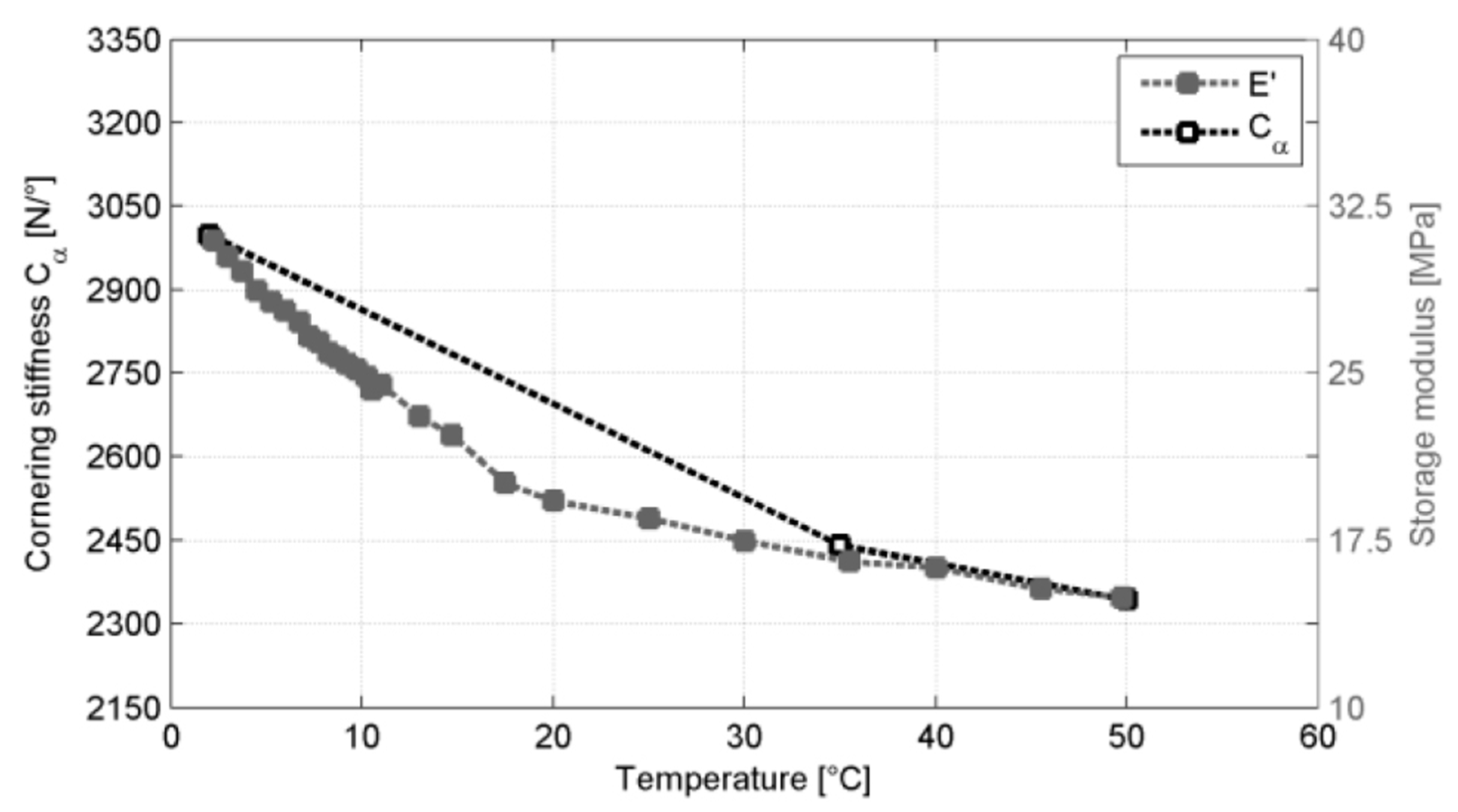
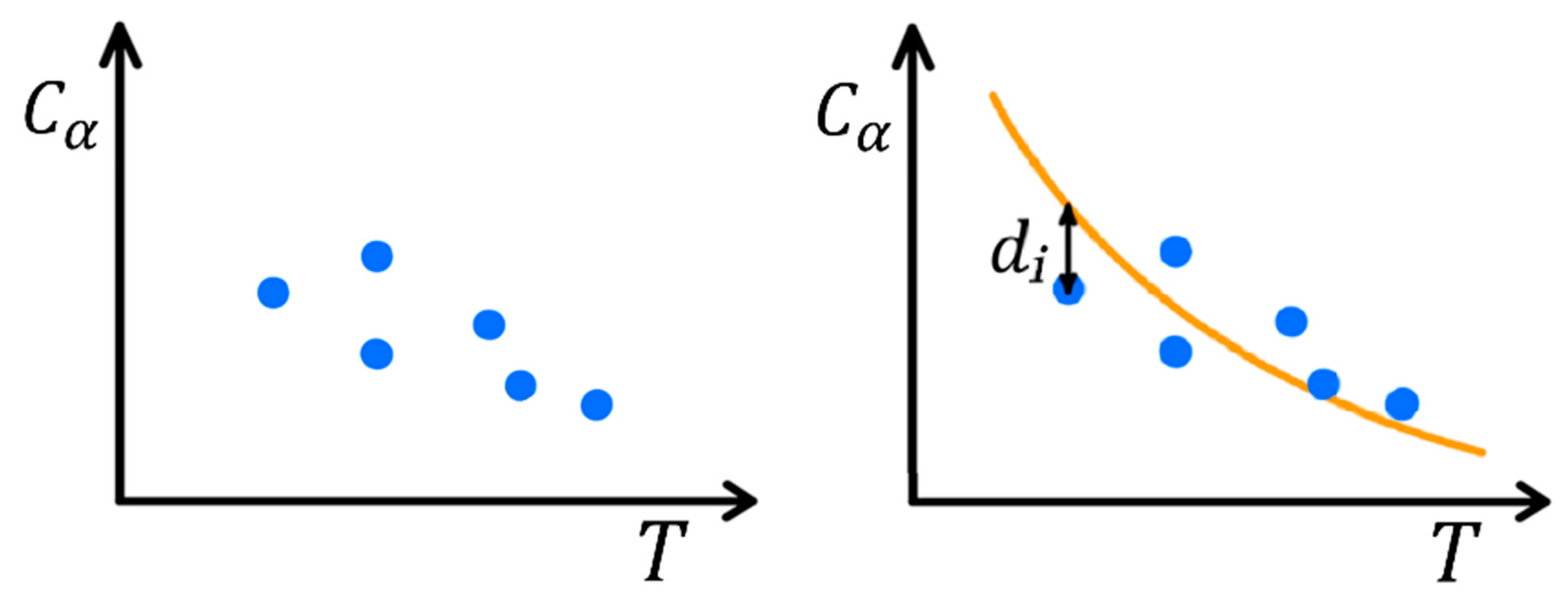
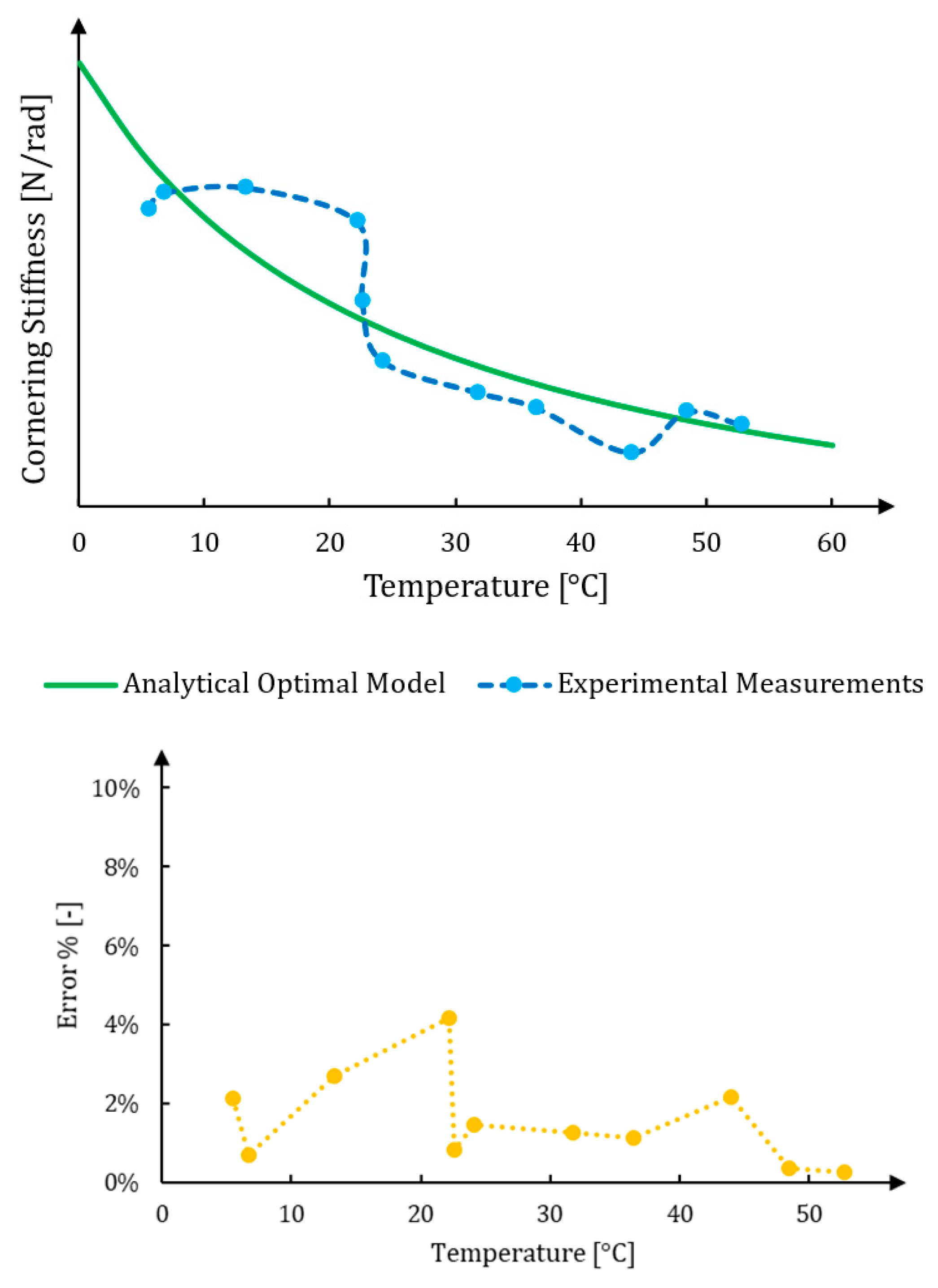
2.2. Cornering Stiffness Analytical Optimal Model
- From a mathematical point of view, is the temperature at which the cornering stiffness is equal to infinity. Physically, this is the so-called glass transition temperature, ;
- From a mathematical point of view, is the cornering stiffness when the temperature is equal to infinity. Physically, this is the decomposition temperature and, depending on the tire compound, it is close to 150 °C.
2.3. MATLAB Optimization Script
3. Model Application
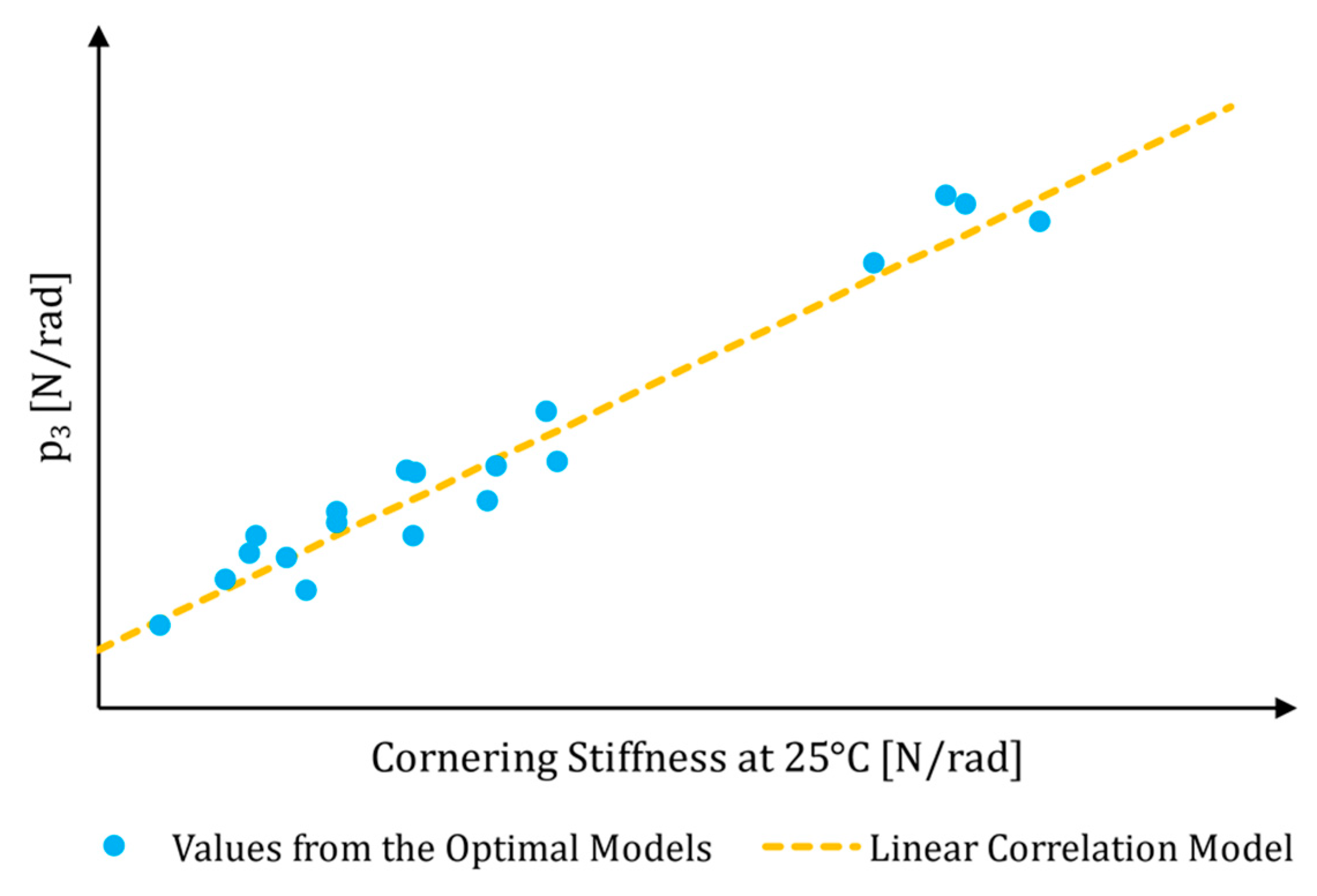
3.1. Linear Correlation Model
3.2. Analysis of the New Results
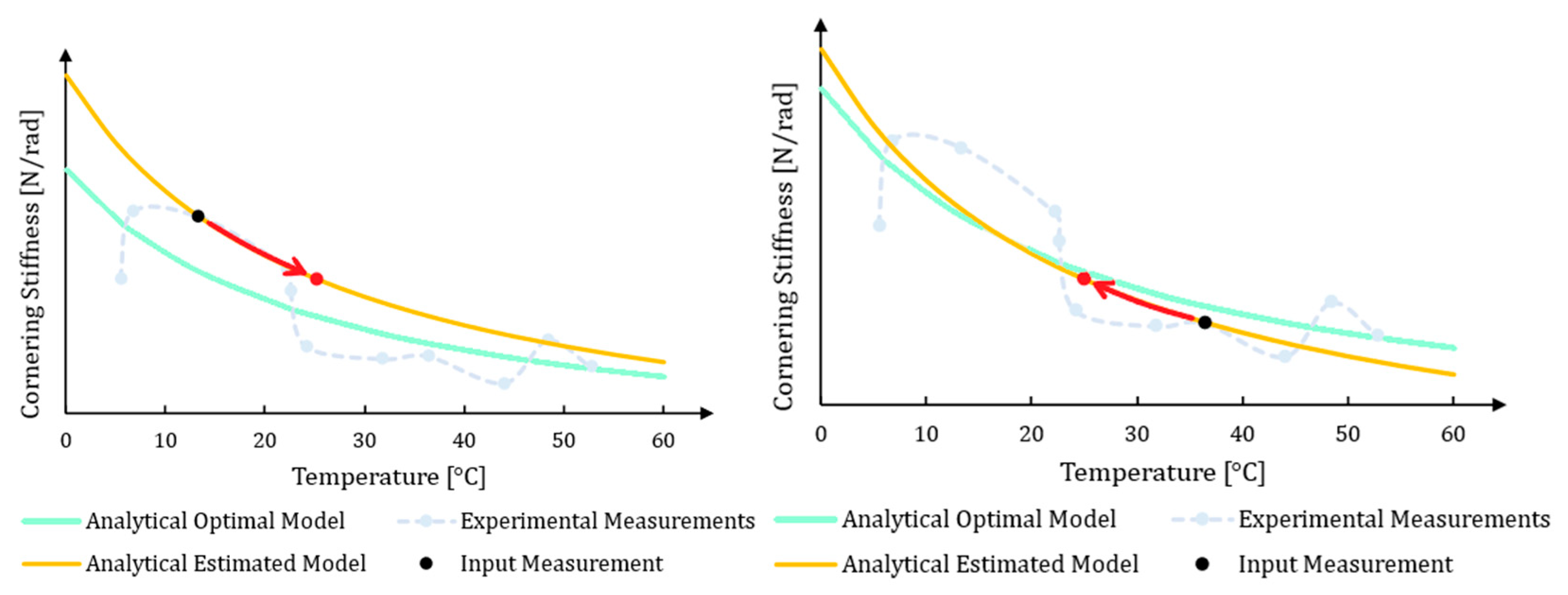
4. Tool Implementation
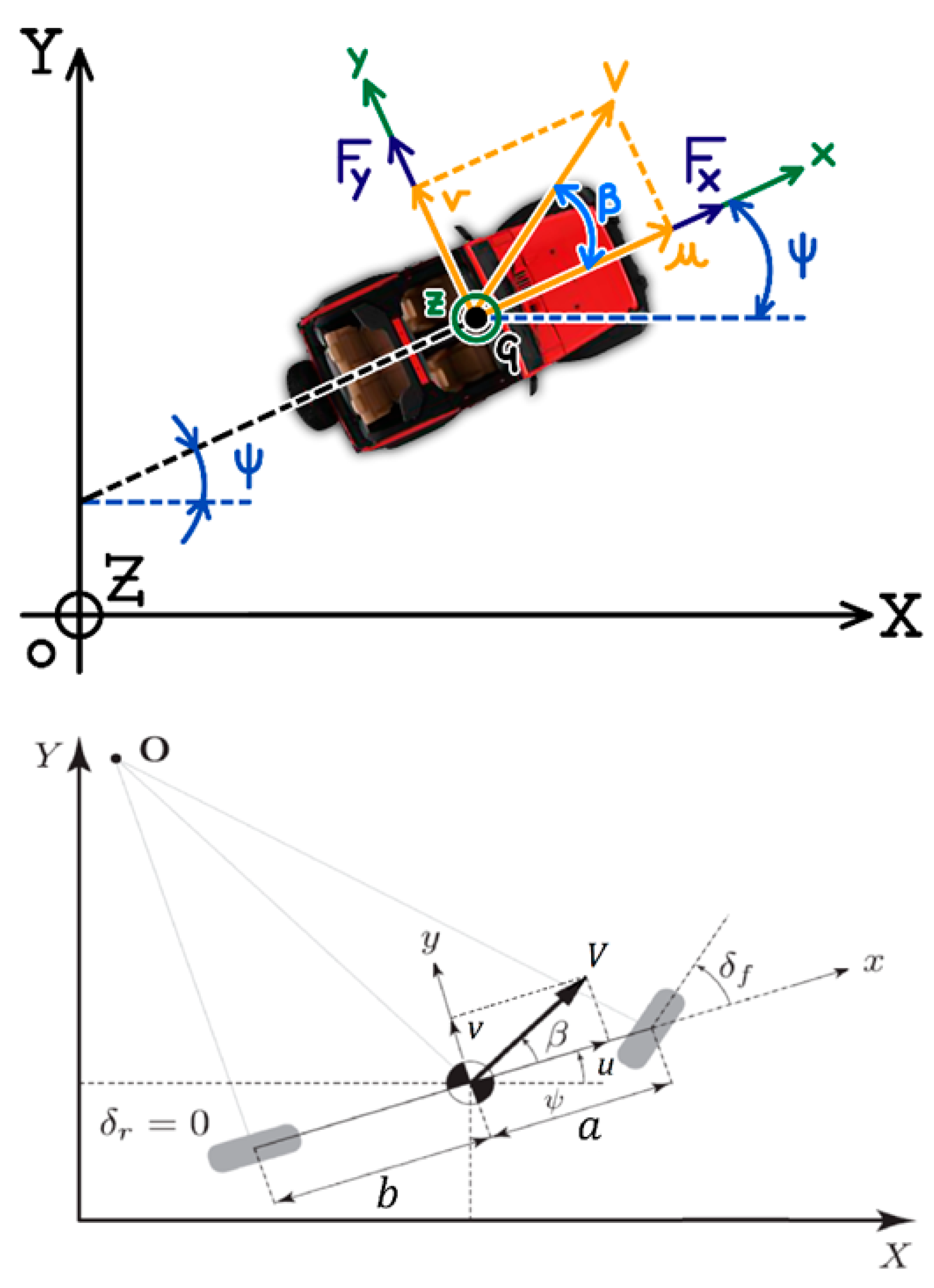
4.1. Lateral Dynamics Bicycle Model
- The entire motion of the vehicle can be described along the XY plane.
- The vehicle is assumed to be rigid: the effects of the suspension system are neglected, and so roll and pitch motions are considered uncoupled from yaw motions.
- The contributions of aerodynamic forces are neglected. This can be done because the maximum speed reached by the vehicle during the maneuvers is always smaller than or equal to 120 km/h. Consequently, even if the aerodynamic force is proportional to the square of the velocity, the values that it assumes are small enough to be ignored without introducing large errors.
- The tire’s self-aligning stiffness—which is the influence of the related torque that is minor compared to the action of the other forces and moments involved—is neglected.
- The generalized forces applied to the vehicle can be expressed quite simply;
- The trigonometric functions can be linearized because, except for the yaw angle, , all the angles are assumed to be small.
4.2. Tire Relaxation Length
4.3. Roll Motion Model
4.4. Computation of the Updated Numerical Transfer Functions
4.5. Analysis of the Scaled Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Al Atat, H.; Ghaffari, M.; Lee, J.; Xi, L.-F. Prognostics of automotive sensors: Tools and case study. Failure Prevention for System Availability. In Proceedings of the 62nd Meeting of the Society for Machinery Failure Prevention Technology, Virginia Beach, VA, USA, 6–8 April 2008. [Google Scholar]
- Armstrong, K.; Das, S.; Cresko, J. The energy footprint of automotive electronic sensors. Sustain. Mater. Technol. 2020, 25, e00195. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Shead, L.; Ivanov, V.; Hoepping, K. Torque Vectoring for Electric Vehicles with Individually Controlled Motors: State-of-the-Art and Future Developments. World Electr. Veh. J. 2012, 5, 617–628. [Google Scholar] [CrossRef] [Green Version]
- Manca, R.; Castellanos Molina, L.M.i.; Hegde, S.; Tonoli, A.; Amati, N.; Pazienza, L. Optimal Torque-Vectoring Control Strategy for Energy Efficiency and Vehicle Dynamic Improvement of Battery Electric Vehicles with Multiple Motors; SAE Technical Paper 2023-01-0563. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 18–20 April 2023. [Google Scholar] [CrossRef]
- Ferraris, A.; De Cupis, D.; de Carvalho Pinheiro, H.; Messana, A.; Sisca, L.; Airale, A.G.; Carello, M. Integrated Design and Control of Active Aerodynamic Features for High Performance Electric Vehicles; SAE Technical Paper 2020-36-0079. In Proceedings of the 2020 SAE Brasil Congress & Exhibition, Sao Paulo, Brazil, 1 December 2021. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H.; Punta, E.; Carello, M.; Ferraris, A.; Airale, A.G. Torque Vectoring in Hybrid Vehicles with In-Wheel Electric Motors: Comparing SMC and PID control. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Carello, M.; Ferraris, A.; Carvalho Pinheiro H de Cruz Stanke, D.; Gabiati, G.; Camuffo, I.; Grillo, M. Human-Driving Highway Overtake and Its Perceived Comfort: Correlational Study Using Data Fusion; SAE Technical Paper 2020-01-1036. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 21–23 April 2020. [Google Scholar] [CrossRef]
- Dingyi, Y.; Haiyan, W.; Kaiming, Y. State-of-the-art and trends of autonomous driving technology. In Proceedings of the 2018 IEEE International Symposium on Innovation and Entrepreneurship (TEMS-ISIE), Beijing, China, 30 March–1 April 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Tramacere, E.; Luciani, S.; Feraco, S.; Bonfitto, A.; Amati, N. Processor-in-the-Loop Architecture Design and Experimental Validation for an Autonomous Racing Vehicle. Appl. Sci. 2021, 11, 7225. [Google Scholar] [CrossRef]
- Yunzheng, Z.; Shaofei, Q.; Huang, A.C.; Jianhong, X. Smart Vehicle Control Unit—An integrated BMS and VCU System. IFAC-Pap. 2018, 51, 676–679. [Google Scholar] [CrossRef]
- de Carvalho Pinheiro, H.; Carello, M. Design and validation of a high-level controller for automotive active systems. SAE Int. J. Veh. Dyn. Stab. NVH 2022, 7, 83–98. [Google Scholar] [CrossRef]
- Dugoff, H.; Fancher, P.S.; Segel, L. An Analysis of Tire Traction Properties and Their Influence on Vehicle Dynamic Performance. SAE Trans. 1970, 79, 1219–1243. [Google Scholar]
- Pacejka, H.B. Analysis of Tire Properties. In Mechanics of Pneumatic Tires; Clark, S.K., Ed.; National Highway Traffic Safety Administration: Washington, DC, USA, 1981; pp. 721–870. [Google Scholar]
- Farroni, F.; Russo, M.; Russo, R.; Terzo, M.; Timpone, F. A combined use of phase plane and handling diagram method to study the influence of tyre and vehicle characteristics on stability. Veh. Syst. Dyn. 2013, 51, 1265–1285. [Google Scholar] [CrossRef]
- Farroni, F. TRICK-Tire/Road Interaction Characterization & Knowledge—A tool for the evaluation of tire and vehicle performances in outdoor test sessions. Mech. Syst. Signal Process. 2016, 72–73, 808–831. [Google Scholar] [CrossRef]
- Farroni, F.; Sakhnevych, A.; Timpone, F. Physical modelling of tire wear for the analysis of the influence of thermal and frictional effects on vehicle performance. Proceedings of the Institution of Mechanical Engineers, Part L. J. Mater. Des. Appl. 2017, 231, 151–161. [Google Scholar] [CrossRef]
- Stellantis Media Official Website. Available online: https://www.media.stellantis.com/em-en/fca-archive/press/fca-what-s-behind-episode-3-balocco-proving-ground (accessed on 1 January 2022).
- Michelin Website. Available online: https://www.michelinman.com/auto/tips-and-advice/advice-auto/tires-101/how-are-tires-made (accessed on 1 January 2022).
- U.S. Tire Manufacturers Association Website. Available online: https://www.ustires.org/whats-tire-0 (accessed on 1 June 2023).
- European Tyre & Rubber Manufacturer’s Association. The ETRMA Statistics Report Edition 2015. Available online: https://www.etrma.org/wp-content/uploads/2019/09/20151214-statistics-booklet-2015-final2.pdf (accessed on 1 June 2023).
- Angrick, C.; van Putten, S.; Prokop, G. Influence of Tire Core and Surface Temperature on Lateral Tire Characteristics. SAE Int. J. Passeng. Cars-Mech. Syst. 2014, 7, 468–481. [Google Scholar] [CrossRef]
- Lugaro, C.; Alirezaei, M.; Konstantinou, I.; Behera, A. A Study on the Effect of Tire Temperature and Rolling Speed on the Vehicle Handling Response. SAE Technical Paper 2020-01-1235. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 21–23 April 2020. [Google Scholar]
- Genta, G.; Morello, L. The Automotive Chassis; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1. [Google Scholar]
- Milliken, W.F. Race Car Vehicle Dynamics. In Society of Automotive Engineers; SAE International: Warrendale, PA, USA, 1995; ISBN 978-0-7680-0103-7. [Google Scholar]
- Ejsmont, J.; Taryma, S.; Ronowski, G. Swieczko-Zurek Mechanical Faculty. Influence of Temperature on the Tire Rolling Resistance. SAE Int. J. Automot. Technol. 2018, 19, 45–54. [Google Scholar] [CrossRef]
- Lu, D.; Lu, L.; Wu, H.; Li, L.; Wang, W.; Lv, M. Study on the Influence of Temperature on Tire Cornering Stiffness and Aligning Stiffness; Preprint (Version 1); Research Square: Durham, UK, 26 June 2020. [Google Scholar] [CrossRef]
- Okubo, R.; Oyama, K. Effects of Tire Thermal Characteristics on Vehicle Performance. In Proceedings of the FISITA 2014 World Automotive Congress, Maastricht, The Netherlands, 2–6 June 2014. [Google Scholar]
- Behera, A. The Influence of Tire Temperature and Velocity on Vehicle Dynamics. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2019. [Google Scholar]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- ISO 7401:2011; Road Vehicles—Lateral Transient Response Test Methods—Open-Loop Test Methods. International Organization for Standardization: Geneva, Switzerland, 2011.
- ISO/TR 8725:1988; Road Vehicles—Transient Open-Loop Response Test Method with One Period of Sinusoidal Input. Available online: https://www.iso.org/standard/16128.html (accessed on 1 June 2023).
- Dörrie, H.; Schröder, C.; Wies, B. Winter Tires: Operating Conditions, Tire Characteristics and Vehicle Driving Behavior. Tire Sci. Technol. 2010, 38, 119–136. [Google Scholar] [CrossRef]
- Farroni, F. Tire/Road Interaction Models. In Analysis of the Results Provided by a Grip and Thermodynamic-Sensitive Tire/Road Interaction Force Characterization Procedure; Tire Technology International: Surrey, UK, 2014. [Google Scholar]
- Warasitthinon, N.; Robertson, C.G. Interpretation of the tanδ Peak Height for Particle-Filled Rubber and Polymer Nanocomposites with Relevance to Tire Tread Performance Balance. Rubber Chem. Technol. 2018, 91, 577–594. [Google Scholar] [CrossRef]
- Rodríguez-Guadarrama, L.; Kounavis, J.; Maldonado, J. Functionalization: A Key Differential Factor in the Design of SSBRs for High Performance Tires; 194th Technical Meeting; Rubber World: Akron, OH, USA, 2018. [Google Scholar]
- Kalman, R. On the general theory of control systems. IRE Trans. Autom. Control 1959, 4, 110. [Google Scholar] [CrossRef]
- Canuto, E.; Novara, C.; Colangelo, L. Embedded model control: Reconciling modern control theory and error-based control design. Control Theory Technol. 2018, 16, 261–283. [Google Scholar] [CrossRef]




| Tires Category | Value of p1 | Units |
|---|---|---|
| Summer Tires | −25 | [°C] |
| Summer GT Tires | −20 | [°C] |
| All Season Tires | −32 | [°C] |
| Winter Tires | −40 | [°C] |
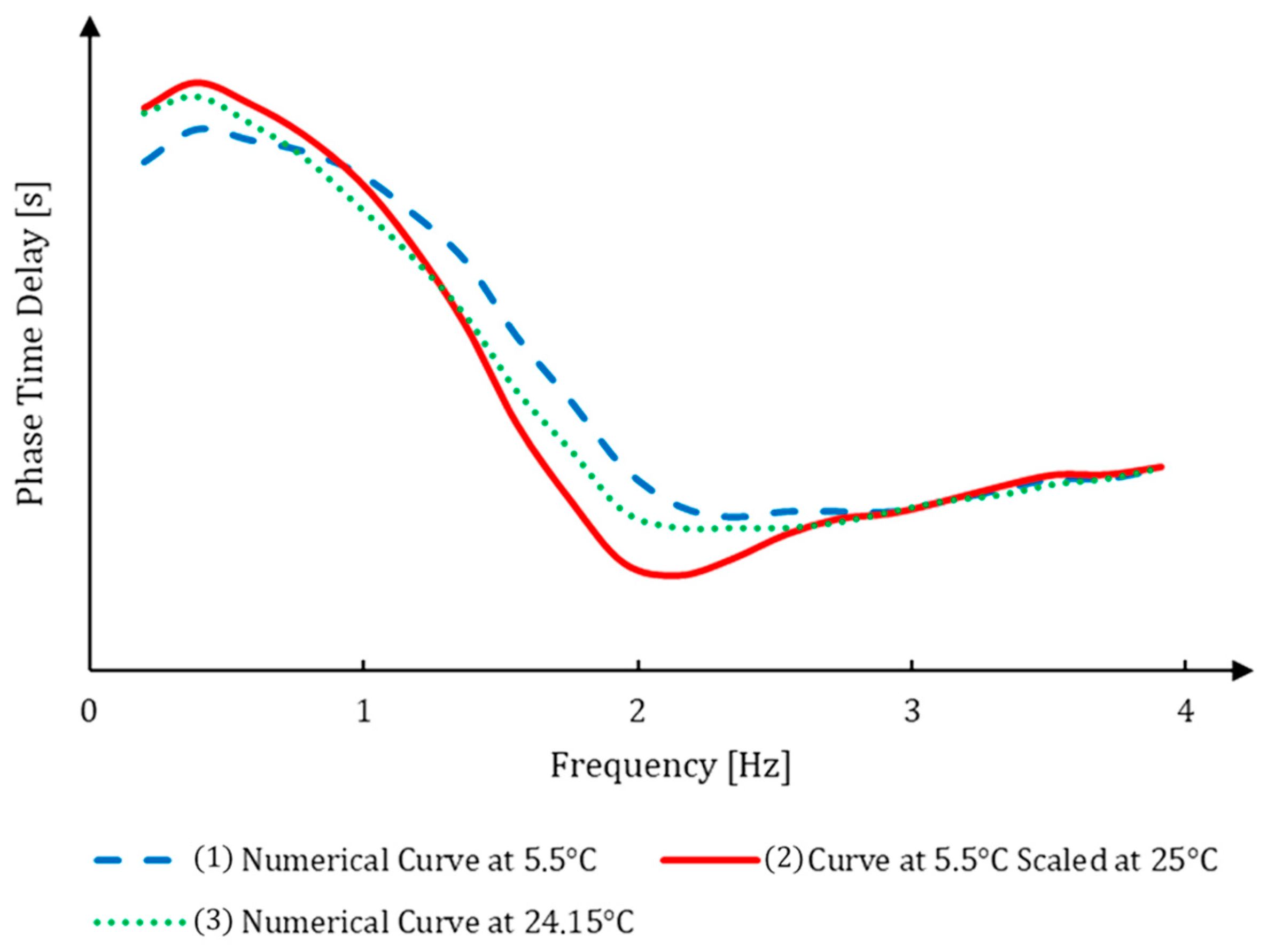
| (Figure 11) | ||||
| Curve ID | Vehicle | Temperature | Maneuver | Cornering Stiffnesses |
| #1—Blue | B-Segment Hybrid Subcompact Crossover SUV | 5.5 °C | Frequency Sweep, 0.5 g | Measured |
| #2—Red | B-Segment Hybrid Subcompact Crossover SUV | 25 °C | Frequency Sweep, 0.5 g | Computed |
| #3—Green | B-Segment Hybrid Subcompact Crossover SUV | 24.15 °C | Frequency Sweep, 0.5 g | Measured |
| (Figure 12) | ||||
| Curve ID | Vehicle | Temperature | Maneuver | Cornering Stiffnesses |
| #1—Blue | B-Segment Subcompact Crossover SUV | 8.1 °C | Frequency Sweep, 0.5 g | Measured |
| #2—Red | B-Segment Subcompact Crossover SUV | 25 °C | Frequency Sweep, 0.5 g | Computed |
| #3—Green | B-Segment Subcompact Crossover SUV | 24.85 °C | Frequency Sweep, 0.5 g | Measured |
| B-Segment Hybrid Subcompact Crossover SUV, Frequency Sweep, 0.5 g , (=) | ||||
| Component | Frequency | Value Measured at 5.5 °C | Value Computed at 25 °C | Value Measured at 24.15 °C |
| Gain | ≈ 0 Hz | 0.021 [-] | 0.027 [-] | 0.025 [-] |
| Phase Delay | −0.144 [s] | −0.153 [s] | −0.184 [s] | |
| Gain | 0.5 Hz | 0.022 [-] | 0.028 [-] | 0.026 [-] |
| Phase Delay | −0.113 [s] | −0.130 [s] | −0.140 [s] | |
| Gain | 1 Hz | 0.025 [-] | 0.032 [-] | 0.029 [-] |
| Phase Delay | −0.137 [s] | −0.156 [s] | −0.164 [s] | |
| B-Segment Subcompact Crossover SUV, Frequency Sweep, 0.5 g , (=) | ||||
| Component | Frequency | Value Measured at 5.5 °C | Value Computed at 25 °C | Value Measured at 24.15 °C |
| Gain | 1 Hz | 0.391 [-] | 0.412 [-] | 0.400 [-] |
| Phase Delay | −0.064 [s] | −0.072 [s] | −0.082 [s] | |
| Gain | 1.5 Hz | 0.385 [-] | 0.363 [-] | 0.363 [-] |
| Phase Delay | −0.113 [s] | −0.122 [s] | −0.116 [s] | |
| Gain | 2 Hz | 0.307 [-] | 0.284 [-] | 0.290 [-] |
| Phase Delay | −0.116 [s] | −0.119 [s] | −0.118 [s] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savant, S.; De Carvalho Pinheiro, H.; Sacchi, M.E.; Conti, C.; Carello, M. Tires and Vehicle Lateral Dynamic Performance: A Corrective Algorithm for the Influence of Temperature. Machines 2023, 11, 654. https://doi.org/10.3390/machines11060654
Savant S, De Carvalho Pinheiro H, Sacchi ME, Conti C, Carello M. Tires and Vehicle Lateral Dynamic Performance: A Corrective Algorithm for the Influence of Temperature. Machines. 2023; 11(6):654. https://doi.org/10.3390/machines11060654
Chicago/Turabian StyleSavant, Simone, Henrique De Carvalho Pinheiro, Matteo Eugenio Sacchi, Cinzia Conti, and Massimiliana Carello. 2023. "Tires and Vehicle Lateral Dynamic Performance: A Corrective Algorithm for the Influence of Temperature" Machines 11, no. 6: 654. https://doi.org/10.3390/machines11060654
APA StyleSavant, S., De Carvalho Pinheiro, H., Sacchi, M. E., Conti, C., & Carello, M. (2023). Tires and Vehicle Lateral Dynamic Performance: A Corrective Algorithm for the Influence of Temperature. Machines, 11(6), 654. https://doi.org/10.3390/machines11060654







