Adaptive Control Strategy for a Pumping System Using a Variable Frequency Drive
Abstract
:1. Introduction
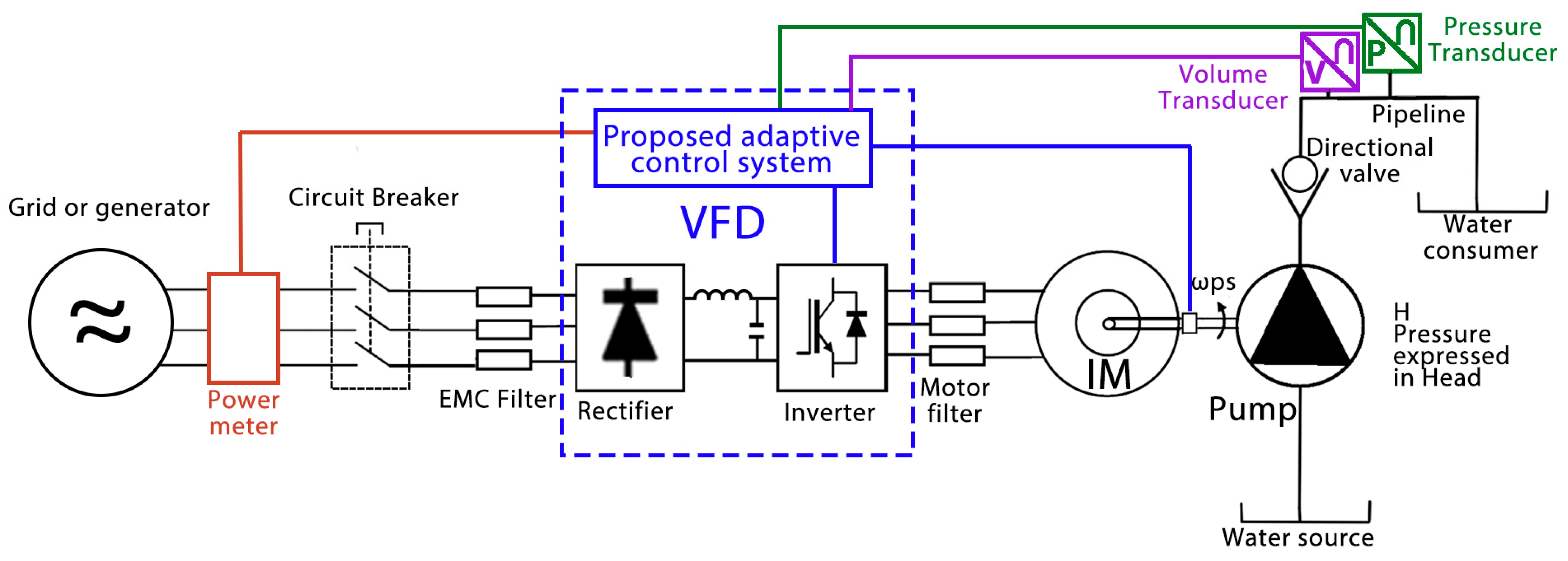
2. Mathematical Model of a Pumping System Driven by a Variable Frequency Drive
2.1. Variable Frequency Drive (VFD) Model
2.2. Induction Motor Model
2.3. Variable Speed Centrifugal Pump Model
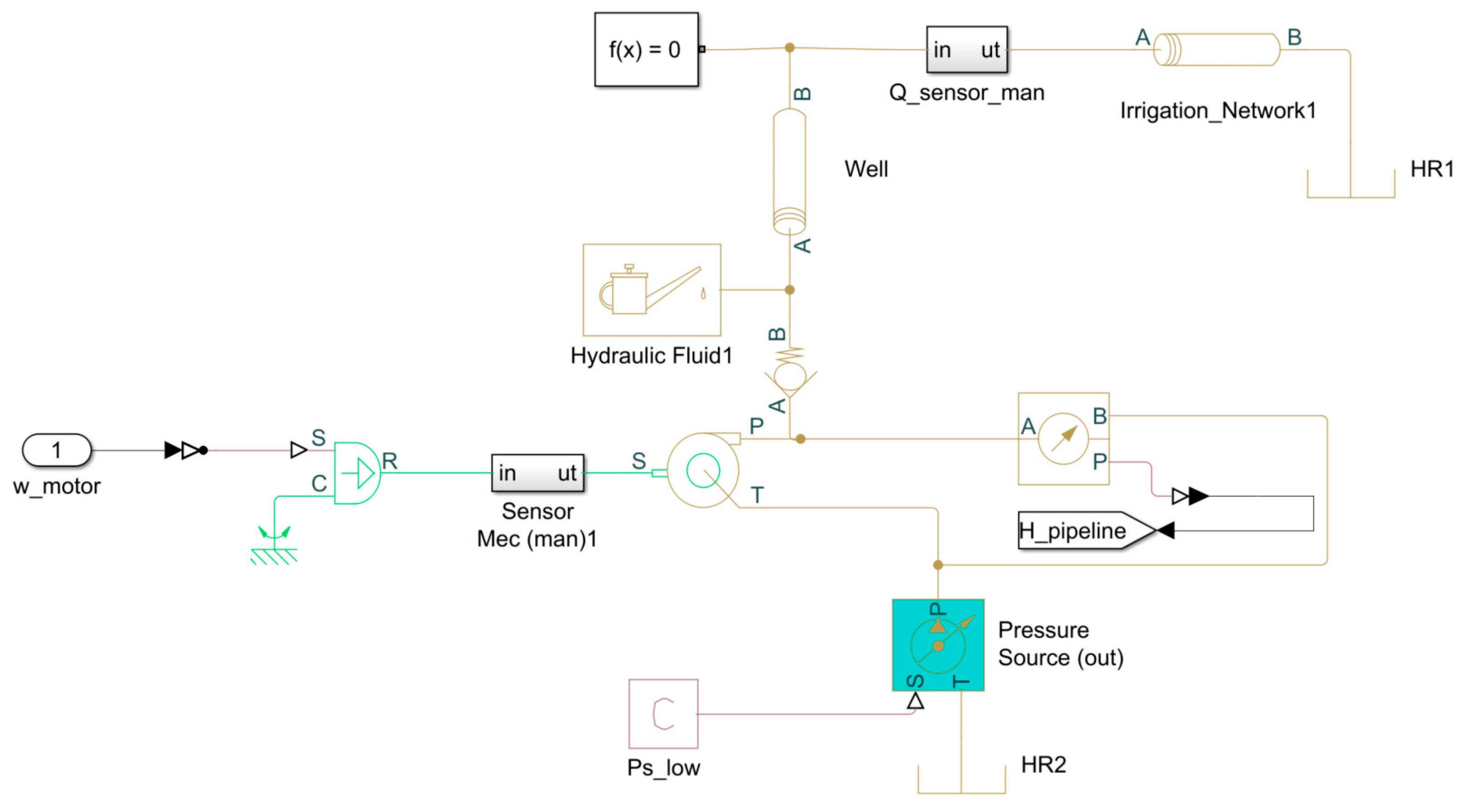
2.4. Hydraulic Network Model
3. The Proposed Adaptive Control Strategy
- G1, G2 and G3 are variable gains obtained in Equations (43), (45) and (47);
- k_T represents the torque coefficient calculated in Equation (12);
- represents the transformation from a stationary (αβ) reference frame into a synchronous (dq) reference frame;
- represents the transformation from a three-phase (abc) complex space vector into a stationary (αβ) reference frame;
- represents the transformation from a synchronous (dq) reference frame into a stationary (αβ) reference frame;
- represents the transformation from a stationary (αβ) reference frame into a three-phase (abc) complex space vector.
3.1. Classical Variable Speed Pump Control Strategy Implemented in a VFD
3.2. Adapting the Variable Speed Pump Control Strategy of the VFD to Operate the Centrifugal Pump at Variable Flow (Pump Discharge)
3.3. Adapting the Variable Speed Pump Control Strategy of the VFD to Operate the Centrifugal Pump at Variable Pressure (Pumping Head)
3.4. Adapting the Variable Speed Pump Control Strategy of the VFD to Operate the Centrifugal Pump at Variable Available Power (Tracking a Fluctuating and Intermittent Power Source)
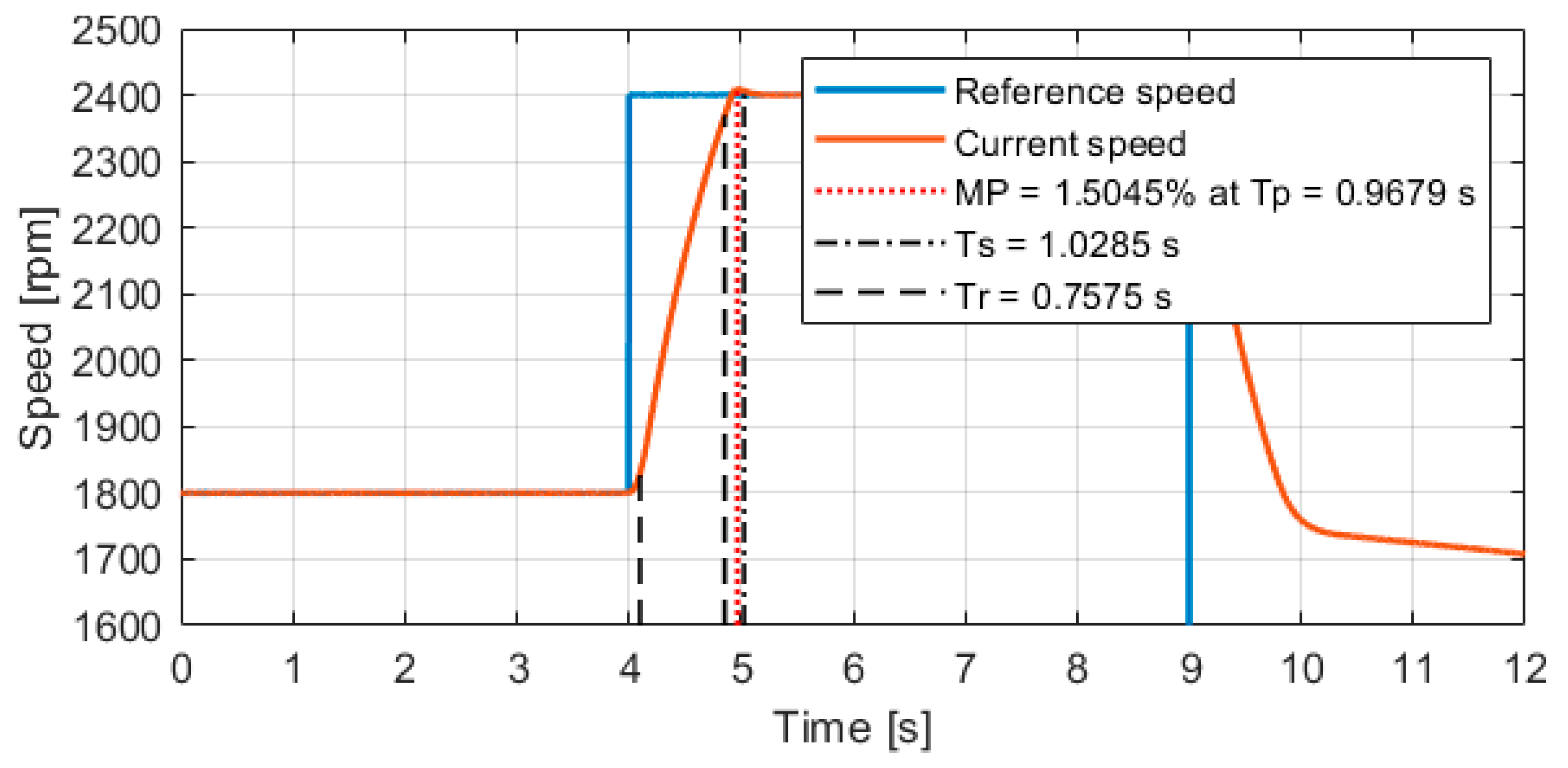
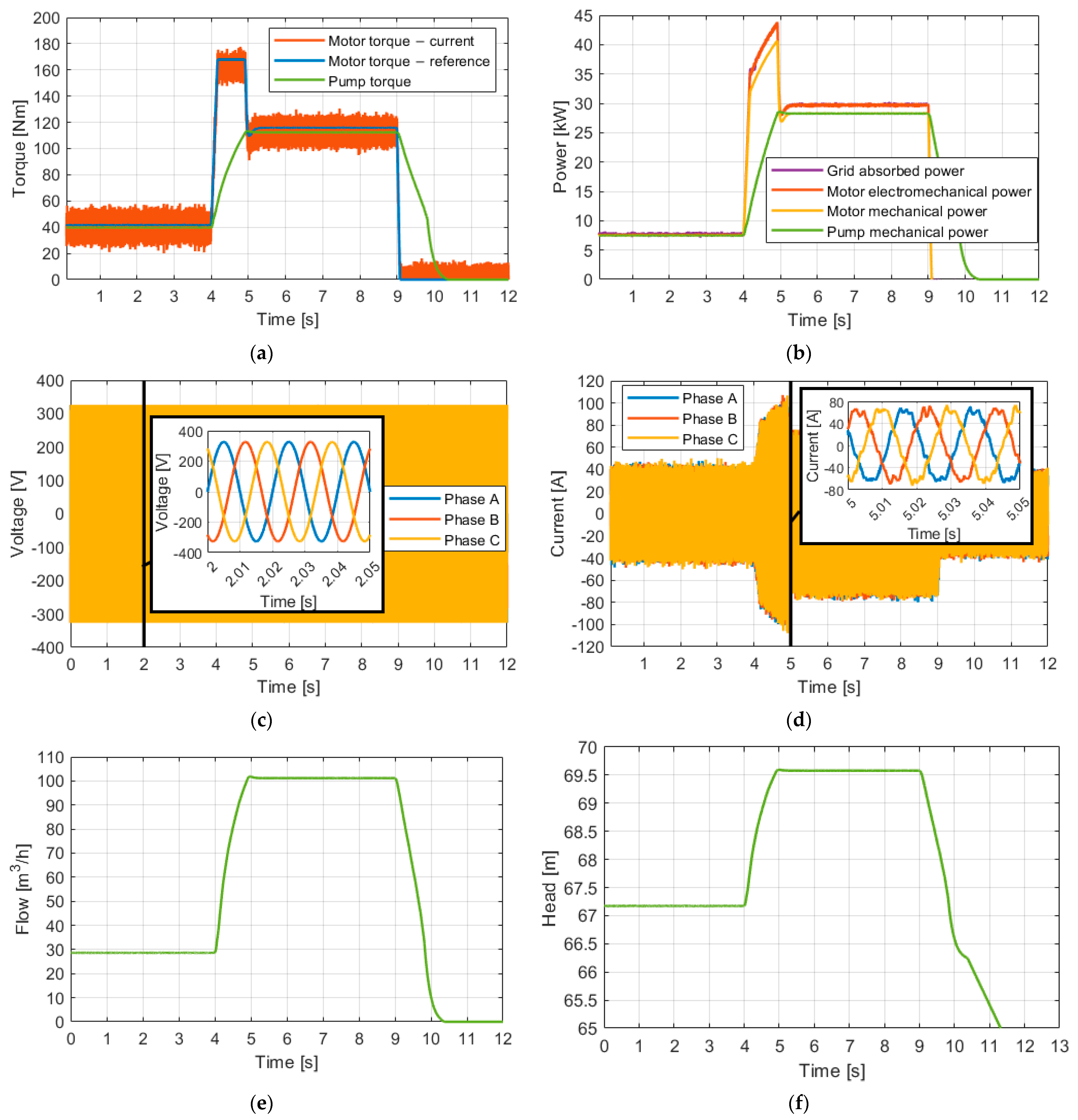
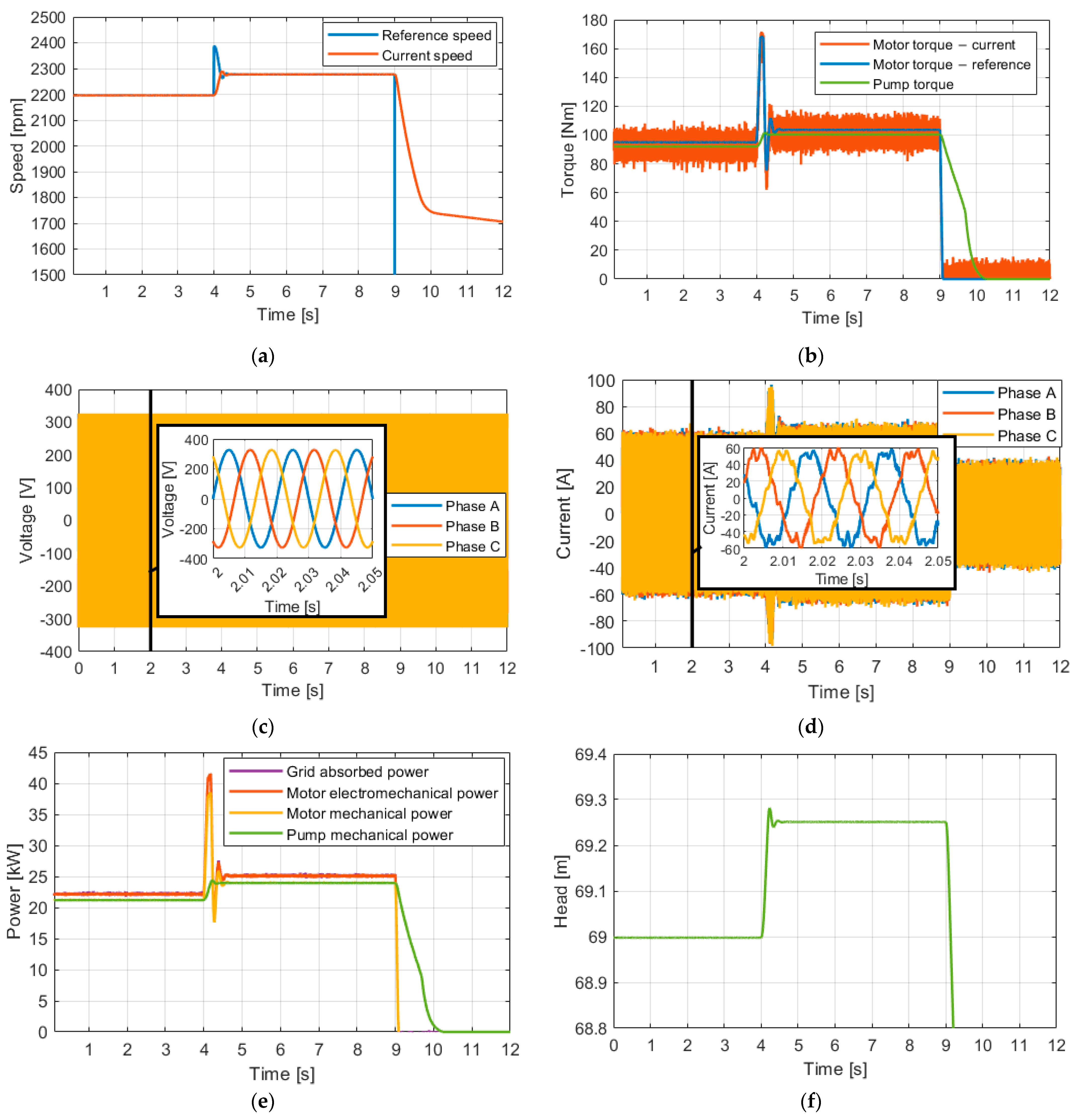
4. Simulation Results
- Variable speed;
- Variable flow (pump discharge);
- Variable pressure (pumping head);
- Variable available power (tracking a fluctuating and intermittent power source).
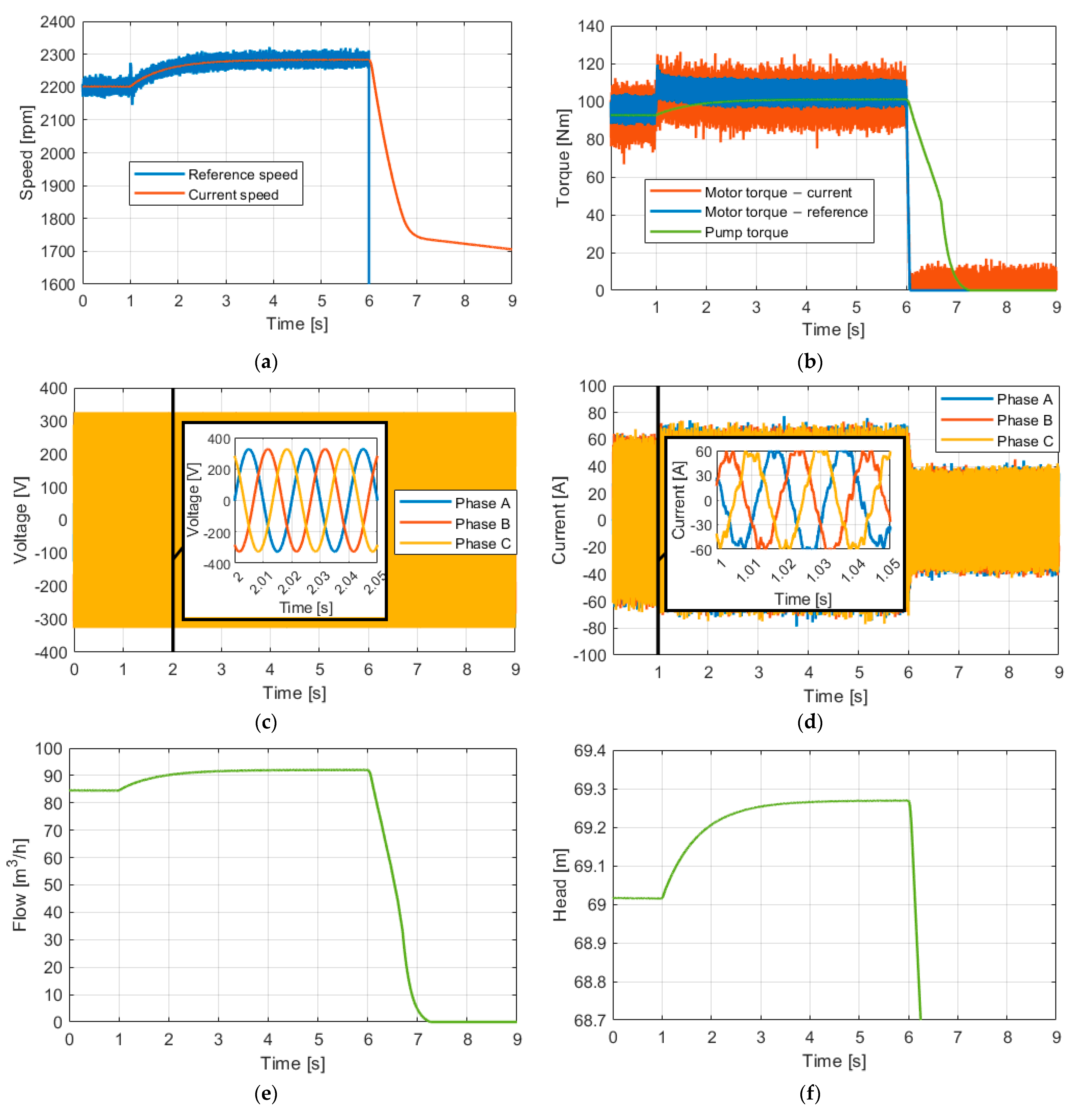
4.1. Response of the Adaptive Control Strategy Operating the Centrifugal Pump at Variable Speed
4.2. Response of the Adaptive Control Strategy Operating the Centrifugal Pump at Variable Flow (Pump Discharge)
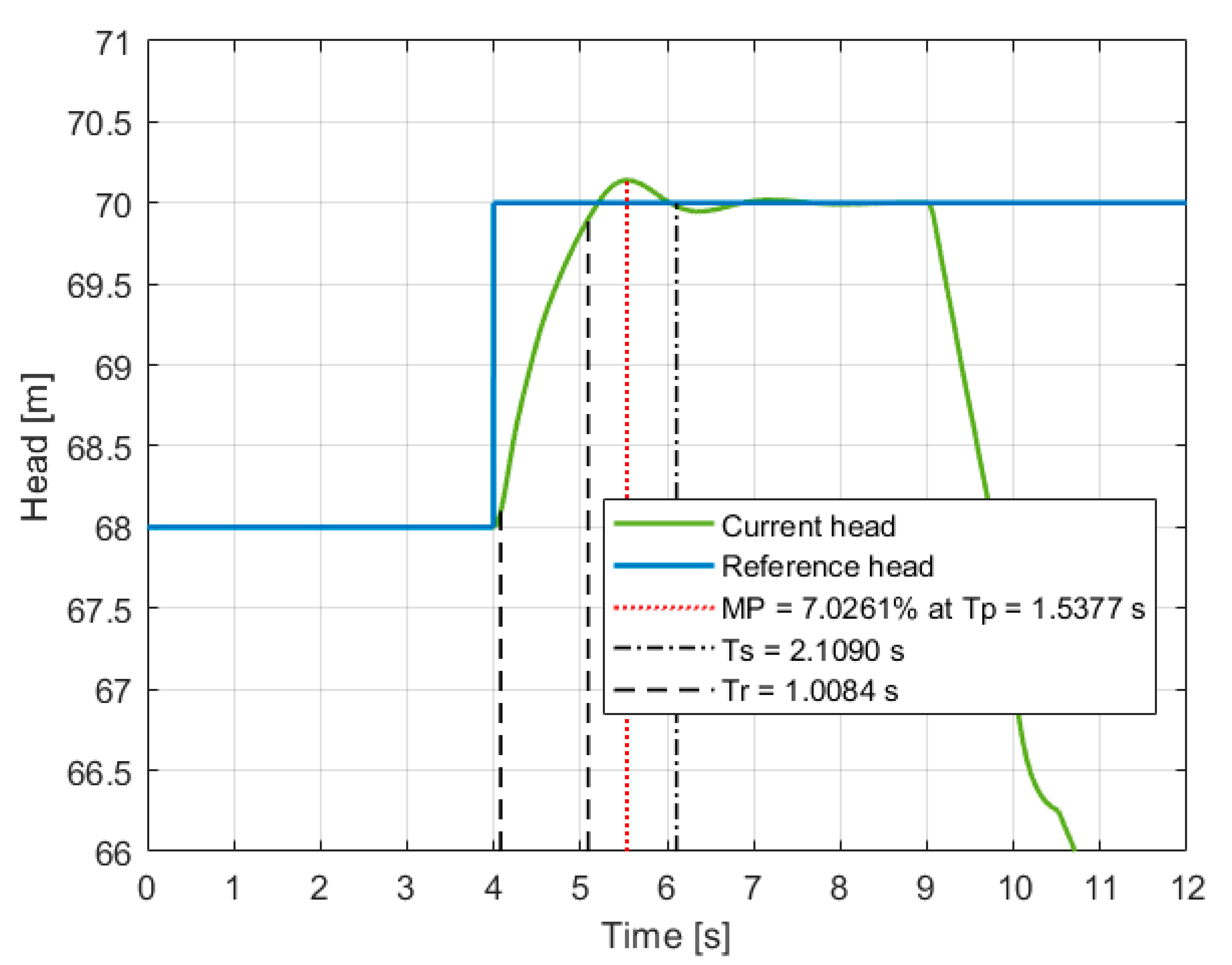
4.3. Response of the Adaptive Control Strategy Operating the Centrifugal Pump at Variable Pressure (Pumping Head)
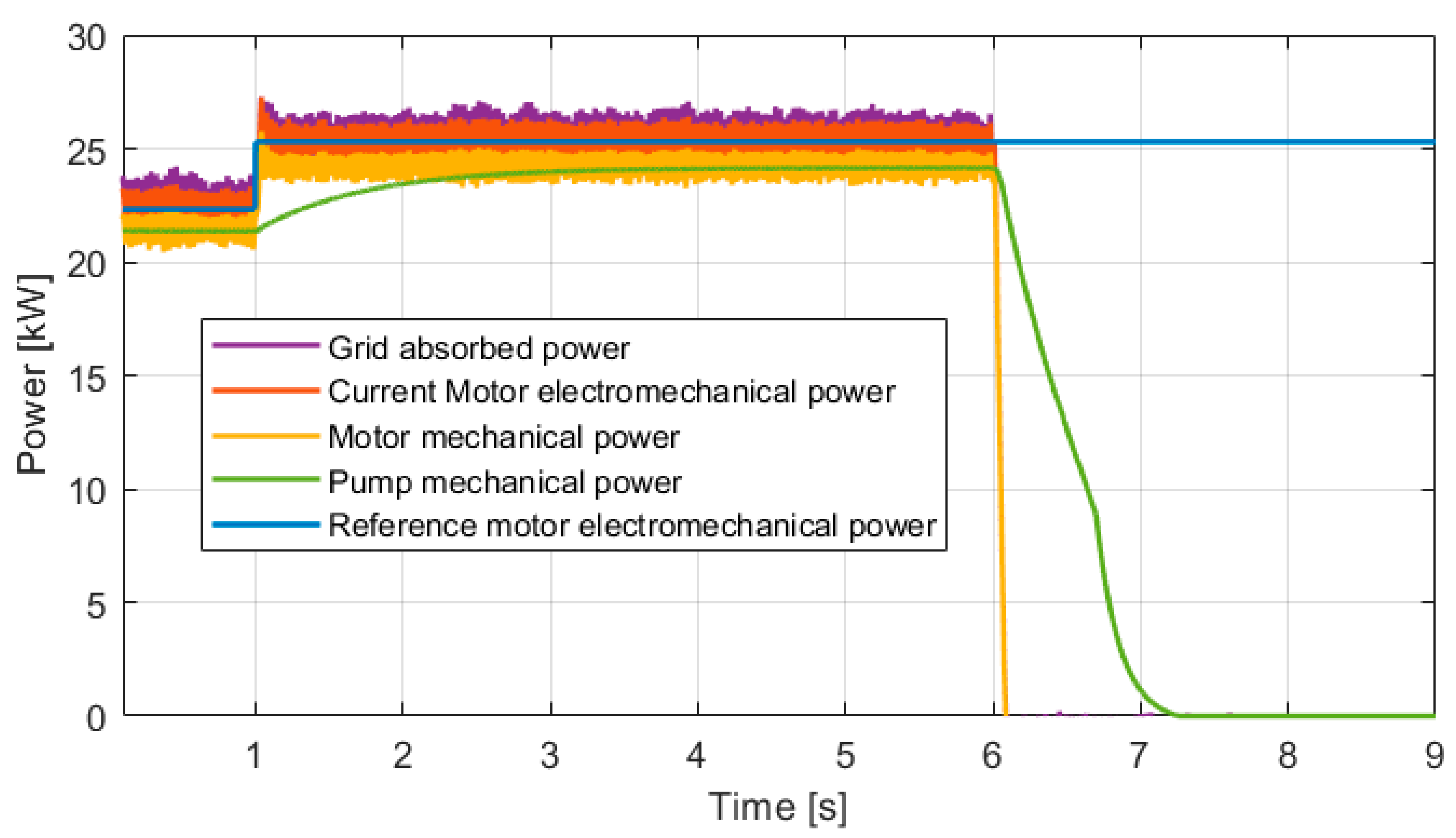
4.4. Response Response of the Adaptive Control Strategy Operating the Centrifugal Pump at Variable Available Power (Tracking a Fluctuating and Intermittent Power Source)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Technical Properties | Variable Frequency Drive | Symbol | Unit |
|---|---|---|---|
| Manufacturer | Nidec Control Techniques | - | - |
| Type | F300 | - | - |
| Maximum DC voltage | 980 | VmaxVFDdc | Vdc |
| MMP DC voltage range | 540–830 | VVFDdc | Vdc |
| AC rated power | 45 | PVFD | kW |
| AC rated voltage | 400 | VVFDac | Vac |
| AC rated frequency | 50 | fVFD | A |
| AC maximum continuous current | 94 | IVFD | A |
| No-load inverter losses | 0.0115 | k0 | - |
| Linear inverter losses | 0.0015 | k1 | - |
| Joule inverter losses | 0.0438 | k2 | - |
| Technical Properties | Submersible Pump Induction Motor | Symbol | Unit |
|---|---|---|---|
| Manufacturer | Caprari | - | - |
| Type | MAC625A-8V | - | - |
| Nominal Power | 18.5 | PIM0 | kW |
| Nominal Efficiency | 83% | ηIM0 | % |
| Nominal Frequency | 50 | fIM | Hz |
| Nominal Voltage | 400 | VIM | V |
| Nominal Current | 40.2 | IIM | A |
| Number of poles | 2 | Poles | - |
| Rotor synchronous speed | 3000 | ωs | rpm |
| Rotor nominal speed | 2875 | ω0 | rpm |
| Rotor operating speed | Variable | ω | rpm |
| Power factor | 0.8 | cos φ | - |
| Properties | Value | Symbol | Unit |
|---|---|---|---|
| Manufacturer | Caprari | - | - |
| Type | E8P95/7ZC | - | - |
| Minimum water speed to cool the jacket of the motor | 0.5 m/s | - | - |
| Maximum number of starts in one hour | 20 | - | - |
| Minimum immersion depth | 507.5 mm | - | - |
| Pump service flow rate | 91.85 m3/h | Q | m3/h |
| Submersible pump service head | 78.12 m | H | m |
| Pump rated efficiency | 75.63% | η | % |
| Pump rated hydraulic power | 25.84 kW | Phydraulic | kW |
| Pump maximum flow rate | 169.2 m3/h | Qmax | m3/h |
| Pump head at theoretical 0 flow rate | 97.35 m | Hmax | m |
| Pump minimum head (at maximum flow rate) | 83.29 m | Hmin | m |
| Pump efficiency at maximum flow rate | 81.5% | η | % |
| Pump hydraulic power at maximum flow rate | 30 kW | Ppump | m3/h |
| Consumer pressure | 1.5 | Hg | bar |
| Well Dynamic head | 35.7 | Hgwell | mca |
| Water level variation | 18.6 | ΔHg | mca |
| Pipe diameter | 0.3 | Dpipe | m |
| Head–flow 1st coefficient | 185.2123 | A | m |
| Head–flow 2nd coefficient | 0.2608 | B | h/m2 |
| Head–flow 3rd coefficient | −0.0076 | C | h/m5 |
| Efficiency-flow 1st coefficient | 1.8274 | D | 1/m2 |
| Efficiency-flow 2nd coefficient | −0.104 | E | 1/m5 |
References
- Bordeașu, D.; Proștean, O.; Filip, I.; Drăgan, F.; Vașar, C. Modelling, Simulation and Controlling of a Multi-Pump System with Water Storage Powered by a Fluctuating and Intermittent Power Source. Mathematics 2022, 10, 4019. [Google Scholar] [CrossRef]
- Al-Khalifah, M.; Mcmillan, G. Control valve versus variable speed drive for flow control. ISA Autom. Week 2012, 60, 42–46. [Google Scholar]
- Brogan, A.; Gopalakrishnan, V.; Sturtevant, K.; Valigosky, Z.; Kissock, K. Improving Variable-Speed Pumping Control to Maximize Savings. ASHRAE Trans. 2016, 122, 141–148. [Google Scholar]
- Priyadarshi, N.; Ramachandaramurthy, V.K.; Padmanaban, S.K.; Azam, F.; Sharma, A.K.; Kesari, J.P. An ANN Based Intelligent MPPT Control for Wind Water Pumping System. In Proceedings of the 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 443–448. [Google Scholar] [CrossRef]
- Sul, S. Control of Electric Machine Drive Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 291–294. [Google Scholar]
- Mourad, E.; Lachhab, A.; Limouri, M.; Dahhou, B.; Essaid, A. Adaptive control of a water supply system. Control. Eng. Pract. 2001, 9, 343–349. [Google Scholar] [CrossRef]
- Kokotovic, V.; Buckman, C. Electric Water Cooling Pump Sensitivity Based Adaptive Control. SAE Int. J. Commer. Veh. 2017, 10, 331–339. [Google Scholar] [CrossRef]
- Kiata, E.; Ngasop, N.; Justin, N.S.J.; Djalo, H. Fuzzy Adaptive Control by Reference Model of a Submerged Electric Pump: Application to Photovoltaic Water Pumping. Glob. J. Eng. Sci. 2023, 10, 861–869. [Google Scholar]
- Torres, L.H.S.; Schnitman, L.; Felippe de Souza, J.A.M. Model Reference Adaptive Control Applied to the Improvement of the Operational Conditions of a Sucker Rod Pump System. IFAC Proc. Vol. 2010, 43, 231–236. [Google Scholar] [CrossRef] [Green Version]
- Bordeașu, D. Study on the implementation of an alternative solution to the current irrigation system. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2022, 65, 593–602. [Google Scholar]
- Nidec. Powerdrive F300; Nidec Control Techniques Ltd.: Newtown, UK, 2017; p. 324. [Google Scholar]
- Janevska, G.; Bitola, R.M. Mathematical Modeling of Pump System. Electron. Int. Interdiscip. Conf. 2013, 2, 455–458. [Google Scholar]
- Muñoz, J.; Martínez-Moreno, F.; Lorenzo, E. On-site characterisation and energy efficiency of grid-connected PV inverters. Prog. Photovolt. Res. Appl. 2011, 19, 192–201. [Google Scholar] [CrossRef]
- Abad, G. Power Electronics and Electric Drives for Traction Applications; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Malinowski, M.; Al-Haddad, K. Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications; John Wiley & Sons Ltd.: Chichester, UK, 2014. [Google Scholar]
- Errouha, M.; Motahhir, S.; Combe, Q.; Derouich, A. Intelligent control of induction motor for photovoltaic water pumping system. SN Appl. Sci. 2021, 3, 777. [Google Scholar] [CrossRef]
- Caprari, Submersible Electric Pump E8P95/7ZC+MAC870-8V Technical Data Sheet. 2019. Available online: https://ipump.caprarinet.net/ (accessed on 9 October 2021).
- Majhi, J.; Nema, S.; Verma, D. Simulation and analysis of solar based water pumping system for hydraulic actuated load. In Proceedings of the 2nd International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 21–23 August 2019. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 7th ed.; University of Rhode Island: Kingston, RI, USA; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Thorley, A.R.D. Fluid Transients in Pipeline Systems; D. & L. George Ltd Publ.: Herts, UK, 1991. [Google Scholar]
- Sabbagh, E.; Sinai, G. A model for optimal real-time computer control of pumping stations in irrigation systems. Comput. Electron. Agric. 1988, 3, 119–133. [Google Scholar] [CrossRef]
- Bordeasu, I. Monografia Laboratorului de Cercetare a Eroziunii Prin Cavitatie al Universitatii Polirehnica Timisoara (1960–2020); Editura Politehnica: Timişoara, Romania, 2020. [Google Scholar]
- Mitelea, I.; Bordeaşu, I.; Belin, C.; Uţu, I.-D.; Crăciunescu, C.M. Cavitation Resistance, Microstructure, and Surface Topography of Plasma Nitrided Nimonic 80 A Alloy. Materials 2022, 15, 6654. [Google Scholar] [CrossRef] [PubMed]
- Bordeasu, I.; Popoviciu, M.O.; Mitelea, I.; Balasoiu, V.; Ghiban, B.; Tucu, D. Chemical and mechanical aspects of the cavitation phenomena. Rev. Chim. 2007, 58, 1300–1304. [Google Scholar]


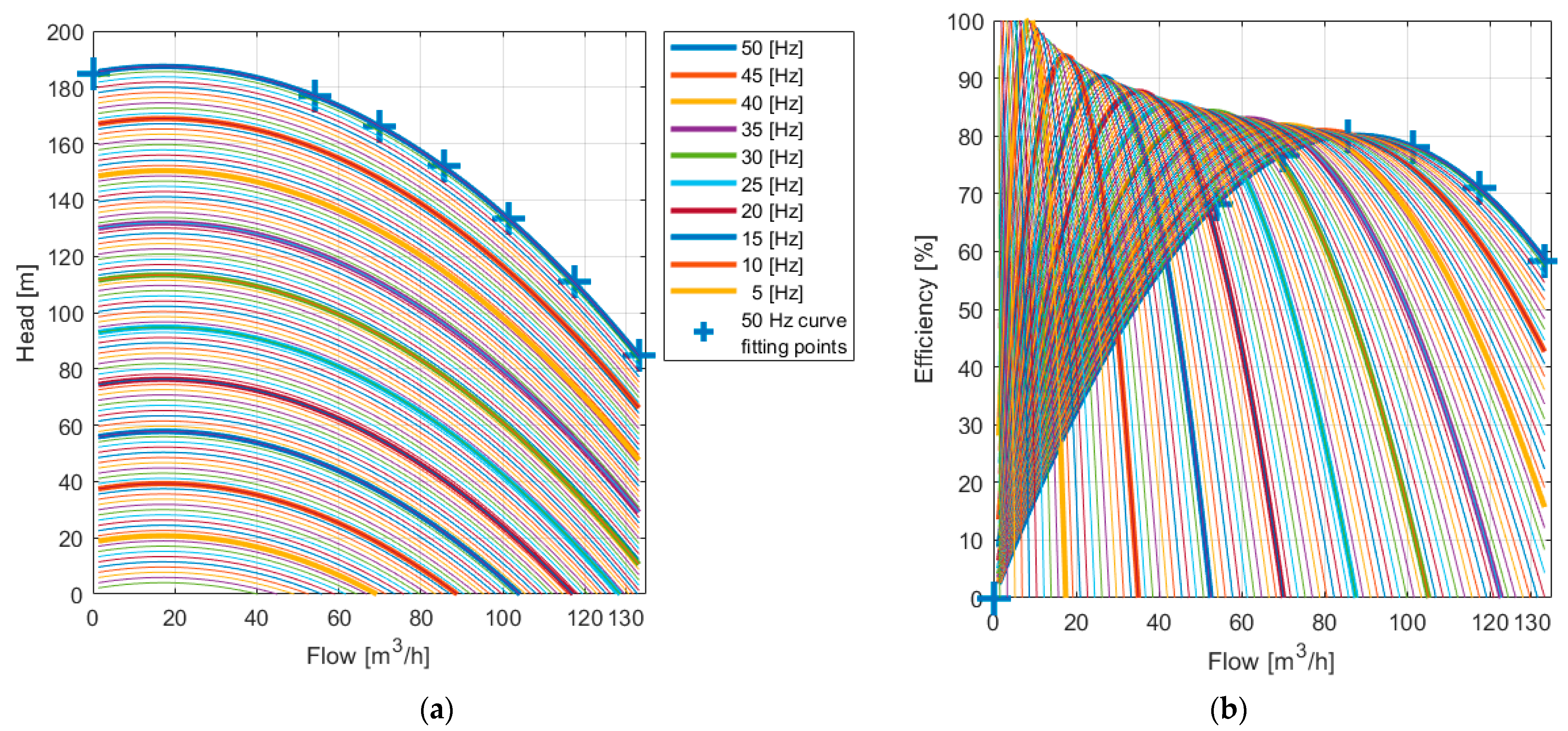




| 50 Hz Curve Fitting Point | Q [m³/h] | H [m] | P [kW] | η [%] | NPSH [m] |
|---|---|---|---|---|---|
| 1 | 0 | 185 | 0 | 0 | 0 |
| 2 | 54 | 177 | 36.8 | 68.1 | 1.8 |
| 3 | 69.84 | 166 | 41.19 | 76.7 | 2.37 |
| 4 | 85.68 | 152 | 45.11 | 80 | 3.22 |
| 5 | 101.52 | 133.5 | 48.09 | 78 | 4.28 |
| 6 | 117.36 | 111 | 50.01 | 71 | 5.6 |
| 7 | 133.2 | 85 | 50.03 | 58.35 | 7.2 |
| Sector | Htotal (mca) | Q (m3/h) | Pressure (bar) | Pressure Reference (bar) | Power (kW) | Frequency (Hz) |
|---|---|---|---|---|---|---|
| 1 | 68 | 54 | 3.4812354 | 3.5 | 12.029 | 33.0518 |
| 2 | 76 | 84 | 4.18822408 | 4.2 | 22.319 | 39.0077 |
| 3 | 76 | 91.5 | 4.42083782 | 4.4 | 25.301 | 40.3471 |
| 4 | 76 | 90 | 4.168346 | 4.2 | 24.676 | 40.0732 |
| 5 | 72 | 85.5 | 3.79069191 | 3.8 | 21.890 | 38.6260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bordeasu, D.; Prostean, O.; Filip, I.; Vasar, C. Adaptive Control Strategy for a Pumping System Using a Variable Frequency Drive. Machines 2023, 11, 688. https://doi.org/10.3390/machines11070688
Bordeasu D, Prostean O, Filip I, Vasar C. Adaptive Control Strategy for a Pumping System Using a Variable Frequency Drive. Machines. 2023; 11(7):688. https://doi.org/10.3390/machines11070688
Chicago/Turabian StyleBordeasu, Dorin, Octavian Prostean, Ioan Filip, and Cristian Vasar. 2023. "Adaptive Control Strategy for a Pumping System Using a Variable Frequency Drive" Machines 11, no. 7: 688. https://doi.org/10.3390/machines11070688
APA StyleBordeasu, D., Prostean, O., Filip, I., & Vasar, C. (2023). Adaptive Control Strategy for a Pumping System Using a Variable Frequency Drive. Machines, 11(7), 688. https://doi.org/10.3390/machines11070688








