A Study of Knee Exoskeleton Configuration Based on Lower Limb Motion Characteristics Analysis
Abstract
:1. Background
2. Analysis of the Biomechanical Characteristics of Lower Limb Movement
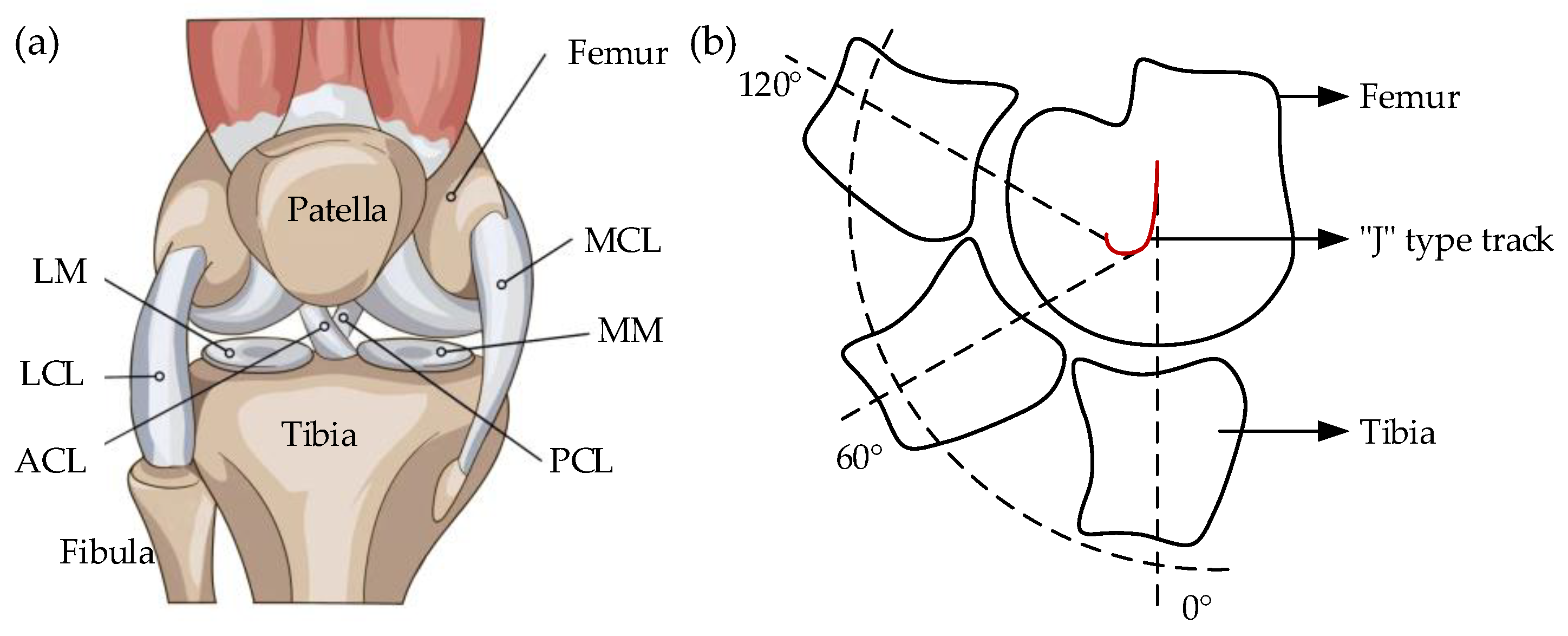
2.1. Physiological Characteristics of Knee Joint Movement
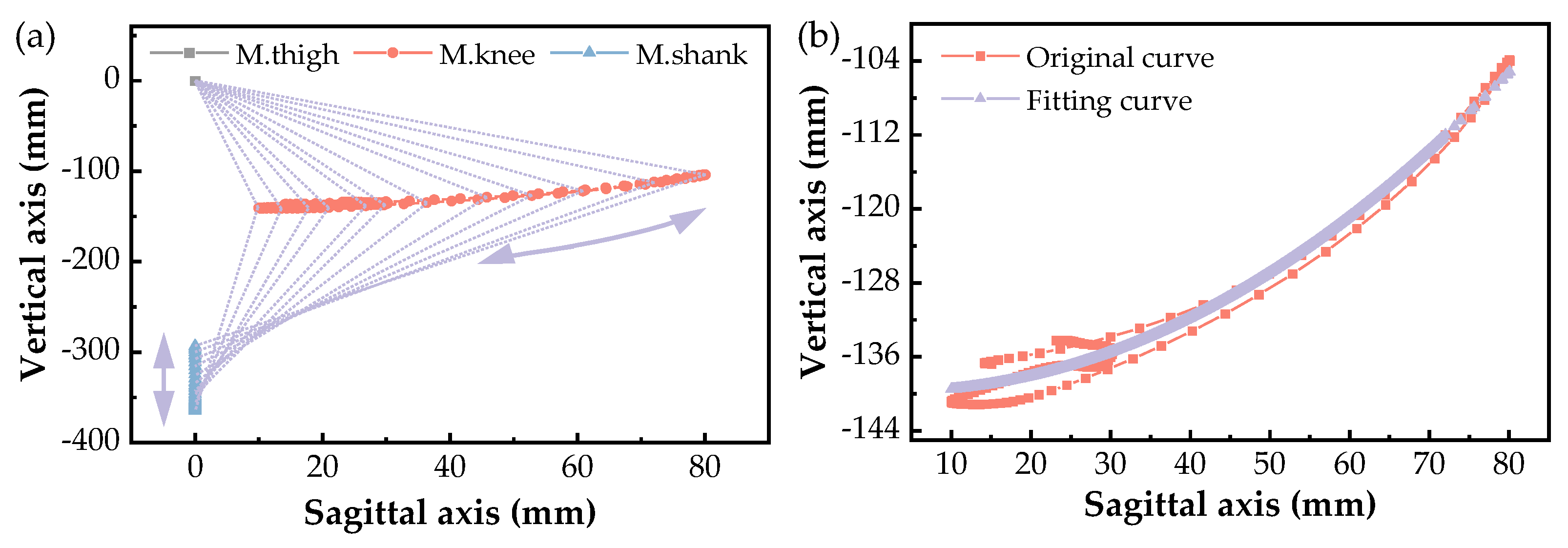
2.2. Motion Space–Time Data Acquisition
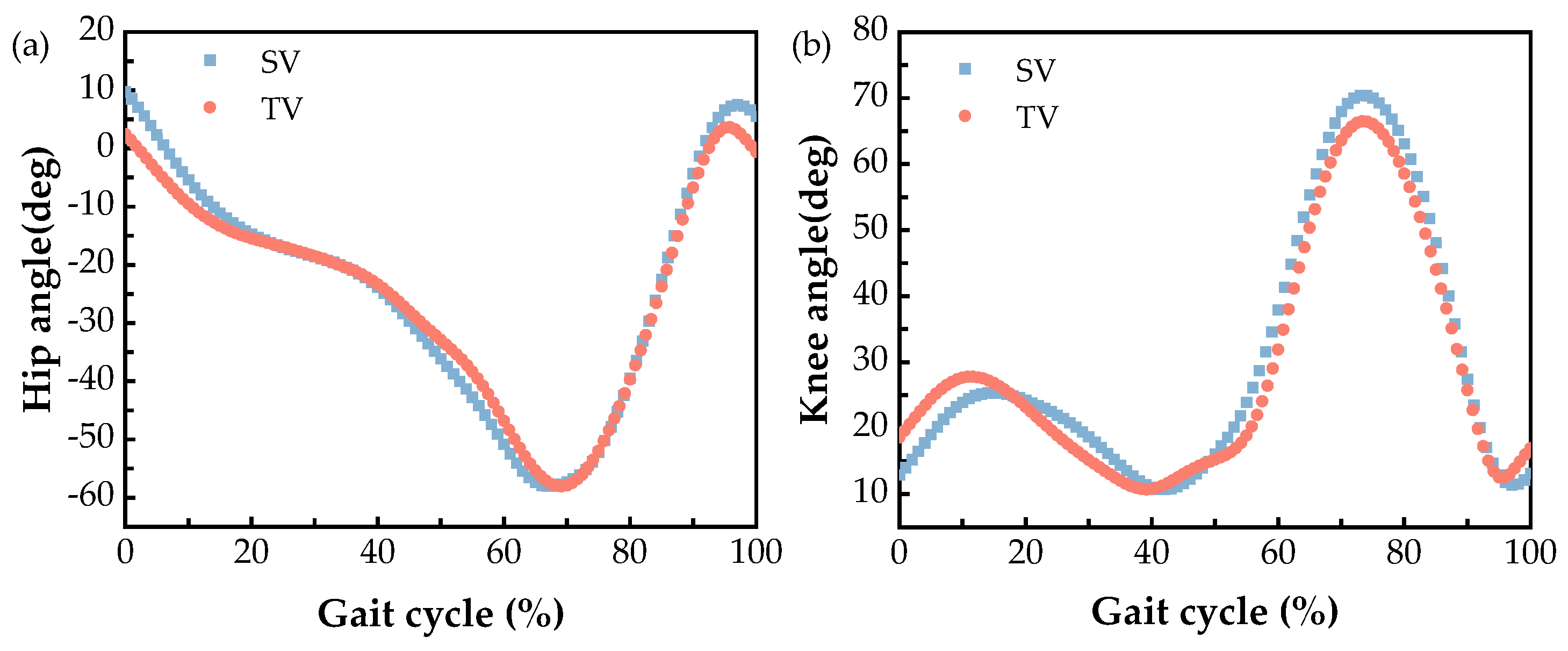
2.3. Movement Gait Characteristics Analysis
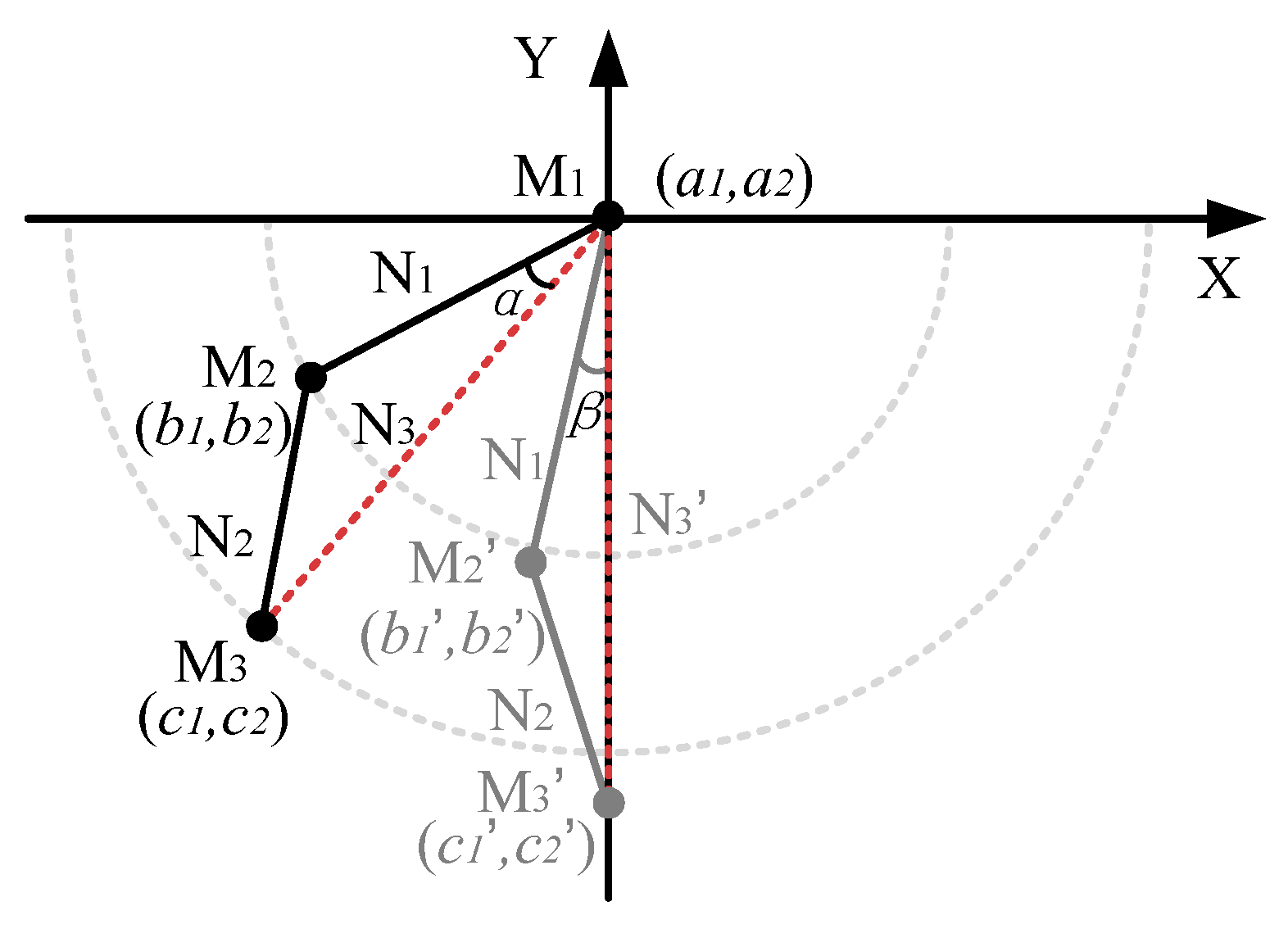
2.4. Four-Link Mechanism Simulating the Knee Joint
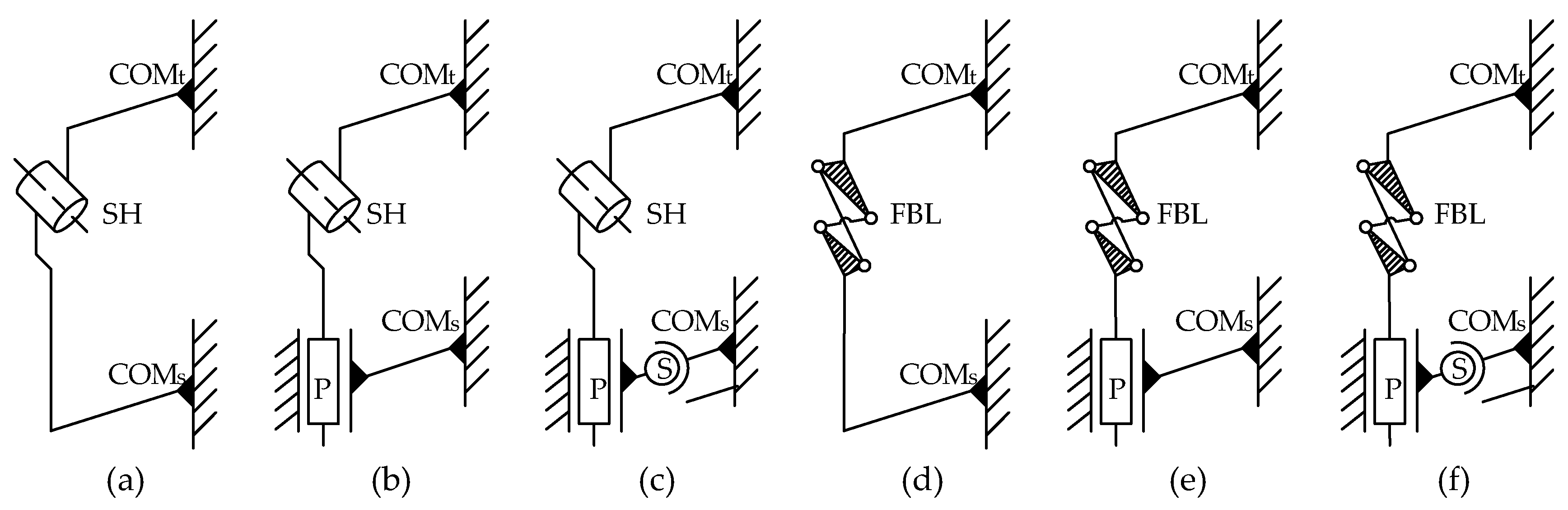
2.5. Knee Exoskeleton Configuration
3. Kinematics and Dynamics Model of Lower Limbs
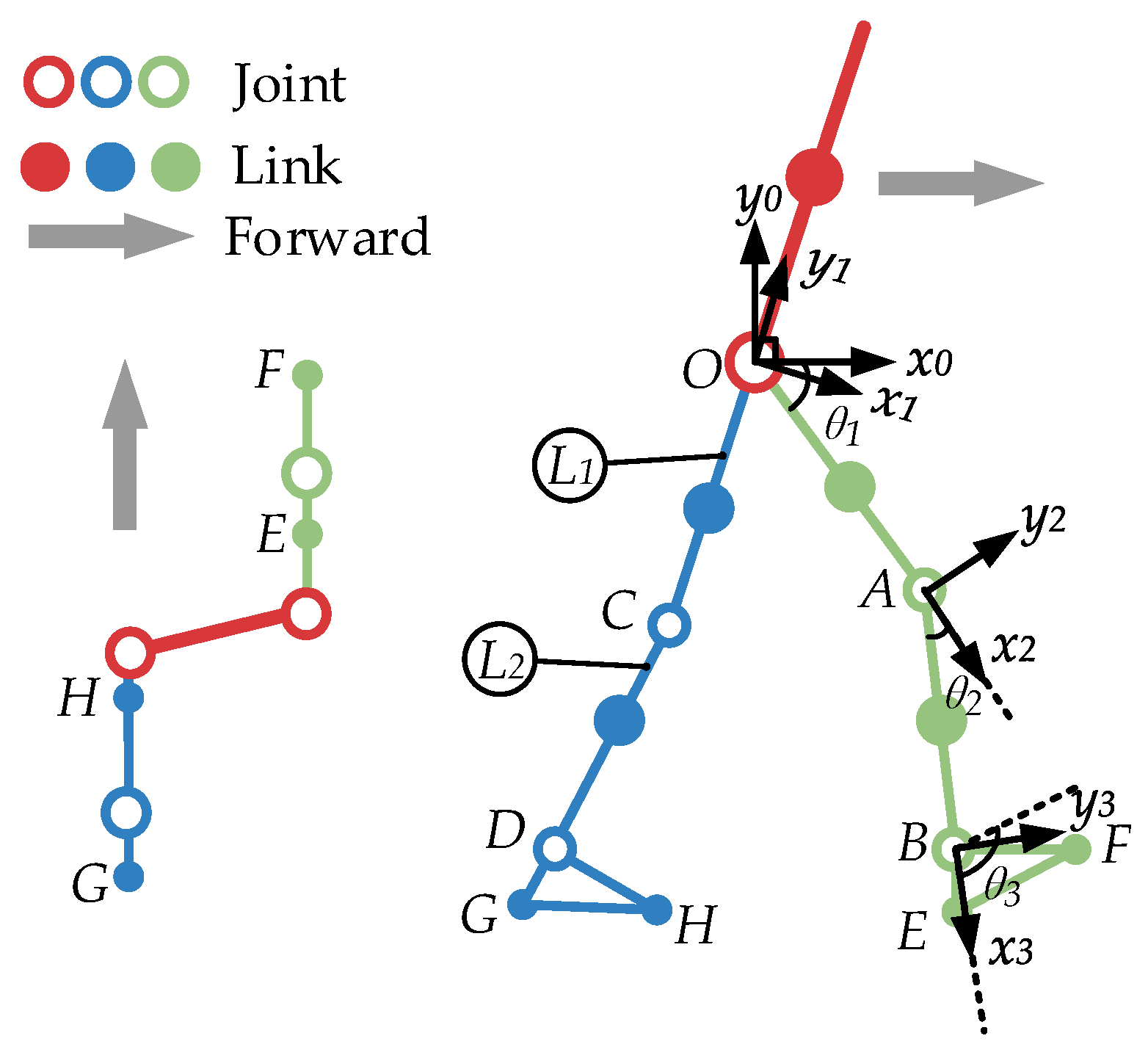
3.1. Manikin Simplification
3.2. Kinematic Model of Human Lower Limbs
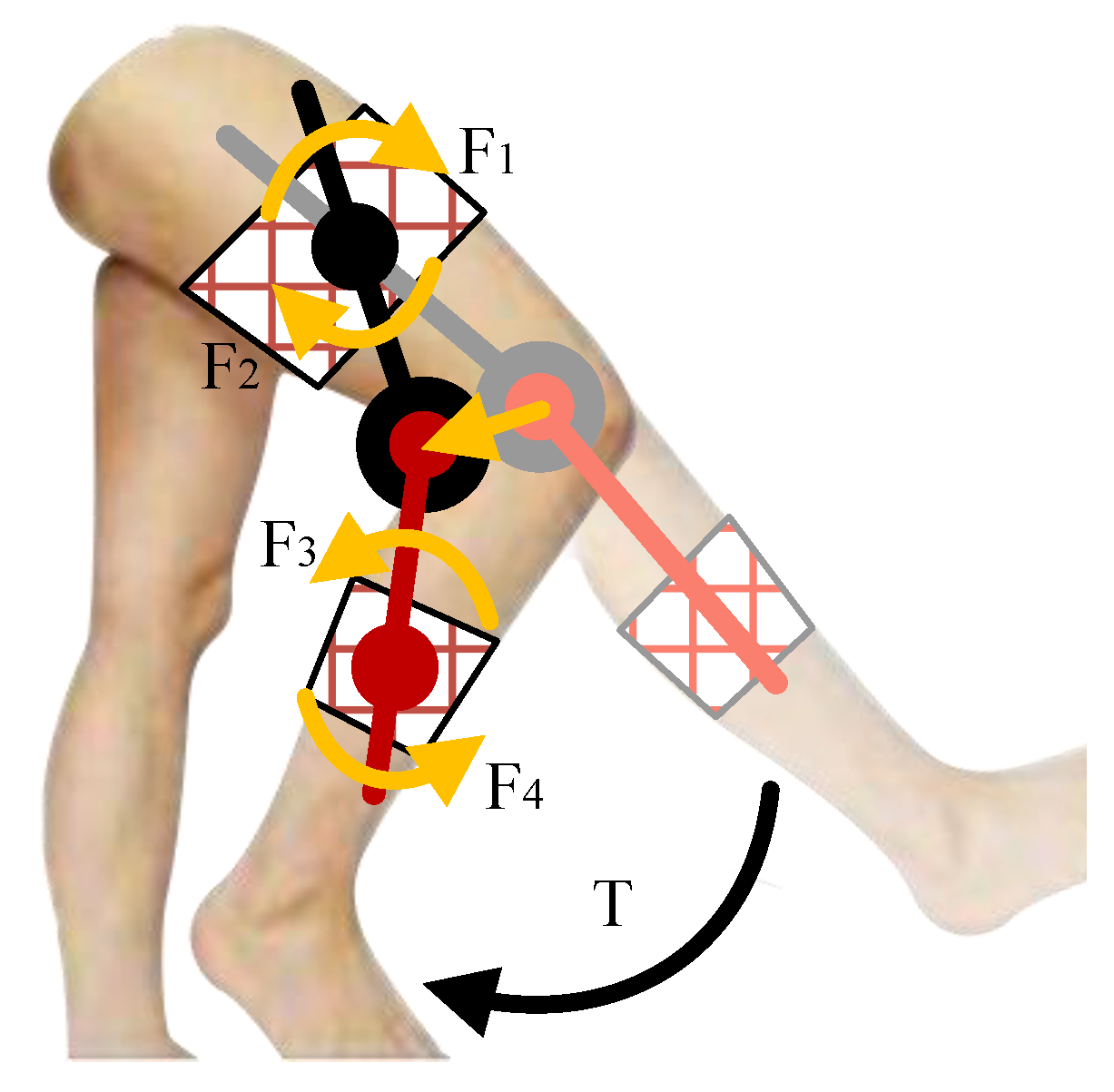
3.3. Man–Machine System Dynamics Model
4. Human Machine Coupling Simulation Experiment
4.1. Establishment of a Three-Dimensional Human Body Model
4.2. Applying Constraints
4.3. Applying Drive and Contact
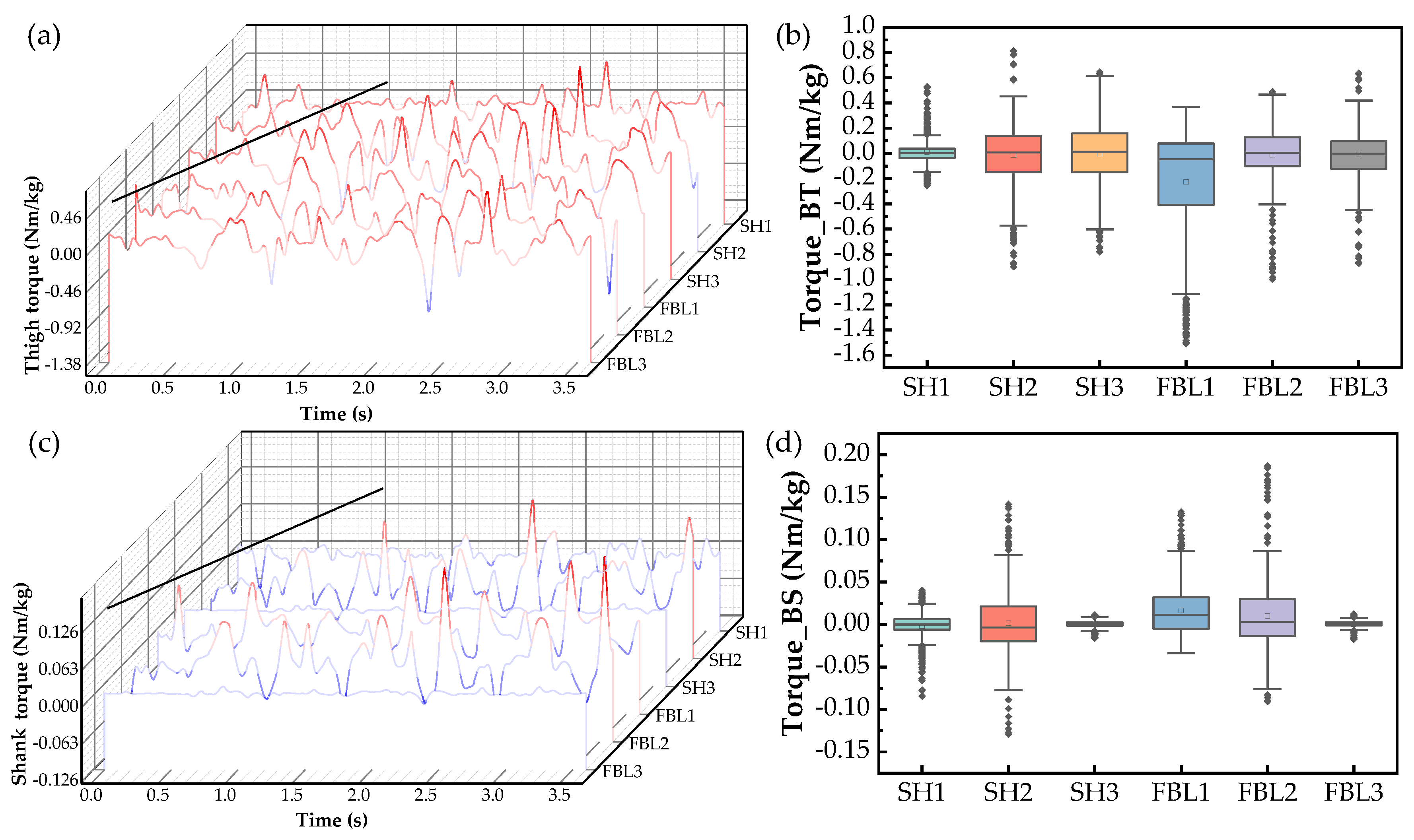
4.4. Simulation and Post-Processing Analysis
4.5. Wearing Exoskeleton Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weber, W.; Weber, E. Mechanik Der Menschlichen Gehwerkzeuge; Göttingen, Germany, 1836; pp. 1–496. [Google Scholar]
- Bresler, B.; Frankel, J. The Forces and Moments in the Leg During Level Walking. J. Appl. Mech. 1950, 72, 27–36. [Google Scholar] [CrossRef]
- Hao, Z.X.; Leng, H.J.; Qu, C.Y.; Wan, C. Biomechanics of the Bone and the Joint. J. Solid Mech. 2010, 31, 603–612. [Google Scholar]
- Fuge, A.; Herron, C.; Beiter, B.; Kalita, B.; Leonessa, A. Design, development, and analysis of the lower body of next-generation 3D-printed humanoid research platform: PANDORA. Robotica 2023, 41, 2177–2206. [Google Scholar] [CrossRef]
- Sun, Z.; Li, Y.; Zi, B.; Chen, B. Design, Modeling, and Evaluation of a Hybrid Driven Knee-Ankle Orthosis With Shape Memory Alloy Actuators. ASME J. Mech. Des. 2023, 145, 063301. [Google Scholar] [CrossRef]
- Sulzer, J.S.; Roiz, R.A.; Peshkin, M.A.; Patton, J.L. A Highly Back Drivable, Lightweight Knee Actuator for Investigating Gait in Stroke. IEEE Trans. Robot. 2009, 25, 539–548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaichaowarat, R.; Kinugawa, J.; Kosuge, K. Unpowered Knee Exoskeleton Reduces Quadriceps Activity during Cycling. Engineering 2018, 4, 471–478. [Google Scholar] [CrossRef]
- Wang, D.; Lee, K.M.; Guo, J.J.; Yang, C.J. Adaptive Knee Joint Exoskeleton Based on Biological Geometries. IEEE/ASME Trans. Mechatron. 2014, 19, 1268–1278. [Google Scholar] [CrossRef]
- Douglas, A.D.; Mohamed, R.M.; Richard, D.K.; William, H. In Vivo Determination of Normal and Anterior Cruciate Ligament-Deficient Knee Kinematics. J. Biomech. 2005, 38, 241–253. [Google Scholar]
- Van Den Bogert, A.J.; Reinschmidt, C.; Lundberg, A. Helical Axes of Skeletal Knee Joint Motion during Running. J. Biomech. 2008, 41, 1632–1638. [Google Scholar] [CrossRef] [Green Version]
- Wolf, A. Instantaneous Screws of Weight-Bearing Knee: What Can the Screws Tell Us About the Knee Motion. J. Biomech. Eng. 2014, 136, 433–440. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.T.; Yang, L.F.; Wang, Y.X.; Long, Q. The New Simulated Knee Prosthesis of Discontinuity Instantaneous Center Curve. Mach. Des. Manuf. 2014, 281, 183–185. [Google Scholar]
- Choi, B.; Lee, Y.; Kim, J.; Lee, M.; Lee, J.; Roh, S.G.; Choi, H.; Kim, Y.-J.; Choi, J.-Y. A Self-aligning Knee Joint for Walking Assistance Devices. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; IEEE: Orlando, FL, USA, 2016; pp. 2222–2227. [Google Scholar]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Li, H.; Jiao, Y. Assistive devices of human knee joint: A review. Robot. Auton. Syst. 2020, 125, 103394. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, P.; Peng, J.; Qiao, X.; Zhu, F.; Zhong, J. Design and Optimization of Lower Limb Rehabilitation Exoskeleton with a Multiaxial Knee Joint. Biomimetics 2023, 8, 156. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.J.; Kim, G.T.; Kim, Y. Optimal Design of Multi-linked Knee Joint for Lower Limb Wearable Robot. Int. J. Precis. Eng. Manuf. 2023, 24, 967–976. [Google Scholar] [CrossRef]
- Shuai, Y.M.; Xu, Z.; Li, S.Z.; Liu, X.H. Selection and Optimization of Multicentre Extremity Knee-Mechanism. J. Jianghan Pet. Inst. 2001, 23, 86–88. [Google Scholar]
- Bertomeu, J.M.; Lois, J.M.; Guillem, R.B.; Pozo, A.P.; Lacuesta, J.; Mollà, C.G.; Luna, P.; Vera, P.; Jaime, P. Development of a Hinge Compatible with the Kinematics of the Knee Joint. Prosthet. Orthot. Int. 2007, 31, 371–383. [Google Scholar] [CrossRef] [Green Version]
- Walker, P.S.; Kurosawa, H.; Rovick, J.S.; Zimmerman, R.A. External Knee Joint Design Based on Normal Motion. J. Rehabil. Res. Dev. 1985, 22, 9–22. [Google Scholar] [CrossRef]
- Jarrasse, N.; Morel, G. Connecting a Human Limb to an Exoskeleton. IEEE Trans. Robot. 2013, 28, 697–709. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.L. Design and Kinematic Analysis of Double Motor Driven Hexapod Upright Walking Mechanism. J. Mech. Transm. 2012, 42, 106–111. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. Closure to “Discussions of ‘Approximate Synthesis of Spatial Linkages’”. ASME J. Appl. Mech. 1960, 27, 757–758. [Google Scholar]
- Bagheri, M.; Naseradinmousavi, P. Analytical and Experimental Nonzero-Sum Differential Game-Based Control of A 7-Dof Robotic Manipulator. J. Vib. Control 2022, 28, 707–718. [Google Scholar] [CrossRef]
- Li, X.; Sun, H.X.; Liao, L.J.; Song, J. Simulation and Comparison Research of Lagrange and Kane Dynamics Modeling for the 4-Dof Modular Industrial Robot. In Proceedings of the 5th International Conference on Advanced Design and Manufacturing Engineering, Shenzhen, China, 19–20 September 2015; Atlantis Press: Shenzhen, China, 2015. [Google Scholar]
- Gao, M.; Wang, Z.; Pang, Z.; Sun, J.; Li, J.; Li, S.; Zhang, H. Electrically Driven Lower Limb Exoskeleton Rehabilitation Robot Based on Anthropomorphic Design. Machines 2022, 10, 266. [Google Scholar] [CrossRef]
- Yu, C.; Yao, K.; Zong, Y.; Ye, J.; Chen, J. Rigid-Body Guidance Synthesis of Noncircular Gear-Five-Bar Mechanisms and Its Application in a Knee Joint Rehabilitation Device. Machines 2022, 10, 1110. [Google Scholar] [CrossRef]
- Shafiei, M.; Behzadipour, S. Adding Backlash to the Connection Elements can Improve the Performance of a Robotic Exoskeleton. Mech. Mach. Theory 2020, 152, 103937. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.M.; Xuan, B.K.; Zhang, Y.C. Motion Analysis and Simulation of Lower Limb based on ADAMS. J. Syst. Simul. 2017, 29, 988–995. [Google Scholar]
- Li, X.H.; Hao, W.Y.; Xiao, X.F.; Wu, C.L. Simulation and Validation of Human Model in Landings Based on ADAMS. LifeMoD. Zhejiang Sport Sci. 2015, 37, 114–116. [Google Scholar]






| Knee Flexion Angle/° | Knee Flexion Angle/° | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 70 | 14 | 129 |
| 10 | 31 | 47 | 80 | 12 | 130 |
| 20 | 31 | 87 | 90 | 11 | 131 |
| 30 | 26 | 107 | 100 | 9 | 132 |
| 40 | 21 | 118 | 110 | 7 | 132 |
| 50 | 18 | 124 | 120 | 5 | 133 |
| 60 | 16 | 127 | 130 | 2 | 133 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Value | 34.131 | 34.126 | 49.626 | 46.667 | 0.175 | 0.523 |
| 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | ||
| 3 | 0 | 0 |
| Body Segment | Coefficient | Mass (kg) | Center of Mass (mm) | |||
|---|---|---|---|---|---|---|
| Neck | 2.9540 | 69.400 | 27,149.40 | 25,082.10 | 18,641.00 | |
| 0.0400 | 0.510 | −115.80 | −177.30 | −105.00 | ||
| 0.0001 | 0.013 | 7.22 | 11.54 | 3.82 | ||
| Trunk | −5.0010 | −66.650 | −234,173.20 | −143,387.90 | −51,335.70 | |
| 0.1110 | −0.330 | 1181.00 | 772.60 | 1702.40 | ||
| 0.0050 | 1.121 | 165.88 | 97.55 | 33.95 | ||
| Upper arm | −0.3230 | 15.150 | −18,962.40 | −18,962.40 | −195.30 | |
| 0.0300 | 0.160 | 165.60 | 165.60 | 3.40 | ||
| 0.0001 | 0.080 | 12.23 | 12.23 | 0.92 | ||
| Forearm | −0.2770 | 12.940 | −8113.50 | −7438.30 | −627.90 | |
| 0.0160 | 0.450 | 42.90 | 41.30 | 21.40 | ||
| 0.0001 | 0.054 | 5.04 | 4.64 | 0.05 | ||
| Hand | −0.4240 | 71.620 | / | / | / | |
| 0.0030 | 0.340 | / | / | / | ||
| 0.0004 | 0.013 | / | / | / | ||
| Thigh | −0.0930 | −122.520 | −370,537.70 | −366,488.90 | 6527.00 | |
| 0.1520 | −0.310 | 428.40 | 554.90 | 716.50 | ||
| −0.0004 | 0.235 | 286.21 | 280.78 | −14.61 | ||
| Shank | −0.8340 | 23.470 | −30,104.40 | −29,916.40 | −1777.60 | |
| 0.0610 | 0.500 | 299.00 | 293.00 | 79.20 | ||
| −0.0002 | 0.095 | 20.12 | 20.09 | −0.33 | ||
| Foot | −0.715 | 35.130 | / | / | / | |
| 0.0060 | −0.020 | / | / | / | ||
| 0.0007 | 0.003 | / | / | / |
| Body Segment | Size (mm) | Mass (kg) | Center of Mass (mm) | |||
|---|---|---|---|---|---|---|
| Neck | 29.487 | 6.134 | 131.05 | 31,460.40 | 32,556.60 | 17,642.00 |
| Trunk | 48.197 | 32.100 | 1057.19 | 565,312.3 | 458,110 | 301,949.50 |
| Upper arm | 33.153 | 2.107 | 171.15 | 15,471.60 | 16,171.10 | 1715.70 |
| Forearm | 25.018 | 1.103 | 143.89 | 4176.00 | 4011.20 | 1067.10 |
| Hand | 15.715 | 0.521 | 120.52 | / | / | / |
| Thigh | 44.100 | 10.587 | 277.23 | 176,770.30 | 180,532.60 | 33,966.50 |
| Shank | 51.300 | 3.381 | 231.97 | 28,536.60 | 28,220.60 | 3568.40 |
| Foot | 7.270 | 0.995 | 39.03 | / | / | / |
| Parameter | Variable | Value |
|---|---|---|
| Stiffness (N/mm) | 100 | |
| Force index | 1.5 | |
| Damping (N·s/mm) | 1.0 | |
| Penetration depth (mm) | 0.0 | |
| Static friction coefficient | 0.3 | |
| Dynamic friction coefficient | 0.3 |
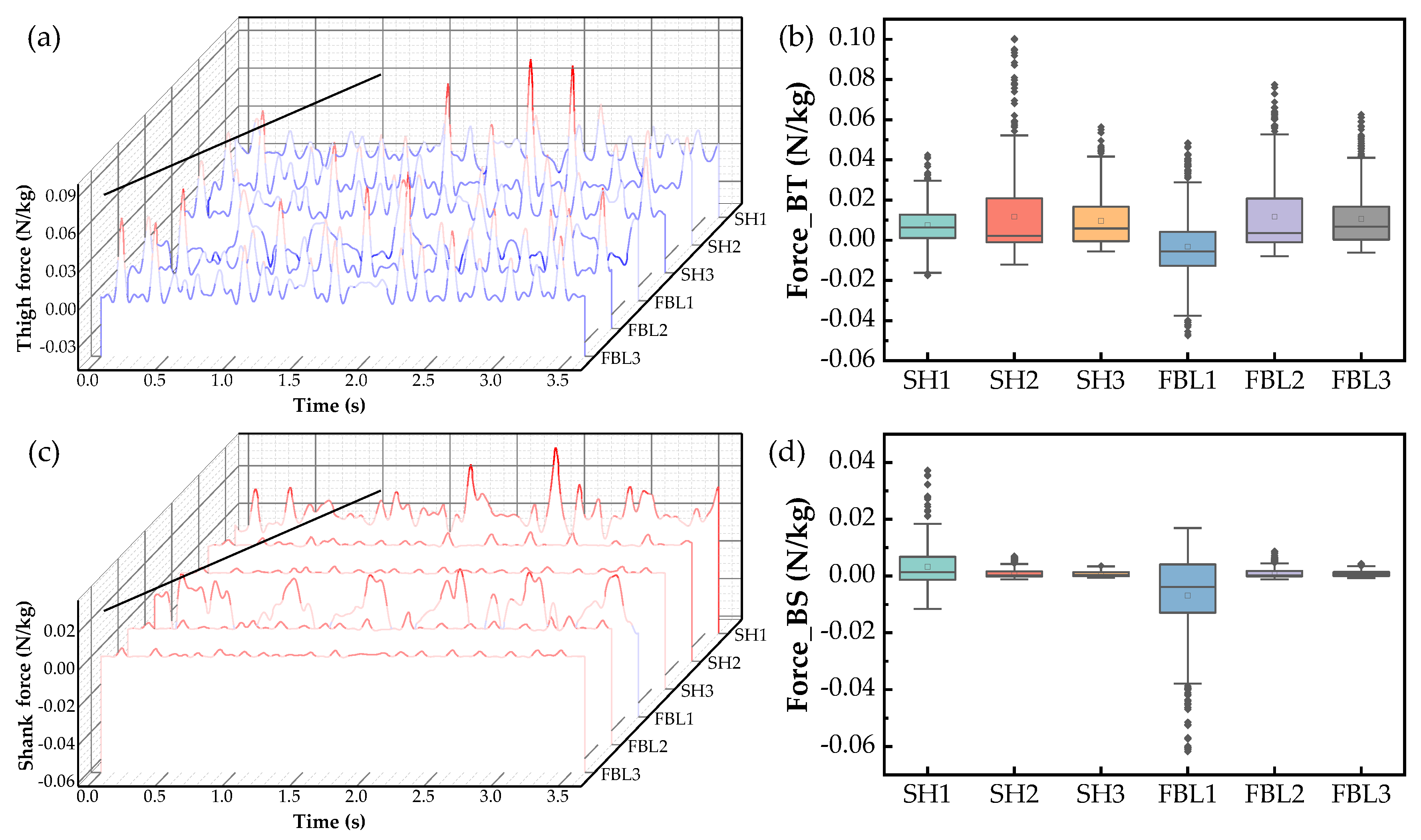
| Parameter | Group 1 | Group 2 | |||||
|---|---|---|---|---|---|---|---|
| SH1 | SH2 | SH3 | FBL1 | FBL2 | FBL3 | ||
| Torque_BT (Nm/kg) | Mean (10−4) | 115.4 | −139.6 | −15.1 | −2256.2 | −100.3 | −95.4 |
| Median (10−4) | 20.6 | 67.3 | 150.3 | −466.9 | 45.5 | −14.5 | |
| (10−2) | 168.1 | 345.1 | 297.2 | 242.0 | 322.1 | 287.2 | |
| (10−3) | 73.9 | 289.1 | 308.6 | 486.3 | 227.8 | 218.8 | |
| Torque_BS (Nm/kg) | Mean (10−4) | −16.7 | 16.8 | 5.0 | 165.8 | 101.2 | 5.4 |
| Median (10−4) | 1.2 | −34.7 | 3.6 | 115.3 | 30.8 | 3.0 | |
| (10−2) | 27.6 | 54.3 | 9.0 | 26.3 | 57.0 | 7.3 | |
| (10−3) | 12.3 | 41.1 | 4.0 | 37.1 | 43.2 | 3.7 | |
| Force_BT (N/kg) | Mean (10−4) | 74.5 | 116.8 | 96.0 | −32.8 | 117.5 | 105.4 |
| Median (10−4) | 64.1 | 22.1 | 58.6 | −55.9 | 35.8 | 66.5 | |
| (10−2) | 12.5 | 42.6 | 20.5 | 16.7 | 26.0 | 21.3 | |
| (10−3) | 11.7 | 21.9 | 17.1 | 16.9 | 21.8 | 16.4 | |
| Force_BS (N/kg) | Mean (10−4) | 32.3 | 9.4 | 7.5 | −68.9 | 10.1 | 8.5 |
| Median (10−4) | 13.8 | 1.9 | 4.1 | −38.0 | 2.6 | 5.8 | |
| (10−2) | 12.7 | 3.7 | 1.2 | 12.7 | 2.8 | 1.4 | |
| (10−3) | 5.5 | 1.8 | 1.4 | 17.0 | 1.9 | 1.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Wang, X.; Xue, Y.; Yin, R.; Yang, J. A Study of Knee Exoskeleton Configuration Based on Lower Limb Motion Characteristics Analysis. Machines 2023, 11, 709. https://doi.org/10.3390/machines11070709
Tang X, Wang X, Xue Y, Yin R, Yang J. A Study of Knee Exoskeleton Configuration Based on Lower Limb Motion Characteristics Analysis. Machines. 2023; 11(7):709. https://doi.org/10.3390/machines11070709
Chicago/Turabian StyleTang, Xinyao, Xupeng Wang, Yanmin Xue, Rong Yin, and Jiayin Yang. 2023. "A Study of Knee Exoskeleton Configuration Based on Lower Limb Motion Characteristics Analysis" Machines 11, no. 7: 709. https://doi.org/10.3390/machines11070709
APA StyleTang, X., Wang, X., Xue, Y., Yin, R., & Yang, J. (2023). A Study of Knee Exoskeleton Configuration Based on Lower Limb Motion Characteristics Analysis. Machines, 11(7), 709. https://doi.org/10.3390/machines11070709





