Monitoring Built-Up Edge, Chipping, Thermal Cracking, and Plastic Deformation of Milling Cutter Inserts through Spindle Vibration Signals
Abstract
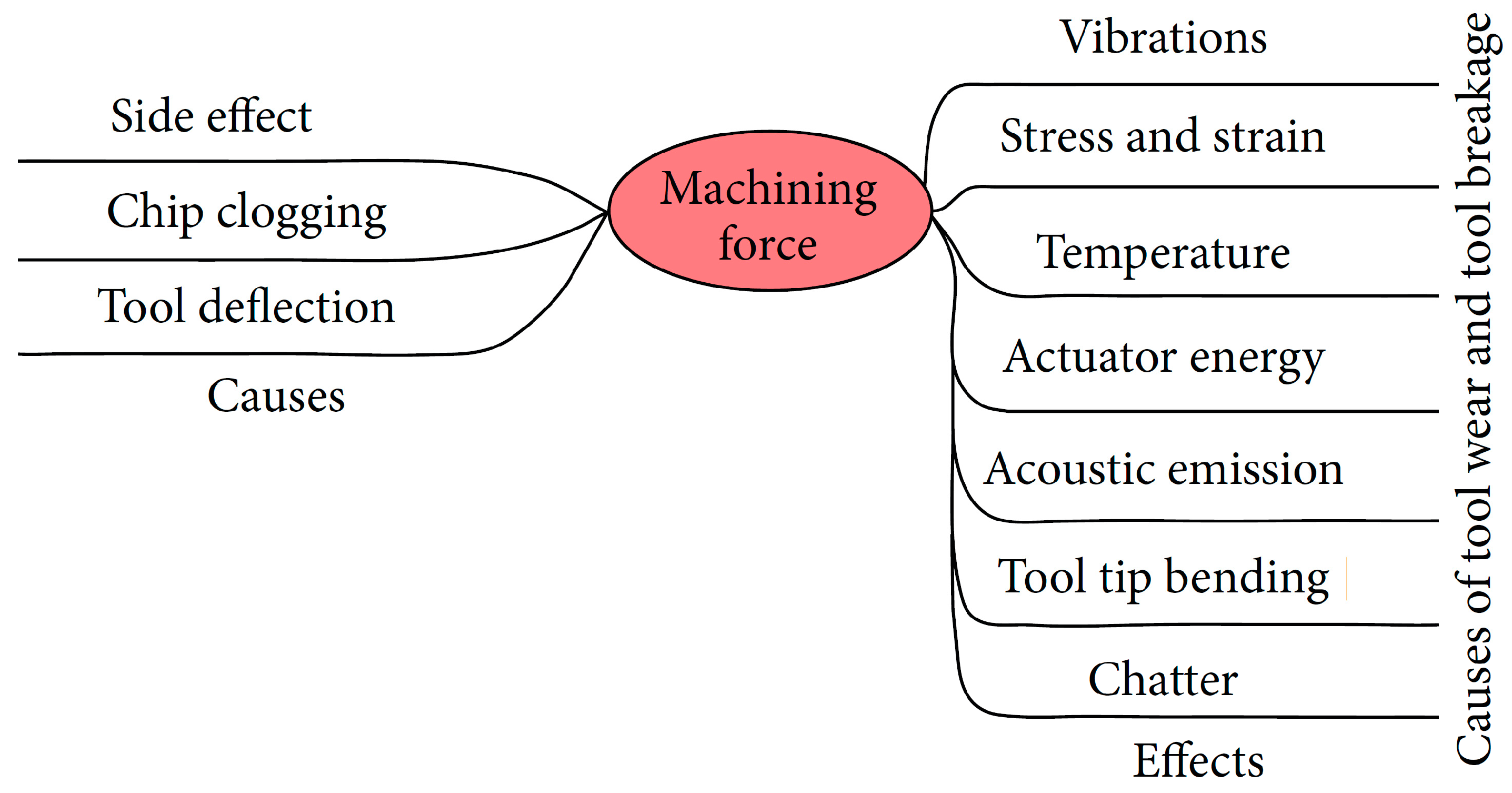
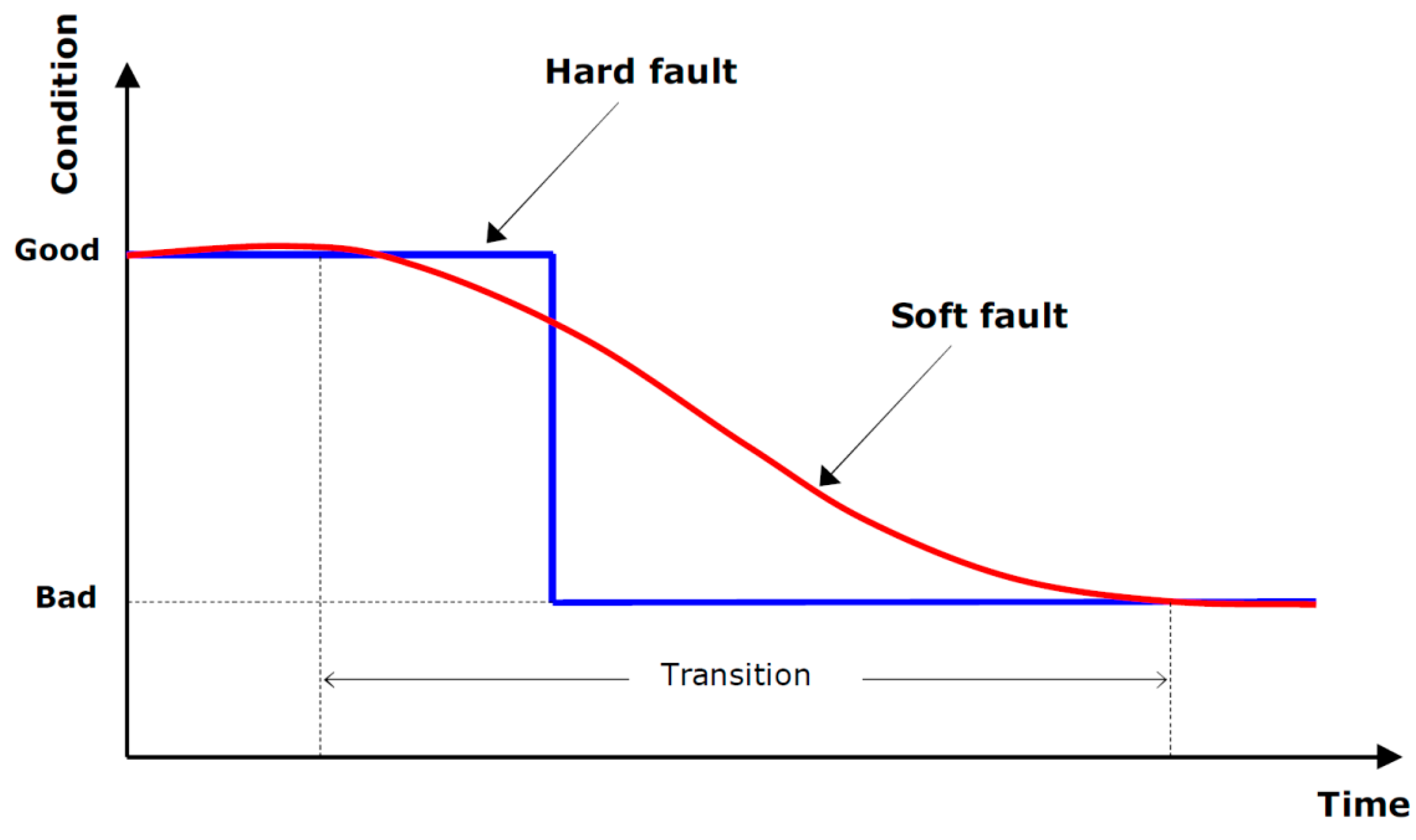
:1. Introduction
| Type of Signal Acquired for Tool Condition Monitoring | Authors (Year), [Ref.] | ||||
|---|---|---|---|---|---|
| Sound | AE | Motor Current | Vibration | Cutting Force | |
| - | - | - | √ | √ | Ross et al. (2023) [22] |
| - | - | - | √ | √ | Laghari et al. (2023) [23] |
| - | √ | - | - | - | Ahmed et al. (2023) [24] |
| - | - | - | √ | √ | Natarajan et al. (2023) [25] |
| - | - | - | - | √ | Mohanraj et al. (2022) [26] |
| - | - | √ | - | - | Ou (2021) [27] |
| - | - | - | √ | - | Mohanraj et al. (2021) [28] |
| - | - | - | √ | √ | Yao et al. (2021) [29] |
| √ | - | √ | - | Shrivastava and Singh (2021) [30] | |
| √ | √ | √ | √ | √ | Kuntoglu et al. (2021) [31] |
| - | - | √ | - | Xu et al. (2021) [32] | |
| - | - | √ | √ | Finkeldey et al. (2020) [33] | |
| - | √ | - | - | Bobyr et al. (2020) [34] | |
| - | - | √ | √ | M. Postel et al. (2020) [35] | |
| - | - | - | √ | - | Hesser and Markert (2019) [36] |
| - | - | √ | - | Herwan et al. (2019) [37] | |
| √ | - | √ | √ | √ | Cuka and Kim (2017) [38] |
| √ | √ | - | √ | √ | Harris et al. (2016) [39] |
| - | - | - | √ | √ | Sevilla et al. (2015) [40] |
| - | - | - | - | √ | Wang et al. (2014) [41] |
| - | - | - | √ | - | Hsieh, Lu and Chiou (2012) [42] |
| - | - | - | √ | - | Xu and Hualing (2009) [43] |
| - | - | - | √ | - | Zhang and Chen (2008) [44] |
| - | - | - | √ | - | Yesilyurt and Ozturk (2006) [45] |
2. Tool Faults Considered
- Built-up edge: Built-up edge is produced due to the adhesion of workpiece material pressure welded to the tooltip as a consequence of sufficient temperature, high pressure, and chemical affinity at the tool–work interface [74]. In due course, the built-up edge breaks down and takes cutting-edge pieces, leading to rapid flank wear and chipping. Built-up edges appear as shiny portions built on the cutting tool’s flank face, leading to cutting-edge chipping and smaller craters or pits on the tool’s rake face [75]. This mode of failure typically occurs while machining stainless steels, superalloys, and non-ferrous materials with lower cutting feeds and speeds. Its prevention requires increased feed rate and speed, selection of a sharper insert with a smoother rake face, and application of coolants at an improved concentration [76].
- Chipping: Chipping occurs due to two main reasons; one is in-built cracks within the material, and the other is the unstable mechanical behavior of the material. Additionally, excessive machining vibrations also lead to cutting-edge chipping. Moreover, rigid inclusions on the surface of the work and intermittent cutting results in localized stress concentrations forming cracks and, ultimately, causing chipping [77]. The appearance of chipping is smaller bits generated due to the breaking of the cutting edge. Machining of hardening work material usually leads to cutting-edge chipping because of abrasion. Its prevention requires controlled tool–workpiece interaction, minimized deflection, and the use of tough carbide grades. Also, reduced feed and higher cutting speed prevent chipping, particularly at cutter entry or exit [78].
- Thermal cracks: Thermal cracks mainly happen due to excessive thermal loadings affected by higher temperatures at the tool–workpiece interface) or changing temperature gradients. Due to these reasons, stress cracks develop approximately perpendicular to the tool edge, ultimately pulling out carbide pieces from the edge to the chip produced [79]. Thermal cracks are primarily witnessed in interrupted turning and milling. This also affects the cooling of tools and workpieces due to the intermittent flow of coolant, leading to thermal cracks. Its prevention requires the application of uninterrupted coolant flow, selecting tough carbide grades, reducing feed and speed, and using a tool with free-cutting geometry to reduce heat [80].
- Plastic deformation: A thermally overloaded tool–workpiece interface leads to plastic deformation. Extreme heating makes the work material soften and is followed by mechanical overloads; the pressure acting on the cutting edge deforms the tooltip and finally breaks down, or rapid flank wear occurs [81]. A deformed cutting edge is the typical appearance of plastic deformation in a tool. One should be cautious when differentiating plastic deformation from flank wear as they resemble one another. Due to their high strength, machining superalloys, strain-hardened surfaces, or hard steels cause plastic deformation. The main reason behind this is the generation of higher cutting temperatures due to high cutting speeds and feeds. Its prevention requires the application of uninterrupted coolant, reduced cutting speeds and feeds, use of a large nose radius, and choosing a wear-resistant and harder carbide grade [82].
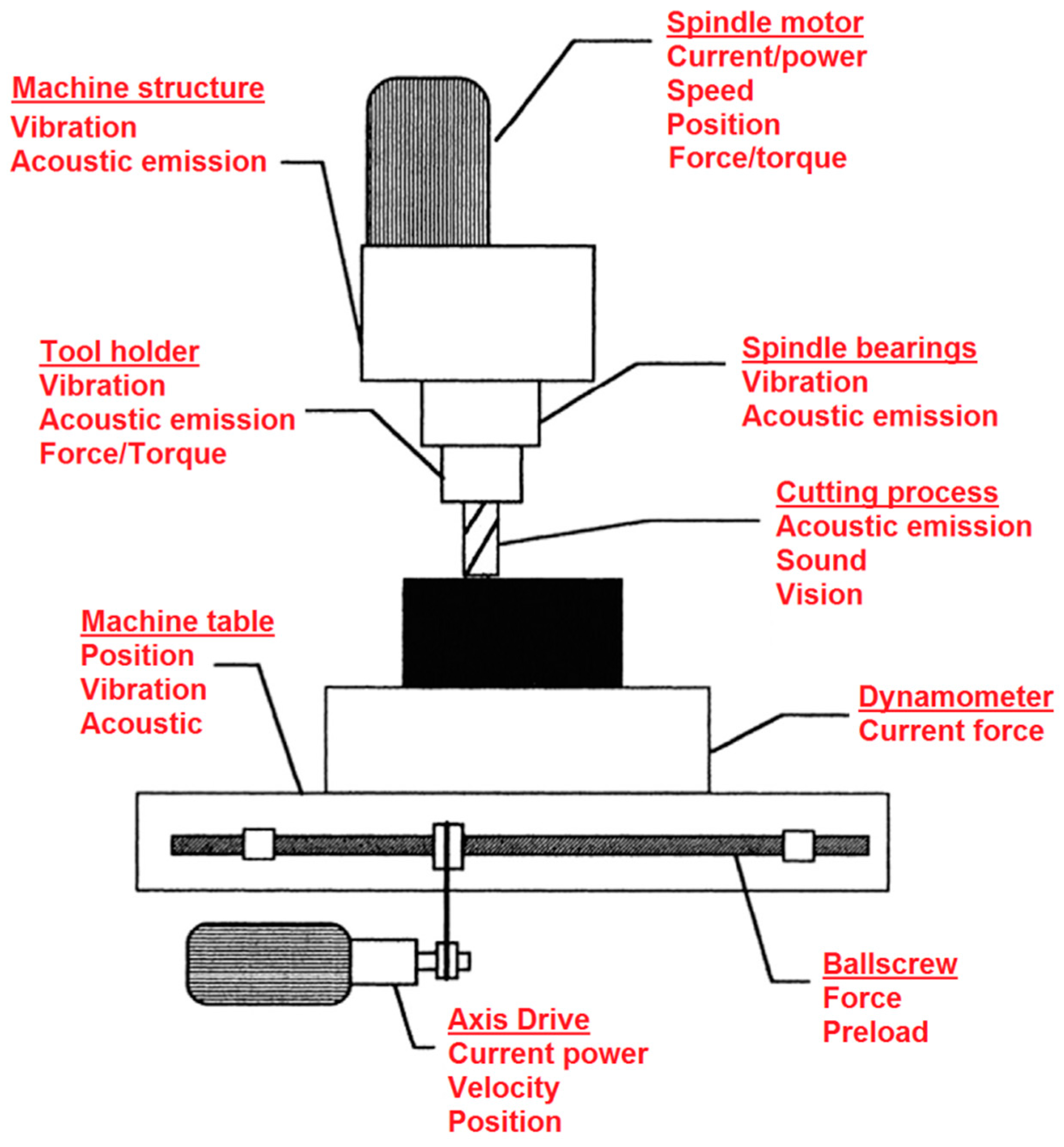
3. Experimentation for Signal Acquisition
4. Signal Representation and Transformation
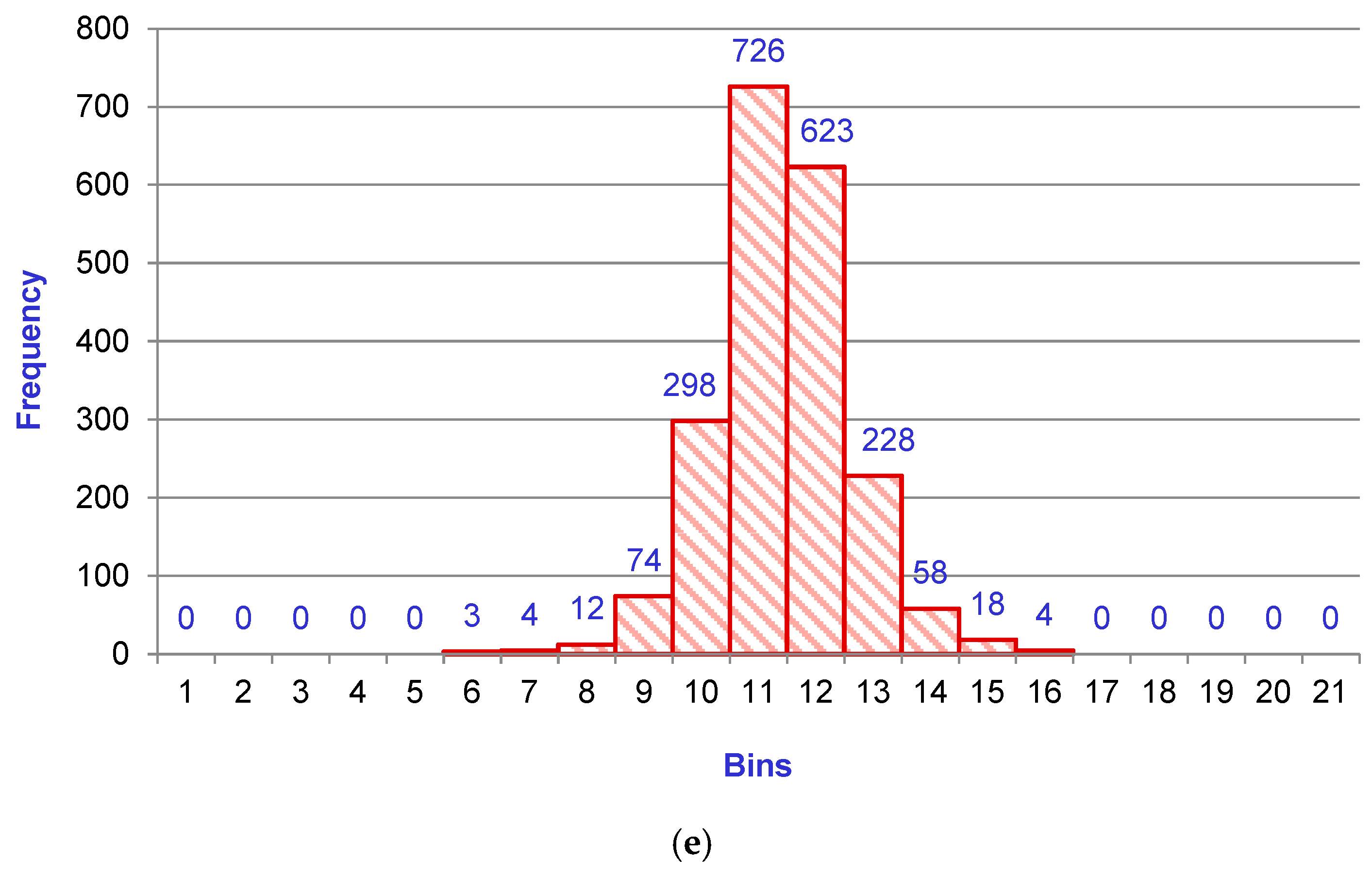
- Amplitude Distribution: A histogram built of vibration signals provides evidence of the amplitude distribution within the collected signal to exhibit its spread and range.
- Peak Values: The histogram highlights the peak frequency and its incidence corresponding to certain abnormalities or events in structures or machine elements being monitored.
- Statistical Parameters: Histograms also assist in the calculation of statistical features of the vibration signal, such as skewness, kurtosis, and standard deviation, to judge the variability, shape, and central tendency of the vibration signal distribution.
- Energy Distribution: Histograms built based on the energy contained inside specific frequency bands allow the analysis of the vibration signals’ frequency-dependent features.
- Signal Characteristics: Histograms also reveal modes or patterns of vibration. For instance, clusters or multi-peaks in a typical histogram designate the existence of different vibration components or modes.
- Trends and Changes: Rapid deviations or shifts in the normal histogram distribution indicate wear, faults, or other changes in structures or machine elements.
5. Feature Engineering
- Bin counts: Bin counts specify that the number of observations falls within every bin of the histogram indicating the frequency of specific incidence.
- Bin heights: Bin height specifies the altitude of every bin of the histogram representing the graphic view of the distribution’s shape through the relative frequency of observations within a particular bin.
- Bin widths: Bin widths specify the thickness of every bin of the histogram determining the range of observations considered by every bin which affects the granularity or smoothness of the distribution.
- Bin centers: Bin centers specify the central value or midpoint of every bin.
- Skewness: Skewness specifies the histogram’s asymmetry indicating whether the observations are skewed to the right or left from its mean value.
- Kurtosis: Kurtosis specifies a histogram’s flatness or peakedness quantifying deviation from a normal distribution.
- Mean: To judge the central tendency, the average value of the observations plays an important role.
- Standard Deviation: Standard deviation measures the spread or dispersion of the observations around their average value indicating the variability of the distribution.
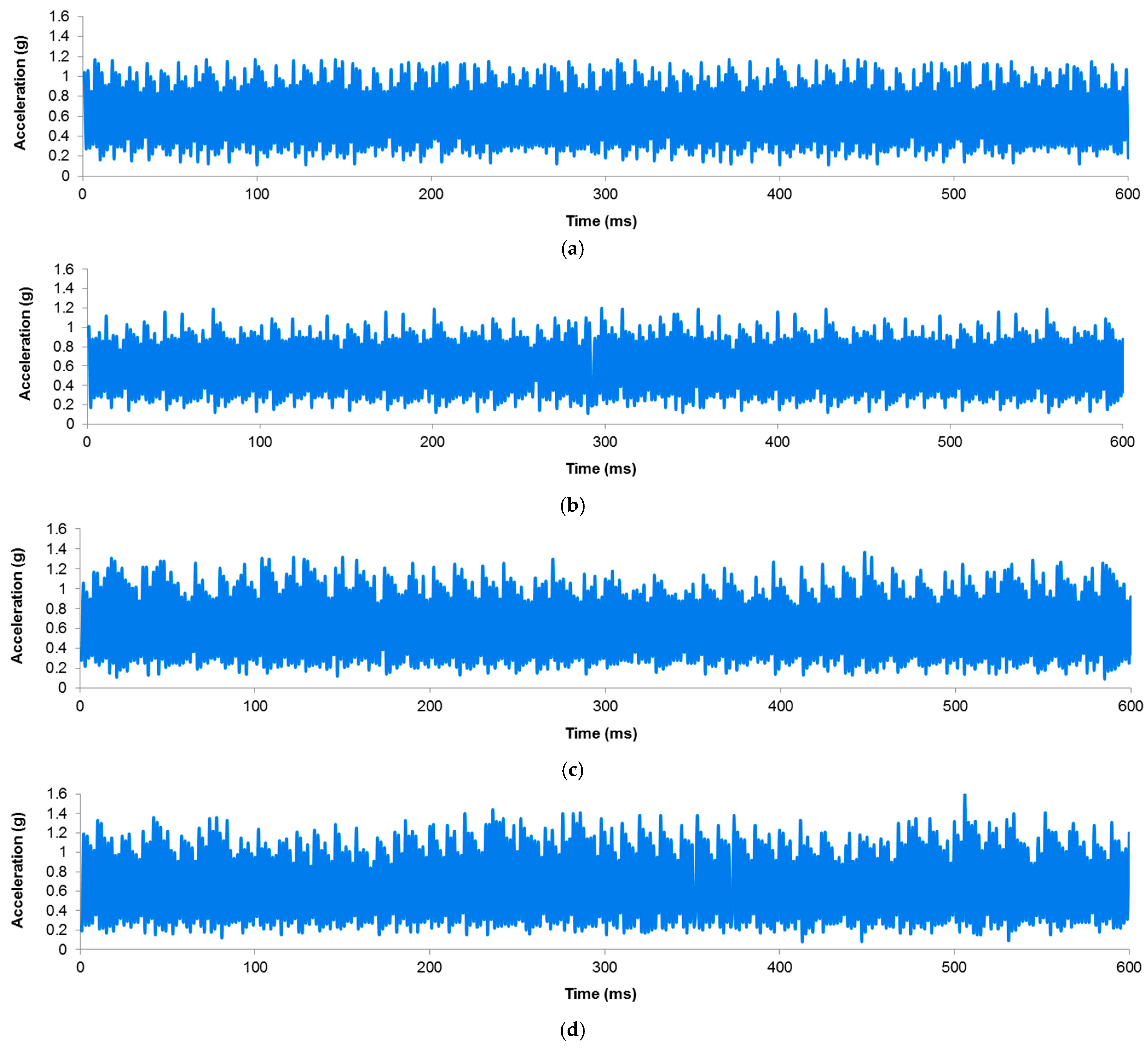
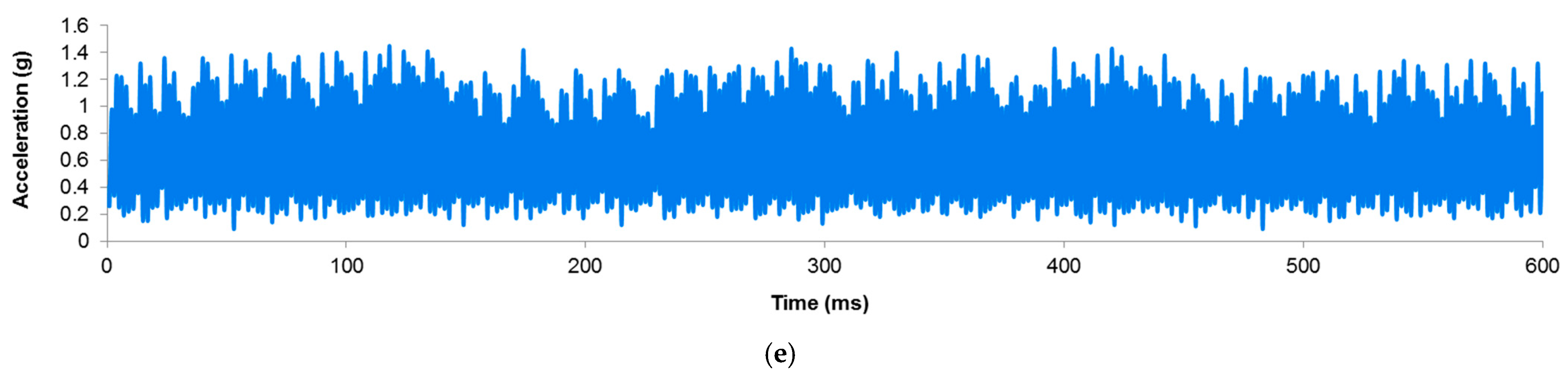
- Signal acquisition: During the face-milling operation, vibration data were collected using the accelerometer, which was located near the milling cutter spindle holder. The accelerometer measures the vibration in terms of acceleration experienced by the milling cutter for various tool conditions. The data were acquired continuously throughout the face-milling operation, considering the vibrations in the Z direction.
- Signal pre-processing: Before constructing histograms, the raw vibration signals were pre-processed using filters to remove noise or irrelevant information.
- Creation of bins: The vibration data were divided into smaller intervals or bins. Each bin signifies a specific range of acceleration. The number of bins and range for each bin were selected based on the data dynamics.
- Counting Observations: The number of acceleration observations that fell within that specific range was counted for each bin. The count represents the frequency of observations within each bin, reflecting how often the acceleration values occur in that range.
- Visualization: Finally, histograms were plotted where the X-axis shows the bins or ranges of acceleration values, and the Y-axis shows the corresponding frequency or count of observations in each bin.
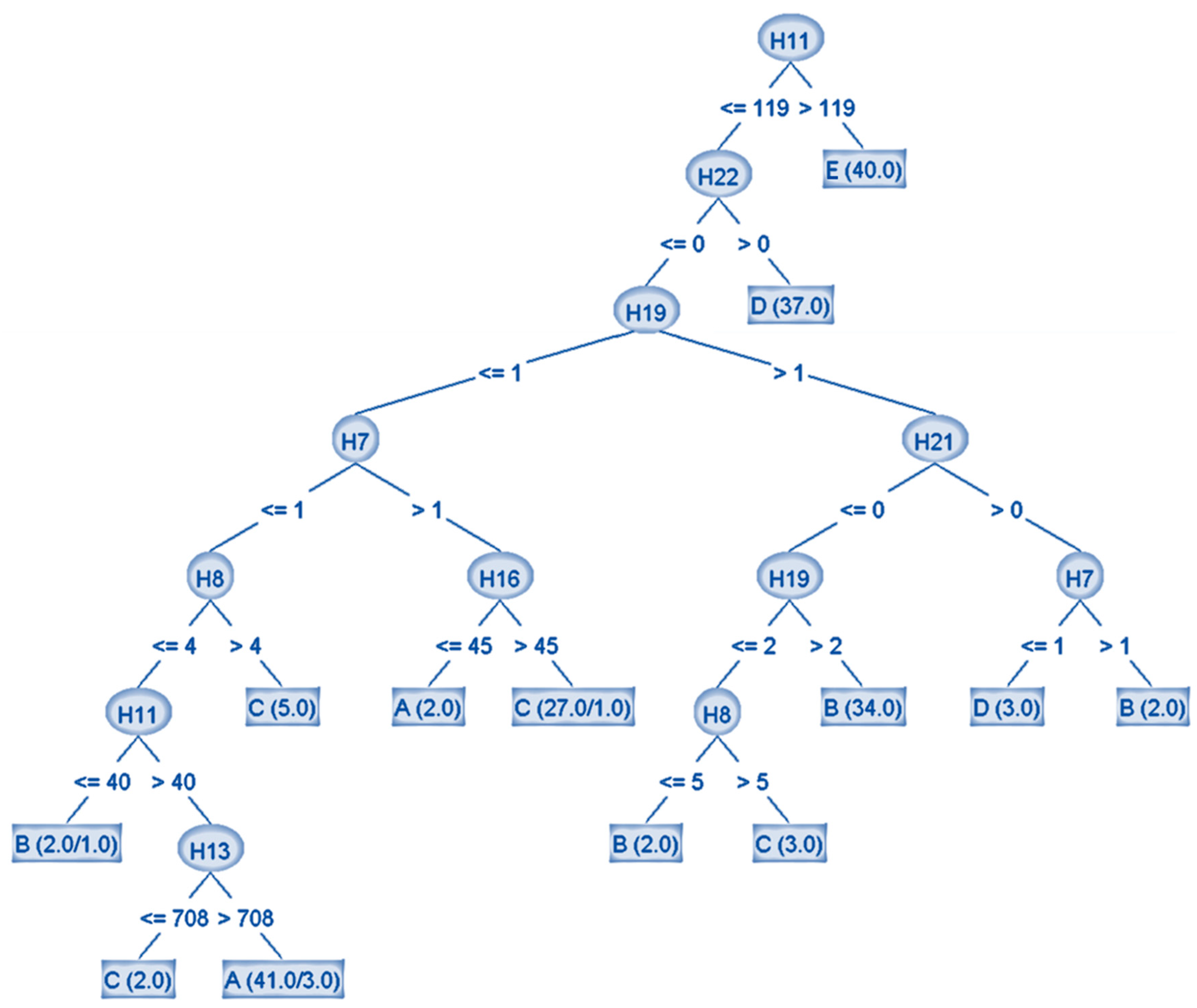
6. Design of Partial C4.5 Decision Tree
- Initialization of the rule set as empty.
- For each data split:
- Construct a rubric with the same class if the split is pure, indicating zero entropy (covers observations of only a single label).
- If the split is impure, indicating entropy more than zero (covers observations of multiple labels), choose the most frequent features-class combination and construct a rubric with the same features-class combination.
- Again, if the split of step “b” is not pure, choose the best attribute according to Gini or information gain criteria.
- Divide the split according to attribute value and make new splits for every value.
- Recurse on every new split until termination is fulfilled.
- Once all partitions have been processed, the algorithm outputs the rules.
- Random Forest (RF): The principle of random forest is an ensemble that constructs multiple decision trees and averages out their predictions. Multiple trees are built using training instances, and their feature subset is selected randomly. Oppositely, PART uses a single set of rubrics by recursive splitting attribute values of the data. RF aims to improve generalization and reduce variance by averaging predictions of multiple random trees, while PART emphasizes generating interpretable rubrics.
- Logistic Model Trees (LMT): The logistic regression is combined with decision trees to design LMTs. The induction of LMT is similar to conventional decision trees; however, while taking decisions at leaf nodes, it estimates class probabilities using logistic regression. LMT captures linear associations between attributes and corresponding labels. On the other hand, PART exhibits rubrics considering attributes and majority labels of every split without explicitly modeling logistic regression.
- Random Tree (RT): Random Tree is another variant of a decision tree that chooses attributes randomly at every partition point using a single tree in place of an ensemble-like random forest. Random Tree handles high-dimensional datasets and helps to reduce overfitting. However, unlike PART, it does not produce rubrics explicitly.
- Hoeffding Tree (HT): Hoeffding Tree handles datasets containing larger instances. A Hoeffding bound decides judgment about the tree structure, avoiding re-processing the complete dataset. They are incremental and adapt to concept drift. In contrast, PART does not address concept drift or streaming situations.
- Rotation Forest with Enhanced Performance Trees (REPT): REPT is an extension of Rotation Forest, an ensemble method based on extracting features using principal component analysis. REPT further augments the performance of the Rotation Forest with the help of Enhanced Performance Trees (EPTs) by splitting attributes through information gain. REPT efficiently trains complex associates between attributes and handles data with higher dimensions. PART, instead, aimed at creating a concise set of rubrics for interpretability instead of engaging feature extraction or ensemble methods.
7. Results and Discussion
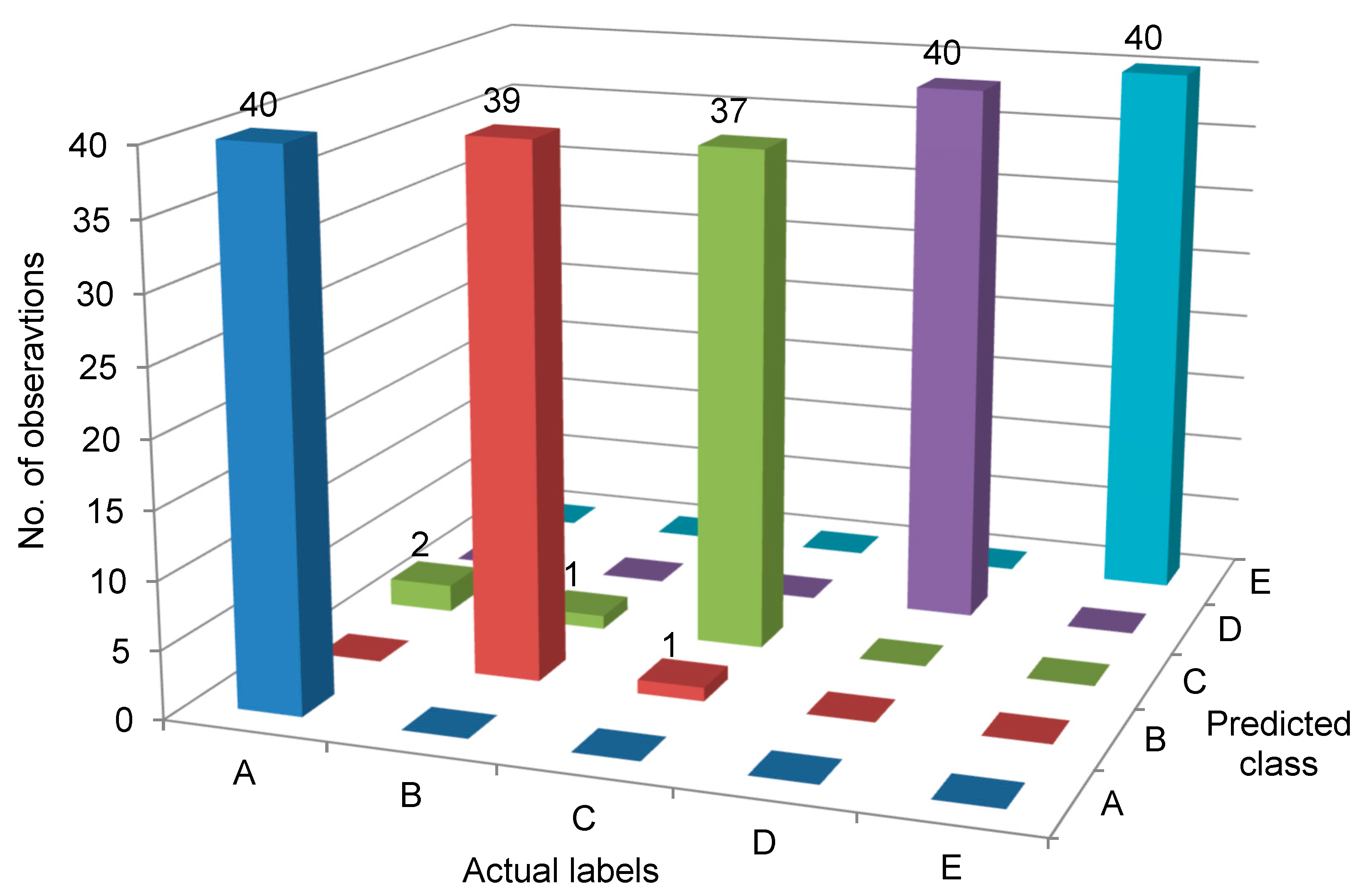
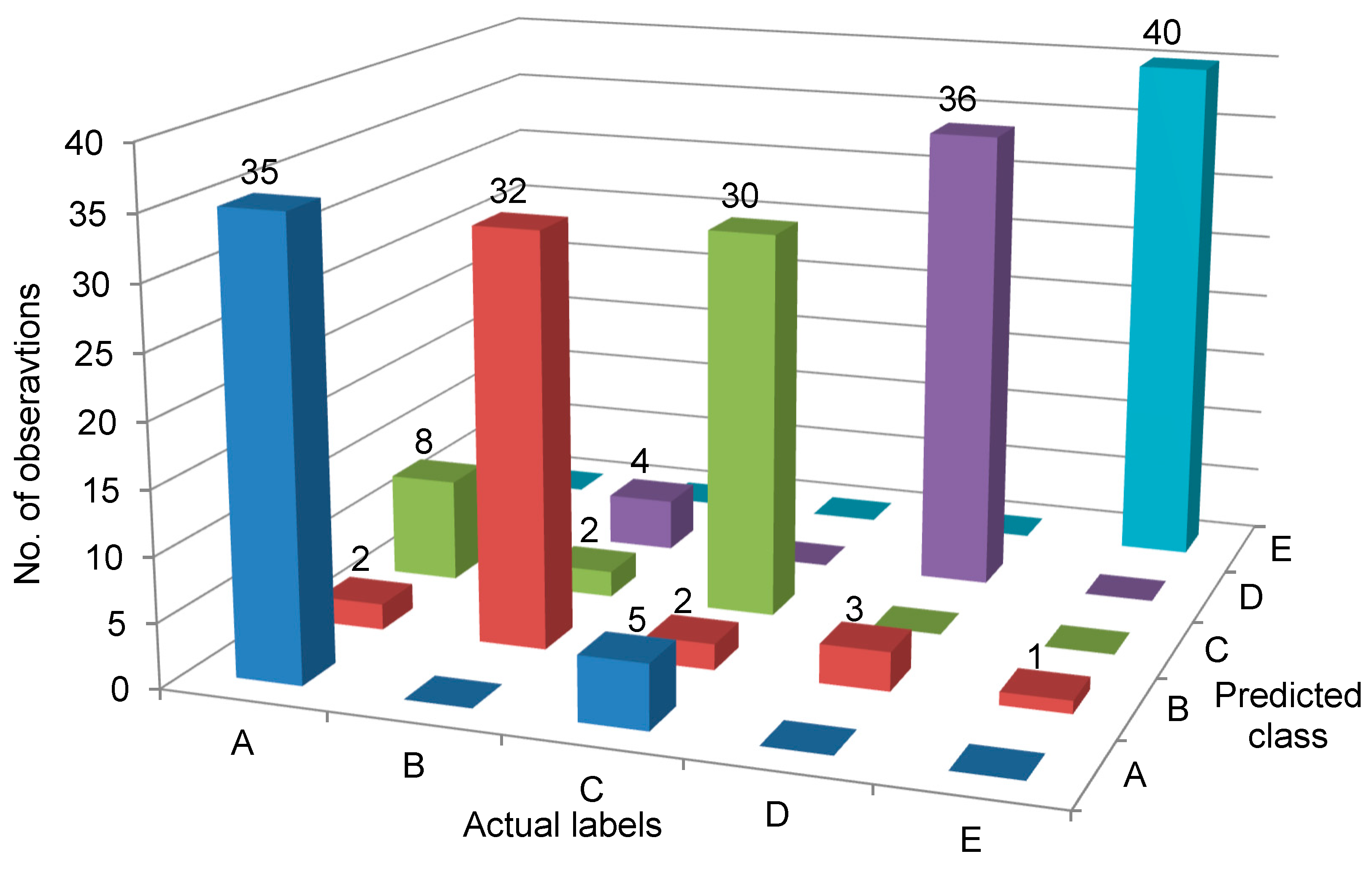
- Label A, i.e., built-up edge (actual) was correctly classified as A (predicted) 40 times and there is no misclassification.
- Label B, i.e., chipping (actual) was correctly classified as B (predicted) 39 times and misclassified as C once.
- Label C, i.e., thermal cracking (actual) was correctly classified as C (predicted) 37 times and misclassified as A twice and B once.
- Label D, i.e., plastic deformation (actual) was correctly classified as D (predicted) 40 times and there is no misclassification.
- Label F, i.e., normal (actual) was correctly classified as F (predicted) 40 times and there is no misclassification.
8. Conclusions
- The decision tree construction comprised 11 branches, 13 leaves, and a total size of 25. Eight features were chosen while training the tree, as there was a difference between the four faulty and normal tool labels, while the rejected ones showed similarity.
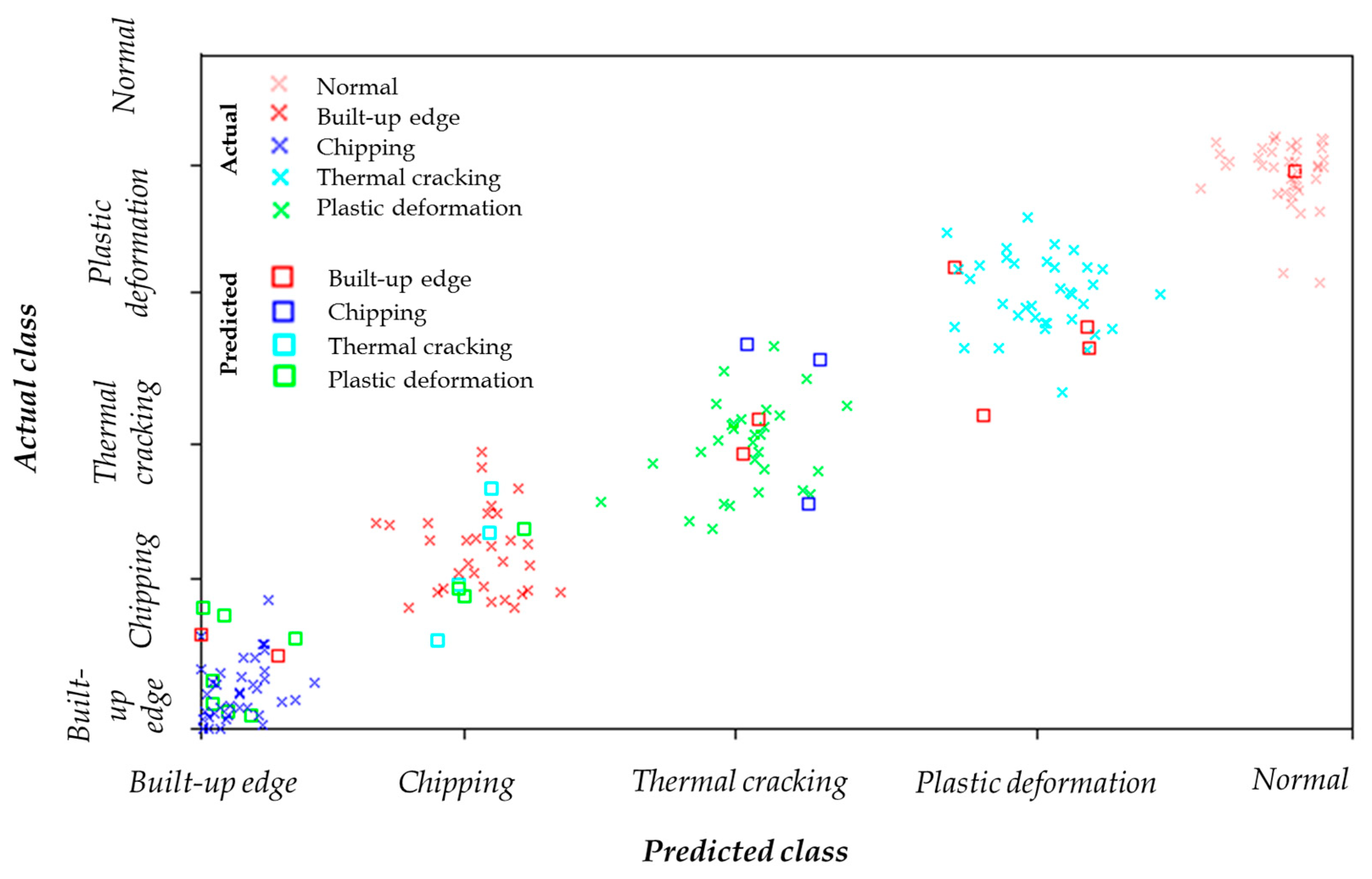
- The PART algorithm attained a desired accuracy of 98% when learning the rubrics on training data. It truly categorized labels A—Built-up edge, D—Plastic deformation, and F—normal tool without a single misclassification. However, the algorithm faced confusion segregating labels B—Chipping and C—Thermal cracking, following some misclassifications. Nonetheless, the overall misclassifications were negligible, signifying a robust model.
- The evaluation metrics further demonstrate the usefulness of the PART algorithm. A Kappa value showed higher agreement between the actual labels and corresponding predictions. The mean absolute and root mean squared error denoted the average prediction errors. The relative absolute and relative squared errors showed insights into the deviance between the actual labels and corresponding predictions.
- Detailed evaluation of the PART algorithm on the training data exhibited higher true positives, Matthews Correlation Coefficient, Recall, F-Measure, Precision, ROC Area, and PRC Area. These metrics specified correct identification and distinction of various tool conditions.
- The robustness of the PART classifier was compared in three scenarios; it executed best on the training data, followed by the k-folds cross-validation and the test data. The assessment metrics exhibited lower error and higher accuracy in all three scenarios, eliminating the potential concern of overfitting.
- In conclusion, the method demonstrated herein appears to be robust for categorizing tool labels based on the histogram features of the vibration dataset. However, it is vital to be careful while applying the model to unlabeled data, as the performance may differ from trained rubrics. The study highlighted the significance of vibration analysis and machine learning for condition monitoring, enabling time-to-time maintenance or replacing cutting tools, therefore improving productivity and efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, S.; Tlusty, J. An Overview of Modeling and Simulation of the Milling Process. J. Eng. Ind. 1991, 113, 169–175. [Google Scholar] [CrossRef]
- Binali, R.; Demirpolat, H.; Kuntoğlu, M.; Sağlam, H. Machinability investigations based on tool wear, surface roughness, cutting temperature, chip morphology and material removal rate during dry and MQL-assisted milling of Nimax mold steel. Lubricants 2023, 11, 101. [Google Scholar] [CrossRef]
- Tlusty, J. Machine Dynamics. In Handbook of High-Speed Machining Technology; Chapman and Hall Advanced Industrial Technology Series; King, R.I., Ed.; Springer: Boston, MA, USA, 1985. [Google Scholar] [CrossRef]
- Morelli, L.; Grossi, N.; Campatelli, G.; Scippa, A. Surface location error prediction in 2.5-axis peripheral milling considering tool dynamic stiffness variation. Precis. Eng. 2022, 76, 95–109. [Google Scholar] [CrossRef]
- Lazkano, X.; Aristimuño, P.X.; Aizpuru, O.; Arrazola, P.J. Roughness maps to determine the optimum process window parameters in face milling. Int. J. Mech. Sci. 2022, 221, 107191. [Google Scholar] [CrossRef]
- Usca, Ü.A.; Uzun, M.; Şap, S.; Kuntoğlu, M.; Giasin, K.; Pimenov, D.Y.; Wojciechowski, S. Tool wear, surface roughness, cutting temperature and chips morphology evaluation of Al/TiN coated carbide cutting tools in milling of Cu–B–CrC based ceramic matrix composites. J. Mater. Res. Technol. 2022, 16, 1243–1259. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Gupta, M.K.; Aslan, A.; Salur, E.; Garcia-Collado, A. Influence of tool hardness on tool wear, surface roughness and acoustic emissions during turning of AISI 1050. Surf. Topogr. Metrol. Prop. 2022, 10, 015016. [Google Scholar] [CrossRef]
- He, Z.; Shi, T.; Xuan, J. Milling tool wear prediction using multi-sensor feature fusion based on stacked sparse autoencoders. Measurement 2022, 190, 110719. [Google Scholar] [CrossRef]
- Shewale, M.S.; Mulik, S.S.; Deshmukh, S.P.; Patange, A.D.; Zambare, H.B.; Sundare, A.P. Novel machine health monitoring system. In Proceedings of the 2nd International Conference on Data Engineering and Communication Technology: ICDECT 2017; Springer: Singapore, 2019; pp. 461–468. [Google Scholar]
- Dhobale, N.; Mulik, S.; Jegadeeshwaran, R.; Patange, A. Supervision of milling tool inserts using conventional and artificial intelligence approach: A review. Sound Vib. 2021, 55, 87–116. [Google Scholar] [CrossRef]
- Binali, R.; Kuntoğlu, M.; Pimenov, D.Y.; Usca, Ü.A.; Gupta, M.K.; Korkmaz, M.E. Advance monitoring of hole machining operations via intelligent measurement systems: A critical review and future trends. Measurement 2022, 111757. [Google Scholar] [CrossRef]
- Gupta, M.K.; Niesłony, P.; Sarikaya, M.; Korkmaz, M.E.; Kuntoğlu, M.; Krolczyk, G.M.; Jamil, M. Tool wear patterns and their promoting mechanisms in hybrid cooling assisted machining of titanium Ti-3Al-2.5 V/grade 9 alloy. Tribol. Int. 2022, 174, 107773. [Google Scholar] [CrossRef]
- Kuntoglu, M. Machining induced tribological investigations in sustainable milling of Hardox 500 steel: A new approach of measurement science. Measurement 2022, 201, 111715. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Acar, O.; Gupta, M.K.; Sağlam, H.; Sarikaya, M.; Giasin, K.; Pimenov, D.Y. Parametric optimization for cutting forces and material removal rate in the turning of AISI 5140. Machines 2021, 9, 90. [Google Scholar] [CrossRef]
- Karali, P.; Pal, S.K.; Bhattacharyya, K. fuzzy radial basis function (FRBF) network based tool condition monitoring system using vibration signals. Mach. Sci. Technol. Int. J. 2010, 14, 280–300. [Google Scholar]
- Sugumaran, V.; Ramachandran, K.I. Effect of number of features on classification of roller bearing faults using SVM and PSVM. Expert Syst. Appl. 2011, 38, 4088–4096. [Google Scholar] [CrossRef]
- Elangovan, M.; Ramachandran, K.I.; Sugumaran, V. Studies on Bayes classifier for condition monitoring of single point carbide tipped tool based on statistical and histogram features. Expert Syst. Appl. 2010, 37, 2059–2065. [Google Scholar] [CrossRef]
- Elangovan, M.; Babu, D.S.; Sakthivel, N.R.; Ramachandran, K.I. Evaluation of expert system for condition monitoring of a single point cutting tool using principle component analysis and decision tree algorithm. Expert Syst. Appl. 2011, 38, 4450–4459. [Google Scholar] [CrossRef]
- Krishnakumar, P.; Rameshkumar, K.; Ramachandran, K.I. Tool Wear Condition Prediction Using Vibration Signals in High Speed Machining (HSM) of Titanium (Ti-6Al-4V) Alloy. In Proceedings of the Procedia Computer Science, 2nd International Symposium on Big Data and Cloud Computing; 2015; Volume 50, pp. 270–275. [Google Scholar]
- Fatima, S.; Mohanty, A.R.; Naikan, V.N.A. Multiple Fault Classification Using Support Vector Machine in a Machinery Fault Simulator. Vib. Eng. Technol. Mach. Mech. Mach. Sci. 2015, 23. [Google Scholar]
- Drouillet, C.; Karandikar, J.; Nath, C.; Journeaux, A.C.; El Mansori, M.; Kurfess, T. Tool life predictions in milling using spindle power with the neural network technique. J. Manuf. Process. 2016, 22, 161–168. [Google Scholar] [CrossRef]
- Ross, N.S.; Sheeba, P.T.; Shibi, C.S.; Gupta, M.K.; Korkmaz, M.E.; Sharma, V.S. A novel approach of tool condition monitoring in sustainable machining of Ni alloy with transfer learning models. J. Intell. Manuf. 2023, 1–19. [Google Scholar] [CrossRef]
- Laghari, R.A.; Mekid, S. Comprehensive Approach Toward IIoT Based Condition Monitoring of Machining Processes. Measurement 2023, 217, 113004. [Google Scholar] [CrossRef]
- Ahmed, M.; Kamal, K.; Ratlamwala TA, H.; Hussain, G.; Alqahtani, M.; Alkahtani, M.; Alzabidi, A. Tool Health Monitoring of a Milling Process Using Acoustic Emissions and a ResNet Deep Learning Model. Sensors 2023, 23, 3084. [Google Scholar] [CrossRef]
- Natarajan, S.; Thangamuthu, M.; Gnanasekaran, S.; Rakkiyannan, J. Digital Twin-Driven Tool Condition Monitoring for the Milling Process. Sensors 2023, 23, 5431. [Google Scholar] [CrossRef]
- Mohanraj, T.; Uddin, M.; Thangarasu, S.K. Review on sensor design for cutting force measurement. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 237, 455–466. [Google Scholar] [CrossRef]
- Ou, J.; Li, H.; Huang, G.; Zhou, Q. A Novel Order Analysis and Stacked Sparse Auto-Encoder Feature Learning Method for Milling Tool Wear Condition Monitoring. Sensors 2020, 20, 2878. [Google Scholar] [CrossRef]
- Mohanraj, T.; Jayanthi, Y.; Krishnan, H.; Nithin Aravind, R.S.; Yameni, R. Development of tool condition monitoring system in end milling process using wavelet features and Hoelder’s exponent with machine learning algorithms. Measurement 2021, 173, 108671. [Google Scholar] [CrossRef]
- Yao, Z.; Luo, M.; Mei, J.; Zhang, D. Position dependent vibration evaluation in milling of thin-walled part based on single-point monitoring. Measurement 2021, 171, 108810. [Google Scholar] [CrossRef]
- Shrivastava, Y.; Singh, B. Tool chatter prediction based on empirical mode decomposition and response surface methodology. Measurement 2021, 173, 108585. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Sağlam, H. Investigation of signal behaviors for sensor fusion with tool condition monitoring system in turning. Measurement 2021, 173, 108582. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J.; Zhong, B.; Ming, W.; Chen, M. Deep learning-based tool wear prediction and its application for machining process using multi-scale feature fusion and channel attention mechanism. Measurement 2021, 177, 109254. [Google Scholar] [CrossRef]
- Finkeldey, F.; Saadallah, A.; Wiederkehr, P.; Morik, K. Real-time prediction of process forces in milling operations using synchronized data fusion of simulation and sensor data. Eng. Appl. Artif. Intell. 2020, 94, 103753. [Google Scholar] [CrossRef]
- Bobyr, M.V.; Yakushev, A.S.; Dorodnykh, A.A. Fuzzy devices for cooling the cutting tool of the CNC machine implemented on FPGA. Measurement 2020, 152, 107378. [Google Scholar] [CrossRef]
- Postel, M.; Bugdayci, B.; Wegener, K. Ensemble transfer learning for refining stability predictions in milling using experimental stability states. Int. J. Adv. Manuf. Technol. 2020, 107, 4123–4139. [Google Scholar] [CrossRef]
- Hesser, D.F.; Markert, B. Tool wear monitoring of a retrofitted CNC milling machine using artificial neural networks. Manuf. Lett. 2019, 19, 1–4. [Google Scholar] [CrossRef]
- Herwan, J.; Kano, S.; Ryabov, O.; Sawada, H.; Kasashima, N.; Misaka, T. Retrofitting old CNC turning with an accelerometer at a remote location towards Industry 4.0. Manuf. Lett. 2019, 21, 56–59. [Google Scholar] [CrossRef]
- Cuka, B.; Kim, D. Fuzzy logic based tool condition monitoring for end-milling. Robot. Comput. -Integr. Manuf. 2017, 47, 22–36. [Google Scholar] [CrossRef]
- Harris, K.; Triantafyllopoulos, K.; Stillman, E.; Mcleay, T. A multivariate control chart for autocorrelated tool wear processes. Qual. Reliab. Eng. Int. 2016, 32, 2093–2106. [Google Scholar] [CrossRef] [Green Version]
- Sevilla, P.; Robles, J.; Jauregui, J.; Jimenez, D. FPGA-based reconfigurable system for tool condition monitoring in high-speed machining process. Measurement 2015, 64, 81–88. [Google Scholar] [CrossRef]
- Wang, G.; Liu, C.; Cui, Y.; Feng, X. Tool wear monitoring based on co-integration modeling of multisensory information. Int. J. Comput. Integr. Manuf. 2014, 27, 479–487. [Google Scholar] [CrossRef]
- Hsieh, W.; Lu, M.; Chiou, S. Application of back-propagation neural network for spindle vibration-based tool wear monitoring in micro-milling. Int. J. Adv. Manuf. Technol. 2012, 61, 53–61. [Google Scholar] [CrossRef]
- Xu, C.; Hualing, C. Fractal analysis of vibration signals for monitoring the condition of milling tool. Wear 2009, 223, 909–918. [Google Scholar]
- Zhang, J.Z.; Chen, J.C. The development of an in-process surface roughness adaptive control system in end milling operations. Int. J. Adv. Manuf. Technol. 2007, 31, 877–887. [Google Scholar] [CrossRef]
- Yesilyurt, I.; Ozturk, H. Tool condition monitoring in milling using vibration analysis. Int. J. Prod. Res. 2006, 45, 1013–1028. [Google Scholar] [CrossRef]
- Rubeo, M.A.; Schmitz, T.L. Global stability predictions for flexible workpiece milling using time-domain simulation. J. Manuf. Syst. 2016, 40, 8–14. [Google Scholar] [CrossRef]
- Liu, R.; Kothuru, A.; Zhang, S. Calibration-based tool condition monitoring for repetitive machining operations. J. Manuf. Syst. 2020, 54, 285–293. [Google Scholar] [CrossRef]
- Samin, R.; Nuawi, M.Z.; Haris, S.M.; Ghani, J.A. Statistical investigation for cutting force and surface roughness of S45C steel in turning processes by I-kazTM method. J. Phys. Conf. Ser. IOP Publ. 2020, 1489, 012028. [Google Scholar] [CrossRef] [Green Version]
- Aralikatti, S.S.; Ravikumar, K.N. Comparative Study on Tool Fault Diagnosis Methods Using Vibration Signals and Cutting Force Signals by Machine Learning Technique. Struct. Durab. Health Monit. 2020, 14, 128–145. [Google Scholar] [CrossRef]
- Alamelu, M.T.M.; Jegadeeshwaran, R. Vibration based brake health monitoring using wavelet features: A machine learning approach. J. Vib. Control 2019, 17, 1–17. [Google Scholar]
- Rakkiyannan, J.; Jakkamputi, L.; Thangamuthu, M.; Patange, A.D.; Gnanasekaran, S. Development of Online Tool Wear-Out Detection System Using Silver–Polyester Thick Film Sensor for Low-Duty Cycle Machining Operations. Sensors 2022, 22, 8200. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Song, Q.; Peng, Y.; Jin, P.; Liu, Z.; Liu, Z. A milling tool wear monitoring method with sensing generalization capability. J. Manuf. Syst. 2023, 68, 25–41. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, H.; Li, S.; Lin, X. Online tool wear monitoring by super-resolution based machine vision. Comput. Ind. 2023, 144, 103782. [Google Scholar] [CrossRef]
- Song, G.; Zhang, J.; Zhu, K.; Ge, Y.; Yu, L.; Fu, Z. Tool wear monitoring based on multi-kernel Gaussian process regression and Stacked Multilayer Denoising AutoEncoders. Mech. Syst. Signal Process. 2023, 186, 109851. [Google Scholar] [CrossRef]
- Huang, C.R.; Lu, M.C. Investigation of Cutting Path Effect on Spindle Vibration and AE Signal Features for Tool Wear Monitoring in Micro Milling. Appl. Sci. 2023, 13, 1107. [Google Scholar] [CrossRef]
- Ma, J.; Luo, D.; Liao, X.; Zhang, Z.; Huang, Y.; Lu, J. Tool wear mechanism and prediction in milling TC18 titanium alloy using deep learning. Measurement 2021, 173, 108554. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, B.; Guo, K.; Liu, J.; Sun, J.; Song, G.; Zhu, S.; Sun, C.; Jiang, Z. Vibration singularity analysis for milling tool condition monitoring. Int. J. Mech. Sci. 2020, 166, 105254. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Papacharalampopoulos, A.; Vasiliadis, E.; Chryssolouris, G. Tool wear predictability estimation in milling based on multi-sensorial data. Int. J. Adv. Manuf. Technol. 2016, 82, 509–521. [Google Scholar] [CrossRef] [Green Version]
- Karandikar, J.; Mcleay, T.; Turner, S.; Schmitz, T. Tool wear monitoring using naïve bayes classifiers. Int. J. Adv. Manuf. Technol. 2015, 77, 1613–1626. [Google Scholar] [CrossRef]
- Ren, Q.; Balazinski, M.; Baron, L.; Jemielniak, K.; Botez, R.; Achiche, S. Type-2 fuzzy tool condition monitoring system based on acoustic emission in micromilling. Inf. Sci. 2014, 255, 121–134. [Google Scholar] [CrossRef]
- Ammouri, A.; Hamade, R. Current rise criterion: A process independent method for tool-condition monitoring and prognostics. Int. J. Adv. Manuf. Technol. 2014, 72, 509–519. [Google Scholar] [CrossRef]
- Bajaj, N.S.; Patange, A.D.; Jegadeeshwaran, R.; Kulkarni, K.A.; Ghatpande, R.S.; Kapadnis, A.M. A Bayesian optimized discriminant analysis model for condition monitoring of face milling cutter using vibration datasets. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2022, 5, 021002. [Google Scholar] [CrossRef]
- Yen, C.; Lu, M.; Chen, J. Applying the self-organization feature map (som) algorithm to AE-based tool wear monitoring in micro-cutting. Mech. Syst. Signal Process. 2013, 34, 353–366. [Google Scholar] [CrossRef]
- Lu, M.; Wan, B. Study of high-frequency sound signals for tool wear monitoring in micro milling. Int. J. Adv. Manuf. Technol. 2013, 66, 1785–1792. [Google Scholar]
- Wang, M.; Wang, J. CHMM for tool condition monitoring and remaining useful life prediction. Int. J. Adv. Manuf. Technol. 2012, 59, 463–471. [Google Scholar] [CrossRef]
- Girardin, F.; Remond, D.; Rigal, J. Tool wear detection in milling—An original approach with a non-dedicated sensor. Mech. Syst. Signal Process. 2010, 24, 1907–1920. [Google Scholar] [CrossRef]
- Hsueh, Y.; Yang, C. Tool breakage diagnosis in face milling by support vector machine. J. Mater. Process. Technol. 2009, 209, 145–152. [Google Scholar] [CrossRef]
- Shao, H.; Wang, H.; Zhao, X. A cutting power model for tool wear monitoring in milling. Int. J. Mach. Tools Manuf. 2004, 44, 1503–1509. [Google Scholar] [CrossRef]
- Chen, S.; Jen, Y. Data fusion neural network for tool condition monitoring in CNC milling machining. Int. J. Mach. Tools Manuf. 2000, 40, 381–400. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y.; Usca, Ü.A.; Salur, E.; Gupta, M.K.; Mikolajczyk, T.; Giasin, K.; Kapłonek, W.; Sharma, S. A review of indirect tool condition monitoring systems and decision-making methods in turning: Critical analysis and trends. Sensors 2020, 21, 108. [Google Scholar] [CrossRef]
- Serin, G.; Sener, B.; Ozbayoglu, A.M.; Unver, H.O. Review of tool condition monitoring in machining and opportunities for deep learning. Int. J. Adv. Manuf. Technol. 2020, 109, 953–974. [Google Scholar] [CrossRef]
- Deo, T.Y.; Patange, A.D.; Pardeshi, S.S.; Jegadeeshwaran, R.; Khairnar, A.N.; Khade, H.S. A white-box SVM framework and its swarm-based optimization for supervision of toothed milling cutter through characterization of spindle vibrations. arXiv 2021, arXiv:2112.08421. [Google Scholar]
- Kale, A.P.; Wahul, R.M.; Patange, A.D.; Soman, R.; Ostachowicz, W. Development of Deep Belief Network for Tool Faults Recognition. Sensors 2023, 23, 1872. [Google Scholar]
- Bajaj, N.S.; Patange, A.D.; Jegadeeshwaran, R.; Pardeshi, S.S.; Kulkarni, K.A.; Ghatpande, R.S. Application of metaheuristic optimization based support vector machine for milling cutter health monitoring. Intell. Syst. Appl. 2023, 18, 200196. [Google Scholar] [CrossRef]
- Kümmel, J.; Braun, D.; Gibmeier, J.; Schneider, J.; Greiner, C.; Schulze, V.; Wanner, A. Study on micro texturing of uncoated cemented carbide cutting tools for wear improvement and built-up edge stabilisation. J. Mater. Process. Technol. 2015, 215, 62–70. [Google Scholar] [CrossRef]
- Gupta, M.K.; Song, Q.; Liu, Z.; Sarikaya, M.; Jamil, M.; Mia, M.; Khanna, N.; Krolczyk, G.M. Experimental characterisation of the performance of hybrid cryo-lubrication assisted turning of Ti–6Al–4V alloy. Tribol. Int. 2021, 153, 106582. [Google Scholar] [CrossRef]
- Varghese, A.; Kulkarni, V.; Joshi, S.S. Modeling cutting edge degradation by chipping in micro-milling. Wear 2022, 488, 204141. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Wang, B. Effect of Cutting Parameters on Tool Chipping Mechanism and Tool Wear Multi-Patterns in Face Milling Inconel 718. Lubricants 2022, 10, 218. [Google Scholar] [CrossRef]
- Peng, R.; Tong, J.; Tang, X.; Chen, R.; Jiang, S. Crack propagation and wear estimation of ceramic tool in cutting inconel 718 based on discrete element method. Tribol. Int. 2020, 142, 105998. [Google Scholar] [CrossRef]
- Salur, E.; Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y. The effects of MQL and dry environments on tool wear, cutting temperature, and power consumption during end milling of AISI 1040 steel. Metals 2021, 11, 1674. [Google Scholar] [CrossRef]
- Zhuang, K.; Fu, C.; Weng, J.; Hu, C. Cutting edge microgeometries in metal cutting: A review. Int. J. Adv. Manuf. Technol. 2021, 116, 2045–2092. [Google Scholar] [CrossRef]
- Doan, D.Q.; Fang, T.H.; Chen, T.H. Machining mechanism and deformation behavior of high-entropy alloy under elliptical vibration cutting. Intermetallics 2021, 131, 107079. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Patange, A.D.; Jegadeeshwaran, R. A machine learning approach for vibration-based multipoint tool insert health prediction on vertical machining centre (VMC). Measurement 2021, 173, 108649. [Google Scholar] [CrossRef]
- Ibarguren, I.; Pérez, J.M.; Muguerza, J.; Gurrutxaga, I.; Arbelaitz, O. UnPART: PART without the ‘partial’condition of it. Inf. Sci. 2018, 465, 505–522. [Google Scholar] [CrossRef]
- Patange, A.D.; Jegadeeshwaran, R. Application of bayesian family classifiers for cutting tool inserts health monitoring on CNC milling. Int. J. Progn. Health Manag. 2020, 11. [Google Scholar] [CrossRef]
- Ibarguren, I.; Lasarguren, A.; Pérez, J.M.; Muguerza, J.; Gurrutxaga, I.; Arbelaitz, O. Bfpart: Best-first part. Inf. Sci. 2016, 367, 927–952. [Google Scholar] [CrossRef]
- Patil, S.S.; Pardeshi, S.S.; Patange, A.D. Health Monitoring of Milling Tool Inserts Using CNN Architectures Trained by Vibration Spectrograms. CMES-Comput. Model. Eng. Sci. 2023, 136, 177–199. [Google Scholar] [CrossRef]




| Workpiece/Milling Cutter | Tool Faults | Method of Monitoring | Authors (Year), [Ref.] |
|---|---|---|---|
| Mild steel/High-Speed Steels (HSS 18:4:1) | Initial, Severe flank wear | Silver–Polyester Thick Film Sensor | Jegadeeshwaran et al. (2022) [51] |
| Ti-6Al-4/End cutter and TiSiN coated | Initial, Severe flank wear | Stacked bidirectional GRU | Wang et al. (2023) [52] |
| - | Initial, Normal, Severe flank wear | Sparse decomposition and machine vision | Zhu et al. (2023) [53] |
| Normalized Steel (HB160 ~ 197)/Sandvik CNMG120408-PM | Flank wear | Stacked Multilayer Denoising AutoEncoders | Song et al. (2023) [54] |
| ISO TC 120 (SK2 steel)/- | Sharp, worn, average tooltip | Spindle Vibration and AE Signal Feature | Huang et al. (2023) [55] |
| Inconel 625/End mill | Fresh, working, and Dull tool | MLP, k-NN, Trees, SVM | Mohanraj et al. (2021) [28] |
| TC18 titanium alloy/Cutter with 2 milling inserts | Initial wear, Normal wear, Severe wear | CNN BIGRU CNN BILSTM | Ma et al. (2021) [56] |
| Titanium alloy TC21/End mill with 2 carbide flutes | - | Back calculation Acceleration | Yao et al. (2021) [29] |
| Low carbon steel (AISI 1018)/Tungsten carbide inserts | Lower to higher Chatter index | ANOVA | Shrivastav and Singh (2021) [30] |
| Med. carbon steel with high chromium/Carbide-coated | Break and flank wear (progressive) | Fuzzy logic | Kuntoglu et al. (2021) [31] |
| Ti–6Al–4V/Cemented carbide end mill | Wear states—initial, steady, and accelerated | TPIM and SVM | Zhou et al. (2020) [57] |
| Grey cast iron (FC250)/CBN insert | Usable and worn tool | ANN | Herwan et al. (2019) [37] |
| AISI 1045 steel/End mill with 2-flutes | small, medium, and accelerated wear | Fuzzy logic inference | Cuka et al. (2017) [38] |
| Titanium alloy Ti–6Al–4V/4-flutes | Broken and normal tool | PCA | Wang et al. (2016) [41] |
| CGI 450/5-flutes face milling | High, medium, and low wear | 3rd deg. regression | Stavropoulos et al. (2016) [58] |
| Aluminum alloy6061-T6/3-flutes face mill | Severe, partially worn, and healthy | Threshold | Sevilla et al. (2015) [40] |
| Steel/1-flute end mill 1018 | Severe, medium, Low wear | Naïve Bayes classifiers | Karandikar et al. (2015) [59] |
| Steel/ball end with 2-flute mill | Sharp tool and worn tool | Fuzzy logic system | Ren et al. (2014) [60] |
| AISI 1020 low carbon steel/HSS 4-flute end mill | Sharp, slightly worn workable, dull | Current rise index | Ammouri et al. (2014) [61] |
| Mild still | Flank, nose, notch, crater wear | Bayesian network | Bajaj et al. (2022) [62] |
| SK2 steel/Steel mill with 2-flutes | Sharp tool and worn tool | Learning vector quantification | Yen et al. (2013) [63] |
| SK2 steel/Micro-end mill | Sharp and worn | HMM | Lu et al. (2013) [64] |
| SK2 steel/Micro-end mill | Normal and broken teeth | BPNN | Hsieh et al. (2012) [42] |
| ASSAB718HH/End mill EGD 4440R | Worst, bad, and medium wear | CHMM | Wang M et al. (2012) [65] |
| Aluminum alloy6061-T6/3-flutes face mill | Tool normal and tool breakage | Arithmetic mean of asymmetry | Sevilla et al. (2011) [40] |
| TA6V Titanium alloy/4-flutes mill | Tool normal and tool breakage | Rotational freq. analysis | Girardin et al. (2010) [66] |
| 7075 aluminum/Face mill cutter | Normal and damage | SVM | Hsueh et al. (2009) [67] |
| Cast iron/Face mill with 1 and 5 flutes | Tool normal and tool breakage | Threshold | Shao H et al. (2004) [68] |
| Carbon steel S45C/TPMN322-CH550 | Break, severe, slight, mid wear | ANN | Chen et al. (2000) [69] |
| Performance Matrices | ||||||
|---|---|---|---|---|---|---|
| Matrices | Value | Percentage | ||||
| Correctly Classified Instances | 196 | 98% | ||||
| Incorrectly Classified Instances | 4 | 2% | ||||
| Kappa statistic | 0.975 | - | ||||
| Mean absolute error | 0.0148 | - | ||||
| Root mean squared error | 0.0861 | - | ||||
| Relative absolute error | - | 4.631% | ||||
| Root relative squared error | - | 21.5196% | ||||
| Detailed performance | ||||||
| Class | A | B | C | D | F | Weighted Avg. |
| TP Rate | 1.000 | 0.975 | 0.925 | 1.000 | 1.000 | 0.980 |
| FP Rate | 0.013 | 0.006 | 0.006 | 0.000 | 0.000 | 0.005 |
| Precision | 0.952 | 0.975 | 0.974 | 1.000 | 1.000 | 0.980 |
| Recall | 1.000 | 0.975 | 0.925 | 1.000 | 1.000 | 0.980 |
| F-Measure | 0.976 | 0.975 | 0.949 | 1.000 | 1.000 | 0.980 |
| MCC | 0.970 | 0.969 | 0.937 | 1.000 | 1.000 | 0.975 |
| ROC Area | 0.994 | 0.997 | 0.989 | 1.000 | 1.000 | 0.996 |
| PRC Area | 0.952 | 0.986 | 0.951 | 1.000 | 1.000 | 0.978 |
| Performance Matrices | ||||||
|---|---|---|---|---|---|---|
| Matrices | Value | Percentage | ||||
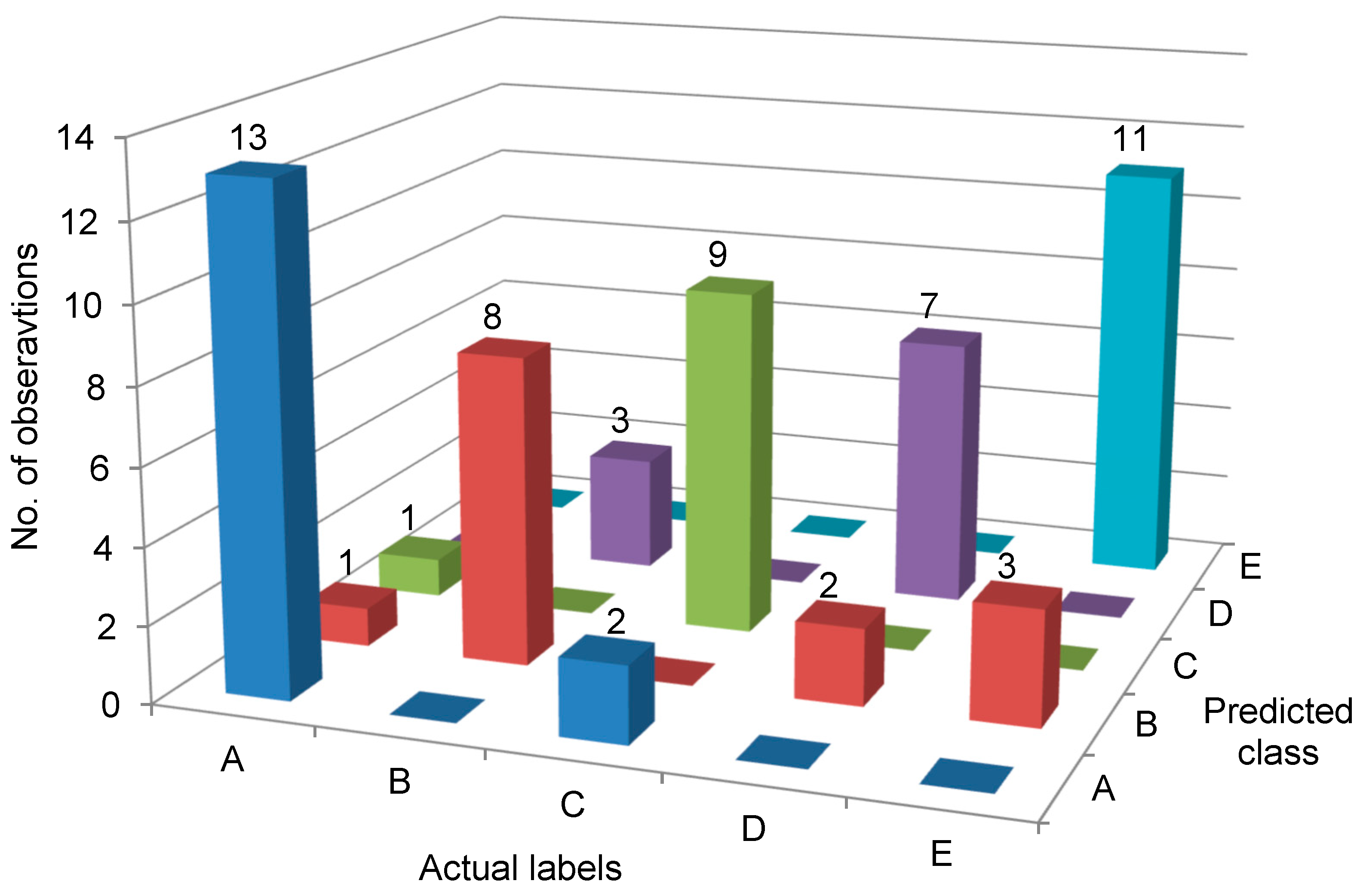
| Correctly Classified Instances | 173 | 86.5% | ||||
| Incorrectly Classified Instances | 27 | 13.5% | ||||
| Kappa statistic | 0.8313 | - | ||||
| Mean absolute error | 0.0575 | - | ||||
| Root mean squared error | 0.2267 | - | ||||
| Relative absolute error | - | 17.958% | ||||
| Root relative squared error | - | 56.6627% | ||||
| Detailed performance | ||||||
| Class | A | B | C | D | F | Weighted Avg. |
| TP Rate | 0.875 | 0.800 | 0.750 | 0.900 | 1.000 | 0.865 |
| FP Rate | 0.063 | 0.038 | 0.044 | 0.019 | 0.006 | 0.034 |
| Precision | 0.778 | 0.842 | 0.811 | 0.923 | 0.976 | 0.866 |
| Recall | 0.875 | 0.800 | 0.750 | 0.900 | 1.000 | 0.865 |
| F-Measure | 0.824 | 0.821 | 0.779 | 0.911 | 0.988 | 0.864 |
| MCC | 0.778 | 0.777 | 0.728 | 0.890 | 0.985 | 0.832 |
| ROC Area | 0.941 | 0.907 | 0.895 | 0.953 | 0.997 | 0.938 |
| PRC Area | 0.748 | 0.779 | 0.753 | 0.894 | 0.976 | 0.830 |
| Performance Matrices | ||||||
|---|---|---|---|---|---|---|
| Matrices | Value | Percentage | ||||
| Correctly Classified Instances | 48 | 80% | ||||
| Incorrectly Classified Instances | 12 | 20% | ||||
| Kappa statistic | 0.7489 | - | ||||
| Mean absolute error | 0.088 | - | ||||
| Root mean squared error | 0.2805 | - | ||||
| Relative absolute error | - | 27.4118% | ||||
| Root relative squared error | - | 69.8654% | ||||
| Detailed performance | ||||||
| Class | A | B | C | D | F | Weighted Avg. |
| TP Rate | 0.867 | 0.571 | 0.900 | 0.700 | 1.000 | 0.800 |
| FP Rate | 0.044 | 0.065 | 0.040 | 0.040 | 0.061 | 0.051 |
| Precision | 0.867 | 0.727 | 0.818 | 0.778 | 0.786 | 0.796 |
| Recall | 0.867 | 0.571 | 0.900 | 0.700 | 1.000 | 0.800 |
| F-Measure | 0.867 | 0.640 | 0.857 | 0.737 | 0.880 | 0.793 |
| MCC | 0.822 | 0.553 | 0.828 | 0.689 | 0.859 | 0.745 |
| ROC Area | 0.911 | 0.702 | 0.964 | 0.830 | 0.969 | 0.868 |
| PRC Area | 0.784 | 0.516 | 0.775 | 0.594 | 0.786 | 0.689 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jatakar, K.; Shah, V.; Binali, R.; Salur, E.; Sağlam, H.; Mikolajczyk, T.; Patange, A.D. Monitoring Built-Up Edge, Chipping, Thermal Cracking, and Plastic Deformation of Milling Cutter Inserts through Spindle Vibration Signals. Machines 2023, 11, 790. https://doi.org/10.3390/machines11080790
Jatakar K, Shah V, Binali R, Salur E, Sağlam H, Mikolajczyk T, Patange AD. Monitoring Built-Up Edge, Chipping, Thermal Cracking, and Plastic Deformation of Milling Cutter Inserts through Spindle Vibration Signals. Machines. 2023; 11(8):790. https://doi.org/10.3390/machines11080790
Chicago/Turabian StyleJatakar, Keshav, Varsha Shah, Rüstem Binali, Emin Salur, Hacı Sağlam, Tadeusz Mikolajczyk, and Abhishek D. Patange. 2023. "Monitoring Built-Up Edge, Chipping, Thermal Cracking, and Plastic Deformation of Milling Cutter Inserts through Spindle Vibration Signals" Machines 11, no. 8: 790. https://doi.org/10.3390/machines11080790
APA StyleJatakar, K., Shah, V., Binali, R., Salur, E., Sağlam, H., Mikolajczyk, T., & Patange, A. D. (2023). Monitoring Built-Up Edge, Chipping, Thermal Cracking, and Plastic Deformation of Milling Cutter Inserts through Spindle Vibration Signals. Machines, 11(8), 790. https://doi.org/10.3390/machines11080790








