Integrated Value Engineering and Risk Assessment Performance Measurement Framework in Ship-Manufacturing Industry towards Net Zero Emissions Using Fuzzy DEMATEL-AHP
Abstract
:1. Introduction
2. Literature and Critical Review
2.1. The Models in Ship-Manufacturing Performance Assessment
2.2. Integrated Value Engineering and Risk Assessment
2.3. Fuzzy DEMATEL and AHP
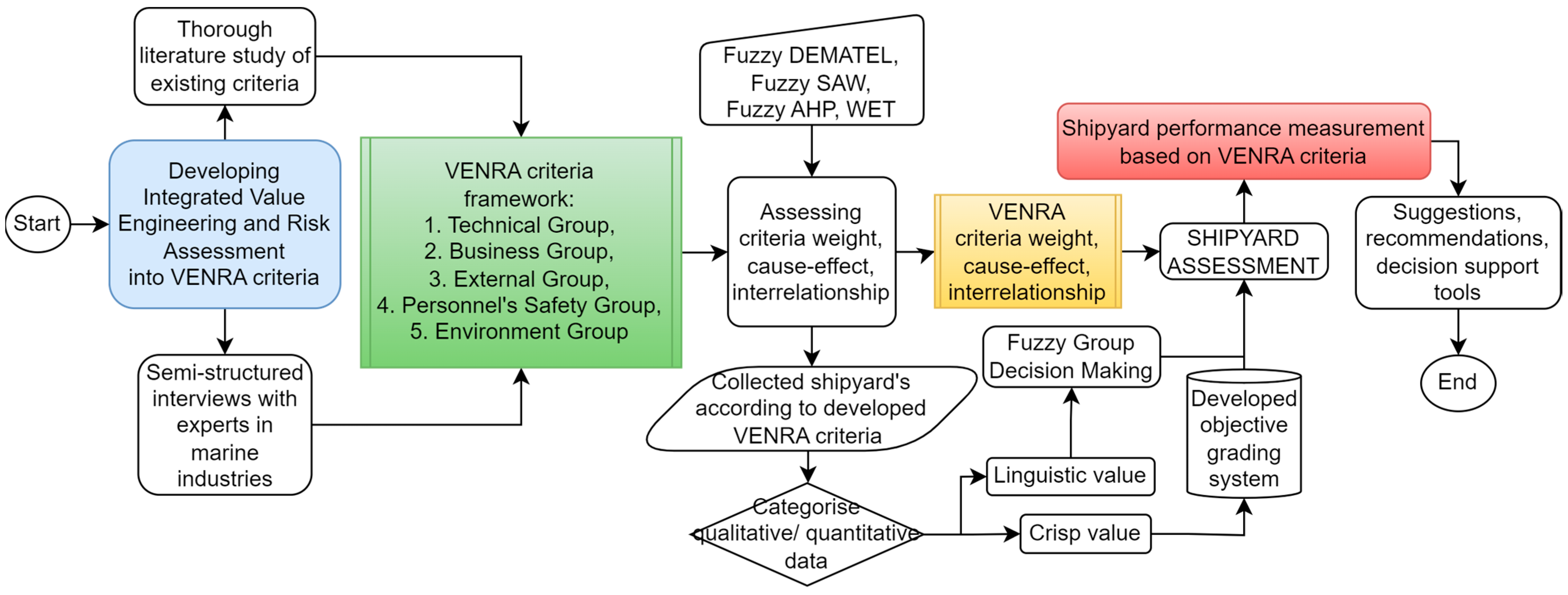
3. The VENRA Framework
3.1. VENRA Criteria Framework
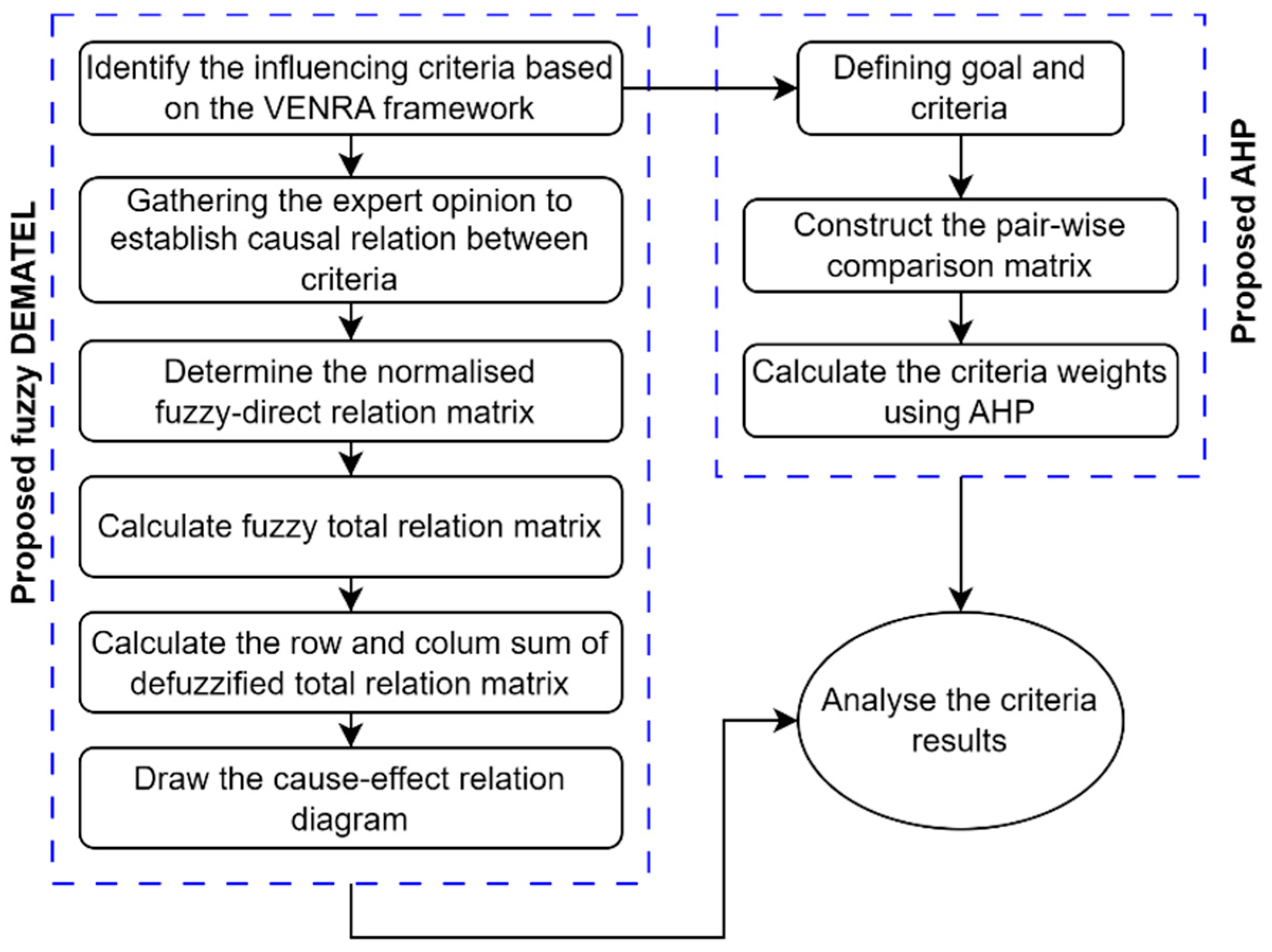
3.2. Methodology
3.2.1. Fuzzy DEMATEL
3.2.2. Analytic Hierarchy Process (AHP)
4. Case Study and Results
4.1. Shipyard Case Study and Data Analysis
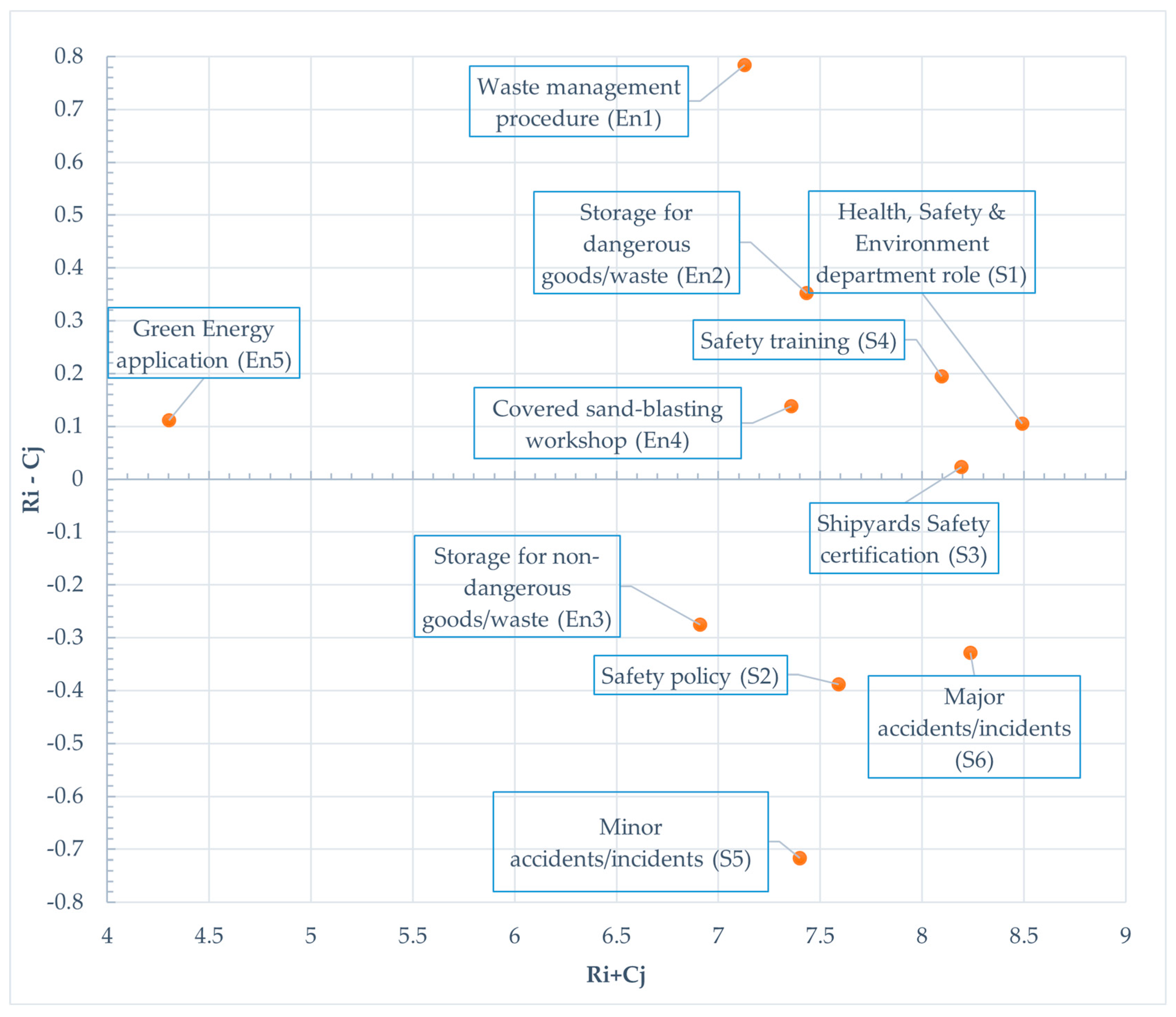
4.2. Criteria Cause-Effect and Ranking Analysis
5. Discussion
5.1. The Causal Factors
5.2. The Causal & Most Important Factors Group Based on Fuzzy DEMATEL & AHP
5.3. Shipyard’s Improvement Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Criteria Code | S1 | S2 | S3 | S4 | S5 | S6 | En1 | En2 | En3 | En4 | En5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | N | FG | G | G | FG | FG | VG | VG | VG | VG | MG |
| S2 | FG | N | FG | L | MG | MG | MG | FG | FG | FG | FG |
| S3 | E | VG | N | FG | FG | FG | FG | VG | VG | VG | MG |
| S4 | FG | ML | VG | N | FG | FG | VG | VG | VG | VG | L |
| S5 | FG | G | G | FG | N | FG | L | MG | MG | VG | L |
| S6 | E | VG | VG | VG | VG | N | L | MG | MG | VG | L |
| En1 | E | G | VG | G | G | G | N | FG | G | G | FL |
| En2 | VG | VG | VG | VG | VG | VG | G | N | FL | VL | VL |
| En3 | G | G | G | G | G | VG | G | VL | N | VL | VL |
| En4 | E | G | E | G | VG | E | FG | ML | VL | N | VL |
| En5 | MG | VL | VL | M | M | M | FG | M | ML | VL | N |
| S1 | S2 | S3 | S4 | S5 | S6 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | |
| S1 | 0.00 | 0.00 | 0.10 | 0.57 | 0.70 | 0.80 | 0.54 | 0.70 | 0.84 | 0.54 | 0.70 | 0.84 | 0.74 | 0.84 | 0.88 | 0.74 | 0.84 | 0.88 |
| S2 | 0.65 | 0.77 | 0.86 | 0.00 | 0.00 | 0.10 | 0.56 | 0.68 | 0.77 | 0.30 | 0.42 | 0.54 | 0.65 | 0.75 | 0.82 | 0.74 | 0.82 | 0.84 |
| S3 | 0.64 | 0.76 | 0.83 | 0.77 | 0.87 | 0.93 | 0.00 | 0.00 | 0.10 | 0.57 | 0.67 | 0.76 | 0.65 | 0.77 | 0.86 | 0.65 | 0.77 | 0.86 |
| S4 | 0.48 | 0.60 | 0.71 | 0.54 | 0.62 | 0.68 | 0.72 | 0.82 | 0.88 | 0.12 | 0.14 | 0.24 | 0.74 | 0.84 | 0.88 | 0.74 | 0.84 | 0.88 |
| S5 | 0.50 | 0.60 | 0.68 | 0.57 | 0.74 | 0.88 | 0.48 | 0.64 | 0.79 | 0.62 | 0.74 | 0.85 | 0.00 | 0.00 | 0.10 | 0.53 | 0.63 | 0.73 |
| S6 | 0.71 | 0.84 | 0.88 | 0.84 | 0.94 | 1.00 | 0.77 | 0.89 | 0.98 | 0.84 | 0.94 | 1.00 | 0.58 | 0.70 | 0.83 | 0.00 | 0.00 | 0.10 |
| En1 | 0.75 | 0.89 | 0.96 | 0.50 | 0.64 | 0.79 | 0.61 | 0.75 | 0.89 | 0.43 | 0.63 | 0.83 | 0.50 | 0.64 | 0.79 | 0.50 | 0.64 | 0.79 |
| En2 | 0.84 | 0.94 | 1.00 | 0.69 | 0.83 | 0.96 | 0.69 | 0.83 | 0.96 | 0.61 | 0.75 | 0.89 | 0.69 | 0.77 | 0.85 | 0.80 | 0.90 | 1.00 |
| En3 | 0.50 | 0.64 | 0.79 | 0.50 | 0.64 | 0.79 | 0.50 | 0.64 | 0.79 | 0.43 | 0.63 | 0.83 | 0.43 | 0.63 | 0.83 | 0.69 | 0.83 | 0.96 |
| En4 | 0.90 | 1.00 | 1.00 | 0.50 | 0.70 | 0.90 | 0.90 | 1.00 | 1.00 | 0.50 | 0.70 | 0.90 | 0.69 | 0.77 | 0.85 | 0.90 | 1.00 | 1.00 |
| En5 | 0.43 | 0.53 | 0.64 | 0.00 | 0.10 | 0.20 | 0.00 | 0.10 | 0.20 | 0.23 | 0.41 | 0.58 | 0.19 | 0.35 | 0.51 | 0.19 | 0.35 | 0.51 |
| En1 | En2 | En3 | En4 | En5 | ||||||||||||||
| l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | ||||
| S1 | 0.69 | 0.77 | 0.85 | 0.69 | 0.83 | 0.96 | 0.69 | 0.83 | 0.96 | 0.80 | 0.90 | 1.00 | 0.50 | 0.55 | 0.60 | |||
| S2 | 0.46 | 0.51 | 0.56 | 0.50 | 0.60 | 0.70 | 0.50 | 0.60 | 0.70 | 0.50 | 0.60 | 0.70 | 0.50 | 0.60 | 0.70 | |||
| S3 | 0.50 | 0.58 | 0.66 | 0.69 | 0.77 | 0.85 | 0.69 | 0.77 | 0.85 | 0.69 | 0.83 | 0.96 | 0.50 | 0.55 | 0.60 | |||
| S4 | 0.69 | 0.83 | 0.96 | 0.61 | 0.75 | 0.89 | 0.61 | 0.75 | 0.89 | 0.61 | 0.75 | 0.89 | 0.10 | 0.30 | 0.50 | |||
| S5 | 0.06 | 0.19 | 0.35 | 0.43 | 0.53 | 0.64 | 0.50 | 0.55 | 0.60 | 0.69 | 0.77 | 0.85 | 0.06 | 0.19 | 0.35 | |||
| S6 | 0.06 | 0.19 | 0.35 | 0.50 | 0.61 | 0.71 | 0.50 | 0.61 | 0.71 | 0.84 | 0.94 | 1.00 | 0.06 | 0.19 | 0.35 | |||
| En1 | 0.00 | 0.00 | 0.10 | 0.65 | 0.77 | 0.86 | 0.65 | 0.81 | 0.94 | 0.41 | 0.59 | 0.77 | 0.30 | 0.40 | 0.50 | |||
| En2 | 0.57 | 0.74 | 0.88 | 0.00 | 0.00 | 0.10 | 0.38 | 0.51 | 0.63 | 0.08 | 0.20 | 0.33 | 0.00 | 0.10 | 0.20 | |||
| En3 | 0.41 | 0.59 | 0.77 | 0.27 | 0.39 | 0.51 | 0.00 | 0.00 | 0.10 | 0.17 | 0.27 | 0.37 | 0.00 | 0.10 | 0.20 | |||
| En4 | 0.32 | 0.42 | 0.51 | 0.23 | 0.31 | 0.40 | 0.18 | 0.28 | 0.38 | 0.00 | 0.00 | 0.10 | 0.22 | 0.30 | 0.38 | |||
| En5 | 0.51 | 0.59 | 0.67 | 0.41 | 0.51 | 0.60 | 0.42 | 0.47 | 0.52 | 0.00 | 0.10 | 0.20 | 0.00 | 0.00 | 0.10 | |||
| S1 | S2 | S3 | S4 | S5 | S6 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | |
| S1 | 0.00 | 0.00 | 0.01 | 0.07 | 0.08 | 0.09 | 0.06 | 0.08 | 0.10 | 0.06 | 0.08 | 0.10 | 0.09 | 0.10 | 0.10 | 0.09 | 0.10 | 0.10 |
| S2 | 0.07 | 0.09 | 0.10 | 0.00 | 0.00 | 0.01 | 0.06 | 0.08 | 0.09 | 0.03 | 0.05 | 0.06 | 0.07 | 0.09 | 0.09 | 0.09 | 0.09 | 0.10 |
| S3 | 0.07 | 0.09 | 0.09 | 0.09 | 0.10 | 0.11 | 0.00 | 0.00 | 0.01 | 0.07 | 0.08 | 0.09 | 0.07 | 0.09 | 0.10 | 0.07 | 0.09 | 0.10 |
| S4 | 0.06 | 0.07 | 0.08 | 0.06 | 0.07 | 0.08 | 0.08 | 0.09 | 0.10 | 0.01 | 0.02 | 0.03 | 0.09 | 0.10 | 0.10 | 0.09 | 0.10 | 0.10 |
| S5 | 0.06 | 0.07 | 0.08 | 0.07 | 0.08 | 0.10 | 0.06 | 0.07 | 0.09 | 0.07 | 0.08 | 0.10 | 0.00 | 0.00 | 0.01 | 0.06 | 0.07 | 0.08 |
| S6 | 0.08 | 0.10 | 0.10 | 0.10 | 0.11 | 0.11 | 0.09 | 0.10 | 0.11 | 0.10 | 0.11 | 0.11 | 0.07 | 0.08 | 0.09 | 0.00 | 0.00 | 0.01 |
| En1 | 0.09 | 0.10 | 0.11 | 0.06 | 0.07 | 0.09 | 0.07 | 0.09 | 0.10 | 0.05 | 0.07 | 0.09 | 0.06 | 0.07 | 0.09 | 0.06 | 0.07 | 0.09 |
| En2 | 0.10 | 0.11 | 0.11 | 0.08 | 0.09 | 0.11 | 0.08 | 0.09 | 0.11 | 0.07 | 0.09 | 0.10 | 0.08 | 0.09 | 0.10 | 0.09 | 0.10 | 0.11 |
| En3 | 0.06 | 0.07 | 0.09 | 0.06 | 0.07 | 0.09 | 0.06 | 0.07 | 0.09 | 0.05 | 0.07 | 0.09 | 0.05 | 0.07 | 0.09 | 0.08 | 0.09 | 0.11 |
| En4 | 0.10 | 0.11 | 0.11 | 0.06 | 0.08 | 0.10 | 0.10 | 0.11 | 0.11 | 0.06 | 0.08 | 0.10 | 0.08 | 0.09 | 0.10 | 0.10 | 0.11 | 0.11 |
| En5 | 0.05 | 0.06 | 0.07 | 0.00 | 0.01 | 0.02 | 0.00 | 0.01 | 0.02 | 0.03 | 0.05 | 0.07 | 0.02 | 0.04 | 0.06 | 0.02 | 0.04 | 0.06 |
| En1 | En2 | En3 | En4 | En5 | ||||||||||||||
| l | m | u | l | m | u | l | m | u | l | m | u | l | m | u | ||||
| S1 | 0.08 | 0.09 | 0.10 | 0.08 | 0.09 | 0.11 | 0.08 | 0.09 | 0.11 | 0.09 | 0.10 | 0.11 | 0.06 | 0.06 | 0.07 | |||
| S2 | 0.05 | 0.06 | 0.06 | 0.06 | 0.07 | 0.08 | 0.06 | 0.07 | 0.08 | 0.06 | 0.07 | 0.08 | 0.06 | 0.07 | 0.08 | |||
| S3 | 0.06 | 0.07 | 0.08 | 0.08 | 0.09 | 0.10 | 0.08 | 0.09 | 0.10 | 0.08 | 0.09 | 0.11 | 0.06 | 0.06 | 0.07 | |||
| S4 | 0.08 | 0.09 | 0.11 | 0.07 | 0.09 | 0.10 | 0.07 | 0.09 | 0.10 | 0.07 | 0.09 | 0.10 | 0.01 | 0.03 | 0.06 | |||
| S5 | 0.01 | 0.02 | 0.04 | 0.05 | 0.06 | 0.07 | 0.06 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 | 0.01 | 0.02 | 0.04 | |||
| S6 | 0.01 | 0.02 | 0.04 | 0.06 | 0.07 | 0.08 | 0.06 | 0.07 | 0.08 | 0.10 | 0.11 | 0.11 | 0.01 | 0.02 | 0.04 | |||
| En1 | 0.00 | 0.00 | 0.01 | 0.07 | 0.09 | 0.10 | 0.07 | 0.09 | 0.11 | 0.05 | 0.07 | 0.09 | 0.03 | 0.05 | 0.06 | |||
| En2 | 0.07 | 0.08 | 0.10 | 0.00 | 0.00 | 0.01 | 0.04 | 0.06 | 0.07 | 0.01 | 0.02 | 0.04 | 0.00 | 0.01 | 0.02 | |||
| En3 | 0.05 | 0.07 | 0.09 | 0.03 | 0.04 | 0.06 | 0.00 | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.00 | 0.01 | 0.02 | |||
| En4 | 0.04 | 0.05 | 0.06 | 0.03 | 0.04 | 0.05 | 0.02 | 0.03 | 0.04 | 0.00 | 0.00 | 0.01 | 0.03 | 0.03 | 0.04 | |||
| En5 | 0.06 | 0.07 | 0.08 | 0.05 | 0.06 | 0.07 | 0.05 | 0.05 | 0.06 | 0.00 | 0.01 | 0.02 | 0.00 | 0.00 | 0.01 | |||
| Low Score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | En1 | En2 | En3 | En4 | En5 | |
| S1 | 0.128 | 0.177 | 0.178 | 0.165 | 0.198 | 0.211 | 0.157 | 0.173 | 0.176 | 0.187 | 0.100 |
| S2 | 0.176 | 0.096 | 0.159 | 0.124 | 0.169 | 0.188 | 0.120 | 0.138 | 0.141 | 0.141 | 0.094 |
| S3 | 0.193 | 0.194 | 0.117 | 0.166 | 0.187 | 0.199 | 0.137 | 0.171 | 0.174 | 0.174 | 0.100 |
| S4 | 0.174 | 0.169 | 0.192 | 0.115 | 0.194 | 0.205 | 0.152 | 0.161 | 0.164 | 0.166 | 0.056 |
| S5 | 0.147 | 0.147 | 0.141 | 0.145 | 0.089 | 0.156 | 0.070 | 0.118 | 0.128 | 0.151 | 0.042 |
| S6 | 0.193 | 0.197 | 0.194 | 0.188 | 0.176 | 0.125 | 0.088 | 0.146 | 0.149 | 0.188 | 0.053 |
| En1 | 0.186 | 0.151 | 0.165 | 0.136 | 0.155 | 0.165 | 0.072 | 0.154 | 0.157 | 0.131 | 0.073 |
| En2 | 0.199 | 0.177 | 0.179 | 0.161 | 0.180 | 0.200 | 0.135 | 0.090 | 0.135 | 0.106 | 0.044 |
| En3 | 0.135 | 0.130 | 0.132 | 0.117 | 0.124 | 0.158 | 0.098 | 0.095 | 0.068 | 0.090 | 0.032 |
| En4 | 0.205 | 0.157 | 0.199 | 0.149 | 0.179 | 0.209 | 0.108 | 0.115 | 0.113 | 0.096 | 0.068 |
| En5 | 0.094 | 0.044 | 0.045 | 0.066 | 0.066 | 0.070 | 0.088 | 0.084 | 0.086 | 0.038 | 0.016 |
| Middle score | |||||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | En1 | En2 | En3 | En4 | En5 | |
| S1 | 0.269 | 0.324 | 0.333 | 0.318 | 0.344 | 0.362 | 0.272 | 0.305 | 0.309 | 0.318 | 0.180 |
| S2 | 0.306 | 0.209 | 0.287 | 0.250 | 0.293 | 0.315 | 0.215 | 0.247 | 0.251 | 0.253 | 0.166 |
| S3 | 0.339 | 0.331 | 0.248 | 0.305 | 0.328 | 0.345 | 0.246 | 0.291 | 0.295 | 0.302 | 0.176 |
| S4 | 0.324 | 0.308 | 0.336 | 0.249 | 0.335 | 0.353 | 0.270 | 0.290 | 0.294 | 0.297 | 0.150 |
| S5 | 0.268 | 0.269 | 0.267 | 0.264 | 0.196 | 0.278 | 0.168 | 0.223 | 0.228 | 0.254 | 0.115 |
| S6 | 0.335 | 0.330 | 0.333 | 0.322 | 0.313 | 0.255 | 0.200 | 0.266 | 0.270 | 0.308 | 0.135 |
| En1 | 0.334 | 0.294 | 0.312 | 0.286 | 0.299 | 0.316 | 0.174 | 0.279 | 0.287 | 0.265 | 0.153 |
| En2 | 0.337 | 0.313 | 0.318 | 0.298 | 0.311 | 0.339 | 0.249 | 0.198 | 0.257 | 0.230 | 0.123 |
| En3 | 0.265 | 0.255 | 0.260 | 0.247 | 0.256 | 0.288 | 0.203 | 0.205 | 0.166 | 0.200 | 0.103 |
| En4 | 0.340 | 0.296 | 0.332 | 0.290 | 0.308 | 0.345 | 0.213 | 0.230 | 0.230 | 0.204 | 0.143 |
| En5 | 0.184 | 0.131 | 0.135 | 0.161 | 0.160 | 0.168 | 0.156 | 0.160 | 0.159 | 0.118 | 0.057 |
| Upper score | |||||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | En1 | En2 | En3 | En4 | En5 | |
| S1 | 0.694 | 0.754 | 0.769 | 0.762 | 0.764 | 0.791 | 0.633 | 0.694 | 0.7 | 0.712 | 0.44 |
| S2 | 0.663 | 0.570 | 0.650 | 0.622 | 0.649 | 0.673 | 0.515 | 0.573 | 0.577 | 0.584 | 0.391 |
| S3 | 0.735 | 0.731 | 0.654 | 0.717 | 0.726 | 0.751 | 0.585 | 0.652 | 0.657 | 0.676 | 0.421 |
| S4 | 0.739 | 0.721 | 0.753 | 0.677 | 0.744 | 0.770 | 0.628 | 0.67 | 0.676 | 0.683 | 0.419 |
| S5 | 0.619 | 0.628 | 0.628 | 0.627 | 0.548 | 0.636 | 0.473 | 0.543 | 0.544 | 0.578 | 0.341 |
| S6 | 0.722 | 0.721 | 0.729 | 0.724 | 0.707 | 0.654 | 0.54 | 0.623 | 0.628 | 0.667 | 0.387 |
| En1 | 0.750 | 0.718 | 0.739 | 0.726 | 0.722 | 0.746 | 0.527 | 0.655 | 0.669 | 0.659 | 0.412 |
| En2 | 0.734 | 0.718 | 0.728 | 0.713 | 0.709 | 0.747 | 0.593 | 0.561 | 0.624 | 0.601 | 0.372 |
| En3 | 0.644 | 0.633 | 0.643 | 0.639 | 0.639 | 0.673 | 0.527 | 0.545 | 0.505 | 0.545 | 0.333 |
| En4 | 0.699 | 0.678 | 0.697 | 0.680 | 0.675 | 0.712 | 0.527 | 0.564 | 0.567 | 0.546 | 0.373 |
| En5 | 0.452 | 0.398 | 0.405 | 0.442 | 0.433 | 0.447 | 0.379 | 0.4 | 0.395 | 0.364 | 0.221 |
| S1 | S2 | S3 | S4 | S5 | S6 | En1 | En2 | En3 | En4 | En5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 0.358 | 0.398 | 0.420 | 0.412 | 0.429 | 0.448 | 0.349 | 0.385 | 0.390 | 0.400 | 0.237 |
| S2 | 0.400 | 0.311 | 0.415 | 0.388 | 0.412 | 0.430 | 0.340 | 0.363 | 0.367 | 0.371 | 0.202 |
| S3 | 0.414 | 0.371 | 0.331 | 0.411 | 0.405 | 0.423 | 0.316 | 0.364 | 0.368 | 0.377 | 0.228 |
| S4 | 0.380 | 0.327 | 0.363 | 0.290 | 0.369 | 0.390 | 0.282 | 0.318 | 0.321 | 0.324 | 0.216 |
| S5 | 0.334 | 0.311 | 0.333 | 0.337 | 0.266 | 0.344 | 0.227 | 0.284 | 0.289 | 0.317 | 0.160 |
| S6 | 0.410 | 0.389 | 0.411 | 0.409 | 0.391 | 0.337 | 0.269 | 0.339 | 0.342 | 0.381 | 0.188 |
| En1 | 0.418 | 0.367 | 0.400 | 0.383 | 0.386 | 0.403 | 0.253 | 0.358 | 0.366 | 0.347 | 0.210 |
| En2 | 0.417 | 0.374 | 0.402 | 0.397 | 0.394 | 0.422 | 0.321 | 0.278 | 0.333 | 0.307 | 0.176 |
| En3 | 0.343 | 0.320 | 0.339 | 0.335 | 0.335 | 0.368 | 0.271 | 0.277 | 0.242 | 0.274 | 0.153 |
| En4 | 0.409 | 0.357 | 0.404 | 0.371 | 0.382 | 0.416 | 0.278 | 0.298 | 0.298 | 0.277 | 0.192 |
| En5 | 0.245 | 0.228 | 0.197 | 0.192 | 0.221 | 0.230 | 0.209 | 0.216 | 0.215 | 0.174 | 0.099 |
| Criteria | Normalised Weight | Cause/Effect | Weight Rank | ||||
|---|---|---|---|---|---|---|---|
| S1 | 4.299 | 4.194 | 8.493 | 0.105 | 0.105 | Cause | 1 |
| S2 | 3.601 | 3.990 | 7.590 | −0.389 | 0.094 | Effect | 5 |
| S3 | 4.108 | 4.085 | 8.194 | 0.023 | 0.101 | Cause | 3 |
| S4 | 4.145 | 3.950 | 8.095 | 0.195 | 0.100 | Cause | 4 |
| S5 | 3.342 | 4.059 | 7.401 | −0.717 | 0.091 | Effect | 7 |
| S6 | 3.955 | 4.283 | 8.238 | −0.328 | 0.102 | Effect | 2 |
| En1 | 3.956 | 3.172 | 7.128 | 0.784 | 0.088 | Cause | 9 |
| En2 | 3.892 | 3.540 | 7.433 | 0.352 | 0.092 | Cause | 6 |
| En3 | 3.318 | 3.592 | 6.910 | −0.275 | 0.085 | Effect | 10 |
| En4 | 3.749 | 3.611 | 7.359 | 0.138 | 0.091 | Cause | 8 |
| En5 | 2.207 | 2.095 | 4.302 | 0.111 | 0.053 | Cause | 11 |
Appendix B
| Group in VENRA | PS | Env | Standardised Matrix (Sum of Columns) | Criteria Weight (Average of Row) | |
|---|---|---|---|---|---|
| Personnel’s Safety (PS) | 1 | 4.2 | 0.788 | 0.808 | 79.80% |
| Environment (Env) | 0.269 | 1 | 0.212 | 0.192 | 20.20% |
| Sum of Columns= | 1.269 | 5.2 | 100% | ||
| Personnel’s Safety Criteria | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|
| * HSE department role (S1) | 1 | 4.067 | 1.080 | 2.680 | 3.800 | 0.491 |
| Safety policy (S2) | 0.897 | 1 | 1.335 | 1.362 | 3.133 | 0.502 |
| Shipyards Safety certification (S3) | 2.467 | 3.240 | 1 | 4.029 | 4.467 | 0.707 |
| Safety training (S4) | 2.269 | 2.733 | 1.575 | 1 | 3.733 | 1.175 |
| Minor accidents/incidents (S5) | 1.844 | 1.335 | 0.764 | 1.307 | 1 | 0.168 |
| Major accidents/incidents (S6) | 4.600 | 4.200 | 2.200 | 4.040 | 7.000 | 1 |
| Sum of columns= | 13.077 | 14.467 | 7.954 | 16.526 | 23.133 | 4.043 |
| Criteria Code | S1 | S2 | S3 | S4 | S5 | S6 | Weight | Criteria Rank |
|---|---|---|---|---|---|---|---|---|
| (S1) | 0.076 | 0.245 | 0.136 | 0.186 | 0.164 | 0.121 | 15.5% | 4 |
| (S2) | 0.069 | 0.060 | 0.168 | 0.094 | 0.135 | 0.124 | 10.8% | 5 |
| (S3) | 0.189 | 0.195 | 0.126 | 0.279 | 0.193 | 0.175 | 19.3% | 2 |
| (S4) | 0.173 | 0.165 | 0.198 | 0.069 | 0.161 | 0.291 | 17.6% | 3 |
| (S5) | 0.141 | 0.081 | 0.096 | 0.091 | 0.043 | 0.042 | 8.2% | 6 |
| (S6) | 0.352 | 0.253 | 0.277 | 0.280 | 0.303 | 0.247 | 28.5% | 1 |
| Criteria Code | S1 | S2 | S3 | S4 | S5 | S6 | Sum of Row | Sum of Row/ Weight |
|---|---|---|---|---|---|---|---|---|
| (S1) | 0.155 | 0.441 | 0.208 | 0.473 | 0.312 | 0.140 | 1.729 | 11.166 |
| (S2) | 0.139 | 0.108 | 0.258 | 0.240 | 0.258 | 0.143 | 1.146 | 10.562 |
| (S3) | 0.382 | 0.351 | 0.193 | 0.710 | 0.367 | 0.202 | 2.205 | 11.435 |
| (S4) | 0.351 | 0.297 | 0.304 | 0.176 | 0.307 | 0.335 | 1.770 | 10.040 |
| (S5) | 0.286 | 0.145 | 0.147 | 0.230 | 0.082 | 0.048 | 0.938 | 11.418 |
| (S6) | 0.712 | 0.456 | 0.424 | 0.712 | 0.575 | 0.285 | 3.165 | 11.094 |
| lambda max | 10.953 | |||||||
| CI | 0.991 | |||||||
| CR | 0.792 | |||||||
| Environment Criteria | En1 | En2 | En3 | En4 | En5 |
|---|---|---|---|---|---|
| Waste management procedure (En1) | 1 | 3.667 | 5.400 | 2.040 | 3.640 |
| Storage for dangerous goods/waste (En2) | 0.924 | 1 | 6.600 | 2.867 | 4.600 |
| Storage for non-dangerous goods/waste (En3) | 0.224 | 0.159 | 1 | 0.947 | 2.240 |
| Covered sandblasting workshop (En4) | 1.507 | 0.947 | 2.867 | 1 | 4.000 |
| Green Energy used (En5) | 1.202 | 0.242 | 1.383 | 0.395 | 1 |
| Sum of column= | 4.857 | 6.015 | 17.250 | 7.249 | 15.480 |
| Criteria Code | En1 | En2 | En3 | En4 | En5 | Weight | Criteria Rank |
|---|---|---|---|---|---|---|---|
| (En1) | 0.206 | 0.610 | 0.313 | 0.281 | 0.235 | 32.9% | 1 |
| (En2) | 0.190 | 0.166 | 0.383 | 0.395 | 0.297 | 28.6% | 2 |
| (En3) | 0.046 | 0.026 | 0.058 | 0.131 | 0.145 | 8.1% | 5 |
| (En4) | 0.310 | 0.157 | 0.166 | 0.138 | 0.258 | 20.6% | 3 |
| (En5) | 0.247 | 0.040 | 0.080 | 0.055 | 0.065 | 9.7% | 4 |
| Criteria Code | En1 | En2 | En3 | En4 | En5 | Sum of Row | Sum of Row/ Weight |
|---|---|---|---|---|---|---|---|
| (En1) | 0.32903 | 1.04993 | 0.43839 | 0.42031 | 0.35455 | 2.5922 | 7.878 |
| (En2) | 0.30396 | 0.28635 | 0.53582 | 0.59063 | 0.44806 | 2.1648 | 7.56 |
| (En3) | 0.07374 | 0.04563 | 0.08118 | 0.19505 | 0.21819 | 0.6138 | 7.561 |
| (En4) | 0.49574 | 0.27107 | 0.23273 | 0.20603 | 0.38962 | 1.5952 | 7.742 |
| (En5) | 0.39546 | 0.06927 | 0.1123 | 0.08143 | 0.0974 | 0.7559 | 7.76 |
| lambda max | 7.7 | ||||||
| CI | 0.675 | ||||||
| CR | 0.608 | ||||||
References
- Bruce, G.; Garrard, I. The Business of Shipbuilding; Informa Law from Routledge: London, UK, 2013; ISBN 1315778572. [Google Scholar]
- Chatzinikolaou, S.D.; Ventikos, N.P. Applications of Life Cycle Assessment in Shipping. In Proceedings of the 2nd International Symposium on Naval Architecture and Maritime, Istanbul, Turkey, 23–24 October 2014. [Google Scholar]
- Harbour, J.L. The Basics of Performance Measurement; Productivity Press: Cambridge, MA, USA, 1999; Volume 21, ISBN 9781439802502. [Google Scholar]
- OECD Compensated Gross Ton (CGT) System; OECD: Paris, France, 2007.
- Roque, P.Z.; Gordo, J.M. A Measurement of Shipbuilding Productivity. In Maritime Technology and Engineering 5 Volume 1; CRC Press: Boca Raton, FL, USA, 2021; pp. 801–809. [Google Scholar] [CrossRef]
- Chao, S.L.; Yeh, Y.H. Comparing the Productivity of Major Shipyards in China, South Korea, and Japan—An Application of a Metafrontier Framework. Marit. Bus. Rev. 2020, 5, 193–210. [Google Scholar] [CrossRef]
- Pires, J.F.; Lamb, T.; Souza, C. Shipbuilding Performance Benchmarking. Int. J. Bus. Perform. Manag. 2009, 11, 216–235. [Google Scholar]
- Rabar, D.; Pavletić, D.; Doboviček, S.; Vlatković, M. Dry-Docking Performance Measurement Model–Multi Criteria Non Parametric Approach. Ships Offshore Struct. 2022, 17, 1286–1293. [Google Scholar] [CrossRef]
- Cook, W.D.; Tone, K.; Zhu, J. Data Envelopment Analysis: Prior to Choosing a Model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Golany, B.; Roll, Y. An Application Procedure for DEA. Omega 1989, 17, 237–250. [Google Scholar] [CrossRef]
- Banker, R.D.; Cooper, W.W.; Swarts, J.; Thomas, D. An Introduction to Data Envelopment Analysis with Some of Its Models and Their Uses. Res. Gov. Nonprofit Account. 1989, 5, 125–163. [Google Scholar]
- Gavalas, D.; Syriopoulos, T.; Tsatsaronis, M. Assessing Key Performance Indicators in the Shipbuilding Industry; an MCDM Approach. Marit. Policy Manag. 2022, 49, 463–491. [Google Scholar] [CrossRef]
- Sahin, B.; Yazir, D.; Soylu, A.; Yip, T.L. Improved Fuzzy AHP Based Game-Theoretic Model for Shipyard Selection. Ocean Eng. 2021, 233, 109060. [Google Scholar] [CrossRef]
- Vakili, S.V.; Ölçer, A.I.; Schönborn, A. Identification of Shipyard Priorities in a Multi-Criteria Decision-Making Environment through a Transdisciplinary Energy Management Framework: A Real Case Study for a Turkish Shipyard. J. Mar. Sci. Eng. 2021, 9, 1132. [Google Scholar] [CrossRef]
- Baihaqi, I.; Lazakis, I.; Kurt, R.E. Development of a Novel Integrated Value Engineering and Risk Assessment (VENRA) Framework for Shipyard Performance Measurement: A Case Study for an Indonesian Shipyard. Ships Offshore Struct. 2023, 1–16. [Google Scholar] [CrossRef]
- Pires, F.C.M.; Lamb, T. Establishing Performance Targets for Shipbuilding Policies. Marit. Policy Manag. 2008, 35, 491–502. [Google Scholar] [CrossRef]
- Kafali, M.; Ozkok, M.; Cebi, S. Evaluation of Pipe Cutting Technologies in Shipbuilding. Teor. I Praksa Brodogr. I Pomor. Teh. 2014, 65, 33–48. [Google Scholar]
- Kaplan, R.S.; Norton, D.P. The Balanced Scorecard: Measures That Drive Performance. Harv. Bus. Rev. 1992, 83, 71–79. [Google Scholar]
- Ozturkoglu, Y.; Kazancoglu, Y.; Ozkan-Ozen, Y.D. A Sustainable and Preventative Risk Management Model for Ship Recycling Industry. J. Clean. Prod. 2019, 238, 117907. [Google Scholar] [CrossRef]
- Dror, S. The Balanced Scorecard versus Quality Award Models as Strategic Frameworks. Total Qual. Manag. Bus. Excell. 2008, 19, 583–593. [Google Scholar] [CrossRef]
- Dell’Isola, A. Value Engineering: Practical Applications for Design, Construction, Maintenance & Operation; R.S. Means Company, Inc.: Kingston, NJ, USA, 1997; ISBN 0876294638. [Google Scholar]
- SAVE International Value Standard and Body of Knowledge; Mount Royal: New Jersey, USA, 2007.
- Dahooie, J.H.; Dehshiri, S.J.H.; Banaitis, A.; Binkytė-Vėlienė, A. Identifying and Prioritizing Cost Reduction Solutions in the Supply Chain by Integrating Value Engineering and Gray Multi-Criteria Decision-Making. Technol. Econ. Dev. Econ. 2020, 26, 1311–1338. [Google Scholar] [CrossRef]
- Ishak, A.; Ginting, R.; Malik, A.F. Integration of Quality Function Deployment (QFD) and Value Engineering in Improving the Quality of Product: A Literature Review. In Proceedings of the AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2020; Volume 2217, p. 30158. [Google Scholar]
- Gunarathne, A.S.; Zainudeen, N.; Perera, C.S.R.; Perera, B.A.K.S. A Framework of an Integrated Sustainability and Value Engineering Concepts for Construction Projects. Int. J. Constr. Manag. 2020, 22, 2178–2190. [Google Scholar] [CrossRef]
- Setti, P.H.P.; Canciglieri Junior, O.; Estorilio, C.C.A. Integrated Product Development Method Based on Value Engineering and Design for Assembly Concepts. J. Ind. Inf. Integr. 2021, 21, 100199. [Google Scholar] [CrossRef]
- Anđelić, O.R.; Rakićević, Z.M.; Nikolić, V.N. Integral Approach to Risk Analysis and Value Engineering. Tehnika 2020, 75, 94–100. [Google Scholar] [CrossRef]
- Masengesho, E.; Wei, J.; Umubyeyi, N.; Niyirora, R. A Review on the Role of Risk Management (RM) and Value Engineering (VE) Tools for Project Successful Delivery. World J. Eng. Technol. 2020, 9, 109–127. [Google Scholar] [CrossRef]
- Baihaqi, I.; Lazakis, I.; Kurt, R.E. Developing a Hybrid Value Engineering and Risk Assessment (VENRA) Framework for Shipbuilding and Ship Repair Industry Performance Measurement. In Proceedings of the International Conference of Ship and Offshore Technology, Surabaya, Indonesia, 19–20 November 2021; pp. 1–10. [Google Scholar]
- Fontela, E.; Gabus, A. The DEMATEL Observer, DEMATEL 1976 Report; Battelle Geneva Research Center: Geneva, Switzerland, 1976. [Google Scholar]
- Gabus, A.; Fontela, E. Perceptions of the World Problematique: Communication Procedure, Communicating with Those Bearing Collective Responsibility; DEMATEL Report No, vol 1; Battelle Geneva Research Centre: Geneva, Switzerland, 1973. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Kuzu, A.C. Risk Analysis of Break-in-Two Accident of Ships Using Fuzzy DEMATEL Method. Ocean Eng. 2021, 235, 109410. [Google Scholar] [CrossRef]
- Soner, O. Application of Fuzzy DEMATEL Method for Analysing of Accidents in Enclosed Spaces Onboard Ships. Ocean Eng. 2021, 220, 108507. [Google Scholar] [CrossRef]
- Gayathri, C.; Kamala, V.; Gajanand, M.S.; Yamini, S. Analysis of Operational and Financial Performance of Ports: An Integrated Fuzzy DEMATEL-TOPSIS Approach. Benchmarking Int. J. 2022, 29, 1046–1066. [Google Scholar] [CrossRef]
- Thakkar, J.J. Multi-Criteria Decision Making; Kacprzyk, J., Ed.; Springer Nature Singapore Pte Ltd.: Singapore, 2021; ISBN 9789813347441. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; Advanced Book Program; McGraw-Hill International Book Company: New York, NY, USA, 1980; ISBN 9780070543713. [Google Scholar]
- Ayan, B.; Abacıoğlu, S.; Basilio, M.P. A Comprehensive Review of the Novel Weighting Methods for Multi-Criteria Decision-Making. Information 2023, 14, 285. [Google Scholar] [CrossRef]
- Chen, S.-J.; Hwang, C.-L. Fuzzy Multiple Attribute Decision Making Methods. In Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. ISBN 978-3-642-46768-4. [Google Scholar]
- Pulli, J.; Heikkilä, J.; Kosomaa, L. Designing an Environmental Performance Indicator for Shipbuilding and Ship Dismantling. Rep. Turku Univ. Appl. Sci. Project ECO-EFFI Final Rep. 2013, 185, 1–54. [Google Scholar]


| Criteria Code | Description |
|---|---|
| S1 | The availability and the role of HSE in the department |
| S2 | Safety policy established and enforced by the HSE department |
| S3 | The availability of safety certificates in the shipyard, e.g., OHSAS certificate |
| S4 | Safety training conducted periodically |
| S5 | Number of minor accidents/incidents annually |
| S6 | Number of Major accidents/incidents annually |
| En1 | Procedure/guideline to handle waste management (for dangerous and non-dangerous) |
| En2 | Availability of dangerous goods storage (chemical, battery, radioactive, etc.) |
| En3 | Availability of non-dangerous goods storage (oil waste, scrapped steel, slag, barnacles/scrapped biofouling, etc.) |
| En4 | Covered sandblasting workshop to prevent air pollution (Availability, condition, function) |
| En5 | The stage of environmentally friendly energy used in the shipyard (plan, application in partial sector, application in major sector), e.g., solar panel energy, gas-energy-driven rather than diesel engine used for electricity power |
| Abbreviation | Linguistic Term | Triangular Fuzzy Number | ||
|---|---|---|---|---|
| Low (l) | Medium (m) | Upper (u) | ||
| N | 0. None | 0 | 0 | 0.1 |
| VL | 1. Very Low | 0 | 0.1 | 0.2 |
| L | 2. Low | 0.1 | 0.3 | 0.5 |
| FL | 3. Fairly Low | 0.3 | 0.4 | 0.5 |
| ML | 4. More or less low | 0.4 | 0.45 | 0.5 |
| M | 5. Medium | 0.3 | 0.5 | 0.7 |
| MG | 6. More or less good | 0.5 | 0.55 | 0.6 |
| FG | 7. Fairly Good | 0.5 | 0.6 | 0.7 |
| G | 8. Good | 0.5 | 0.7 | 0.9 |
| VG | 9. Very Good | 0.8 | 0.9 | 1 |
| E | 10. Excellent | 0.9 | 1 | 1 |
| Formal Academic Background (Weight: 15%) | Practical Experience in the Industry (In Years) (Weight: 70%) | Experience in Academic Working (In Years) (Weight: 15%) | |||
|---|---|---|---|---|---|
| Group | Score | Year Range | Score | Year Range | Score |
| High School | 25% | ≤5 | 40% | <5 | 35% |
| Diploma (Pre-University) | 35% | 6–10 | 60% | 5–10 | 50% |
| S1/Bachelor’s degree | 60% | 11–15 | 85% | 11–15 | 75% |
| S2/Master’s degree | 85% | 16–20 | 90% | 16–20 | 90% |
| S3/Doctoral/PhD | 100% | ≥21 | 100% | ≥21 | 100% |
| Rating | Definition |
|---|---|
| 9 | Row extremely more important |
| 8 | Row very strongly to extremely more important |
| 7 | Row very strongly more important |
| 6 | Row strongly to very strongly more important |
| 5 | Row strongly more important |
| 4 | Row moderately to strongly more important |
| 3 | Row moderately more important |
| 2 | Row equally important to moderately more important |
| 1 | Row and column equally important |
| Size of Matrix | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Random Index (RI) | 0 | 0 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.4 | 1.45 | 1.49 |
| Criteria Code | Assessed Data from the Shipyard | Data Acquired | |
|---|---|---|---|
| Verbal Assessment | Score | ||
| S1 | The significant role of HSE in the safety plan, process and control in the shipyard | 90 | Interview |
| S2 | Safety policies are implemented, such as regular safety toolbox checks and safety induction for personnel and visitors. | 70 | Interview |
| S3 | ISO 45001:2018: Health and Safety Management System | 90 | Shipyard’s data |
| S4 | Conducted periodically (possibly) | 75 | Interview, Assumption |
| S5 | Four minor accidents occurred and were recorded within the last six month | 55 | Interview |
| S6 | Possibly less than two non-fatal major accidents/incidents in a year (but not recorded) | 65 | Assumption |
| En1 | ISO 14000:2015: Environmental Management | 90 | Shipyard’s data |
| En2 | Dangerous and poisonous substances storages are available in the shipyard, the stored waste is collected by a legal waste collection company and reported to the Ministry of Environment (government) | 80 | Interview |
| En3 | Available, but limited capacity | 50 | Interview |
| En4 | A covered workshop for plate-blasting is available, but not for site-erection blasting, which is conducted outdoors and uncovered, it may use prohibited sand material for blasting | 50 | Interview |
| En5 | The application of environmentally friendly energy has not been planned yet | 15 | Interview |
| No | Edu. | Exper. | Acad. | Level’s Grade | Occupation Sector | Job’s Position |
|---|---|---|---|---|---|---|
| 1 | MSc | 17 | 10 | Senior | Shipyard | Technical and development director |
| 2 | MSc | 8 | 10 | Middle | Academia | Senior Lecturer |
| 3 | MSc | 6 | 8 | Middle | Academia | Lecturer staff |
| 4 | MSc | 6 | 8 | Middle | Academia | Lecturer staff |
| 5 | MSc | 6 | 8 | Middle | Academia | Lecturer staff |
| VENRA Group | Weight | Criteria Code | Fuzzy DEMATEL Results | AHP Results | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fuzzy DEMATEL | AHP | Weight | Rank | Cause/ Effect | Local Weight | Local Group Rank | Global Weight | Global Rank | ||
| Personnel Safety | 58.99% | 79.80% | (S1) | 10.47% | 1 | Cause | 15.49% | 4 | 12.36% | 4 |
| (S2) | 9.35% | 5 | Effect | 10.85% | 5 | 8.66% | 5 | |||
| (S3) | 10.10% | 3 | Cause | 19.29% | 2 | 15.39% | 2 | |||
| (S4) | 9.98% | 4 | Cause | 17.63% | 3 | 14.07% | 3 | |||
| (S5) | 9.12% | 7 | Effect | 8.22% | 6 | 6.56% | 7 | |||
| (S6) | 10.15% | 2 | Effect | 28.53% | 1 | 22.77% | 1 | |||
| Environment | 41.01% | 20.20% | (En1) | 8.78% | 9 | Cause | 32.90% | 1 | 6.65% | 6 |
| (En2) | 9.16% | 6 | Cause | 28.63% | 2 | 5.78% | 8 | |||
| (En3) | 8.52% | 10 | Effect | 8.12% | 5 | 1.64% | 11 | |||
| (En4) | 9.07% | 8 | Cause | 20.60% | 3 | 4.16% | 9 | |||
| (En5) | 5.30% | 11 | Cause | 9.74% | 4 | 1.97% | 10 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baihaqi, I.; Lazakis, I.; Supomo, H. Integrated Value Engineering and Risk Assessment Performance Measurement Framework in Ship-Manufacturing Industry towards Net Zero Emissions Using Fuzzy DEMATEL-AHP. Machines 2023, 11, 799. https://doi.org/10.3390/machines11080799
Baihaqi I, Lazakis I, Supomo H. Integrated Value Engineering and Risk Assessment Performance Measurement Framework in Ship-Manufacturing Industry towards Net Zero Emissions Using Fuzzy DEMATEL-AHP. Machines. 2023; 11(8):799. https://doi.org/10.3390/machines11080799
Chicago/Turabian StyleBaihaqi, Imam, Iraklis Lazakis, and Heri Supomo. 2023. "Integrated Value Engineering and Risk Assessment Performance Measurement Framework in Ship-Manufacturing Industry towards Net Zero Emissions Using Fuzzy DEMATEL-AHP" Machines 11, no. 8: 799. https://doi.org/10.3390/machines11080799
APA StyleBaihaqi, I., Lazakis, I., & Supomo, H. (2023). Integrated Value Engineering and Risk Assessment Performance Measurement Framework in Ship-Manufacturing Industry towards Net Zero Emissions Using Fuzzy DEMATEL-AHP. Machines, 11(8), 799. https://doi.org/10.3390/machines11080799







