A Hybrid Approach for Predicting Critical Machining Conditions in Titanium Alloy Slot Milling Using Feature Selection and Binary Whale Optimization Algorithm
Abstract
:1. Introduction
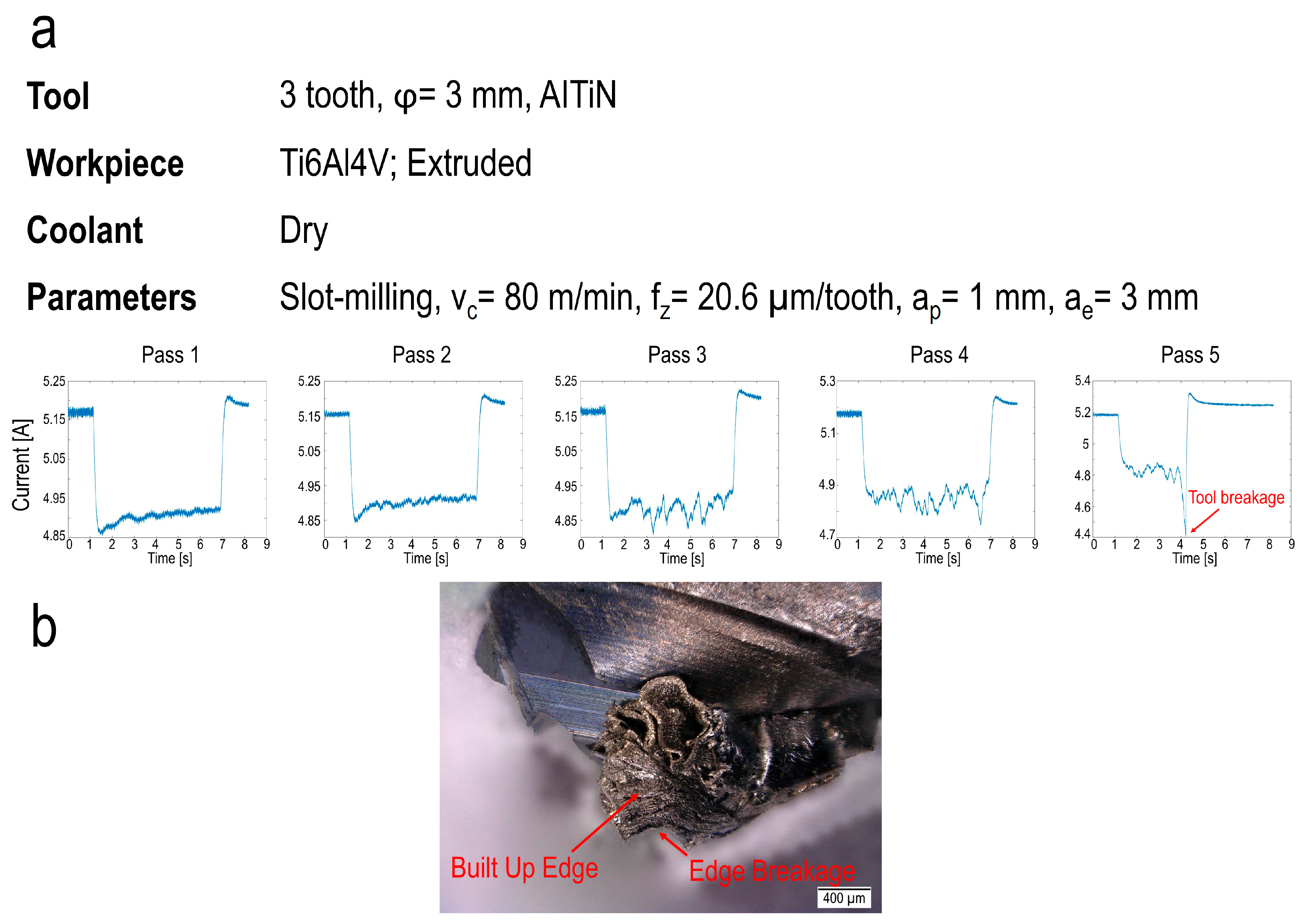
2. Experimental Setup
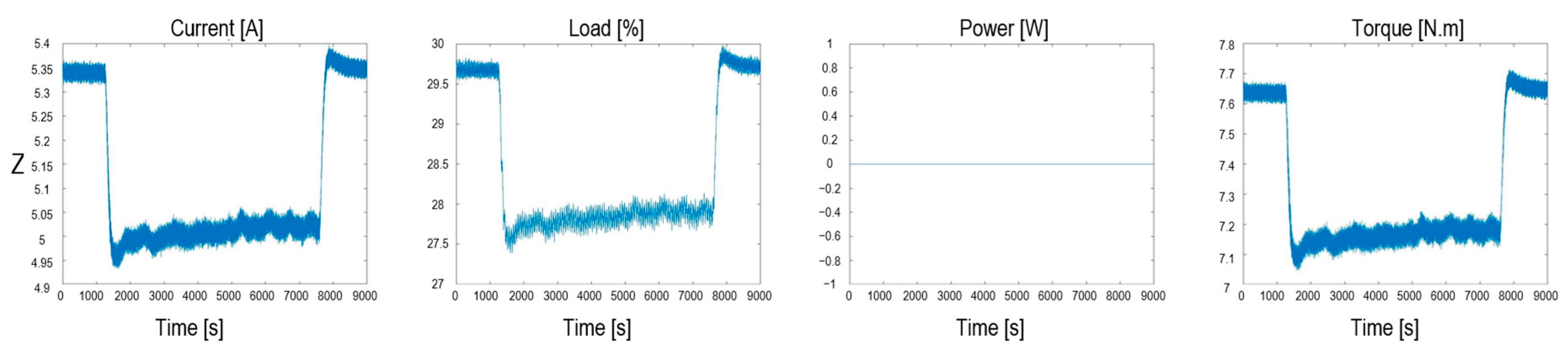
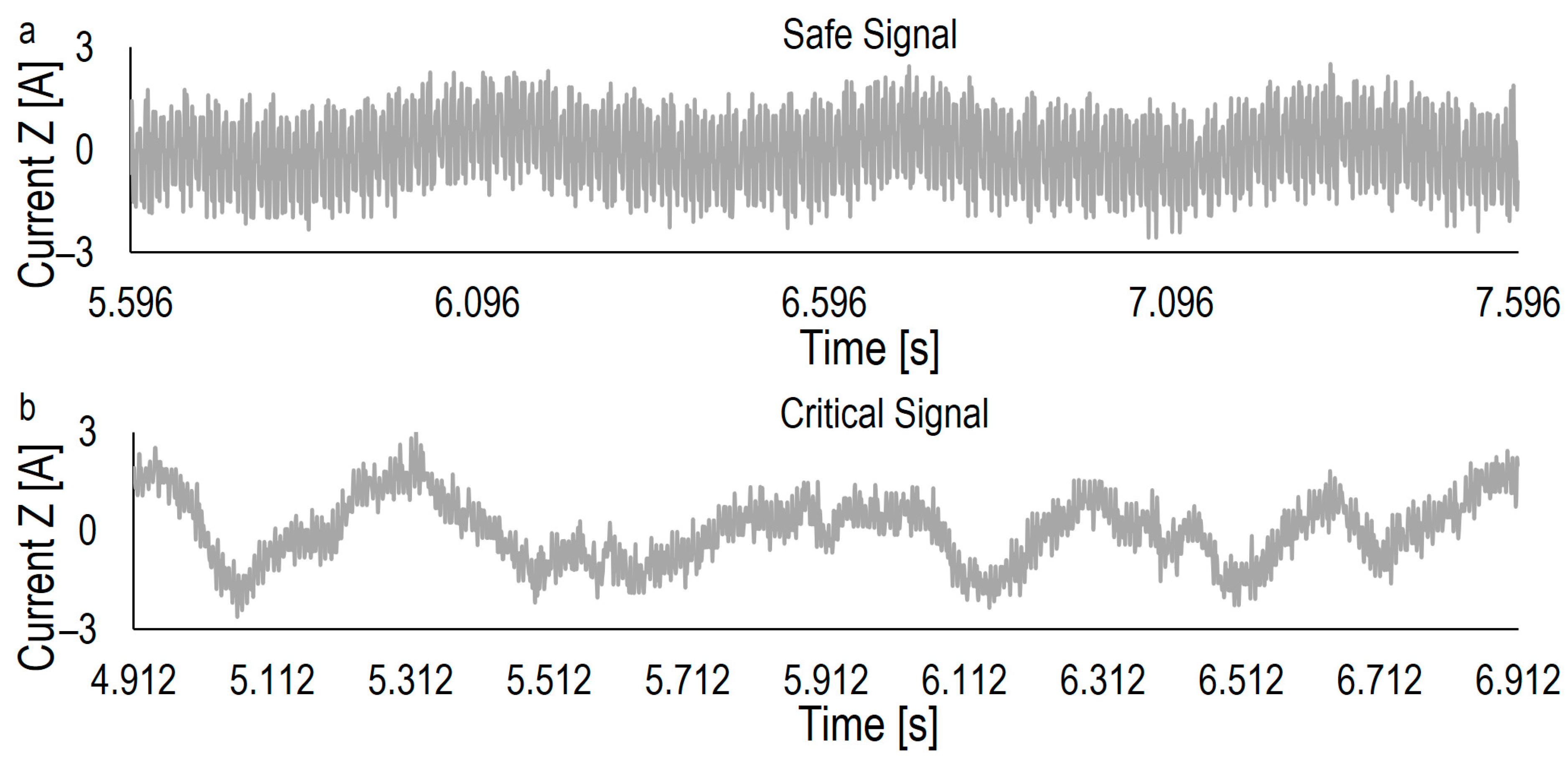
3. Signal Selection
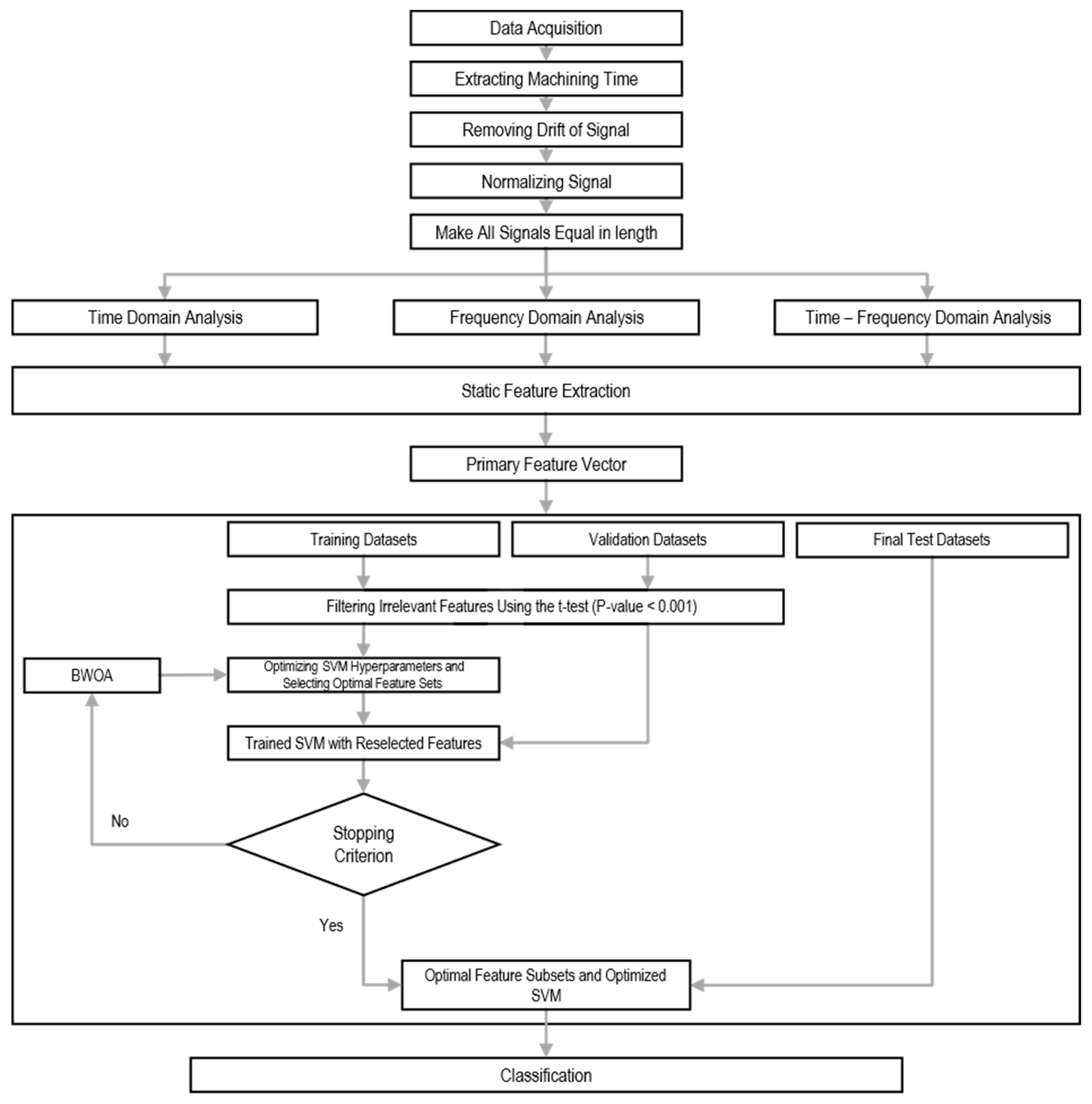
4. Methods
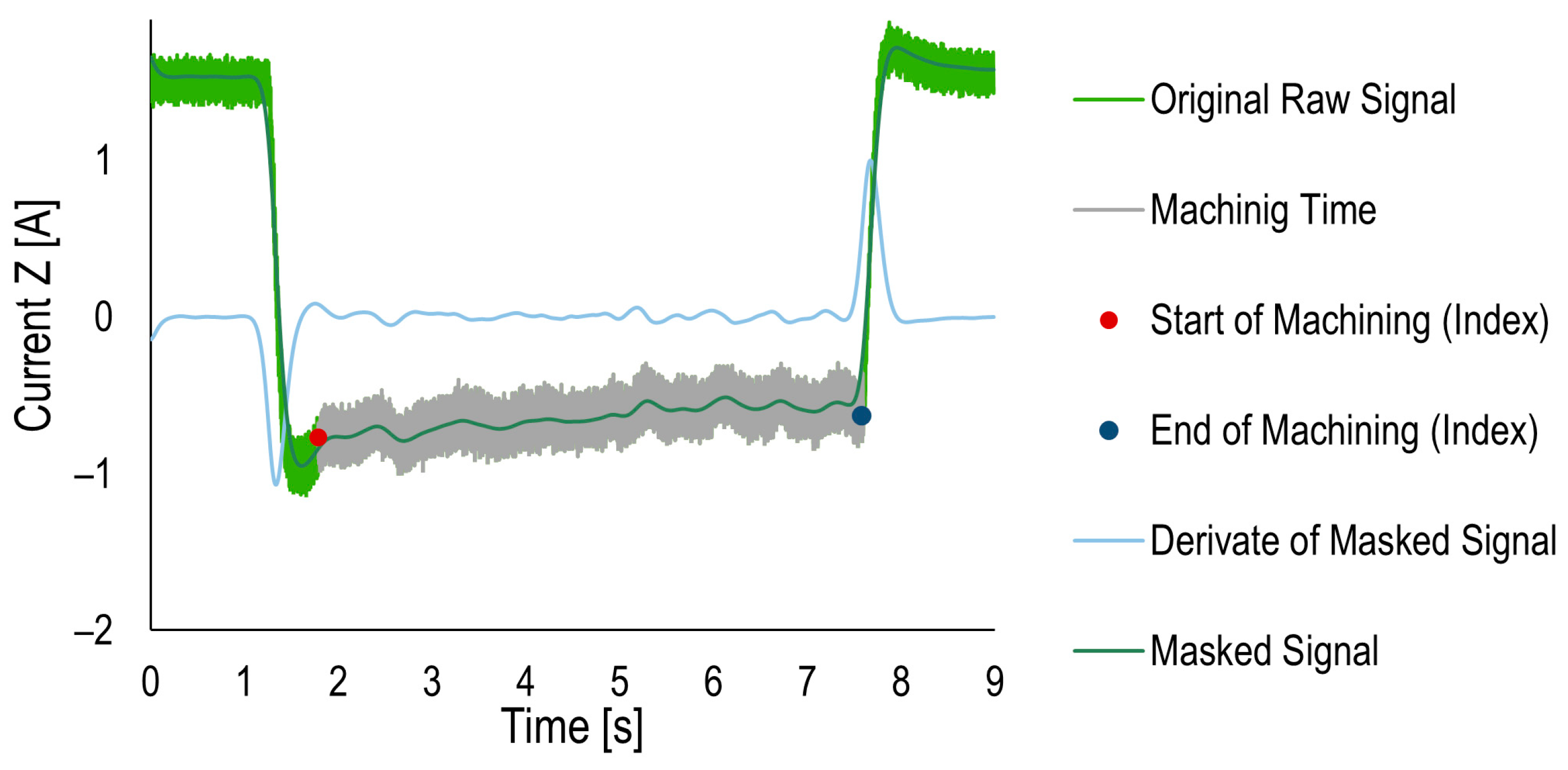
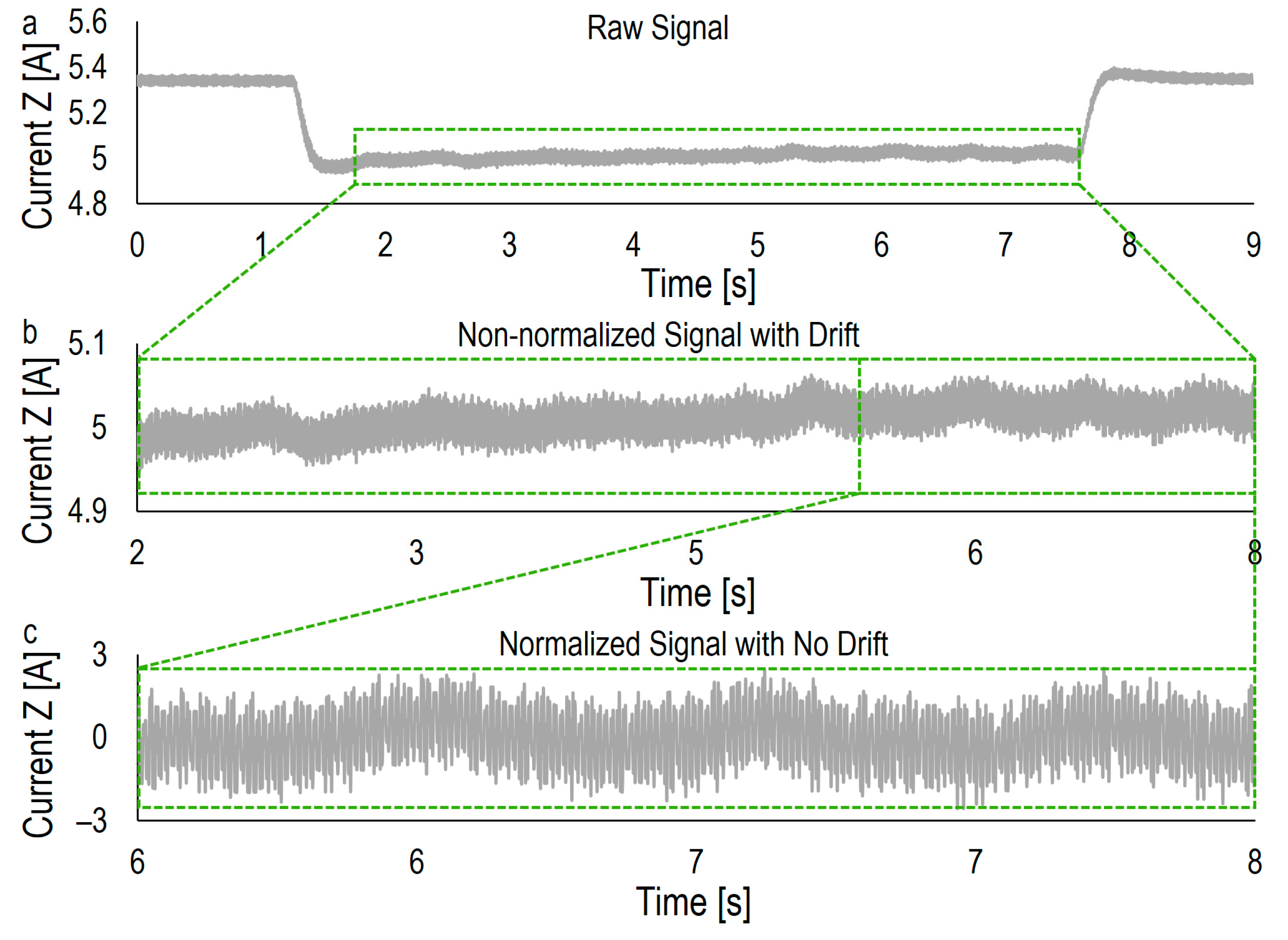
4.1. Preprocessing Signal
4.2. Signal Analysis
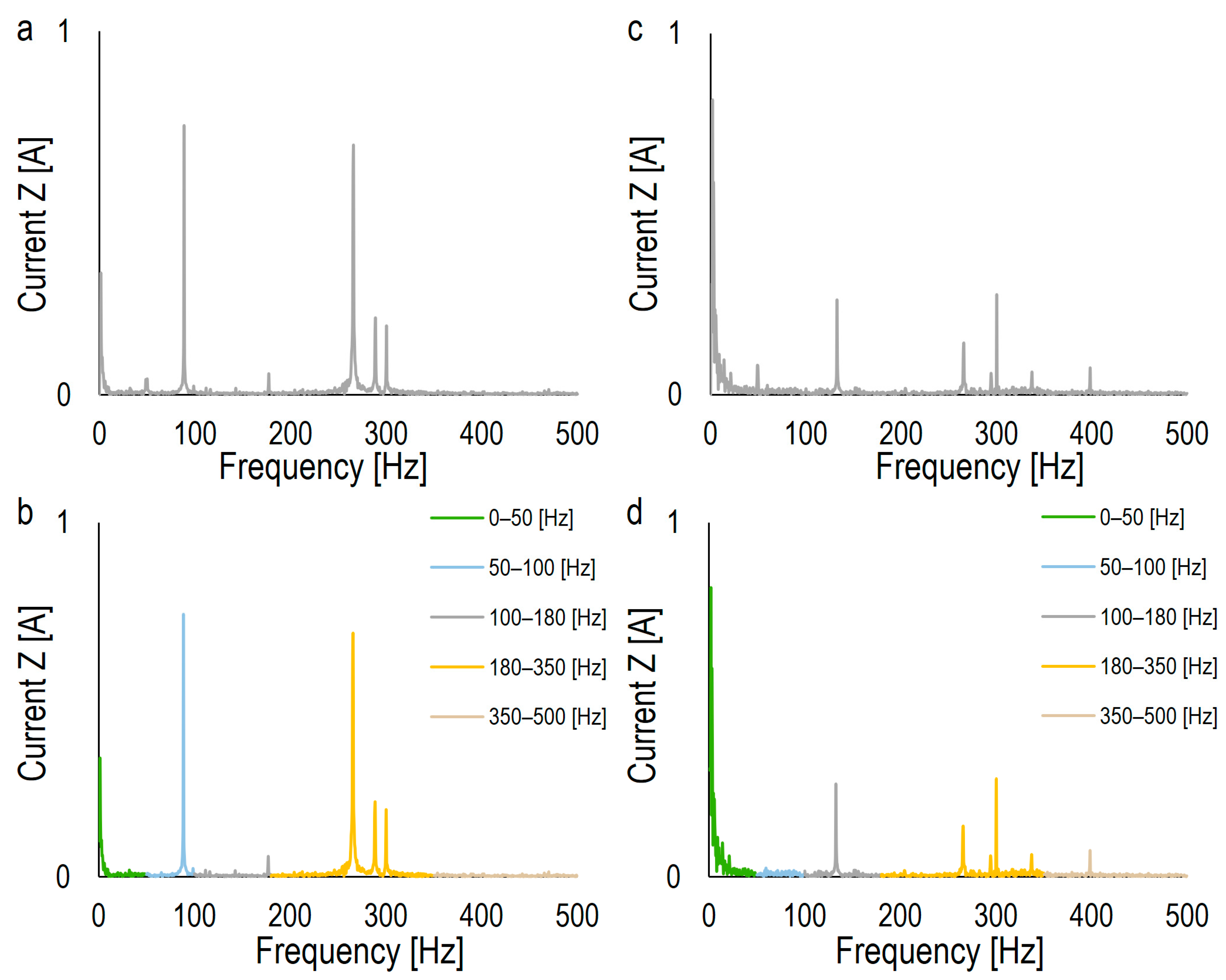
4.2.1. Frequency Domain
4.2.2. Time Domain
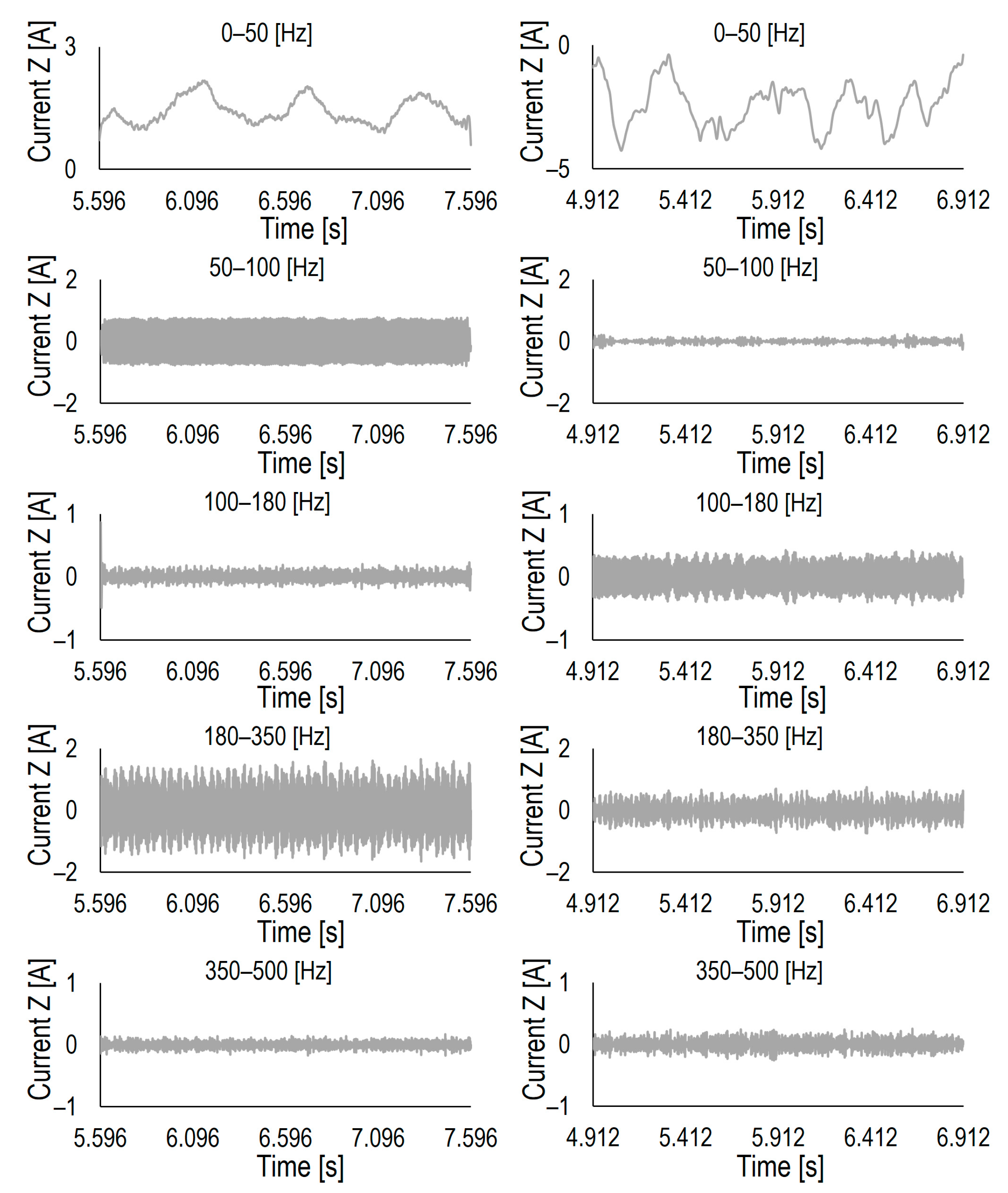
4.2.3. Time–Frequency Domain
4.3. Feature Extraction
4.4. Feature Selection
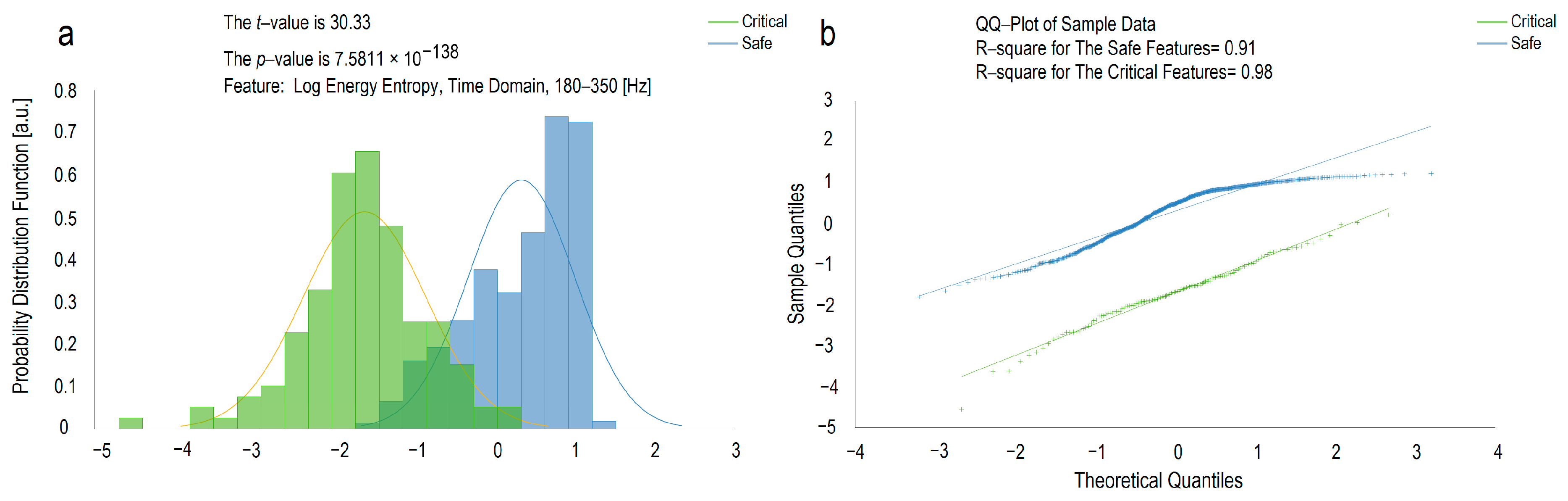
4.4.1. t-Test
4.4.2. Whale Optimization Algorithm (WOA)
4.5. Support Vector Machine (SVM)
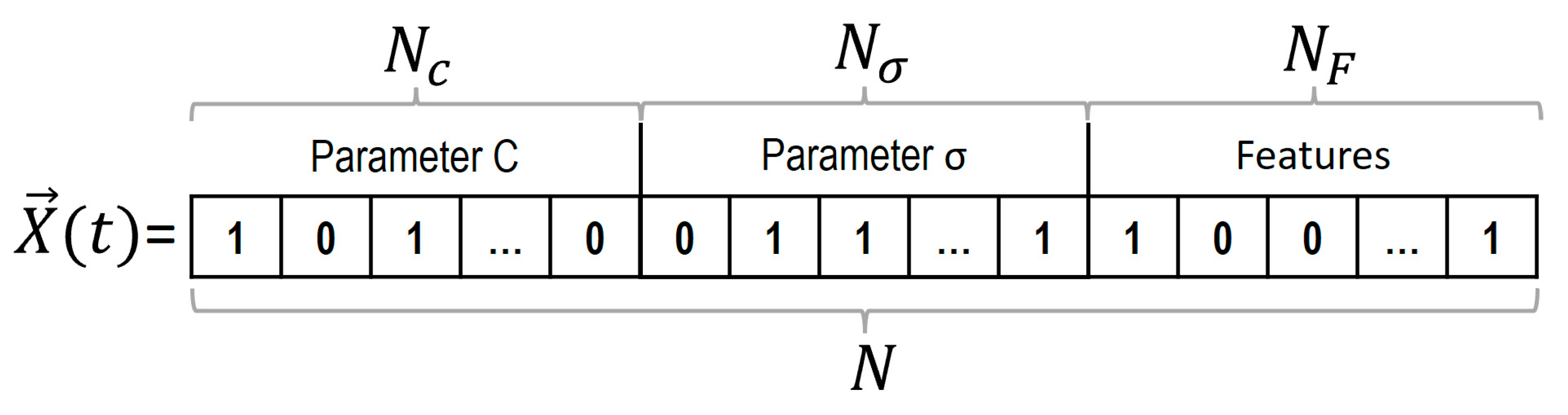
4.6. Encoding and WOA Parameters
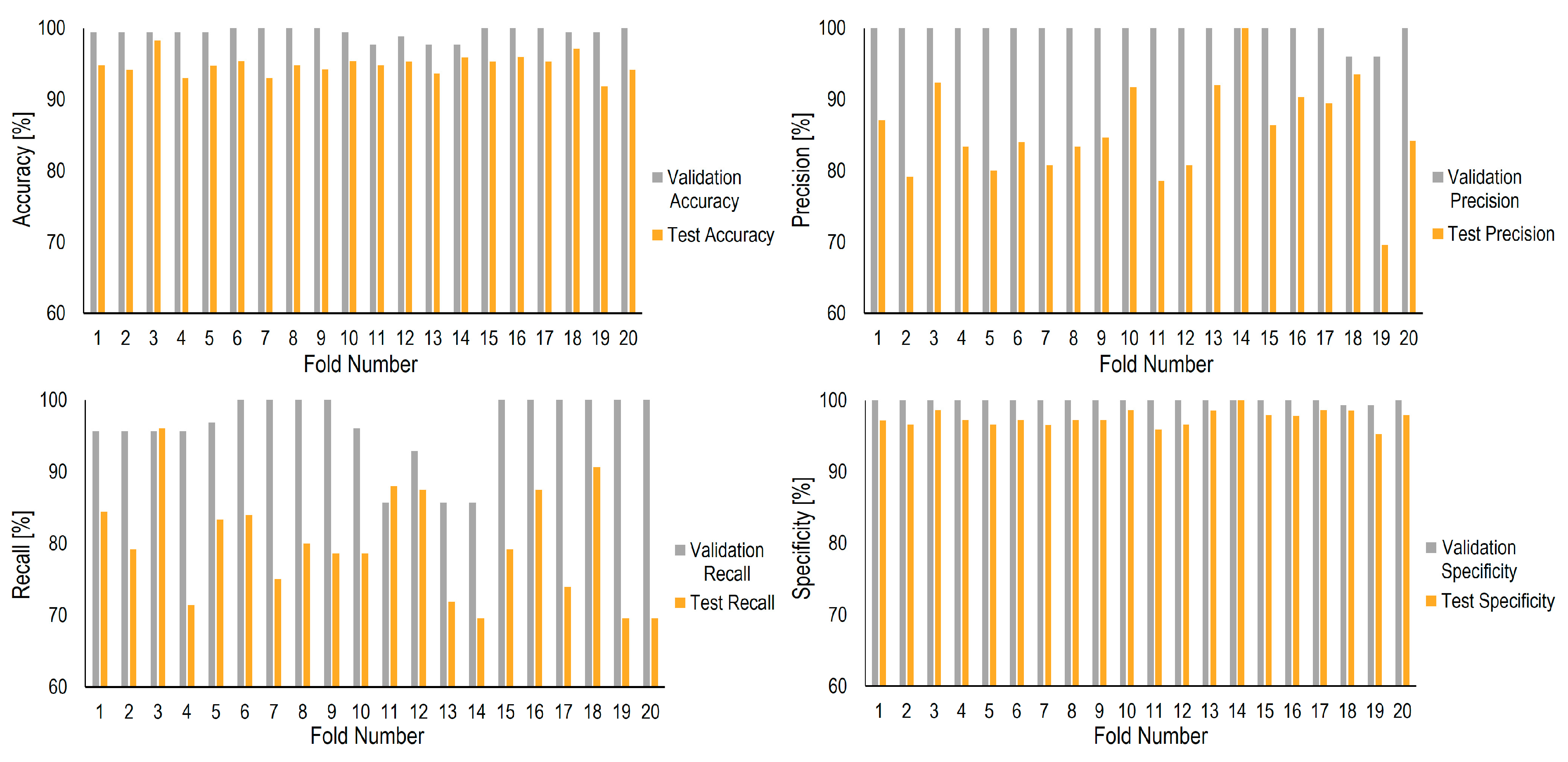
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michelsen, K.-E. Industry 4.0 in Retrospect and in Context. In Technical, Economic and Societal Effects of Manufacturing 4.0; IDEAS: Paris, France, 2020; pp. 1–14. [Google Scholar]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Bajaj, N.S.; Patange, A.D.; Jegadeeshwaran, R.; Pardeshi, S.S.; Kulkarni, K.A.; Ghatpande, R.S. Application of metaheuristic optimization based support vector machine for milling cutter health monitoring. Intell. Syst. Appl. 2023, 18, 200196. [Google Scholar] [CrossRef]
- He, Z.; Shi, T.; Xuan, J.; Li, T. Research on tool wear prediction based on temperature signals and deep learning. Wear 2021, 478–479, 203902. [Google Scholar] [CrossRef]
- Polini, W.; Turchetta, S. Cutting force, tool life and surface integrity in milling of titanium alloy Ti-6Al-4V with coated carbide tools. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 694–700. [Google Scholar] [CrossRef]
- Aghazadehkouzekonani, F. A Contribution to Online Tool Wear Detection Using Deep Learning Methodology. Ph.D. Thesis, École de Technologie Supérieure, Montréal, QC, Canada, 2020. [Google Scholar]
- Zhu, K.P.; Wong, Y.S.; Hong, G.S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results. Int. J. Mach. Tools Manuf. 2009, 49, 537–553. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Kumar Gupta, M.; da Silva, L.R.R.; Kiran, M.; Khanna, N.; Krolczyk, G.M. Application of measurement systems in tool condition monitoring of Milling: A review of measurement science approach. Meas. J. Int. Meas. Confed. 2022, 199, 111503. [Google Scholar] [CrossRef]
- Liu, M.K.; Tseng, Y.H.; Tran, M.Q. Tool wear monitoring and prediction based on sound signal. Int. J. Adv. Manuf. Technol. 2019, 103, 3361–3373. [Google Scholar] [CrossRef]
- García Plaza, E.; Núñez López, P.J. Application of the wavelet packet transform to vibration signals for surface roughness monitoring in CNC turning operations. Mech. Syst. Signal Process. 2018, 98, 902–919. [Google Scholar] [CrossRef]
- Segreto, T.; D’Addona, D.; Teti, R. Tool wear estimation in turning of Inconel 718 based on wavelet sensor signal analysis and machine learning paradigms. Prod. Eng. 2020, 14, 693–705. [Google Scholar] [CrossRef]
- Nezamivand Chegini, S.; Bagheri, A.; Najafi, F. A new intelligent fault diagnosis method for bearing in different speeds based on the FDAF-score algorithm, binary particle swarm optimization, and support vector machine. Soft Comput. 2020, 24, 10005–10023. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, X.; Yan, B.; Qiao, L.; Wang, Z. The time-frequency analysis of the acoustic signal produced in underwater discharges based on Variational Mode Decomposition and Hilbert–Huang TransforQm. Sci. Rep. 2023, 13, 22. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Ming, W.; An, Q.; Chen, M. Tool wear monitoring in milling of titanium alloy Ti–6Al–4 V under MQL conditions based on a new tool wear categorization method. Int. J. Adv. Manuf. Technol. 2019, 104, 4117–4128. [Google Scholar] [CrossRef]
- Li, X.; Dong, S.; Yuan, Z. Discrete wavelet transform for tool breakage monitoring. Int. J. Mach. Tools Manuf. 1999, 39, 1935–1944. [Google Scholar] [CrossRef]
- Li, G.; Yang, X.; Chen, D.; Song, A.; Fang, Y.; Zhou, J. Tool breakage detection using deep learning. In Proceedings of the 2018 IEEE/ACIS 3rd International Conference on Big Data, Cloud Computing, Data Science and Engineering, BCD 2018, Yonago, Japan, 12–13 July 2018; IEEE: New York, NY, USA, 2018; pp. 37–42. [Google Scholar]
- Kolar, P.; Burian, D.; Fojtu, P.; Masek, P.; Fiala, S.; Chladek, S.; Petracek, P.; Sveda, J.; Rytir, M. Indirect Drill Condition Monitoring Based on Machine Tool Control System Data. MM Sci. J. 2022, 2022-Octob, 5905–5912. [Google Scholar] [CrossRef]
- Tahir, N.H.M.; Muhammad, R.; Ghani, J.A.; Nuawi, M.Z.; Haron, C.H.C. Monitoring the flank wear using piezoelectric of rotating tool of main cutting force in end milling. J. Teknol. 2016, 78, 45–51. [Google Scholar] [CrossRef]
- Aghazadeh, F.; Tahan, A.; Thomas, M. Tool condition monitoring using spectral subtraction and convolutional neural networks in milling process. Int. J. Adv. Manuf. Technol. 2018, 98, 3217–3227. [Google Scholar] [CrossRef]
- Niaki, F.A.; Ulutan, D.; Mears, L. Wavelet based sensor fusion for tool condition monitoring of hard to machine materials. In Proceedings of the 2015 IEEE International Conference on Multisensor Fusion and Integration for Intelligent, San Diego, CA, USA, 14–16 September 2015; pp. 271–276. [Google Scholar]
- Hojati, F.; Azarhoushang, B.; Daneshi, A.; Hajyaghaee Khiabani, R. Prediction of Machining Condition Using Time Series Imaging and Deep Learning in Slot Milling of Titanium Alloy. J. Manuf. Mater. Process. 2022, 6, 145. [Google Scholar] [CrossRef]
- Pagani, L.; Parenti, P.; Cataldo, S.; Scott, P.J.; Annoni, M. Indirect cutting tool wear classification using deep learning and chip colour analysis. Int. J. Adv. Manuf. Technol. 2020, 111, 1099–1114. [Google Scholar] [CrossRef]
- Tabakhi, S.; Moradi, P. Relevance-redundancy feature selection based on ant colony optimization. Pattern Recognit. 2015, 48, 2798–2811. [Google Scholar] [CrossRef]
- Nouri-Moghaddam, B.; Ghazanfari, M.; Fathian, M. A novel bio-inspired hybrid multi-filter wrapper gene selection method with ensemble classifier for microarray data. In Neural Computing and Applications; Springer: London, UK, 2021; Volume 9. [Google Scholar] [CrossRef]
- Kusy, M.; Zajdel, R.; Kluska, J.; Zabinski, T. Fusion of Feature Selection Methods for Improving Model Accuracy in the Milling Process Data Classification Problem. In Proceedings of the 2020 International Joint Conference on Neural Networks, Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Xie, Z.; Li, J.; Lu, Y. Feature selection and a method to improve the performance of tool condition monitoring. Int. J. Adv. Manuf. Technol. 2019, 100, 3197–3206. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, G.; Zhang, Z.; Lu, J.; Ma, J. Tool wear state recognition based on GWO–SVM with feature selection of genetic algorithm. Int. J. Adv. Manuf. Technol. 2019, 104, 1051–1063. [Google Scholar] [CrossRef]
- Chen, Y.; Li, H.; Hou, L.; Wang, J.; Bu, X. An intelligent chatter detection method based on EEMD and feature selection with multi-channel vibration signals. Meas. J. Int. Meas. Confed. 2018, 127, 356–365. [Google Scholar] [CrossRef]
- Binsaeid, S.; Asfour, S.; Cho, S.; Onar, A. Machine ensemble approach for simultaneous detection of transient and gradual abnormalities in end milling using multisensor fusion. J. Mater. Process. Technol. 2009, 209, 4728–4738. [Google Scholar] [CrossRef]
- Kossakowska, J.; Bombiński, S.; Ejsmont, K. Analysis of the suitability of signal features for individual sensor types in the diagnosis of gradual tool wear in turning. Energies 2021, 14, 6489. [Google Scholar] [CrossRef]
- Lei, Z.; Zhu, Q.; Zhou, Y.; Sun, B.; Sun, W.; Pan, X. A GAPSO-Enhanced Extreme Learning Machine Method for Tool Wear Estimation in Milling Processes Based on Vibration Signals. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 8, 745–759. [Google Scholar] [CrossRef]
- García Plaza, E.; Núñez López, P.J. Analysis of cutting force signals by wavelet packet transform for surface roughness monitoring in CNC turning. Mech. Syst. Signal Process. 2018, 98, 634–651. [Google Scholar] [CrossRef]
- Khazaee, M.; Banakar, A.; Ghobadian, B.; Agha Mirsalim, M.; Minaei, S.; Jafari, S.M. Detection of inappropriate working conditions for the timing belt in internal-combustion engines using vibration signals and data mining. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 418–432. [Google Scholar] [CrossRef]
- Avijit Chakraborty, D.O. Frequency-time decomposition of seismic data using wavelet-based methods. Geophysics 1995, 60, 1058–1065. [Google Scholar] [CrossRef]
- Khazaee, M.; Ahmadi, H.; Omid, M.; Banakar, A.; Moosavian, A. Feature-level fusion based on wavelet transform and artificial neural network for fault diagnosis of planetary gearbox using acoustic and vibration signals. Insight Non-Destr. Test. Cond. Monit. 2013, 55, 323–330. [Google Scholar] [CrossRef]
- Moosavian, A.; Ahmadi, H.; Tabatabaeefar, A.; Khazaee, M. Comparison of two classifiers; K-nearest neighbor and artificial neural network, for fault diagnosis on a main engine journal-bearing. Shock Vib. 2013, 20, 263–272. [Google Scholar] [CrossRef]
- Potochnik, A.; Colombo, M.; Wright, C. Statistics and Probability. Recipes Sci. 2018, 167–206. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 2009; pp. 1–967. Available online: https://darmanto.akakom.ac.id/pengenalanpola/PatternRecognition4thEd.(2009).pdf (accessed on 11 August 2022). [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education India: Delhi, India, 2009. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Nezamivand Chegini, S.; Amini, P.; Ahmadi, B.; Bagheri, A.; Amirmostofian, I. Intelligent bearing fault diagnosis using swarm decomposition method and new hybrid particle swarm optimization algorithm. Soft Comput. 2022, 26, 1475–1497. [Google Scholar] [CrossRef]
- Nezamivand, C.S.; Bagheri, A.; Najafi, F. A New Hybrid Intelligent Technique Based on Improving the Compensation Distance Evaluation Technique and Support Vector Machine for Bearing Fault Diagnosis. Modares Mech. Eng. 2019, 19, 865–875. [Google Scholar]
- Eid, H.F. Binary whale optimisation: An effective swarm algorithm for feature selection. Int. J. Metaheuristics 2018, 7, 67. [Google Scholar] [CrossRef]
- Xu, H.; Fu, Y.; Fang, C.; Cao, Q.; Su, J.; Wei, S. An improved binary whale optimization algorithm for feature selection of network intrusion detection. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems, IDAACS-SWS 2018, Lviv, Ukraine, 20–21 September 2018; IEEE: New York, NY, USA, 2018; pp. 10–15. [Google Scholar]
- Da Li, A.; Xue, B.; Zhang, M. Multi-objective feature selection using hybridization of a genetic algorithm and direct multisearch for key quality characteristic selection. Inf. Sci. 2020, 523, 245–265. [Google Scholar]
- Abdar, A.K.; Sadjadi, S.M.; Bashirgonbadi, A.; Naghibi, M.; Soltanian-Zadeh, H. Extended VGG16 Deep-Learning Detects COVID-19 from Chest CT Images. AUT J. Electr. Eng. 2022, 54, 79–90. [Google Scholar]





| Cutting Speed, (m/min) | Feed Per Tooth, (μm/tooth) | Radial Depth of Cut, (mm) | Axial Depth of Cut, (mm) | Coolant |
|---|---|---|---|---|
| 50–113 | 17–50 | 3 | 1 | Oil/Dry |
| t-Test Rank | Domain | Frequency Band (Hz) | Feature Name |
|---|---|---|---|
| 1 | Time | 180–350 | Log Energy Entropy |
| 2 | Time | 180–350 | Hybrid Feature 1 |
| 3 | Frequency | 350–500 | Mean |
| 4 | Frequency | 350–500 | Hybrid Feature 1 |
| 5 | Time | 180–350 | Max |
| Total Selected Features | Validation Accuracy | Validation Precision | Validation Recall | Validation Specificity |
|---|---|---|---|---|
| 99.36 ± 0.78 | 99.60 ± 1.23 | 96.27 ± 5.06 | 99.93 ± 0.21 | |
| 16.45 ± 6.06 | Test Accuracy | Test Precision | Test Recall | Test Specificity |
| 94.84 ± 1.43 | 85.55 ± 6.79 | 79.89 ± 7.69 | 97.52 ± 1.13 | |
| Caverage | σaverage | CBest fold | σBest fold | |
| 41.75 ± 23.19 | 5.41 ± 1.32 | 75.39 ± 0 | 5.04 ± 0 |
| Number | Number of Repetitions across 20 Folds | Domain | Frequency Band (Hz) | Feature Name |
|---|---|---|---|---|
| 1 | 9 | Time–Frequency | 0–15.6 | Teager Kaiser |
| 2 | 8 | Frequency | 350–500 | Teager Kaiser |
| 3 | 5 | Time–Frequency | 78.1–93.7 | Log Energy Entropy |
| 4 | 4 | Time–Frequency | 359.3–375 | Range |
| 5 | 3 | Frequency | 350–500 | Log Energy Entropy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmani, A.; Hojati, F.; Hadad, M.; Azarhoushang, B. A Hybrid Approach for Predicting Critical Machining Conditions in Titanium Alloy Slot Milling Using Feature Selection and Binary Whale Optimization Algorithm. Machines 2023, 11, 835. https://doi.org/10.3390/machines11080835
Rahmani A, Hojati F, Hadad M, Azarhoushang B. A Hybrid Approach for Predicting Critical Machining Conditions in Titanium Alloy Slot Milling Using Feature Selection and Binary Whale Optimization Algorithm. Machines. 2023; 11(8):835. https://doi.org/10.3390/machines11080835
Chicago/Turabian StyleRahmani, Amirsajjad, Faramarz Hojati, Mohammadjafar Hadad, and Bahman Azarhoushang. 2023. "A Hybrid Approach for Predicting Critical Machining Conditions in Titanium Alloy Slot Milling Using Feature Selection and Binary Whale Optimization Algorithm" Machines 11, no. 8: 835. https://doi.org/10.3390/machines11080835
APA StyleRahmani, A., Hojati, F., Hadad, M., & Azarhoushang, B. (2023). A Hybrid Approach for Predicting Critical Machining Conditions in Titanium Alloy Slot Milling Using Feature Selection and Binary Whale Optimization Algorithm. Machines, 11(8), 835. https://doi.org/10.3390/machines11080835








