Mass Flow Function Correlation for Solid and Honeycomb Land Labyrinth Seals including Fin Front Angle, Clearance, Fin Number and Honeycomb Geometry

Abstract

In this study, the effects of several geometry factors (fin front angle, clearance, number of fins, and honeycomb cell diameter and depth) on the mass flow function of solid and honeycomb land were studied experimentally. The fin front angle considered in the experiment ranged from 60 to 90 degrees, the number of fins was varied between two and three, and the diameter and depth of the honeycomb cell ranged from 1.33 to 4.00 times and 8.08 to 13.08 times the thickness of the fin tip, respectively. The experimental results showed that the mass flow function decreased as the number of fins increased for the solid land labyrinth seal, and the mass flow function increased as the clearance increased. A fin front angle of 60 degrees was found to have the minimum mass flow function. For the honeycomb land labyrinth seal, the mass flow function decreased as the number of fins increased, and the effect of the cell depth was shown to be insignificant compared to the effect of the cell diameter. The effects of cell diameter and cell depth on the mass flow function depended on the conditions of other variables. In addition, the correlation equations of the mass flow functions of the solid land and honeycomb land labyrinth seals are presented based on the experimental results, which represent the effects of the fin front angle, clearance, pressure ratio, and diameter and depth of the honeycomb cell. The correlation equation for the solid land labyrinth seal had an $r^2$ value of 0.9822, while the correlation equation for honeycomb land had an $r^2$ value of 0.9621.

1. Introduction

The existence of clearances between blade tips and the casing is inevitable for gas turbines. The leakage flows that occur in these clearances contribute to a large part of the overall turbine efficiency loss [1]. To reduce losses due to tip leakage, various sealing techniques, such as the optimization of the blade cross-sectional shape, brush seal, and labyrinth seal [2,3], are applied to the blade tip. Labyrinth-sealing techniques have been studied since the 20th century. The primary advantages of labyrinth seals are their simple structure and high thermal resistance [4], which lead to them still being applied in modern gas turbines [5,6,7].

A common principle of labyrinth seals at gas turbine blades is to reduce leakages by increasing the flow resistance with fins installed above the blade tip at the clearance. The sealing performance of a labyrinth seal is strongly influenced by associated variables, including the angle, thickness, and number of fins, and the clearance between the casing and fin tips [8,9,10,11,12].

Labyrinth seals are classified into two types, namely solid land labyrinth seals and honeycomb land labyrinth seals, depending on whether a honeycomb structure is applied to the land part. A casing with a honeycomb labyrinth seal has the advantage of being lighter in weight than a casing with a solid land, which can reduce turbine vibration [13], and it has the advantage of being less abrasive than a solid land labyrinth seal when the fin and the casing are in contact due to thermal expansion [14]. For honeycomb land labyrinth seals, it is known that the geometric factors of the honeycomb cells (diameter, depth, thickness, etc.) greatly affect the airtight performance of the seal [15,16,17].

Previous research works on labyrinth sealing techniques have mainly reported the effects of geometric factors. Desando et al. [18] experimentally studied the effect of fin thickness on the performance of a solid land labyrinth seal, showing that the leakage flow rate decreases with increasing fin thickness. Kuwamura et al. [19] studied the effect of the position of the fin and the shape of the cavity on the sealing performance in a stepped labyrinth seal, and found that the position of the fin has a significant effect on the sealing performance, and that circular-shaped cavities have a high sealing performance in all pressure ranges. Lee et al. [20] experimentally investigated the effects of factors such as the fin front angle (FFA), number of fins, and clearance on the sealing performance of a solid land labyrinth seal and presented experimental correlations for each variable. In addition, flow visualization using the Schlieren technique was used to observe the flow separation at the fin tip and the vortex structure inside the cavity. Li et al. [21] compared the effects of the cell depth and cell diameter in honeycomb labyrinth seals through computational analysis and found that an optimal cell depth and diameter exist under each condition. Using experimental and computational results, Zhang et al. [22] proposed a correlation equation involving the thickness of the fin tip and the number of fins, FFA, clearance, and pressure ratio in a stepped labyrinth seal, and proposed a correction factor based on the FFA. Chun and Ahn [23] conducted a computational study to investigate the effect of the geometric parameters of a stepped labyrinth seal on the discharge coefficient. Their research underscored that among these parameters, the step height within the stepped labyrinth seal exhibited the highest degree of sensitivity in relation to the discharge coefficient. Hu et al. [24] carried out a computational analysis to examine the effect of the geometry of honeycomb cells on the flow characteristics in a honeycomb labyrinth seal. They observed that, in honeycomb lands with relatively large diameters, an increase in the honeycomb cell depth led to a noticeable increase in the mass flow rate.

In this study, we conducted experimental research to investigate the impact of various geometric factors on the actual performance of a labyrinth seal. The factors examined in this research include the number of fins, fin frontal angle, clearance, and honeycomb cell depth and diameter. Tests were performed in a test rig with a straight flow path, and both solid and honeycomb lands were considered. Based on the experimental results, the mass flow function correlation equations for each geometric factor are presented in the paper.

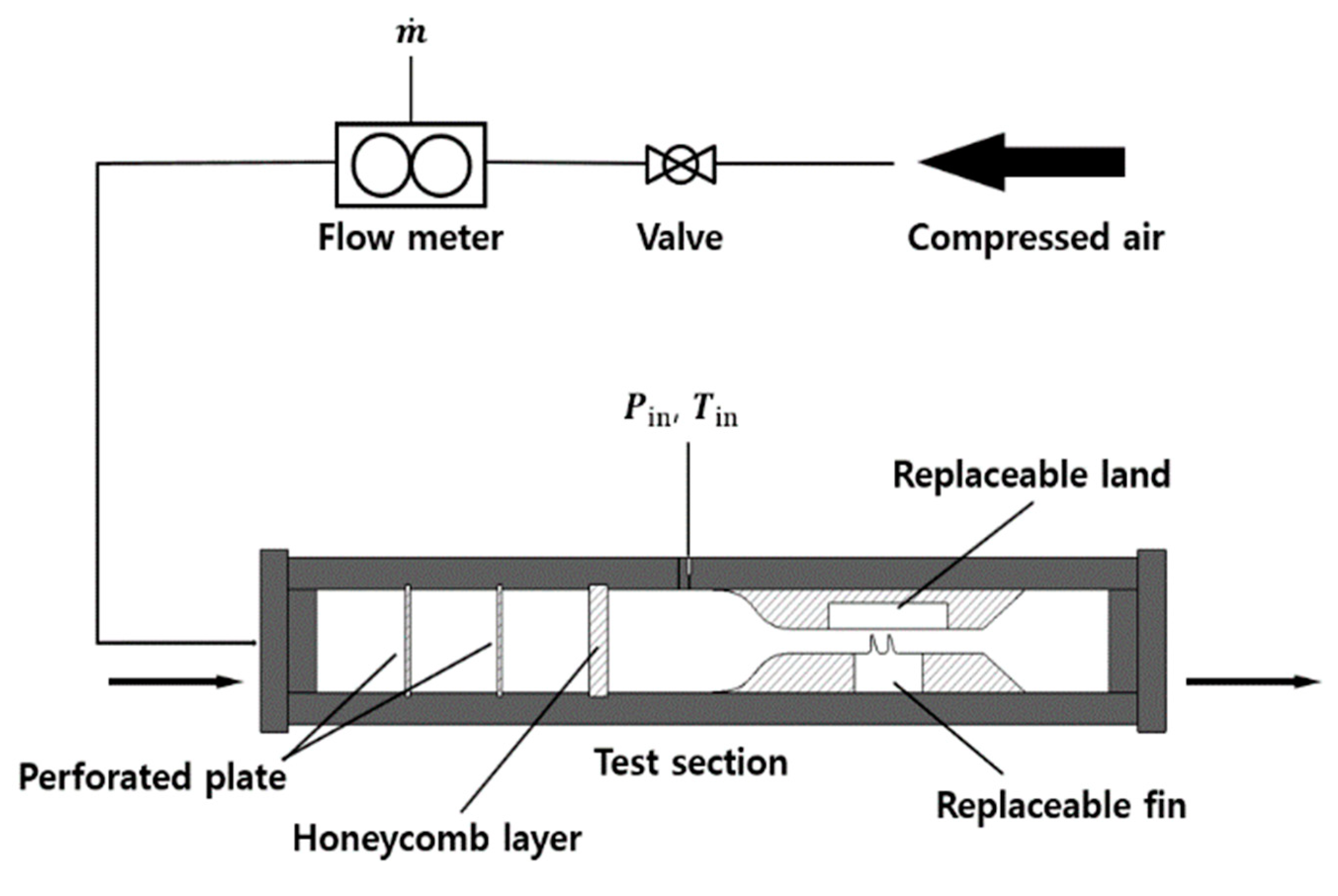
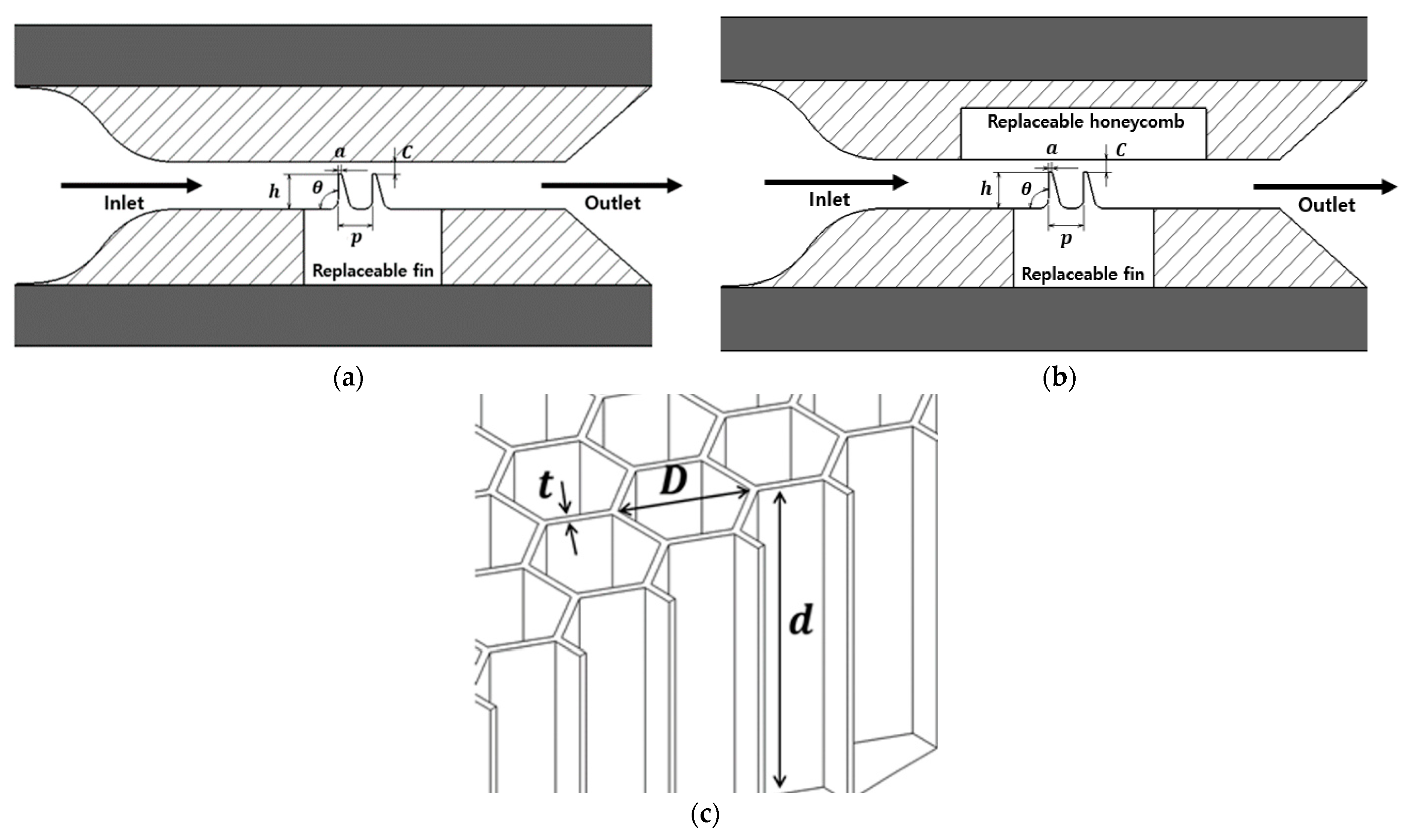
2. Experimental Methods

The experimental setup of this study is shown in the schematic diagram of Figure 1. Compressed air at 8.6 bar enters the test section after passing through a valve and a flow meter. The width of the test section was 40 mm, and the outlet was exposed to the atmosphere. The flow was controlled by adjusting the inlet and outlet pressure ratio. The inlet pressure of the flow was measured using a manometer (PX409-050GL, OMEGA, USA), and the mass flow rate corresponding to each pressure ratio was measured using a thermal mass flow meter (FD-TMS-50 mm, Republic of Korea). To ensure a uniform inlet flow, a perforated plate and a honeycomb layer were installed in the main flow path before the test section.

Figure 2a,b shows the geometry of the test piece and the shape factors of the labyrinth seal, where a is the thickness of the fin, C is the clearance between the land and the fin tip, h is the height of the fin, p is the distance between the fin, and θ is the FFA. Figure 2c shows the parameters of the honeycomb cell used in the honeycomb labyrinth seal. D is the diameter of the honeycomb cell, d is the depth of the honeycomb cell, and t is the thickness of the honeycomb cell. Figure 3 shows the replaceable fins used in the experiments, which were conducted using varying FFA and N.

Table 1. Geometry of labyrinth seal.

Seal Type	Solid Land	Honeycomb Land
FFA (θ)	60°, 75°, 90°
Number of fin (N)	2, 3
Fin tip thickness (a)	1.2 mm
Pitch (p/a)	10
Clearance (C/a)	1.16~2.82	1.15~3.65
Honeycomb cell thickness (t/a)	-	0.25
Honeycomb cell diameter (D/a)	-	1.33~4.00
Honeycomb cell depth (d/a)	-	8.08~13.08

shows the range of each geometric factor used in this study.

$$\varphi =\frac{\dot{m}\sqrt{T_0}}{A_c{P}_0}$$

(1)

The performance of the seal with each geometric factor was analyzed using the mass flow function [25], which is defined by Equation (1). In Equation (1), $\dot{m,}{T}_0,A_c,P_0$ are the mass flow rate, total temperature, clearance area, and total pressure, respectively. The clearance area was calculated by physically measuring the size of the clearance during the installation. The predicted measurement uncertainty of the mass flow function was estimated to be 2.3% [26].

3. Results and Discussions

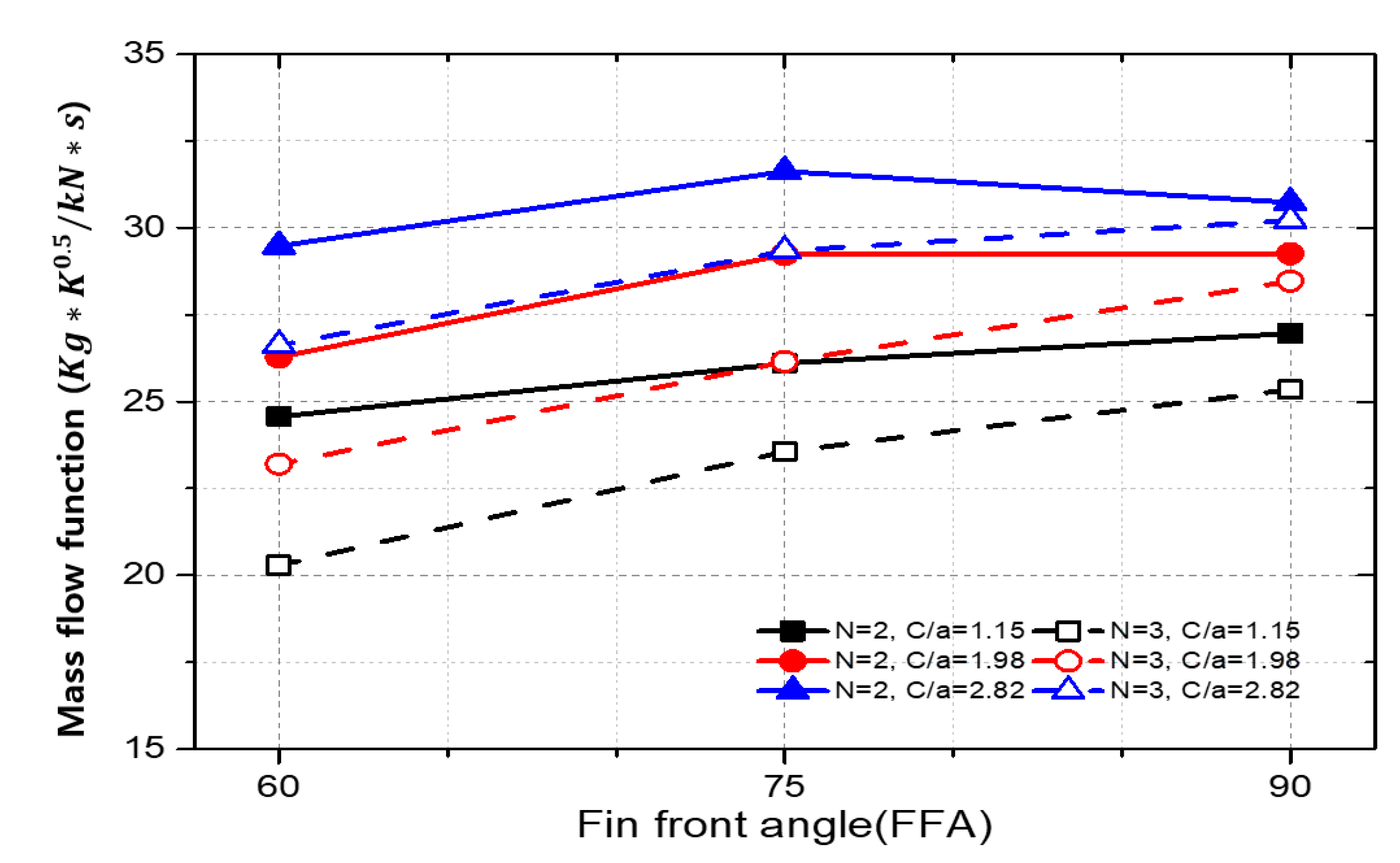
3.1. Solid Land Labyrinth Seal

Figure 4 shows the measured mass flow function as a function of the pressure ratio, clearance, and the number of fins for each FFA. For all three angles, the mass flow function decreases as the number of fins increases from two to three, which confirms the same trend as Zhang et al. [22]. In addition, the mass flow function increases as the pressure ratio increases, and the mass flow function increases as the clearance increases in all cases. The trend observed in the tests was similar to previous studies [15,16,22].

Figure 5 shows the effect of FFA on the size of the clearance and the number of fins at a pressure ratio of 1.7. Smaller FFAs resulted in lower mass flow functions in all cases. This effect was greater when the number of fins was three.

Based on the measured data and Zhang’s correlation equation [22], a new correlation equation of the mass flow function, Equation (2), with the FFA, clearance, pressure ratio, and number of fins as variables, was derived.

Table 2. Coefficient of correlation of solid land labyrinth seal.

Parameters	Constraints
FFA (θ)	90~60°
Clearance (C/a)	1.1~2.82
Number of fin (N)	2, 3
PR	1.1~1.7
$r^2$	0.9822
i	0.1915
j	22.5635
k	0.2250
l	−0.2230
m	0.4594

shows the range of geometric factors reflected in the correlation equation and the coefficient of determination. The coefficient of determination, $r^2$, was 0.9822, showing a good fit.

$$\varphi =(i\theta +j){\left(\frac{C}{a}\right)}^k{\left(1-0.9\frac{N-1}{N}\right)}^l{\left(\frac{1-{PR}^{-2}}{N}\right)}^m$$

(2)

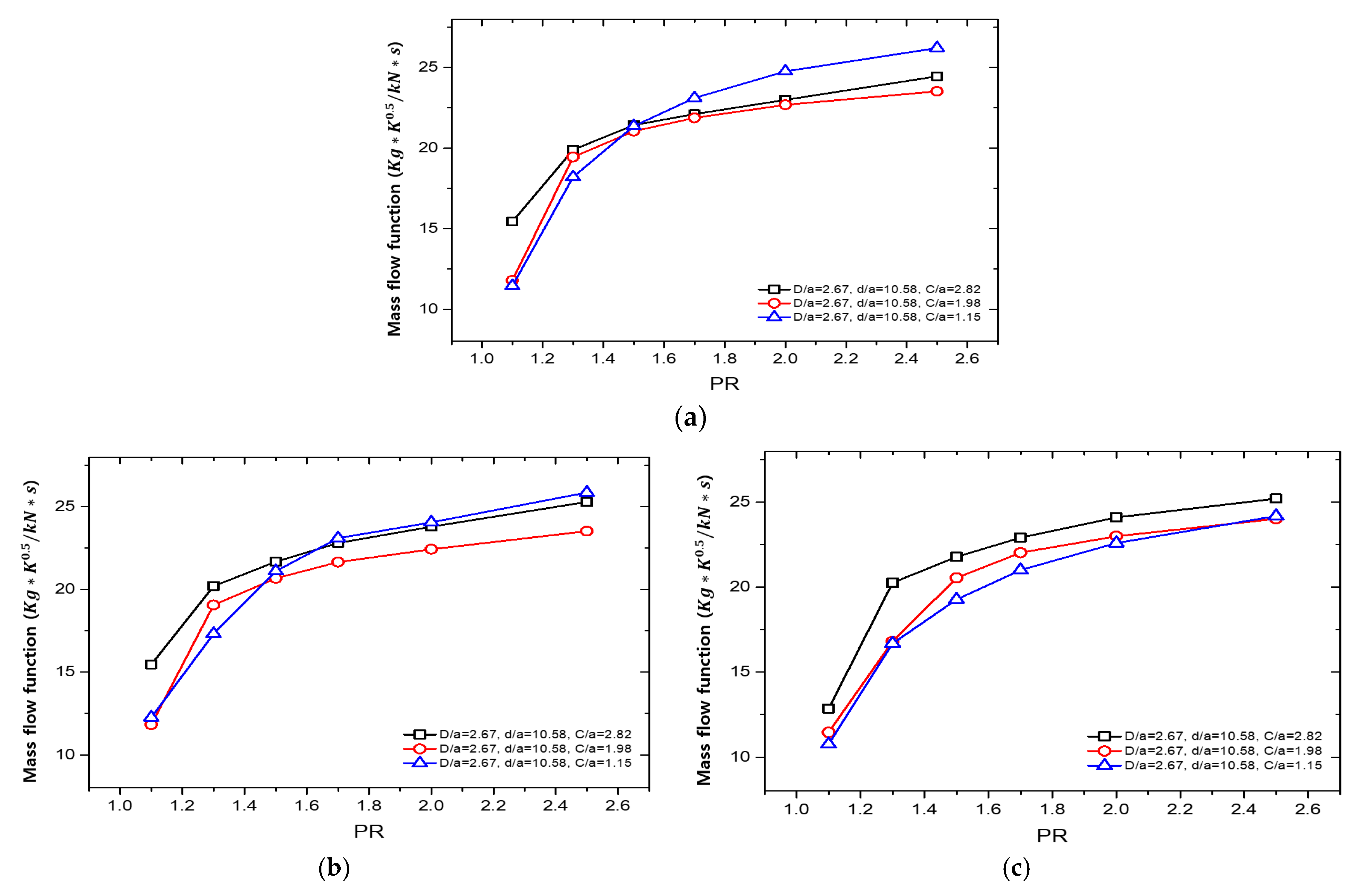
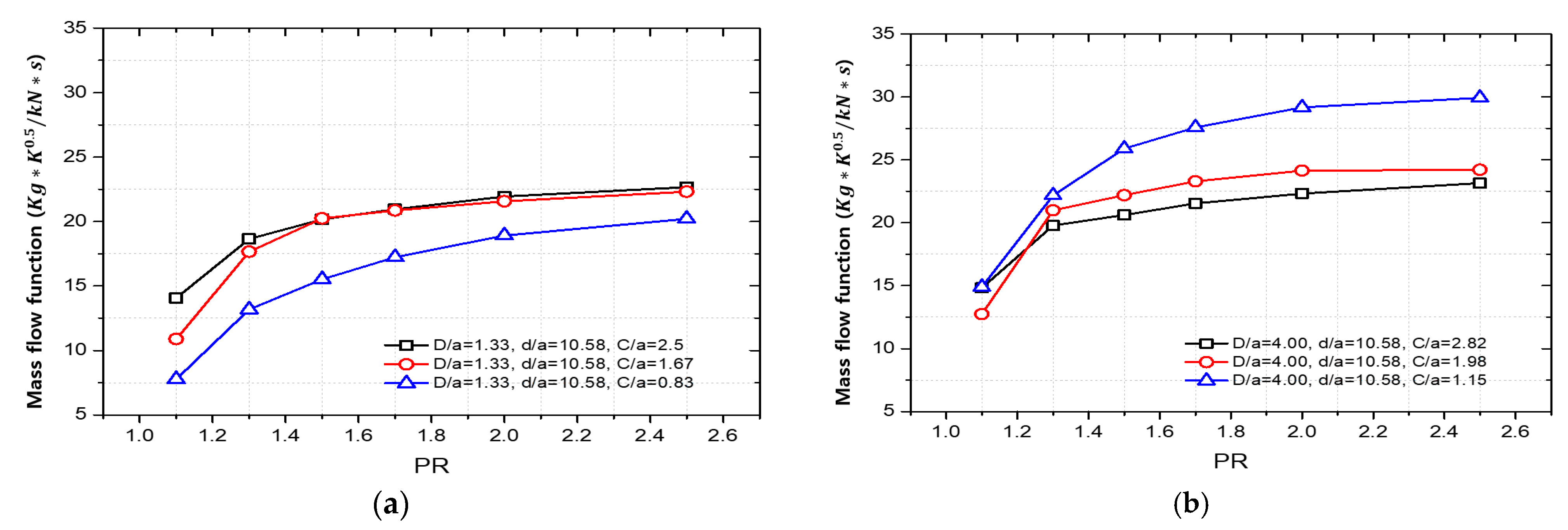
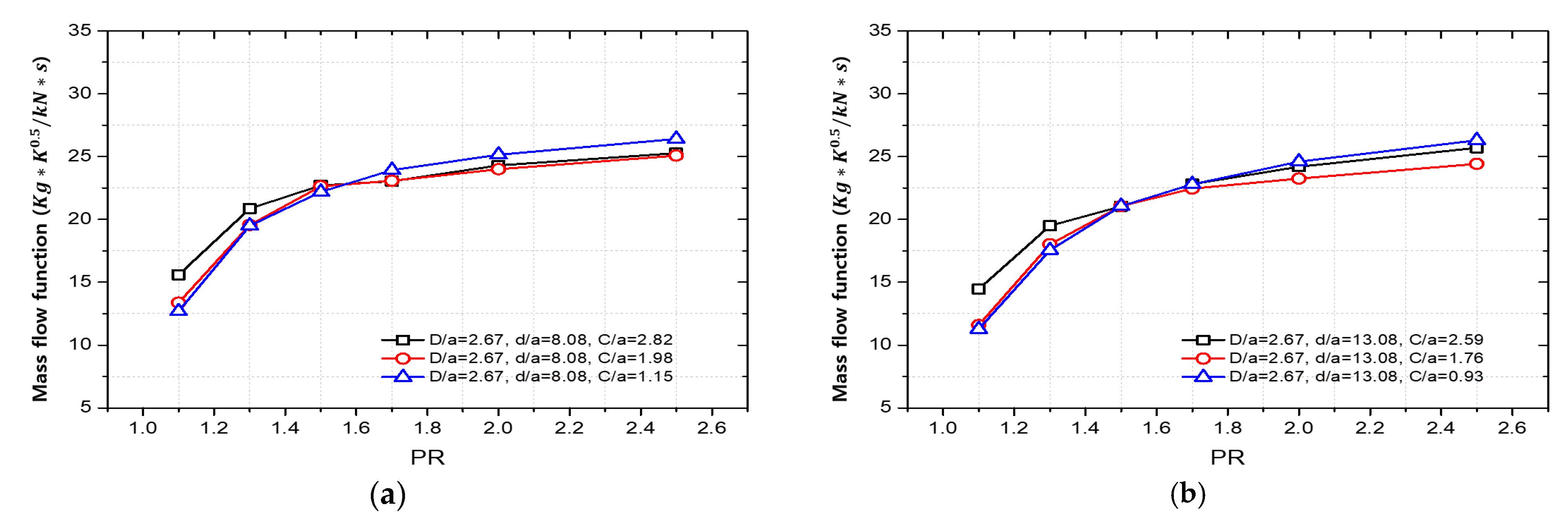
3.2. Honeycomb Land Labyrinth Seal

Figure 6 compares the effect of the number of fins for the honeycomb land application at FFA = 90°. As the pressure ratio increases, the mass flow function tends to increase. The mass flow function tends to decrease when the number of fins increases from two to three, as in the case of the solid land.

Figure 7 shows the effect of clearance per FFA in a honeycomb labyrinth seal with the same honeycomb cell size (D/a = 2.67, d/a = 10.58). Below the pressure ratio of 1.5, all FFAs showed higher mass flow functions with larger clearances, but this trend was not observed above the pressure ratio of 1.5, except for the case of FFA = 60°. In other words, for the honeycomb land labyrinth seal, the effect of clearances on the mass flow function depends on the FFA and pressure ratio. Kaczyński et al. [15] found that the flow pattern of a labyrinth seal changes with the clearance and FFA. According to that, our results in Figure 7 can be understood as the changed effect of the clearance due to the changed flow pattern.

Figure 8 shows a comparison of the effects of cell diameters and clearances for a given cell depth. The mass flow function increased with the increasing clearance for D/a = 1.33 (Figure 8a), but the opposite trend was observed for D/a = 4.00 (Figure 8b). The trend in Figure 8b shows the same trend as in the study of Frączek et al. [16], whereas Figure 8a shows the same trend as the experimental results of the solid land labyrinth seal. This is interpreted as the tendency of the leakage flow to behave in a similar way as the solid land, as it decreases to enter the cell as the cell diameter decreases. On the other hand, the leakage flow entering the cell increases as the cell diameter increases, and the changed flow pattern increases the effective clearance, causing the mass flow function to increase. In other words, the effect of the clearance on the mass flow function depends on the cell diameter.

Figure 9 compares the effects of cell depth and clearance for a given cell diameter, and Figure 9a,b shows the mass flow function graphs for d/a = 8.08 and 10.58, respectively. In both cases, the mass flow function increased with increasing clearance under a PR below 1.5. However, the mass flow function showed the maximum at the smallest clearance under a PR above 1.5. Therefore, the effect of cell diameter on the mass flow function showed dependence on the pressure ratio and clearance. The effect of clearance was not significant for a given cell depth. This is because the effect of cell diameter is stronger than that of cell depth, as explained by Desando et al. [18].

Based on the measured results and Zhang’s correlation equation [22], we derived a new correlation equation with FFA, clearance, honeycomb cell depth, and diameter as variables. The honeycomb shape factors, cell diameter and depth, were added as variables, and the correlation equation is shown in Equation (3).

Table 3. Coefficient of correlation of honeycomb land labyrinth seal.

Parameters	Constraints
FFA (θ)	90~60°
Clearance (C/a)	0.83~1.98
Number of fin (N)	2, 3
Cell diameter (D/a)	1.33~2.67
Cell depth (d/a)	8.08~13.08
PR	1.1~1.7
$r^2$	0.9621
i	0.1019
j	34.1676
k	0.0465
l	0.1790
m	−0.2072
n	0.4824

shows the range of shape factors reflected in the correlation equation and the coefficient of the correlation equation. The coefficient of the determinant for the correlation equation, $r^2$, was 0.9621, which is lower than that of solid land. This is because the influence of the diameter and depth of the honeycomb cell tended to vary depending on the clearance, as described earlier.

$$\varphi =\left(i\theta +j\right){\left(\frac{C}{a}\right)}^k{\left(\frac{D}{d}\right)}^l{\left(1-0.9\frac{N-1}{N}\right)}^m{\left(\frac{1-{PR}^{-2}}{N}\right)}^n$$

(3)

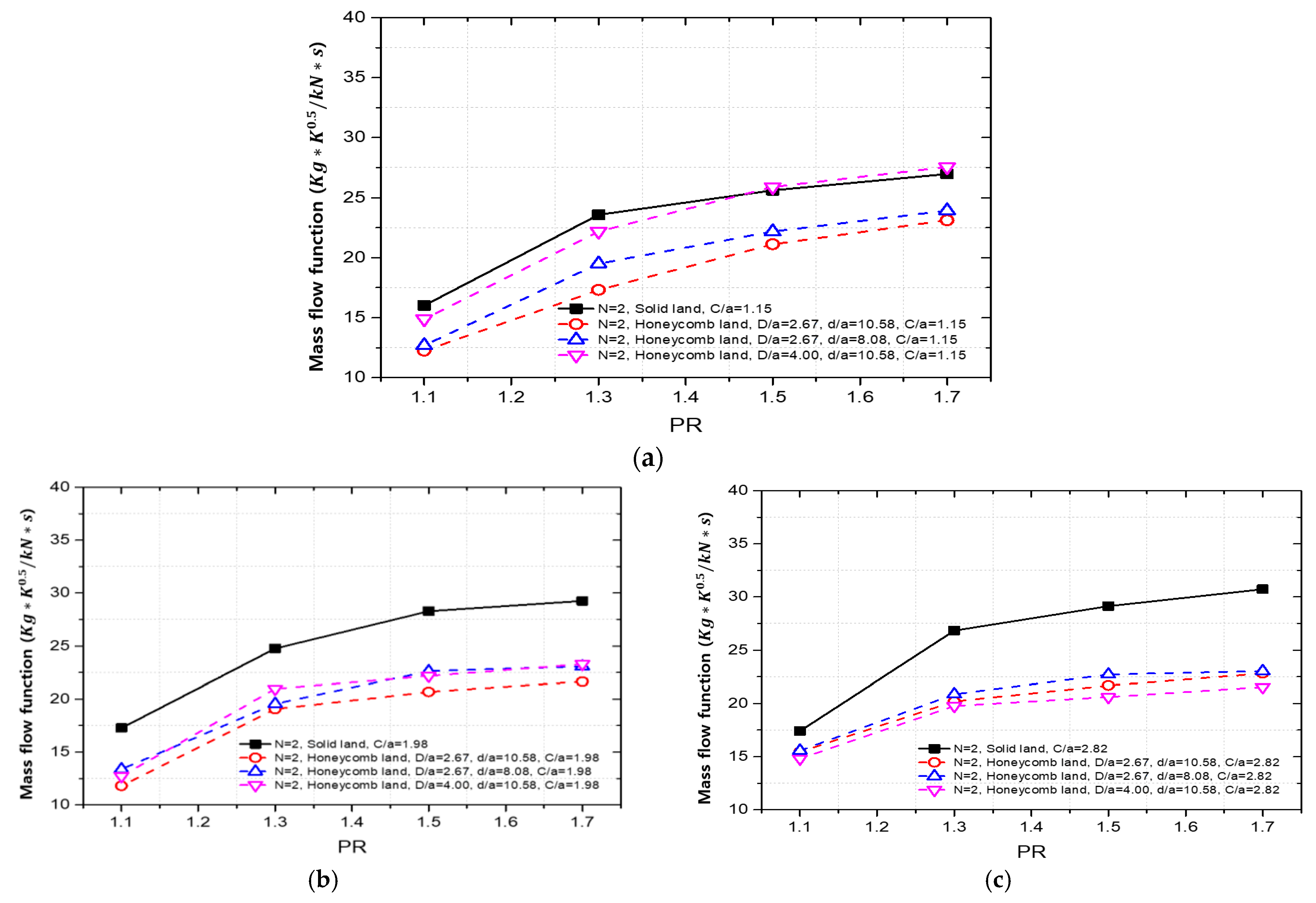
3.3. Comparison of Solid Land and Honeycomb Land Labyrinth Seal

Figure 10 is a graph comparing the solid land labyrinth seal and the honeycomb land labyrinth seal with the same number of fins, clearance, and FFA. In most cases, the honeycomb land application showed lower mass flow function values, indicating that the honeycomb land application improved the sealing performance.

4. Conclusions

In this study, the effects of various geometric factors on the sealing performance of solid land labyrinth seals and honeycomb land labyrinth seals were experimentally verified. The experimental results were used to derive a correlation equation of the mass flow function with the relevant geometric factors. The main results are as follows.

(1)

Regarding the solid land labyrinth seal, the mass flow function exhibited its lowest value at the FFA (forward facing angle) of 60°. Additionally, the mass flow function demonstrated a decreasing trend as the clearance decreased.

(2)

In both solid and honeycomb lands, employing three fins resulted in a higher sealing performance compared to using two fins.

(3)

The effect of the honeycomb cell diameter on the flow rate function varied depending on the clearance, while the effect of cell depth on the flow rate function was relatively minor compared to the influence of cell diameter.

(4)

In general, the honeycomb land labyrinth seal exhibited lower mass flow function values compared to the solid land seal with the same number of fins, FFA, and clearance.

(5)

Based on the experimental results, correlation equations were derived for both solid and honeycomb lands. It is expected that these equations can be applied to various seal designs.

In this study, experiments were conducted in a simplified test rig to establish flow rate function correlations for honeycomb land and solid land labyrinth seals. In the future, it is suggested that similar studies are carried out in experimental setups that simulate the real operational conditions of gas turbines, such as under rotational conditions or using annular-shaped devices.