A Theoretical and Experimental Identification with Featured Structures for Crucial Position-Independent Geometric Errors in Ultra-Precision Machining
Abstract
:1. Introduction
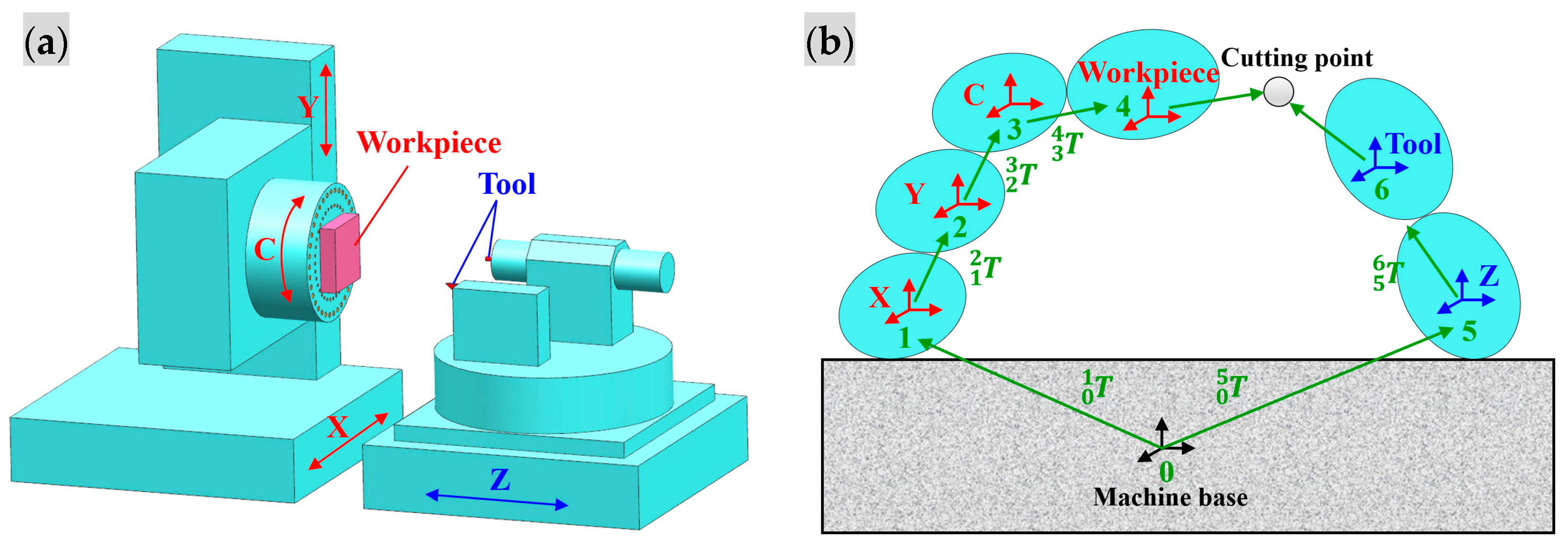
2. Volumetric Error Modelling for PIGEs
3. Recognition of the Crucial PIGEs with the Featured Structures
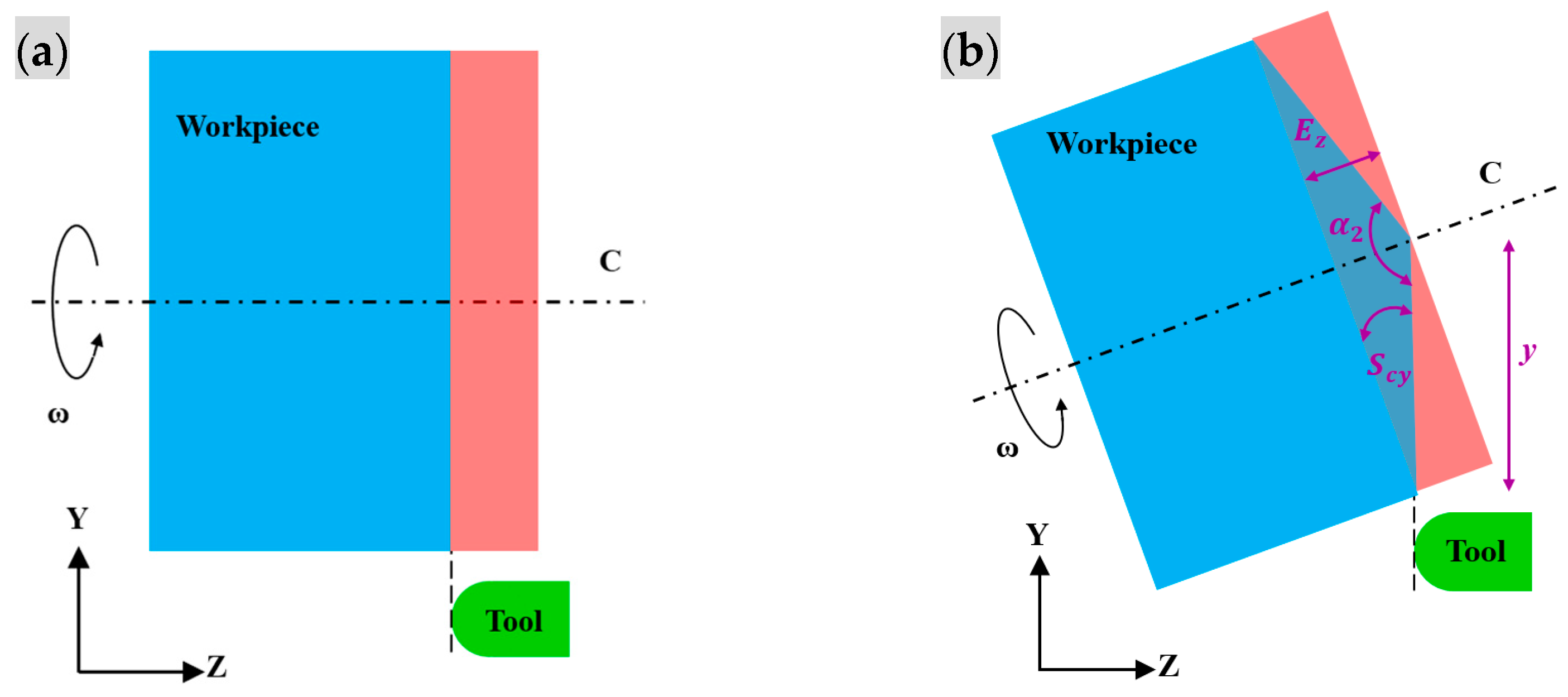
3.1. Specific Squareness Errors Scx and Scy under End-Face Turning
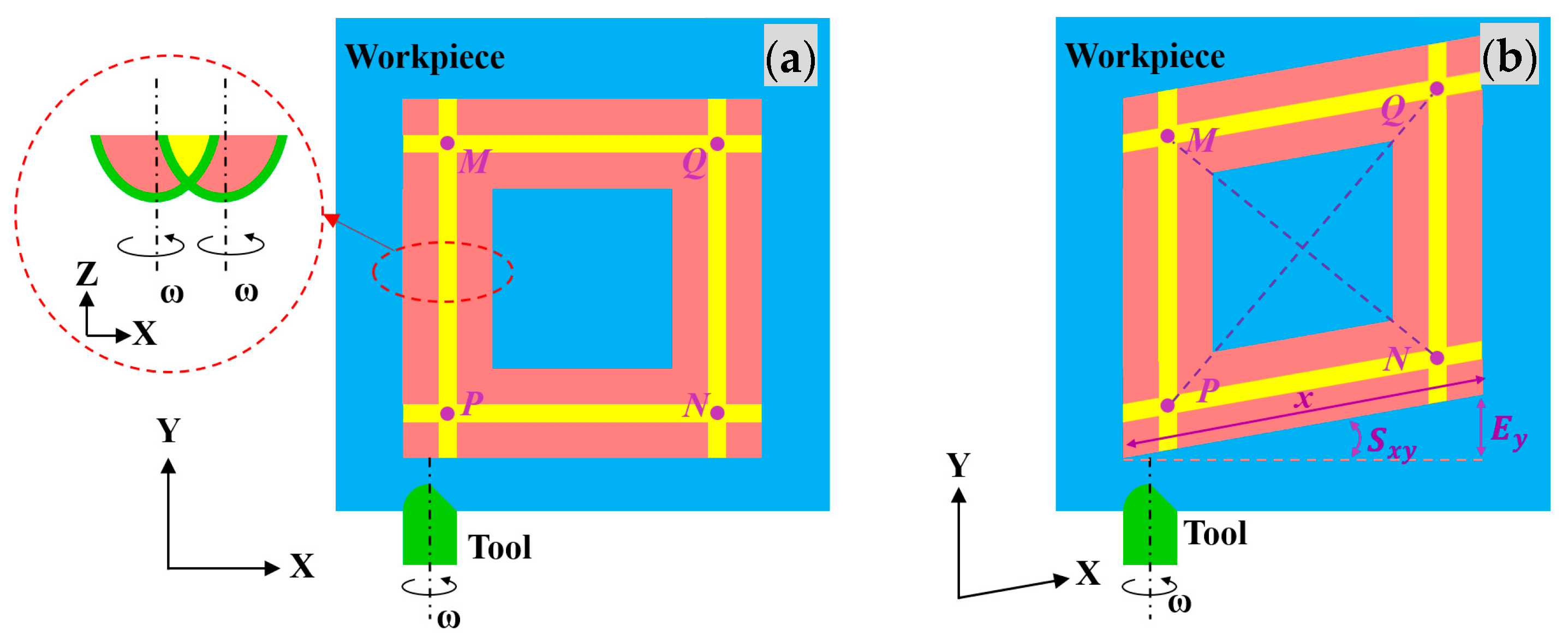
3.2. Specific Squareness Error Sxy under End-Square Milling
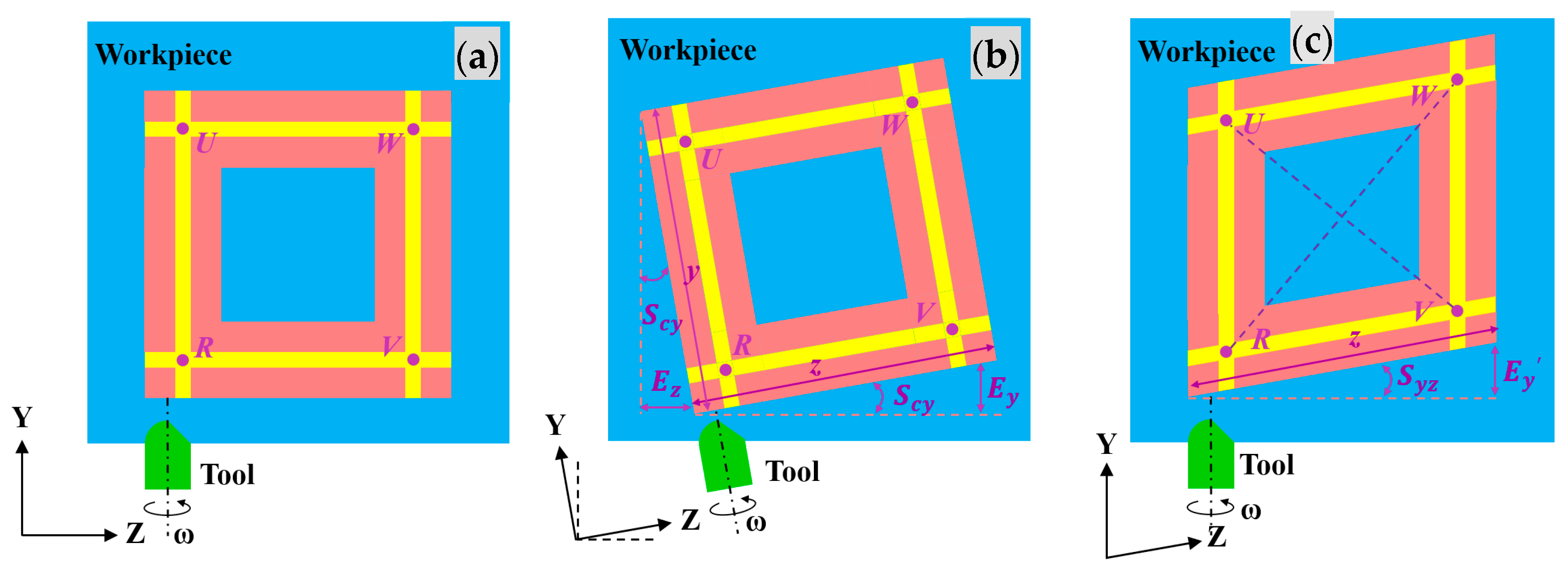
3.3. Specific Squareness Error Syz under Lateral-Square Milling
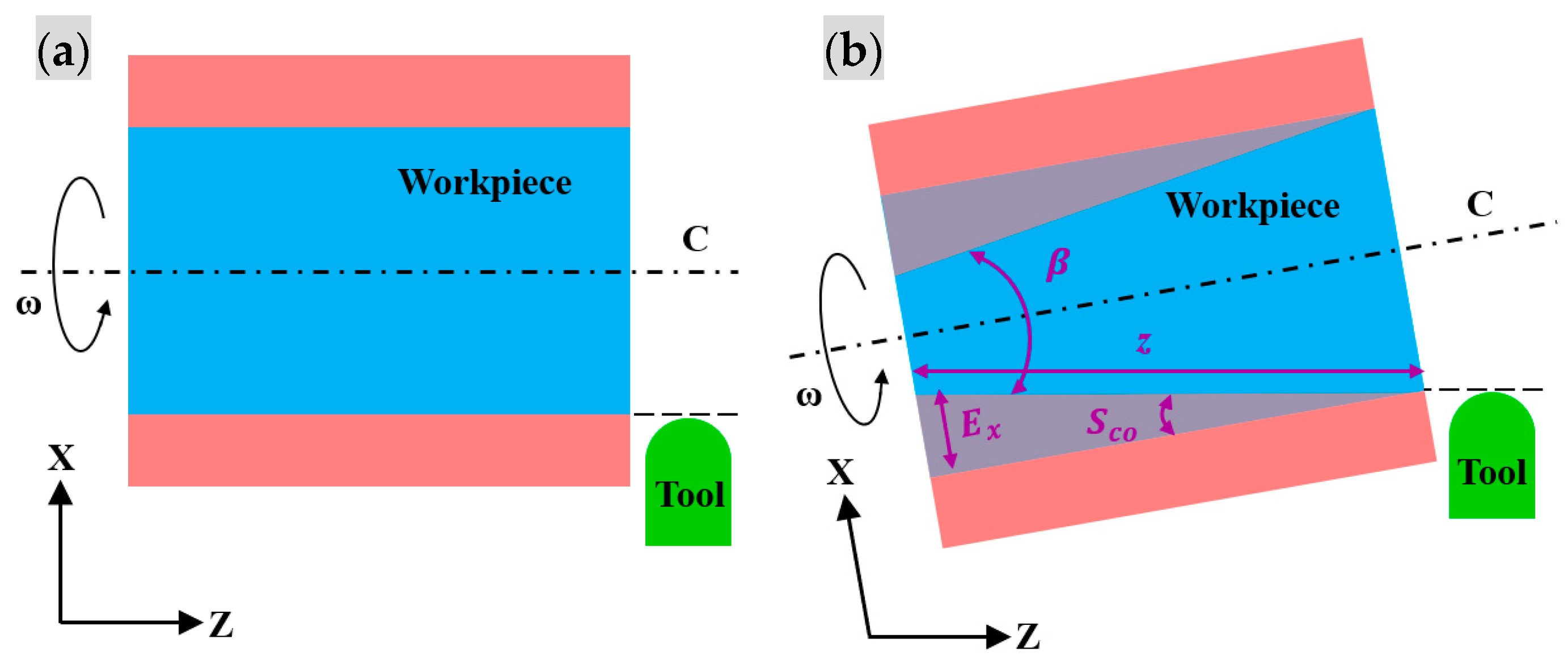
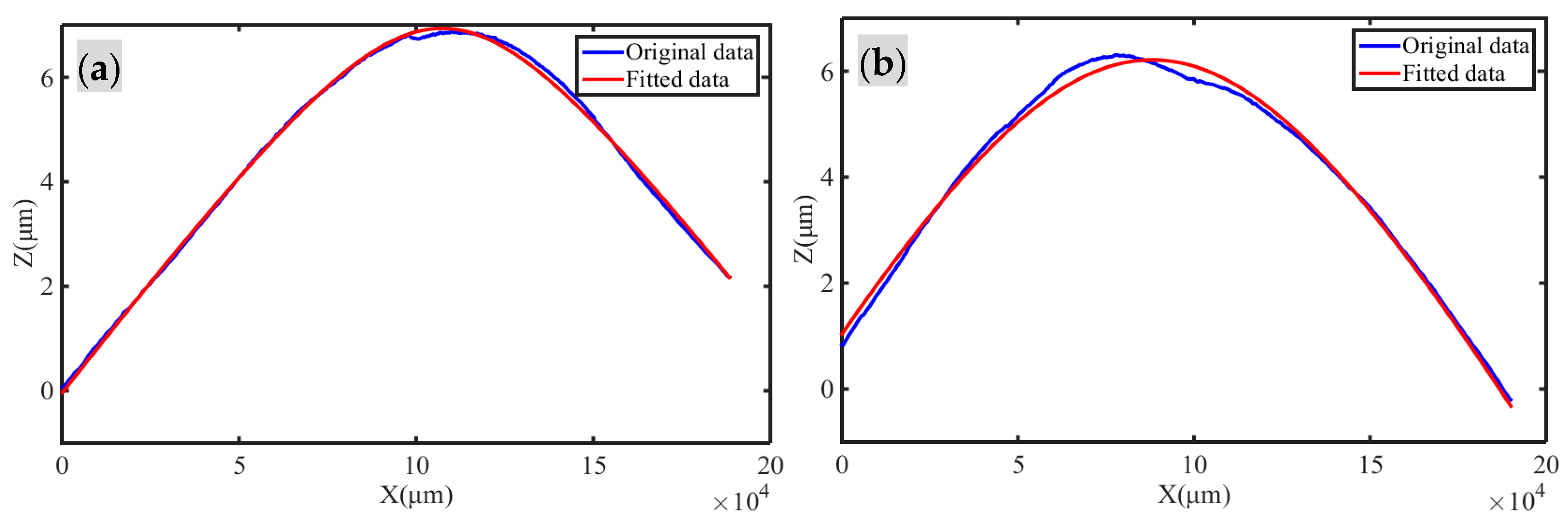
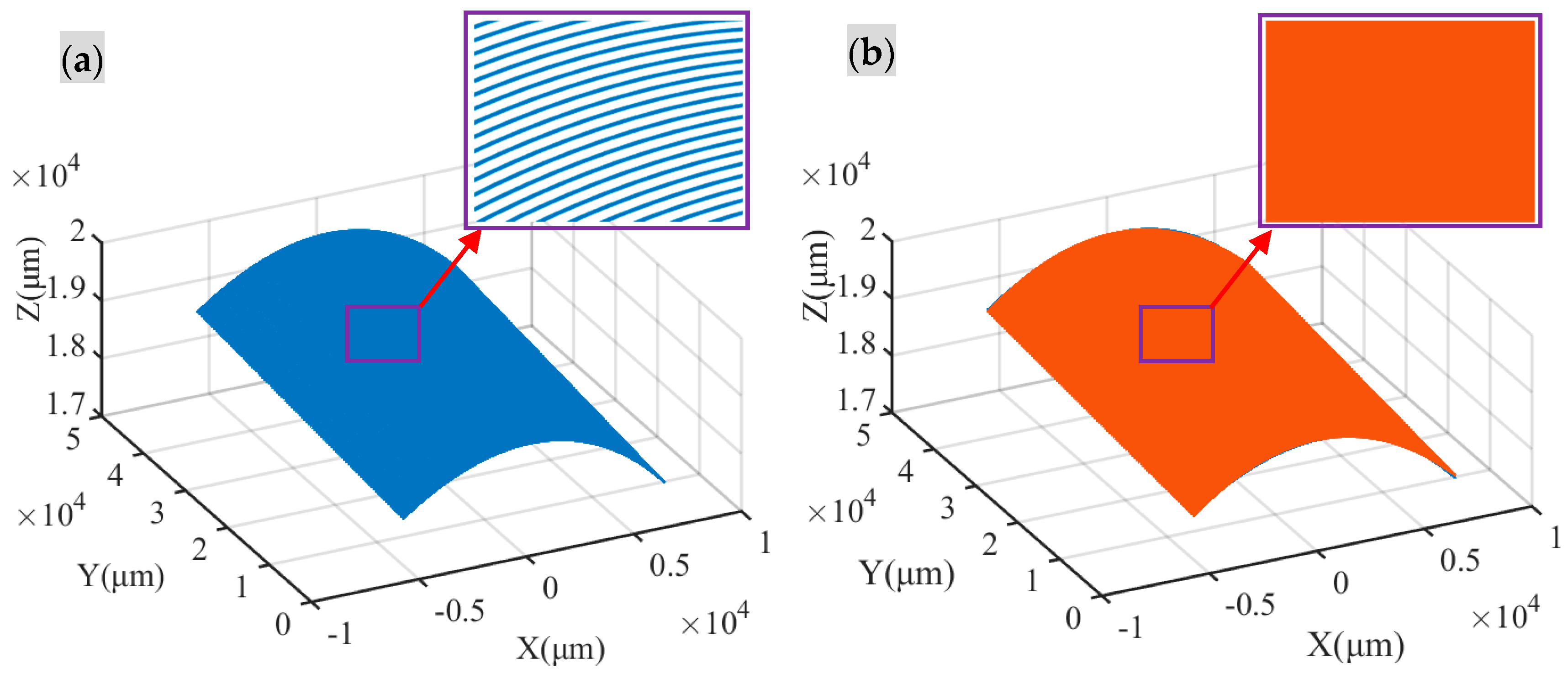
3.4. Specific Squareness Error Sxz under Cylinder Turning
4. Experimental Setup
5. Results and Discussion
6. Conclusions
- (1)
- A volumetric error model has been proposed for PIGEs, to significantly reveal the relationship between the five squareness errors and their resulting machining form errors in UPM. The volumetric error is coupled with other squareness errors, and changes with the motion position along each axis.
- (2)
- Moreover, the featured structures have been designed, machined, and measured to efficiently decouple the specific squareness errors from their form errors in UPM, and to successfully recognize crucial PIGEs. The values of the five specific squareness errors identified are between 15″ and 26″.
- (3)
- Further, it is a potential means to improve the form accuracy of UPM, through the identification of crucial PIGEs with compensation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; To, S.; Chan, C.Y. Investigation on the influence of tool-tip vibration on surface roughness and its representative measurement in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2013, 69, 20–29. [Google Scholar] [CrossRef]
- Geng, Z.; Tong, Z.; Jiang, X. Review of geometric error measurement and compensation techniques of ultra-precision machine tools. Light Adv. Manuf. 2021, 2, 211–227. [Google Scholar] [CrossRef]
- Xing, T.; Zhao, X.; Song, L.; Cui, Z.; Zou, X.; Sun, T. On-machine measurement method and geometrical error analysis in a multi-step processing system of an ultra-precision complex spherical surface. J. Manuf. Process. 2022, 80, 161–177. [Google Scholar] [CrossRef]
- Guo, P.; Li, Z.; Xiong, Z.; Zhang, S. A theoretical and experimental investigation into tool setting induced form error in diamond turning of micro-lens array. Int. J. Adv. Manuf. Technol. 2023, 124, 2515–2525. [Google Scholar] [CrossRef]
- Wu, L.; Liu, H.; Zong, W. Analysis and compensation for the dominant tool error in ultra-precision diamond ball-end milling. J. Mater. Process. Technol. 2023, 318, 118034. [Google Scholar] [CrossRef]
- Sun, L.; Ren, M.; Hong, H.; Yin, Y. Thermal error reduction based on thermodynamics structure optimization method for an ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2017, 88, 1267–1277. [Google Scholar] [CrossRef]
- Fedorynenko, D.; Nakao, Y. Evaluation of thermal stability of ultra-precision water-lubricated spindle. Precis. Eng. 2023, 80, 127–137. [Google Scholar] [CrossRef]
- Chen, G.D.; Sun, Y.Z.; Zhang, F.H.; Lu, L.H.; Chen, W.Q.; Yu, N. Dynamic accuracy design method of ultra-precision machine tool. Chin. J. Mech. Eng. 2018, 31, 8. [Google Scholar] [CrossRef]
- He, S.; Wu, J.; Xuan, J.; Du, W.; Xia, Q.; Zhang, L.; Shi, T. Freeform surface topography model for ultraprecision turning under the influence of various errors. J. Manuf. Process. 2021, 71, 429–449. [Google Scholar] [CrossRef]
- Gu, J.; Agapiou, J.S.; Kurgin, S. CNC machine tool work offset error compensation method. J. Manuf. Syst. 2015, 37, 576–585. [Google Scholar] [CrossRef]
- ISO230-1; Test Code for Machine Tools-Part 1: Geometric Accuracy of Machines Operating under No-Load or Quasi-Static Conditions. ISO, BS: Geneva, Switzerland, 2012.
- ISO230-7; Test Code for Machine Tools-Part 7: Geometric Accuracy of Axes of Rotation. ISO, BS: Geneva, Switzerland, 2015.
- Lee, K.I.; Yang, S.H. Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar. Int. J. Precis. Eng. Manuf. 2013, 14, 231–239. [Google Scholar] [CrossRef]
- Jiang, X.; Cripps, R.J. A method of testing position independent geometric errors in rotary axes of a five-axis machine tool using a double ball bar. Int. J. Mach. Tools Manuf. 2015, 89, 151–158. [Google Scholar] [CrossRef]
- Chen, Q.; Maeng, S.; Li, W.; Zhou, Z.; Min, S. Geometric-and force-induced errors compensation and uncertainty analysis of rotary axis in 5-axis ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2020, 109, 841–856. [Google Scholar] [CrossRef]
- Osei, S.; Wang, W.; Ding, Q. A new method to identify the position-independent geometric errors in the rotary axes of five-axis machine tools. J. Manuf. Process. 2023, 87, 46–53. [Google Scholar] [CrossRef]
- Lai, T.; Peng, X.; Tie, G.; Liu, J.; Guo, M. High accurate squareness measurement squareness method for ultra-precision machine based on error separation. Precis. Eng. 2017, 49, 15–23. [Google Scholar] [CrossRef]
- Maeng, S.; Min, S. Simultaneous geometric error identification of rotary axis and tool setting in an ultra-precision 5-axis machine tool using on-machine measurement. Precis. Eng. 2020, 63, 94–104. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, F.; Li, D.; Wu, Y.; Xue, J.; Wang, W.; Wang, B. Machining accuracy improvement for a dual-spindle ultra-precision drum roll lathe based on geometric error analysis and calibration. Precis. Eng. 2020, 66, 401–416. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Jiang, C.; Zhou, Z.; Min, S. Separation and compensation of geometric errors of rotary axis in 5-axis ultra-precision machine tool by empirical mode decomposition method. J. Manuf. Process. 2021, 68, 1509–1523. [Google Scholar] [CrossRef]
- Song, L.; Zhao, X.; Zhang, Q.; Shi, D.; Sun, T. A geometric error measurement method for five-axis ultra-precision machine tools. Int. J. Adv. Manuf. Technol. 2023, 126, 1379–1395. [Google Scholar] [CrossRef]
- Gao, H.; Fang, F.; Zhang, X. Reverse analysis on the geometric errors of ultra-precision machine. Int. J. Adv. Manuf. Technol. 2014, 73, 1615–1624. [Google Scholar] [CrossRef]
- Pezeshki, M.; Arezoo, B. Kinematic errors identification of three-axis machine tools based on machined work pieces. Precis. Eng. 2016, 43, 493–504. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Fang, F.; Liu, S. Identification and compensation of main machining errors on surface form accuracy in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2016, 105, 45–57. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Lin, J.; Yi, A.; Zhou, X. Effects of Machining Errors on Optical Performance of Optical Aspheric Components in Ultra-Precision Diamond Turning. Micromachines 2020, 11, 331. [Google Scholar] [CrossRef]
- Tao, H.; Chen, R.; Xuan, J.; Xia, Q.; Yang, Z.; Zhang, X.; Shi, T. A new approach to identify geometric errors directly from the surface topography of workpiece in ultra-precision machining. Int. J. Adv. Manuf. Technol. 2020, 106, 5159–5173. [Google Scholar] [CrossRef]
- Zha, J.; Villarrazo, N.; Martínez de Pisson, G.; Li, Y.; Zhang, H.; López de Lacalle, L.N. An accuracy evolution method applied to five-axis machining of curved surfaces. Int. J. Adv. Manuf. Technol. 2023, 125, 3475–3487. [Google Scholar] [CrossRef]
- Yang, S.H.; Lee, K.I. Machine tool analyzer: A device for identifying 13 position-independent geometric errors for five-axis machine tools. Int. J. Adv. Manuf. Technol. 2021, 115, 2945–2957. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Sun, Y.; Chen, W.; Wang, B. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2013, 68, 2525–2534. [Google Scholar] [CrossRef]
- Tao, H.; Chen, R.; Xuan, J.; Xia, Q.; Yang, Z.; Zhang, X.; Shi, T. Prioritization analysis and compensation of geometric errors for ultra-precision lathe based on the random forest methodology. Precis. Eng. 2020, 61, 23–40. [Google Scholar] [CrossRef]




| Number | Symbol | Description |
|---|---|---|
| 1 | Sxy | Squareness error between X-axis and Y-axis |
| 2 | Sxz | Squareness error between X-axis and Z-axis |
| 3 | Syz | Squareness error between Y-axis and Z-axis |
| 4 | Scx | Squareness error between C-axis and X-axis |
| 5 | Scy | Squareness error between C-axis and Y-axis |
| Adjacent Bodies | ||
|---|---|---|
| 0–1 (X-axis) | ||
| 1–2 (Y-axis) | ||
| 2–3 (C-axis) | ||
| 3–4 (workpiece) | ||
| 0–5 (Z-axis) | ||
| 5–6 (tool) |
| Squareness Error | Featured Structure | Feed Direction | Feed Rate (mm min−1) | Spindle Speed (rpm) | Feed Distance (mm) | Cutting Depth (μm) |
|---|---|---|---|---|---|---|
| Scx | End-face turning in the X-direction | X | 10 | 1000 | 105 | 2 |
| Scy | End-face turning in the Y-direction | Y | 10 | 1000 | 105 | 2 |
| Sxy | End-square milling in the X–Y plane | X and Y | 10 | 20,000 | 70 | 5 |
| Syz | Lateral-square milling in the Y–Z plane | Y and Z | 10 | 20,000 | 70 | 5 |
| Sxz | Cylinder turning in the Z-direction | Z | 10 | 1000 | 70 | 2 |
| Tool | Tool Nose Radius (mm) | Tool Rake Angle (°) | Front Clearance Angle (°) |
|---|---|---|---|
| Turning tool | 0.3258 | 0 | 12 |
| Milling tool | 0.3700 | 0 | 7 |
| Item | Result |
|---|---|
| The taper angle α1 (°) | 179.9896 |
| The taper angle α2 (°) | 179.9858 |
| The lengths LMN and LPQ (μm) | 98,996.126 and 99,003.545 |
| The lengths LUV and LRW (μm) | 99,000.582 and 99,008.822 |
| The taper angle β (″) | 19.80 |
| Squareness Error | Result (″) |
|---|---|
| Squareness error Scx | 18.72 |
| Squareness error Scy | −25.56 |
| Squareness error Sxy | 15.46 |
| Squareness error Syz | 17.17 |
| Squareness error Sxz | 23.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, S. A Theoretical and Experimental Identification with Featured Structures for Crucial Position-Independent Geometric Errors in Ultra-Precision Machining. Machines 2023, 11, 909. https://doi.org/10.3390/machines11090909
Zhang L, Zhang S. A Theoretical and Experimental Identification with Featured Structures for Crucial Position-Independent Geometric Errors in Ultra-Precision Machining. Machines. 2023; 11(9):909. https://doi.org/10.3390/machines11090909
Chicago/Turabian StyleZhang, Li, and Shaojian Zhang. 2023. "A Theoretical and Experimental Identification with Featured Structures for Crucial Position-Independent Geometric Errors in Ultra-Precision Machining" Machines 11, no. 9: 909. https://doi.org/10.3390/machines11090909
APA StyleZhang, L., & Zhang, S. (2023). A Theoretical and Experimental Identification with Featured Structures for Crucial Position-Independent Geometric Errors in Ultra-Precision Machining. Machines, 11(9), 909. https://doi.org/10.3390/machines11090909





