Multi-Rate Vibration Signal Analysis for Bearing Fault Detection in Induction Machines Using Supervised Learning Classifiers
Abstract
:1. Introduction
2. Multi-Rate Sampling Methodology
2.1. Fractional Resampling
- STEP 1—Upsampling through Interpolation: The first step in fractional resampling consists in interpolating the signal. An interpolation of rate q consists in a multi-rate signal process, which generates interpolated samples between two original signals [44]. Therefore, due to the interpolation of q times, the SF becomes a resampled , according toThis step is important in fractional sampling, because it effectively increases the source SR, without acquiring additional physical samples. In other words, by generating interpolated samples between the existing ones, one can obtain a higher temporal resolution of the signal, which is particularly valuable when dealing with signals that change rapidly over time, similarly to vibrations. As a result of (1), as the increases, the data sequence is similarly increased by a factor q of the interpolation rate.
- STEP 2—Low-Pass Filter (LPF): By interpolating a signal, spectral distortion can be introduced due to the underlying mathematical principles and limitations of the interpolation process, e.g., due to signal aliasing or simply the time variation in the signal. This distortion can result in the introduction of quantization noise into the interpolated signal [44]. As a consequence, introducing a LPF is important to deal with such interpolation effects and reduce spectral distortion. The LPF has a cut off frequency, , respecting
- STEP 3—Downsampling by Decimation: Decimating a digital signal consists of the opposite of interpolating it. Through the decimation process, the number of samples in the original signal is reduced by a factor p, and the is modified due to the decimation [44], as follows:By definition, the decimation step acts as a LPF because it reduces the number of samples and deletes the high-frequency bands of the original signal. However, similarly to the length modification of the signal after interpolation, the length of the original sequence after decimation is decreased by a factor p.

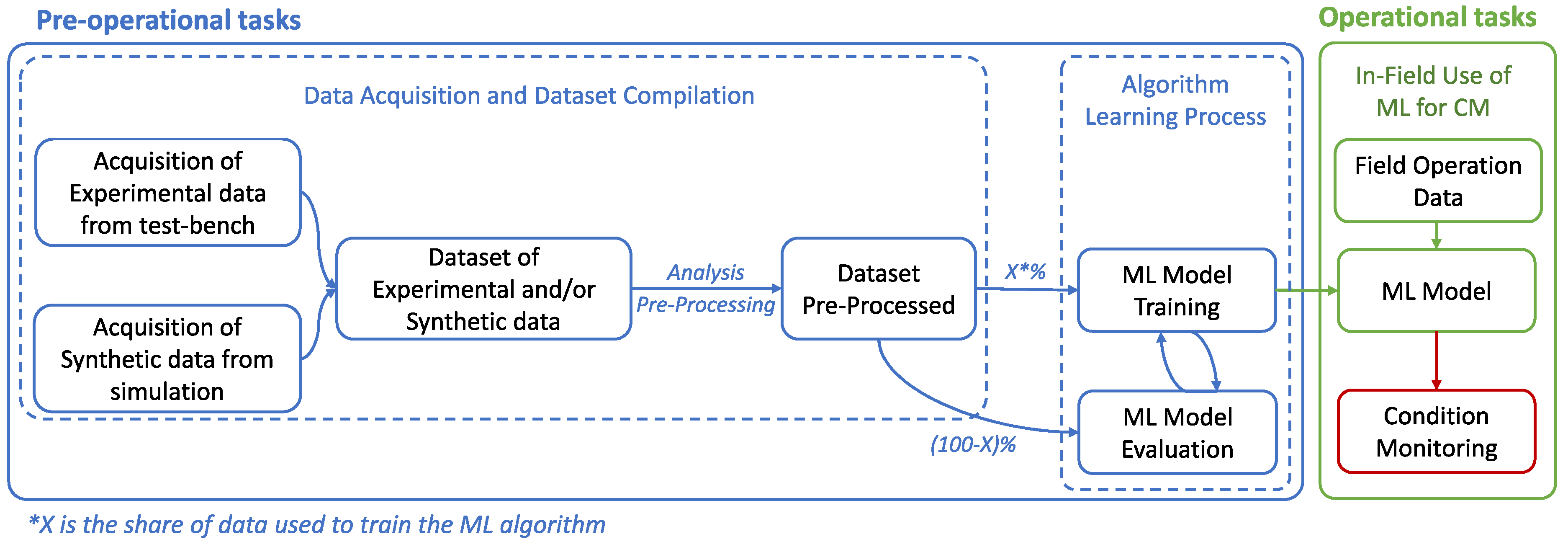
2.2. Multi-Fractional Resampling in Machine Learning
3. Machine Learning Classifiers
3.1. Linear Classifier
3.1.1. SVM
3.1.2. MNLR
3.2. Tree-Based Methods
3.3. Neural Networks
- Weighted Sum: Each input is assigned a weight . Hence, the i-th neuron computes as the addition of a weighted sum and a bias term , as
- Activation Function: After computing , the neuron applies an activation function that introduces non-linearity into the neuron’s response according toThe choice of the activation function is particularly important in the context of a study about vibrations, because it introduces non-linearities and enables the effective capture of dynamic and time-varying behaviors.
3.3.1. MLP
3.3.2. RNN
- Hidden State Update: For a layer with m neurons, taking an input ∈ at time t, the hidden state update is defined as∈ represents the hidden state at time t, is the activation function, ∈ and ∈ are weight matrices for recurrent and input connections, and ∈ is the bias vector;
- Output Computation: At every time t, for a K-class classification task, the output ∈ is computed from the hidden state as follows:
- Categorical Cross-Entropy Loss to Minimize for Classification: Similarly to the MLP, the cross-entropy loss as defined in (24) is an objective function which is then minimized during training.
4. Methodology
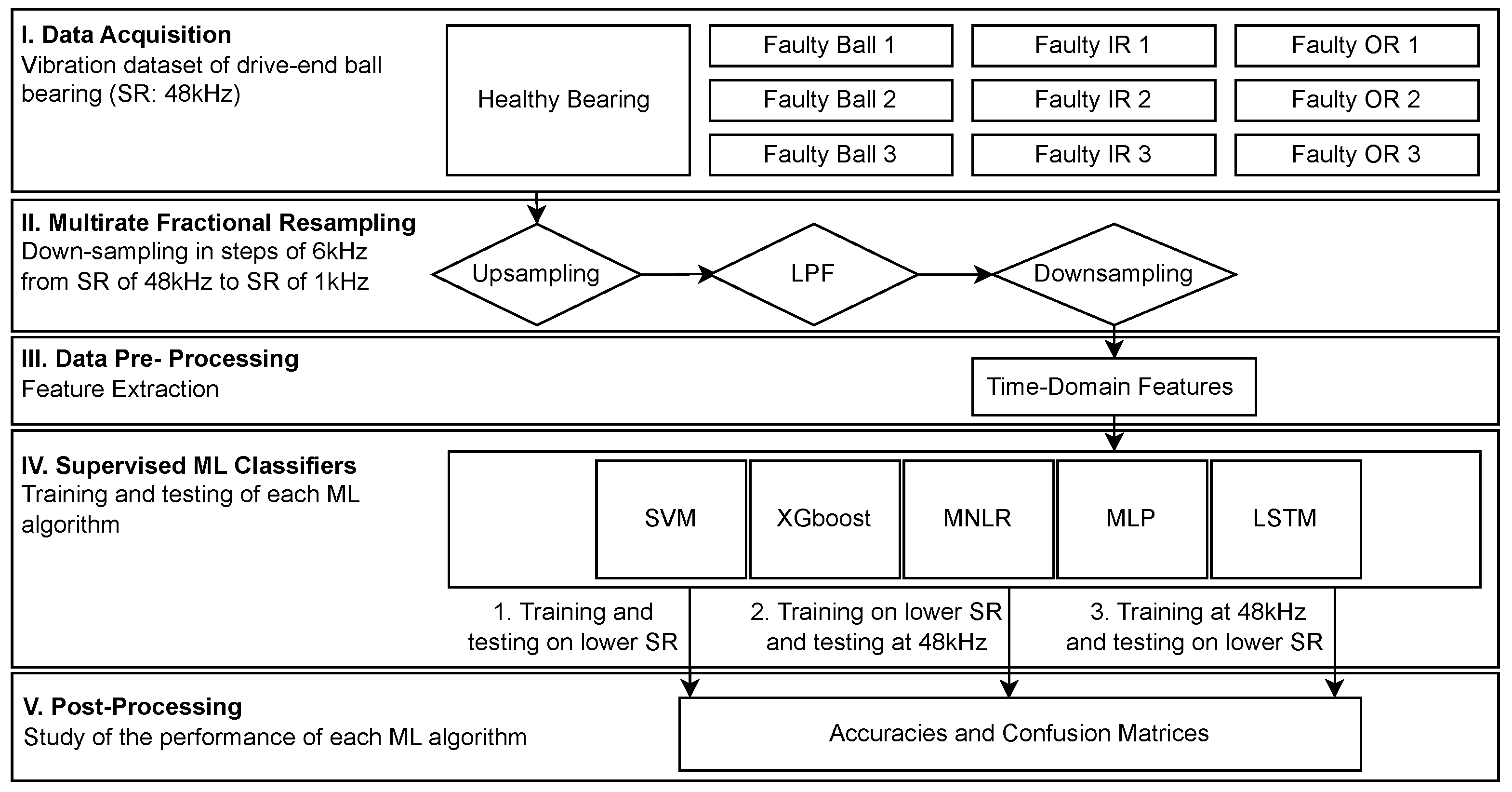
4.1. Numerical Experimentation Flowchart
- I.
- Data Acquisition: Experimental data about vibration signals related to ball bearing faults in an IM acquired at a SF of 48 kHz were obtained from an the CWRU dataset [33] detailed in Section 4.2;
- II.
- Multirate Fractional Resampling: Each vibration signal for each bearing state (faulty ball, faulty inner ring (IR), faulty outer ring (OR), healthy bearing) was resampled using a step of 6 kHz from the initial SR, i.e., 48 kHz. Therefore, vibration signals for each of the time-series were downsampled to 1 kHz, 6 kHz, 12 kHz, 18 kHz, 24 kHz, 30 kHz, 36 kHz, and 42 kHz. The design choice of resampling the signals by a step of 6 kHz was driven by the fact that, in the literature, most datasets of bearing vibration acquired their signals at a SF which was multiple of 6 or relatively close to it, e.g., 12, 20, or 48 kHz [12,33]. It was thus concluded that 6 was a good metric to cover a large number of SRs, while remaining close to actual figures.Afterward, the downsampled signals were studied separately in the following steps;
- III.
- Data Pre-processing: The downsampled signals for each respective SR were then preprocessed and time-domain features were calculated as a preparation for the training and evaluation of the ML algorithms;
- IV.
- Supervised ML classifiers: Supervised ML classifiers were trained and tested based on data from the different time-series previously generated. These classifiers learned and accurately recognized patterns within the features extracted from the vibration signals. Three scenarios were studied:
- The objective was to train the ML classifiers to detect various bearing faults for each SR and to test the performance of the classifiers at the respective SR. By doing so, the ML algorithm’s ability to classify at low(er) SR was studied, i.e., under varying data acquisition conditions;
- This step was similar to the first one but tested the performance of the classifiers on the initial data sampled at 48 kHz. By doing so, the robustness of the ML classifiers was evaluated, as they were tested on finer data;
- Vice-versa, this step trained the ML classifiers on the initial data sampled at 48 kHz and evaluated the algorithms on vibration signals sampled at a lower SF.
- V.
- Post-Processing: The accuracy of each ML algorithm was evaluated for both training and testing according to the metric previously described in Section 3. Afterwards, the length of the downsampled signals, i.e., the number of data-points after feature extraction, was calculated for each SF and evaluated, to observe the correlation with the performance of the algorithms.
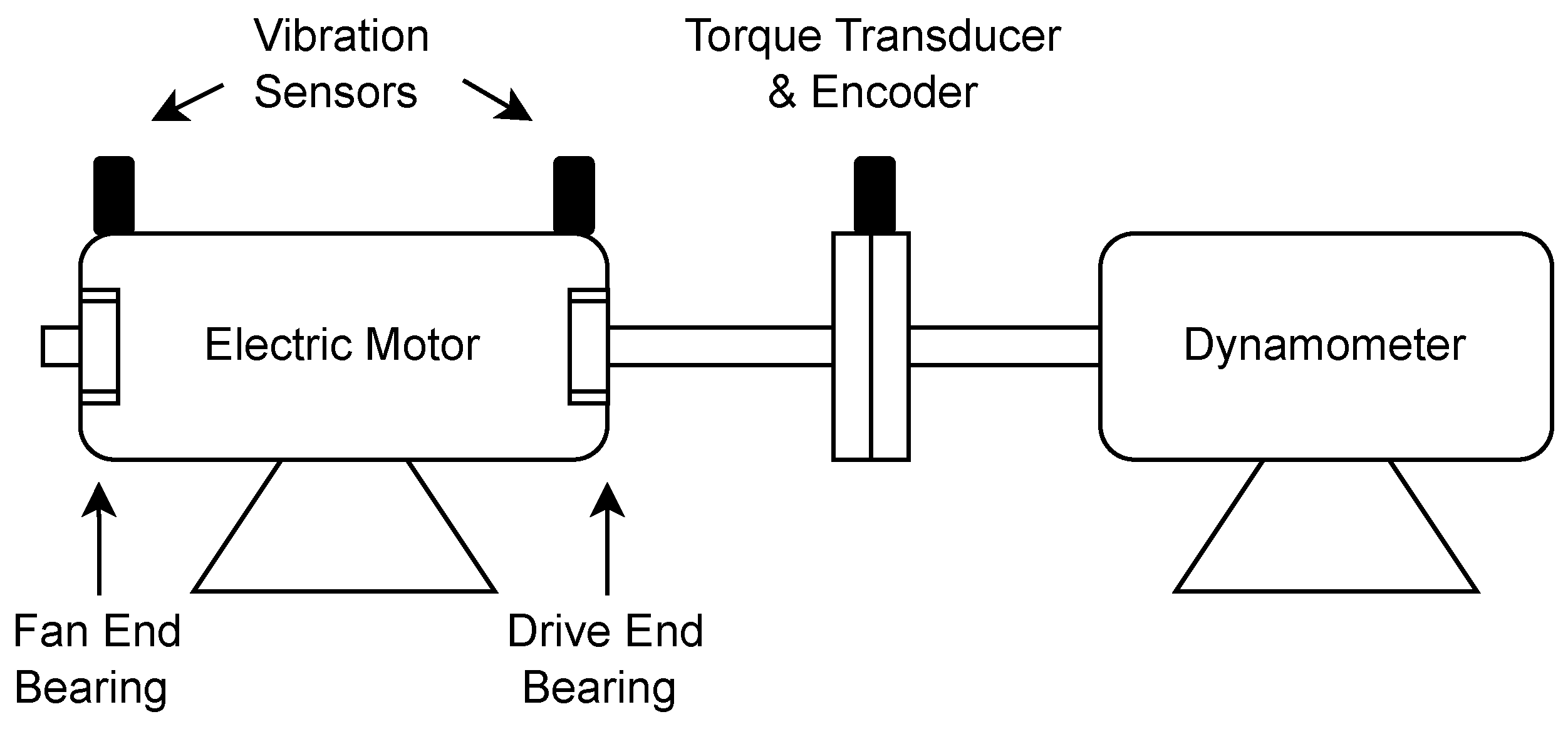
4.2. Experimental Set-Up and Data Acquisition
4.3. Dataset Pre-Processing
5. Results
5.1. Evaluation and Verification of the Downsampling Method
- Kurtosis: The kurtosis of a signal measures the sharpness of the peaks in a probability distribution; i.e., how often outliers stand in the signal. In the present case, the kurtosis values for both scenarios were close, with a difference of 0.05, which means that the tails of the two scenarios were fairly similar, yet slightly more pronounced in the downsampled signal;
- Variance: The variance of a signal measures the spread of data points in a signal with respect to the mean value of this same signal. Here, the two cases share similar variance values, meaning that the dispersion of the data was consistent between the downsampled and experimental signals;
- Skewness: The skewness measures the asymmetry of a probability distribution. In the two scenarios studied here, the skewness was very low, suggesting that the distributions were rather symmetrical, with a tendency towards positive skewness;
- Energy: The energy is a measure of the total signal power. Here, the downsampled signal had a higher overall power compared to the experimental signal, but the values in the two cases only had a difference of 0.66%.
5.2. ML Classifiers Performance
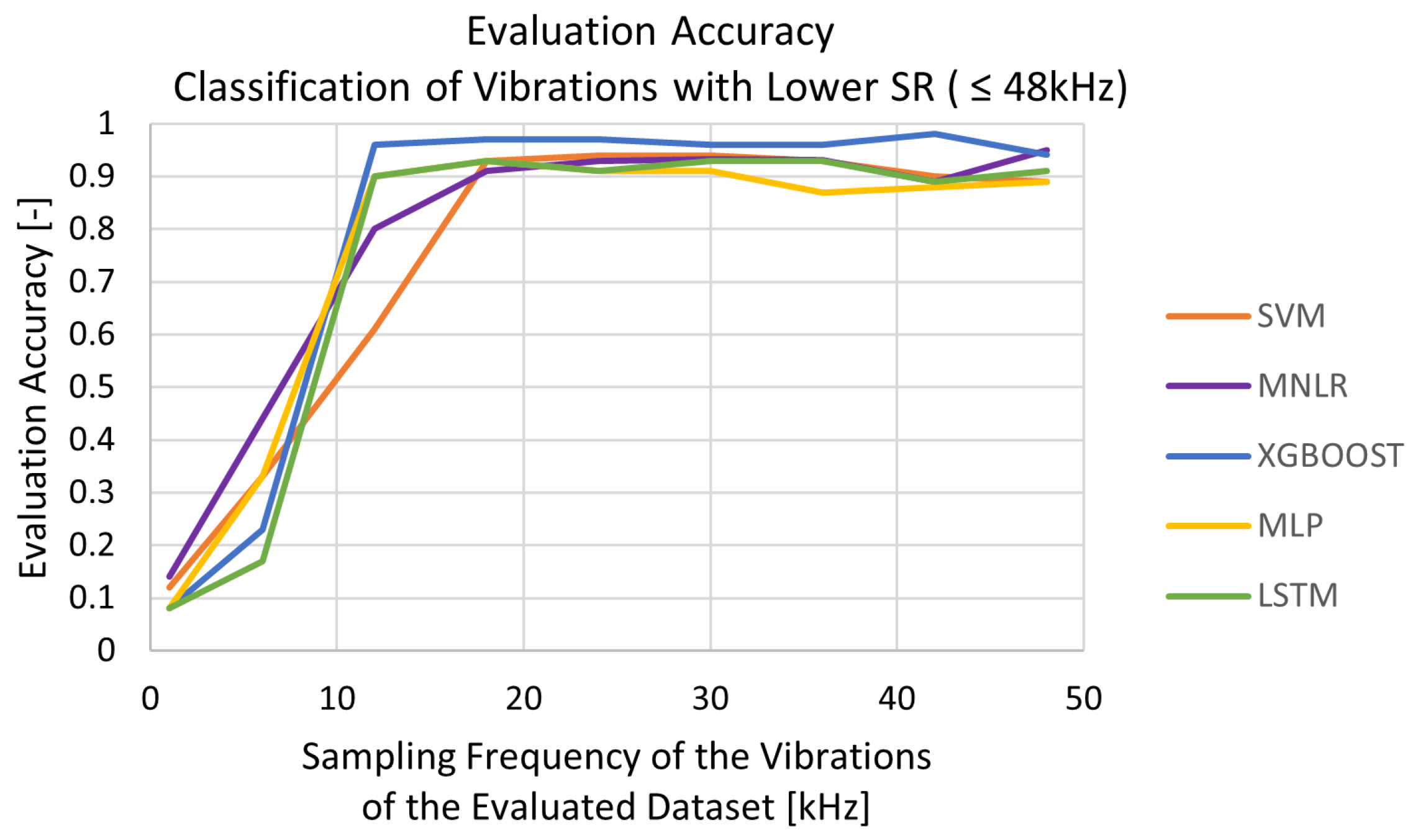
5.2.1. Training and Evaluation at Respective SRs
- SVM and MNLR: The linear classifiers were able to classify bearing faults but showed a lower performance for signals sampled at 1 and 6 kHz. This means that for these SRs, these algorithms did not learn from the training dataset in order to define the decision boundaries between the classes;
- XGBoost: XGBoost, as a tree based model, is the ML algorithm which was the least sensitive to the downsampling of the vibration data. Indeed, the training accuracy remained at its maximum value, despite the change in SR. It was able to learn well from lower sampled datasets, while maintaining a high performance. Based on theory (Section 3.2), the training procedure in XGBoost is inherently robust to variations in dataset size and distribution. It uses an ensemble of decision trees with features like gradient boosting and regularization, which allows it to adapt effectively to different data representations, ensuring a stable performance, even with a reduced sample density. During the evaluation, the highest performance of XGBoost was achieved at 24 kHz. This did not seem to imply anything or result from any specific feature of the dataset at this SF, especially as the evaluation performance remained in the same range as the other performances obtained, i.e., above 90% accuracy;
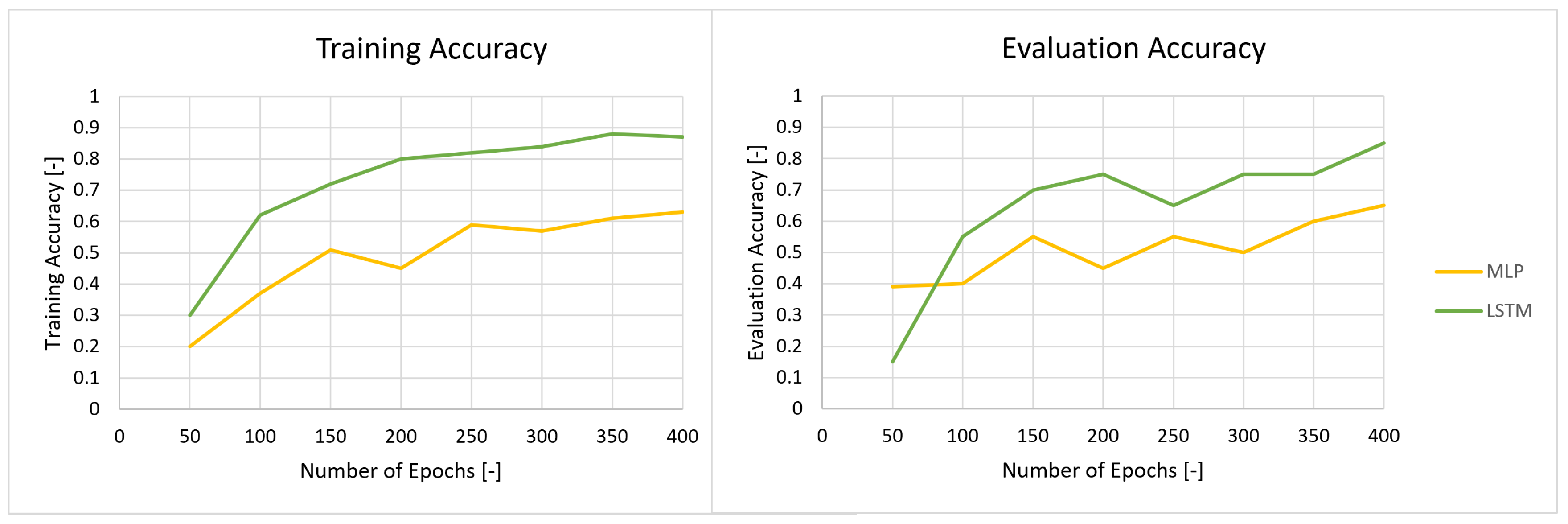
- MLP and LSTM: As neural networks, MLP and LSTM are by definition more sensitive to the amount of samples [12,13]. The low SR lost fine-grained information about the health conditions of the bearing, which made it harder for these neural networks to learn patterns and achieve high performances. However, due to its architecture, LSTM can capture longer-term dependencies in sequential data and this provides some advantages in scenarios with limited data. Therefore, at a SR of 6 kHz, LSTM was already catching up with performance of the other ML algorithms and even surpassed the linear models. As far as the MLP is concerned, it seemed to globally lag behind compared to the other ML algorithms, no matter the SR. At a lower SR, MLP suffered from lack of qualitative information to learn correctly, but at high-frequency, MLP might not have been able to generalize higher dimensional spaces as well.
5.2.2. Training at Lower SRs and Evaluation at 48 kHz
5.2.3. Training at 48 kHz and Evaluation at Lower SR
- SVM and MNLR: The two linear classifiers showed different trends before classification of signals with a SR below 18 kHz and a similar behavior above. Particularly, the SVM algorithm lagged behind in classifying the signals sampled at 12 kHz, while being trained with data sampled at 48 kHz. This might have been due to the fact that the SVM relied on maximizing the margin between different classes, which can be challenging when working with a low number of features;
- XGBOOST: XGBoost was the best algorithm after 12 kHz. Before the SR of 12 kHz, the XGBoost performance decreased drastically. XGBoost has an enhanced training mechanism that excels at capturing intricate patterns and complex relationships within high-dimensional datasets. When trained with complex data and evaluated with signals sampled at or above 12 kHz, the feature space became more informative, allowing XGBoost to leverage its boosting learning techniques effectively;
- MLP and LSTM: The two neural networks showed the same trends across all the SRs, with MLP slightly lagging behind for higher SRs, as was the case earlier.
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| CM | Condition Monitoring |
| DL | Deep Learning |
| FR | Frequency Resolution |
| IM | Induction Machine |
| IR | Inner Ring |
| LFP | Low-Pass Filter |
| LSTM | Long short-term memory |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MNLR | Multinomial Logistic Regression |
| LPF | Low-Pass Filter |
| OR | Outer Ring |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| SF | Sampling Frequency |
| SR | Sampling Rate |
| SVM | Support Vector Machines |
References
- Desnica, E.; Ašonja, A.; Radovanović, L.; Palinkaš, I.; Kiss, I. Selection, Dimensioning and Maintenance of Roller Bearings. In Proceedings of the 31st International Conference on Organization and Technology of Maintenance (OTO 2022), Osijek, Croatia, 12 December 2022; pp. 133–142. [Google Scholar]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Leffler, J.; Trnka, P. Failures of Electrical Machines—Review. In Proceedings of the 8th International Youth Conference on Energy, Eger, Hungary, 6–9 July 2022; pp. 1–4. [Google Scholar]
- El Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M. Induction machine faults detection using stator current parametric spectral estimation. Mech. Syst. Signal Process. 2015, 52–53, 447–464. [Google Scholar] [CrossRef]
- Gupta, P.K. Dynamics of Rolling-Element Bearings—Part III: Ball Bearing Analysis. ASME J. Lubr. Technol. 1979, 101, 312–318. [Google Scholar] [CrossRef]
- Hadi, R.H.; Hady, H.N.; Hasan, A.M.; Al-Jodah, A.; Humaidi, A.J. Improved Fault Classification for Predictive Maintenance in Industrial IoT Based on AutoML: A Case Study of Ball-Bearing Faults. Processes 2023, 11, 1507. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K.; Zhang, Y.; Lin, D.; Zheng, J. Data-driven bearing health management using a novel multi-scale fused feature and gated recurrent unit. Reliab. Eng. Syst. Saf. 2023, 242, 109753. [Google Scholar] [CrossRef]
- Mansouri, M.; Harkat, M.F.; Nounou, H.N.; Nounou, M.N. Data-Driven and Model-Based Methods for Fault Detection and Diagnosis; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–10. [Google Scholar]
- Khan, M.A.; Asad, B.; Kudelina, K.; Vaimann, T.; Kallaste, A. The Bearing Faults Detection Methods for Electrical Machines—The State of the Art. Energies 2022, 16, 296. [Google Scholar] [CrossRef]
- Heidari, M. Fault Detection of Bearings Using a Rule-based Classifier Ensemble and Genetic Algorithm. Int. J. Eng. 2017, 30, 604–609. [Google Scholar]
- Quinde, I.R.; Sumba, J.C.; Ochoa, L.E.; Vallejo Guevara, A., Jr.; Morales-Menendez, R. Bearing Fault Diagnosis Based on Optimal Time-Frequency Representation Method. IFAC-PapersOnLine 2019, 52, 194–199. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Rezaeianjouybari, B.; Shang, Y. Deep learning for prognostics, and health management: State of the art, challenges and opportunities. Measurement 2020, 163, 107929. [Google Scholar] [CrossRef]
- Bouharrouti, N.E.B.; Martin, F.; Belahcen, A. Radial Lumped-parameter Model of a Ball Bearing for Simulated Fault Signatures. In Proceedings of the 14th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives, Chania, Greece, 28–31 August 2023; pp. 403–409. [Google Scholar]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Ball bearing defect models: A study of simulated and experimental fault signatures. J. Sound Vib. 2017, 400, 86–112. [Google Scholar] [CrossRef]
- Saberi, A.N.; Sandirasegaram, S.; Belahcen, A.; Vaimann, T.; Sobra, J. Multi-sensor fault diagnosis of induction motors using random forests and support vector machine. In Proceedings of the 2020 ICEM, Gothenburg, Sweden, 23–26 August 2020; pp. 1404–1410. [Google Scholar]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing by using multinomial logistic regression and wavelet packet transform. Soft Comput. Fusion Found. Methodol. Appl. 2014, 18, 255–266. [Google Scholar] [CrossRef]
- Rojas, A.; Nandi, A.K. Detection and Classification of Rolling-Element Bearing Faults using Support Vector Machines. In Proceedings of the IEEE Workshop on Machine Learning for Signal Processing, Mystic, CT, USA, 28–30 September 2005; pp. 153–158. [Google Scholar]
- Qian, L.; Pan, Q.; Lv, Y.; Zhao, X. Fault Detection of Bearing by Resnet Classifier with Model-Based Data Augmentation. Machines 2022, 10, 521. [Google Scholar] [CrossRef]
- Kahr, M.; Kovács, G.; Loinig, M.; Brückl, H. Condition Monitoring of Ball Bearings Based on Machine Learning with Synthetically Generated Data. Sensors 2022, 22, 2490. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Raouf, I.; Kim, H.S. Review on prognostics and health management in smart factory: From conventional to deep learning perspectives. Eng. Appl. Artif. Intell. 2023, 126 Pt D, 107126. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Patil, A.A.; Desai, S.S.; Patil, L.N.; Patil, S.A. Adopting Artificial Neural Network for Wear Investigation of Ball Bearing Materials Under Pure Sliding Condition. Appl. Eng. Lett. J. Eng. Appl. Sci. 2022, 7, 81–88. [Google Scholar] [CrossRef]
- Hotait, H.; Chiementin, X.; Rasolofondraibe, L. Intelligent Online Monitoring of Rolling Bearing: Diagnosis and Prognosis. Entropy 2021, 23, 791. [Google Scholar] [CrossRef]
- Brusa, E.; Delprete, C.; Di Maggio, L.G. Deep Transfer Learning for Machine Diagnosis: From Sound and Music Recognition to Bearing Fault Detection. Appl. Sci. 2021, 11, 11663. [Google Scholar] [CrossRef]
- Park, Y.-J.; Fan, S.-K.S.; Hsu, C.-Y. A Review on Fault Detection and Process Diagnostics in Industrial Processes. Processes 2020, 8, 1123. [Google Scholar] [CrossRef]
- Ru, X.; Gu, N.; Shang, H.; Zhang, H. MEMS Inertial Sensor Calibration Technology: Current Status and Future Trends. Micromachines 2022, 13, 879. [Google Scholar] [CrossRef] [PubMed]
- Aburakhia, S.A.; Myers, R.; Shami, A. A Hybrid Method for Condition Monitoring and Fault Diagnosis of Rolling Bearings with Low System Delay. IEEE Trans. Instrum. Meas. 2022, 71, 3519913. [Google Scholar] [CrossRef]
- Kim, D.W.; Lee, E.S.; Jang, W.K.; Kim, B.H.; Seo, Y.H. Effect of data preprocessing methods and hyperparameters on accuracy of ball bearing fault detection based on deep learning. Adv. Mech. Eng. 2022, 14, 16878132221078494. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Lee, J.; Qiu, H.; Yu, G.; Lin, J.; Rexnord Technical Services. Bearing Data Set. University of Cincinnati, NASA Prognostics Data Repository. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 10 October 2023).
- Case Western Reserve University. Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter/welcome (accessed on 7 October 2023).
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset With Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Liu, L.; Wei, Y.; Song, X.; Zhang, L. Fault Diagnosis of Wind Turbine Bearings Based on CEEMDAN-GWO-KELM. Energies 2023, 16, 48. [Google Scholar] [CrossRef]
- Smith, W.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Wei, X.; Söffker, D. Comparison of CWRU Dataset-Based Diagnosis Approaches: Review of Best Approaches and Results. In Proceedings of the European Workshop on Structural Health Monitoring (EWSHM 2020), Palermo, Italy, 6–9 July 2020; Lecture Notes in Civil Engineering. Springer: Berlin/Heidelberg, Germany, 2021; Volume 127, p. 51. [Google Scholar]
- Xie, W.; Li, Z.; Xu, Y.; Gardoni, P.; Li, W. Evaluation of Different Bearing Fault Classifiers in Utilizing CNN Feature Extraction Ability. Sensors 2022, 22, 3314. [Google Scholar] [CrossRef]
- Wei, X.; Lee, T.; Söffker, D. A New Unsupervised Learning Approach for CWRU Bearing State Distinction. In Proceedings of the European Workshop on Structural Health Monitoring, Palermo, Italy, 4–7 July 2022; Springer International: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Wei, J.; Huang, H.; Yao, L.; Hu, Y.; Fan, Q.; Huang, D. New imbalanced bearing fault diagnosis method based on Sample-characteristic Oversampling TechniquE (SCOTE) and multi-class LS-SVM. Appl. Soft Comput. 2021, 101, 107043. [Google Scholar] [CrossRef]
- Mohiuddin, M.; Islam, M.S.; Islam, S.; Miah, M.S.; Niu, M.-B. Intelligent Fault Diagnosis of Rolling Element Bearings Based on Modified AlexNet. Sensors 2023, 23, 7764. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Chen, Z.; Yang, Y.; Geng, C.; Zuo, M.J. Time-frequency ridge estimation: An effective tool for gear and bearing fault diagnosis at time-varying speeds. Mech. Syst. Signal Process. 2023, 189, 110108. [Google Scholar] [CrossRef]
- AlShalalfeh, A.; Shalalfeh, L. Bearing Fault Diagnosis Approach under Data Quality Issues. Appl. Sci. 2021, 11, 3289. [Google Scholar] [CrossRef]
- de Jesus Romero-Troncoso, R. Multirate Signal Processing to Improve FFT-Based Analysis for Detecting Faults in Induction Motors. IEEE Trans. Ind. Inform. 2017, 13, 1291–1300. [Google Scholar] [CrossRef]
- Jung, A. Machine Learning: The Basics; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Kerdsiri, T.; Gullayanon, R. Early Fault Detection based on Ball Bearing Vibration Analysis using Multinomial Logistic Regression. In Proceedings of the 2017 International Conference on Intelligent Systems, Metaheuristic & Swarm Intelligence, Hong Kong, China, 25–27 March 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 152–156. [Google Scholar]
- Nielsen, D. Tree Boosting with XGBoost: Why Does XGBoost Win “Every" Machine Learning Competition? Department of Mathematical Sciences, Norwegian University of Science and Technology: Trondheim, Norway, 2016. [Google Scholar]
- Xie, J.; Li, Z.; Zhou, Z.; Liu, S. A Novel Bearing Fault Classification Method Based on XGBoost: The Fusion of Deep Learning-Based Features and Empirical Features. IEEE Trans. Instrum. Meas. 2021, 70, 3506709. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, W.; Wang, L.; Xie, T. Intelligent Diagnosis of Rolling Bearing Fault Based on Improved Convolutional Neural Network and LightGBM. Shock Vib. 2021, 2021, 1205473. [Google Scholar] [CrossRef]
- Wei, C.; Xiang, C.; Ren, Z.; Shi, P.; Zhao, H. Data-Driven Fault Diagnosis for Rolling Bearing Based on DIT-FFT and XGBoost. Complexity 2021, 2021, 4941966. [Google Scholar]
- Tarek, K.; Abdelaziz, L.; Zoubir, C.; Kais, K.; Karim, N. Optimized multi-layer perceptron artificial neural network based fault diagnosis of induction motor using vibration signals. Diagnostyka 2021, 22, 65–74. [Google Scholar] [CrossRef]
- Sabir, R.; Rosato, D.; Hartmann, S.; Guehmann, C. LSTM Based Bearing Fault Diagnosis of Electrical Machines using Motor Current Signal. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 16–19 December 2019; pp. 613–618. [Google Scholar]
- Martinez-Figueroa, G.D.J.; Morinigo-Sotelo, D.; Zorita-Lamadrid, A.L.; Morales-Velazquez, L.; Romero-Troncoso, R.D.J. FPGA-Based Smart Sensor for Detection and Classification of Power Quality Disturbances Using Higher Order Statistics. IEEE Access 2017, 5, 14259–14274. [Google Scholar] [CrossRef]
- Ross, S.M. Introductory Statistics, 4th ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 17–63. [Google Scholar]
- Han, S.; Oh, S.; Jeong, J. Bearing Fault Diagnosis Based on Multiscale Convolutional Neural Network Using Data Augmentation. J. Sens. 2021, 2021, 6699637. [Google Scholar] [CrossRef]
- Doukim, C.A.; Dargham, J.A.; Chekima, A. Finding the number of hidden neurons for an MLP neural network using coarse to fine search technique. In Proceedings of the 10th International Conference on Information Science, Signal Processing and Their Applications (ISSPA 2010), Kuala Lumpur, Malaysia, 10–13 May 2010; pp. 606–609. [Google Scholar]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Wang, C.; Deng, C.; Wang, S. Imbalance-XGBoost: Leveraging weighted and focal losses for binary label-imbalanced classification with XGBoost. Pattern Recognit. Lett. 2020, 136, 190–197. [Google Scholar] [CrossRef]




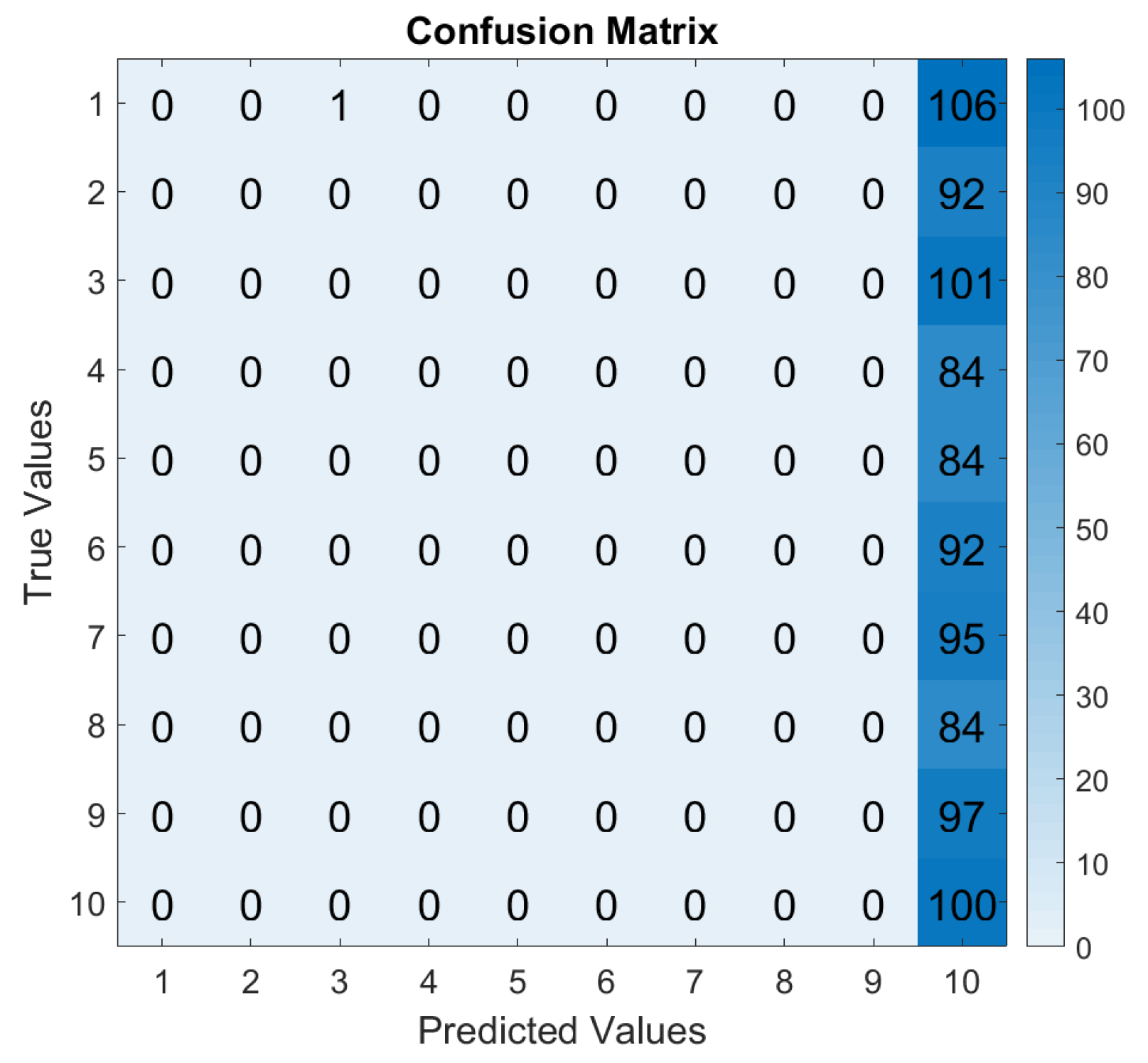
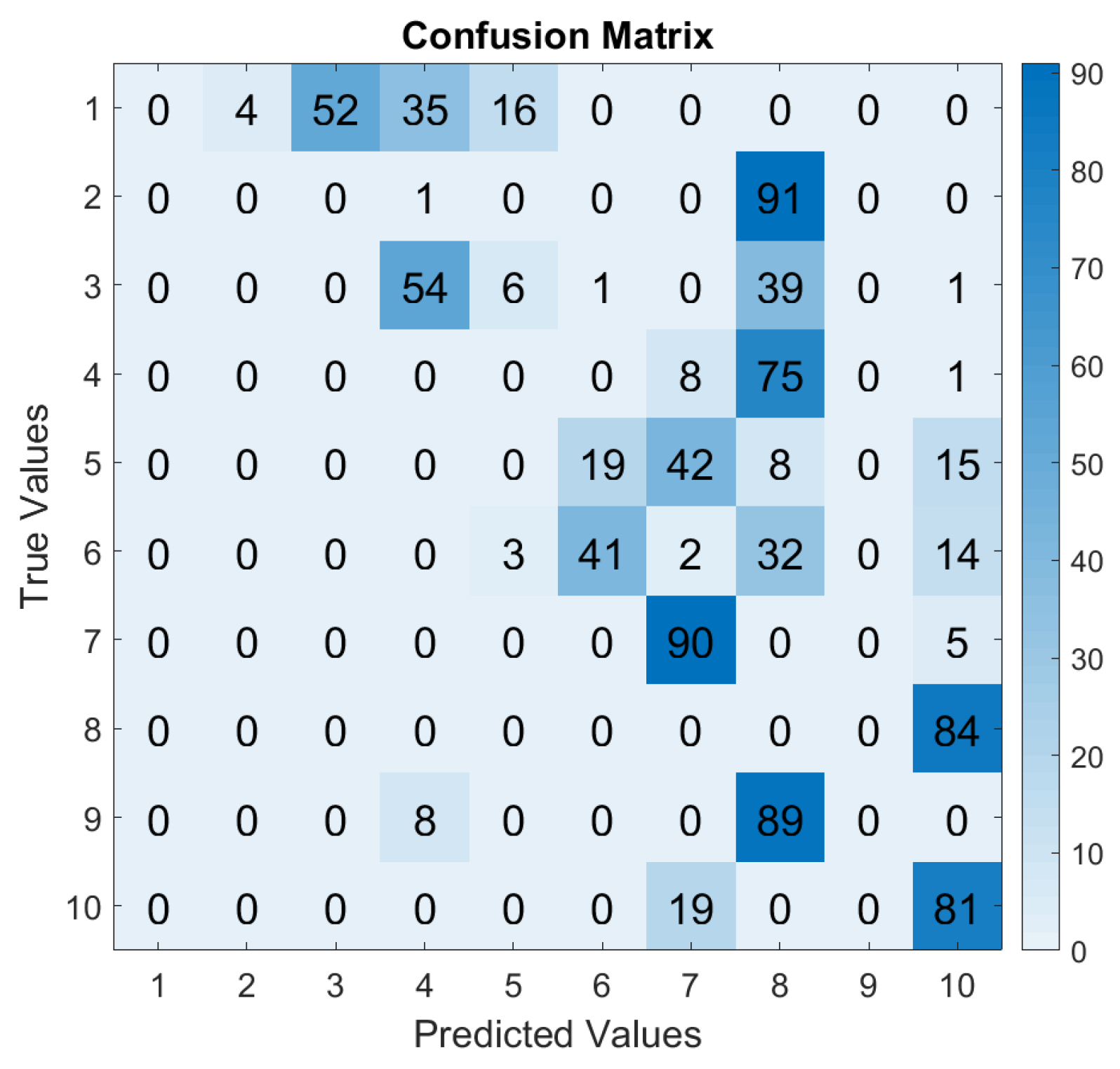

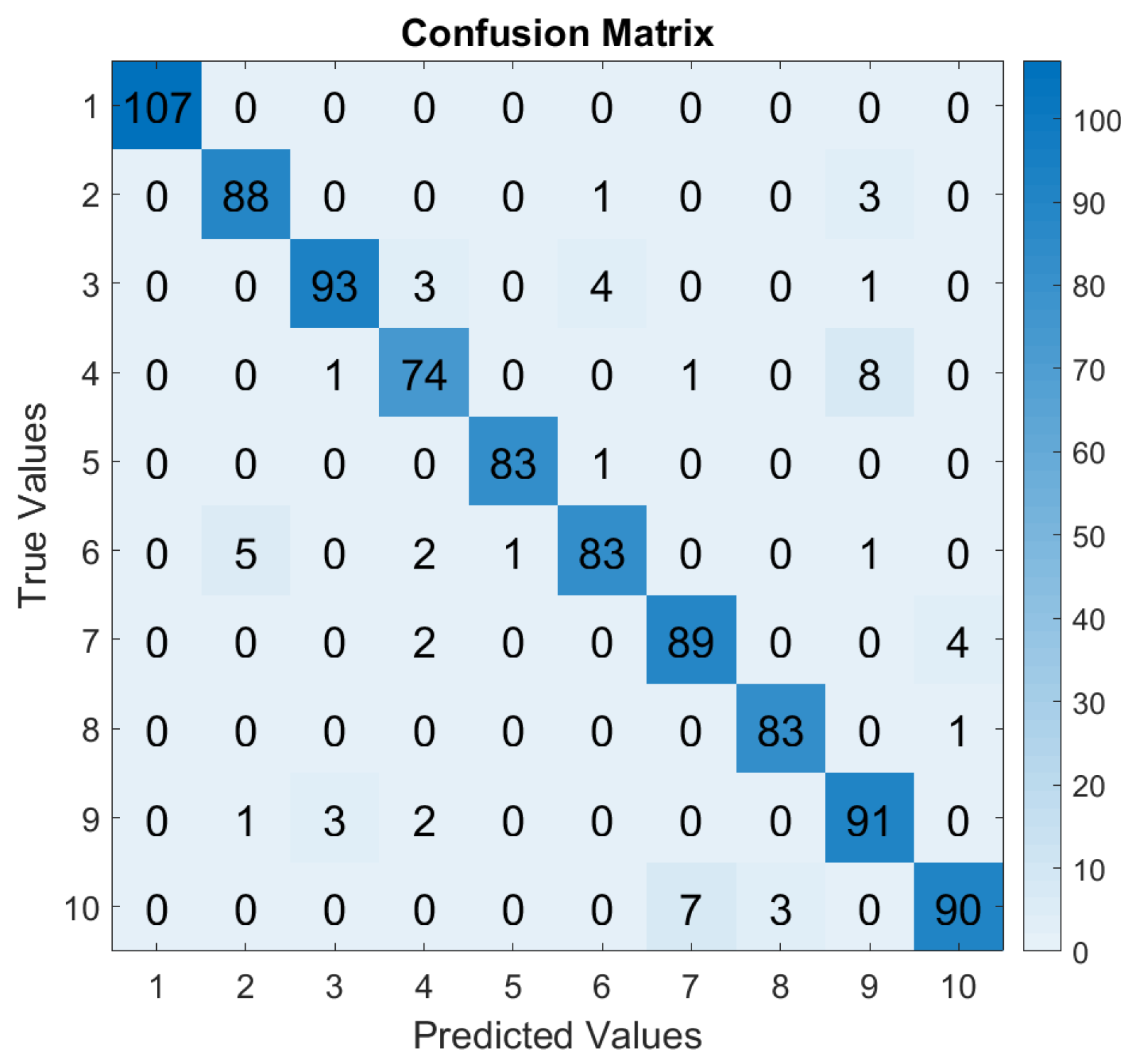
| Faulty Component | Fault Diameter [mm] | Label |
|---|---|---|
| None (Healthy) | - | 1 |
| Ball | 0.178 | 2 |
| Ball | 0.356 | 3 |
| Ball | 0.533 | 4 |
| IR | 0.178 | 5 |
| IR | 0.356 | 6 |
| IR | 0.533 | 7 |
| OR | 0.178 | 8 |
| OR | 0.356 | 9 |
| OR | 0.533 | 10 |
| Time-Domain Features | |
|---|---|
| T = max() | T = |
| T = | T = |
| T = | T = |
| T = | T = |
| T = min() | |
| T = | T = |
| T = T − T | T = |
| T = | = |
| T = | = |
| T = | = |
| 12 kHz Down-Sampled | 12 kHz Experimental | |
|---|---|---|
| Kurtosis | 3.01 | 2.96 |
| Variance | 0.02 | 0.02 |
| Skewness | 0.01 | 0.01 |
| Energy | 2363.50 | 2348.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Bouharrouti, N.; Morinigo-Sotelo, D.; Belahcen, A. Multi-Rate Vibration Signal Analysis for Bearing Fault Detection in Induction Machines Using Supervised Learning Classifiers. Machines 2024, 12, 17. https://doi.org/10.3390/machines12010017
El Bouharrouti N, Morinigo-Sotelo D, Belahcen A. Multi-Rate Vibration Signal Analysis for Bearing Fault Detection in Induction Machines Using Supervised Learning Classifiers. Machines. 2024; 12(1):17. https://doi.org/10.3390/machines12010017
Chicago/Turabian StyleEl Bouharrouti, Nada, Daniel Morinigo-Sotelo, and Anouar Belahcen. 2024. "Multi-Rate Vibration Signal Analysis for Bearing Fault Detection in Induction Machines Using Supervised Learning Classifiers" Machines 12, no. 1: 17. https://doi.org/10.3390/machines12010017
APA StyleEl Bouharrouti, N., Morinigo-Sotelo, D., & Belahcen, A. (2024). Multi-Rate Vibration Signal Analysis for Bearing Fault Detection in Induction Machines Using Supervised Learning Classifiers. Machines, 12(1), 17. https://doi.org/10.3390/machines12010017







