Structural Design with Self-Weight and Inertial Loading Using Simulated Annealing for Non-Gradient Topology Optimization
Abstract
:1. Introduction
2. Materials and Methods
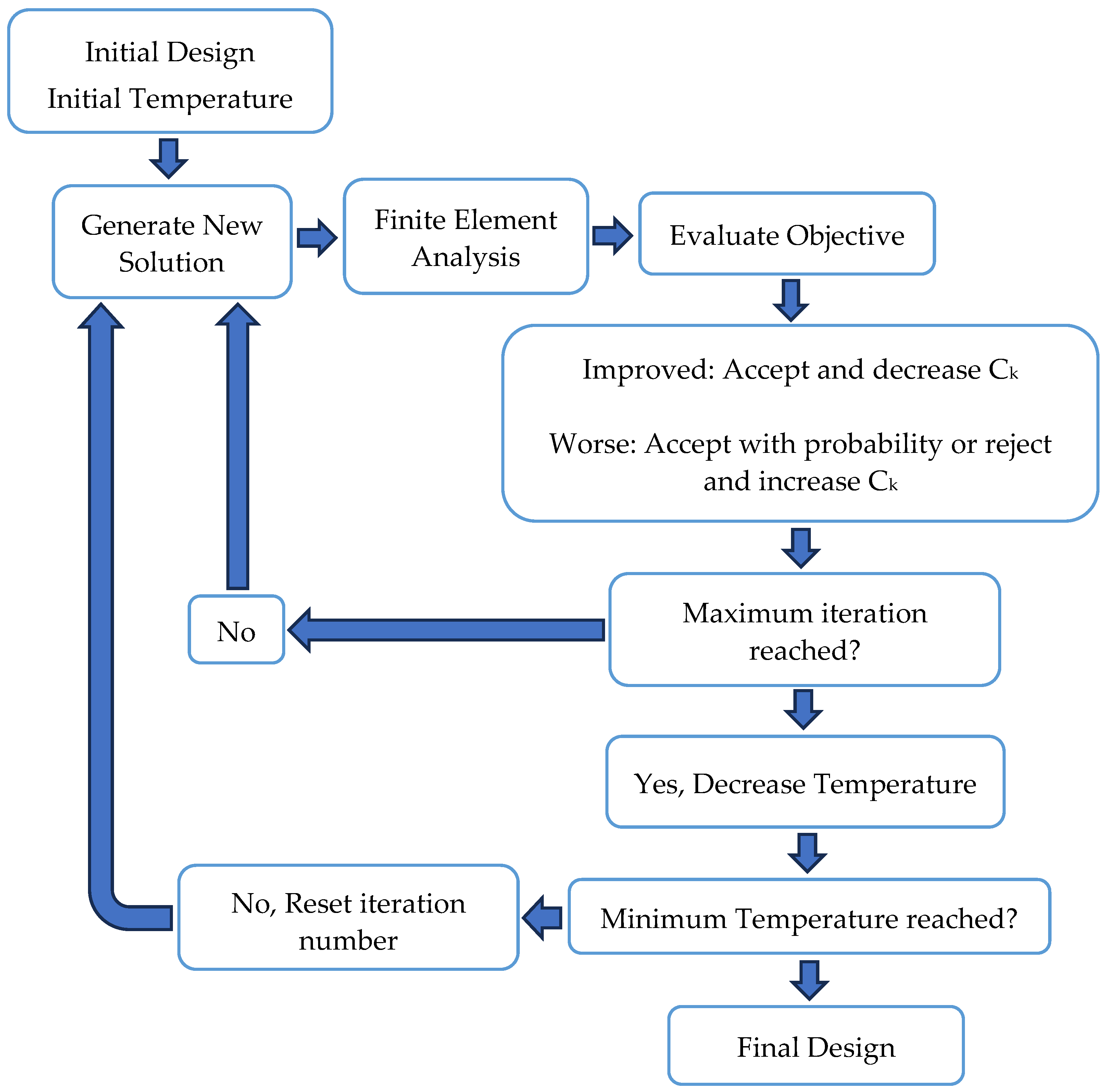
2.1. Topology Optimization Algorithm
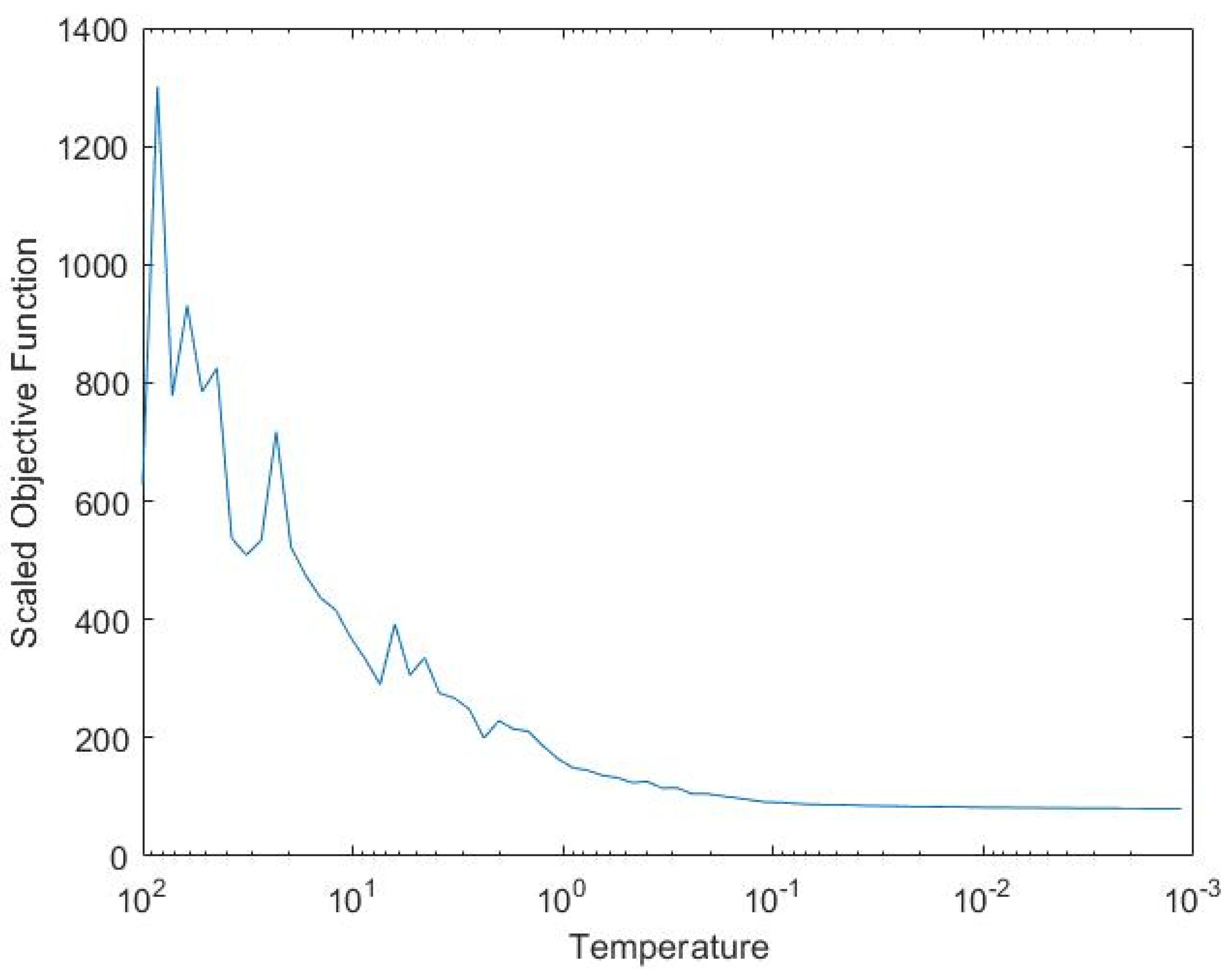
2.2. Simulated Annealing in TO
3. Results
- (a)
- Case with no self-weight effect and only a point load equal to the weight of the structure;
- (b)
- Case with self-weight effect and a point load equal to 25% percent of the weight;
- (c)
- Another scenario with self-weight effect and a point load equal to a 50% of the weight;
- (d)
- Yet another scenario with self-weight effect and a point load equal to the weight;
- (e)
- Lastly, a case with self-weight effect and a point load equal to 200% of the weight.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barari, A.; ElMaraghy, H.; Knopf, G. Evaluation of geometric deviations in sculptured surfaces using probability density estimation. In Proceedings of the Models for Computer Aided Tolerancing in Design and Manufacturing, Arizona State University, Tempe, AZ, USA, 10–12 April 2005; pp. 135–146. [Google Scholar]
- Rosso, R.S., Jr.; Tsuzuki, M.d.S.G.; Barari, A.; Macchi, M. Transition towards Smart Factories; Taylor & Francis: Abingdon, UK, 2022; Volume 35, pp. 341–344. [Google Scholar]
- Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [Google Scholar] [CrossRef]
- Hurtado-Pérez, A.B.; Pablo-Sotelo, A.d.J.; Ramírez-López, F.; Hernández-Gómez, J.J.; Mata-Rivera, M.F. On Topology Optimisation Methods and Additive Manufacture for Satellite Structures: A Review. Aerospace 2023, 10, 1025. [Google Scholar] [CrossRef]
- Alnowibet, K.A.; Mahdi, S.; El-Alem, M.; Abdelawwad, M.; Mohamed, A.W. Guided hybrid modified simulated annealing algorithm for solving constrained global optimization problems. Mathematics 2022, 10, 1312. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. A review of the application of the simulated annealing algorithm in structural health monitoring (1995–2021). Frat. E Integrita Strutt. 2023, 64, 51–76. [Google Scholar] [CrossRef]
- De, S.; Hampton, J.; Maute, K.; Doostan, A. Topology optimization under uncertainty using a stochastic gradient-based approach. Struct. Multidiscip. Optim. 2020, 62, 2255–2278. [Google Scholar] [CrossRef]
- Jalalpour, M.; Tootkaboni, M. An efficient approach to reliability-based topology optimization for continua under material uncertainty. Struct. Multidiscip. Optim. 2016, 53, 759–772. [Google Scholar] [CrossRef]
- Baumann, B.; Kost, B. Structure assembling by stochastic topology optimization. Comput. Struct. 2005, 83, 2175–2184. [Google Scholar] [CrossRef]
- Najafabadi, H.R.; Goto, T.G.; Martins, T.C.; Barari, A.; Tsuzuki, M.S. Multi-objective topology optimization using simulated annealing method. In Proceedings of the ICGG 2020-Proceedings of the 19th International Conference on Geometry and Graphics, 9–13 August 2020; pp. 343–353. [Google Scholar]
- Jamiolahmadi, S.; Barari, A. Surface topography of additive manufacturing parts using a finite difference approach. J. Manuf. Sci. Eng. 2014, 136, 061009. [Google Scholar] [CrossRef]
- Barari, A.; ElMaraghy, H.A.; Knopf, G.K. Search-guided sampling to reduce uncertainty of minimum deviation zone estimation. J. Comput. Inf. Sci. Eng. 2007, 7, 360–371. [Google Scholar] [CrossRef]
- Najafabadi, H.R.; Goto, T.G.; Falheiro, M.S.; Martins, T.C.; Barari, A.; Tsuzuki, M.S.G. Smart topology optimization using adaptive neighborhood simulated annealing. Appl. Sci. 2021, 11, 5257. [Google Scholar] [CrossRef]
- Bochenek, B.; Tajs-Zielińska, K. TABASCO—Topology Algorithm that Benefits from Adaptation of Sorted Compliances Optimization. Appl. Sci. 2023, 13, 10595. [Google Scholar] [CrossRef]
- Tajs-Zielińska, K.; Bochenek, B. Multi-domain and multi-material topology optimization in design and strengthening of innovative sustainable structures. Sustainability 2021, 13, 3435. [Google Scholar] [CrossRef]
- Xue, H.; Yu, H.; Zhang, X.; Quan, Q. A novel method for structural lightweight design with topology optimization. Energies 2021, 14, 4367. [Google Scholar] [CrossRef]
- Najafabadi, H.R. Design of Surface Micro-Machined Inertial MEMS Sensor with Meta-Heuristic Topology Optimization. Doctoral Dissertation, Universidade de São Paulo, São Paulo, Brazil, 2023. [Google Scholar]
- Kanno, Y. Topology optimization of tensegrity structures under self-weight loads. J. Oper. Res. Soc. Jpn. 2012, 55, 125–145. [Google Scholar] [CrossRef]
- Holmberg, E.; Thore, C.-J.; Klarbring, A. Worst-case topology optimization of self-weight loaded structures using semi-definite programming. Struct. Multidiscip. Optim. 2015, 52, 915–928. [Google Scholar] [CrossRef]
- Xu, H.; Guan, L.; Chen, X.; Wang, L. Guide-weight method for topology optimization of continuum structures including body forces. Finite Elem. Anal. Des. 2013, 75, 38–49. [Google Scholar] [CrossRef]
- Garaigordobil, A.; Ansola, R.; Canales, J.; Borinaga, R. Addressing topology optimization with overhang constraints for structures subjected to self-weight loads. Struct. Multidiscip. Optim. 2022, 65, 358. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Huang, Y. An improved multi-objective topology optimization model based on SIMP method for continuum structures including self-weight. Struct. Multidiscip. Optim. 2021, 63, 211–230. [Google Scholar] [CrossRef]
- Han, Y.; Xu, B.; Wang, Q.; Liu, Y. Bi-directional evolutionary topology optimization of continuum structures subjected to inertial loads. Adv. Eng. Softw. 2021, 155, 102897. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Evolutionary topology optimization of continuum structures including design-dependent self-weight loads. Finite Elem. Anal. Des. 2011, 47, 942–948. [Google Scholar] [CrossRef]
- Garcez, G.L.; Pavanello, R.; Picelli, R. Stress-based structural topology optimization for design-dependent self-weight loads problems using the BESO method. Eng. Optim. 2023, 55, 197–213. [Google Scholar] [CrossRef]
- Khosravinia, K.; Kiani, A. Optimizing the Ultrashort Laser Pulses for In Situ Nanostructure Generation Technique for High-Performance Supercapacitor Electrodes Using Artificial Neural Networks and Simulated Annealing Algorithms. ACS Omega 2023, 8, 17220–17233. [Google Scholar] [CrossRef] [PubMed]
- Najafabadi, H.R.; Goto, T.G.; Martins, T.C.; Barari, A.; Tsuzuki, M.d.S.G. Topology Optimization of Capacitive MEMS Accelerometers for Seismic Applications. In Proceedings of the International Conference on Geometry and Graphics, Online, 15–19 August 2022; pp. 760–772. [Google Scholar]
- Brown, N.K.; Garland, A.P.; Fadel, G.M.; Li, G. Deep reinforcement learning for engineering design through topology optimization of elementally discretized design domains. Mater. Des. 2022, 218, 110672. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Ghasemi, H.; Zhuang, X.; Rabczuk, T. Multilevel Monte Carlo method for topology optimization of flexoelectric composites with uncertain material properties. Eng. Anal. Bound. Elem. 2022, 134, 412–418. [Google Scholar] [CrossRef]
- He, Y.; Cai, K.; Zhao, Z.-L.; Xie, Y.M. Stochastic approaches to generating diverse and competitive structural designs in topology optimization. Finite Elem. Anal. Des. 2020, 173, 103399. [Google Scholar] [CrossRef]
- Wang, X.; Ni, B.; Wang, L. Quantum-Inspired Topology Optimization. In Modern Trends in Structural and Solid Mechanics 3: Non-Deterministic Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 177–201. [Google Scholar]
- Wang, X.; Ni, B.; Wang, L. A Modified Quantum-Inspired Genetic Algorithm for Continuum Structural Topology Optimization. Int. J. Comput. Methods 2023, 20, 2250056. [Google Scholar] [CrossRef]
- Ye, Z.; Qian, X.; Pan, W. Quantum Topology Optimization via Quantum Annealing. IEEE Trans. Quantum Eng. 2023, 4, 3100515. [Google Scholar] [CrossRef]
- Garcia-Lopez, N.; Sanchez-Silva, M.; Medaglia, A.; Chateauneuf, A. A hybrid topology optimization methodology combining simulated annealing and SIMP. Comput. Struct. 2011, 89, 1512–1522. [Google Scholar] [CrossRef]
- Sonmez, F.O.; Tan, C. Structural optimization using simulated annealing. Simulated Annealing 2008, 2008, 281–306. [Google Scholar]
- Garcia-Lopez, N.; Sanchez-Silva, M.; Medaglia, A.; Chateauneuf, A. An improved hybrid topology optimization approach coupling Simulated Annealing and SIMP (SA-SIMP). In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sydney, Australia, 19–23 July 2010; p. 012183. [Google Scholar]
- Najafabadi, H.R.; Goto, T.; Falheiro, M.; Martins, T.C.; Barari, A.; Tsuzuki, M.S. Post-processing of non gradient-based topology optimization with simulated annealing. IFAC-Pap. 2021, 54, 755–760. [Google Scholar] [CrossRef]
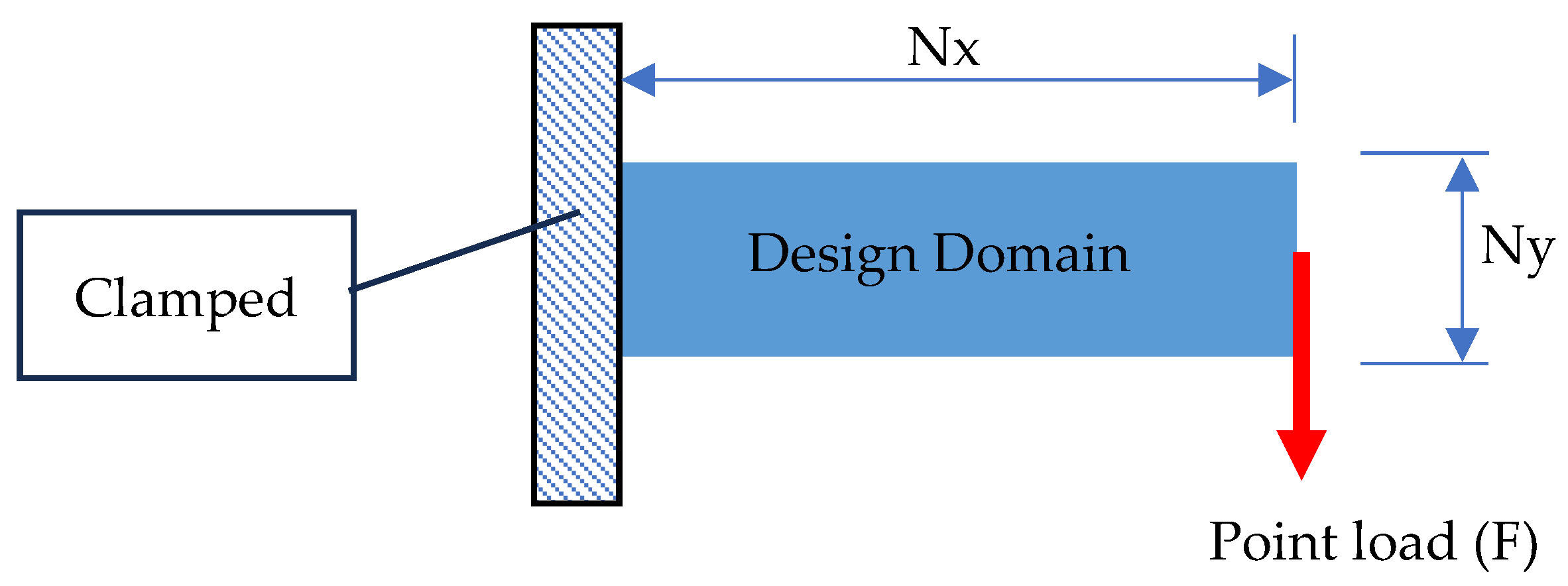


| Parameter | Symbol | Value |
|---|---|---|
| Number of elements in horizontal direction | Nx | 160 |
| Number of elements in vertical direction | Ny | 100 |
| Thickness | t | 1 |
| Density range | ρ | [0, 1] |
| Poisson’s ratio | υ | 0.3 |
| Young’s modulus | E | 1 |
| Penalization factor | p | 3 |
| Initial temperature | Tmax | 10000 |
| Minimum temperature | Tmin | 0.00001 |
| Cooling factor | α | 0.9 |
| Maximum iteration | n | 1000 |
| Crystallization factor range | Ci | (1, 20) |
| Loading Condition | Compliance from Reference [23] | Calculated Compliance from the Proposed Method |
|---|---|---|
| Without self-weight and only point load equal to weight | 4.9062 × 105 | 5.5563 × 105 |
| Self-weight with point load 25% of weight | 5.0291 × 104 | 7.6035 × 104 |
| Self-weight with point load 50% of weight | 1.8725 × 105 | 2.2347 × 105 |
| Self-weight with point load 100% of weight | 6.7959 × 105 | 7.1928 × 105 |
| Self-weight with point load 200% of weight | 2.4241 × 106 | 2.5515 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rostami Najafabadi, H.; Martins, T.C.; Tsuzuki, M.S.G.; Barari, A. Structural Design with Self-Weight and Inertial Loading Using Simulated Annealing for Non-Gradient Topology Optimization. Machines 2024, 12, 25. https://doi.org/10.3390/machines12010025
Rostami Najafabadi H, Martins TC, Tsuzuki MSG, Barari A. Structural Design with Self-Weight and Inertial Loading Using Simulated Annealing for Non-Gradient Topology Optimization. Machines. 2024; 12(1):25. https://doi.org/10.3390/machines12010025
Chicago/Turabian StyleRostami Najafabadi, Hossein, Thiago C. Martins, Marcos S. G. Tsuzuki, and Ahmad Barari. 2024. "Structural Design with Self-Weight and Inertial Loading Using Simulated Annealing for Non-Gradient Topology Optimization" Machines 12, no. 1: 25. https://doi.org/10.3390/machines12010025
APA StyleRostami Najafabadi, H., Martins, T. C., Tsuzuki, M. S. G., & Barari, A. (2024). Structural Design with Self-Weight and Inertial Loading Using Simulated Annealing for Non-Gradient Topology Optimization. Machines, 12(1), 25. https://doi.org/10.3390/machines12010025









