Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers
Abstract
:1. Introduction
- (1)
- This paper devises two different control algorithms, including an AESO-based geometric fault-tolerant control (AESOGFTC) method (passive FTC method) and an AESO-based attitude control method (active FTC method), and they both ensure that the closed-loop signals can exponentially converge to a bounded set.
- (2)
- In both approaches, the AESO-based control framework, without known upper bounds of the lumped disturbance, has a few parameters which need to be tuned; this makes the structure of the proposed control method more simple. In the active FTC method, while actuator failure, inertia matrix uncertainty and external perturbations occur, the AESO-based attitude control method actively estimates and compensates with an AESO. In the passive FTC method, inertia matrix uncertainty and external perturbation are regarded as the lumped disturbances that can be dealt with by the AESO.
- (3)
- In the passive FTC method, an FTC framework is proposed to address the attitude actuator failure problem by a constant partial LOE. As a result of the actuator failures that occur in the attitude subsystem, the model proposed in [18] does not apply to this article. Then, an improved method is developed by using the generalized inverse matrix.
- (4)
- By introducing the novel control laws, the actuator failures, inertia matrix uncertainty and external perturbations are simultaneously addressed.
2. Problem Statement and Preliminaries
2.1. A Model of UAVs
2.2. Design and Stability Analysis of the AESO
3. Geometric Fault-Tolerant Tracking Control with AESOs
3.1. Method I: AESO-Based Fault-Tolerant Control
3.2. Method II: AESO-Based Geometric Control Method
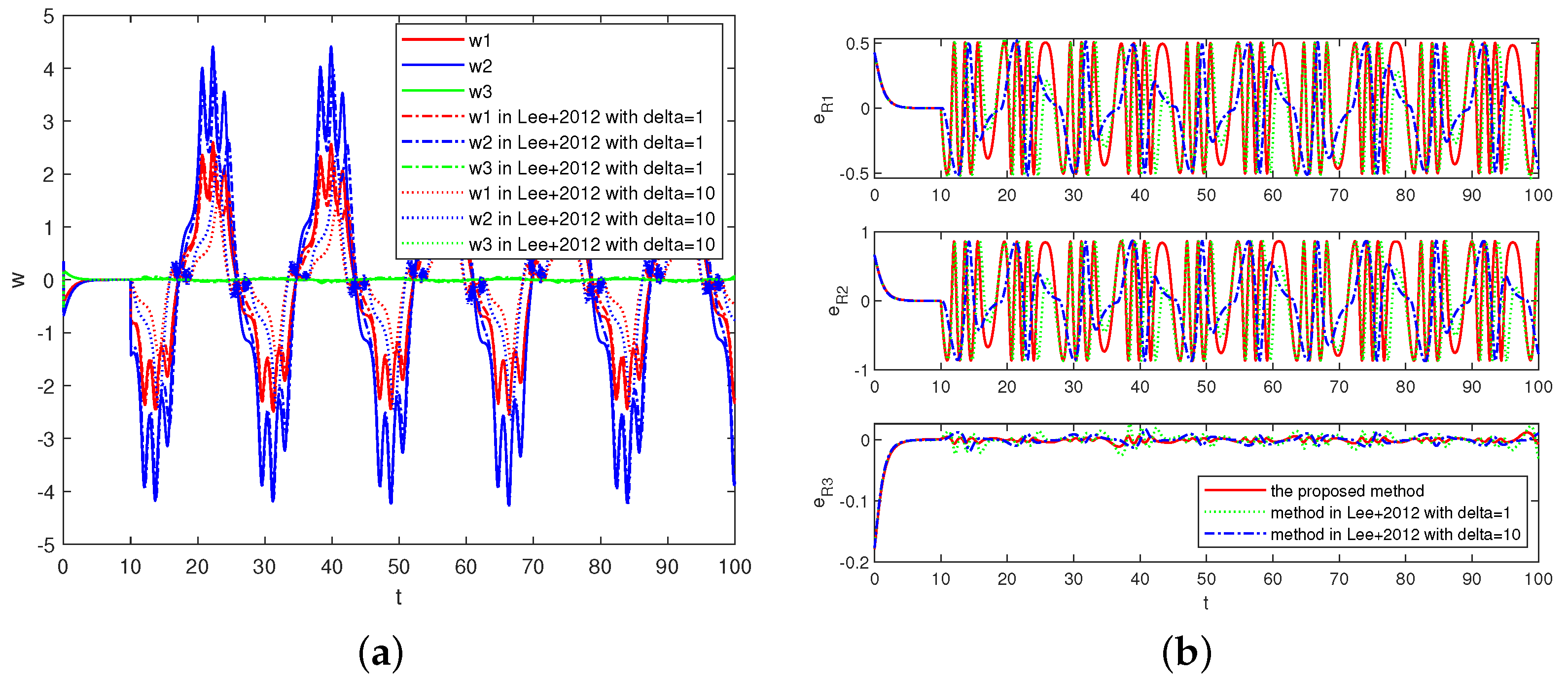
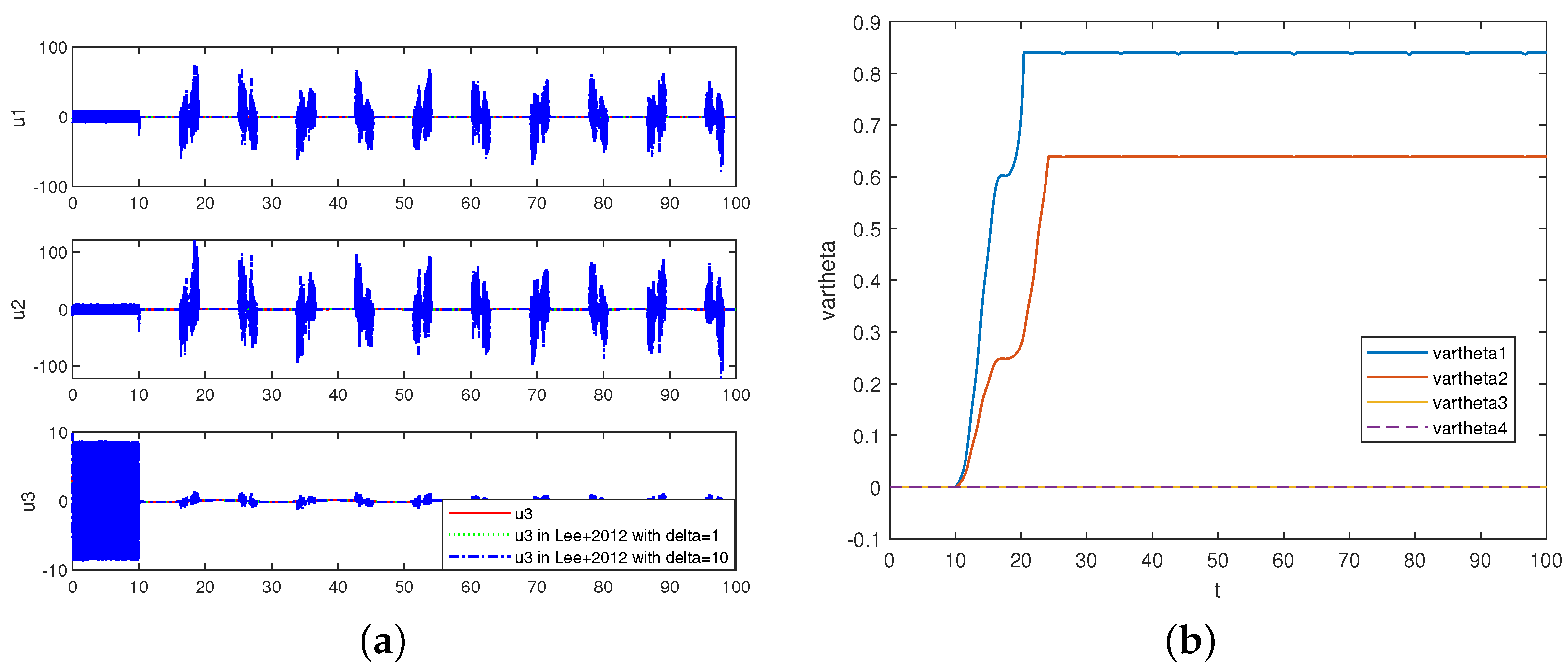
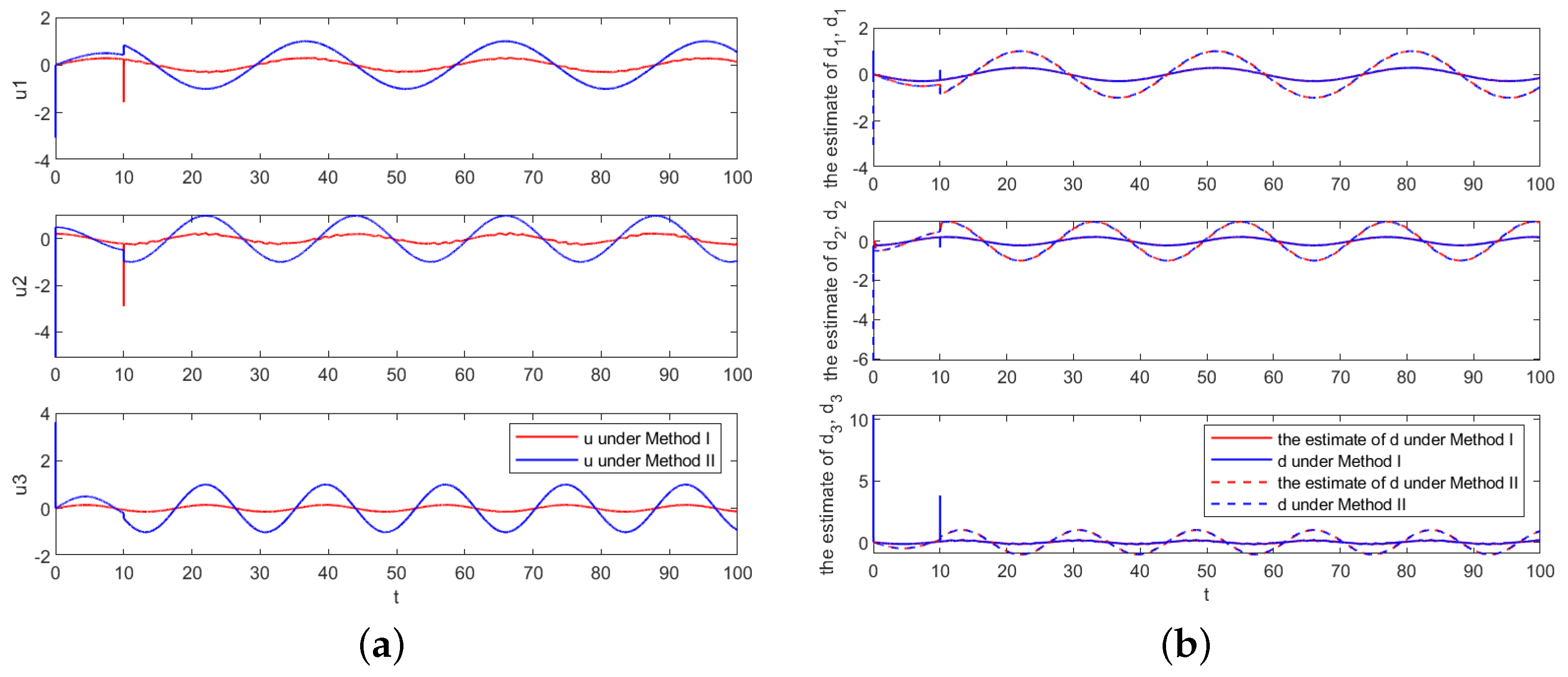
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| AESO | Adaptive Extended State Observer |
| NESO | Nonlinear Extended State Observer |
| LESO | Linear Extended State Observer |
| LOE | Loss of Effectiveness |
| FTC | Fault-Tolerant Control |
| SISO | Single-Input, Single-Output |
| MIMO | Multiple-Input, Multiple-Output |
| AESOGFTC | AESO-based Geometric Fault-Tolerant Control |
References
- Lee, T.; Leok, M.; Mcclamroch, N. Control of complex maneuvers for a quadrotor UAV using geometric methods on SE(3). Mathematics 2010, 15, 391–408. [Google Scholar]
- Yun, Y.; Yang, S.; Wang, M.; Li, C.; Li, Z. High performance full attitude control of a quadrotor on SO(3). In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1698–1703. [Google Scholar]
- Alattas, K.A.; Vu, M.T.; Mofid, O.; El-Sousy, F.F.M.; Fekih, A.; Mobayen, S. Barrier Function-Based Nonsingular Finite-Time Tracker for Quadrotor UAVs Subject to Uncertainties and Input Constraints. Mathematics 2022, 10, 1659. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, H.; Chen, X.; Lu, T.; Tan, S.; Yang, H.; Gulliver, T.A. Tracking performance of the coaxial counter-paddle flight system using fractional active disturbance rejection controller. Appl. Math. Model. 2023, 121, 800–827. [Google Scholar] [CrossRef]
- Han, J.Q. A class of extended state observers for uncertain systems. Control. Decis. 1995, 10, 85–88. [Google Scholar]
- Han, J.Q. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertainties; National Defense Industry Press: Beijing, China, 2008; pp. 197–270. [Google Scholar]
- Han, J.Q. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z. On convergence of nonlinear extended state observer for multi-input multi-output systems with uncertainty. IET Control Theory Appl. 2012, 6, 2375–2386. [Google Scholar] [CrossRef]
- Guo, B.Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Shao, X.; Zhang, W.; Zhang, W. Improved prescribed performance anti-disturbance control for UAVs. Appl. Math. Model. 2021, 97, 501–521. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A class of adaptive extended state observers for nonlinear disturbed systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Wu, X.; Wang, C.; Hua, S. Adaptive extended state observer-based nonsingular terminal sliding mode control for the aircraft skin inspection robot. J. Intell. Robot. Syst. 2020, 98, 721–732. [Google Scholar] [CrossRef]
- Tang, X.; Tao, G.; Joshi, S.M. Adaptive actuator failure compensation for nonlinear MIMO systems with an aircraft control application. Automatica 2007, 43, 1869–1883. [Google Scholar] [CrossRef]
- Lu, K.; Xia, Y. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence. Automatica 2013, 49, 3591–3599. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, D.; Zhu, S.; Poh, E.K. Inertia-free fault-tolerant spacecraft attitude tracking using control allocation. Automatica 2015, 62, 114–121. [Google Scholar] [CrossRef]
- Avram, R.C.; Zhang, X.; Muse, J. Quadrotor actuator fault diagnosis and accommodation using nonlinear adaptive estimators. IEEE Trans. Control Syst. Technol. 2017, 25, 2219–2226. [Google Scholar] [CrossRef]
- Avram, R.C.; Zhang, X.; Muse, J. Nonlinear adaptive fault-tolerant quadrotor altitude and attitude tracking with multiple actuator faults. IEEE Trans. Control Syst. Technol. 2018, 26, 701–707. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.; Yu, Y.; Ma, G. Observer-based fault-tolerant attitude control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2572–2582. [Google Scholar] [CrossRef]
- Ran, D.; Chen, X.; de Anton, R.; Xiao, B. Adaptive extended-state observer-based fault tolerant attitude control for spacecraft with reaction wheels. Acta Astronaut. 2018, 145, 501–514. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.P. Fault-tolerant spacecraft attitude control under actuator saturation and without angular velocity. Int. J. Robust Nonlinear Control 2019, 29, 6483–6506. [Google Scholar] [CrossRef]
- Mallavalli, S.; Fekih, A. A fault tolerant tracking control for a quadrotor UAV subject to simultaneous actuator faults and exogenous disturbances. Int. J. Control. 2020, 93, 655–668. [Google Scholar] [CrossRef]
- Najafi, A.; Vu, M.T.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics 2022, 10, 3009. [Google Scholar] [CrossRef]
- Liu, Z.B.; Wang, L.; Song, Y.C.; Dang, Q.Q.; Ma, B.D. Fault diagnosis and accommodation for multi-actuator faults of a fixed-wing unmanned aerial vehicle. Meas. Sci. Technol. 2022, 33, 075903. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.; Liu, Y.; Xue, H. Finite-time prescribed performance optimal attitude control for quadrotor UAV. Appl. Math. Model. 2023, 120, 752–768. [Google Scholar] [CrossRef]
- Bullo, F.; Murray, R.M. Proportional Derivative (PD) Control on the Euclidean Group; California Institute of Technology: Pasadena, CA, USA, 1995; Available online: https://citeseerx.ist.psu.edu (accessed on 18 March 2020).
- Lee, T. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers. Syst. Control Lett. 2012, 61, 231–237. [Google Scholar] [CrossRef]
- Lee, T. Robust adaptive geometric tracking controls on SO(3) with an application to the attitude dynamics of a quadrotor UAV. In Proceedings of the 50th IEEE Conf. on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2012. [Google Scholar]
- Silverman, L.M. Transformation of time-variable systems to canonical (phase-variable) form. IEEE Trans. Automat. Control 1966, 11, 300–303. [Google Scholar] [CrossRef]
- Zhu, J. A unified spectral theory for linear time-varying systems-progress and challenges. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995. [Google Scholar]
- Ma, K. Comment on ‘Quasi-continuous higher order sliding-mode controller for spacecraft-attitude-tracking maneuvers’. IEEE Trans. Ind. Electron. 2013, 60, 2771–2773. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Pei, H.; Cheng, Z. Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers. Machines 2024, 12, 47. https://doi.org/10.3390/machines12010047
Wang L, Pei H, Cheng Z. Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers. Machines. 2024; 12(1):47. https://doi.org/10.3390/machines12010047
Chicago/Turabian StyleWang, Liping, Hailong Pei, and Zihuan Cheng. 2024. "Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers" Machines 12, no. 1: 47. https://doi.org/10.3390/machines12010047
APA StyleWang, L., Pei, H., & Cheng, Z. (2024). Geometric Attitude Fault-Tolerant Control of Quadrotor Unmanned Aerial Vehicles with Adaptive Extended State Observers. Machines, 12(1), 47. https://doi.org/10.3390/machines12010047






